On the Dynamics of Solitary Waves to a (3+1)-Dimensional Stochastic Boiti–Leon–Manna–Pempinelli Model in Incompressible Fluid
Abstract
:1. Introduction
2. Wave Equation for SBLMPE
3. Exact Solutions of SBLMPE
3.1. HSI-Method
3.2. GREM Method
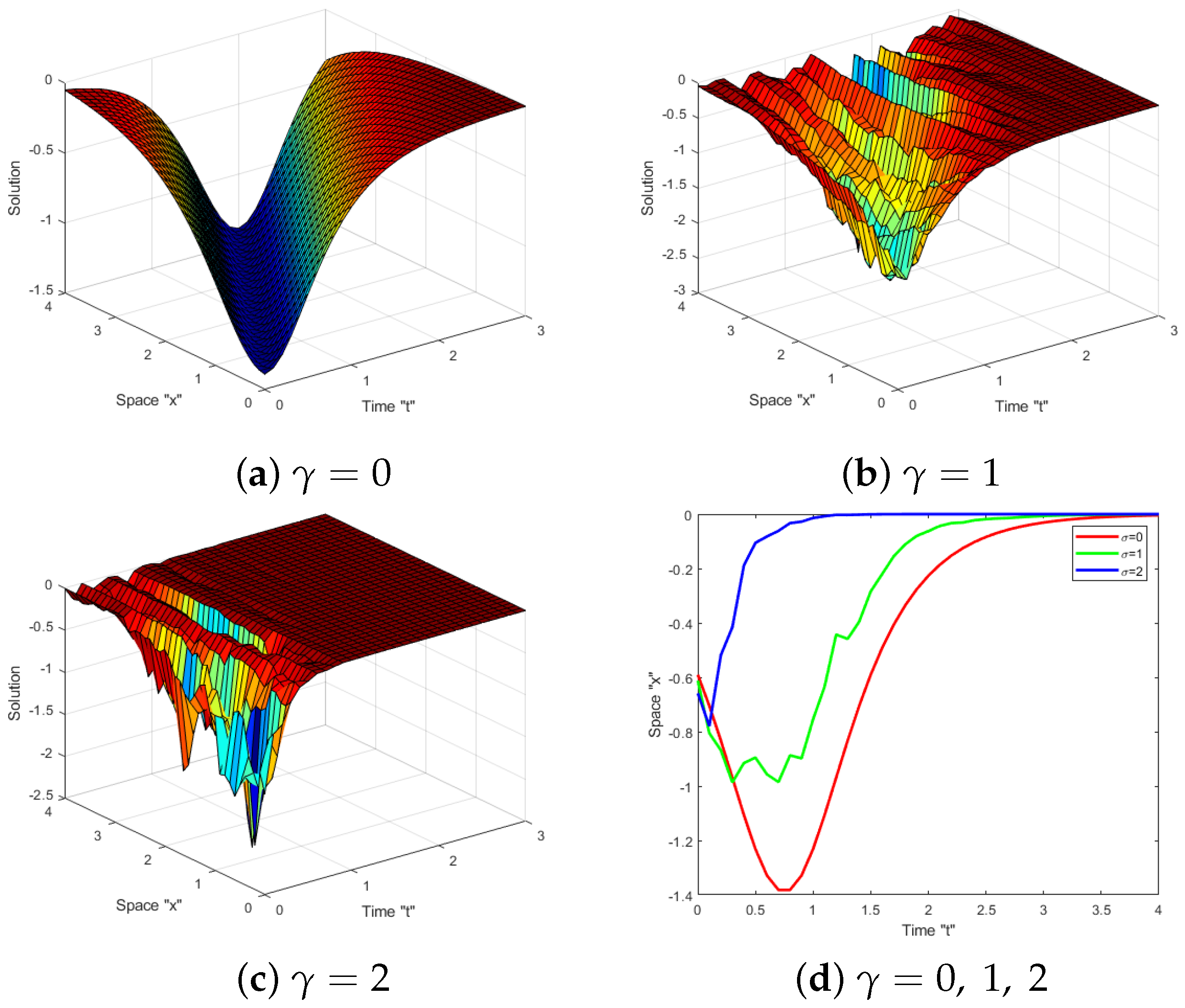
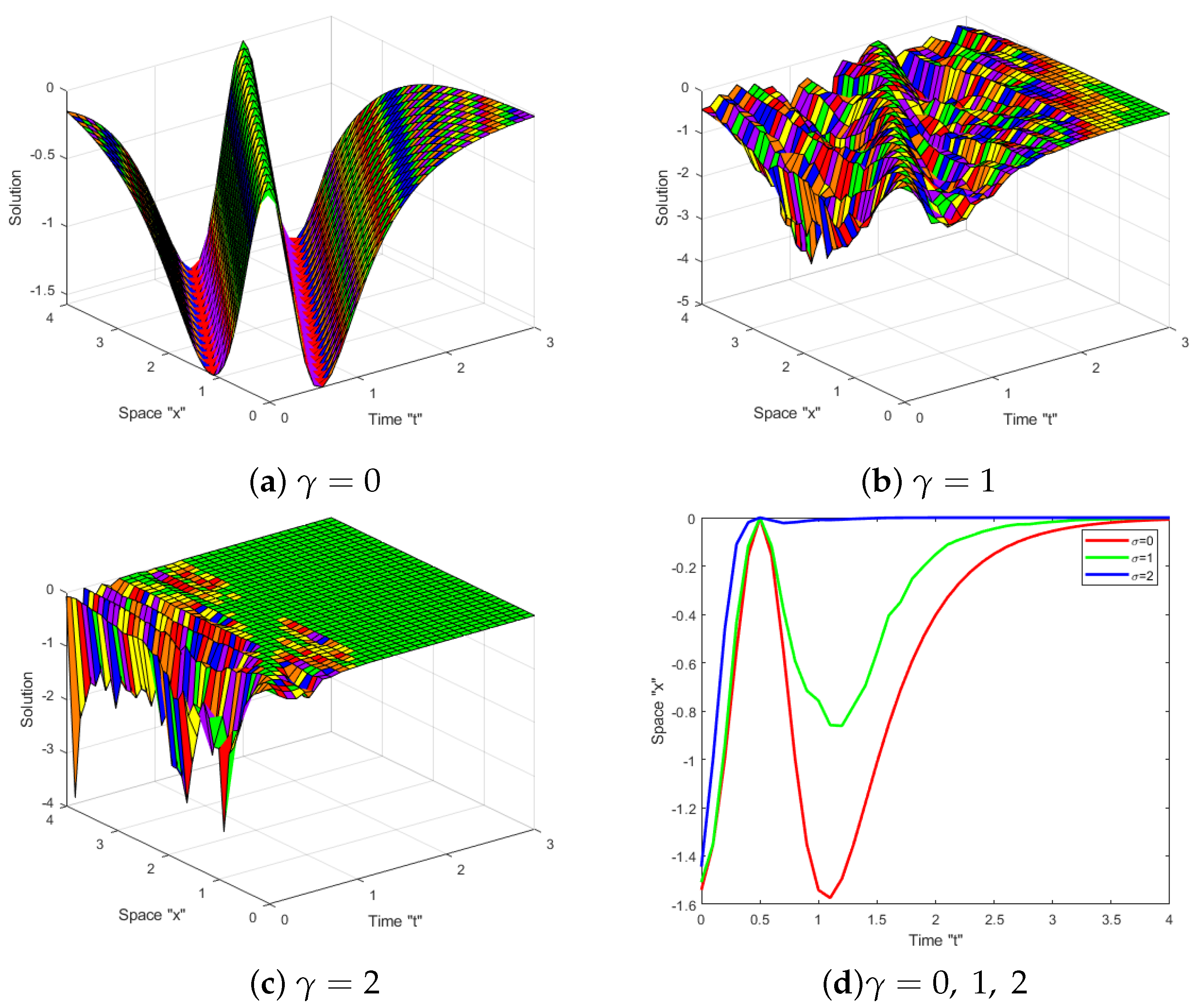
4. Impacts of Brownian Motion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Zhang, H. New application of the (G′/G)-expansion method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3220–3225. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The tanh method: Exact solutions of the Sine–Gordon and Sinh–Gordon equations. Appl. Math. Comput. 2005, 167, 1196–1210. [Google Scholar] [CrossRef]
- Malfliet, W.; Hereman, W. The tanh method. I. Exact solutions of nonlinear evolution and wave equations. Phys Scr. 1996, 54, 563–568. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. The exp(−ϕ(ς))-expansion method for finding travelling wave solutions of Vakhnenko–Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar]
- Yang, X.; Zhao, C.; Cao, J. Dynamics of the discrete coupled nonlinear Schrödinger–Boussinesq equations. Appl. Math. Comput. 2013, 219, 8508–8524. [Google Scholar] [CrossRef]
- Bekir, A.; Gner, A. Topological (dark) soliton solutions for the Camassa–Holm type equations. Ocean Eng. 2013, 74, 276–279. [Google Scholar] [CrossRef]
- Hirota, R. Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar] [CrossRef]
- Mohammed, W.W. Approximate solution of the Kuramoto–Shivashinsky equation on an unbounded domain. Chin. Ann. Math. Ser. B 2018, 39, 145–162. [Google Scholar] [CrossRef]
- Mohammed, W.W. Modulation equation for the Stochastic Swift–Hohenberg equation with cubic and quintic nonlinearities on the Real Line. Mathematics 2019, 7, 1217. [Google Scholar] [CrossRef]
- Yan, Z.L. Abunbant families of Jacobi elliptic function solutions of the dimensional integrable Davey–Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Arnold, L. Random Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Imkeller, P.; Monahan, A.H. Conceptual stochastic climate models. Stoch. Dynam. 2002, 2, 311–326. [Google Scholar] [CrossRef]
- Duan, J. An Introduction to Stochastic Dynamics; Cambridge University Press: Cambridge, UK, 2015; Volume 51. [Google Scholar]
- Al-Askar, F.M.; Mohammed, W.W.; Aly, E.S.; EL-Morshedy, M. Exact solutions of the stochastic Maccari system forced by multiplicative noise. ZAMM J. Appl. Math. Mech. 2022, 103, e202100199. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C. The analytical solutions of the stochastic mKdV equation via the mapping method. Mathematics 2022, 10, 4212. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W. The analytical solutions of the stochastic fractional RKL equation via Jacobi elliptic function method. Adv. Math. Phys. 2022, 2022, 1534067. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Cesarano, C. The soliton solutions for the (4 + 1)-dimensional stochastic Fokas equation. Math. Methods Appl. Sci. 2023, 46, 7589–7597. [Google Scholar] [CrossRef]
- Elmandouh, A.; Fadhal, E. Bifurcation of Exact Solutions for the Space-Fractional Stochastic Modified Benjamin–Bona–Mahony Equation. Fractal Fract. 2022, 6, 718. [Google Scholar] [CrossRef]
- Elmandouh, A.A. Integrability, qualitative analysis and the dynamics of wave solutions for Biswas–Milovic equation. Eur. Phys. J. Plus 2021, 136, 638. [Google Scholar] [CrossRef]
- Boiti, M.; Leon, J.; Manna, M.; Pempinelli, F. On the spectral transform of a Korteweg–de Vries equation in two spatial dimension. Inverse Probl. 1986, 2, 271–279. [Google Scholar] [CrossRef]
- Ali, K.K.; Mehanna, M.S. On some new soliton solutions of (3+1)-dimensional Boiti–Leon–Manna–Pempinelli equation using two different methods. Arab J. Basic Appl. Sci. 2021, 28, 234–243. [Google Scholar] [CrossRef]
- Guiqiong, X. Painlevé analysis, lump-kink solutions and localized excitation solutions for the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation. Appl. Math. Lett. 2019, 97, 81–87. [Google Scholar]
- Yel, G.; Aktürk, T. A new approach to (3+1) dimensional Boiti–Leon–Manna–Pempinelli equation. Appl. Math. Nonlinear. Sci. 2020, 5, 309–316. [Google Scholar] [CrossRef]
- Pinar, Z. Analytical studies for the Boiti–Leon-Monna-Pempinelli equations with variable and constant coefficients. Asymptot. Anal. 2020, 117, 279–287. [Google Scholar] [CrossRef]
- Peng, W.; Tian, S.; Zhang, T. Breather waves and rational solutions in the (3+1)-dimensional Boiti–Leon–Manna–Pempinelli equation. Comput. Math. Appl. 2019, 77, 715–723. [Google Scholar] [CrossRef]
- Liu, J. Double-periodic soliton solutions for the (3+1)-dimensional Boiti–Leon–Manna–Pempinelli equation in incompressible fluid. Comput. Math. Appl. 2018, 75, 3604–3613. [Google Scholar] [CrossRef]
- Liu, J.; Tian, Y.; Hu, J. New non-traveling wave solutions for the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation. Appl. Math. Lett. 2018, 79, 162–168. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. Abundant Solitary Wave Solutions for the Boiti–Leon–Manna–Pempinelli Equation with M-Truncated Derivative. Axioms 2023, 12, 466. [Google Scholar] [CrossRef]
- Osman, M.S.; Wazwaz, A.M. A general bilinear form to generate different wave structures of solitons for a (3+1)-dimensional Boiti–Leon–Manna–Pempinelli equation. Math. Methods Appl. Sci. 2019, 42, 6277–6283. [Google Scholar] [CrossRef]
- Duan, X.; Lu, J. The exact solutions for the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation. Results Phys. 2021, 21, 103820. [Google Scholar] [CrossRef]
- Shen, Y.; Tian, B.; Zhang, C.R.; Tian, H.Y.; Liu, S.H. Breather-Wave, Periodic-Wave and Traveling-Wave Solutions for a (2+1)-Dimensional Extended Boiti-Leon-Manna-Pempinelli Equation for an Incompressible Fluid. Mod. Phys. Lett. B 2021, 35, 2150261. [Google Scholar] [CrossRef]
- Song, L.L.; Pu, Z.L.; Dai, Z.D. Spatio-Temporal Deformation of Kink-Breather to the (2 + 1)-Dimensional Potential Boiti–Leon–Manna–Pempinelli Equation. Commun. Theor. Phys. 2017, 67, 493. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Ali, A.; Helal, M.A. Analytical Wave Solutions of the (2+1)-Dimensional Boiti-Leon-Pempinelli and Boiti-Leon-Manna-Pempinelli Equations by Mathematical Methods. Math. Appl. Sci. 2021, 44, 14292–14315. [Google Scholar] [CrossRef]
- Zhu, S. The generalizing Riccati equation mapping method in non-linear evolution equation: Application to (2 + 1)-dimensional Boiti-Leon-Pempinelle equation. Chaos Solitons Fractals 2008, 37, 1335–1342. [Google Scholar] [CrossRef]
- Li, M.; Tan, W.; Dai, H. Integrability Tests and Some New Soliton Solutions of an Extended Potential Boiti–Leon–Manna–Pempinelli Equation. J. Appl. Math. Phys. 2022, 10, 2895–2905. [Google Scholar] [CrossRef]
- He, J.H. Semi-inverse method of establishing generalized variational principles for fluid mechanics with emphasis on turbomachinery aerodynamics. Int. Turbo-Jet-Engines 1997, 14, 23–28. [Google Scholar] [CrossRef]
- He, J.H. Variational principles for some nonlinear partial dikerential equations with variable coencients. Chaos Solitons Fractals 2004, 19, 847–851. [Google Scholar] [CrossRef]
- He, J.H. Some asymptotic methods for strongly nonlinear equations. Internat. Mod. Phys. B 2006, 20, 1141–1199. [Google Scholar] [CrossRef]
- Ye, Y.H.; Mo, L.F. He’s variational method for the Benjamin–Bona–Mahony equation and the Kawahara equation. Comput. Math. Appl. 2009, 58, 2420–2422. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; El-Morshedy, M. On the Dynamics of Solitary Waves to a (3+1)-Dimensional Stochastic Boiti–Leon–Manna–Pempinelli Model in Incompressible Fluid. Mathematics 2023, 11, 2390. https://doi.org/10.3390/math11102390
Mohammed WW, Al-Askar FM, Cesarano C, El-Morshedy M. On the Dynamics of Solitary Waves to a (3+1)-Dimensional Stochastic Boiti–Leon–Manna–Pempinelli Model in Incompressible Fluid. Mathematics. 2023; 11(10):2390. https://doi.org/10.3390/math11102390
Chicago/Turabian StyleMohammed, Wael W., Farah M. Al-Askar, Clemente Cesarano, and M. El-Morshedy. 2023. "On the Dynamics of Solitary Waves to a (3+1)-Dimensional Stochastic Boiti–Leon–Manna–Pempinelli Model in Incompressible Fluid" Mathematics 11, no. 10: 2390. https://doi.org/10.3390/math11102390
APA StyleMohammed, W. W., Al-Askar, F. M., Cesarano, C., & El-Morshedy, M. (2023). On the Dynamics of Solitary Waves to a (3+1)-Dimensional Stochastic Boiti–Leon–Manna–Pempinelli Model in Incompressible Fluid. Mathematics, 11(10), 2390. https://doi.org/10.3390/math11102390






