A Connectome-Based Digital Twin Caenorhabditis elegans Capable of Intelligent Sensorimotor Behavior

Abstract

Despite possessing a simple nervous system, the Caenorhabditis elegans exhibits remarkably intelligent behavior. However, the underlying mechanisms involved in sensory processing and decision making, which contribute to locomotion behaviors, remain unclear. In order to investigate the coordinated function of neurons in achieving chemotaxis behavior, we have developed a digital twin of the C. elegans that combines a connectome-based neural network model with a realistic digital worm body. Through training the digital worm using offline chemotaxis behavioral data generated with a PID controller, we have successfully replicated faithful sinusoidal crawling and intelligent chemotaxis behavior, similar to real worms. By ablating individual neurons, we have examined their roles in modulating or contributing to the regulation of behavior. Our findings highlight the critical involvement of 119 neurons in sinusoidal crawling, including B-type, A-type, D-type, and PDB motor neurons, as well as AVB and AVA interneurons, which was experimentally demonstrated. We have also predicted the involvement of DD04 and DD05 neurons and the lack of relevance of DD02 and DD03 neurons in crawling, which have been confirmed through experimentation. Additionally, head motor neurons, sublateral motor neurons, layer 1 interneurons, and layer 1 and layer 5 sensory neurons are expected to play a role in crawling. In summary, we present a novel methodological framework that enables the establishment of an animal model capable of closed-loop control, faithfully replicating realistic animal behavior. This framework holds potential for examining the neural mechanisms of behaviors in other species.

1. Introduction

The Caenorhabditis elegans (C. elegans) nematode is an excellent model organism for studying neural mechanisms due to its compact nervous system and diverse range of behavior. Despite having only 302 neurons, the C. elegans can adapt to different environmental stimuli for survival and reproduction [1], exhibiting behaviors such as chemotaxis [2], thermotaxis [3], escape responses [4], mating [5], and learning [6,7]. Its stereotyped behavior and fully mapped connectome [8,9] make it ideal for investigating the neural mechanisms of perception, decision making, and intelligent behavioral control using both experimental and computational approaches.

Previous computational studies have focused on modeling the circuit network of the C. elegans to simulate certain behaviors, particularly motion behavior in the OpenWorm project [10,11] and other studies [12,13]. Some of these studies have explored certain sensory–motion mechanisms, such as gait adaptation [14] and the touch response circuit with corresponding tap withdrawal behavior [15]. However, these studies have mainly focused on basic sensory and locomotion behavior and less on the sensory–decision–motor closed-loop control of body behavior in response to environmental stimuli, such as chemotaxis [16], thermotaxis [3], and phototaxis [17].

In particular, the C. elegans exhibits chemotaxis behavior in response to various volatile and water-soluble cues, such as NaCl, as it seeks attractants and avoids repellents in its surrounding environment [2], which demonstrates its sensorimotor intelligence. The chemotaxis behavior of the worm involves two mechanisms known as pirouette and weathervane mechanisms [16,18]. During its crawling motion, the worm undergoes long runs interspersed with occasional pirouettes. The weathervane mechanism predominates during the long runs, gradually guiding the worm towards regions with higher concentrations [18]. However, when encountering a steep decrease in concentration, the worm increases the frequency of pirouettes, leading to significant changes in its movement direction [16]. Despite extensive research on the chemotaxis behavior and chemosensory circuitry of the C. elegans [19,20,21], previous studies have primarily focused on modeling the worm’s chemosensory circuit and the processing of chemical signals [22,23,24,25] with limited emphasis on behavioral experiments and analysis.

Furthermore, although previous studies have simulated locomotion behavior, they typically employ virtual C. elegans body and physics dynamics using open-loop control [13,14,25]. This approach does not accurately represent the neural network’s adaptation in response to proprioceptive feedback and external stimuli. Furthermore, while the OpenWorm project [10] has released a highly detailed biophysical model of the C. elegans [26] based on the Sibernetic physics engine [27], its slow rendering and limited adaptability make it difficult to use for simulating other behavioral tasks. Developing a biophysical model of the C. elegans body and its surrounding environment remains a challenge, as it necessitates both biological realism to accurately replicate C. elegans behavior and high computational efficiency for rapid interaction with the neural controller.

To address these challenges, we draw inspiration from the OpenWorm project [10,28] and Zador et al. [29] to build an in silico model of the C. elegans for closed-loop chemotaxis behavioral simulation. Our goal is to examine the role of C. elegans neurons in behavioral modulation and the underlying neural mechanisms. The proposed model integrates a connectome-based C. elegans neural network and a realistic virtual worm body, creating an autonomous digital twin C. elegans that allows for grounded study of its embodied intelligence. Modeling digital twin organisms successfully can bridge the fields of neuroscience and artificial intelligence, leading to brain-inspired artificial agents with higher capabilities and greater robustness.

2. Materials and Methods

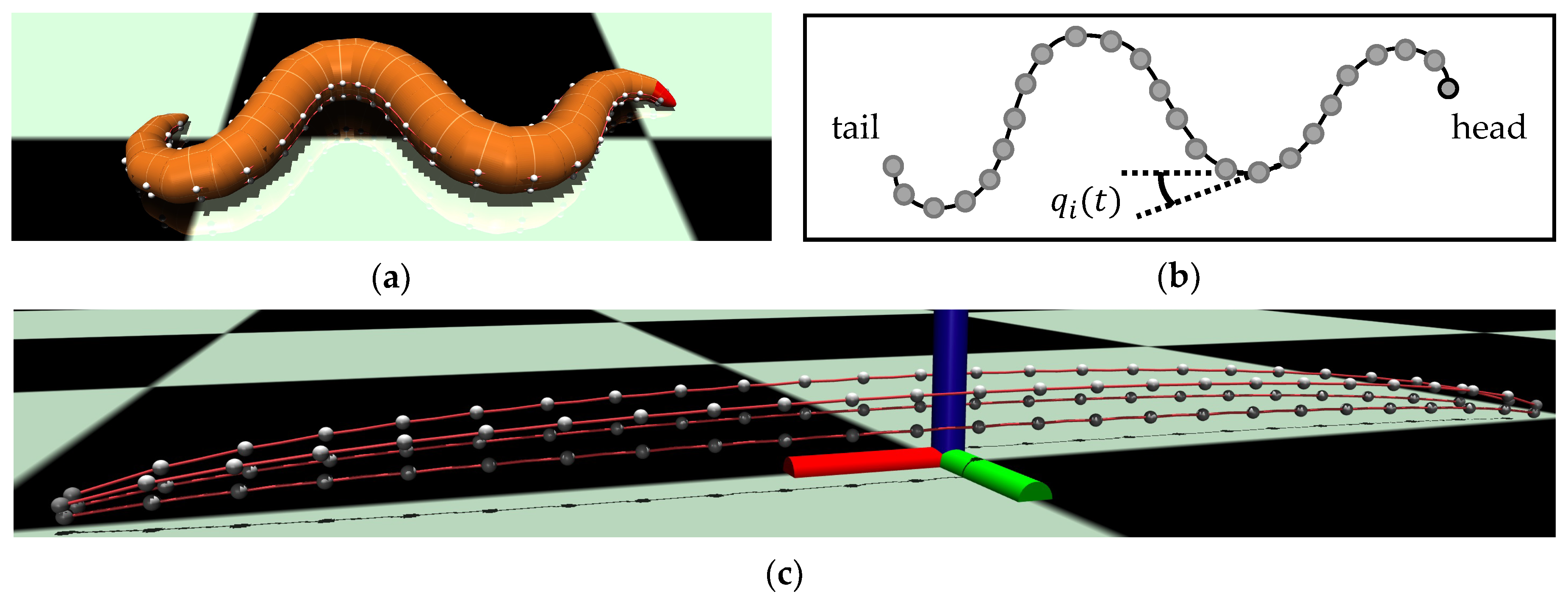
2.1. Digital C. elegans Body

We developed a digital model of the C. elegans in MuJoCo [30], which is illustrated in Figure 1. The digital worm closely resembles the shape and muscle arrangement of a real worm, as shown in Figure A1. It is vermiform and bilaterally symmetrical, with a length of 1 mm and a radius of 0.04 mm. It is composed of 25 segments connected via 24 joints, and its posture and behavior are determined by the rotation of its joints. Therefore, the angles $q\left(t\right)$ of its 24 joints define its posture and are provided by the physics engine, as depicted in Figure 1b. Furthermore, these joint angles serve as proprioceptive information for the worm.

The digital worm body is actuated by 95 body wall muscles, which are arranged in four quadrants: dorsal left (DL), dorsal right (DR), ventral left (VL), and ventral right (VR), as shown in Figure 1c. Each of the 24 joints is controlled by 4 corresponding muscles, 1 in each quadrant, except for the last joint, which is actuated by 3 muscles due to the absence of its VL muscle [8,31]. Thus, there are 24 muscles in the DL, DR, and VR quadrants but only 23 in the VL quadrant. The worm’s motion is limited to the dorsal–ventral plane and is updated every 0.04 s.

MuJoCo offers cutting-edge physics simulation capabilities [30], allowing us to recreate the interactive dynamics between the C.elegans and its realistic crawling environment in a laboratory setting by adjusting the environmental parameters. By using appropriate control signals, the digital C. elegans body can replicate the nematode’s natural locomotion behavior, such as forward movement, shallow turns, gradual turns, and omega turns, in real-time [32].

2.2. Virtual Chemotaxis Environment and the Chemotaxis Task

Radial gradients of attractant sodium chloride (NaCl) are commonly used in biological experiments to study the chemotaxis behavior of the C. elegans [16,33]. The concentration of the attractant follows the solution of the diffusion equation [34,35], resulting in a radial Gaussian distribution. In our virtual environment for studying chemotaxis behavior of the digital C. elegans, we also use a radial Gaussian distribution of attractant NaCl, as depicted in Figure 2. The concentration distribution in the environment is given by the following:

$$C\left(r\right)=exp(-\frac{r^2}{2{\sigma }^2})$$

(1)

where r (mm) is the distance from the center $(0,0)$ and $\sigma =2$. The concentration is constant over time and has a range from the highest at the center ($C(r=0)=1$) to the lowest at the edge ($C(r=\infty )=0$).

The digital worm’s goal in the chemotaxis task is to navigate towards the center and remain in a region with a high concentration, based on the chemical gradient information detected at its front tip. The performance of the digital worm’s chemotaxis behavior can be quantified using the chemotaxis index [16,36], which is defined as follows:

$$I_C=\frac{1}{T}\sum _{t=1}^T\frac{C\left(r\right(t\left)\right)}{C(r=0)}$$

(2)

where T (steps) is the duration of the simulation, and $r\left(t\right)$ (mm) is the distance from the center $(0,0)$ at time t. It ranges from 0 to 1, with a higher value indicating better chemotaxis performance. Thus, the objective of the digital worm in the chemotaxis task is to achieve the highest possible chemotaxis index within a given time frame.

2.3. C. elegans Neural Network Model

Figure 3 shows the structure of the C. elegans neural network (CENN) model, which is based on the adult hermaphrodite connectome of C. elegans [8]. The model consists of 469 nodes, including 329 neurons, 95 body wall muscles, 21 end organs, and 24 sex-specific motor neurons and muscles. It also includes 4869 chemical connections and 1433 electrical connections.

2.3.1. Nodes

To simplify the modeling process, all nodes in the model are assumed to be homologous, and a single-compartment membrane equation is used to model the membrane potential $V_i$ of node i [37], which is given by the following:

$$C_i\frac{d{V}_i\left(t\right)}{dt}=-G_i(V_i\left(t\right)-V_i^{leak})+I_i^{syn}\left(t\right)+I_i^{gap}\left(t\right)+I_i^{prop}\left(t\right)+I_i^{chem}\left(t\right),i=1,2,\cdots ,N$$

(3)

where ${\tau }_i$ is the time constant, $V_i^{leak}$ is the leakage potential, $I_i\left(t\right)$ is input current, and $N=469$ is the number of nodes.

The ordinary differential equation (ODE) of $V_i\left(t\right)$ shown in Equation (3) can adopt an explicit form using the Euler method [38] as follows:

$$V_i(t+\Delta t)=(1-\frac{\Delta t}{{\tau }_i})V_i\left(t\right)+\frac{\Delta t}{{\tau }_i}[V_i^{leak}+\frac{1}{G_i}(I_i^{syn}\left(t\right)+I_i^{gap}\left(t\right)+I_i^{prop}\left(t\right)+I_i^{chem}\left(t\right))]$$

(4)

After updating $V_i\left(t\right)$ at each time step with Equation (4), it is further limited to a range using a version of the sigmoid function $S\left(x\right)$, given by the following:

$$S\left(V_i\left(t\right)\right)=(b-a)\frac{1}{1+exp(-\frac{V_i\left(t\right)-(a+b)/2}{b-a})}+a$$

(5)

where $a=-80$ mV and $b=35$ mV. As a result, its value is further constrained within a reasonable range of $S\left(V_i\left(t\right)\right)\in (-80,35)$ mV.

Since the majority of the neurons in the C. elegans do not exhibit spiking behavior [1,31], the activation $y_i\left(t\right)$ of node i is determined by a sigmoid function [37,39,40] as follows:

$$y_i\left(t\right)=\frac{1}{1+exp(-\beta (V_i\left(t\right)-V_{th}))}$$

(6)

where $\beta =0.375$ mV${}^{-1}$ and $V_{th}=-24$ mV as Kunert et al. [39] suggests. In addition, the activations of the 95 muscle nodes are used as action signals for actuating the digital worm body.

2.3.2. Chemical Connections and Electrical Connections

As stated in Equation (3), the input currents to node i at time t include the chemical connection input $I_i^{syn}$ and electrical connection input $I_i^{gap}\left(t\right)$, given, respectively, by the following:

$$I_i^{syn}\left(t\right)=\sum _{j=1}^N(E_{ij}-V_i\left(t\right))w_{ij}{y}_j\left(t\right)/N_i^{syn}$$

(7)

$$I_i^{gap}\left(t\right)=\sum _{j=1}^N(V_j\left(t\right)-V_i\left(t\right))g_{ij}/N_i^{gap}$$

(8)

where $w_{ij}$ and $E_{ij}$ are the weight and reversal potential of the chemical connection from nodes j to i, respectively, $g_{ij}$ is the weight of the electrical connection between nodes i and j, $N_i^{syn}$ is the indegree of chemical connections, and $N_i^{gap}$ is the degree of electrical connections.

The connection matrices of chemical and electrical connections are defined based on the connectome of the adult hermaphrodite C. elegans [8]. If there is no chemical connection from nodes j to i, $w_{ij}=0$. Similarly, if there is no electrical connection between nodes i and j, $g_{ij}=0$. The weight matrix of electrical connection is symmetric; therefore, $g_{ij}=g_{ji}$.

Furthermore, the polarity of a chemical connection is determined by the type of neurotransmitter released by the presynaptic neuron and the type of receptor expressed by the postsynaptic neuron [41]. The polarity of some of the chemical connections in the C. elegans has already been elucidated [42]. Out of the 4869 chemical connections, 1141 are excitatory and 404 are inhibitory [42]. The reversal potentials of the excitatory and inhibitory chemical connections are set as $E_{ij}^{+}=5$ mV and $E_{ij}^{-}=-50$ mV, respectively.

2.3.3. Proprioceptive Feedback

Proprioceptive feedback is essential for closed-loop control in behavioral simulation, as it allows the neural network to continuously modulate its behavior. Previous studies have shown that B-type and A-type motor neurons are responsible for transducing proprioceptive feedback during undulatory locomotion [43,44,45]. Specifically, the bending of a body region during forward locomotion requires the anterior ∼0.2 mm region to bend and directly activates B-type motor neurons [43]. However, these motor neurons only control the muscles in the body region (DL08-24, DR08-24, VL08-23, VR08-24), leaving the mechanism of proprioceptive feedback for the muscles in the head region (DL01-07, DR01-07, VL01-07, VR01-07) largely unknown. As a result, previous studies simulating sinusoidal locomotion often exclude the head muscles and their related motor neurons [11,12]. In order to achieve closed-loop behavioral simulation using all body wall muscles, proprioceptive feedback must be applied to the motor neurons controlling the head muscles as well. Therefore, we propose that the head motor neurons (HMNs) and sublateral motor neurons (SMNs), which are the upstream motor neurons of the head muscles, also receive proprioceptive feedback.

The CENN model incorporates proprioceptive feedback into B-type (DB01-07, VB01-11) and A-type (DA01-09, VA01-12) motor neurons from their anterior and posterior regions, respectively, extending over 5 joints, as shown in Figure 4a. Furthermore, head motor neurons and sublateral motor neurons receive proprioceptive feedback from all regions. The connection matrix of proprioceptive feedback is presented in Figure 4b.

In addition to chemical connection input and electrical connection input, specific motor neurons also receive proprioceptive feedback $I_i^{prop}\left(t\right)$, which is given by the following:

$$I_i^{prop}\left(t\right)=\sum _{k=1}^Q{w}_{ik}^{prop}{q}_k\left(t\right)/N_i^{prop}$$

(9)

The weight of the proprioceptive feedback from joint k to node i is given by $w_{ik}^{prop}$. The angle $q_k\left(t\right)$ of joint k serves as the corresponding proprioceptive feedback. The number of proprioceptive feedback connections to node i is denoted by $N_i^{prop}$.

2.3.4. Chemosensory Stimuli

The model includes ASEL and ASER chemosensory neurons that detect NaCl, and they receive chemosensory stimuli $I_i^{chem}\left(t\right)$ as in the C. elegans. The chemical stimuli to ASEL and ASER are modeled based on their response to NaCl concentration steps and the ON–OFF functional asymmetry between them [46]. Specifically, they are given by the following:

$$I_{ASEL}^{chem}\left(t\right)=\left\{\begin{array}{cc}{w}_{ASEL}^{+}g\left(t\right)\hfill & \mathrm{if}g\left(t\right)>0\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(10)

$$I_{ASER}^{chem}\left(t\right)=\left\{\begin{array}{cc}-w_{ASER}^{+}g\left(t\right)\hfill & \mathrm{if}g\left(t\right)>0\hfill \\ -w_{ASER}^{-}g\left(t\right)\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(11)

where $g\left(t\right)=\Delta C\left(t\right)/\Delta t$ is the chemical gradient detected at the head and $w_{ASEL}^{+}$, $w_{ASER}^{+}$, and $w_{ASER}^{-}$ are the positive scales of the incoming chemical stimuli.

2.4. Closed-Loop Simulation of Chemotaxis Behavior with the PID Controller

We propose a closed-loop controller for the digital worm body to realize chemotaxis behavior that is similar to a real worm. To enable the digital worm body to exhibit chemotaxis behavior, the controller must consistently generate suitable action signals for muscle actuation, minimizing the disparity between the digital worm body’s posture and the desired posture. Initially, we establish the desired posture for chemotaxis behavior. Subsequently, we utilize the controller to govern the movements of the digital worm body, facilitating the manifestation of chemotaxis behavior.

Through closed-loop simulation of chemotaxis behavior with the digital worm body, we can establish a baseline of chemotaxis simulation with the digital C. elegans body. Furthermore, by collecting behavior data in chemotaxis simulation, we can build an offline behavior dataset for optimizing the C. elegans neural network model, leading to the realization of a digital twin C. elegans.

2.4.1. Posture of Chemotaxis Behavior

The behavior of the digital C. elegans is determined by the angles of its 24 joints, as depicted in Figure 1b. During crawling locomotion, the desired angle of each joint ${\widehat{q}}_i\left(t\right)$ can be approximated by a sinusoidal function, as suggested by Soh et al. [25]:

$${\widehat{q}}_i\left(t\right)=q_{max}sin(\omega t-2\pi \psi (i-1)-\pi )+\kappa \left(t\right),i=1,2,\cdots ,Q$$

(12)

where $q_{max}$ is the maximum joint angle, $\omega$ is the angular velocity of bending, $\psi$ is determined by the body wavelength, and $Q=24$ is the number of joints.

Furthermore, although both mechanisms contribute to chemotaxis navigation, the weathervane mechanism alone is sufficient in producing chemotaxis behavior [18]. For simplicity, this study focuses solely on the weathervane mechanism. Through this mechanism, the worm gradually curves towards higher concentrations by using gradual turns in response to the spatial gradient of the attractant. Therefore, the bias angle $\kappa \left(t\right)$ is determined by the weathervane mechanism, which can be described as follows:

$$\kappa \left(t\right)=-k_w{g}_w\left(t\right)$$

(13)

where $g_w\left(t\right)$ is the chemical gradient perpendicular to the traveling direction at the digital C. elegans’ center of mass and $k_w=1$.

Based on the midline skeleton extracted from recordings of a freely moving C. elegans [47,48], we set $q_{max}=0.6$, $\omega =1.6\pi$, and $\psi =0.07$ to produce sinusoidal movement that closely resembles the movement of C. elegans.

2.4.2. Closed-Loop Control with the PID Controller

To achieve closed-loop control of the digital worm’s behavior, we employ a proportional–integral–derivative (PID) controller to continuously generate the required action signals of muscles $y\left(t\right)$, so that the angles of its joints $q\left(t\right)$ can reach the desired values $\widehat{q}\left(t\right)$ and form the corresponding posture, as shown in Figure 5. The PID controller minimizes the error of posture $e_i\left(t\right)={\widehat{q}}_i\left(t\right)-q_i\left(t\right)$ with the control variable $u_i\left(t\right)$. The equation governing the control variable is:

$$u_i\left(t\right)=K_{P,i}{e}_i\left(t\right)+K_I\sum _{\tau =1}^t{e}_i\left(\tau \right)\Delta \tau +K_D\frac{\Delta e_i\left(t\right)}{\Delta t},i=1,2,\cdots ,Q$$

(14)

where the coefficients for the proportional, integral, and derivative terms are $K_{P,i}=3.3-0.2|12.5-i|$, $K_I=0$, and $K_D=0.15$, respectively. Additionally, the error’s rate of change is defined as $\Delta e_i\left(t\right)=e_i\left(t\right)-e_i(t-1)$.

However, since the digital C. elegans is actuated by its body wall muscles instead of joint rotors, $u_i\left(t\right)$ cannot be used for actuation directly. Therefore, the action signals of muscles $y\left(t\right)$ need to be generated by converting $u_i\left(t\right)$ using the following equations:

$$\left\{\begin{array}{cc}{y}_{DL,i}\left(t\right)=y_{DR,i}\left(t\right)=-min(0,u_i\left(t\right))\hfill & i=1,2,\cdots ,Q\hfill \\ y_{VL,i}\left(t\right)=max(0,u_i\left(t\right))\hfill & i=1,2,\cdots ,Q-1\hfill \\ y_{VR,i}\left(t\right)=max(0,u_i\left(t\right))\hfill & i=1,2,\cdots ,Q\hfill \end{array}\right.$$

(15)

Thus, $y\left(t\right)$ can be applied for the actuation of its 95 muscles.

At each time step, the PID controller generates the appropriate action signal $y\left(t\right)$ based on the current error of posture $e_i\left(t\right)$. Under the control of the controller, the errors of the digital worm body’s posture are continuously minimized. Therefore, the digital worm body can produce the desired chemotaxis behavior defined by Equation (12). As a result, the closed-loop control of chemotaxis behavior can be achieved with this PID controller.

Furthermore, an offline dataset of behavioral control sequences can be built during the simulation of chemotaxis behavior. This dataset includes proprioceptive feedback $q\left(t\right)$, the chemical gradient $g\left(t\right)=\Delta C\left(t\right)/\Delta t$, and the corresponding action signals of muscles $y\left(t\right)$ at each time step. The collected dataset can be processed and utilized to optimize the connectome-based C. elegans neural network model, which can then acquire the ability to control chemotaxis behavior.

2.5. Chemotaxis Behavioral Training of the C. elegans Neural Network Model

The CENN model can be trained using machine learning methods on an offline behavioral dataset to enable closed-loop control of chemotaxis behavior. The model is expected to generate appropriate muscle actions $y\left(t\right)$ based on proprioceptive feedback $q\left(t\right)$ and the chemical gradient $g\left(t\right)$ and perform chemotaxis navigation.

By simulating chemotaxis behavior with the PID controller, 6000 sequences of chemotaxis behavioral data are collected, each lasting 136 steps (5.44 s). The digital worm starts at a random position within a radius of 6 mm from the center with a random initial direction in each sequence. Each sequence is divided into 10 overlapping sets of equally sized chunks, each lasting 64 steps (2.56 s) with a stride of 8 steps, which are then used for behavioral training. A detailed explanation of the training and testing procedure for the model is provided in Appendix B.

The model has a set of trainable parameters listed in

Table 1. Trainable parameters of the C. elegans neural network model.

Parameter	Unit	Initialization	Constraint	Number
${\tau }_i$	second (s)	$U(0.01,0.2)$	$(0.01,0.2)$ 1	469
$V_i^{leak}$	millivolt (mV)	$N(-35,1)$	-	469
$E_{ij}$	millivolt (mV)	$N(-24,1)$	$(-50,5)$ 1	3324 2
$w_{ij}$	-	$U(0,1)$	$[0,+\infty )$ 3	4869
$g_{ij}$	-	$U(0,1)$	$[0,+\infty )$ 3	1433
$w_{ik}^{prop}$	-	$U(-1,1)$	-	1223
$w_{ASE}$ 4	-	1	$[0,+\infty )$ 3	3

¹ Constraint of the parameter is realized with sigmoid function $S\left(x\right)$ as shown in Equation (5). ² Reversal potentials of the chemical connections with known polarities are fixed and thus not included here. ³ Only the absolute value of the parameter is trained. ⁴ The parameter $w_{ASE}$ includes $w_{ASEL}^{+}$, $w_{ASER}^{+}$, and $w_{ASER}^{-}$.

, which include neuron parameters, connection parameters, and weights of sensory stimuli. These parameters can be optimized using backpropagation through time (BPTT), a supervised learning method [49]. Since the end-to-end chemotaxis navigation can be viewed as a regression task, the mean square error (MSE) function is adopted as the training and evaluation loss function [12], which is given by the following:

$$E=\frac{1}{T}\frac{1}{M}\sum _{t=1}^T\sum _{m=1}^M\frac{1}{2}{(y_m\left(t\right)-{\widehat{y}}_m\left(t\right))}^2$$

(16)

where T is the length of the sequence, $y_m\left(t\right)$ is the activation of the muscles, ${\widehat{y}}_m\left(t\right)$ is the target action signals, and $M=95$ is the number of muscles.

3. Results

3.1. Chemotaxis Simulation with the Digital Twin C. elegans

After undergoing chemotaxis behavioral training, the CENN model is capable of achieving closed-loop chemotaxis behavioral control. Combining the CENN model with the digital C. elegans body allows for the simulation of an autonomous digital twin C. elegans, as explained in Appendix B.2.

The simulation results validate the effectiveness of the training process, as the digital twin of C. elegans autonomously exhibits chemotaxis behavior by crawling towards the target (represented by the green cylinder positioned at the center). This behavior is visually depicted in Figure 6 and can be observed in Video S1, closely resembling the chemotaxis behavior observed in experimental studies of live worms [16,18]. In this trial of chemotaxis simulation, the worm crawls towards the target and travels 9.20 mm in 100 s (Figure 6a). During chemotaxis navigation, the angles of the worm’s 24 joints exhibit a sinusoidal pattern, indicating that the worm crawls with a sinusoidal posture with a cycle of ∼0.64 s, as shown in Figure 6b. These joint angles serve as proprioceptive feedback to the digital C. elegans. The activation of the model’s 95 muscles is used as the action signals for the digital body’s muscle actuators. Each muscle activates periodically every ∼1.28 s, each time lasting ∼0.64 s, followed by ∼0.64 s of resting (Figure 6c). The dorsal and ventral muscles activate in turns to generate dorsal–ventral sinusoidal movement and propel itself forward (Figure 6d). In general, the sinusoidal crawling of the digital C. elegans is in line with the behavior of a natural worm.

The digital C. elegans starts the chemotaxis simulation at $(4,0)$ mm, with an initial concentration of 0.14. The worm gradually steers towards the center by sinusoidal crawling, as shown in Figure 6d. As a result, the concentration along its track gradually increases (Figure 6e), reaching a final chemotaxis index of 0.74, which is similar to the chemotaxis performance of a real worm [16,18]. During chemotaxis navigation, the ASEL neuron activates when the concentration increases, while the ASER neuron activates when the concentration decreases, as shown in Figure 6e–g. This ON–OFF functional asymmetry of ASE neurons is consistent with experiment findings [46].

Furthermore, the results demonstrate that the CENN model can achieve comparable chemotaxis behavior to the PID controller (Figure A2). This indicates that the CENN model is able to effectively learn chemotaxis behavior through optimization with offline behavioral data generated by the PID controller. Additionally, the comparison further validates the feasibility of our proposed method for digital twin C. elegans simulation. More details regarding the results of the chemotaxis simulation with the PID controller can be found in Appendix D.1.

3.2. Behavioral Analysis of the Digital Twin C. elegans

To further validate the chemotaxis performance of the digital twin C. elegans, we conducted behavioral analysis on multiple trials of chemotaxis simulation with random initialization. This analysis aims to verify the robustness and generalization ability of the CENN model in chemotaxis behavior control. The details of the multiple-trial chemotaxis simulation are explained in Appendix C.

3.2.1. Behavioral Performance

To comprehensively evaluate the chemotaxis performance of the digital twin C. elegans in radial gradients, chemotaxis simulation was conducted under several initial position settings, including random initialization and three fixed positions at different distances from the center. The chemotaxis performance of the PID controller was also tested for comparison.

Table 2. Behavioral performance comparison between the C. elegans neural network model and the PID controller over 100 trials (each 100 s) with different initial positions. The crawling distance and chemotaxis index represent the performance of sinusoidal crawling and chemotaxis navigation, respectively. Results are presented as mean ± standard deviation (s.d.).

Controller	PID Controller			C. elegans Neural Network
Initial Position (mm)	Crawling Distance (mm)	Chemotaxis Index	Initial Concentration	Crawling Distance (mm)	Chemotaxis Index	Initial Concentration
Random	$9.74\pm 0.15$	$0.65\pm 0.33$	$0.38\pm 0.33$	$9.09\pm 0.86$	$0.72\pm 0.34$	$0.44\pm 0.36$
$(2,0)$	$9.63\pm 0.11$	$0.80\pm 0.17$	0.61	$8.95\pm 0.81$	$0.89\pm 0.11$	0.61
$(4,0)$	$9.80\pm 0.06$	$0.63\pm 0.31$	0.14	$9.19\pm 0.73$	$0.65\pm 0.35$	0.14
$(6,0)$	$9.95\pm 0.08$	$0.24\pm 0.34$	0.01	$9.36\pm 0.88$	$0.26\pm 0.37$	0.01

presents the average crawling distance and chemotaxis performance of the digital twin C. elegans and the PID controller in different initial position settings. The results quantitatively confirm the ability of the digital C. elegans to perform sinusoidal crawling and chemotaxis navigation. For instance, when the worm starts at $(4,0)$ mm, it travels an average distance of 9.19 mm and achieves an average chemotaxis index of 0.65, which is in line with the crawling speed of a natural worm [1] and its chemotaxis performance [16,18]. Additionally, the performance of the CENN model is comparable to that of the PID controller, further demonstrating the effectiveness of the CENN model in behavioral learning.

Furthermore, Figure 7 displays the two-dimensional density plot of the digital C. elegans’ tracks under different scenarios. In the virtual chemotaxis environment, the worm’s tracks start at random positions and converge at the center (Figure 7a) with an average chemotaxis index of $0.72\pm 0.34$ (Table 2). In contrast, the tracks are much less concentrated at the center in an environment without chemical gradients (Figure 7b). In another setting where the worm starts at $(6,0)$ mm in an environment with chemical gradients, the tracks disperse from the starting point and eventually converge at the center (Figure 7c) with an average chemotaxis index of $0.26\pm 0.37$ (Table 2). However, the tracks do not converge without chemical gradients (Figure 7d). In summary, the convergence of tracks aligns with the distribution of real worms’ tracks on an assay plate with a similar concentration distribution [16], which further demonstrates the chemotaxis ability of the digital twin C. elegans. Additionally, the density plot of the tracks is similar to the results obtained with the PID controller (Figure A3), verifying that the CENN model has mastered the ability of chemotaxis navigation.

3.2.2. Behavioral Statistics

To conduct a more detailed analysis of the digital C. elegans’ chemotaxis behavior, we define the following variables, following Iino and Yoshida [18]. The curving rate (degree/mm) refers to the change in direction per unit distance of crawling, while the bearing (degree) is the difference between the direction of the center and the direction of the worm’s locomotion. By analyzing these variables based on the worm’s tracks, we can further verify its chemotaxis performance.

In the virtual chemotaxis environment, the statistical analysis of the digital C. elegans’ tracks reveals that the worm makes the largest gradual turn when moving perpendicular to the direction of the center, as illustrated in Figure 8a. However, in an environment without chemical gradients there is no significant correlation between the curving rate and bearing (Figure 8b). Furthermore, Figure 8c demonstrates the positive correlation between the curving rate and chemical gradient in the normal direction, indicating that the gradual turns are biased towards areas with higher concentrations. These results confirm that the digital twin C. elegans exhibits statistical patterns similar to natural worms [18], demonstrating the high biological realism of the chemotaxis simulation.

Overall, the results demonstrate that the CENN model is capable of achieving closed-loop chemotaxis behavioral control. The statistical analysis shows that the CENN model performs comparably to the PID controller and exhibits chemotaxis behavior that closely resembles that of the real C. elegans in both environments with and without chemical gradients, as reported in previous studies [18].

4. Discussion

In this study, we establish a biologically constrained model of a digital twin C. elegans, capable of generating realistic sinusoidal crawling and chemotaxis navigation behavior with its neuronal circuit’s intrinsic sensory–decision–motion closed-loop control mechanism. By performing ablation experiments on each individual neuron of the circuit, the level of behavioral impairment can be measured step-by-step, which allow us to step deeper into the role of each node in behavioral control.

4.1. Behavioral Mechanism of the Digital Twin C. elegans

Building on the success of cell ablation experiments in investigating neuronal function, such as those performed by Schafer [50], similar experiments can be performed in silico on the digital twin C. elegans to study the effect of individual neuron ablation on its behavior. This involves removing all chemical and electrical connections connected to a specific node [39,40]. In other words, if node i is to be ablated, the connectivity of the CENN model is altered as follows:

$$w_{ij}=w_{ji}=g_{ij}=g_{ji}=0,j=1,2,\cdots ,N$$

(17)

After performing node ablation, multiple trials of chemotaxis simulation were conducted using the altered model, and the crawling distance and chemotaxis index were measured to assess the impact on the digital C. elegans’ behavior. A larger decrease in crawling distance and chemotaxis index indicates more severe impairments of crawling locomotion and chemotaxis navigation, respectively.

During multiple trials of simulation, the worm started at $(4,0)$ mm with a random initial direction. In this scenario, the average crawling distance ($9.19\pm 0.73$ mm), chemotaxis index ($0.65\pm 0.35$), and initial concentration (0.14) were measured as control values (Table 2). These values are used as a baseline for comparison with the results obtained after individual neuron ablation.

4.1.1. Behavioral Mechanism of Sinusoidal Crawling

By conducting ablation experiments on individual nodes of the model, the corresponding average crawling distances were measured. If the average crawling distance is below the overall average (5.81 mm), the node is considered significant for behavioral modulation of sinusoidal crawling. Figure 9 presents the resulting average crawling distances grouped by cell types after ablation.

Firstly, the ablation experiments reveal that, among ventral cord motor neurons, B-type (DB, VB), A-type (DA, VA), and D-type (DD, VD) motor neurons are vital for sinusoidal crawling, as shown in Figure 9b. This finding is consistent with previous experimental studies [43,44,51] and simulation results [11,52]. Notably, although D-type motor neurons (DD, VD) do not receive direct proprioceptive feedback like B-type and A-type motor neurons, they are found to play an important role in modulating the worm’s sinusoidal crawling. Moreover, the ventral cord motor neuron PDB (2.23 mm) is predicted to be essential for crawling, which is supported by experiment findings [52]. Additionally, among the DD motor neurons, DD04 (1.01 mm) and DD05 (1.51 mm) are identified as pivotal for sinusoidal crawling, while DD02 (9.34 mm) and DD03 (8.84 mm) are found to be irrelevant, which is consistent with experiment results [52].

Secondly, the simulation results show that ablating AVBL (0.64 mm), AVBR (0.99 mm), AVAL (1.75 mm), and AVAR (0.95 mm) interneurons all lead to severe impairment of crawling, and they are experimentally proven to be involved in crawling behavior [44,51,53].

Thirdly, the simulation results indicate that head motor neurons (HMNs), sublateral motor neurons (SMNs), and ventral cord motor neurons (VCMNs) all exhibit a significant impact on sinusoidal crawling, with their average results dipping below the overall average (5.81 mm), as shown in Figure 9a. Additionally, layer 1 interneurons (IN1s), layer 1 sensory neurons (SN1s), and layer 5 sensory neurons (SN5s) are also pivotal for crawling, indicating their possible role in processing proprioceptive feedback.

Furthermore, we can identify the subcircuit responsible for sinusoidal crawling by selecting nodes with ablation results lower than the overall average (5.81 mm), as depicted in Figure 9c. This subcircuit comprises 119 neurons, including 69 motor neurons, 22 interneurons, and 28 sensory neurons.

Table A2. Detailed list of 119 neurons whose ablation results in an average crawling distance that falls below the overall average (5.81 mm).

Type	Not Yet Experimentally Proven	Experimentally Proven
SN6	ADFR, ASGR, AWBR
SN5	ADLR, ASHR
SN4	ALNL, ALNR, PLNL, SDQL
SN3	ADEL, ALML, DVA
SN1	CEPDL, CEPVL, CEPVR, IL1DR, IL1R, IL1VL, IL1VR, IL2DR, OLLL, OLLR, OLQDL, OLQVR, URYDL, URYDR, URYVL, URYVR
IN3	AIAR, AIZR, AVFL, AVHL, AVHR, PVQR, PVR
IN2	AVJR, AVKR, RICR, RMGL, SAAVL, SAAVR
IN1	AVEL, AVER, RIAR, RIPR	AVAL, AVAR, AVBL, AVBR, PVCL
HMN	RIVL, RIVR, RMDDL, RMDDR, RMDL, RMDR, RMDVR, RMED, RMEL, RMER, RMEV, RMHR, URADR, URAVL, URAVR
SMN	SABD, SABVR, SIAVL, SIBDL, SIBVL, SMBDL, SMBDR, SMBVR, SMDDL, SMDDR, SMDVL, SMDVR
VCMN	AS03, AS11	DA (DA01, DA02, DA03, DA04, DA07, DA08, DA09), DB (DB01, DB02, DB03, DB05, DB06, DB07), DD (DD01, DD04, DD05, DD06), PDB, VA (VA01, VA02, VA03, VA04, VA05, VA08, VA09, VA11, VA12), VB (VB01, VB02, VB03, VB09, VB10, VB11), VD (VD03, VD07, VD09, VD10, VD11, VD12, VD13)

provides a comprehensive list of these neurons and their respective cell types.

4.1.2. Behavioral Mechanism of Chemotaxis Navigation

Similarly, the chemotaxis index resulting from the ablation of each node is used to assess its significance in chemotaxis navigation. However, if the ablation of a node leads to severe crawling impairment, it indirectly affects its chemotaxis index, making it unreliable for accurately assessing its impact on chemotaxis navigation. Therefore, nodes identified as responsible for sinusoidal crawling are excluded from further analysis.

Nodes with an average chemotaxis index after ablation lower than the overall average (0.43) are pivotal for chemotaxis navigation, as shown in Figure 10 and listed in

Table A3. Detailed list of 40 neurons whose ablation results in an average chemotaxis index that falls below the overall average (0.43).

Type	Not Yet Experimentally Proven	Experimentally Proven
Pharynx	I1R
SN6	AFDR, AWBL	ASEL, ASER
SN4	SDQR
SN3	AVM
SN1	IL1L, IL2DL, IL2L, IL2R
IN4	AIML, AINL, RIH, RIR
IN3	ADAR, AIAL, AUAL, PVPL, RIS
IN2	AVJL, DVC, PVT, RIGL, RMGR
IN1	RIAL
HMN	RMDVL
SMN	SIAVR, SIBDR, SIBVR
VCMN	AS02, VA06, VA07, VB04, VB07, VD02, VD06
Sex Motor Neurons	HSNR, VC01, VC06

. The list includes 40 nodes: 10 sensory neurons, 15 interneurons, and 11 motor neurons. ASEL (0.23) and ASER (0.26) neurons directly receive chemical stimuli, and their ablation significantly affects chemotaxis navigation, as experimentally proven [46]. Among the eight sensory neurons predicted to be significant in chemotaxis navigation, AFD, AWB, IL1, and IL2 are associated with ASE in the amphid [2], suggesting their involvement in ASE sensory processing.

4.2. Limitations

However, certain assumptions and simplifications are made in modeling the digital C. elegans, due to the lack of corresponding experiment findings, which may weaken the result’s validity. Firstly, as the mechanism of proprioceptive feedback in the head region is still unknown, the involvement of head motor neurons and sublateral motor neurons in receiving proprioceptive feedback is assumed. Secondly, all nodes in the C. elegans neural network model are considered homologous and generate graded responses, despite some neurons being found to fire spikes in experiments [54,55,56]. Thirdly, we employ the sinusoidal function (Equation (12)) to simulate crawling locomotion for simplicity, which does not accurately capture the complex dynamics of a real worm. Furthermore, there is a notable difference between simulation result and biological experiment result in Figure 8c, showing the relationship between the curving rate and chemical gradient in the normal direction. This discrepancy is likely due to the oversimplification of the bias angle $\kappa \left(t\right)$ (Equation (13)), which lacks biological realism. Therefore, further experiment discoveries are necessary to refine the model and construct a more biologically plausible digital C. elegans to validate the simulation results.

Furthermore, the digital twin C. elegans is optimized with offline behavioral data, which means that certain neurons and their connections that do not participate in sinusoidal crawling and chemotaxis navigation in real worms are not biologically constrained in behavioral training. Consequently, the neurons identified to be essential in behavioral control in this study may include a few neurons that are irrelevant. For instance, even though sex motor neurons are not involved in chemotaxis navigation, the ablation of HSN (0.52) and VC (0.54) still leads to a moderate decrease in the chemotaxis index, as listed in Table A3. To create a more biologically constrained digital twin C. elegans and obtain more conclusive results of node ablation experiments, neuronal calcium imaging data [5,57] can be incorporated into the optimization of the CENN model.

5. Conclusions

This study presents a novel model of the digital twin C. elegans, designed to investigate its neural mechanisms of behavioral modulation. The model seamlessly integrates a connectome-based C. elegans neural network model and a realistic virtual worm body with realistic physics dynamics, allowing for closed-loop behavioral simulation. This integration enables a more comprehensive study of the organism’s behavior and neural mechanisms. The digital twin C. elegans is trained using backpropagation through time on extensive offline data of chemotaxis behavior generated with a PID controller. The simulation results demonstrate the efficacy of this approach, as the model successfully achieves realistic closed-loop control of sinusoidal crawling and chemotaxis behavior.

By conducting node ablation experiments on the digital twin C. elegans, this study identifies 119 pivotal neurons for sinusoidal crawling, including B-type, A-type, D-type, and PDB motor neurons and AVB and AVA interneurons, which have been experimentally proven to be involved. The results correctly predicted the involvement of DD04 and DD05, as well as the irrelevance of DD02 and DD03, in line with experiment findings. Additionally, head motor neurons (HMNs), sublateral motor neurons (SMNs), layer 1 interneurons (LN1s), layer 1 sensory neurons (SN1s), and layer 5 sensory neurons (SN5s) also exhibit significant impact on sinusoidal crawling. Furthermore, 40 nodes are found to be essential for chemotaxis navigation, including 10 sensory neurons, 15 interneurons, and 11 motor neurons, which may be associated with ASE sensory processing and turning behavior. Our findings shed light on the role of neurons in the behavioral modulation of sinusoidal crawling and chemotaxis navigation, which are consistent with experimental results.

This study represents a significant advancement in the field of C. elegans modeling and simulation, providing a promising approach for investigating the neural mechanisms underlying the complex behavior of the C. elegans. The proposed model has the potential to facilitate further research and advance our understanding of this fascinating organism.