Rib Reinforcement Bionic Topology Optimization under Multi-Scale Cyclic Excitation

Abstract

Thin-walled structures have problems such as low stiffness, large deflection, and vibration. The layout of rib reinforcement in thin-walled structures plays a vital role in providing structural strength and rigidity and reducing structural weight. A multi-scale bionic topology optimization method with a cyclic variable load is proposed in this paper to optimize dynamic flexibility by simulating the growth law of leaf vein formation and distribution. A material interpolation method is adopted to penalize the material attributes of rib reinforcement according to their thickness, based on polynomial interpolation. Combined with the layout of rib reinforcement and SIMP, the mathematical model of rib reinforcement layout optimization with cyclic variable loading is proposed, and the sensitivity of thin-walled dynamic flexibility to the rib reinforcement thickness is analyzed. Two typical examples of thin-walled structures are presented to validate the proposed method. Considering the impact effect of multi-scale cyclic loads such as wind speed, pressure, and raindrops acting on the leaf vein, the natural frequencies of bionic topological structures of heart-shaped and elliptical leaf veins are increased by 63.44% and 47.2%, respectively. Considering the change in radial thickness, the mass of the automotive door inner panel with a bionic topological structure increased by 3.2%, the maximum stress value was reduced by 1.4% and 36.8%, and deformation was reduced by 37.6% and 27.1% under the anti-concave and sinking conditions, respectively. Moreover, the first-order natural frequency of the automotive door’s inner panel with a bionic topological structure increased to 30.45%, 3.7% higher than the original.

1. Introduction

Reinforcement structures are widely used in various critical industrial fields, such as the building of reinforced concrete ribbed arch bridges [1,2], unmanned aerial vehicles (UAVs) [3], the vehicle body structures [4], and prosthetic component design [5]. Thin-walled structures subjected to internal or external pressure usually need to be reinforced with ribs. Maximizing the load and minimizing the self-weight are the lightweight design goals of ribs. Design variables such as the geometrical structural shape, uniformity of stress distribution, and standard form are essential factors influencing the performance of ribs. Four surface forms of basalt fiber-reinforced polymer (BFRP) bars, such as circular, rectangular, cross-wound, and spiral wound bars, were used to evaluate the reinforcement’s static and fatigue bonding behavior in concrete under cyclic loading [6]. In order to evaluate the influence of the design parameters, such as the ratio of the rib’s thickness above the upper plate, the ratio of the longitudinal rib width to the spacing, and the ratio of the transverse rib spacing to the longitudinal rib spacing, Zhu et al. [7] calculated and compared the elastic flexural capacity of submarine beams using six specimens. Chen et al. [8] studied the influence of the geometric shape of reinforcement bars on the structural strength, including interfacial porosity, the distribution of chloride ions in different positions, and the distribution of reinforcement bars with different diameters. By increasing the number of reinforcement bars, compressive strength, diameter, and yield strength, the structural design of shear joints with various shapes of reinforcement bars was proposed in the literature [9]. The bonding stress transfer mechanism is the fundamental reason why the reinforcement length and the embedded–bond length ratio affect the reinforcement effect on the fiber-reinforced polymer of building concrete. In order to reduce the radial force imposed on the surrounding concrete and improve the effectiveness of stress transfer in the cracking failure of concrete, the influence of the reinforcement number and bond length on the strength of carbon fiber-reinforced plastic reinforcement was studied in the literature [10]. Jakubovskis et al. proposed that the height of the reinforcement bars is the most critical parameter to control model calibration and pointed out that the role of steel bar mesh should be further studied [11]. Moreover, a relationship between the surface stress of reinforcement bars and the fatigue performance caused by cyclic loading was proposed. Based on the analysis of residual compressive stress and longitudinal residual tensile stress on the surface of reinforcement bars, a reinforcement bar’s geometric shape design method was proposed [12]. On the other hand, the size of reinforcement bars and the diameter of reinforcement bars do not function independently. Because transverse prehensile stress accelerates concrete cracking, it is necessary to consider the size, shape, thickness, and stress transfer performance of different reinforcement bars [13]. Peng et al. proposed that the local strain of reinforcement varies in different positions due to mechanical interaction, which is related to the surface shape of reinforcement. In other words, when the gradient of the reinforcement surface changes gently, the compressive stress transfer is slight, and local strain heterogeneity is not apparent [14]. The thickness of the reinforcing ribs (depth of the ribs) significantly influences the ultimate tensile strength, elastic modulus, and ultimate elongation. It was proposed in the literature [15] that the tensile strength and elastic modulus of shallow ribs are significantly higher than those of deep ribs. Choi et al. [16] proposed an alternating structure of high and low ribs alongside a conventional structure and one with a high relative rib area. A limit load numerical analysis was conducted to study the rib forms in the continuous and discontinuous regions of a structure and find the rational ribs that provided the most effective reinforcement to the structure [17]. By integrating surface cutting optimization and a multi-patch stitching scheme on the parametric space, an explicit layout optimization method was developed to design rib-reinforced thin-walled structures with complex geometries [18]. How to find the most effective and reasonable reinforcement type of structure and realize the lightweight design of a structure is a crucial problem that urgently needs to be solved [19].

Nature is known as the best manufacturer to bring complex structures to life with existing materials [20]. Based on the observation of the natural morphogenesis of leaf veins, Li et al. [21] proposed a simple and practical multi-discipline topology optimization method to produce a stiffener layout for plate/shell structures. Azikov et al. [22] used the finite-element modeling method to compare the service loads, bearing capacities, and weight efficiencies of two structural design schemes of a composite wing. The effective elastic parameters and deformation behavior of rib reinforcement were studied in [23]. A level-set strategy for the optimization of composite structures was employed for the structural optimization of a fiber-reinforced aircraft wing box with design variables and constraints [24]. Kalgutkar et al. [25] analyzed the influence of the arrangement, depth, and width of stiffeners and the influence of an elliptical cutout reinforced with a different pattern of ribs on the stability performance of stiffened composite panels subjected to non-uniform edge loads by employing the finite-element technique. Applying the finite-element method makes researchers pay attention to the influence of different layouts of reinforcing bars or the distribution of holes on the mechanical properties under cyclic loading [26]. Even by using finite-element analysis, reinforcing bars can be added to the base of a porous mold to pad it, providing essential technology for artificial kidney implantation of porous nanoparticle molds [27]. Under the impact of instantaneous loads, for example, in the case of a low-speed impact of aircraft mesh shell protection pads, elastoplastic reinforcement bars should be used between the aerodynamic sheath and the bearing lattice. Kondakov et al. [28] established a calculation model of UD carbon fiber reinforcement bars under an immediate load impact using finite-element simulations. However, the finite-element method only provides simulation analysis and not a design process. Topology optimization is a method for optimizing the structure design of material distribution in a given area according to the given load, constraint conditions, and performance indicators [29]. It can be used to find the thickness and geometry of rib-reinforced thin-walled structures [30,31]. A simple and efficient method to obtain the terrain surface using a structural shell finite-element model was proposed in [32]. To meet the functional and lightweight requirements, Fonseca et al. [33] used topological optimization and free-size optimization techniques to determine the optimal rib shape and position of stiffeners and realized the design of a recycled carbon fiber-reinforced plastic/metal hybrid engine support. By simultaneously taking into account the membrane, shear, and bending strains and stiffnesses of structures, a unified adaptive approach was investigated in [34]. A new empirical stress–strain model was developed with the application of the particle swarm optimization technique in [35]. Recently, honeycomb reinforcement [36], carbon fiber-reinforced plastic reinforcement [37], bionic composite reinforcement [38,39], and other reinforcement configurations were proposed. The bionic optimization algorithm [40], structural optimization algorithm [41], and multi-objective and multi-scale optimization algorithm [42] have been widely used in the macroscopic and microscopic structure design of reinforcing bars. The formation of plant leaves and veins was generated under the impact of long-term wind and rain loads in nature, and it has excellent mechanical properties for impact, deformation, and energy absorption [43]. A mesoscale, also known as unidirectional ply-level-based finite-element modeling, was employed while assuming an individual homogenized lamina with transversely isotropic material principal directions in [44]. Following the above analysis, a bionic topology optimization method with multi-scale cyclic variable loading is proposed in this paper. The main contributions of this paper are summarized as follows:

(1)

Considering the leaf vein mechanical properties and structural composition, bionic topology optimization with minimum compliance and the maximum strain energy is proposed.

(2)

The proposed method was applied to the design of reinforcement ribs of plant leaf veins and an automotive door’s inner panel. The mechanical properties of the obtained topological configurations are superior to the original structures.

The rest of this paper is structured as follows. In Section 2, the bionic topology optimization algorithm is proposed. The reinforcement ribs of the leaf veins and an automotive door’s inner panel are derived, and the corresponding simulations and discussions are also given in Section 3 and Section 4. Finally, conclusions are drawn in Section 5.

2. Bionic Vein Topology Optimization Model

The branch structure of leaves can transfer nutrients and effectively withstand loads such as self-weight, wind, and rain, adapt to the surrounding environment, and finally obtain the optimal branch structure. Similarly, the optimization process of reinforcing bars can adopt the growth process of the branch structure of leaves to obtain the optimal layout shape of reinforcement bars and achieve optimal performance. In this paper, linear hexahedral elements are used to discretize the reinforcement bar structure, and shell elements with specific thicknesses are constructed on the surface of the reinforcement bar model based on node information to represent the outer wall of the reinforcement bar structure.

A material interpolation scheme is introduced to penalize the material attributes of rib reinforcement according to their thickness, based on the following polynomial interpolation scheme [45]:

$$E_e=\left\{\begin{array}{cc}\frac{15{\left(T_e/T_m\right)}^5+T_e/T_m}{16}E& T_0⩽T_e⩽T_m\hfill \\ E& T_m⩽T_e⩽T_{max}\hfill \end{array}\right.$$

(1)

$${\rho }_e=\left\{\begin{array}{cc}\left(T_e/T_m\right)\rho \hfill & T_0⩽T_e⩽T_m\hfill \\ \rho \hfill & T_m⩽T_e⩽T_{max}\hfill \end{array}\right.$$

(2)

where $E_e$ and ${\rho }_e$ are the elastic modulus and density of the e element in the optimization process, respectively, E and $\rho$ are the elastic modulus and density of the actual reinforcement materials, respectively, and $T_0$, $T_{max}$, and $T_m$ are the initial thickness, maximum thickness, and optimized thickness of the reinforcement rib, respectively.

Regarding the supporting structure, its dynamic equation can be expressed as

$$M{\ddot{U}}_0+K{U}_0=F_0$$

(3)

where $F_0$ is the external load acting on the supporting structure, $U_0$ is the structural displacement under external loads, and M and K are the mass matrix and stiffness matrix of the supporting structure, respectively, which satisfy

$$M=M_p+M_s,K=K_p+K_s$$

(4)

where the subscripts P and S denote the outer wall and stiffener of the reinforcement rib, respectively.

By using the finite-element method, the mass matrix and stiffness matrix can be given by

$$K_s=\sum _{e=1}^N{k}_e^s,K_p=\sum _{j=1}^M{k}_j^p$$

(5)

and

$$M_s=\sum _{e=1}^N{m}_e^s,M_p=\sum _{j=1}^M{m}_j^p$$

(6)

where N and M are the unit numbers of the reinforcement ribs and outer wall of the supporting structure, respectively, $k_e^s$ and $m_e^s$ are the stiffness matrix and mass matrix of the element e of the reinforcement rib, respectively, and $k_j^p$ and $m_j^p$ are the stiffness matrix and mass matrix of the element j of the outer wall, respectively.

The mathematical model of reinforcement layout optimization of the support structure under harmonic loading can be expressed as

$$\begin{array}{cc}\hfill & \mathrm{find}T=\left[T_1,T_2,\cdots ,T_N\right]\hfill \\ \hfill & min\tilde{J}\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\widehat{v}\left(T\right)=v-\lambda v_0⩽0\hfill \\ \hfill & 0<T_{min}⩽T_e⩽T_{max}e=[1,\cdots ,N]\hfill \end{array}$$

(7)

where $T_{max}$ and $T_{min}$ are the maximum and minimum values of the reinforcement thickness, respectively, v and $v_0$ are the actual and initial volumes of the supporting structure, respectively, $\lambda$ is the volume fraction, and $\lambda ⩾0$. The optimization objective $\tilde{J}$ is the dynamic flexibility of the support structure and is given by

$$\left\{\begin{array}{c}J\left(w\right)=U^{T}F=U^T\left(K-w^{2}M\right)U\\ \tilde{J}={\int }_0^{w_0}J\left(w\right)dw\end{array}\right.$$

(8)

where $J\left(w\right)$ is the dynamic flexibility of the support structure when the excitation frequency is w.

Using the optimization criteria algorithm, the iterative optimization formula of the design variable $T_e$ is given by

$$T_e=\left\{\begin{array}{c}{T}_{min}\mathrm{if}{T}_e⩽T_{min}\hfill \\ \alpha \left(\frac{-\eta }{\delta A_e}{T}_e\right)+(1-\alpha )T_e\mathrm{if}{T}_{min}<T_e<T_{max}\hfill \\ T_{max}\mathrm{if}{T}_e>T_{max}\hfill \end{array}\right.$$

(9)

where $\alpha$ is the iteration step size, $\eta$ is the sensitivity of the stiffener of unit e to the objective function, $A_e$ is the cross-sectional area of the stiffener of the e unit, and $\delta$ is the Lagrange operator, which satisfies

$$\delta =\sum _{e=1}^N\frac{T_e{S}_e}{\lambda v_0}$$

(10)

The formula for calculating the sensitivity of the dynamic flexibility of the support structure to the thickness of the reinforcement rib can be given by

$$\frac{\partial J\left(w\right)}{\partial T_e}=-U^T\frac{\partial \left(K-w^{2}M\right)}{\partial T_e}U=\sum _{e=1}^N-u_e^T\frac{\partial \left(k_e^s-w^2{m}_e^s\right)}{\partial T_e}{u}_e$$

(11)

where the element stiffness matrix $k_e^s$ consists of the plane stress $k_e^p$ and bending stress $k_e^b$, given by

$$k_e^p=\frac{E_e{T}_e}{1-{\mu }^2}{K}_0^p$$

(12)

and

$$k_e^b=\frac{E_e{T}_e^3}{1-{\mu }^2}{K}_0^b$$

(13)

where $K_0^p$ and $K_0^b$ are the stress stiffness matrix and bending stress matrix of the shell element, respectively, which are determined by the size and Poisson’s ratio of the shell element.

By interpolating the elastic modulus of the reinforcement rib, the sensitivity of the shell element stiffness matrix $E_0^p$ to the design variable can be derived as follows:

$$\frac{\partial k_e^p}{\partial T_e}=\partial \left(\frac{{15}^{T_e^6}/T_m^3+T_e^2/T_m}{16\left(1-{\mu }^2\right)}{K}_0^p\right)/\partial T_e=\left(9T_e^5/T_m^6+2T_e/T_m^2\right)/16k_m^p$$

(14)

where $k_m^p$ is the plane stress stiffness matrix of the reinforcement ribs when the thickness is equal to $T_m$.

When $T_m⩽T_e⩽T_{max}$, the elastic modulus of the reinforcement rib reaches the design optimization value:

$$\frac{\partial k_e^p}{\partial T_e}=\partial \left(\frac{E{T}_e}{1-{\mu }^2}{K}_0^p\right)/\partial T_e=\frac{k_m^p}{T_m}$$

(15)

The sensitivity of the shell element’s bending stiffness matrix to the design variable $E_0^b$ is given by

$$\frac{\partial k_e^b}{\partial T_e}=\partial \left(\left(\left({15}_e^8/T_m^5+T_e^4/T_m\right)/16\left(1-{\mu }^2\right)\right)K_0^b\right)/\partial T_e=\left(\frac{1}{16}\left(\frac{120T_e^7}{T_m^8}+\frac{4T_e^3}{T_m^4}\right)\right)k_m^b.$$

(16)

When $T_m⩽T_e⩽T_{max}$, the elastic modulus interpolation of the bending item of the reinforcement rib can be expressed as

$$\frac{\partial k_e^b}{\partial T_e}=\partial \left(\left(E{T}_e^3/\left(1-{\mu }^2\right)\right)K_0^b\right)/\partial T_e=\frac{3T_e^2}{T_m^3}{k}_m^b$$

(17)

Similarly, the sensitivity of the mass matrix with respect to the design variable can be derived as follows:

$$\frac{\partial m_e^s}{\partial T_e}=\left\{\begin{array}{c}\frac{2T_e}{T_m^2}{M}_m{T}_{min}⩽T_e⩽T_m\hfill \\ \frac{M_m}{T_m}{T}_m⩽T_e⩽T_{max}\hfill \end{array}\right.$$

(18)

where $M_m$ is the mass matrix of the reinforcement rib when the thickness is $T_m$.

3. Topology Optimization of the Veins

3.1. Conditions of Topology Optimization

The wind acts on the blade in the form of plane pressure perpendicular to the airflow direction. The relationship between the wind speed and wind pressure can be obtained according to the Bernoulli equation. The aerodynamic pressure applied per unit area can be given by

$$P_F=\frac{1}{2}{\rho }_0·v^2$$

(19)

where $P_F$ is the wind pressure, $KN$. ${\rho }_0$ is the air mass density, and kg/m${}^3$. v is the wind speed (m/s).

When a raindrop falls from the sky, it first passes through the acceleration stage under the action of gravity, and the air resistance increases with the increase in speed. When the air resistance and gravity reach a balance, the raindrop enters the uniform falling stage. The relation between the raindrop diameter and its equilibrium velocity is

$$V_m=\left\{\begin{array}{c}{10}^6{\left(\frac{0.787}{{(d/2)}^2}+\frac{503}{\sqrt{d/2}}\right)}^{-1}d⩽1.0\mathrm{mm}\\ (17.02-0.844d)\sqrt{0.1d}1.0\mathrm{mm}⩽d⩽3.0\mathrm{mm}\\ \frac{d}{0.113+0.0845d}3.0\mathrm{mm}⩽d⩽6.0\mathrm{mm}\end{array}\right.$$

(20)

The interaction time between the raindrops and the blade is short, and the interaction is a momentum change process. Assuming that the final velocity before the collision between the raindrop and the blade is $v_s$, the mass is m, and the collision time is t, we obtain

$${\int }_0^{\tau }f\left(t\right)dt+{\int }_{v_s}^{0}mdv=0$$

(21)

The impact force of a raindrop on a blade can be calculated as follows:

$$F\left(t\right)=\frac{m{v}_s}{t}$$

(22)

3.2. Bionic Topology Optimization of the Blade Veins

In this paper, heart-shaped leaves (such as buckwheat or sorrel) and ellipsoidal leaves (such as from a camphor tree or tea tree) were selected, as shown in Figure 1.

The shell element modeling method was adopted to define the density of the leaves as 700 kg/m${}^3$, the elastic modulus of the leaf veins as 200 MPa, the thickness of the mesophylls as 0.1 mm, and the total thickness as 1 mm. The wind speed changed from 2 m/s to 15 m/s, the raindrop diameter was 2.5 mm, and its impact force on the blade was 4.33 × 10${}^{-4}$ N [46]. The finite-element meshing of the two leaves is shown in Figure 2.

By using the growth bionic topology optimization method proposed in this paper, the topologies of the two kinds of leaves and their iterative processes are shown in Figure 3 and Figure 4, respectively.

Figure 3 and Figure 4 show that the topological configuration has a main vein and some lateral veins. The change in density nephograms is mainly concentrated in the edge area, and the change is not obvious. The topological structure with bionic reinforcement ribs had a significant increase in its natural frequency, as shown in

Table 1. Comparison of natural frequency before and after optimization.

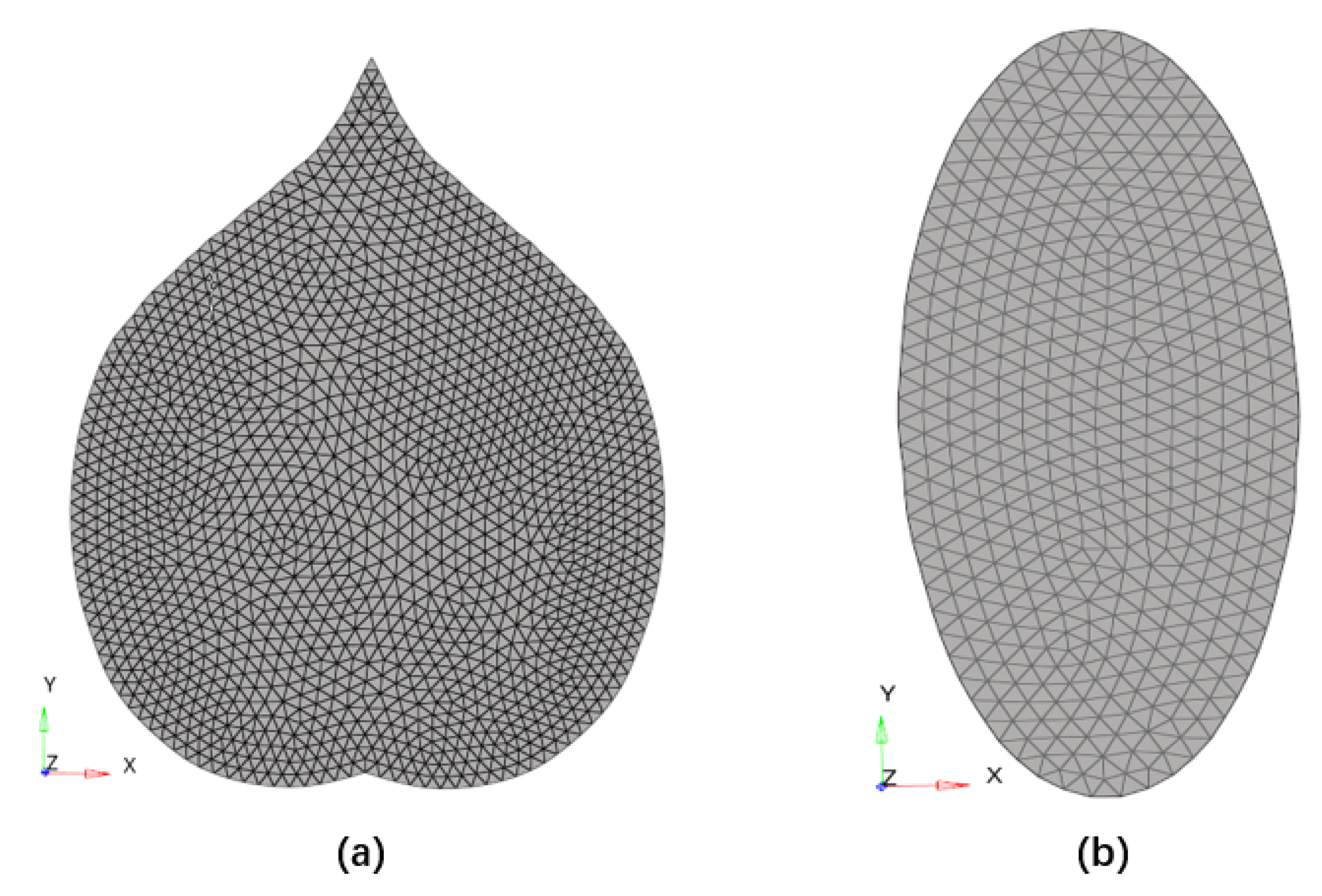
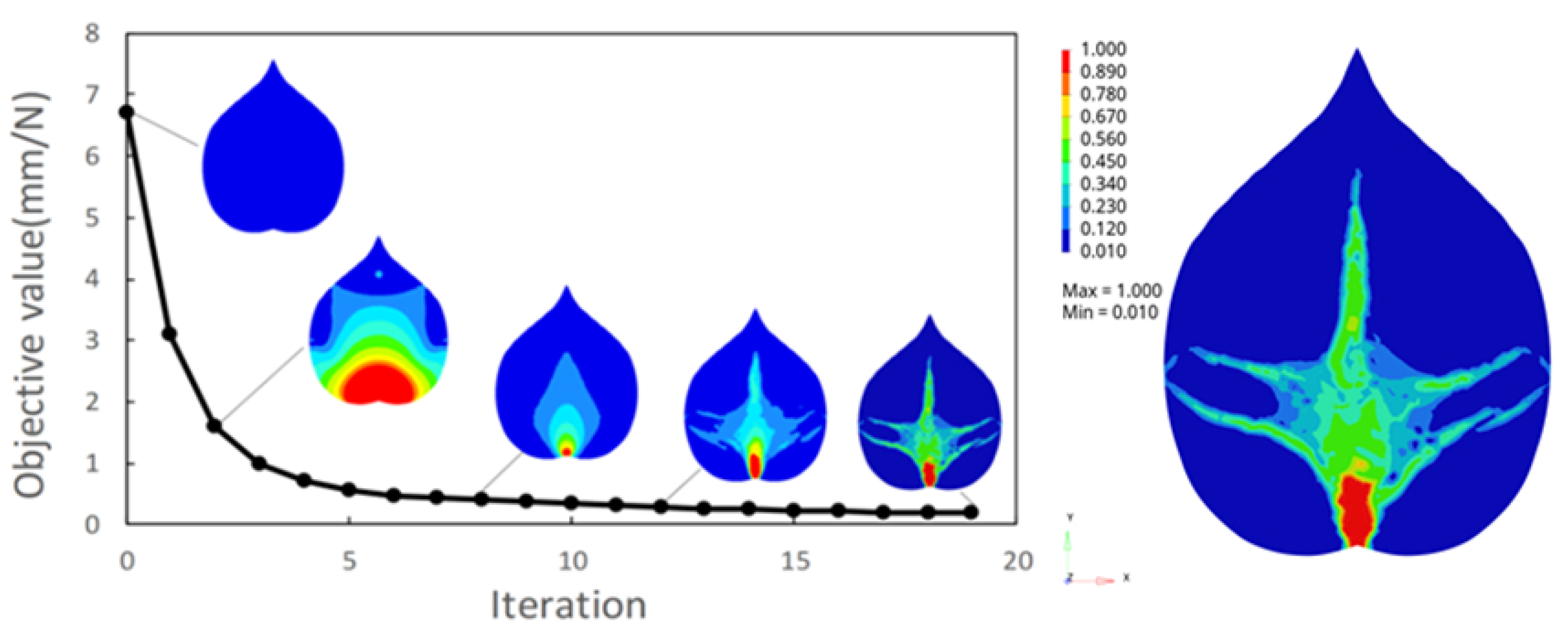
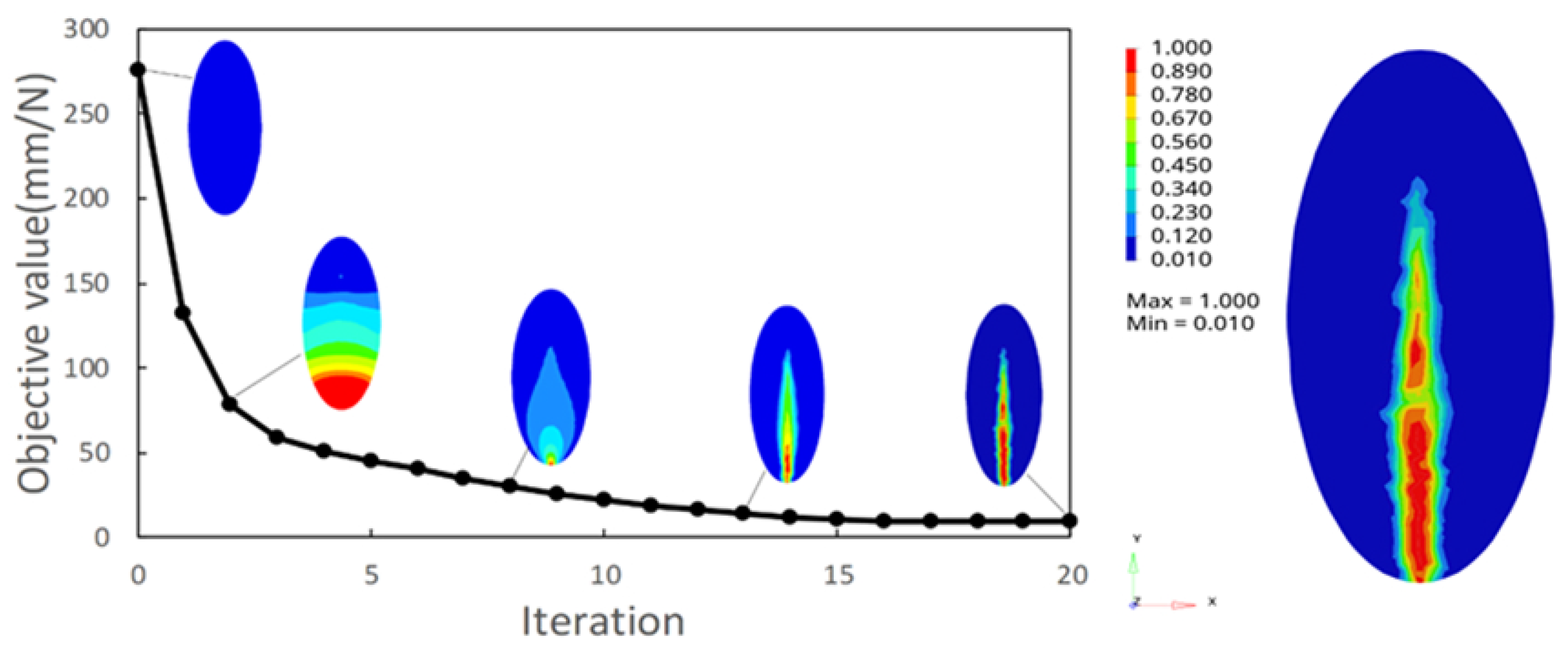
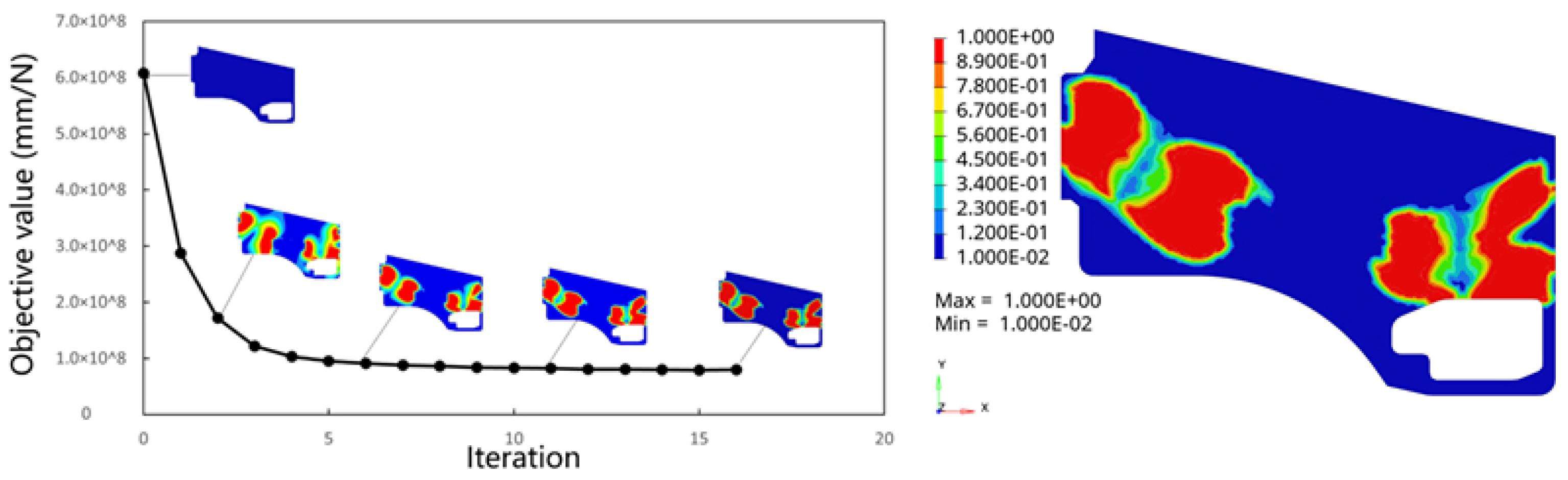
	Heart-Shaped Blade Vein	Elliptic Blade Vein
Before Optimization	$8.37$	$9.72$
After Optimization	$13.68$	$14.29$
Increase	$63.44\%$	$47.02\%$

.

4. Bionic Topology Optimization of Automotive Door’s Inner Panel

In this section, the inner panel of an automotive door is taken as the research object, and four working conditions, including subsidence, anti-concave, lateral column collision, and first-order modal, are established. The inner panel structure of the automotive door was mainly composed of sheet stamping parts, and a shell element was used to simulate the structure. The number of nodes was 3750, and the number of units was 3860. The finite-element mesh division of the automotive door’s inner panel is shown in Figure 5.

The thickness of the automotive door’s inner panel was 0.7 mm, and the material was 6061 aluminum alloy. The material’s parameters are shown in

Table 2. The material’s parameters of the automotive door’s inner panel.

Density ($\mathrm{kg}·{\mathrm{m}}^{-3}$)	Elasticity Modulus ($E/\mathrm{GPa}$)	Poisson’s Ratio ($\mathsf{\mu }$)	Strength of Extension ($R_{\mathrm{m}}/\mathrm{MPa}$)
2.70	70.00	0.27	227.00

.

The iterative processes and topological structures under four working conditions are shown in Figure 6, Figure 7, Figure 8 and Figure 9.

Figure 6 and Figure 7 show that the bionic design of the automotive door’s inner panel had a lighter mass, being $3.2\%$ lower than the original door’s mass. According to the data of the maximum stress value, shown in

Table 3. Maximum stresses of original and bionic rib reinforcement forms of automotive door’s inner panel.

Conditions	Anti-Concave Condition ($\mathrm{Mpa}$)	Sinking Condition ($\mathrm{Mpa}$)
Original	177.30	185.00
Bionic	174.80	117.00

, the maximum stress value of the automotive door’s inner panel with bionic reinforcement ribs was reduced by $1.4\%$ under the anti-concave condition and $36.8\%$ under the sinking condition. Under the above two conditions, the deformation of the automotive door’s inner panel was reduced by $37.6\%$ and $27.1\%$, respectively. The results show that the bionic structure of the automotive door’s inner panel is better than the original in terms of strength and bearing capacity.

Figure 8 shows that the automotive door’s inner panel with the bionic reinforcement rib had higher resistance to lateral column collisions, with the invasion of the rigid column being decreased by 1.5%, kinetic energy attenuation being increased by 4.5%, and total energy loss being decreased by 0.2%.

Figure 9 shows that the first-order natural frequency of the automotive door’s inner panel with the bionic reinforcement rib increased to 30.45 Hz, $3.7\%$ higher than that of the original, and the excitation frequency (20–25 Hz) was effectively avoided.

5. Conclusions

This paper proposed a bionic topology optimization method based on leaf vein growth to optimize the minimum flexibility and elastic strain energy under multi-scale, cyclic variable excitation loading. Considering the impact of multi-scale cyclic loads, such as wind speed, wind pressure, and raindrops acting on the leaf vein, the topological structures were derived using the proposed method with the Matlab program. The topological structures were saved as STL files, input into HyperWorks software, and simulated and compared with those obtained using the traditional SIMP method. The results show that the natural frequencies of the bionic topological structures of heart-shaped and elliptical leaf veins were increased by $63.44\%$ and $47.2\%$, respectively. Considering the change in radial thickness, the bionic topology optimization method was used to design the rib reinforcement of an automotive door’s inner panel, and the topological structure was input into HyperWorks software and simulated and compared with that obtained with the traditional SIMP method under subsidence, anti-concave, lateral column collision, and first-order modal conditions. The results show that the mass of the automotive door’s inner panel with a bionic topological structure increased by $3.2\%$, the maximum stress value was reduced by $1.4\%$ and $36.8\%$, and deformation was reduced by $37.6\%$ and $27.1\%$ under the anti-concave and sinking conditions, respectively. Moreover, the first-order natural frequency of the automotive door’s inner panel with a bionic topological structure increased to $30.45\%$, $3.7\%$ higher than the original.