An Evolutionarily Based Type-2 Fuzzy-PID for Multi-Machine Power System Stabilization
Abstract
:1. Introduction
- A.
- An independent PID fuzzy controller is proposed using a developed virus colony search algorithm that can adapt to different system structures and operating conditions;
- B.
- In order to reduce computation time, the fuzzy controller parameters are adjusted in several phases, including: (1) adjusting the coefficients and membership functions, (2) adjusting the weight coefficients of rules, and (3) adjusting the fuzzy rules;
- C.
- A multi-machine model with nonlinear parameters is used to approximate the behavior of the real system being studied;
- D.
- The proposed controller’s performance is compared with other available methods in different working conditions.
2. Studying the Problem from a Mathematical Perspective
2.1. Multi-Machine Nonlinear Modeling
2.2. Type-2 Fuzzy—PID
3. Improved Virus Colony Search Algorithm
3.1. The Standard Virus Colony Search Algorithm
- A.
- Virus Spread
- B.
- Vulnerability of the Host Cell
- C.
- Performance of the Safety System
3.2. Proposed Improved Algorithm
- Initial Production
- Chaos Theory
4. Design Controller Application of the Proposed Algorithm
5. Simulation Results
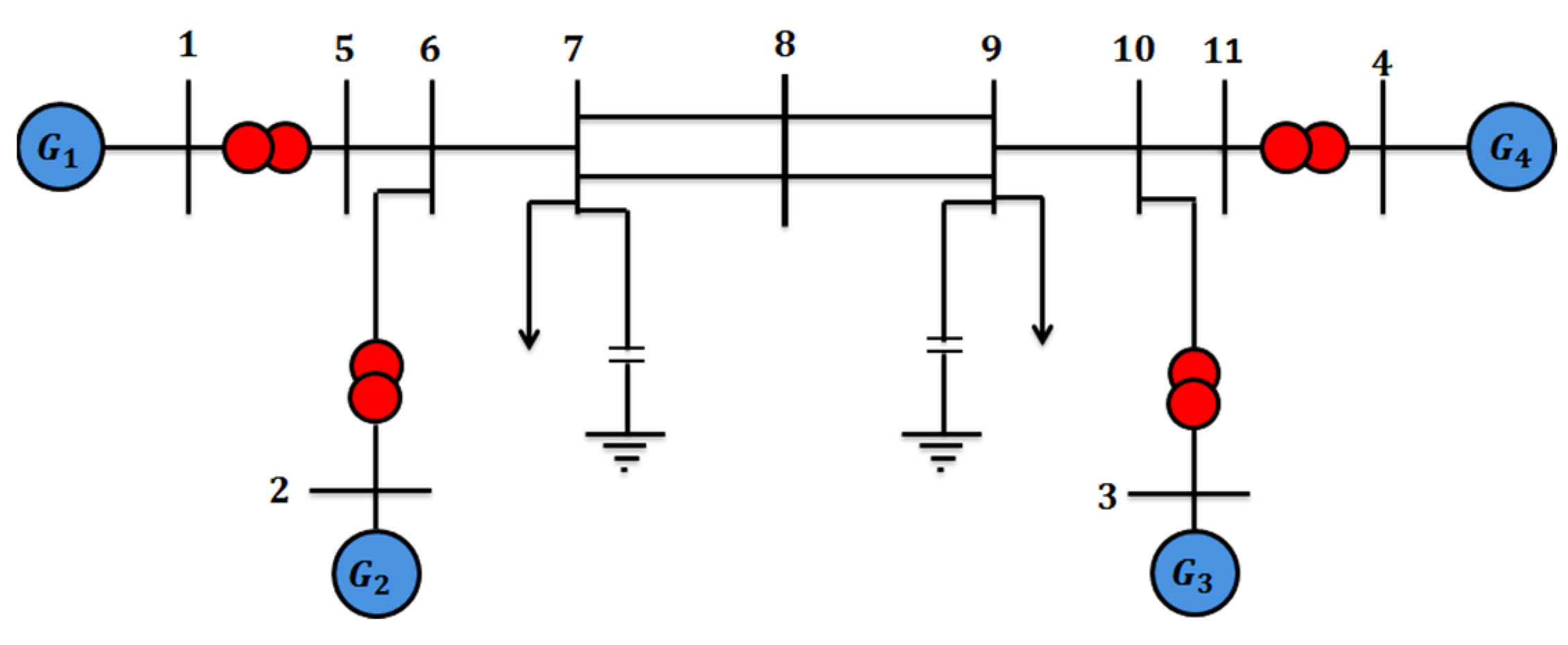
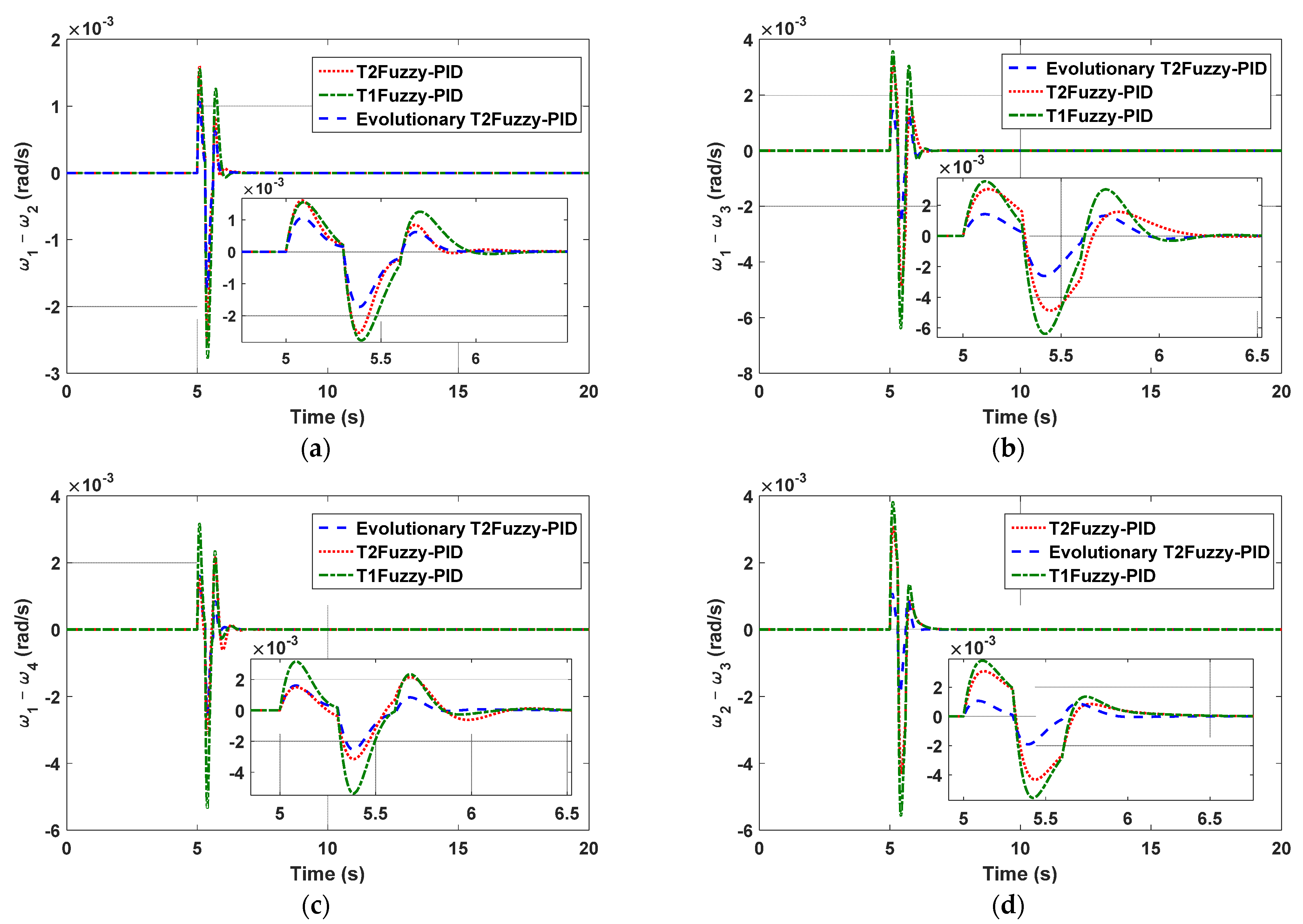
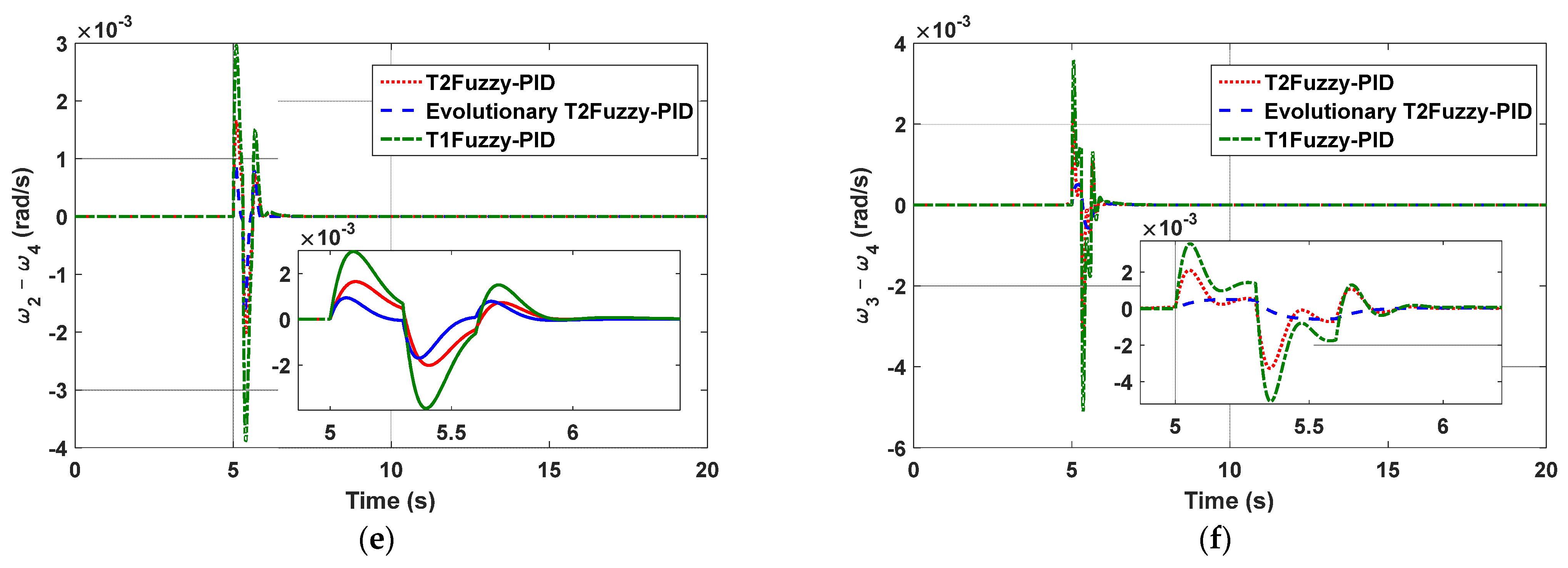
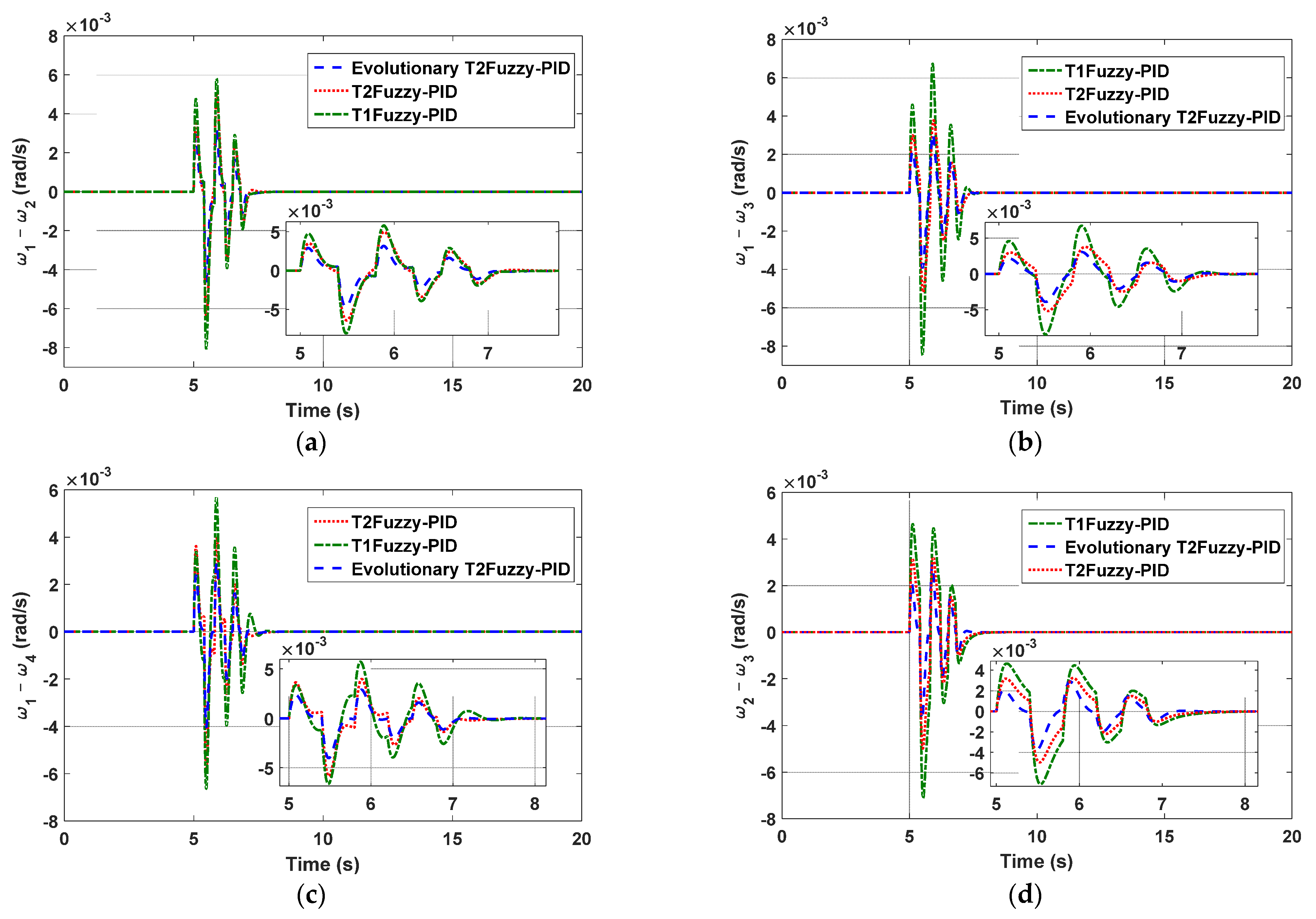
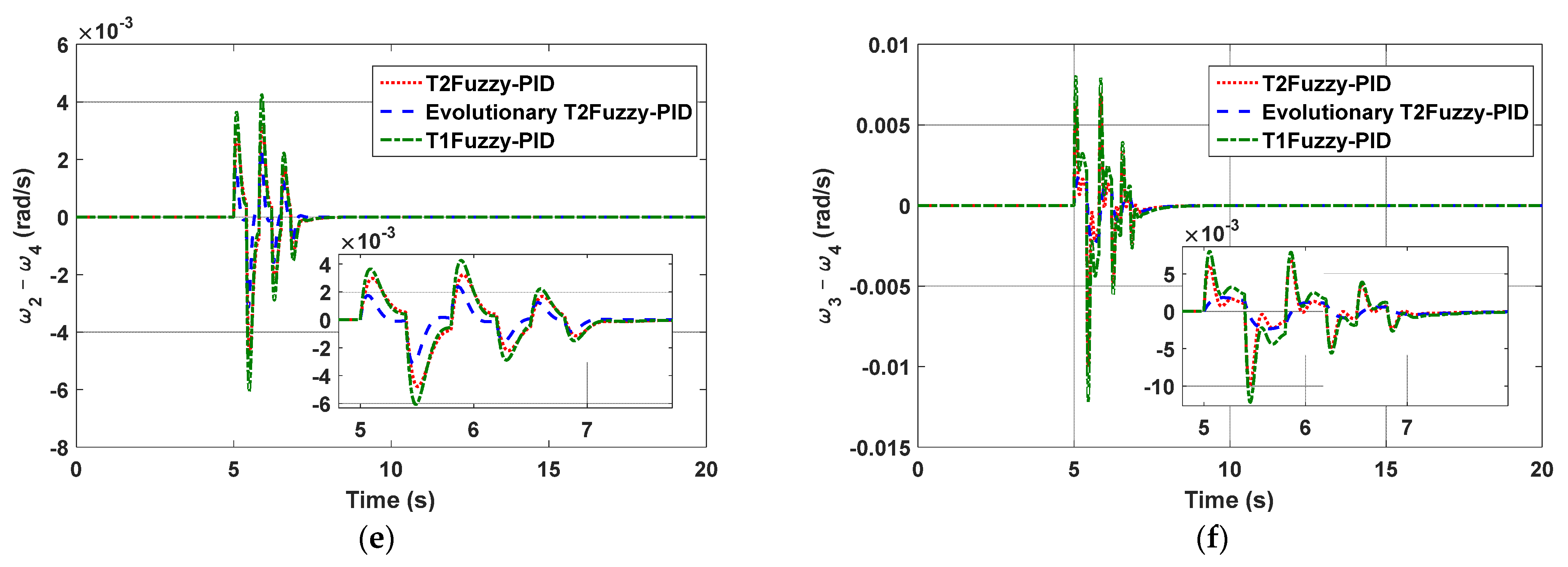
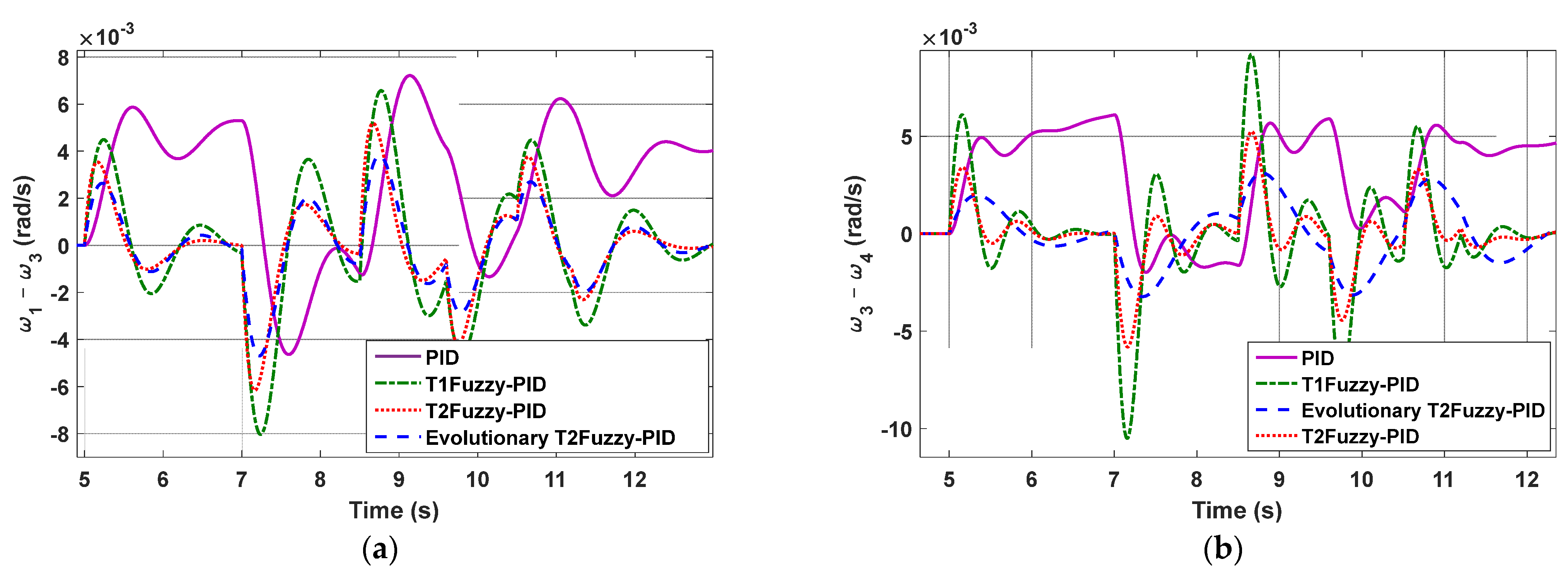
5.1. Simulation Results in Four-Machine System
- (A)
- Transient short-circuit with nominal load;
- (B)
- Transient short-circuit with increasing the load by 25%, that is, a heavy load;
- (C)
- Permanent short-circuit with nominal load (failure of breakers and protection relays).
5.2. A Comparison of Various Control Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Description | Symbol | Description | Symbol |
|---|---|---|---|
| Electric torque | Rotor angle | ||
| Stimulus time constant of the excitation circuit | Rotor speed | ||
| Regulator gain | Mechanical input power | ||
| Regulator time constant | Electric output power | ||
| Reference voltage | Generator internal voltage | ||
| Terminal voltage | Equivalent excitation voltage | ||
| Inertia of the ith machine | Mechanical torque of the ith machine | ||
| Electrical torque of the ith machine | Current iteration of the program | ||
| Dimension of the problem | Composition coefficient | ||
| Number of operating points of the system | Number of generators | ||
| The response session time | The simulation time for the optimization process |
References
- Gu, C.; Chi, E.; Guo, C.; Salah, M.M.; Shaker, A. A New Self-Tuning Deep Neuro-Sliding Mode Control for Multi-Machine Power System Stabilizer. Mathematics 2023, 11, 1616. [Google Scholar] [CrossRef]
- Tavoosi, J.; Shirkhani, M.; Azizi, A.; Din, S.U.; Mohammadzadeh, A.; Mobayen, S. A hybrid approach for fault location in power distributed networks: Impedance-based and machine learning technique. Electr. Power Syst. Res. 2022, 210, 108073. [Google Scholar] [CrossRef]
- Kumar, A.; Bhagat, S.K. Application of Lyapunov’s Method for Multi-Machine Power System Stability Analysis. In Proceedings of the 2022 Second International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 21–22 April 2022; pp. 1–6. [Google Scholar]
- Guo, X.; Shirkhani, M.; Ahmed, E.M. Machine-Learning-Based Improved Smith Predictive Control for MIMO Processes. Mathematics 2022, 10, 3696. [Google Scholar] [CrossRef]
- Aazami, R.; Heydari, O.; Tavoosi, J.; Shirkhani, M.; Mohammadzadeh, A.; Mosavi, A. Optimal Control of an Energy-Storage System in a Microgrid for Reducing Wind-Power Fluctuations. Sustainability 2022, 14, 6183. [Google Scholar] [CrossRef]
- Liu, S.; Niu, B.; Zong, G.; Zhao, X.; Xu, N. Adaptive Neural Dynamic-Memory Event-Triggered Control of High-Order Random Nonlinear Systems with Deferred Output Constraints. IEEE Trans. Autom. Sci. Eng. 2023; Early Access. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, X.; Wang, H.; Zong, G.; Xu, N. Hierarchical sliding-mode surface-based adaptive actor–critic optimal control for switched nonlinear systems with unknown perturbation. IEEE Trans. Neural Netw. Learn. Syst. 2022; Early Access. [Google Scholar] [CrossRef]
- Iranmehr, H.; Aazami, R.; Tavoosi, J.; Shirkhani, M.; Azizi, A.R.; Mohammadzadeh, A.; Mosavi, A.H.; Guo, W. Modeling the price of emergency power transmission lines in the reserve market due to the influence of renewable energies. Front. Energy Res. 2022, 9, 944. [Google Scholar] [CrossRef]
- Latif, S.; Irshad, S.; Ahmadi Kamarposhti, M.; Shokouhandeh, H.; Colak, I.; Eguchi, K. Intelligent Design of Multi-Machine Power System Stabilizers (PSSs) Using Improved Particle Swarm Optimization. Electronics 2022, 11, 946. [Google Scholar] [CrossRef]
- Danyali, S.; Aghaei, O.; Shirkhani, M.; Aazami, R.; Tavoosi, J.; Mohammadzadeh, A.; Mosavi, A. A New Model Predictive Control Method for Buck-Boost Inverter-Based Photovoltaic Systems. Sustainability 2022, 14, 11731. [Google Scholar] [CrossRef]
- Huang, H.; Shirkhani, M.; Tavoosi, J.; Mahmoud, O. A New Intelligent Dynamic Control Method for a Class of Stochastic Nonlinear Systems. Mathematics 2022, 10, 1406. [Google Scholar] [CrossRef]
- Mohammadi, F.; Mohammadi-Ivatloo, B.; Gharehpetian, G.B.; Ali, M.H.; Wei, W.; Erdinç, O.; Shirkhani, M. Robust control strategies for microgrids: A review. IEEE Syst. J. 2021, 16, 2401–2412. [Google Scholar] [CrossRef]
- Zhang, H.; Zou, Q.; Ju, Y.; Song, C.; Chen, D. Distance-based support vector machine to predict DNA N6-methyladenine modification. Curr. Bioinform. 2022, 17, 473–482. [Google Scholar]
- Cao, C.; Wang, J.; Kwok, D.; Cui, F.; Zhang, Z.; Zhao, D.; Li, M.J.; Zou, Q. webTWAS: A resource for disease candidate susceptibility genes identified by transcriptome-wide association study. Nucleic Acids Res. 2022, 50, D1123–D1130. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhao, X.; Zhang, L.; Niu, B.; Zong, G.; Xu, N. Observer-based adaptive fuzzy hierarchical sliding mode control of uncertain under-actuated switched nonlinear systems with input quantization. Int. J. Robust Nonlinear Control 2022, 32, 8163–8185. [Google Scholar] [CrossRef]
- Tang, F.; Niu, B.; Zong, G.; Zhao, X.; Xu, N. Periodic event-triggered adaptive tracking control design for nonlinear discrete-time systems via reinforcement learning. Neural Netw. 2022, 154, 43–55. [Google Scholar] [CrossRef]
- Zhao, Y.; Niu, B.; Zong, G.; Xu, N.; Ahmad, A.M. Event-triggered optimal decentralized control for stochastic interconnected nonlinear systems via adaptive dynamic programming. Neurocomputing 2023, 539, 126163. [Google Scholar] [CrossRef]
- Cheng, F.; Liang, H.; Niu, B.; Zhao, N.; Zhao, X. Adaptive neural self-triggered bipartite secure control for nonlinear MASs subject to DoS attacks. Inf. Sci. 2023, 631, 256–270. [Google Scholar] [CrossRef]
- Kamarposhti, M.A.; Colak, I.; Iwendi, C.; Band, S.S.; Ibeke, E. Optimal coordination of PSS and SSSC controllers in power system using ant colony optimization algorithm. J. Circuits Syst. Comput. 2022, 31, 2250060. [Google Scholar] [CrossRef]
- Xue, B.; Yang, Q.; Xia, K.; Li, Z.; Chen, G.Y.; Zhang, D.; Zhou, X. An AuNPs/mesoporous NiO/nickel foam nanocomposite as a miniaturized electrode for heavy metal detection in groundwater. Engineering 2022, in press. [CrossRef]
- Li, P.; Yang, M.; Wu, Q. Confidence interval based distributionally robust real-time economic dispatch approach considering wind power accommodation risk. IEEE Trans. Sustain. Energy 2020, 12, 58–69. [Google Scholar] [CrossRef]
- Ammari, C.; Belatrache, D.; Touhami, B.; Makhloufi, S. Sizing, optimization, control and energy management of hybrid renewable energy system—A review. Energy Built Environ. 2022, 3, 399–411. [Google Scholar] [CrossRef]
- Si, Z.; Yang, M.; Yu, Y.; Ding, T. Photovoltaic power forecast based on satellite images considering effects of solar position. Appl. Energy 2021, 302, 117514. [Google Scholar] [CrossRef]
- Gönenç, A.; Acar, E.; Demir, İ.; Yılmaz, M. Artificial Intelligence Based Regression Models for Prediction of Smart Grid Stability. In Proceedings of the 2022 Global Energy Conference (GEC), Batman, Turkey, 26–29 October 2022; pp. 374–378. [Google Scholar]
- Tang, F.; Wang, H.; Chang, X.H.; Zhang, L.; Alharbi, K.H. Dynamic event-triggered control for discrete-time nonlinear Markov jump systems using policy iteration-based adaptive dynamic programming. Nonlinear Anal. Hybrid Syst. 2023, 49, 101338. [Google Scholar] [CrossRef]
- Cheng, F.; Wang, H.; Zhang, L.; Ahmad, A.M.; Xu, N. Decentralized adaptive neural two-bit-triggered control for nonstrict-feedback nonlinear systems with actuator failures. Neurocomputing 2022, 500, 856–867. [Google Scholar] [CrossRef]
- Tavoosi, J.; Shirkhani, M.; Abdali, A.; Mohammadzadeh, A.; Nazari, M.; Mobayen, S.; Asad, J.H.; Bartoszewicz, A. A New General Type-2 Fuzzy Predictive Scheme for PID Tuning. Appl. Sci. 2021, 11, 10392. [Google Scholar] [CrossRef]
- Ansari, J.; Abbasi, A.R.; Heydari, M.H.; Avazzadeh, Z. Simultaneous design of fuzzy PSS and fuzzy STATCOM controllers for power system stability enhancement. Alex. Eng. J. 2022, 61, 2841–2850. [Google Scholar] [CrossRef]
- Cheng, Y.; Niu, B.; Zhao, X.; Zong, G.; Ahmad, A.M. Event-triggered adaptive decentralised control of interconnected nonlinear systems with Bouc-Wen hysteresis input. Int. J. Syst. Sci. 2023, 54, 1275–1288. [Google Scholar] [CrossRef]
- Tavoosi, J.; Shirkhani, M.; Azizi, A. Control engineering solutions during epidemics: A review. Int. J. Model. Identif. Control. 2021, 39, 97–106. [Google Scholar] [CrossRef]
- Wang, M.; Yang, M.; Fang, Z.; Wang, M.; Wu, Q. A Practical Feeder Planning Model for Urban Distribution System. IEEE Trans. Power Syst. 2022, 38, 1297–1308. [Google Scholar] [CrossRef]
- Dekaraja, B.; Saikia, L.C. Impact of energy storage and flexible alternating current transmission devices in combined voltage and frequency regulation of multiarea Multisource Interconnected Power System. Energy Storage 2022, 4, e317. [Google Scholar] [CrossRef]
- Penchalaiah, G.; Ramya, R. Investigation on Power System Stability Improvement Using Facts Controllers. In Proceedings of International Conference on Power Electronics and Renewable Energy Systems: ICPERES 2021; Springer: Singapore, 2021; pp. 499–506. [Google Scholar]
- Tan, J.; Liu, L.; Li, F.; Chen, Z.; Chen, G.Y.; Fang, F.; Guo, J.; He, M.; Zhou, X. Screening of endocrine disrupting potential of surface waters via an affinity-based biosensor in a rural community in the Yellow River Basin, China. Environ. Sci. Technol. 2022, 56, 14350–14360. [Google Scholar] [CrossRef]
- Jebali, M.; Kahouli, O.; Hadj Abdallah, H. Optimizing PSS parameters for a multi-machine power system using genetic algorithm and neural network techniques. Int. J. Adv. Manuf. Technol. 2017, 90, 2669–2688. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Zhao, X.; Xu, N. Event-triggered adaptive tracking control for uncertain fractional-order nonstrict-feedback nonlinear systems via command filtering. Int. J. Robust Nonlinear Control 2022, 32, 7987–8011. [Google Scholar] [CrossRef]
- Alshammari, F.A.; Alshammari, G.A.; Guesmi, T.; Alzamil, A.A.; Alshammari, B.M.; Alshammari, A.S. Local search-based non-dominated sorting genetic algorithm for optimal design of multimachine power system stabilizers. Eng. Technol. Appl. Sci. Res. 2021, 11, 7283–7289. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, W.; Sun, B. BDI Agent and QPSO-based Parameter Optimization for a Marine Generator Excitation Controller. Intell. Autom. Soft Comput. 2019, 25, 423–431. [Google Scholar] [CrossRef]
- Amiri, M.S.; Ramli, R.; Ibrahim, M.F. Hybrid design of PID controller for four DoF lower limb exoskeleton. Appl. Math. Model. 2019, 72, 17–27. [Google Scholar] [CrossRef]
- Afolabi, T.; Farzaneh, H. Optimal Design and Operation of an Off-Grid Hybrid Renewable Energy System in Nigeria’s Rural Residential Area, Using Fuzzy Logic and Optimization Techniques. Sustainability 2023, 15, 3862. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Sadati, N.; Zamani, I. H∞ disturbance attenuation of fuzzy large-scale systems. In Proceedings of the 2011 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011), Taipei, Taiwan, 27–30 June 2011. [Google Scholar]
- Yan, S.-R.; Alattas, K.A.; Bakouri, M.; Alanazi, A.K.; Mohammadzadeh, A.; Mobayen, S.; Zhilenkov, A.; Guo, W. Generalized Type-2 Fuzzy Control for Type-I Diabetes: Analytical Robust System. Mathematics 2022, 10, 690. [Google Scholar] [CrossRef]
- Kumbasar, T. Robust stability analysis and systematic design of single-input interval type-2 fuzzy logic controllers. IEEE Trans. Fuzzy Syst. 2015, 24, 675–694. [Google Scholar] [CrossRef]
- Wen, S.; Wang, Y.; Tang, Y.; Xu, Y.; Li, P.; Zhao, T. Real-time identification of power fluctuations based on LSTM recurrent neural network: A case study on Singapore power system. IEEE Trans. Ind. Inform. 2019, 15, 5266–5275. [Google Scholar] [CrossRef]
- Kundr, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Ghanamijaber, M. A hybrid fuzzy-PID controller based on gray wolf optimization algorithm in power system. Evol. Syst. 2019, 10, 273–284. [Google Scholar] [CrossRef]
- Sokólski, P.; Rutkowski, T.A.; Ceran, B.; Horla, D.; Złotecka, D. Power system stabilizer as a part of a generator MPC adaptive predictive control system. Energies 2021, 14, 6631. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ma, Z.; Salah, M.M.; Shaker, A. An Evolutionarily Based Type-2 Fuzzy-PID for Multi-Machine Power System Stabilization. Mathematics 2023, 11, 2500. https://doi.org/10.3390/math11112500
Wang Y, Ma Z, Salah MM, Shaker A. An Evolutionarily Based Type-2 Fuzzy-PID for Multi-Machine Power System Stabilization. Mathematics. 2023; 11(11):2500. https://doi.org/10.3390/math11112500
Chicago/Turabian StyleWang, Ye, Zhaiaibai Ma, Mostafa M. Salah, and Ahmed Shaker. 2023. "An Evolutionarily Based Type-2 Fuzzy-PID for Multi-Machine Power System Stabilization" Mathematics 11, no. 11: 2500. https://doi.org/10.3390/math11112500
APA StyleWang, Y., Ma, Z., Salah, M. M., & Shaker, A. (2023). An Evolutionarily Based Type-2 Fuzzy-PID for Multi-Machine Power System Stabilization. Mathematics, 11(11), 2500. https://doi.org/10.3390/math11112500








