Uncertainty Analysis and Optimization Modeling with Application to Supply Chain Management: A Systematic Review

Abstract

In recent years, there have been frequent cases of impact on the stable development of supply chain economy caused by uncertain events such as COVID-19 and extreme weather events. The creation, management, and impact coping techniques of the supply chain economy now face wholly novel requirements as a result of the escalating level of global uncertainty. Although a significant literature applies uncertainty analysis and optimization modeling (UAO) to study supply chain management (SCM) under uncertainty, there is a lack of systematic literature review and research classification. Therefore, in this paper, 121 articles published in 44 international academic journals between 2015 and 2022 are extracted from the Web of Science database and reviewed using the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA). Bibliometric analysis and CiteSpace software are used to identify current developments in the field and to summarize research characteristics and hot topics. The selected published articles are classified and analyzed by author name, year of publication, application area, country, research purposes, modeling methods, research gaps and contributions, research results, and journals to comprehensively review and evaluate the SCM in the application of UAO. We find that UAO is widely used in SCM under uncertainty, especially in the field of decision-making, where it is common practice to abstractly model the decision problem to obtain scientific decision results. This study hopes to provide an important and valuable reference for future research on SCM under uncertainty. Future research could combine uncertainty theory with supply chain management segments (e.g., emergency management, resilience management, and security management), behavioral factors, big data technologies, artificial intelligence, etc.

1. Introduction

The demand generated by an increasingly competitive global economy has led to a widespread interest in supply chain (SC) and supply chain management (SCM). The exploding growth of the global economy, driven by the internet, technological innovation, and demand, has evolved the SC into a complex heterogeneous grouping [1]. SCM has evolved towards globalization, sustainability, and resilience based on the wider domestic and international environment. According to the Council of SCM Professionals, SCM comprises the full range of planned and managed sourcing and procurement, transformation, and logistics management operations [2]. In addition, it most often involves the coordination of alliances with network partners, which may include suppliers, promoters, external service providers, and customers. In essence, SCM is the co-ordination of the management of supply and demand within and between companies [2]. While SCM has always been the foundation of business, currently, it is more important than ever as a marker of business success [3,4]. In order to live and thrive in the quickly evolving, technologically driven business environment of today, businesses must manage their SCs effectively and adjust as necessary.

The growing awareness of the importance of SCM has generated substantial literature. This literature focuses on how to manage a global supply chain (GSC) (e.g., [5]), sustainability management of supply chain (e.g., [6,7,8,9,10,11,12]), closed-loop supply chain (e.g., [13]), risk management (RM) (e.g., [14,15,16]), and disruption recovery (DR) (e.g., [17]). Within the research stream of SCM globalization, Koberg and Longoni [5] provided a comprehensive analysis of the crucial components of sustainable management in GSC. Through a literature review, they identify two key elements of sustainable supply chain management (SSCM) in GSCs: the structural dimension of GSCs, i.e., SSCM configuration, and the relational dimension of GSCs, i.e., SSCM governance mechanisms. In the context of tariffs and price premiums, Chen et al. [18] analyzed the sourcing decisions of global manufacturers who maintain production sites in a competitive environment and sell their products in domestic and international markets.

There has been a considerable amount of research on SSCM. Silvestre [4] explored how SC sustainability can be implemented and managed in a developing and emerging economic environment. The paper argues that SCs in developing and emerging economies face additional sustainability challenges due to institutional weaknesses and highly variable business environments, which increase the level of complexity and uncertainty. Farooque et al. [6] classified terms related to SC sustainability and provided a unified definition of SC sustainability management. Jia et al. [7] reviewed 55 articles published between 2000 and 2019, identifying four themes in soy SSCM: drivers, global value chain management, consequences, and potential barriers. Nilsson and Goransson [8] identified, categorized, and evaluated the importance of key factors in achieving SSC innovation through a systematic review and analysis of the relevant sustainable supply chain (SSC) innovation literature. Calmon et al. [9] analyzed sustainable business strategies for innovative durable goods distributors serving customers in the supply chain, including pricing issues and distribution issues.

Risk management plays a critical role in the effective operation of SCs under various uncertainties. Numerous scholars have contributed to defining, operationalizing, and mitigating risks and SC disruptions brought on by risks over the years by concentrating on supply chain risk management (SCRM) [14]. Ho et al. [14] provided a new definition of SC risk and SCRM and proposed five common risks present in SCs based on a review and synthesis of 224 papers published in SCRM from 2003 to 2013, including macro risk, demand risk, manufacturing risk, supply risk, and infrastructure risk. Ivanov et al. [17] addressed different disruption risks and recovery measures, and the research streams of different quantitative methods and application areas are structured and classified. Behzadi et al. [15] conducted a comprehensive review of the literature on the agricultural SCRM model, identifying robustness and resilience as two key techniques for managing risk. Huang et al. [19] provided an in-depth look at how downstream purchasers work with upstream suppliers to improve accountability and reduce risk.

The COVID-19 outbreak has increased SC uncertainty for companies. Due to the dynamic and imprecise nature of COVID-19 growth, there are not enough data to adequately estimate the probability distribution of the unknown parameters [20]. In order to better cope with emergencies, companies need to grasp SC uncertainty and implement supply chain resilience management to enhance SC resilience. Abouee-Mehrizi et al. [21] considered the data-driven inventory management of a single, periodically reviewed perishable product (e.g., platelets) with zero lead time and random demand under unit residual shelf-life uncertainty. Li and Mizuno [22] studied the problem of cycle review, joint dynamic pricing, and inventory in a dual-channel SC where demand is stochastic, and price is sensitive. Niu et al. [23] examined the manufacturing or purchasing decisions of retailers under uncertain production quantities. Niu and Shen [24] proposed a programmatic model of two competing SCs to examine the question of whether manufacturers would invest in process innovation considering knowledge spillovers, absorptive capacity, and innovation uncertainty. Saberi et al. [25] modeled the interaction between firms in a heterogeneous SC under uncertainty in the price of carbon permits and carbon demand. Zhao et al. [26] investigated the recovery strategies of SC firms under uncertain demand.

In recent years, various studies have been conducted that combine different theories and methods in various areas of SCM for a systematic review. For example, quantitative method combined with empirical study [17] and structural equation modeling [27]. Guo and He [28] argued that game modeling is the most common method used in research to achieve supply chain optimization of platform services. Global supply chains face serious challenges, and uncertainties are widespread in the supply chain management process. Conventional optimization models assume that the input data are accurate, but this approach does not take into account the quality and feasibility of the model as affected by data uncertainty. In reality, the uncertainty of the parameters may affect the feasibility of the resulting solution, rendering the optimal solution meaningless in practice. However, if the effect of uncertain parameters is over-considered, the decision will often result in the decision-maker not obtaining a satisfactory value of the objective function. Therefore, the decision-maker wants to find a solution that is optimal without the influence of uncertainty parameters. In order to provide a more reasonable and accurate description of the uncertainty problem, uncertainty optimization is gradually gaining attention in the academic community. The research on SCM on the basis of uncertainty analysis and optimization modeling (UAO) is of great importance due to the different levels of uncertainty that are faced. Therefore, a review of published articles about SCM using the method of UAO is necessary to provide a comprehensive perspective for the next generation of applying UAO to the study of SCM. In this review study, we provide a systematic review and classification of articles published between 2015 and 2022 that consider UAO in the field of SCM research. Research publications prior to 2015 are excluded from this review because we aim to provide a new overview of recent trends related to the above-mentioned scope of research, and there are fewer articles that combine uncertainty and supply chain management for research prior to 2015. In addition, 2015 saw an increase in adverse factors and uncertainties in world economic performance following the low growth of world industrial production, the continued downturn in trade, and the increased turbulence in financial markets.

Most of the current literature reviewed in the most relevant fields combines supply chain risk management or a specific type of supply chain with uncertainty, and less of the literature has reviewed the uncertainty as well as its solutions in each segment of supply chain management from the perspective of the whole supply chain management. The purpose of this study is to present the application of UAO in SCM and the outlook of its future application direction in the field of the supply chain. This paper bridges this research gap and reviews the literature on optimization modeling as a method to solve uncertainty problems in supply chain management. This study attempts to address the following questions: (1) What are the main uncertainties in supply chain management? (2) What is the status of previous literature on the use of optimization modeling to solve uncertainty in supply chain management? (3) How are the three types of uncertainty methods applied in different areas of the supply chain?

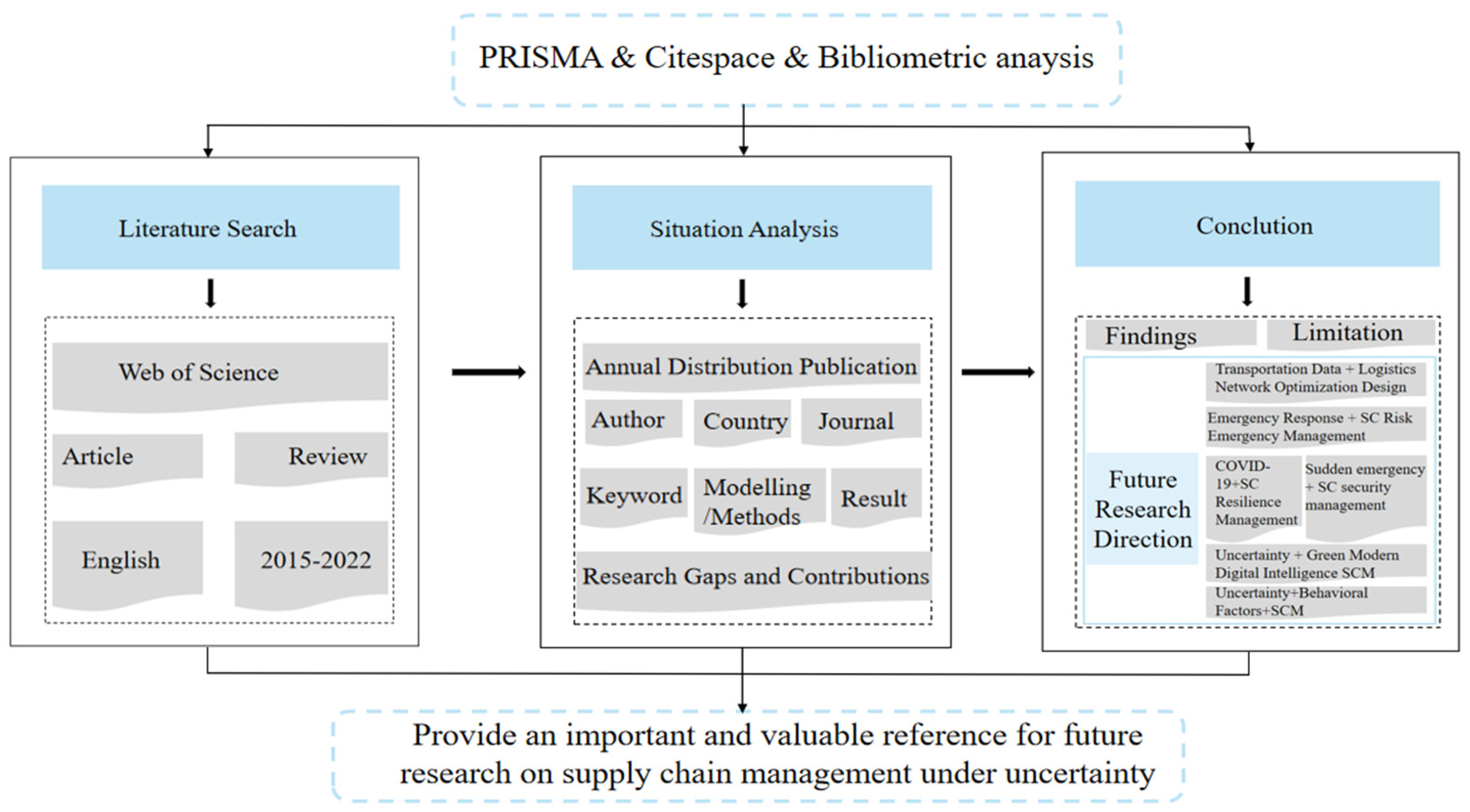
Figure 1 illustrates the research framework of this paper. In terms of analysis, this study carefully and systematically searched research papers involving UAO in SC published from 2015 to 2022, categorized and summarized them for analysis, and then assessed the future research potential of UAO. The top dashed boxes denote the research methodology, while the three solid boxes in the center, linked by thick black arrows, represent the primary research content at various stages.

The rest of the article is organized as follows. In Section 2, we present the theory of UAO and its development. The literature search process and the research analysis methods used in this paper are briefly summarized in Section 3. In Section 4 and Section 5, all selected articles are summarized and reviewed according to different criteria. Section 6 and Section 7 describe the research findings, conclusions, future directions, and limitations.

2. The Evolution of Uncertainty Analysis and Optimization Modeling

As the intersection of combinatorial optimization and uncertainty theory, uncertain network optimization problems have been a hot topic of research. The shortest route problem, minimum spanning tree problem, and other common network optimization issues come in a wide variety. Numerous researchers have been motivated to model network optimization issues mathematically by these appealing challenges [29,30]. When the sample size is too small or when there is no population for calculating a probability distribution, we must enlist the assistance of subject-matter experts in order to determine their level of confidence that each event will occur [31]. Although the probability is one of the theories most commonly used by scholars and practitioners to model uncertainty and subsequently explore the principles inherent in random occurrences, it may not be adequate to address all types of uncertainty associated with unique human beliefs. However, it may not be adequate for addressing virtually all types of uncertainty, especially those associated with unique human beliefs, as it may lead to counterintuitive results [32]. In order to distinguish it from randomness, this phenomenon is called uncertainty [33]. To better deal with this uncertainty, Liu [34] proposed uncertainty theory, which thus became a branch of mathematics to model uncertainty through trustworthiness. Zhou et al. [35] analyzed a review of 1004 journal papers in the field of uncertainty from 2008 to 2019 to derive seven key sub-fields of uncertainty theory and their research potential. The study finds a linear growth trend in the literature of uncertainty theory, involving an extensive network of 1000 scholars published in 300 journals worldwide, indicating the growing attractiveness of uncertainty theory and its gradual expansion of academic influence.

Mathematical models typically explain engineering problems, and in order to solve these models, it is often assumed that the parameters in the mathematical models are deterministic. However, in practical applications, many parameters are difficult to obtain accurately, leading to uncertainty in the parameters. The response of the theoretical analysis may differ considerably from the actual situation because of uncertain parameters. Consideration of uncertainty in design optimization enhances the design solution’s dependability and durability. UAO can be dated back to the 1950s [36,37], and research in this area has proliferated since then [38].

Based on different theories, uncertainty methods can be classified into three categories, as follows:

(1) Uncertainty programming based on probability theory. Probability theory, a branch of mathematics, deals with the analysis of random phenomena. A random phenomenon is such an objective phenomenon that when one observes it, the result obtained cannot be predetermined, but is only one of many possible outcomes. The outcome of a random event cannot be determined before it occurs. However, it may be any one of several possible outcomes. The actual outcome is considered to be determined by chance. The keyword for uncertainty programming based on probability theory is random.

(2) Uncertainty programming based on fuzzy set theory. Fuzzy set theory is a research method that deals with problems related to fuzzy, subjective, and imprecise judgments, which quantifies linguistic aspects of available data and preferences for individual or group decisions. This method treats the object to be examined and the fuzzy concepts reflecting it as a certain fuzzy set, establishes an appropriate affiliation function, and analyzes the fuzzy object through the relevant operations and transformations of the fuzzy set. Fuzzy set theory is based on fuzzy mathematics to study phenomena related to non-exactness. The keyword for uncertainty programming based on fuzzy set theory is fuzzy.

(3) Uncertainty programming based on uncertainty theory. Expert confidence-based data are concerned with the subjective judgments of different experts about the likelihood of an uncertain event occurring. Such judgments are different from the random sampling studied in classical statistics. Therefore, it is not appropriate to directly adopt the framework of classical statistics for statistical inference. Liu [34] proposed an uncertainty theory to build a basis for solving the analysis problem of such data. The theory introduces uncertain variables to portray uncertain phenomena by establishing a new axiomatic system, which mainly includes uncertainty measures, uncertain variables and their distributions, and inverse distributions and applications. The keyword of uncertainty planning based on uncertainty theory is uncertain.

The difference between these three uncertainty approaches is that both probability theory and uncertainty theory try to model the degree of human beliefs, the former using possibility measurement tools and the latter using uncertainty measurement tools [39]. Nevertheless, the fuzzy theory, on the other hand, considers that the degree of belief is a subjective probability or a fuzzy set.

3. Research Methodology

In our retrospective study, combined with the visualization tool CiteSpace and bibliometric analysis, we complete the three main steps of Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA), including literature search, article eligibility, data extraction, and summarization. CiteSpace presents the structure, patterns, and distribution of scientific knowledge in a visual way, and this software is now widely used to analyze changes in research hotspots and trends. PRISMA is a set of standard specifications established for the quality of systematic reviews and is applicable to analyses of published papers using primary data sources, with the aim of improving the objectivity and consistency of systematic reviews.

3.1. Literature Search

In this phase, we demonstrate the use of UAO in SCM using the well-known database Web of Science (WoS). The database is chosen for several reasons. First, it meets the two core quality criteria for literature databases required in leading literature review approaches, such as those of Tranfield et al. [40] and Fink [41]. (1) The scope of the database is consistent with our study design and questions. WoS provides access to over 22,000 journals from all major publishers. This is probably the broadest range of high-quality scientific journals of any database [42]. In addition, it is one of the most complete and most cited reference databases in the field of supply chain management [43]. (2) This data is compiled in a database that can be searched in a consistent manner using Boolean operators to construct customized search strings. Thus, we can provide a consistent set of literature covering the topics of supply chain management and uncertainty in the present paper. Second, the database is widely considered to be the standard and most widely used tool for generating citation data for scientific research and other evaluation purposes [44], and bibliometric studies frequently use the Web of Science as their data source [45]. Finally, Wang and Waltman [46] compared the data coverage of WoS, Scopus, and Google Scholar, respectively. The results of the study showed that the journal classification system of WoS is more accurate and, therefore, superior to the other systems. Consistent with Xu et al. [47] and Saini et al. [48], the authors rely on WoS because it guarantees standardization, credibility, and high-quality publications and ensures the quality of the analyzed papers. Searching by topic “supply chain management” and “uncertainty”, restricting the paper type to “review literature”, “SCM”, “sustainable SCM”, “supply chain network design (SCND)”, “emergency network optimization”, “logistics network optimization”, “SCN disruption”, and “closed-loop SCM” appear more frequently in the titles. The literature search, therefore, uses these seven keywords (specifically examining the period of COVID-19 when studying supply chain disruption), as well as uncertainty and optimization modeling, to gather the available literature for the period 2015–2022. According to our strategic search, a total of 6591 academic papers are extracted. The following stage is looking for duplicate papers with redundant information, reducing the number to the remaining 275 documents. After that, we exclude irrelevant papers, leaving 153 papers after filtering by title and abstract. We add 18 classic papers for reference, keeping just the final 171 potentially pertinent publications for review (see Figure 2). In this paper, each article is reviewed according to Amstar entries in the final step of the literature search to determine the final articles used for this review paper.

3.2. Article Eligibility

In order to qualify, we independently review the entire text of each paper that was taken from the previous step in this review process. We carefully select the pertinent items for which consensus has been established in the last step. Literature that considers uncertainty in SCM or has applied UAO is selected, excluding unpublished working papers, editor’s notes, master’s theses, doctoral dissertations, textbooks, and non-English papers. Previous studies considered other approaches to SCM, such as quantitative analysis, so in this step, we also exclude these studies. Finally, we select 121 articles related to UAO methods in SCM that meet the inclusion criteria from 44 international academic journals from 2015 to 2022. We use CiteSpace software to analyze the keyword, and author of the de-duplicated articles, as shown in Figure 3 and Figure 4, respectively.

3.3. Data Extraction and Summarizing

A total of 121 papers are reviewed and distilled in the literature as the final step of our methodology. In the subsequent analysis, all chosen articles are classified into different categories, including general SCM, sustainable SCM, SCND, emergency network optimization, logistics network optimization, closed-loop SCM, and SCN disruption during the COVID-19 pandemic period (see

Table 1. Distribution of papers based on application areas.

Application Areas	Number of Paper	Percentage (%)
General SCM	19	15.57
SSCM	15	12.30
SCND	20	16.39
Emergency network optimization	15	12.30
Logistics network optimization	15	12.30
CLSCM	20	16.39
SCN disruption during the COVID-19 pandemic	18	14.75
Total	121	100

). In addition, the literature is synthesized and evaluated according to a variety of standards, such as authors’ names, year of publication, application areas, countries, research objectives, modeling methods, research gaps and contributions, research results, and journals in which they appear. Moreover, we consider this review article to be meticulously crafted and a thorough resource on the application of the UAO to SCM. Therefore, we need to go through the article in its entirety and conduct a more in-depth study with more details in order to fully analyze the application of UAO in the field of SCM. Although the selection process is time consuming, it allows us to identify the most appropriate publications.

4. Distribution of Articles by Journal, Year of Publication, and Nationality of Authors

4.1. Distribution of Articles by Journal

The distribution of selected articles by journal is presented in

Table 2. Distribute of papers based on the name of journals.

Name of Journal	Frequency of Publication	Percentage (%)
Computers & Industrial Engineering	11	9.02
Journal of Cleaner Production	11	9.02
International Journal of Production Research	10	8.19
Annals of Operations Research	8	6.55
Omega	7	5.73
Soft Computing	6	4.91
Applied Mathematical Modeling	4	3.28
Applied Soft Computing	4	3.28
International Journal of Production Economics	4	3.28
Journal of Ambient Intelligence and Humanized Computing	4	3.28
Journal of Intelligent & Fuzzy Systems	4	3.28
Environment, Development, and Sustainability	3	2.46
Journal of Intelligent Manufacturing	3	2.46
Operational Research	3	2.46
Transportation Research Part E: Logistics and Transportation Review	3	2.46
European Journal of Operational Research	2	1.64
Expert Systems with Applications	2	1.64
IEEE Transactions on Fuzzy Systems	2	1.64
Information Sciences	2	1.64
International Journal of General Systems	2	1.64
International Journal of Machine Learning and Cybernetics	2	1.64
Production and Operations Management	2	1.64
Applied Mathematics and Computation	2	1.64
Applied Energy	1	0.82
Asia-Pacific Journal of Operational Research	1	0.82
Cleaner Logistics and Supply Chain	1	0.82
Complex & Intelligent Systems	1	0.82
Computers & Operations Research	1	0.82
Energy	1	0.82
Engineering Applications of Artificial Intelligence	1	0.82
Fuzzy Sets and Systems	1	0.82
International Transactions in Operational Research	1	0.82
Journal of Industrial and Management Optimization	1	0.82
Journal of Manufacturing Systems	1	0.82
Journal of Modeling in Management	1	0.82
Kybernetes	1	0.82
Management Science	1	0.82
Neural Computing and Application	1	0.82
RAIRO-Operation Research	1	0.82
Safety Science	1	0.82
Socio-Economic Planning Sciences	1	0.82
The International Journal of Logistics Management	1	0.82
Transportation Science	1	0.82
Sustainable Production and Consumption	1	0.82
Total	121	100

. The articles related to UAO and SCM issues are selected from 44 different international academic journals in the Web of Science database. As shown in Table 2, Computers & Industrial Engineering and Journal of Cleaner Production tie for the top ranking with 11 papers among the 44 journals. The finding also indicates that these two journals contribute more to the application of UAO in SCM. International Journal of Production Research ranks second with 10 papers. Annals of Operations Research, in addition, ranked third with eight articles. Among the other journal rankings, Omega, an international journal with seven published papers ranks fourth, and Soft Computing has six published papers tied for fifth place. Table 2 demonstrates the distribution of other selected literature.

4.2. Distribution of Articles by Year of Publication

In recent years, the use of UAO in SCM has been increasing. There has been a long-standing historical growth rate of UAO in SCM concerns. Based on the frequency of distribution by year of publication, Figure 5 depicts the pertinent evidence. The results show that the amount of literature on UAO applications in SCM has increased from 2015 to 2022. The results in this section indicate that 4 articles in 2015 had references to UAO, and 14 articles did so in 2017. In 2018 and 2019, each year had 12 articles on UAO and SCM, a minor decrease from 2017. Starting in 2019, the number of studies on UAO and SCM will increase annually. In addition, the number of papers published between 2020 and 2021 increased from 15 to 30 in one year. This shows that UAO is currently being used by researchers in different areas of SCM and that this number is expected to increase in the coming years.

4.3. Distribution of Papers by Nationality of Authors

We also provide the findings from the analysis of the writers’ nationalities.

Table 3. Distribution of papers based on the nationality of authors.

Name of Country	Number of Publications	Percentage (%)
China	60	49.18
Iran	22	18.03
India	9	7.38
Canada	5	4.09
USA	4	3.28
Australia	3	2.46
Korea	3	2.46
France	2	1.64
Morocco	2	1.64
Turkey	2	1.64
Russia	1	0.82
Denmark	1	0.82
Dubai	1	0.82
Finland	1	0.82
Germany	1	0.82
Iceland	1	0.82
Italy	1	0.82
Oman	1	0.82
Portugal	1	0.82
UK	1	0.82
Total	121	100

lists authors using UAO in SCM from 20 different countries, which are shown in Figure 6. The most published papers are from China (49.18%), followed by Iran (18.03%). The study found that Chinese authors are more interested in research on UAO and SCM, especially in recent years.

5. Publication Areas Classification

Pishvaee et al. [49] proposed a RO model to deal with the inherent uncertainty of the input data for the CLSCND problem. Initially, a deterministic mixed-integer linear programming model for CLSCND is developed. The robust equivalent of the mixed-integer linear programming model is then demonstrated using the most recent extensions of RO theory. Finally, in order to evaluate the robustness of the solutions derived from the new RO model, they are compared with some implementations of the deterministic mixed integer linear programming model under different test problems. Lalmazloumian et al. [50] also developed a robust mixed integer linear programming model to study the agile manufacturing firm in a make-to-order production environment for the supply chain planning problem and used a scenario-based RO approach to absorb the effects of uncertain parameters and variables. Shabani and Sowlati [51] put forward a hybrid multi-stage SO-RO model for maximizing the SC of a forest biomass power plant with uncertainty. Zokaee et al. [52] addressed the uncertainty in demand, supply capacity, and key cost data. A RO model for SSND is proposed to minimize the total SC cost to determine the optimal siting and allocation strategy.

In this era of black swans, events such as the “car core shortage” and the “shipping shutdown” have overturned many traditional SCM concepts and “uncertainty” has become an element that has to be considered when designing SCs. Uncertainty is not a concept that has only emerged in recent years. The term “VUCA”, i.e., Volatile, Uncertain, Complex, and Ambiguous, which emerged in the 1990s, refers to uncertainty, which has become the norm in SCM due to the high number of unexpected events, high demand for volatility, and high demand for agile response. Klibi et al. [53] reviewed the optimization models proposed in the literature. They state that the model developed should strike a balance between realism and manageability or solvability, using data available in typical real-world situations.

Today’s world is increasingly characterized by VUCA, i.e., instability, uncertainty, complexity, and ambiguity. The uncertainty faced by SCs is increasing, and SCs are facing more and more unexpected risks, which can easily lead to SC disruptions [54]. The industry is increasingly concerned with SC safety and security, is committed to dealing with uncertainty in a variety of ways to enhance the SC’s resilience, and has conducted extensive research on this topic using UAO methods. For example, Saghaei et al. [55] constructed a two-stage stochastic mixed integer nonlinear programming (MINLP) model incorporating opportunity constraints to minimize the total cost of woody biomass power generation in a four-stage integrated bioenergy SC that allows the supply chain to remain resilient in the presence of disruptions. Razavi et al. [56] modeled the crisis response management phase using a multi-objective mathematical model under conditions of uncertainty. Uncertain data generated under disaster conditions are treated with a RO methodology. In light of this, a hybrid solution method based on a genetic algorithm and multiple-choice objective planning is proposed. Foroozesh et al. [57] designed new multi-objective mixed-integer linear programming models for multi-product, multi-cycle, multimodal G-elastic SCs by proposing new strategies to minimize the impact of disruptions. Subsequently, using credibility measures and affiliation functions of generalized interval type II fuzzy variables, a new robust possibility planning strategy is suggested to respond with facility supply capacity, customer demand, transportation cost, and CO₂ emission issues.

We grouped and combined articles that considered both UAO and SCM into seven different application areas, including general SCM, sustainable SCM, closed-loop SCM, SCND, emergency network optimization, logistics network optimization, and SCN disruption during the COVID-19 pandemic. In the next sections, all selected articles are summarized and reviewed according to different criteria, including author name, uncertainty conditions, research objectives, modeling methods, research gaps and contributions, and research results.

5.1. Distribution Papers Based on General SCM

In a highly competitive and changing market environment, there are many uncertainties in SCM. In fact, there are three main types of uncertainty in the SC: supply uncertainty, cost uncertainty, and demand uncertainty.

Among the articles in this field selected for this study, Refs. [27,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73] applied uncertainty methods based on uncertainty theory. For example, Liu et al. [49,50] studied the supply risk from suppliers. In their paper published in 2020, they investigated the optimal decision choice of a retailer when the primary supplier faces supply uncertainty, and the output of the alternate supplier is infinite or uncertain [58]. Subsequently, in 2021, a brand-new idea known as the channel supply risk level (SRL) was put forth to measure the channel supply risk that arises from supply uncertainty [59]. To explore the impact of environmental uncertainty on decision-makers’ behavior, Farham-Nia and Ghaffari-Hadigheh [65] described the demand function as a price-dependent, service-dependent, and channel-dependent uncertainty function to investigate the optimal pricing decision for SCs with dual distribution channels in centralized and decentralized decision systems. Ke et al. [70] proposed uncertainty measures to deal with these artificial degrees of trust and used three uncertainty planning models to derive how channel members should make pricing decisions under three power structures.

Refs. [74,75] applied the uncertainty method based on probability theory. Zhao et al. [74] studied supply chain coordination based on incomplete contracts by using production costs as a random variable. Ma et al. [75] looked at the distribution of substitutable goods to the same market with a pricing decision dilemma by two risk-sensitive makers in an uncertain environment using a shared dominant and risk-neutral retailer.

Based on the above literature and previous studies,

Table 4. Distribution papers based on general SCM.

Author(s)	Uncertainty	Study Purpose	Modeling/Method	Research Gap and Contribution	Results and Outcomes
Liu et al. [58]	Supply	The retailer’s optimal decision selection problem under uncertainty	Profit maximization model for participants based on benchmark confidence level	The reliability of uncertain supply is recommended to be characterized by reliability level for service market (RLSM)	For different RLSMs, the retailer does not choose a mixed strategy
Liu et al. [59]	Supply	The ordering strategies of integrated and decentralized SCs under different SC constraints	Confidence-based decision rule to assess the uncertain supply of two channels	To quantify the supply risk caused by channel supply uncertainty, a channel supply risk level is proposed	The ideal ordering method is directly impacted by the differing trust costs for the two channels due to the distinct SC limitations
Liu et al. [60]	Variable cost	Contract design issues for two competing heterogeneous suppliers working with a common retailer	Confidence-based contract design model for SC with uncertain information	A confidence-based decision rule is applied under incomplete demand information	The inverse distribution and confidence level of external demand determine the optimal order quantity for the retailer
Liu et al. [61]	Cost	Use uncertainty theory to portray uncertain information under different market structures	Competitive models for integrated, hybrid and decentralized SCs	Representing cost and retail price noise as uncertain variables	when cost uncertainty increases or cost uncertainty in competitive chains decreases, chains should order more products
Chen et al. [62]	Operational risk and uncertain demand	The impact of uncertain demand on original equipment manufacturers (OEMs) and original design manufacturers (ODMs)	Multi-stage model with external demand and product substitution degree as uncertain variables	The impact of uncertain demand and different risk attitudes on business outsourcing is revealed	When the OEM is sufficiently risk-averse, the party’s preference for pricing timing remains the same
Chen et al. [63]	Degree of substitution and external demand	How risk attitudes affect outsourcing leadership preferences in uncertain demand	Using confidence level from uncertainty theory to portray the risk attitudes	Focuses on the effect of risk attitudes of OEMs and their CCMs on leadership/following incentives	When both OEMs and CCMs are willing to take the lead, wholesale prices and outsourcing to CCMs are relatively low
Liu et al. [64]	Demand and product evaluation	A two-stage pricing and strategy selection problem for an SC under uncertainty	Profit risk level is proposed to describe the profit risk under double uncertain information	The introduction of decision-makers’ risk attitudes into two-stage dynamic pricing	The profits of supply chain participants increase with the level of supply chain profit risk
Farham-Nia and Ghaffari-Hadigheh [65]	Environmental Uncertainty	The optimal pricing for SCs with dual distribution channels under centralized and decentralized decision systems	Two-stage optimization, the Stackelberg game and the Bertrand-Nash game	Combine uncertainty theory with game theory for the pricing of SC distribution systems	In both centralized and decentralized SCs where manufacturers predominate, retail services play a vital role
Liu et al. [66]	Demand	The implementation of a green strategy by retailers in cooperation with suppliers under uncertainty	A model based on the profit risk level of retailers (PRLR) for different levels of service market reliability	Decision-makers’ risky attitude is introduced into the green strategy implementation problem	For a specific PRLR, the ideal order quantity for a non-green (green) product is not exactly equal to its market demand
Chen et al. [67]	Marketing cost and demand	Problem of optimal sales for a provider providing the same good to two rival shops	Uncertainty theory and game theory-based modeling	The cost of trust in retailers and the size of trust in the market in the SC are proposed	The higher the risk level, the lower the trust cost for the retailer
Chen et al. [68]	Demand and manufacturing and sales effort cost	Pricing and effort decision problems in SCs under uncertain information	Game models are developed based on the expectation criterion	Considering an SC with sales effort and price-dependent demand	Pricing and effort decisions are significantly impacted by how uncertain sales effort elasticity is
Huang and Ke [69]	Manufacturing costs, selling costs, and demand	The pricing decision problem of substitutable products under different power structures	Uncertainty theory and game theory-based modeling approaches	A study of pricing decision problems based on uncertainty theory	If the cost of goods sold is higher, consumers can enjoy lower prices in the face of powerful retailers
Ke et al. [70]	Recycling costs, remanufacturing costs, and demand	The closed-loop SC pricing issue with two rival risk-averse retailers under uncertainty	The objective function of a risk-sensitive retailer is described by an opportunity constraint function	How the degree of parameter uncertainty affects channel members’ pricing and remanufacturing decisions	Both stores will experience lesser profitability if either of the two retailers becomes more risk-averse
Chen et al. [71]	Demand status and production costs	Supplier encroachment is examined from SC members’ attitudes toward risk and upstream production investment	Confidence level is used to describe risk attitude	Consider the impact of supplier investment and uncertainties on reducing production costs and supplier encroachment	Where upstream investment and spillover effects exist, suppliers and retailers can benefit from encroachment strategies at the same time
Chen et al. [72]	Cost and demand	Study whether e-retailers and manufacturers can agree on the introduction of a marketplace channel	Manufacturers’ and e-tailers’ different risk aversions are described by the uncertain sales cost and confidence level	To completely consider the uncertainty brought on both demand and cost, a new risk management method is presented	Manufacturers and e-retailers are less willing to develop online markets as players become more risk-averse.
Ke et al. [73]	Demand, costs, and market size	The pricing decision problem of a dual-channel SC	Uncertain two-level planning model	Consider the impact of the power structure and parameters uncertainty	The existence of dominance will reduce the profitability of the entire SC
Chen et al. [27]	Operational risk	Addressing the choice of sourcing strategy for multinational companies	Game model of MNC and OEM under different sourcing structures	Consider the local sourcing strategies of multinational companies under tax policies and uncertain business risks	As MNCs become more risk-averse and non-refundable VAT rates increase, MNCs’ sourcing strategies will move from consignment to control and then back to consignment
Zhao et al. [74]	Production costs	The effect of uncertain production costs on optimal decisions and expected profits under the centralized and decentralized decision-making	Uncertainty is modeled using the scatter of the mean-holding distribution	For the first time, incomplete contracts are used for coordination	Production cost uncertainty favors centralized supply chains
Ma et al. [75]	Market	Choosing between two risk-sensitive manufacturers whose products are distributed to the same market by a single, dominant retailer	Opportunity-constrained planning model	Provides some important management insights on how risk-averse managers of SMEs can manage risk in an uncertain market environment	The impact of the risk sensitivity depends primarily on estimated demand, and manufacturing costs vary with the risk sensitivity level

shows the results of the value distribution of UAO based on the authors’ names, uncertainty conditions, research objectives, modeling methods, research gaps and contributions, and research results. The finding in this table indicates that 19 papers applied the UAO method in the general SCM, and most of them used confidence levels for uncertainty analysis and decision modeling. The information for all articles published in the field of general SCM is included in Table 4.

5.2. Distribution Papers Based on Sustainable SCM

The most common definition of SSCM is the process of managing SCM activities while considering environmental, economic, and social challenges to advance the long-term financial objectives of specific enterprises and their SCs [76]. Green SCs are closely related to environmental issues in SSC, and many scholars have studied the optimization of Green SCs in an uncertain environment.

Among the articles in this field selected for this study, Refs. [77,78,79,80,81,82,83,84,85] applied uncertainty methods based on uncertainty theory. For example, Shen [79] studied a two-level Green SC network in an uncertain environment where the market base, customer demand, production cost, and sensitivity to price are assumed to be uncertain variables. A food SSC network that considered the three facets of sustainability (economic, social, and environmental) was designed by Krishnan et al. [82] using an integrated resilient multi-objective optimization model while considering the perishability of the food SC, the valuing of food waste, and the uncertainty of supply.

Refs. [85,86,87,88] applied an uncertainty method based on fuzzy set theory. In these, Zhang et al. [85] focused on social aspects, the effectiveness of relief efforts, and financial costs. For the problem of designing a sustainable last-mile relief network in the face of partial probabilistic uncertainty, a multi-objective distributed RO model is designed. For the pharmaceutical SCND problem in uncertain environments, Zahiri et al. [86] came up with a new multi-objective integrated sustainable-resilient mixed integer linear programming model.

Refs. [89,90,91] applied uncertainty method based on probability theory. To study the impact of uncertainty on decision variables in SSCs, Shen [89] developed a multi-objective opportunity constraint model under uncertainty scenarios. Jabbarzadeh et al. [90] put forward a delayed strategy with the RO model for efficient Green SC planning. Kazancoglu et al. [91] examined the reactivity of sustainable GSCs during the COVID-19 pandemic while concentrating on the resilience of sustainable (GSCs) to prevent disruptions brought on by epidemics like COVID-19.

For the literature cited above and previous articles,

Table 5. Distribution papers based on sustainable SCM.

Author(s)	Uncertainty	Study Purpose	Modeling/Method	Research Gap and Contribution	Results and Outcomes
Gao and Zhang [77]	Demand	Pricing, greenness and sales effort decisions in green SCs under demand uncertainty	Expected value model	Provides some management insights into pricing, greenness and sales effort decisions for an SC under uncertain demand	Greenness factor and sales effort factor have a positive effect on pricing, greenness and sales effort
Ma et al. [78]	Shipping costs, demand and return rates	The design of a multi-scenario CLSCN under uncertainty conditions and a robust mean CVaR criterion	A new distributed RO model for multi-product, multi-stage CLSCN	The model uses a flexible network allocation strategy	The model can effectively balance the expected cost and CVaR
Shen [79]	Market base, demand, price sensitivity	The problem of a two-level green SC network under an uncertain environment	A retailer-led bargaining expectation game model under revenue-sharing contracts	Consider joining a revenue-sharing pact to better coordinate the green SC network	Revenue-sharing contracts significantly increase greening and reduce retail prices
Gao and Zhao [80]	Product requirements	Solving the green SC pricing problem under uncertainty considering extended warranty services	Confidence-based decision rules	The study provides some management perspectives on the greening of the two-stage green SC, extended warranty service levels and pricing issues	The cost-sharing ratio is positively impacted by the extended warranty service cost rate and the greening investment factor
Eskandari-Khanghahi et al. [81]	Environmental uncertainty	Improve the blood supply chain while taking the network’s overall social and environmental impact into account	Multi-period mixed integer SCND model	Integrate sustainability into the decision-making process	The proposed solution algorithm obtains acceptable solutions in almost all cases
Krishnan et al. [82]	Supply uncertainty	Studying Robust Optimization of Sustainable Food Supply Chain Networks with Food Waste Valorization and Supply Uncertainty	Integrated robust multi-objective optimization model	Providing a robust MOMILP model to that simultaneously considers economic, environmental and social sustainability dimensions	The results of robust optimization models can help decision-makers to make extra efforts to address uncertainty
Belhadi et al. [83]	Sustainable performance of supply chain partners	The behavioral tendencies of supply and demand sides under complexity and uncertainty	A theoretical framework based on three behavioral motivators	Improved the discussion of sustainable governance by offering a comprehensive understanding of behavioral factors	Positive relationship experiences help increase trust
Ahmed and Sarkar [84]	Resource consumption, residual biomass production in agricultural regions and market center demand	Develop a supply chain model to minimize the total cost to meet the uncertain demand at the center of the market	The model is built by making these parameters uncertain and expressing them as fuzzy numbers	The proposed sustainable distribution of second-generation biofuel supply chains enables decision-makers to minimize the total cost and carbon emissions	Model is feasible for second-generation biofuel supply chain design under uncertainty
Zhang et al. [85]	Five types of uncertainty in the last mile network	Solve last-mile relief network design problems	Multi-objective distributed RO model	Established the equitable distribution of disaster relief networks	The difficulty of designing the last-mile disaster assistance network incorporates sustainability, resilience, and reliability
Zahiri et al. [86]	Environmental uncertainty	A sustainable and resilient pharmaceutical SCN integration design approach for multi-stage planning in an uncertain environment	A new fuzzy possibility-random programming method	A new multi-stage pharmaceutical network design is proposed that includes strategic and tactical decisions	Where fixed costs exceed variable costs, increasing the number of distribution centers will result in an increase in total costs
Pei et al. [87]	Demand with vague uncertainty	The dual-channel green SC pricing decision problem with market size uncertainty	Robust pricing game model	Combining RO and game theory applied to the pricing decision problem of a dual-channel green SC	A direct channel is not always lucrative for manufacturers but always advantageous for retailers when market is uncertain
Fazli-Khalaf et al. [88]	Uncertainty of unexpected events	Designing a sustainable and resilient CLSCN through real-life case studies	A new hybrid fuzzy possibility flexible programming method	A method to achieve network resilience by extending the effective demand coverage plan is proposed	The objective function assessing greenness is primarily influenced by the network’s decentralization and tire supply chain cost
Shen [89]	Costs, environmental impact and social benefits	The impact of uncertainty on SC sustainability and how to develop optimal SC strategies under uncertainty	Multi-objective opportunity constraint model	On the basis of binary mapping patterns and variable-length chromosomal coding, an effective mixed integer genetic algorithm is developed	Decision-makers should think about using greater resources to cope with uncertainty in the system when confidence levels are high
Jabbarzadeh et al. [90]	Demand	The impact of decision-makers’ risk appetite and deferral strategies on the trade-off between economic and environmental goals	Bi-objective RO model	Incorporates delay strategies into SC planning	Deferral strategies can provide ongoing cost savings to the SC
Kazancoglu et al. [91]	Uncertainty due to unexpected events	Focus on the resilience of sustainable GSCs to avoid disruptions caused by pandemics	Partial least squares (PLS) model	Explain the connections between a few concepts in the context of power transition theory and dynamic capacities	SC flexibility directly affects agility

displays the results of the significant distribution of UAO based on author name, uncertainty condition, research purpose, modeling methods, research gap and contribution, and research results. This table reveals that 16 articles utilized the UAO approach in the SSCM. Table 5 provides additional information on the articles published in the SSCM field.

5.3. Distribution Papers Based on Supply Chain Network Design

SCND is one of the most critical planning problems in SCM. SCND under uncertainty has received considerable attention from both theoretical and practical communities in recent years [92]. To design SCN under uncertainty, numerical optimization processes based on SC objectives often consider single or multiple objectives. In this section, we address UAO in SCND in terms of mathematical models, solution approaches, and optimization techniques, mainly including SCND problems with continuous stochastic parameters, risk measures in the context of SCND, RO in the context of SCND, fuzzy mathematical planning in SCND environment, and SCND optimization methods with interruptions.

Among the articles in this field selected for this study, Govindan et al. [92] explored existing optimization techniques for dealing with uncertainty, such as recourse-based stochastic programming, risk-averse stochastic programming, robust optimization, and fuzzy mathematical programming in terms of mathematical modeling and solution approaches.

Refs. [93,94,95,96,97,98] applied uncertainty method based on uncertainty theory. For example, Tirkolaee et al. [94] attempted to optimally a multilevel blood SC under uncertainty in demand, capacity, and blood disposal rates. Yan and Ji [96] developed an uncertainty planning model to design a three-level SCN with disruption risk, where disruptions are considered uncertain events. There are also studies that consider both stochastic planning and RO methods.

Refs. [99,100,101,102,103,104,105,106] applied uncertainty method based on fuzzy set theory. In these, Salehi et al. [103] used the optimization approach to design a resilient and sustainable bioenergy supply network based on the uncertainty of bioenergy demand and the disturbance of biorefineries. Yang and Liu [98] studied the SCND problem under uncertainty, where both customer demand and transportation cost are characterized by fuzzy variables with known likelihood distributions.

Refs. [107,108,109,110,111] applied uncertainty method based on probability theory. For the SCND problem under uncertainty, Yang and Liu [109] constructed a new equilibrium optimization method. The approach uses probability and likelihood distributions to describe the unknown transportation costs and client demand, respectively.

Based on the above discussion,

Table 6. Distribution papers based on supply chain network design.

Author(s)	Uncertainty	Study Purpose	Modeling/Method	Research Gap and Contribution	Results and Outcomes
Govindan et al. [92]	Uncertain environment	A review of research on RL network design and SCM in uncertain environments	Stochastic planning, risk-averse stochastic planning, RO, and fuzzy mathematical planning	SCM aspects and optimization techniques in the field of supply chain and reverse logistics (RL) network design under uncertainty	Solving reliable and resilient SCN under the risk of disruption will be a promising future research direction
Tan et al. [93]	Retailer demand and operating costs	A new model for SCND based on different decision criteria under mixed uncertainty	Expectation cost minimization model, β-cost minimization model, opportunity metric maximization model	Three models of the SCND problem under mixed uncertainty environment are developed	Different decision criteria can result in significantly different SCNDs
Tirkolaee et al. [94]	Demand, volume, and blood disposal rates	Optimally configure a multi-echelon blood SC network under uncertainty	Bi-objective mixed integer linear programming model	A new fuzzy optimization model was introduced to determine the optimal blood SCND variables	The approach used can handle both the bi-objective nature of the model and the uncertainty
Dehghani et al. [95]	Uncertain environment	Design and planning photovoltaic cell supply chain (PVSC) under uncertainty	Data envelopment analysis (DEA) and a two-stage approach to RO models	A two-stage optimization method based on DEA and RO model is proposed to integrate the strategic and tactical decisions of PVSC	The mean and standard deviation of the proposed robust model are better when the electricity demand shortfall is within the acceptable range
Yan and Ji [96]	Interruption uncertainty	Designing a three-tier SCN with risk of disruption	Uncertain nonlinear mixed integer programming model	Proposed a combination of multi-backup and cross-echelon transport strategies	Lagrangian relaxation algorithm for solving linearized models and genetic algorithm for solving simplified models are proposed
Peng et al. [97]	Information uncertainty in big data	The study of SCN’s retail optimization and transportation planning under uncertainty	Uncertainty optimization models under different carbon control policies	Uncertainty theory is used to deal with uncertainty in big data information	Cap-and-trade regulations can aid businesses in cutting expenditures overall and carbon emissions
Diabat et al. [98]	Interruption uncertainty	Study the problem of designing a network of perishable SC for reliability and disruption	Bi-objective RO model	Fills the gap from the SCND perspective on the impact of disruptions on the timely and cost-effective delivery of perishable products during disasters	As base models and communication issues increase, the time to deliver products to customers becomes longer
Yang et al. [99]	Shipping costs and customer demand	Solving multi-objective SCND problems under uncertainty	Two-stage optimization approach	Combining the approximation method and multi-objective biogeography-based optimization method	The main benefits of using the proposed multi-objective optimization approach can help companies reduce costs
Ghahremani-Nahr et al. [100]	Demand, return rates, transportation costs, raw material prices and shortage	Designing facility siting/distribution models under s uncertainty	Mixed integer nonlinear programming (MINLP) model	A new WHALE optimization algorithm is proposed for the model built is the NP-hard model	The algorithm can find the approximate optimal solution in a reasonable computation time
Tavana et al. [101]	Demand	Designing sustainable CLSC networks	Multi-objective mixed integer linear programming (MOMILP) model	Developed an integrated MOMILP model for designing and optimizing sustainable CLSC networks	The proposed model has validity and logical performance
Hosseini-Motlagh et al. [102]	Electricity demand	Studying uncertainty in the design of resilient and sustainable power SCN	Multi-objective RO model	A new fuzzy robustness method is proposed	The proposed multi-objective framework achieves increased resilience and CSR
Salehi et al. [103]	Bio-energy demand	Designing a resilient and sustainable bio-energy supply network	Multi-criteria decision-making method	A single-objective model that considers resilience and sustainability indicators	The proposed model has important applications in improving the performance of biomass SC
Yang and Liu [104]	Shipping costs and customer demand	Study the SCND problem under uncertainty	Two-stage mean-risk fuzzy optimization method	A new two-stage average risk SCND problem is proposed	Larger gains were obtained by solving the two-stage mean-risk SCND problem
Dotoli et al. [105]	Uncertain environment	Research on the SCND method under uncertainty	Fuzzy linear integer programming model	An SCND approach is proposed to maximize the overall efficiency of the SCN under uncertainty, considering possible price discounts	The proposed approach allows for solving the SCND problem of make-to-order production
Farrokh et al. [106]	Mixed uncertainty	RO framework for CLSCND using robust method under mixed uncertainty	Mixed integer programming model	A new robust fuzzy SO by extending the RO method to a fuzzy scenario-based SO model	The model is better at reducing the total variability as the optimal robustness measure
Lim et al. [107]	Demand	Design a responsive SCN considering the agility of the system	Programmatic modeling approach	A programmatic modeling approach is used to study the optimal network design problem under two inventory-sharing models	When the agility dimensions are jointly optimized, it is optimal to allocate more distribution centers (DCS) and each DCS to handle smaller demand volumes when the cost per unit of shortage penalty increases
Cheng et al. [108]	Shipping costs and customer demand	Discuss the influence of international factors on siting decisions	Transformation of the model into a mixed integer programming using the sample approximation method	An uncertain global SCND model with rules of origin (ROOS) and finite import quota is proposed	ROOs and limited import quotas can affect the optimal choice of factory and distribution center locations
Yang and Liu [109]	Shipping costs and customer demand	Study of equilibrium SCND under uncertainty	The optimization model introduces combined service level constraints and cost-risk level constraints	A new method is proposed for dealing with plausibility constraints based on dominance sets and valid inequalities	The corresponding plausibility-constrained planning of the initial equilibrium SCND model is developed
Ghomi-Avili et al. [110]	Demand	Designing a green competitive CLSC network considering demand uncertainty under disruption risk	Robust two-layer model	Bridging the research gap in the design of competitive CLSCN in mixed uncertainty environments	Percentage of total loss requirements is reduced by reducing the risk of disruption
Hosseini-Motlagh et al. [111]	Supply, demand, costs and climate	Optimizing the total cost of wheat SCND	Robust model	The proposed mathematical model considers the various dimension, seeking to minimize the total cost of the network	Robust models yield better results at all levels of perturbation and reliability

shows the results of the significant distribution of UAO based on author names, uncertainty conditions, research objectives, modeling methods, research gaps and contributions, and research results. The result provided in this table indicates that 21 previous studies used UAO in the area of SCND. The information in Table 6 pertains to articles published in the field of SCND.

5.4. Distribution Papers Based on Emergency Network Optimization

Emergency SCM is the process of planning and executing the efficient and cost-effective transportation of supplies (including food, water, medicine, etc.) from the place of production to the disaster zone for effective distribution and application to the affected population in the face of disasters and uncertain environments. Emergency SCM is a vital component of the emergency management system for public health emergencies and the prerequisite for constructing a flawless emergency management system.

Among the articles in this field selected for this study, Refs. [112,113,114,115,116,117,118] applied uncertainty method based on uncertainty theory. For example, Li et al. [112] employed uncertainty planning methods to deal with the medical material dispatching problem in emergency events. Zhang et al. [116] investigated the site-routing issue for a sustainable multi-depot emergency facility. Using uncertainty theory, an uncertain multi-objective emergency response site-route planning model that considers travel time, emergency response costs, and CO₂ emissions is developed.

Refs. [119,120,121] applied uncertainty method based on fuzzy set theory. In these, Wang and Sun [119] established a multi-cycle homogeneous procurement optimization model under uncertainty to obtain optimal emergency supply deployment. Zhu et al. [121] put forward a collaborative optimization model based on a comprehensive evaluation framework for emergency supply suppliers using interval type-II fuzzy sets for the uncertainty and fuzziness of disaster relief information.

Refs. [122,123,124,125,126] applied uncertainty method based on probability theory. Vaezi et al. [123] investigated the design of emergency networks for railroad hazardous materials transportation under uncertainty and proposed a two-stage stochastic planning model to determine the storage locations of response facilities and equipment packages. Song et al. [125] investigated the SC operation of rescue equipment in disaster relief under demand uncertainty. The goal is to minimize total and peak delays in product delivery within a multi-period plan.

Based on the above literature and previous papers,

Table 7. Distribution papers based on emergency network optimization.

Author(s)	Uncertainty	Study Purpose	Modeling/Method	Research Gap and Contribution	Results and Outcomes
Li et al. [112]	Demand and runtime	Handling medical supplies dispatch in emergencies	Uncertain planning methods	Introducing uncertainty planning as a new tool for dealing with real-world uncertainties	The designed algorithm has good robustness to the parameters set in the genetic algorithm
Dalal and Üster [113]	The location and intensity of the disaster	A challenge in designing emergency response networks that incorporates the relief (supply) and evacuation (demand) sides	Stochastic planning framework	Decision models with data uncertainty are treated with SO and RO by weighting the relevant cost components	The impact of changing parameters on shelter siting decisions depends on the variability between potential demand and scenarios
Rahmani [114]	Demand uncertainty and disruption risk	Study of dynamic emergency blood network design issues	RO method	Capture the relationship between disruption and changes in blood demand	Discrete-continuous hybrid approach solved the disruption and uncertainty
Zhang et al. [115]	Response time and node requirements	Application of uncertainty theory to study the siting of emergency service facilities under uncertainty	Uncertain site-set coverage model, ($\alpha$, $\beta$)-maximum coverage siting model, and α-opportunity maximum coverage siting model	Models further improve the ability to model and solve emergency services facility siting problems under uncertainty	The relationship between the ($\alpha$, $\beta$)-maximum coverage siting model and the α-opportunity maximum coverage siting model is given
Zhang et al. [116]	Trip times, emergency response costs and CO2	Sustainable multi-warehouse emergency facility siting-routing problems with uncertain information	Multi-objective emergency response site-selection path planning model	A hybrid intelligent algorithm is designed considering real-time, economy and CO2 emission	Solved the problem of siting paths for sustainable multi-bank emergency facilities with uncertain information
Boutilier and Chan [117]	Travel time	Optimizing the location and routing of emergency response vehicles	RO method	The model offers a broad foundation for travel time uncertainty based on edges	In comparison to typical ambulance vehicles, a fleet of miniature ambulances could perform substantially better
Zhang et al. [118]	Time-varying demand, and the state of the associated transport network	Provide a new optimization model to provide by balancing response capacity and total response cost	Dynamic multi-objective triage distribution location path model	Considers the interrelationship between the decision-making environment and emergency response	The model supports a practical emergency response to large-scale oil spill incidents
Wang and Sun [119]	Fuzzy random information, road network destruction and other uncertainties	Development of a risk metric for multi-cycle material allocation and road rehabilitation under uncertainty	Optimization model for multi-cycle homogeneous procurement under uncertainty	A risk measure for path transportation risk and road network rehabilitation risk during multi-cycle emergency material deployment is designed	The proposed risk measurement method can effectively measure the multi-cycle transportation risk and route rehabilitation risk
Zhang et al. [120]	Demand	Design emergency relief networks for responding to disasters under uncertainty	Distributed RO (DRO) model	Uncertainty requirements are described by fuzzy sets based on mean, mean absolute deviation and support sets	The out-of-sample performance of the proposed DRO model is better
Zhu et al. [121]	Relief information	Evaluation of emergency supplies suppliers to optimize logistics operations	A collaborative optimization model	A dynamic collaborative decision-making model based on interval binary trapezoidal fuzzy set EMR is proposed	The proposed optimization method can optimize the emergency material plan
Fazli-Khalaf et al. [122]	Practical applications	Designing a blood SCN for emergencies	Robust possibility flexible chance constraint planning (RPFCCP) and possibility flexible chance constraint planning (PFCCP) models	Considers laboratories and hospitals in the blood SCN to design the most efficient blood SC	The PFCCP model can handle the uncertainty of the objective function parameters and constraints more effectively
Vaezi et al. [123]	Hazardous material events	Identify storage locations for response facilities and kits	Two-stage SO model	For the first time, the unique characteristics of hazardous railroad materials transportation are incorporated into academic research incidents	Decisions on the design of strategic emergency response networks based primarily on empirical evidence will compromise the network’s efficacy
Liu et al. [124]	Uncertainties inherent in medical services (EMS) systems	Assist disaster relief planners with the construction of long-term EMS systems	A distributed robust model	The study represents the first time that DRO has addressed the location and size of an EMS station	The DRM obtains higher reliability in terms of the performance of the solution method
Song et al. [125]	Demand	The SC operation of rescue equipment in disaster relief in the context of a practical application	Optimization model to minimize the total delay in delivering rescue kits	The impact of different SC flexibility on SC demand satisfaction is examined	Increased SC flexibility can significantly reduce delays in the delivery of relief tools
Ke et al. [126]	Possible disruptions to emergency facilities and road links	The impact of possible system disruptions on the performance of hazardous materials emergency logistics systems	Two mixed integer programming models are developed using a two-stage RO approach	First attempt to incorporate multi-facility, multi-link random interruptions into system development	Determine emergency response facilities’ locations and their capacities for a variety of scenarios quickly

provides valuable information about UAO based on the authors’ names, uncertainty conditions, research objectives, modeling methods, research gaps and contributions, and research results. The result of Table 7 shows that 14 scholars have conducted research on UAO in the field of emergency network optimization in the past. Table 7 provides some highlights of published research in the area of emergency network optimization.

5.5. Distribution Papers Based on Logistics Network Optimization

Logistics network optimization plays a crucial role in modern logistics planning and SCND [127]. Logistics managers may greatly increase the effectiveness of the overall freight transportation system and more effectively and promptly meet the needs of their clients with the help of well-designed transportation and logistics networks. Many scholars have studied issues related to logistics network optimization, including sustainable logistics network design issues, RL network design, collaborative logistics network design], and transportation problems.

Among the articles in this field selected for this study, Refs. [128,129,130,131,132,133] applied uncertainty method based on uncertainty theory. For example, Govindan and Golizadeh [128] studied the robust network design of a sustainable, resilient RL network based on big data using end-of-life vehicles as an example. Chen et al. [131] examined a class of uncertain two-particle solid transportation problems, where supply demand, transportation capacity, transportation cost, and transportation time are considered uncertain variables. Based on the two types of methods for ordering uncertain variables, an expectation value objective planning model and an opportunity-constrained objective planning model for the two-particle solids transportation problem are developed, respectively.

Refs. [134,135,136,137] applied uncertainty method based on fuzzy set theory. In these, a new scenario-based resilient bi-objective optimization model for logistics networks was developed by Sun et al. [133]. It incorporates the placement of medical facilities, the transfer of casualties, and the distribution of aid materials while taking triage into account. Gupta et al. [137] explored the multi-objective optimization of a multi-product SCN logistics problem in an intuitionistic fuzzy environment to optimally obtain the best distribution order for products from different sources and destinations.

Refs. [138,139,140,141,142] applied uncertainty method based on probability theory. In order to help decision-makers select the best collaborative logistics network design option under uncertainty, Xu et al. [140] suggested a general two-stage quantitative methodology. Jiang et al. [141] investigated the problem of designing regional multi-modal logistics networks with CO₂ reduction targets and uncertain demand in the context of urban cluster development.

Based on the above literature and previous papers,

Table 8. Distribution papers based on logistics network optimization.

Author(s)	Uncertainty	Study Purpose	Modeling/Method	Research Gap and Contribution	Results and Outcomes
Govindan and Gholizadeh [128]	Location uncertain	To study the physical and uncertain locations where information between RL facilities has big data characteristics	Robust model optimization	Recycling technology options and reuse concepts for end-of-life vehicle RL and their corresponding social impacts	Organizational cost savings can be achieved by optimally planning the center’s capabilities
Yang et al. [129]	Multiple Uncertainties	Study of type II uncertain variable approximation method and their application to the solid transport problem	Approximate expectation value model with opportunity constraint	Give a definition of type II uncertainty variables by introducing a generalized uncertainty measure	The suggested method converts the mathematical model into a reduced expectation value model with chance limitations
Zhang et al. [130]	Supply, demand, transportation capacity, direct and fixed costs	Study the problem of transporting fixed-charge solids under uncertain conditions	Expected value, time-constrained planning, and metric opportunity planning models	A hybrid intelligent algorithm for solving near-optimal solutions is proposed	Uncertainty theory is an effective method for dealing with uncertain parameters
Chen et al. [131]	Supply, demand, transportation capacity, transportation costs and transportation time	Study of an uncertain class of two-particle solid transport problems	Expectation value objective planning model and opportunity-constrained objective planning model	The total transportation cost and total transportation time are considered	The expected value and opportunity-constrained models can be transformed into corresponding deterministic equivalence models, respectively
Shen and Zhu [132]	Demand, supply, availability, fixed costs, and transport volumes	A class of two-level fixed charge transport problems under uncertainty to maximize total profit	Expected value, opportunity constraint, and measured opportunity models	Considering more realistic and important factors	The suggested technique is effective in finding a close-to-ideal solution
Sun et al. [133]	The risk of disruption	Optimize the humanitarian logistics network	Robust scenario-based bi-objective optimization model	The possibility of medical facilities being disrupted in crisis scenarios is considered	More casualties can be accommodated in open temporary hospitals and medical facilities
Hashemi [134]	Uncertain environment	Integrated design of multi-objective models for RL networks using fuzzy mathematical planning	Mixed integer linear programming model	Simultaneously use two meta-heuristics and compare the results	The swarm algorithm is better able to explore and extract feasible solutions for the region and obtain near-optimal answers
Gong and Zhang [135]	The quality of earnings	A pricing and RL network design problem with return quality uncertainty	Distributionally robust risk aversion model	The first use of price-dependent fuzzy degree sets to describe quality uncertainty	The robust distribution model can effectively hedge against high uncertainties
Du et al. [136]	Fuzzy environment	Study of hazardous materials transportation to minimize risk to life, travel time and fuel consumption	Fuzzy multi-objective planning model	A fuzzy multi-objective planning model for the transportation of hazardous chemicals	The model is valid, and the hybrid intelligence algorithm is stable and convergent for large-scale problems
Gupta et al. [137]	Intuitive blurred environment	Obtain the best distribution order for products	Fuzzy goal planning (FGP) method	The company to follow a structured approach to shipping and distributing orders from multiple sources to destinations	The results obtained give the optimal quantities to be transported from different sources to different destinations
Yang and Chen [138]	Supply	Arguing that the robustness of RL network can be improved and modeled for decision-making by acquiring facility capacity	RO method	A new RO model is proposed	The model can adjust the robustness of the RL network
Shahparvari et al. [139]	Uncertain SC	Redesigning sustainable RL network in uncertain SC	Robust stochastic optimization model	A sustainable RL optimization model is developed for minimizing carbon emissions	Determine the optimal flow of products by using chance constrained robust
Xu et al. [140]	Discrete uncertainty	Investigation of a novel approach to solve CLNDOP resource combination problems with discrete uncertainty (DU-CLNDOP)	Expectation value model with robust constraints	A generic two-stage decision framework is proposed to solve DU-CLNDOP	Allows decision-makers to select the best CLN design option in uncertain situations
Jiang et al. [141]	Demand	Design of regional multimodal logistics networks with CO2 reduction targets and uncertain demand	Tunable RO method	A new two-layer planning model is developed	The proposed method is an effective way to solve the problem of designing regional multimodal logistics networks with uncertain demand
Gao et al. [142]	Fixed charges and transportation costs	The design of a frequency service network in a rail freight system with uncertain fixed and transport costs	Budget constraint model and possibility constraint model	Uncertain variables are introduced in the rail freight model to describe transportation costs and fixed charges	An algorithm for calculating the distribution function is proposed

shows valuable information about the UAO model based on the authors’ names, uncertainty conditions, research objectives, modeling methods, research gaps and contributions, and research results. The result of Table 8 shows that 15 papers have studied UAO in the field of logistics network optimization in the past. Table 8 provides some highlights of the published research in the area of logistics network optimization.

5.6. Distribution Papers Based on Closed-Loop SCM

CLSCM refers to all forward logistics in the SC (e.g., material procurement, production, and distribution) and RL in collecting and disposing of returned (used or unused) products and/or product components to ensure socioeconomic and ecologically sustainable recovery [143]. In the last decade, CLSCM has attracted considerable attention from industry and academia.

Among the articles in this field selected for this study, Refs. [144,145,146,147,148,149,150,151] applied uncertainty method based on uncertainty theory. For example, Goltsos et al. [144] and Peng et al. [145] conducted review studies of the literature related to CLSC and uncertainty. Goltsos et al. [144] conducted a systematic review of the literature in the field of CLSC dynamics in uncertain environments, which investigates how material and information fluxes interact over time in the various supply chain components for remanufacturing. Peng et al. [145] reviewed earlier research on uncertainty in the fundamental properties of CLSCs, examined the factors that contribute to uncertainty at different stages of production and chose the most effective methods to measure its effects.

Refs. [152,153,154] applied uncertainty method based on fuzzy set theory. In these, Kisomi et al. [152] built an integrated mathematical planning model based on RO theory to address the uncertain environment in these two problems. Considering global factors such as exchange rates and tariffs, Amin and Baki [154] developed a mathematical model of a CLSC. The model is a mixed integer linear programming model with several objectives and uncertain demand. SC integration and supplier selection are two important strategic decision problems in SCM.

Refs. [155,156,157,158,159,160,161,162] applied the uncertainty method based on probability theory. Gholizadeh et al. [156] studied a multi-layered CLSC for a disposable appliance recycling network, using discrete stochastic situations with uncertainty in demand and cost parameters. Dutta et al. [160] constructed a recycling framework using buy-back offers at the retailer level. For the purpose of helping to meet the minimum recycling requirements established by legislators and reduce the overall cost of the integrated system, the suggested recycling framework is combined with a multi-period CLSC optimization model with uncertain demand and capacity to determine the best recycling price to offer to consumers.

Based on the above statements about the field of CLSCM,

Table 9. Distribution papers based on closed-loop SCM.

Author(s)	Uncertainty	Study Purpose	Modeling/Method	Research Gap and Contribution	Results and Outcomes
Goltsos et al. [144]	Demand, and control uncertainty	A systematic review of developments in the field of CLSCs in the literature	Forecasting, collection, inventory and production control provide ways to reduce uncertainty	Considering the practical challenges faced by SC managers, and suggesting avenues for future research	Present a structured review of the current state of knowledge in the CLSC field
Peng et al. [145]	Uncertainties	To study the characteristics of CLSC with previously inherent uncertainties	Integrating uncertainty factors, methods and solutions into one analytical framework	Analyze the root causes of different uncertainties and their impact on production	Uncertainty factors in RL/CLSC are identified
Kim et al. [146]	RL and demand	Develop a CLSC planning model	Mixed integer optimization model and robust correspondence model	The offsetting effect of different uncertainties is found	Collectors with low uncertainty have a positive impact on profits
Abdolazimi et al. [147]	Demand, returns and on-time delivery	Provide a model for developing and improving forward SC and improving overall SC performance under uncertainty	Mixed integer linear programming model	Considering uncertainty, supplier selection and the quality of the final product delivered to the customer	Supply chain modeling in terms of uncertainty and product quality to select the best supplier
Yan et al. [148]	The cost of manufacturing sales, retailer sales costs, etc	Study pricing and recycling strategies in a CLSC consisting of manufacturers, retailers, and third-party recycling centers	Decentralized pricing model	A pricing and recycling decision model for CLSC with different recycling channels in an uncertain environment	The recovery rates of all models remain constant
Yan et al. [149]	Costs, demand, manufacturers’ total carbon emissions, and the amount of recycled product	Research in CLSC pricing and recovery decision problems	Decentralized game model	Using game theory, three decentralized pricing models based on uncertainty theory are discussed	When the variance of the retailer’s cost of goods sold increases, the retailer can charge a higher markup price
Marcos et al. [150]	Supply, demand, control uncertainty, and environmental uncertainty	Identification of uncertainty in CLSC management of automotive lithiumion batteries	Uncertainties in CLSC in qualitative and quantitative form	Enable practitioners to develop a design and management approach for CLSC of lithiumion batteries for electric vehicles	Environmental uncertainty, in addition to closed-loop control and supply system uncertainty
Kisomi et al. [151]	Uncertain environment for SC and supplier selection	Research on SC integration and procurement management under uncertainty	Integrated mathematical planning model based on RO theory	Combining supplier selection with quantity discounting and CLSC network design	Enough to provide robust and stable solutions to overcome the inherent uncertainty of inexact parameters, thus saving significant costs
Tavakkoli-Moghaddam et al. [152]	Demand, cost factors, transit time and capacity constraints	Designing bidirectional facility networks in logistics networks under uncertainty	Fuzzy possibility planning and fuzzy multi-objective planning	Inclusion of supplier selection procedures where different levels of quality exist	Minimizes total costs as well as total defect, waste, and pollution generation rates
Gholamian et al. [153]	Some key parameters in the SC	Solving a multi-product, multi-cycle, multi-stage, large-scale sustainable CLSC model	Fuzzy multi-stage, multi-level, multi-objective mixed integer nonlinear programming (MOMINLP) model	For the fuzzy MOMINLP problem, a new interactive fuzzy planning method is proposed	The proposed fuzzy method is more effective than other available methods
Amin and Baki [154]	Demand	Mathematical model of CLSC network considering global factors such as exchange rates and tariffs	Multi-objective mixed integer linear programming model	The model considers global factors in the CLSC	Exchange rates and tariffs play an important role in the global CLSC network
Ghomi-Avili et al. [155]	Interruption risk	Build an optimization model to design a CLSCN	Multi-objective model	Consider disruption risk and uncertainty and investigate lateral transit strategies	A company can save money by increasing the use of lateral transfer strategies and collecting products returned from customers
Gholizadeh et al. [156]	Demand and costs	Maximize the value of returned products in the reverse network and manufactured products in the forward network	Combination of genetic algorithm and RO	The proposed genetic algorithm is slightly different from other algorithms in the literature	The model can effectively solve the problem of one-time appliance CLSCN
Krug et al. [157]	Demand, the amount of returned products and the time required to reprocess them	Help managers better assess risks and opportunities while determining SC design	Two-stage multi-cycle mixed integer planning	This paper introduces the R* criterion for the CLSC design problem, which assumes that decision-makers are pessimistic in the danger zone and optimistic in the opportunity zone to distinguish between danger and opportunity	The use of the R* criterion allows for better exploration of the opportunity domain without losing robustness control
Ghasemzadeh et al. [158]	Demand and returns	Develop a mathematical model of the tire SC in order to simultaneously consider the most practical factors	Mixed integer linear programming model	Developed a CLSCND formula that includes demand uncertainty and product return rates	The optimal CLSCND can be very different in terms of global factors
Xu et al. [159]	Demand and carbon prices	Designing a CLSC in a multi-cycle planning environment under a carbon trading mechanism	Two-stage stochastic model	The modeling strategy suggested in this study enables businesses to base their carbon trading decisions on the quantity of carbon credits	Stochastic models generate networks with capacity redundancy and can science changes in customer demand and carbon prices
Dutta et al. [160]	Demand and capacity	Propose a recycling framework using a buy-back strategy at the retailer level	Multi-cycle CLSC optimization model	Provides a proactive mitigation strategy for disruptions caused by manufacturing facility capacity uncertainty	There is a trade-off between the additional benefits generated by remanufacturing and the cost of acquiring the old product
Liao et al. [161]	Acquisition rates and market demand	Use collaboration between forward and reverse production streams to balance uncertain sourcing rates and market demand	Optimization model	Consider the rate of return and market demand are both stochastic and independent of each other	Despite low processing costs, remanufactured products do not necessarily mean greater cost efficiency
Gaur et al. [162]	Risks in the supply chain	Compare the impact of single versus multiple sources of new and modified products on SC profitability under potential SCD	MINLP model	The new product demand dynamics are explicitly considered when building the multi-source CLSC model	Multiple sources yield higher total profit compared to a single source

provides valuable information about the UAO method based on the authors’ names, uncertainty conditions, research objectives, modeling methods, research gaps and contributions, and research results. The result of Table 9 demonstrates that 19 scholars have applied UAO in CLSCM research in the past. Some of the key points from the published studies in the area of CLSCM are presented in Table 9.

5.7. Distribution Papers Based on Supply Chain Network Disruption during the COVID-19 Pandemic

Public emergencies have a significant impact on SCs, and the COVID-19 pandemic led to a huge impact and influence on economic trade in countries around the world. The issue of SC disruptions once again became a global concern. Scholars have studied SC disruptions in the context of the epidemic, and extensive research has been conducted into coping strategies for SCs.

Among the articles in this field selected for this study, Refs. [163,164,165,166,167,168,169,170,171,172] applied uncertainty methods based on uncertainty theory. For example, in a two-supplier-one-retailer SC setting, Gupta et al. [164] studied the impact of supply capacity disruption times on pricing decisions for alternative products. They derived optimal pricing strategies and order levels that considered both disruption times and product substitution. Rahman et al. [170] examined a consistent set of strategies and recovery plans to minimize costs and maximize the availability of necessary items to cope with GSC disruptions.

Ref. [173] applied an uncertainty method based on fuzzy set theory. In order to observe the elasticity of economic sectors and rank them using three predefined categories, Kan et al. [173] proposed using a new fuzzy method, VIKORSort.

Refs. [174,175,176,177,178,179,180] applied uncertainty methods based on probability theory. A two-layer optimization model was created by Timonina-Farkas et al. [174] that took demand uncertainty and production disruptions into account. This model took into account how opportunity limitations and dual probability service level demand affected the connection between demand distribution and production disruptions. Optimization models that consider production uncertainty and enable the identification of elasticity strategies are essential to mitigate SC disruptions. Liu et al. [176] investigated a new disruption propagation management problem for a multilevel SC with a limited intervention budget. The goal was to reduce the risk of interruption as determined by the SC’s target participants’ likelihood of disturbance.

Based on current literature and previously published articles on SCN disruption during COVID-19,

Table 10. Distribution papers based on supply chain network disruption during COVID-19.

Author(s)	Uncertainty	Study Purpose	Modeling/Method	Research Gap and Contribution	Results and Outcomes
El Baz and Ruel [163]	SC risk	Analyzing how SCRM functions in the context of the COVID-19 outbreak to reduce the effects of disruptions on SC robustness and resilience	Structural equation model	The findings help identify key processes that companies may deploy to improve the resilience and robustness of their SC	Explains how SCRM practices work as mediators and the crucial part they play in fostering SC resilience and robustness
Gupta et al. [164]	Supply interruption	The impact of supply disruptions on the ability to time alternative product pricing decisions for two suppliers in a retailer supply chain setting	Nash and Stackelberg game model	Helps explain the pricing behavior of firms under supply disruptions and provides recommendations for improving their operations	The number of orders affecting the supplier depends on the price leader
Dohale et al. [165]	Disruptive SC risks caused by natural or man-made activities	Identifying key operationalized barriers to the humanitarian supply chain (HSC) in India during the COVID-19 pandemic	Explanatory structural model (ISM) by merging neutrosophic methods	First research work to identify and analyze key barriers to HSC operation during COVID-19 in India	The most critical barriers during the COVID-19 outbreak are unlike other disruptions
Dohmen et al. [166]	SC disruption	Observe and find strategies to better understand disruptions	Experimental design and discrete-event simulation	Improve service and inventory performance during COVID-19 disruption	Decision changes have a greater impact on business continuity
Ghadir et al. [167]	SC risk	Exploring the impact of the COVID-19 outbreak on SC risk	To assess the discovered SCRs, a better failure mode and impacts analysis is proposed	A reliable multi-attribute decision method is proposed for evaluating the weight vector of the current SCR caused by the COVID-19 outbreak	Discussed how the COVID-19 outbreak affects SC risk as well as what the key SCRs are for the COVID-19 pandemic
Ramani et al. [168]	SC disruption	Explores how disruptions begin, propagate, and persist	Linear programming-based SC planning model	A programmatic analytical model was developed to illustrate how disruptions propagate over time	Interaction of external shocks and reactions of different participants in the SC prolong disruptions in the SC
Kähkönen et al. [169]	SC risk	Analyzing the impact of COVID-19 on capacity development and SC resilience improvement in the medical device industry	Dynamic capability view as a theoretical framework	Provides empirical evidence and theoretical insights into the impact of large-scale SC disruptions on firms’ dynamic capabilities and their impact on SC resilience	The impact of COVID-19 on a company’s upstream SC can affect a company’s ability to seize opportunities or eliminate threats
Rahman et al. [170]	SC disruption	Review a consistent strategy and recovery plan to minimize costs and maximize the availability of necessary items to respond to global SC disruptions	Agent-based modeling approach	Demonstrated how simulation-based methodologies can analyze and predict the impact of pandemic situations on SCs using simulation modeling software	By minimizing risk response time and maximizing production capacity, thereby reducing financial shocks to the business
Singh et al. [171]	SC disruption	Propose an action plan to address disruptions in the supply due to the pandemic	Simulation model of a public distribution system (PDS) network	Simulation models can help create a resilient food SC that adapts to changes in demand	The consolidation of warehouses helps to achieve demand fulfillment from alternate warehouses in the event of an outage at the assigned warehouse
Rozhkov et al. [172]	Uncertainty in the COVID-19 pandemic	To study the impact of the COVID-19 pandemic and the proactive mediation	Simulation model based on analytical model of perishable goods inventory control	The model combines three levels, which are not common in the operations management literature	Two-stage SC exhibit higher vulnerability in case of disruptions
Khan et al. [173]	SC disruption	Observe the resilience of the economic sector and perform ranking using three predefined classes	A novel approach to fuzzy VIKOR	No studies classify economic sectors based on SC disruptions	Rank the economic sectors based on severe, moderate, and low disruptions
Timonina-Farkas et al. [174]	Uncertainty in disruptions and demand distribution	Study the impact of limiting SC disruptions under uncertainty in demand allocation	Two-layer stochastic optimization model with chance constraints	An efficient numerical solution scheme combining a robust scenario reduction method and a customized Benders decomposition process is proposed	In the case of disruptions following a peak in demand, the optimality gap can be closed if the service level is reduced
Sundarakani et al. [175]	Cost and fulfillment, trade uncertainty, the risk of environmental trade-off	Examine the question of building or shifting distribution centers in the GSC in the face of uncertainty	RO and mixed integer linear programming (ROMILP)	For the first time, the sustainability dimension of global logistics corridors is examined and investigated from the perspective of global container transport	Along the planned global logistics corridor, the system offers optimality for all tested market situations
Liu et al. [176]	Disruption risk	The investigation of a novel interruption propagation control issue in multi-echelon SC interventions with constrained funding	Mixed integer nonlinear programming model	A new multi-level supply chain survival problem with a limited intervention budget is investigated	The proposed model allows for minimizing the risk of disruption with a limited intervention budget
Chen et al. [177]	SC disruption	SC disruption recovery strategy motivated by changing the original product type is proposed	Mixed integer linear programming model	Study the special case of supply chain disruptions during a pandemic, and develop a disruption recovery strategy	The proposed disruption recovery strategy effectively reduces manufacturers’ profit losses due to late deliveries and order cancellations
Mohammed et al. [178]	SC risk	A real-life case study of a manufacturing company motivated by changes in supply and demand to improve its SCR	Hybrid integrated multi-attribute decision-possibility bi-objective planning model (MADM-PBOPM)	First time to combine a flexible supplier selection (RSS) approach with demand variation through the development of MADM-PBOPM	The developed methodology can potentially be used to build SC that are resilient to supply disruptions and demand uncertainty
Sawik [179]	Interruption risk	Solving ripple optimization problems in SC operations	Multi-combination methods and scenario-based stochastic mixed integer programming models	Developed a scenario-based stochastic mixed-integer programming formulation	Successfully used to mitigate the effects of multi-regional pandemic disturbances and ripple responses
Vali-Siar and Roghanian [180]	SC disruption	Research on the design of hybrid open and CLSCN with responsiveness, resilience, and sustainability	Robust-stochastic hybrid optimization methods	The model can be used as an effective tool for designing SSC and their related decisions	Using a resilience strategy at the same time delivers the best results for SC objectives

shows the significant distribution of authors’ names, uncertainty conditions, research objectives, modeling method, research gaps and contributions, and UAO of research results. As can be observed from the table, 18 scholars have applied the UAO approach in the past in their studies of SCN disruption during the COVID-19 pandemic. Table 10 provides some highlights of published research in the area of SCN disruption during the COVID-19 pandemic.

6. Findings and Discussions

Our findings show that UAO is an effective decision-making tool when faced with SCM uncertainties, such as uncertainty in demand and uncertainty in costs. Combined with the fact that companies often try to make optimal decisions that satisfy as many objectives as possible, the current environment is characterized by a variety of uncertainties. The UAO approach is frequently utilized in SCM because it can easily handle multi-objective function problems with unclear parameters, which is undoubtedly an appealing characteristic for most researchers. The UAO approach is used to find the best solution when complexity and uncertainty are present. Once the ideal answer has been found, it is converted into suggestions for management decisions.

In addition, the main sources of uncertainty in SCM are supply and demand uncertainty, cost uncertainty, and supply chain disruption risk, and decision-makers often need to make optimal decisions under these uncertainties. According to the results of this review, UAO frequently models the decision problem abstractly before utilizing the appropriate optimization techniques to solve it. This practice is carried out in order to produce scientific decision results in the field of decision-making in SCM. Among the three methods of uncertainty modeling for an optimal solution, RO is the most widely used in SCM, followed by SO.

The construction of RO models has been proposed in the literature, such as characterizing the risk due to uncertainty with confidence in the uncertainty theory. Therefore, future research can extend the results of these models to study supply chain risk contingency management under unexpected contingencies in order to assess risks more effectively and make optimal decisions more quickly. In addition, the literature has used RO models, multi-objective opportunity constraint models recognized uncertainty modeling paradigms, and multi-objective particle swarm optimization solution methods that can only optimize algorithms to solve decision-making problems in SSC. In the future, the conventional paradigm of uncertainty modeling can be combined with big data and algorithms to study green modern digital intelligence SCM in uncertain environments.

Moreover, transportation problems under uncertainty have been studied in the literature, and the expected value model and chance-constrained programming model have been constructed. Future research can combine these models with transportation-related big data to study the optimal design of logistics networks. The SC disruption problem during the COVID-19 pandemic has also been studied in the literature, and various optimization models have been constructed to enhance SC resilience and mitigate SC disruption. After the SC crisis caused by COVID-19, the EU focused its industrial policy on increasing the SC resilience of industrial chains. We should keep an eye on the latest developments in EU industrial policy, analyze and assess any potential effects on China’s SC and industrial chain, plan appropriate responses, and intensify efforts to build resilient SC and industrial chain policies. Therefore, future research can be conducted in the direction of SC resilience management under the impact of a global epidemic. In addition, the theme of promoting high-quality development should be adopted, and efforts should be made to improve the resilience and safety of industrial chains and SCs, as pointed out in the report of the 20th National Congress. Therefore, an important research direction is also the SC safety management of industrial chains under unexpected emergency events. There is also some literature that utilizes the UAO approach in order to obtain the maximization of SC performance based on economic, environmental, social, and other sustainability indicators. In this regard, similar studies can be conducted to consider maximizing SC performance from different perspectives, while UAO can be applied together with some other complex methods, such as game theory. In addition, uncertainty in the attitudes of SC members toward risk has been studied in the literature. In addition to the uncertainty of the external environment, there is also a large amount of uncertainty in the behavior of SC members, such as overconfidence and risk aversion, so UAO can be applied to study the SCM based on behavioral factors in an uncertain environment.

7. Conclusions and Recommendations

Whether it is due to the increase of uncertainty in the external environment, such as natural disasters, political impact, or major public health events, or the increase of uncertainty in the internal environment, such as product quality, lack of capacity, etc., all lead to the increase of uncertainty in supply chain management, and how to effectively deal with and reduce losses after the occurrence of uncertainty in supply chain management is a key challenge for relevant companies. It is a key challenge for the enterprises concerned to deal with the supply chain management uncertainty effectively and reduce the loss after it occurs. By reviewing the literature on the application of UAO in various areas of supply chain management, we provide scholars and practitioners with understanding, decision ideas and insights and future directions on the effective implementation of UAO in SCM under uncertainty.

We tried to classify these papers into the following seven application areas: general SCM, sustainable SCM, SCND, emergency network optimization, logistics network optimization, CLSCM, and SC disruption during the COVID-19 pandemic. The results show that 19 papers apply the UAO approach to general SCM, and 15 studies used the UAO approach in sustainable SCM. In addition, 20 papers applied the UAO approach in the area of CLSCM. A further result shows that 18 studies of papers related to the UAO approach have been conducted in the area of SC disruptions during the COVID-19 pandemic. In addition, 20, 15 and 15 papers have applied the UAO approach in the areas of SCND, emergency network optimization, and logistics network optimization, respectively. In the above literature, the main sources of uncertainty are as follows: (1) uncertainty in demand due to factors such as fierce market competition and variable consumer demand makes it difficult for supply chain companies to obtain full information about the market demand, (2) supply-side uncertainty due to uncertainty in supplier supply quality, quantity, and extended delivery time, and (3) operating cost uncertainty, risk uncertainty, and disruption uncertainty are caused by various internal and external environmental factors. This study only addresses the literature that uses the UAO method for the management of different SCs and different aspects of SCM. Therefore, other methods can be considered for further research in the application of SCM.

In terms of journal distribution, Computers & Industrial Engineering and Journal of Cleaner Production tie for first place with 11 articles, and Annals of Operations Research ranks third with nine articles related to UAO methodology and SCM. In terms of ethnicity-based classification, there are 20 ethnicities and countries applying the UAO approach to SCM issues. Finally, among SCM, Chinese scholars published the most contributions of UAO-related papers, followed by Iran.

The findings of the study indicate that the UAO method is appropriate for resolving uncertainty in SCM. By merging the academic literature on SCM under uncertainty and reviewing the outcomes of UAO research in many application domains, we obtain a better knowledge of both the specific results and the solution to uncertainty problems in SCM. These results are intended to contribute to SCM and UAO literature and to assist academic researchers and managers in SCM areas where uncertainty exists to make optimal decisions in SCM through modeling and optimal resolution of uncertainty.

The theoretical contributions of this paper are to complement the existing literature by demonstrating the application of the UAO approach to SCM and to validate the applicability and importance of the uncertainty model optimization approach in the field of supply chain management. By summarizing the application of UAO in the seven areas of supply chain management subdivided in this paper, an overview of UAO research in these areas is derived, with relatively more research applying UAO methods in the areas of general SCM, CLSCM, and SCND. Many unexpected events, high demand volatility, and high demand for agile response have become the norm in supply chain management. Supply chain uncertainty optimization enables supply chains to operate as planned. The practical contributions of this paper are to provide a reference for researchers in this research direction of uncertainty and supply chain management in the future by reviewing the literature on the use of uncertainty optimization models to solve uncertainty problems in supply chain management, which in turn enlightens decision-makers to better solve a series of uncertainty problems in SCM, improve the efficiency of decision-making, and keep the supply chain stable.

Like with any study, this article contains some limitations that can be considered in future investigations. These limitations can provide opportunities and suggestions for future research. First, this study divided the 121 articles into seven application areas. We recommend that future research reviews papers in different subfields of these categories. Second, this paper reviews the application of UAO in various areas of SCM and identifies the most used UAO and its solution methods for SCM uncertainty problem solving, mainly the three more traditional optimization modeling solution paradigms of SO, chance constraint, and RO. In this regard, it is recommended that other number-wise techniques be used in future research for modeling solution optimization analysis of uncertainty problems in SCM. Third, the data were collected from journals, and the literature does not include textbooks, PhD and MSc theses and dissertations, or unpublished papers on UAO methods and SCM. As a result, information for future studies can be gathered from these sources, and the results can then be compared with the findings and reports of previous research. Fourth, the paper presents the selection and summary of articles by different publishers in the Web of Science. However, it is possible that some of the relevant outlets are still outside the scope of this study. Therefore, the evaluation of papers that were not part of the present study should be the subject of future research. Fifth, this research reviews numerous journal articles that describe the use of the UAO methodology to supply management concerns. Nevertheless, this review does not include recently published book-length approaches. Finally, this paper classifies papers based on seven different areas of SCM rather than different uncertainty analysis modeling optimization solution methods, so the classification of papers based on the UAO approach needs further study.