1. Introduction
Interest in improving STEM education continues to grow in many countries. Improving STEM education can also increase technology and science literacy for all people across the population [
1].
Researchers in the education field point out that teachers do not know how to form connections between STEM disciplines [
2]. STEM education is an approach to teaching and learning that is a unique combination of science, technology, engineering, and mathematics [
3]. Consequently, students show very little interest in science and mathematics, often learning these subjects in isolation and in a disconnected way (i.e., without links to cross-curricular concepts and applications of the real world) [
4]. Recently, STEM education has focused on improving science and mathematics, not treating them as isolated disciplines [
5]. In [
6], it is stated that integrated STEM education is an approach that explores teaching and learning between two or more STEM-related subject areas. Additionally, also between STEM subjects and one or more subjects taught at school. Mathematics is a crucial part of the STEM areas, but also of other teaching subjects, as stated in [
7].
Mathematics is considered difficult to implement into STEM lesson plans. When connections between mathematics and other STEM disciplines are required, teachers typically use mathematics only as a tool or an algorithmic method [
8].
We have presented the results published in the paper in two levels. The first level consists of a stereometry test, containing four tasks exploring students’ spatial abilities to solve space-related problems. Given the unfavorable results and our findings, we designed math trails that are appropriate for eliminating the described findings related to geometry education. Therefore, the second level in the paper consists of creating tasks for a stereometry test using math trails. We prepared the final tasks for implementation in the town.
STEM Education and Math Trails
We deal with the role of mathematics within STEM education through an inter-disciplinary approach using the math trail. Research in [
9] indicated the efficiency of promoting STEM education. This is needed to advance STEM education in general and also the essential role of mathematics in this education. The emphasis on the diversity of STEM subjects is not balanced, and the role of mathematics, in particular, is usually underestimated. Many problems are based on real situations; teachers try to implement this in the teaching process. Such modeling of mathematical real-world problems makes it easier for educators to integrate mathematics into STEM disciplines and, thus, make mathematics teaching and learning activities more meaningful [
10]. Also, Ref. [
11] states that teachers can use mathematics as a tool or use it in an algorithmic way, so there is a need to connect mathematics with other STEM disciplines. These issues are also of interest to various researchers [
12,
13,
14].
In this article, we have created a math trail with problems related to the development of spatial ability linked to selected places in one city in Slovakia. The math trail we designed covers spots in our town. We aim to show that even such a complex issue can be implemented in the teaching process in an interesting way. In the math trail, the goal is not only to create tasks but to show that students will also experience success from solving problems and understand the meaning of problem-solving in practice.
2. Materials and Methods
The research consists in determining the achievement of students in a stereometry test who attend technical vocational schools.
2.1. Research Objectives
The objectives of this research are:
2.2. Description of the Research Sample
The research was carried out in 2022 (from May to September) and the sample consisted of 455 second- and third-year students at technical vocational schools. The students were selected from these fields of study: mechanical engineering, the construction industry, operators of construction production, geodesy, cartography and land register, technical and information services, and technical lyceum.
We have created a stereometry test based on the analysis of state educational programs. The stereometry test contains four tasks that examine students’ spatial abilities, and the test also examines students’ ability to solve spatial displaying tasks.
2.3. Research Tools
The stereometry test (see
Appendix A) contains four stereometrical tasks. All tasks are related to the spatial abilities of the students.
The first task is focused on constructing a plane intersection of the cube by three points of a given plane. This task was also aimed at marking the visibility of sides to the resulting polygon intersection. The first task was divided into two subtasks. There was a non-standard view of the cube (bottom left view of the cube) and a standard view of the cube (top right view of the cube). The second task was oriented to find the vertices of two points, which are located at the edges of a given solid (rectangular prism). The third task dealt with choosing the correct options for the different views of the object (top, front, and side) from the given alternatives. The fourth task is targeted on drawing the correct top view, front view, and side view of the given object.
3. Data Analysis and Interpretation of Results
3.1. Quantitative Analysis
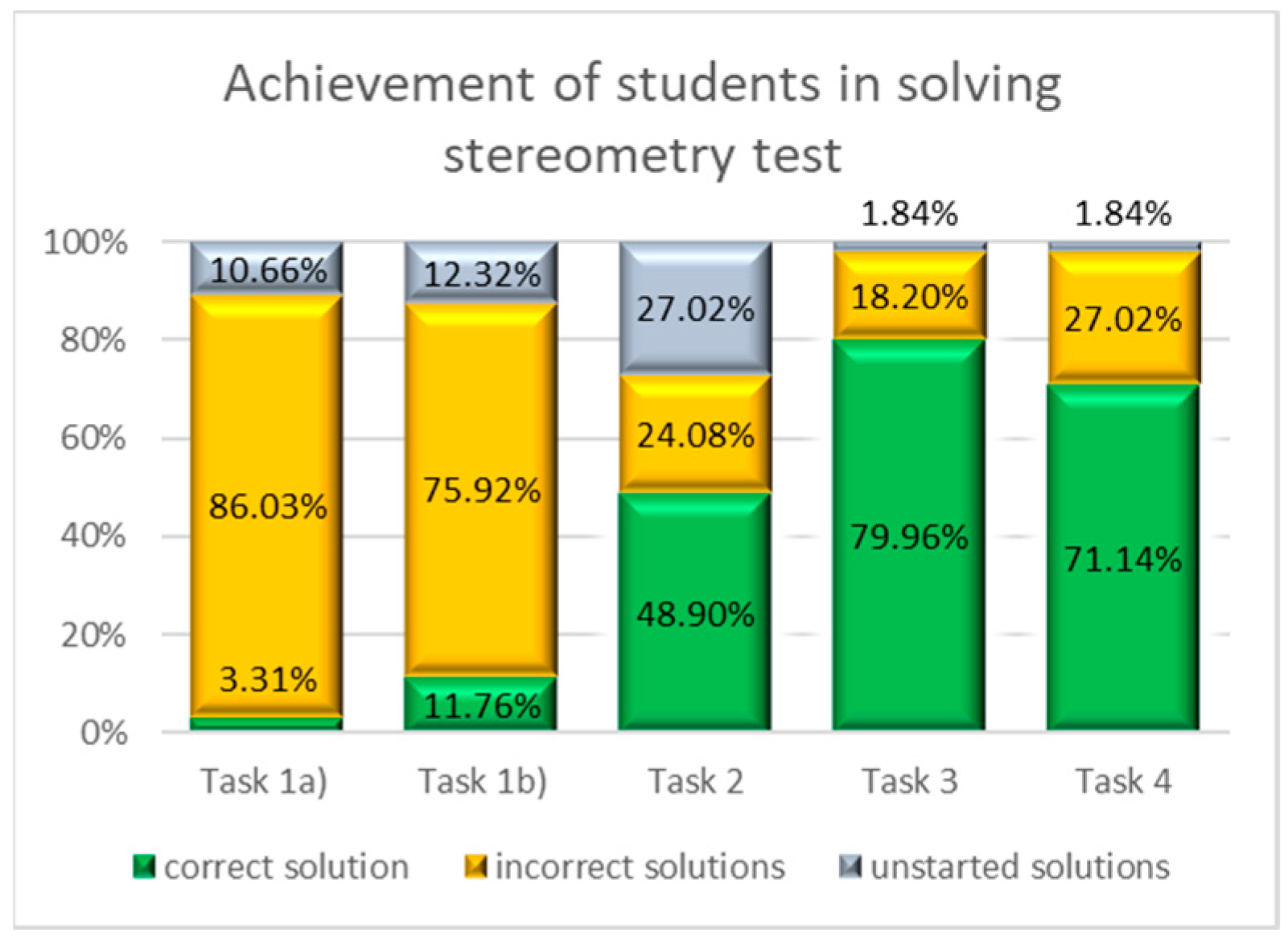
We evaluated the tasks using a quantitative assessment standard. We can see the students’ success in solving the stereometry test in
Figure 1. This graph shows correct solutions, incorrect solutions, and not-yet-started solutions. We can see that students had problems with solving Task 1(a) and Task 1(b), which were solved correctly by only 3.31% and 11.76% of them, respectively. More successful was the task where the cube was given in the standard view mostly used in the teaching process.
Figure 2 presents a graph detailing the correct solutions, incorrect solutions, and not-yet-started solutions in Task 3 and Task 4.
We scored the tasks in such a way that each of the following steps was assigned one point. Each student could achieve a maximum of 12 points in total (see
Figure 3):
construct a plane intersection of the cube (Task 1a);
mark the visibility of sides to the resulting polygon intersection (Task 1a);
construct a plane intersection of the cube (Task 1b);
mark the visibility of sides to the resulting polygon intersection (Task 1b);
find the vertices of the points X (Task 2);
find the vertices of the points F (Task 2);
choose the correct options for the top view (Task 3);
choose the correct options for the front view (Task 3);
choose the correct options for the side view (Task 3);
draw the top view of the given object (Task 4);
draw the front view of the given object (Task 4);
draw the side view of the given object (Task 4).
We also used statistical implicative analysis methods to evaluate the results; specifically, we used statistical software CHIC. For this evaluation, we need didactic variables, and these didactic variables are present in
Table 1.
3.2. Statistical Processing of the Obtained Data
The statistical program CHIC was used to analyze individual steps of student solutions to tasks. The didactic variables mentioned above were used to create implicative trees.
Figure 4 shows the relationship between the correct solutions of the tasks. An implication tree is given there for the complete correct solution of all tasks. We used the statistical program CHIC to analyze individual steps of student solutions to tasks. The didactic variables mentioned above were used to create implicative trees.
Figure 4 shows the relationship between the correct solutions of the tasks. An implication tree is given there for the complete correct solution.
The implication relation U1A→U3 (cohesion: 0.974) shows that if students correctly constructed a plane intersection of the cube by three points of a given plane and marked the visibility of sides to the resulting polygon intersection in Task 1a), they correctly chose options of the different view of the object in Task 3.
In
Figure 5, we present an implication tree that represents an individual strategies analysis of the student´s solutions.
There is the implication . We can see that if the student correctly finds the vertices of point F that student correctly finds the vertices of point X (cohesion: 1). The implications (cohesion: 1) and (cohesion: 1) show that if students correctly constructed a plane intersection of the cube by three points of a given plane, then the students marked the visibility of the sides to the resulting polygon intersection.
The implications (cohesion: 1) and (cohesion: 1) show that if students correctly choose or draw the side view of the given object then students correctly choose or draw the front view of the given object.
Since
Figure 1 shows that the students have success less than 79.96% in Task 3 and less than 71.14% in Task 4. We created a math trail which could support students’ spatial abilities. Students can see the use of theoretical spatial ability knowledge in real situations and objects by realizing the math trail. This math trail is called “Math trail on the Ľudovít Štúr square in Bánovce and Bebravou” and it is focused on developing spatial abilities in city streets. The math trail is available to all in the MathCityMap application. Anyone can search for it by the name of the walk or by using the code 3514190.
4. Description of the Math Trail with an Emphasis on Developing Spatial Abilities in City Streets
In [
15], five components of spatial ability are differentiated. They are spatial perception, visualization, mental rotation, spatial relations, and spatial orientation.
The mental processes of the elements of spatial abilities are either dynamic or static. The test person’s spatial position is an outside or inside position. We can see this in
Table 2, which shows an overview of the elements of spatial ability [
15].
During a math trail, students can solve mathematical problems related to real objects. It is one of the types of outdoor education. Students use mobile technologies during the math trail. Each task in the MathCityMap contains these main points: task assignment, task type, as well as hints. A sample solution to the task is also presented [
16].
We created a math trail on the Ľudovít Štúr square in Bánovce and Bebravou (a town in Slovakia). It is a math trail focused on spatial ability, stereometry, and descriptive geometry. It will be solved by secondary-school students. The math trail comprises six tasks related to real objects located on the square. Each task is focused on one of the elements of spatial ability. We present the individual tasks together with elements of spatial ability.
4.1. Task Related to Visualization
Task assignment: The figure of Ľudovít Štúr is placed on a pedestal in the shape of a truncated cone (see
Figure 6). His cloak extends to the upper base of this pedestal. The cone is imaginatively formed from the pedestal (a truncated cone). Compare the height of the cone and Štúr’s coat. Approximately, what is the ratio of the height of the cone and the length of Ľudovít Štúr’s coat?
Students were offered the following type of answer—multiple choice and these hints:
1/6 or 10–13%, or 1/7 or 14–16%, or 40–50%, or 25–30%;
hint 1: you take a photo of the memorial and on the photo you mark the approximate top of the cone;
hint 2: Ľudovít has his coat on and his cloak billows behind him.
A sample solution to the task is shown in
Figure 7 and the result is 10–13%.
4.2. Task Related to Mental Rotation
Task assignment: Move your finger on the map from your current location. Walk down the street going in the south-west direction. Turn left at the nearest Y-shaped crossroads. Then, go to the nearest crossroads and continue straight. Now, you are near a block of flats that looks similar to a star. Turn right, and continue along the street. At the second crossroads, turn around the perimeter of the grass quadrangle. Move along the street called K. Zornici. Next to the pharmacy, turn south-east. At the intersection of your street with Radiša, walk to the river and follow the flow of the river. On the second bridge, go along the street to the north-west. When the name of the street changes, walk on the street named after A. Braxatoris. Then, walk into the parking area. Now, you have walked the entire street named after one Slovak poet. Where did you end your walk?
Students were offered multiple-choice-type answers and they were given these hints:
ODES, or Tesco, or a sports hall (on the map: “športová hala”) or Lidl, or ADM motor, or the Ľudovít Štúr square (on the map: “Námestie Ľudovíta Štúra”), or a post office (on the map: “Pošta”);
hint 1: the compass on the map will help you;
hint 2: two blocks of flats that look similar to a star with 12 floors are also located at the Vystrkov-Strážovská–Na vrštek crossroads.
In
Figure 8 is sample solution: the Ľudovít Štúr square (on the map: “Námestie Ľudovíta Štúra”).
4.3. Task Related to Spatial Orientation
Task assignment: The Church of the Most Holy Trinity which stands in Bánovce to this day was built in 1803 in a classical style. Formerly an older Baroque church stood on the same spot. The old Baroque church was not oriented according to the typical Baroque orientation. The last rays of the sun entered the church through the side door. The front door under the tower were located on the north side. Look at the new Church of the Most Holy Trinity (
Figure 9). Compare the axis of the old church and the main axis of the new church. Calculate the difference between these axes. Write the difference in the positive direction of the oriented angle by integers without the symbol of degree.
This task required a written answer. The students’ answers had to fit into a given interval shown in the
Figure 10. The orange-colored interval indicates a not perfect, but correct, answer, and the green-colored interval indicates a more precise answer.
Students were also offered hints:
We present a sample solution out of interest and a description of the student’s solution to the task. First, you determine the orientation of the old church. The front door under the tower was oriented to the north and the side door was oriented to the west. Secondly, we determine the orientation of the new church. We can use a well-known fact about where the sun sets, find a map of the square, or, simply, use a compass on a phone. We draw the orientation of both the old church and the new church on paper and calculate the difference.
4.4. Task Related to Spatial Perception
Task assignment: The trunk of the well-known planetree of Bánovce (see in
Figure 12) is surrounded by a curb. A tactile path is also built near it. Find the point of the curb which is closest to the tactile path. Hold a camera lens at a height of one meter above this point. Take a photo. You will see a monoclinic one-point linear perspective, horizon, vanishing point line, and a vanishing point. Choose the correct options. Where is the vanishing point in the photo located?
The students were given multiple-choice-type answers and the following hints:
the grocery store Coop Jednota, a hill in the background of the apartment buildings, trees in the foreground of the apartment buildings, one of the trees in the square in a row with the same curb as the planetree, the sky above the hill, or the department store Tesco;
Figure 13.
Hints were related to the specific measurements used in solving of the task: (a) hint 1; (b) hint 2.
Figure 13.
Hints were related to the specific measurements used in solving of the task: (a) hint 1; (b) hint 2.
A sample solution is shown in
Figure 14, where there are trees in the foreground of the apartment buildings.
4.5. Task Related to Spatial Relations
We created two tasks related to spatial relations present in the math trails. Their assignments are listed below with hints that were given to the students and the solutions.
Task 1: The central object of the town is the Church of the Most Holy Trinity (
Figure 15). It was built in 1803. Pictures of different ground plans of the church are in the hints. Mark the correct top view of the church in the answers.
Students had to find the orthogonal projection of the church into the plane. The type of answer (multiple choice) and hints can be seen in
Figure 16.
Task 2: Several doctors have their offices on the first floor of this historical building (
Figure 17). There is a top view and a roof plan of the building in the hints. Using the hints, try to choose and mark the correct top view and roof plan for the historical building.
Figure 18 shows the answers in the form of pictures (multiple choice) along with hints.
5. Score of Components of Spatial Ability
We have created a graph (see
Figure 19) that shows the score in percentages for each component of spatial ability related to task-solving from our math trail.
This graph shows that spatial perception scores the highest among the five components of spatial ability listed in
Table 2. The graph also reveals that the score of spatial orientation is the lowest among the components of spatial ability.
6. Conclusions
Schools have been teaching mathematics the traditional way for a very long time. Hence, is mathematics crucial in STEM? We believe that such an explanation provides additional educational benefits through the STEM model, but it is different. It is important to note that the traditional method of teaching mathematics is inevitable. As stated in [
17], there is abundant empirical evidence of a significant correlation between spatial ability, which is a part of mathematics, and educational performance in STEM. STEM is a comprehensive approach that integrates disciplines to make learning connected, focused, relevant, and meaningful for students.
Our test results show a lack of spatial ability and mental rotation in pupils which is also one of the crucial components of spatial ability. We also think that geometry teaching needs to be linked to the real world and activities. Everyday activities require spatial ability. This ability is a major factor in mathematics because it is used to understand the properties of objects, such as their position, size, and shape, as well as the relationships between objects.
We have also found that incorporating outdoor activities, such as math trails, can help to develop spatial ability in a non-formal context. This finding is beneficial for stereometry and mathematics proficiency more generally. We can also conclude that the motivation of students increased during the experience, despite the problems of the trail not being easy for all students.
The math trail was created as one of many activities that can develop a student’s spatial ability. Our most important findings are based on the results of the stereometry test as well as the realization of the math trail. The score in the stereometry test and the math trail for spatial orientation is the lowest of the other components of spatial ability. The achievement of students in tasks in the stereometry test related to spatial relations is almost 80%. We can also see the achievement of students in tasks related to spatial relations is close to 85%. We can state that the results are comparable. We can state that the important relationship between spatial orientation and spatial relation was shown to be similar in both the stereometry test and the math trail. Similarly, it shows that the achievement of students in tasks related to spatial orientation is lower than the achievement of students in tasks related to visualization. This comparison of achievements of students in solving tasks related to spatial orientation and visualization was shown in solving tasks in the stereometry test and tasks in the math trail as well. Although the cohesion in the implication graph is not significant, we can see that there is some relationship between spatial orientation and visualization. These findings are well grounded by the graphs we have presented.
Our results show students developing a more positive attitude towards geometry, broadening their perspective about the connections between mathematics, other school subjects, and also everyday life.
Author Contributions
Conceptualization, K.L. and L.R.; methodology, K.L. and L.R.; software, K.L.; validation, L.R.; resources, L.R.; data curation, K.L.; writing—original draft preparation, K.L.; writing—review and editing, L.R.; project administration, L.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by the Slovak Research and Development Agency (under contract no. APVV-14-0446) and the Cultural and Educational Grant Agency of the Ministry of Education, Science, Research, and Sports of the Slovak Republic (no. KEGA 013UKF-4/2023).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Stereometry test for students.
Task 1(a)
Construct a plane intersection of the cube by three points of that plane . Mark the visibility of sides to the resulting polygon intersection.
Figure A1.
Cube for solving Task 1a.
Figure A1.
Cube for solving Task 1a.
Task 1(b)
Construct a plane intersection of the cube by three points of that plane . Mark the visibility of sides to the resulting polygon intersection.
Figure A2.
Cube for solving Task 1b.
Figure A2.
Cube for solving Task 1b.
Task 2
If , , are the vertices of a rectangular prism ABCDEFGH, find the vertices of the points and , which are located at the edges of this solid. For a point X: .
Figure A3.
Rectangular prism for solving Task 2.
Figure A3.
Rectangular prism for solving Task 2.
Task 3
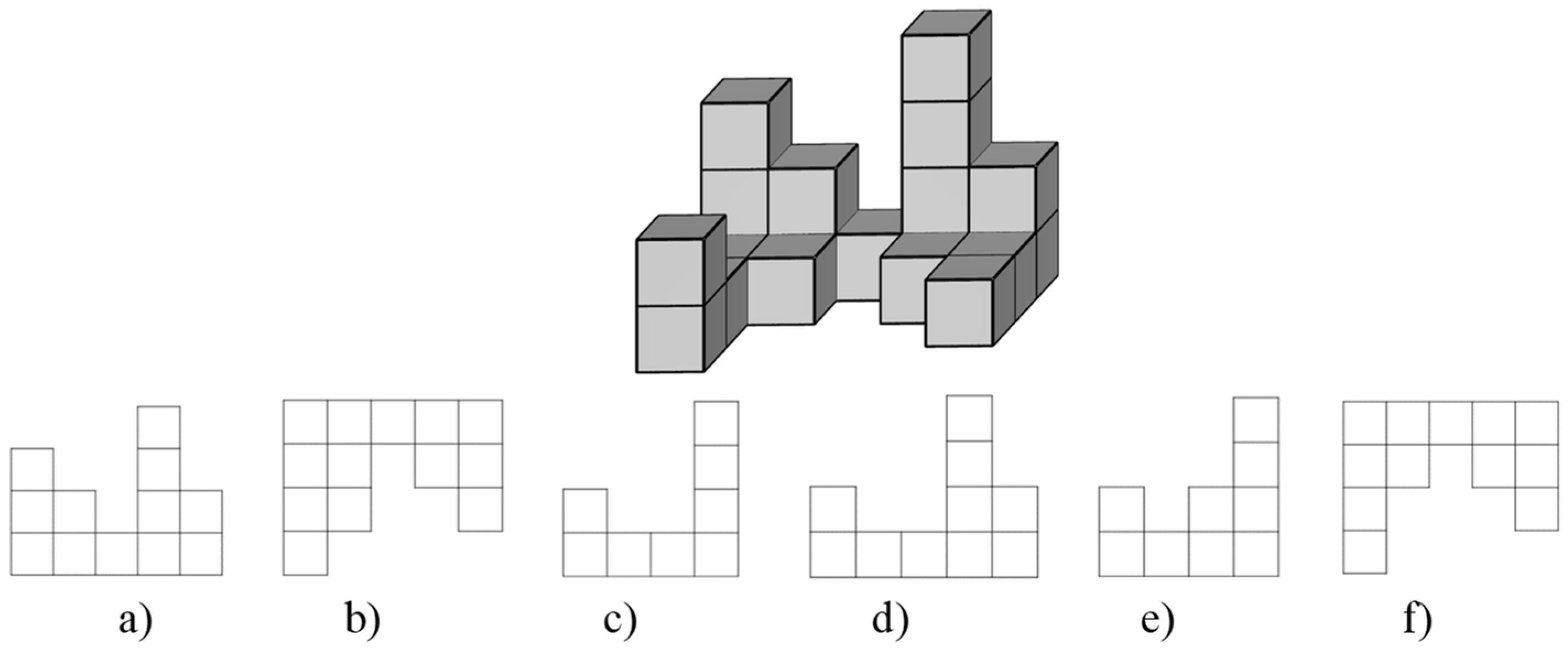
From the given alternatives (a)–(f), choose the correct options for the different view of the object (top, front, and side).
Figure A4.
Object for solving Task 3.
Figure A4.
Object for solving Task 3.
Task 4
Draw the top view of the given object, front view of the given object, and also side view of the given object.
Figure A5.
Object for solving Task 4.
Figure A5.
Object for solving Task 4.
Appendix B
Math trail with an emphasis on developing spatial abilities in city streets.
Figure A6.
Math trail in mobile application.
Figure A6.
Math trail in mobile application.
Task 1: The Church of the Most Holy Trinity—right-angled projection of the plane.
Figure A7.
Task 1 in mobile application.
Figure A7.
Task 1 in mobile application.
Task 2: Plane tree—linear perspective.
Figure A8.
Task 2 in mobile application.
Figure A8.
Task 2 in mobile application.
Task 3: Ľudovít Štúr memorial—visualization.
Figure A9.
Task 3 in mobile application.
Figure A9.
Task 3 in mobile application.
Task 4: Grocery store—orthographic projection.
Figure A10.
Task 4 in mobile application.
Figure A10.
Task 4 in mobile application.
Task 5: Map—mental rotation.
Figure A11.
Task 5 in mobile application.
Figure A11.
Task 5 in mobile application.
Task 6: The Church of the Most Holy Trinity—astronomical orientation.
Figure A12.
Task 6 in mobile application.
Figure A12.
Task 6 in mobile application.
References
- Li, Y.; Schoenfeld, A.H. Problematizing Teaching and Learning Mathematics as “Given” in STEM Education. Int. J. STEM Educ. 2019, 6, 44. [Google Scholar] [CrossRef]
- Fitzallen, N. STEM Education: What Does Mathematics Have to Offer? In Proceedings of the 38th Annual Conference of the Mathematics Education Research Group of Australasia (MERGA), Adelaide, SA, Australia, 28 June–2 July 2015. [Google Scholar]
- Bennett, C.A.; Ruchti, W. Bridging STEM with Mathematical Practices. J. STEM Teach. Educ. 2014, 49, 17–28. [Google Scholar] [CrossRef]
- Kelley, T.R.; Knowles, J.G. A Conceptual Framework for Integrated STEM Education. Int. J. STEM Educ. 2016, 3, 1. [Google Scholar] [CrossRef]
- Breiner, J.M.; Harkness, S.S.; Johnson, C.C.; Koehler, C.M. What is STEM? A Discussion about Conceptions of STEM in Education and Partnerships. Sch. Sci. Math. 2012, 112, 3–11. [Google Scholar] [CrossRef]
- Sanders, M. STEM, STEM Education, STEMmania. Technol. Teach. 2009, 68, 20–26. [Google Scholar]
- Coufal, P. Project-Based STEM Learning Using Educational Robotics as the Development of Student Problem-Solving Competence. Mathematics 2022, 10, 4618. [Google Scholar] [CrossRef]
- Wang, H.H.; Moore, T.J.; Roehrig, G.H.; Park, M.S. STEM Integration: Teacher Perceptions and Practice. J. Pre-Coll. Eng. Educ. Res. 2011, 1, 2. [Google Scholar]
- Maass, K.; Geiger, V.; Ariza, M.R.; Goos, M. The Role of Mathematics in Interdisciplinary STEM Education. ZDM 2019, 51, 869–884. [Google Scholar] [CrossRef]
- Blum, W. Mathematical Modelling in Mathematics Education and Instruction. In Teaching and Learning Mathematics in Context; Breiteig, T., Huntley, I., Kaiser-Messmer, G., Eds.; Ellis Horwood Limited: Chichester, UK; New York, NY, USA, 1993; pp. 3–14. [Google Scholar]
- Wang, H. A New Era of Science Education: Science Teachers ‘Perceptions and Classroom Practices of Science, Technology, Engineering, and Mathematics (STEM) Integration. Doctoral Dissertation, Minnesota University, Minneapolis, MN, USA, 2012. [Google Scholar]
- Yabas, D.; Boyacı, H.S.; Corlu, M.S. Mathematical Modelling in STEM Education: A Math Trail Using LABSTARTM. In Proceedings of the Research on Outdoor STEM Education in the Digital Age, Online Conference, 16–19 June 2020. [Google Scholar]
- Haringová, S.; Medová, J. Identification of Domains of Mathematics Teachers’ Knowledge Addressed in Reflection on Technology-Supported Math Trails. In Proceedings of the 13th ERME Topic Conference (ETC13), Nitra, Slovakia, 7–9 September 2022. [Google Scholar]
- Gurjanow, I.; Zender, J.; Ludwig, M. MathCityMap–Popularizing mathematics around the globe with math trails and smartphone. In Research on Outdoor STEM Education in the Digital Age, Proceedings of the ROSETA; Online Conference, 10 June 2020, WTM: London, UK, 2020. [Google Scholar]
- Maier, P.H. Spatial Geometry and Spatial Ability-How to Make Solid Geometry Solid? In Proceedings of the Annual Conference of Didactics of Mathematics, Rosenburg, Germany, 15–20 September 1996. [Google Scholar]
- Haringová, S.; Medová, J. Math trails supporting the collaboration between mathematics teachers in professional development. In Proceedings of the Twelfth Congress of the European Society for Research in Mathematics Education (CERME12), Bolzano, Italy, 2–6 February 2022. [Google Scholar]
- Buckley, J.; Seery, N.; Canty, D. A Heuristic Framework of Spatial Ability: A Review and Synthesis of Spatial Factor Literature to Support its Translation into STEM Education. Educ. Psychol. Rev. 2018, 30, 947–972. [Google Scholar] [CrossRef]
Figure 1.
Achievement of students in the stereometry test.
Figure 1.
Achievement of students in the stereometry test.
Figure 2.
Achievement of students in Task 3 and Task 4.
Figure 2.
Achievement of students in Task 3 and Task 4.
Figure 3.
Students’ achievements in the stereometry test.
Figure 3.
Students’ achievements in the stereometry test.
Figure 4.
Implicative tree for the correct solutions of all tasks.
Figure 4.
Implicative tree for the correct solutions of all tasks.
Figure 5.
Implicative tree for individual variables of the students’ solutions.
Figure 5.
Implicative tree for individual variables of the students’ solutions.
Figure 6.
Photo of the Ľudovít Štúr memorial for visualization in the task.
Figure 6.
Photo of the Ľudovít Štúr memorial for visualization in the task.
Figure 7.
Task for dynamic mental processes (visualization).
Figure 7.
Task for dynamic mental processes (visualization).
Figure 8.
Sample solution on the map—task for dynamic mental processes (mental rotation).
Figure 8.
Sample solution on the map—task for dynamic mental processes (mental rotation).
Figure 9.
The main object, the Church of the Most Holy Trinity.
Figure 9.
The main object, the Church of the Most Holy Trinity.
Figure 10.
Students´ answer to the task on spatial orientation in the interval.
Figure 10.
Students´ answer to the task on spatial orientation in the interval.
Figure 11.
Picture hints for the task related to astronomical orientation: (a) hint 2; (b) hint 3.
Figure 11.
Picture hints for the task related to astronomical orientation: (a) hint 2; (b) hint 3.
Figure 12.
The main photo of the object (plane tree) from the task related to static mental processes (linear perspective).
Figure 12.
The main photo of the object (plane tree) from the task related to static mental processes (linear perspective).
Figure 14.
Sample solution of the task related to linear perspective.
Figure 14.
Sample solution of the task related to linear perspective.
Figure 15.
Photo of the Church of the Most Holy Trinity.
Figure 15.
Photo of the Church of the Most Holy Trinity.
Figure 16.
(a) Hints and all answers of the task related to static mental processes (right-angled projection of the plane); (b) a sample solution of task.
Figure 16.
(a) Hints and all answers of the task related to static mental processes (right-angled projection of the plane); (b) a sample solution of task.
Figure 17.
The main photo of the object—grocery store (static mental processes—orthographic projection).
Figure 17.
The main photo of the object—grocery store (static mental processes—orthographic projection).
Figure 18.
(a) Hints and all answers of the task related to static mental processes (orthographic projection with roof plan); (b) correct roof plan marked in the real photo of the building.
Figure 18.
(a) Hints and all answers of the task related to static mental processes (orthographic projection with roof plan); (b) correct roof plan marked in the real photo of the building.
Figure 19.
Score of the components of spatial ability.
Figure 19.
Score of the components of spatial ability.
Table 1.
Didactic variables for each task of stereometry test.
Table 1.
Didactic variables for each task of stereometry test.
| Task | Didactic Variables |
|---|
| Task 1a (type U1A) | U1A—students’ correct solution of Task 1(a)
U1A_r—correctly constructing a plane intersection of the cube by three points of that given plane of Task 1(a)
U1A_v—correctly marking the visibility of sides to the
resulting polygon intersection of Task 1(a) |
| Task 1b (type U1B) | U1B—students’ correct solution of Task 1(b)
U1B_r—correctly constructing a plane intersection of the cube by three points of that given plane od Task 1(b)
U1B_v—correctly marking the visibility of sides to the
resulting polygon intersection of Task 1(b) |
| Task 2 (type U2) | U2—students´ correct solution of Task 2
U2_X—correctly finding the vertices of point X of Task 2
U2_F—correctly finding the vertices of point F of Task 2 |
| Task 3 (type U3) | U3—students´ correct solution of Task 3
U3_n—choosing the correct options for the front view
of the object of Task 3
U3_p—choosing the correct options for the top view
of the object of Task 3
U3_b—choosing the correct options for the side view
of the object of Task 3 |
| Task 4 (type U4) | U4—students´ correct solution of Task 4
U4_n—correctly drawing the front view of the
given object of Task 4
U4_p—correctly drawing the top view of the
given object of Task 4
U4_b—correctly drawing the side view of the
given object of Task 4 |
Table 2.
Overview of the elements of spatial ability.
Table 2.
Overview of the elements of spatial ability.
Spatial Position
of Test Person | Dynamic
Mental Processes | Static
Mental Processes |
|---|
| outside person | visualization | spatial relations |
| mental rotation | spatial perception |
| inside person | spatial orientation |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).