Review of Reliability Assessment Methods of Drone Swarm (Fleet) and a New Importance Evaluation Based Method of Drone Swarm Structure Analysis
Abstract
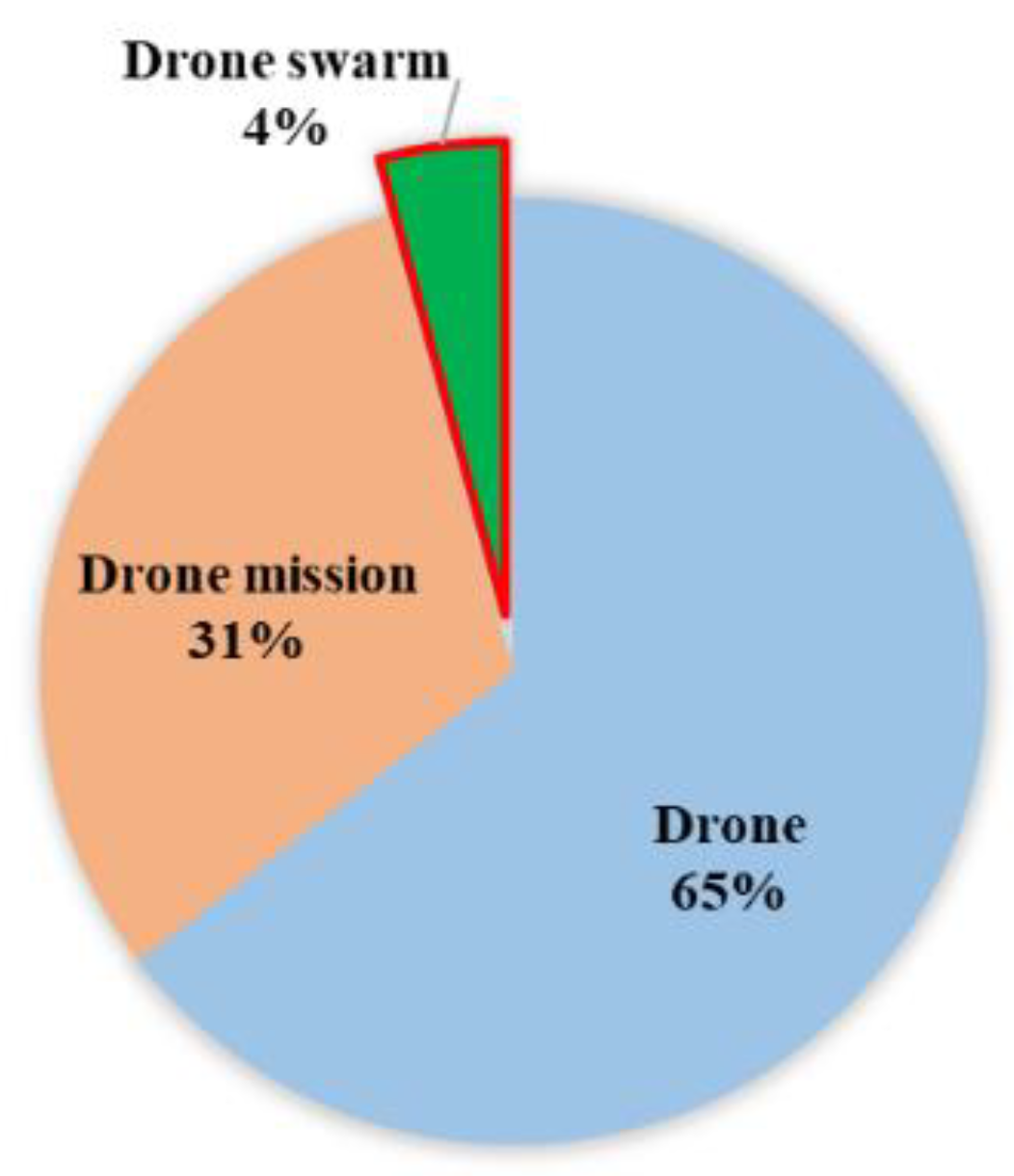
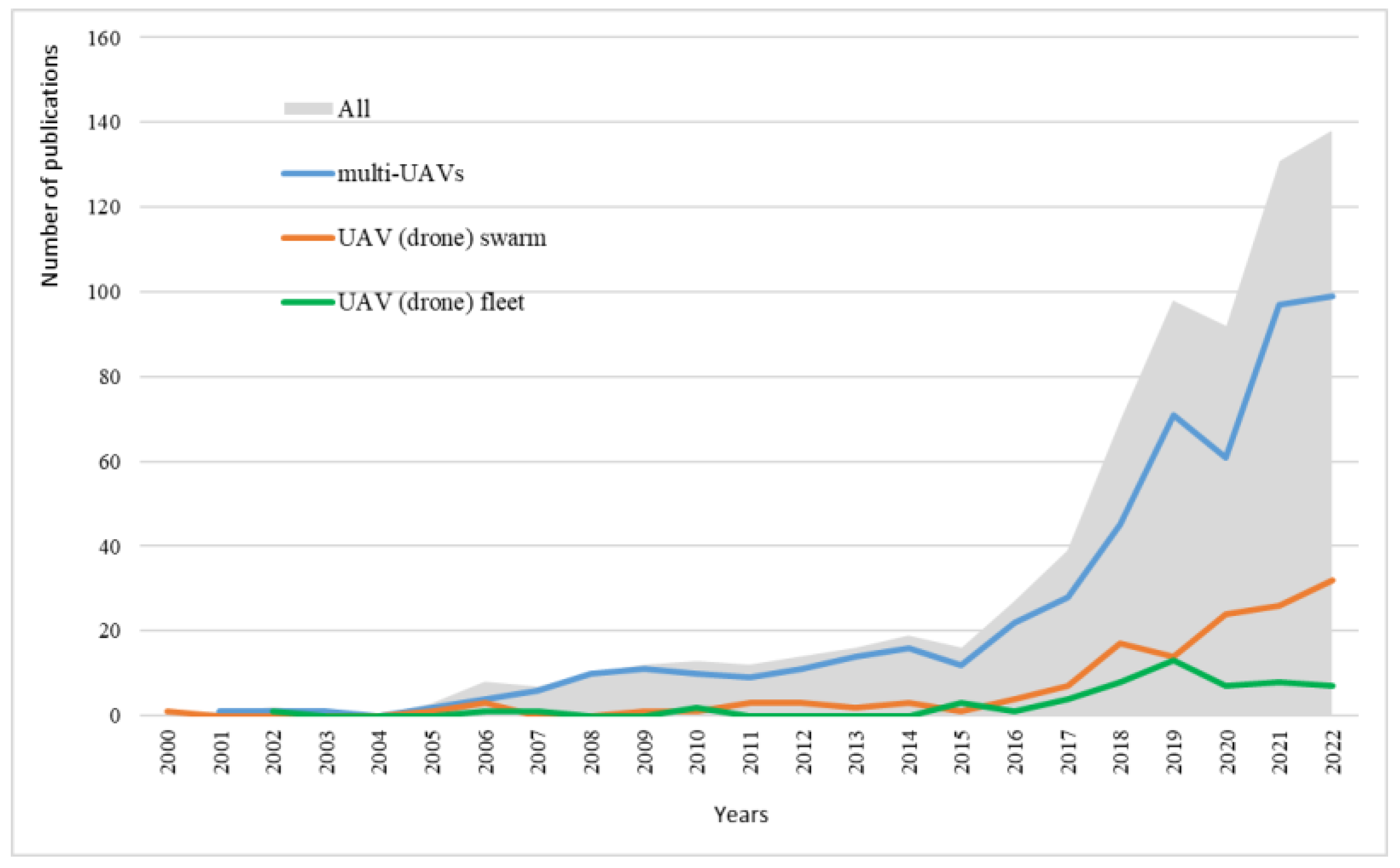
:1. Introduction
- Reliability analysis of a single drone. In this case, a drone is a system from the point of view of reliability analysis. The components of the drone are considered system components and impact its operation and reliability [5]. There are many investigations of drone components. These components can be divided into two groups. The first group comprises the hardware and mechanical components of drones, for example, the propellers [6], motors and power system [7,8,9], communication platform and sensors [8,10,11,12], and mechanical components [13]. The other group of components consists of the software used for drone mission support, for which the methods of software reliability are applied [14,15,16,17]. There is one more direction for drone reliability improvement: the development of machine-learning-based and AI-based methods to improve some of a drone’s components’ functioning [18,19,20,21,22]. However, in these studies, the proposed methods do not evaluate drone reliability directly and consider reliability as one of the positive characteristics of developed methods.
- Reliability evaluation of a drone mission. In these studies, as a rule, the problem of the fulfillment or non-fulfillment of the assigned mission by the drone is considered and this mission result is evaluated by reliability or risk. Many of the developed methods focus on the tasks of planning or optimizing the flight path [23,24,25]. However, reliability and risk are not considered according to the reliability of engineering designs. An important tendency in reliable drone missions is the application of artificially intelligent and machine learning methods in the mission’s development and support [26,27,28]. A discussion of reliability analysis methods for drone missions is in some papers: redundancy of drone components [29], maintenance [30], prognostic and health management [31], importance analysis [32], safety [33], and defense [34] analysis.
- Reliability analysis of drone swarm (fleet) or multi-UAVs. A drone swarm (in some publications it is called a “fleet”) is group of drones that implement one mission or are joined by one control center [35]. In some studies, this concept is named “multi-UAVs” [36]. From the point of view of reliability analysis, the reliability of a drone swarm is influenced by many factors such as: its structure or topology [32,37], type of redundancy [38], drone characteristics [39], heterogeneity [40], and others.
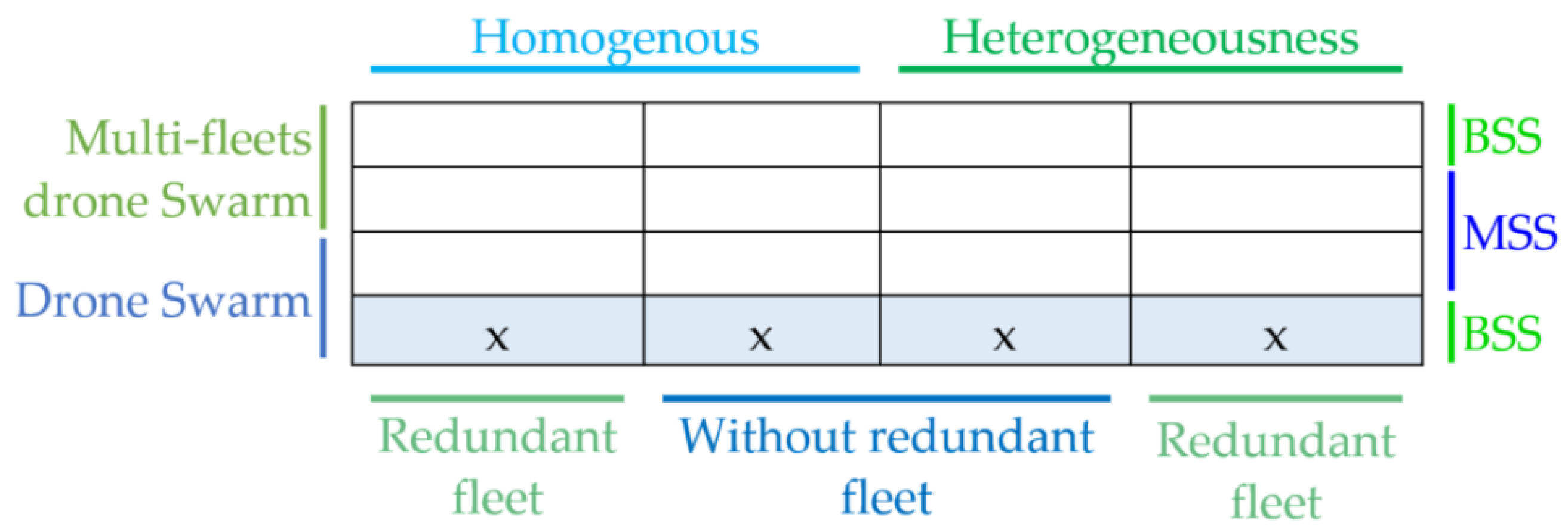
2. Reliability Analysis of Drone Swarm Review
- The swarm structure, which can include one fleet (drome swarm) or more than one drone fleet (multi-fleets drone swarm).
- The heterogeneous or homogenous types of swarms; in the case of homogenous drone swarms, all drones have similar characteristics and properties.
- The presence of a reserved fleet of drones in the overall structure of drone swarm.
- The number of states in swarm performance: a mathematical model of a Binary-state system (BSS) allows the representation of two states in swarm performance (failure and functioning) and a mathematical model of a Multi-state system (MSS) [43,44] allows for the investigation of degradation in swarm performance.
3. Structure Function-Based Approach of Reliability Analysis
3.1. Structure Function
3.2. Availability Defined Based on a Structure Function
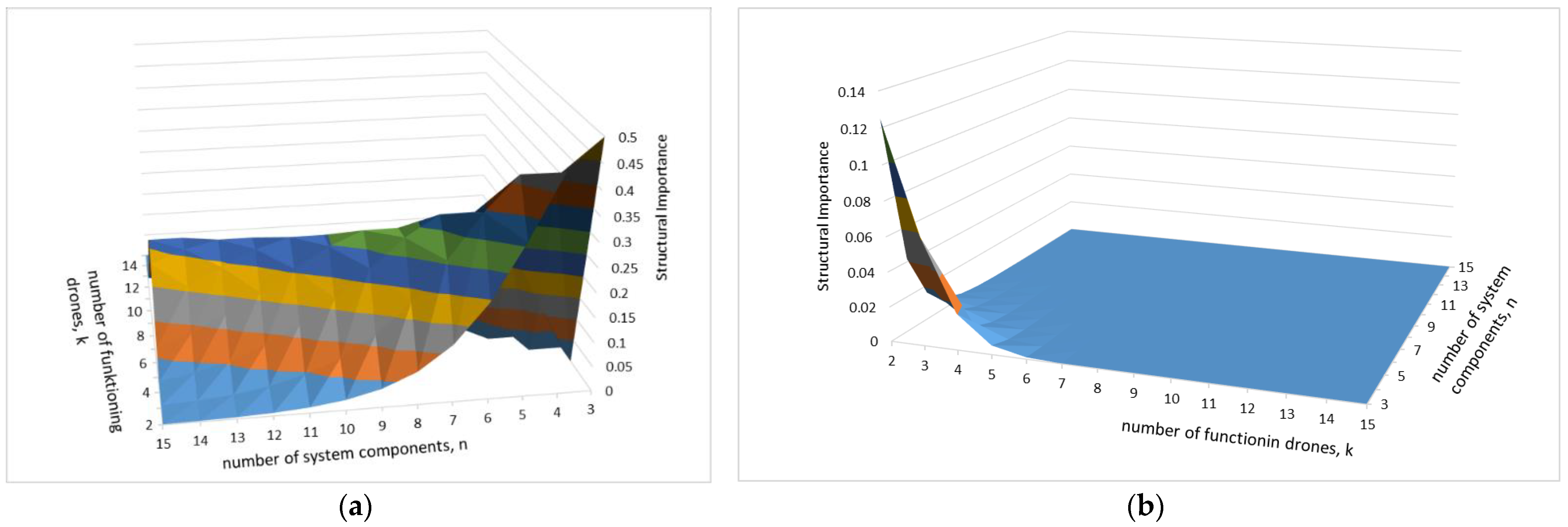
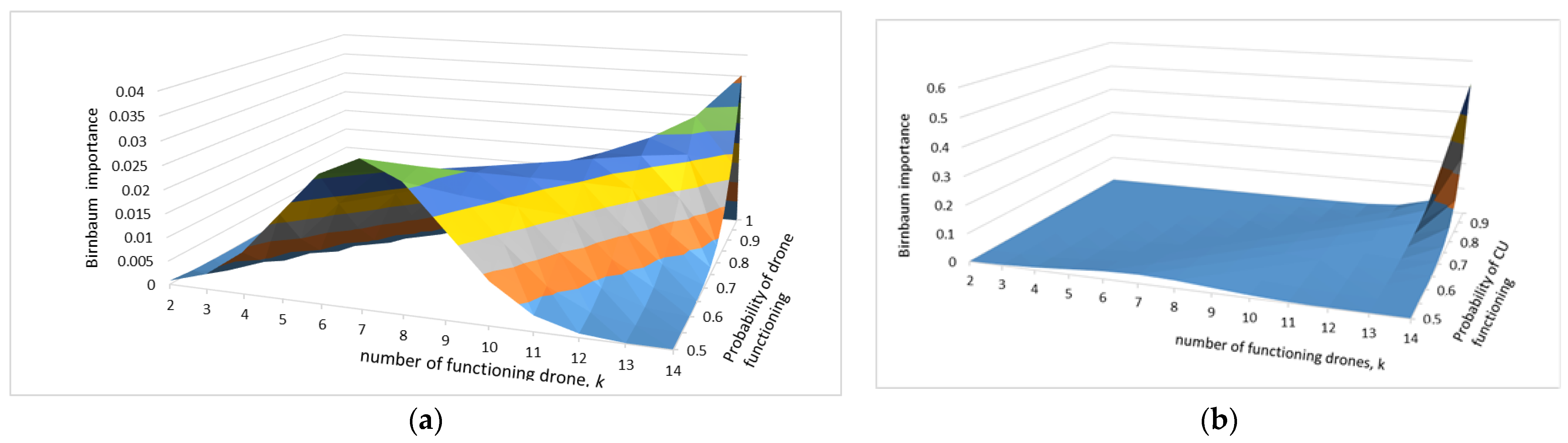
3.3. Importance Analysis of UAV Fleets
3.4. Hand-Calculated Example
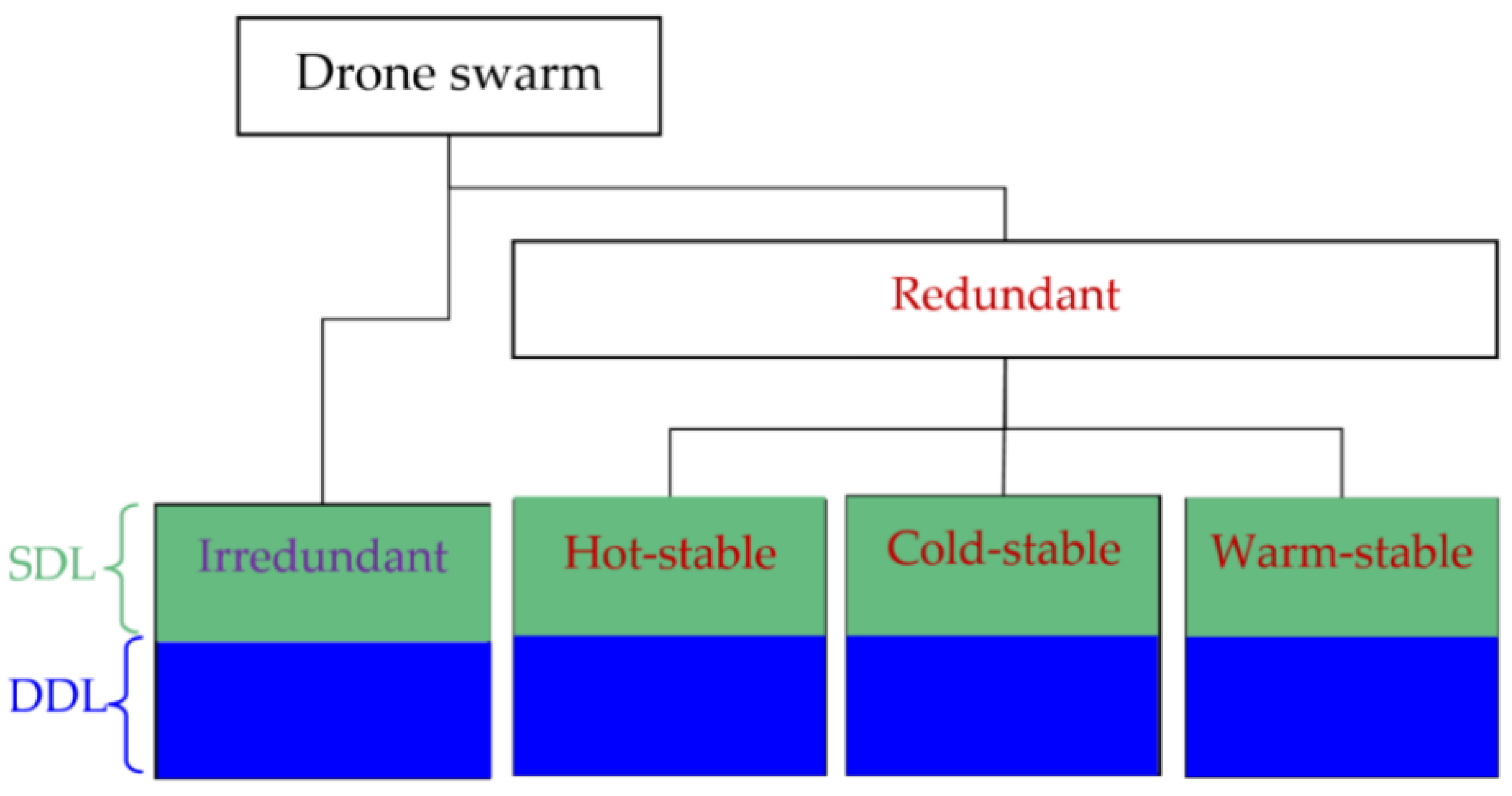
4. Typical Structures of Drone Swarms
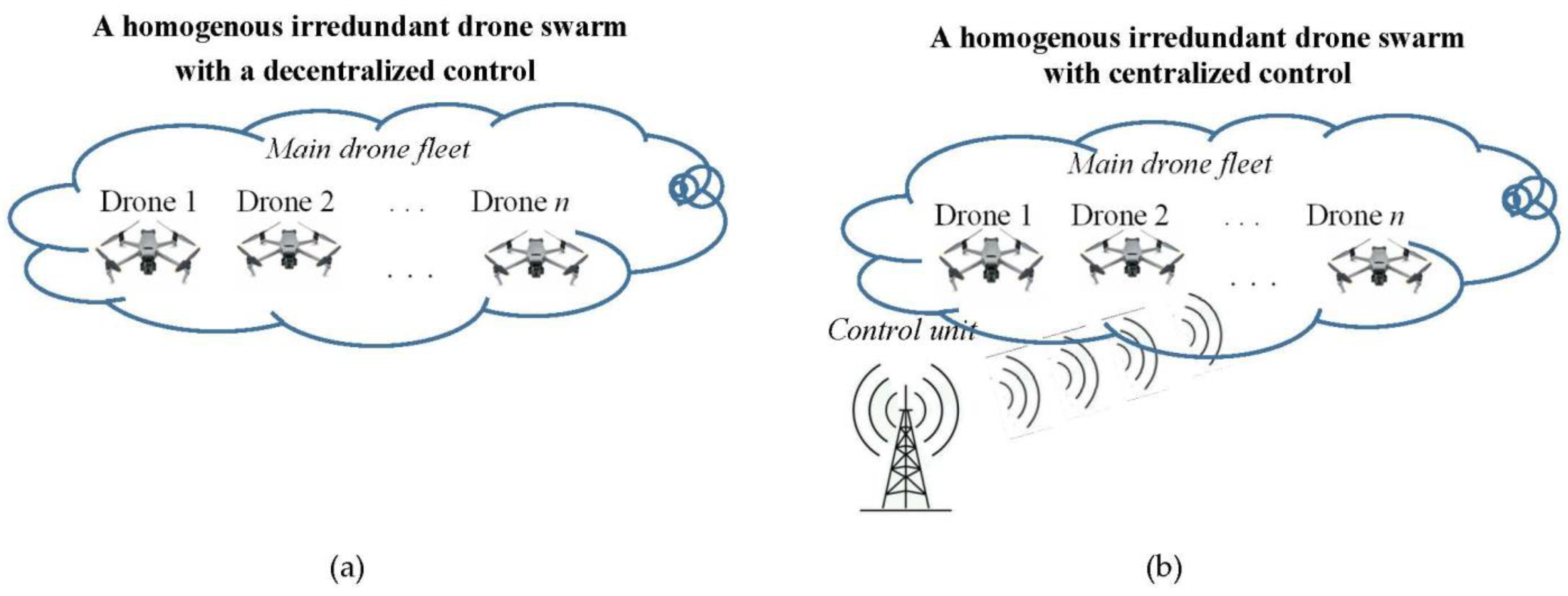
- Homogenous irredundant drone swarm;
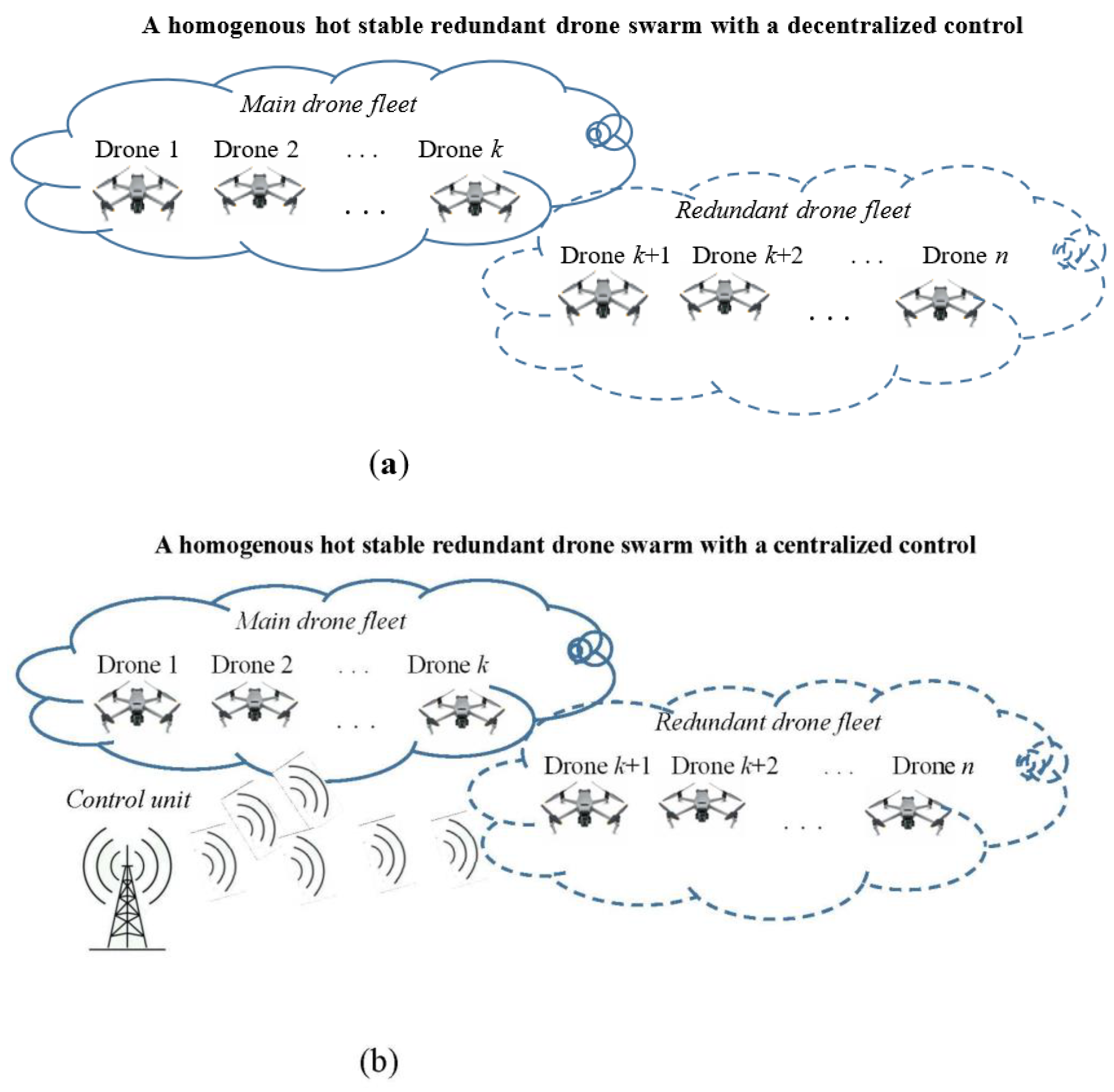
- Homogenous hot stable redundant drone swarm;
- Heterogeneous irredundant drone swarm;
- Heterogeneous hot stable redundant drone swarm.
4.1. Homogenous Irredundant Drone Swarms
4.2. Homogenous Hot Stable Redundant Drone Swarms
4.3. Heterogeneous Irredundant Drone Swarm
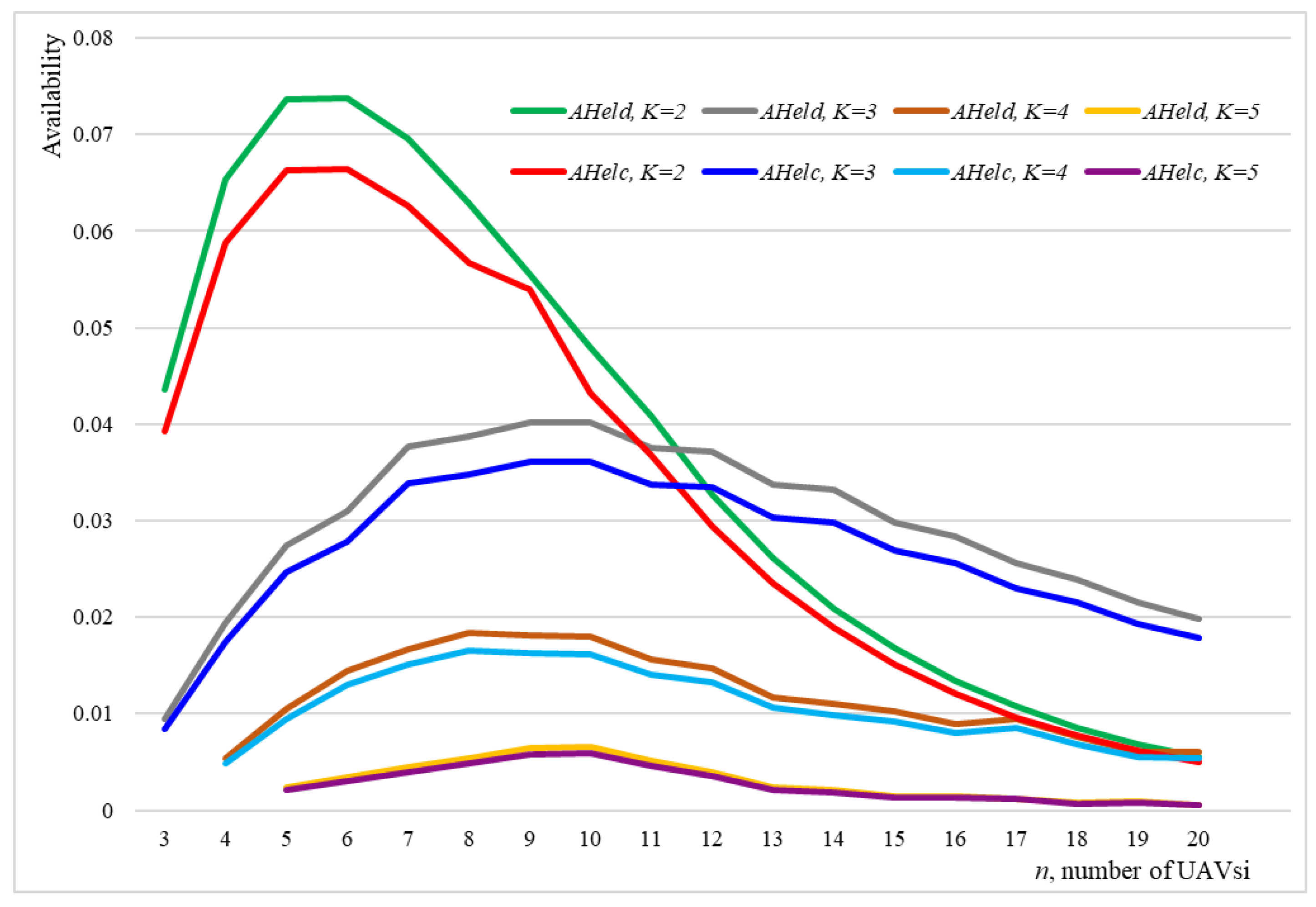
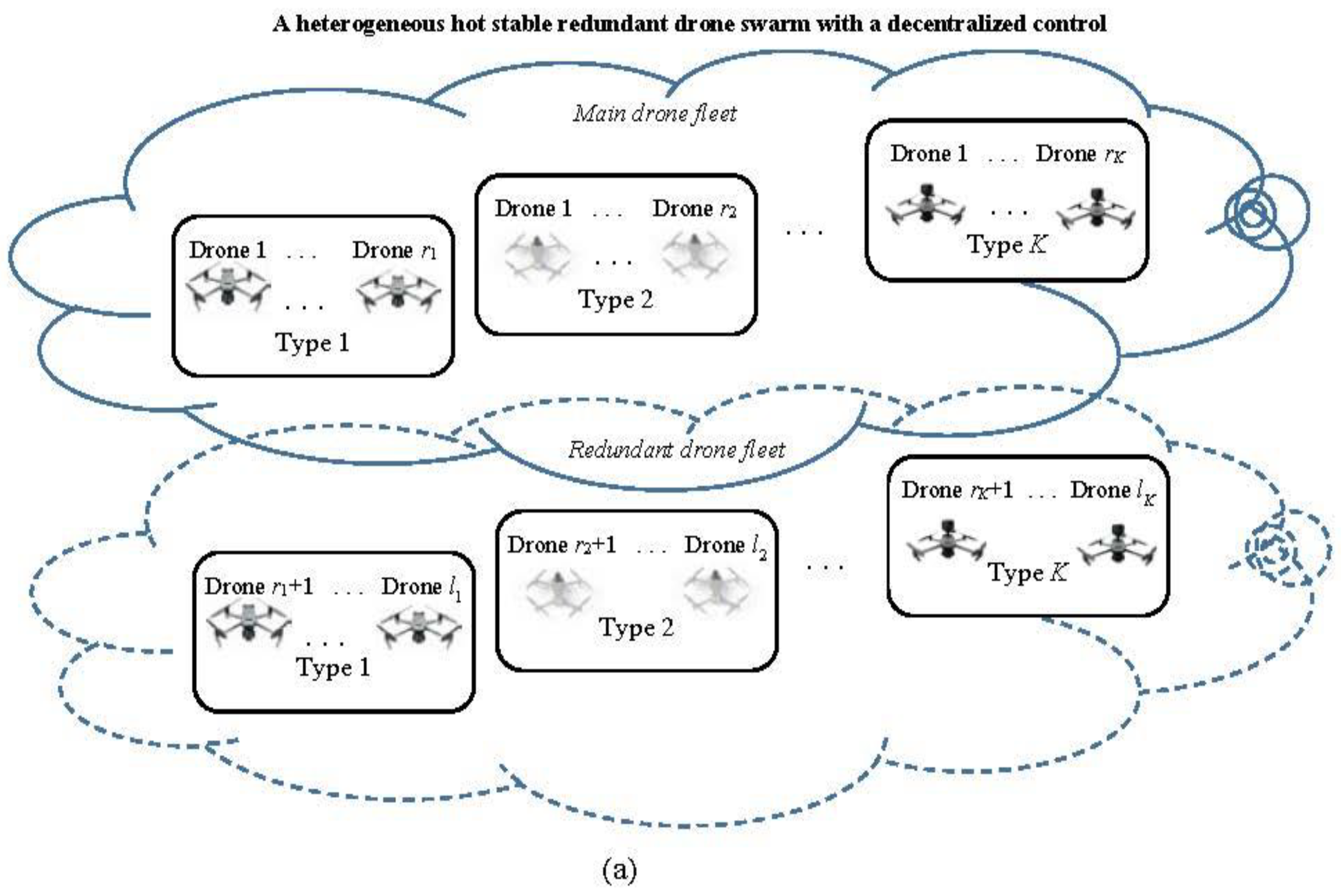
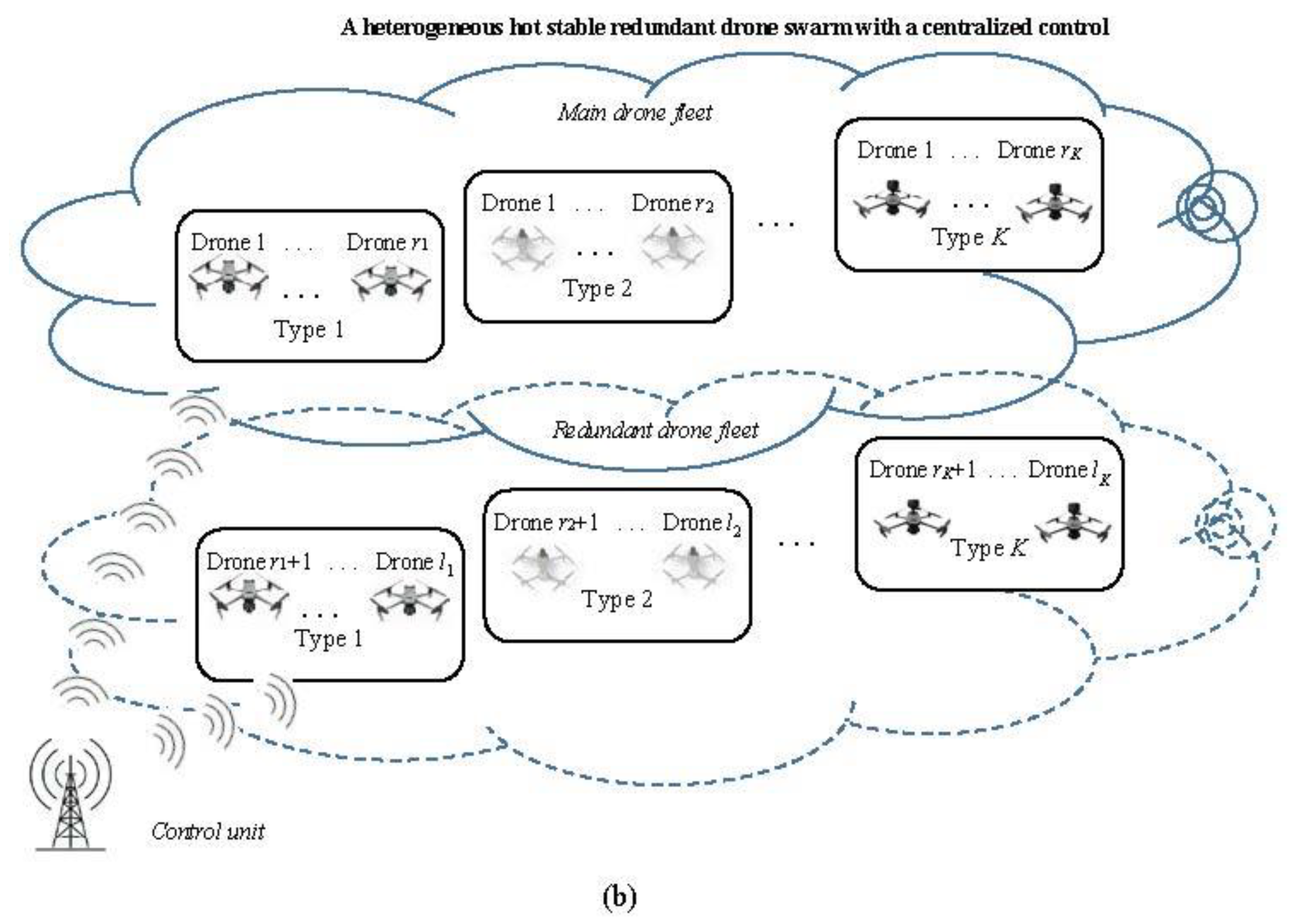
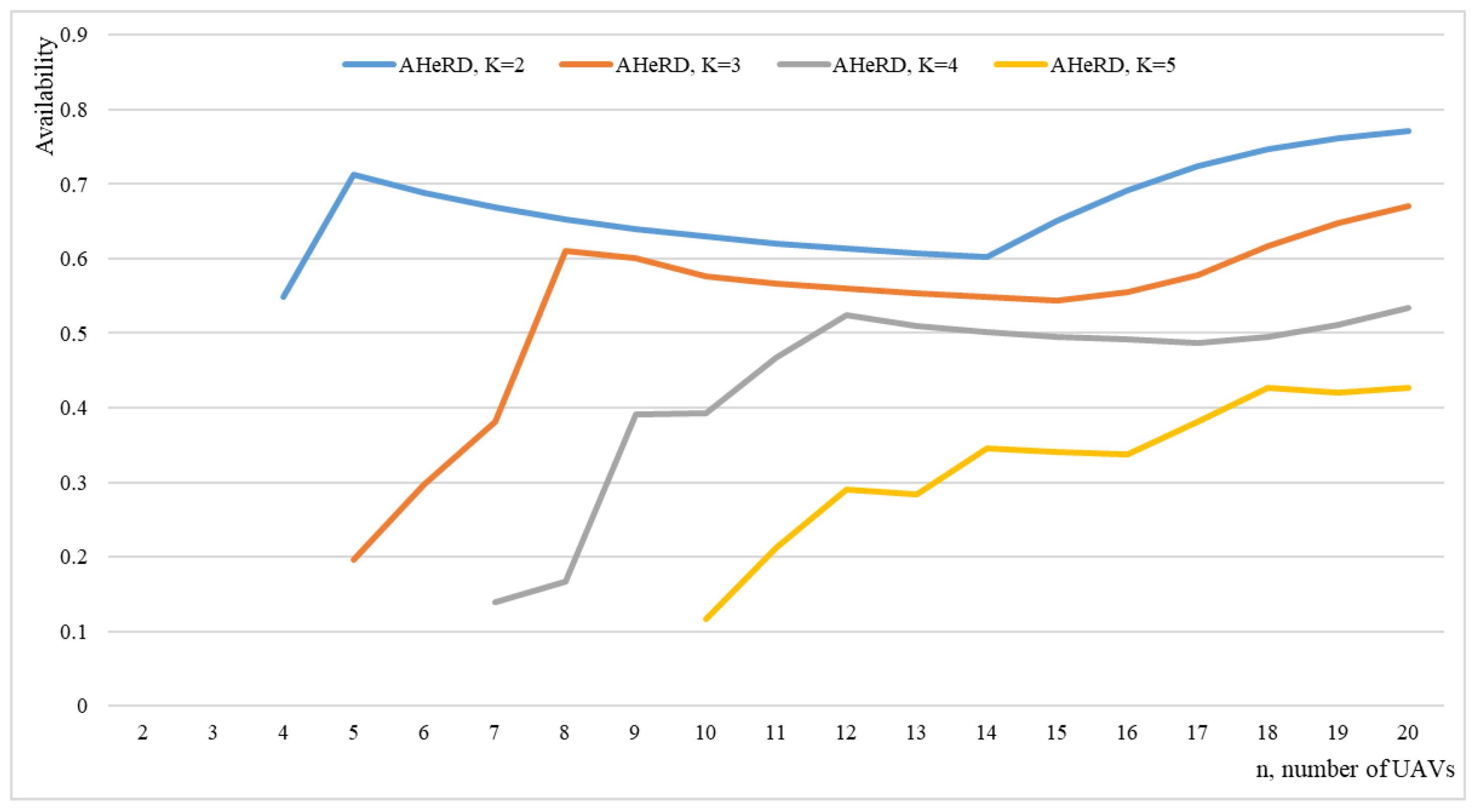
4.4. Heterogeneous Hot Stable Redundant Drone Swarm
5. Conclusions
- Homogenous irredundant drone swarm;
- Homogenous hot stable redundant drone swarm;
- Heterogeneous irredundant drone swarm;
- Heterogeneous hot stable redundant drone swarm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chittoor, P.K.; Chokkalingam, B.; Mihet-Popa, L. A Review on UAV Wireless Charging: Fundamentals, Applications, Charging Techniques and Standards. IEEE Access 2021, 9, 69235–69266. [Google Scholar] [CrossRef]
- Kumar, A.; Augusto de Jesus Pacheco, D.; Kaushik, K.; Rodrigues, J.J.P.C. Futuristic View of the Internet of Quantum Drones: Review, Challenges and Research Agenda. Veh. Commun. 2022, 36, 100487. [Google Scholar] [CrossRef]
- Li, Y.; Liu, M.; Jiang, D. Application of Unmanned Aerial Vehicles in Logistics: A Literature Review. Sustainability 2022, 14, 14473. [Google Scholar] [CrossRef]
- Mukhamediev, R.I.; Symagulov, A.; Kuchin, Y.; Zaitseva, E.; Bekbotayeva, A.; Yakunin, K.; Assanov, I.; Levashenko, V.; Popova, Y.; Akzhalova, A.; et al. Review of Some Applications of Unmanned Aerial Vehicles Technology in the Resource-Rich Country. Appl. Sci. 2021, 11, 10171. [Google Scholar] [CrossRef]
- Puchalski, R.; Giernacki, W. UAV Fault Detection Methods, State-of-the-Art. Drones 2022, 6, 330. [Google Scholar] [CrossRef]
- Shelare, S.; Belkhode, P.; Nikam, K.C.; Yelamasetti, B.; Gajbhiye, T. A Payload Based Detail Study on Design and Simulation of Hexacopter Drone. Int. J. Interact. Des. Manuf. (IJIDeM) 2023, in press. [CrossRef]
- Abouelghit, F.A.; Alkady, G.I.; Daoud, R.M.; Amer, H.H.; Adly, I. Motor Failure Detection in FPGA-Based Fault-Tolerant Quadcopters. In Proceedings of the 2020 32nd International Conference on Microelectronics (ICM), Aqaba, Jordan, 14–17 December 2020. [Google Scholar] [CrossRef]
- Petritoli, E.; Leccese, F.; Ciani, L. Reliability and Maintenance Analysis of Unmanned Aerial Vehicles. Sensors 2018, 18, 3171. [Google Scholar] [CrossRef]
- Schiestl, M.; Marcolini, F.; Incurvati, M.; Capponi, F.G.; Starz, R.; Caricchi, F.; Rodriguez, A.S.; Wild, L. Development of a High Power Density Drive System for Unmanned Aerial Vehicles. IEEE Trans. Power Electron. 2021, 36, 3159–3171. [Google Scholar] [CrossRef]
- Ghazali, M.H.M.; Rahiman, W. An Investigation of the Reliability of Different Types of Sensors in the Real-Time Vibration-Based Anomaly Inspection in Drone. Sensors 2022, 22, 6015. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U. A Systematic Review of Advanced Sensor Technologies for Non-Destructive Testing and Structural Health Monitoring. Sensors 2023, 23, 2204. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.-H. Trustworthy Transaction Spreading Using Node Reliability Estimation in IoT Blockchain Networks. Appl. Sci. 2022, 12, 8737. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Qin, Z.; Eizad, A.; Lyu, S.-K. Numerical Investigation of the Mechanical Component Design of a Hexacopter Drone for Real-Time Fine Dust Monitoring. J. Mech. Sci. Technol. 2021, 35, 3101–3111. [Google Scholar] [CrossRef]
- Foreman, V.L.; Favaró, F.M.; Saleh, J.H.; Johnson, C.W. Software in Military Aviation and Drone Mishaps: Analysis and Recommendations for the Investigation Process. Reliab. Eng. Syst. Saf. 2015, 137, 101–111. [Google Scholar] [CrossRef]
- Khan, A.; Ivaki, N.; Madeira, H. Are UAVs’ Flight Controller Software Reliable? In Proceedings of the 2022 IEEE 27th Pacific Rim International Symposium on Dependable Computing (PRDC), Beijing, China, 28 November–1 December 2022. [Google Scholar] [CrossRef]
- Watanabe, K.; Machida, F. Availability Analysis of a Drone System with Proactive Offloading for Software Life-Extension. In Proceedings of the 2022 IEEE International Conference on Omni-layer Intelligent Systems (COINS), Barcelona, Spain, 1–3 August 2022. [Google Scholar] [CrossRef]
- Zhu, X.; Liang, C.; Yin, Z.; Shao, Z.; Liu, M.; Chen, H. A New Hierarchical Software Architecture towards Safety-Critical Aspects of a Drone System. Front. Inf. Technol. Electron. Eng. 2019, 20, 353–362. [Google Scholar] [CrossRef]
- Bithas, P.S.; Michailidis, E.T.; Nomikos, N.; Vouyioukas, D.; Kanatas, A.G. A Survey on Machine-Learning Techniques for UAV-Based Communications. Sensors 2019, 19, 5170. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, Z.; Kou, L. Reliable UAV Monitoring System Using Deep Learning Approaches. IEEE Trans. Reliab. 2022, 71, 973–983. [Google Scholar] [CrossRef]
- Favarò, F.M.; Saleh, J.H. Application of Temporal Logic for Safety Supervisory Control and Model-Based Hazard Monitoring. Reliab. Eng. Syst. Saf. 2018, 169, 166–178. [Google Scholar] [CrossRef]
- Petritoli, E.; Leccese, F.; Ciani, L. Reliability Assessment of UAV Systems. In Proceedings of the 2017 IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), Padua, Italy, 21–23 June 2017. [Google Scholar] [CrossRef]
- Toma, C.; Popa, M.; Iancu, B.; Doinea, M.; Pascu, A.; Ioan-Dutescu, F. Edge Machine Learning for the Automated Decision and Visual Computing of the Robots, IoT Embedded Devices or UAV-Drones. Electronics 2022, 11, 3507. [Google Scholar] [CrossRef]
- Czyża, S.; Szuniewicz, K.; Kowalczyk, K.; Dumalski, A.; Ogrodniczak, M.; Zieleniewicz, Ł. Assessment of Accuracy in Unmanned Aerial Vehicle (UAV) Pose Estimation with the REAL-Time Kinematic (RTK) Method on the Example of DJI Matrice 300 RTK. Sensors 2023, 23, 2092. [Google Scholar] [CrossRef]
- Debus, P.; Rodehorst, V. Multi-Scale Flight Path Planning for UAS Building Inspection. In Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2020; pp. 1069–1085. [Google Scholar] [CrossRef]
- Shao, P.-C. Risk Assessment for UAS Logistic Delivery under UAS Traffic Management Environment. Aerospace 2020, 7, 140. [Google Scholar] [CrossRef]
- Ashush, N.; Greenberg, S.; Manor, E.; Ben-Shimol, Y. Unsupervised Drones Swarm Characterization Using RF Signals Analysis and Machine Learning Methods. Sensors 2023, 23, 1589. [Google Scholar] [CrossRef] [PubMed]
- Feuerriegel, S.; Geraldes, R.; Goncalves, A.; Liu, Z.; Prendinger, H. Interface Design for Human-Machine Collaborations in Drone Management. IEEE Access 2021, 9, 107462–107475. [Google Scholar] [CrossRef]
- Sakib, M.N.; Chaspari, T.; Behzadan, A.H. A Feedforward Neural Network for Drone Accident Prediction from Physiological Signals. Smart Sustain. Built Environ. 2021, 11, 1017–1041. [Google Scholar] [CrossRef]
- Pogorzelski, T.; Zielińska, T. Vision Based Navigation Securing the UAV Mission Reliability. In Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2022; pp. 251–263. [Google Scholar] [CrossRef]
- Xing, L.; Johnson, B.W. Reliability Theory and Practice for Unmanned Aerial Vehicles. IEEE Internet Things J. 2023, 10, 3548–3566. [Google Scholar] [CrossRef]
- Schacht-Rodríguez, R.; Ponsart, J.-C.; García-Beltrán, C.D.; Astorga-Zaragoza, C.M. Prognosis & Health Management for the Prediction of UAV Flight Endurance. IFAC-PapersOnLine 2018, 51, 983–990. [Google Scholar] [CrossRef]
- Dui, H.; Zhang, C.; Bai, G.; Chen, L. Mission Reliability Modeling of UAV Swarm and Its Structure Optimization Based on Importance Measure. Reliab. Eng. Syst. Saf. 2021, 215, 107879. [Google Scholar] [CrossRef]
- Basavaraju, S.; Rangan, V.A.; Rajgopal, S. Unmanned Aerial System (UAS) Hazard Identification, Reliability, Risk Analysis & Range Safety. In Proceedings of the 2019 International Conference on Range Technology (ICORT), Balasore, India, 15–17 February 2019. [Google Scholar] [CrossRef]
- Papakonstantinou, N.; Bashir, A.Z.; O’Halloran, B.; Bossuyt, D.L.V. Early Assessment of Drone Fleet Defence in Depth Capabilities for Mission Success. In Proceedings of the 2019 Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 28–31 January 2019. [Google Scholar] [CrossRef]
- Almeida, M.; Hildmann, H.; Solmaz, G. Distributed UAV-swarm-based real-time geomatic data collection under dynamically changing resolution requirements. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W6, 5–12. [Google Scholar] [CrossRef]
- Silva, M.R.; Souza, E.S.; Alsina, P.J.; Leite, D.L.; Morais, M.R.; Pereira, D.S.; Nascimento, L.B.P.; Medeiros, A.A.D.; Junior, F.H.C.; Nogueira, M.B.; et al. Performance Evaluation of Multi-UAV Network Applied to Scanning Rocket Impact Area. Sensors 2019, 19, 4895. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, M.; Dui, H.; Ren, Y.; Sun, B.; Yang, D.; Wang, Z. Importance Measure-Based Phased Mission Reliability and UAV Number Optimization for Swarm. Reliab. Eng. Syst. Saf. 2022, 223, 108478. [Google Scholar] [CrossRef]
- Fesenko, H.; Kharchenko, V.; Zaitseva, E. Evaluating Reliability of a Multi-Fleet with a Reserve Drone Fleet: An Approach and Basic Model. In Proceedings of the 2019 International Conference on Information and Digital Technologies (IDT), Zilina, Slovakia, 25–27 June 2019. [Google Scholar] [CrossRef]
- Tahir, A.; Böling, J.; Haghbayan, M.-H.; Toivonen, H.T.; Plosila, J. Swarms of Unmanned Aerial Vehicles—A Survey. J. Ind. Inf. Integr. 2019, 16, 100106. [Google Scholar] [CrossRef]
- Rusnak, P.; Kvassay, M.; Zaitseva, E.; Kharchenko, V.; Fesenko, H. Reliability Assessment of Heterogeneous Drone Fleet With Sliding Redundancy. In Proceedings of the 2019 10th International Conference on Dependable Systems, Services and Technologies (DESSERT), Leeds, UK, 5–7 June 2019. [Google Scholar] [CrossRef]
- Kuo, W.; Zhu, X. Importance Measures in Reliability, Risk, and Optimization; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Coppola, M.; McGuire, K.N.; De Wagter, C.; de Croon, G.C.H.E. A Survey on Swarming With Micro Air Vehicles: Fundamental Challenges and Constraints. Front. Robot. AI 2020, 7, 18. [Google Scholar] [CrossRef] [PubMed]
- Kliushnikov, I.; Kharchenko, V.; Fesenko, H. An Unmanned Aerial Vehicle as a Multi-State System. In Proceedings of the 2022 IEEE 16th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 22–26 February 2022. [Google Scholar] [CrossRef]
- Zaitseva, E.; Levashenko, V.; Kvassay, M.; Kharchenko, V. Reliability Evaluation of Heterogeneous Drone Fleet by Structure Function Based Method. In Proceedings of the 30th European Safety and Reliability Conference and 15th Probabilistic Safety Assessment and Management Conference, Venice, Italy, 1–5 November 2020. [Google Scholar] [CrossRef]
- Zaitseva, E.; Levashenko, V.; Brinzei, N.; Kovalenko, A.; Yelis, M.; Gopejenko, V.; Mukhamediev, R. Reliability Assessment of UAV Fleets. In Emerging Networking in the Digital Transformation Age, Proceedings of the IEEE lnternational Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering, Lviv-Slavske, Ukraine, 22–26 February 2022; Springer: Cham, Switzerland, 2023; pp. 335–357. [Google Scholar] [CrossRef]
- Abdallah, R.; Sarraf, C.; Kouta, R.; Gaber, J.; Wack, M. Communication Failure Analysis for a Fleet Formation Flight of Drones Based on Absorbing Markov Chain. In Safety and Reliability—Safe Societies in a Changing World; CRC Press: Boca Raton, FL, USA, 2018; pp. 2595–2601. [Google Scholar] [CrossRef]
- Morio, J.; Levasseur, B.; Bertrand, S. Drone Ground Impact Footprints with Importance Sampling: Estimation and Sensitivity Analysis. Appl. Sci. 2021, 11, 3871. [Google Scholar] [CrossRef]
- Xu, B.; Liu, T.; Bai, G.; Tao, J.; Zhang, Y.; Fang, Y. A Multistate Network Approach for Reliability Evaluation of Unmanned Swarms by Considering Information Exchange Capacity. Reliab. Eng. Syst. Saf. 2022, 219, 108221. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, Y.; Dui, H. Phased-Mission Reliability and Importance Measure Analysis for Linear and Circular UAV Swarms. Int. J. Math. Eng. Manag. Sci. 2023, 8, 176–193. [Google Scholar] [CrossRef]
- Guo, J.; Wang, L.; Wang, X. A Group Maintenance Method of Drone Swarm Considering System Mission Reliability. Drones 2022, 6, 269. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Z. Towards a Robust FANET: Distributed Node Importance Estimation-Based Connectivity Maintenance for UAV Swarms. Ad Hoc Netw. 2022, 125, 102734. [Google Scholar] [CrossRef]
- Bai, G.; Li, Y.; Fang, Y.; Zhang, Y.-A.; Tao, J. Network Approach for Resilience Evaluation of a UAV Swarm by Considering Communication Limits. Reliab. Eng. Syst. Saf. 2020, 193, 106602. [Google Scholar] [CrossRef]
- Floriano, B.; Borges, G.A.; Ferreira, H. Planning for Decentralized Formation Flight of UAV Fleets in Uncertain Environments with Dec-POMDP. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019. [Google Scholar] [CrossRef]
- Yuan, Z.; Jin, J.; Sun, L.; Chin, K.-W.; Muntean, G.-M. Ultra-Reliable IoT Communications with UAVs: A Swarm Use Case. IEEE Commun. Mag. 2018, 56, 90–96. [Google Scholar] [CrossRef]
- Guldenring, J.; Koring, L.; Gorczak, P.; Wietfeld, C. Heterogeneous Multilink Aggregation for Reliable UAV Communication in Maritime Search and Rescue Missions. In Proceedings of the 2019 International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Barcelona, Spain, 21–23 October 2019. [Google Scholar] [CrossRef]
- Gupta, R.; Shukla, A.; Mehta, P.; Bhattacharya, P.; Tanwar, S.; Tyagi, S.; Kumar, N. VAHAK: A Blockchain-Based Outdoor Delivery Scheme Using UAV for Healthcare 4.0 Services. In Proceedings of the IEEE INFOCOM 2020—IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, ON, Canada, 6–9 July 2020. [Google Scholar] [CrossRef]
- Patil, R.B.; Al-Dahidi, S.; Newale, S.; Arezki Mellal, M. Reliability Analysis of Centerless Grinding Machine Using Fault Tree Analysis. In Springer Series in Reliability Engineering; Springer: Cham, Switzerland, 2022; pp. 191–211. [Google Scholar] [CrossRef]
- Amari, S.V.; Dill, G. A New Method for Reliability Analysis of Standby Systems. In Proceedings of the 2009 Annual Reliability and Maintainability Symposium, Fort Worth, TX, USA, 26–29 January 2009. [Google Scholar] [CrossRef]
- Tannous, O.; Xing, L.; Rui, P.; Xie, M.; Ng, S.H. Redundancy Allocation for Series-Parallel Warm-Standby Systems. In Proceedings of the 2011 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 6–9 December 2011. [Google Scholar] [CrossRef]
- Fesenko, H.; Kharchenko, V. Reliability Models for a Multi-Fleet of Drones with Two-Level Hot Standby Redundancy Considering a Control System Structure. In Proceedings of the 2019 10th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Metz, France, 18–21 September 2019. [Google Scholar] [CrossRef]
- Pashchuk, Y.M.; Salnyk, Y.P.; Pashkovskyi, V.V.; Zaiets, Y.H.; Miskiv, V.M.; Shkiliuk, O.P. Method for Structural Optimization of Avionics of Unmanned Aerial Vehicle. Math. Model. Comput. 2020, 7, 373–388. [Google Scholar] [CrossRef]
- Guo, J.; Elsayed, E.A. Reliability of Balanced Multi-Level Unmanned Aerial Vehicles. Comput. Oper. Res. 2019, 106, 1–13. [Google Scholar] [CrossRef]
- Alshaibani, W.T.; Shayea, I.; Caglar, R.; Din, J.; Daradkeh, Y.I. Mobility Management of Unmanned Aerial Vehicles in Ultra–Dense Heterogeneous Networks. Sensors 2022, 22, 6013. [Google Scholar] [CrossRef]
- Shirey, R.; Rao, S.; Sundaram, S. Chimera: Exploiting UAS Flight Path Information to Optimize Heterogeneous Data Transmission. In Proceedings of the 2021 IEEE 29th International Conference on Network Protocols (ICNP), Dallas, TX, USA, 1–5 November 2021. [Google Scholar] [CrossRef]
- Osmic, N.; Tahirbegovic, A.; Tahirovic, A.; Bogdan, S. Failure Mode and Effects Analysis for Large Scale Multirotor Unmanned Aerial Vehicle Controlled by Moving Mass System. In Proceedings of the 2018 IEEE International Systems Engineering Symposium (ISSE), Rome, Italy, 1–3 October 2018. [Google Scholar] [CrossRef]
- Shafiee, M.; Zhou, Z.; Mei, L.; Dinmohammadi, F.; Karama, J.; Flynn, D. Unmanned Aerial Drones for Inspection of Offshore Wind Turbines: A Mission-Critical Failure Analysis. Robotics 2021, 10, 26. [Google Scholar] [CrossRef]
- Straub, J. Anti-Drone Capabilities: Using a Quality Assurance Technology to Identify Exploitable UAV Weaknesses. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021. [Google Scholar] [CrossRef]
- Walker, M.G. Next Generation Prognostics and Health Management for Unmanned Aircraft. In Proceedings of the 2010 IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2010. [Google Scholar] [CrossRef]
- Dingeldein, L. Simulation Framework for Real-Time PHM Applications in a System-of-Systems Environment. Aerospace 2023, 10, 58. [Google Scholar] [CrossRef]
- Paixao de Medeiros, I.; Ramos Rodrigues, L.; Strottmann Kern, C.; Duarte Coelho dos Santos, R.; Hideiti Shiguemori, E. Integrated Task Assignment and Maintenance Recommendation Based on System Architecture and PHM Information for UAVs. In Proceedings of the 2015 Annual IEEE Systems Conference (SysCon) Proceedings, Vancouver, BC, Canada, 13–16 April 2015. [Google Scholar] [CrossRef]
- Fan, H.; Fang, H.; Dong, Y.; Shi, H.; Ren, S. UAV Engine Fault and Diagnosis with Parameter Models Based on Telemetry Data. In Proceedings of the 2017 Prognostics and System Health Management Conference (PHM-Harbin), Harbin, China, 9–12 July 2017. [Google Scholar] [CrossRef]
- Barlow, R.E.; Proschan, F. Statistical Theory of Reliability and Life Testing; Holt, Rinehart and Winston: New York, NY, USA, 1975. [Google Scholar]
- Akers, S.B. Binary Decision Diagrams. IEEE Trans. Comput. 1978, C–27, 509–516. [Google Scholar] [CrossRef]
- Ibáñez-Llano, C.; Rauzy, A.; Meléndez, E.; Nieto, F. Hybrid Approach for the Assessment of PSA Models by Means of Binary Decision Diagrams. Reliab. Eng. Syst. Saf. 2010, 95, 1076–1092. [Google Scholar] [CrossRef]
- Rauzy, A.; Yang, L. Decision Diagram Algorithms to Extract Minimal Cutsets of Finite Degradation Models. Information 2019, 10, 368. [Google Scholar] [CrossRef]
- Reay, K.A.; Andrews, J.D. A Fault Tree Analysis Strategy Using Binary Decision Diagrams. Reliab. Eng. Syst. Saf. 2002, 78, 45–56. [Google Scholar] [CrossRef]
- Fesenko, H.; Kharchenko, V.; Bardis, N.; Kor, A.-L.; Brezhniev, Y. Drone Fleet Survivability Evaluation Based on Lanchester’s Modified Deterministic Model. Int. J. Circuits Syst. Signal Process. 2020, 14, 775–781. [Google Scholar] [CrossRef]
- Brînzei, N.; Aubry, J.-F. Graphs Models and Algorithms for Reliability Assessment of Coherent and Non-Coherent Systems. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2018, 232, 201–215. [Google Scholar] [CrossRef]
- Schneeweiss, W.G. A Short Boolean Derivation of Mean Failure Frequency for Any (Also Non-Coherent) System. Reliab. Eng. Syst. Saf. 2009, 94, 1363–1367. [Google Scholar] [CrossRef]
- Zhai, Q.; Xing, L.; Peng, R.; Yang, J. Aggregated Combinatorial Reliability Model for Non-Repairable Parallel Phased-Mission Systems. Reliab. Eng. Syst. Saf. 2018, 176, 242–250. [Google Scholar] [CrossRef]
- Zaitseva, E.; Levashenko, V.; Kostolny, J. Importance Analysis Based on Logical Differential Calculus and Binary Decision Diagram. Reliab. Eng. Syst. Saf. 2015, 138, 135–144. [Google Scholar] [CrossRef]
- Steinbach, B.; Posthoff, C. Boolean Differential Equations; Springer: Cham, Switzerland, 2013; pp. 49–127. [Google Scholar] [CrossRef]
- Armstrong, M.J. Joint Reliability-Importance of Components. IEEE Trans. Reliab. 1995, 44, 408–412. [Google Scholar] [CrossRef]
- Heidtmann, K.D. Improved Method of Inclusion-Exclusion Applied to k-out-of-n Systems. IEEE Trans. Reliab. 1982, R-31, 36–40. [Google Scholar] [CrossRef]





| 0 0 0 | 0 | − | − | − |
| 0 0 1 | 0 | − | − | 0 |
| 0 1 0 | 0 | − | 0 | − |
| 0 1 1 | 1 | − | 1 | 1 |
| 1 0 0 | 0 | 0 | − | − |
| 1 0 1 | 1 | 1 | − | 1 |
| 1 1 0 | 1 | 1 | 1 | − |
| 1 1 1 | 1 | 0 | 0 | 0 |
| SI | 0.5 | 0.5 | 0.5 | |
| BI | 0.375 | 0.350 | 0.350 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaitseva, E.; Levashenko, V.; Mukhamediev, R.; Brinzei, N.; Kovalenko, A.; Symagulov, A. Review of Reliability Assessment Methods of Drone Swarm (Fleet) and a New Importance Evaluation Based Method of Drone Swarm Structure Analysis. Mathematics 2023, 11, 2551. https://doi.org/10.3390/math11112551
Zaitseva E, Levashenko V, Mukhamediev R, Brinzei N, Kovalenko A, Symagulov A. Review of Reliability Assessment Methods of Drone Swarm (Fleet) and a New Importance Evaluation Based Method of Drone Swarm Structure Analysis. Mathematics. 2023; 11(11):2551. https://doi.org/10.3390/math11112551
Chicago/Turabian StyleZaitseva, Elena, Vitaly Levashenko, Ravil Mukhamediev, Nicolae Brinzei, Andriy Kovalenko, and Adilkhan Symagulov. 2023. "Review of Reliability Assessment Methods of Drone Swarm (Fleet) and a New Importance Evaluation Based Method of Drone Swarm Structure Analysis" Mathematics 11, no. 11: 2551. https://doi.org/10.3390/math11112551
APA StyleZaitseva, E., Levashenko, V., Mukhamediev, R., Brinzei, N., Kovalenko, A., & Symagulov, A. (2023). Review of Reliability Assessment Methods of Drone Swarm (Fleet) and a New Importance Evaluation Based Method of Drone Swarm Structure Analysis. Mathematics, 11(11), 2551. https://doi.org/10.3390/math11112551









