Optimal Robust Tracking Control of Injection Velocity in an Injection Molding Machine

Abstract

Injection molding is a critical component of modern industrial operations, and achieving fast and stable control of injection molding machines (IMMs) is essential for producing high-quality plastic products. This paper focuses on solving an optimal tracking control problem of the injection velocity that arises in a typical nonlinear IMM. To this end, an efficient optimal robust controller is proposed and designed. The nonlinear injection velocity servo system is first approximately linearized at iteration points using the first-order Taylor expansion approach. Then, at each time node in the optimization process, the relevant algebraic Riccati equation is introduced, and the solution is used to construct an optimal robust feedback controller. Furthermore, a rigorous Lyapunov theorem analysis is employed to demonstrate the global stability properties of the proposed feedback controller. The results from numerical simulations show that the proposed optimal robust control strategy can successfully and rapidly achieve the best tracking of the intended injection velocity trajectory within a given time.

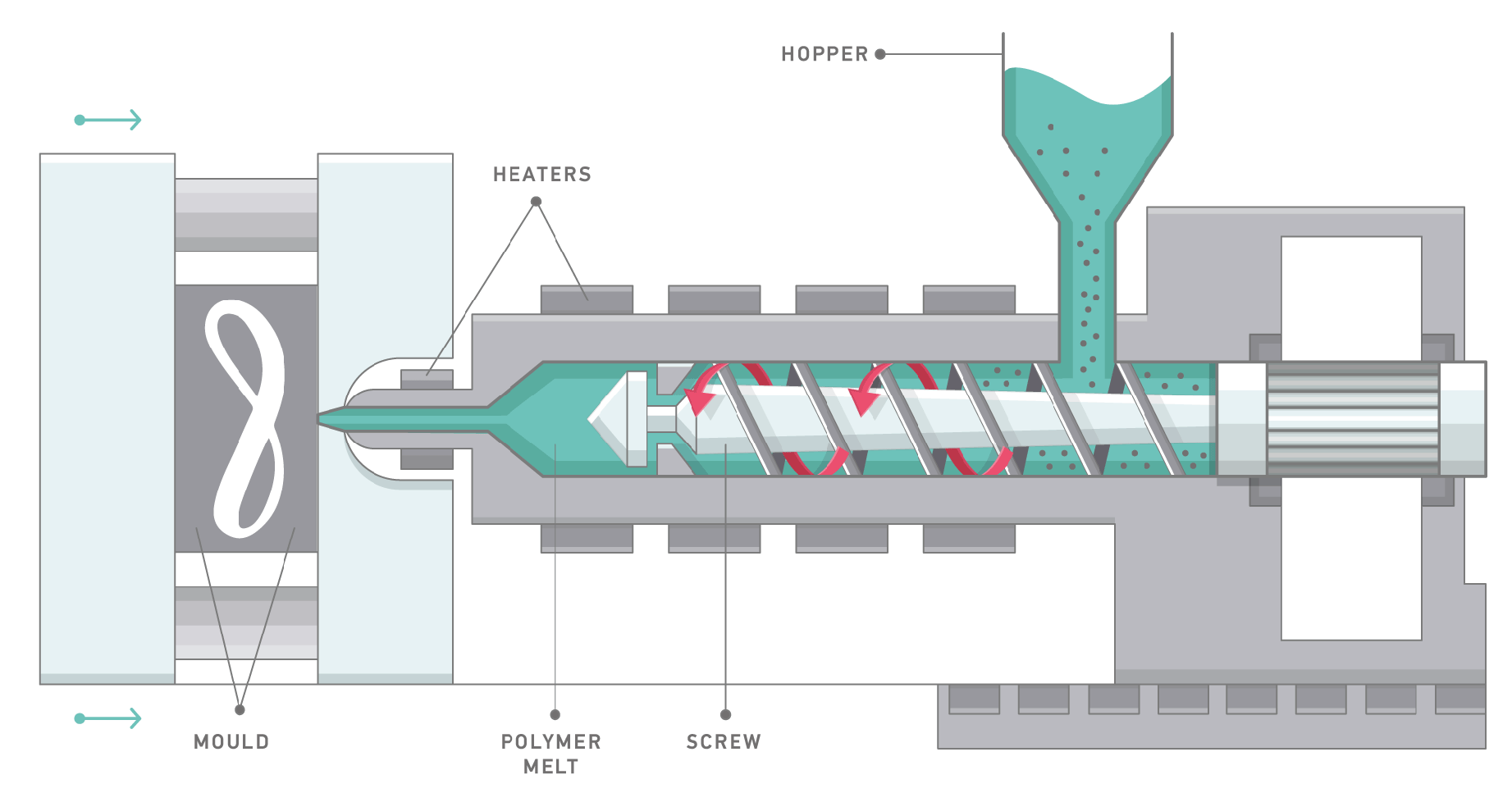
1. Introduction

Plastic products are extensively used in our daily life and industries, such as in the automobile industry, aerospace, military technology, and other fields, due to their good plasticity, chemical stability, and lightweight [1,2]. According to market statistics, the total plastic production in the world in 2021 was 399 million tons (384 million tons in 2020), an increase of 3.7% over 2020 (the same increase of 4.6% in 2020). Data shows that plastic products have become an indispensable part of all walks of life and people’s daily life. From now until 2030, the injection plastic market is anticipated to develop at a compound annual growth rate of 4.90%.

Injection molding (IM) technology has the advantages of high production speed, high efficiency, process automation, and the ability to manufacture complex shaped parts [3,4,5]. Currently, due to its dependable, high-quality performance, IM has become one of the most widely commonly applied processes for producing plastic components. IM is a sophisticated and continuous cycle operation, wherein various requirements for the IMM (as shown in Figure 1) settings for different products and stages are required. The quality of plastic products is directly connected to processing facilities, product cooling time, and subsequent processing technology. Poor management of variables such as temperature, pressure, and molding cycle will result in poor quality of the final molded plastic and affect their use [6,7,8]. However, as we are now in the field of intelligent manufacturing, the overall automation level of IM equipment is still very low, and the vast majority of process parameters still need to be adjusted manually, which often leads to unstable product quality and poor product consistency, which requires an urgent need for technological innovation to improve competitiveness. The development of related technologies, such as plastic molding, will have a profound impact on the competitiveness of the discrete manufacturing industry in the future and will also have an important radiative impact on the industrial sector. Therefore, the intelligent automation of various IMMs has become a hotspot in the study of discrete industrial manufacturing [9,10,11,12,13,14,15,16,17,18,19].

Recent years have seen a large number of pertinent studies on control and optimization methods for the temperature, pressure, and injection velocity in various IMMs [20,21,22,23,24,25,26,27,28,29,30,31,32,33]. For instance, Cho et al. [20] presented an open-loop control approach to realizing the pre-position tracking control of the melt injection flow inside an IMM. Dubay [22] developed an all-encompassing learning and self-optimizing model predictive control approach to regulate the melt temperature in an IMM. Yao et al. [23] studied a time-optimal control problem for the barrel temperature regulation in an IMM. Ruan et al. [29] proposed an intelligent temperature compensation control strategy for the injection molding process under dynamic conditions using feedforward iterative learning control and the Q-learning method. Stemmler et al. [30] proposed a norm-optimal iterative learning controller to track the desired cavity pressure value of an IMM throughout the cycle. Guo et al. [31] proposed a novel reinforcement learning framework and a self-predictive artificial neural network model to set appropriate process parameters. Tian et al. [32] proposed a double-controller scheme for the injection velocity control in thermoplastic injection molding. Yang et al. [33] proposed an improved PID method using the unsaturated integral and passivation differential to achieve injection velocity control. Although these control methods have proven good dynamic performance, on the one hand, most methods focus on open-loop control of IMMs and often have problems such as poor robustness in practical applications. On the other hand, some of the above-mentioned methods are more complex and often involve tedious calculations that are difficult to implement in practical physical environments. Therefore, it is very meaningful to design more efficient optimization and control methods to achieve quality control in the injection molding process. Motivated and inspired by the above, in this paper, we carry out further research on the velocity control approach for a typical type of injection machines, and we will consider designing a robust optimal feedback controller to realize the optimal tracking control of the intended injection velocity trajectory.

In an IMM, in addition to controlling the injection temperature and injection pressure, controlling the injection velocity has also been recognized as a key variable in the molten polymer. It indicates the rate of the polymer melt flowing to the mold cavity during the filling phase. The velocity has a significant impact on cavity pressure, which in turn may affect the quality of the product in terms of residual stress, shrinkage, impact strength, product morphology, and surface characteristics. For example, during the high-speed filling process, when the melt is injected into the cavity via the nozzle and gating system, a significant amount of frictional heat is generated, thereby increasing the melt temperature. However, if the cavity is filled at a low injection speed, the filling time will be prolonged. Conversely, if the mold cavity is filled at a high injection speed, the welding of the insert rear may be unsatisfactory, leading to a reduction in product strength. The melt injected into the cavity initially cools down rapidly and becomes more viscous, requiring higher pressure for subsequent filling [34]. Thus, selecting an appropriate injection velocity is also crucial for controlling the properties of injection-molded products.

In this paper, we study an optimal tracking control problem of the injection velocity in a typical class of IMMs with nonlinear characteristics, and an effective optimal robust state feedback controller is proposed and designed to achieve the fast-tracking of the given injection velocity at the given time. In practice, maintaining the actual injection velocity to follow a desired profile can be challenging due to the complex effects of numerous factors on velocity dynamics. Achieving high precision and robust control of injection velocity is therefore critical to improving product quality and reducing cycle-to-cycle variation. Furthermore, due to the nonlinearity of electrohydraulic actuators in the IMMs, the solutions of the related control and the proof of global stability and robustness for such methods remain a challenging task. In conventional methods, control of such systems is a non-trivial problem because of the nonlinearities and underactuation in their dynamics. In this current work, our aim mainly focuses on developing an efficient computational optimal control method using advanced control technology for the fast and robust tracking of injection velocity in a typical IMM. To address this issue, we first formulate a nonlinear tracking control problem for the injection velocity in the injection molding process. Given the nonlinear characteristics and the need for simplified controller design, we use Taylor’s first-order expansion to linearize the original nonlinear dynamical system at the iterative point. This transforms the optimal tracking control problem governed by the original continuous nonlinear system into one governed by a set of simplified linear systems. From a computational optimal control perspective, we propose an optimal feedback robust controller based on solving Riccati equations. This converts the design of a closed-loop controller for linear systems into solving a series of Riccati equations. We then use the Lyapunov theory to prove that our proposed controller has global stability properties. The optimal robust control strategy we propose can efficiently and quickly achieve optimal tracking of the desired injection velocity trajectory within a given time frame. Numerical simulations confirm the feasibility and efficiency of our feedback stabilization controller design. The proposed control method retains the advantages of classical linear optimal control and it has fast and accurate tracking of reference setpoints under moderate variations. This is a first step and quite a preliminary attempt in the intelligent injection molding process manufacturing area. Compared with traditional control methods for IMMs, such as PID and model predictive control (MPC) strategies, our proposed control strategy has some advantages. For example, unlike traditional PID control and MPC in IMMs, the proposed optimal control method is of proven global stability. Moreover, in traditional PID control, the selection of the controller’s parameters usually relies on a heuristic tuning procedure. The approach recommended in this work is simple and efficient, and can also be easily generalized to other types of industrial process optimal control systems.

In summary, the contributions in current work are listed as follows:

(1)

The dynamic mathematical modeling of the speed servo system of the variable speed pump-controlled hydraulic cylinder in a typical IMM is carried out, and the differential plane flatness characteristics of the nonlinear dynamic system are proven.

(2)

The underlying nonlinear dynamic system is high-fidelity linearized using Taylor series expansion, which can help further streamline the design of the ensuing robust controller.

(3)

A stabilizing optimal controller is proposed for the actuator, and it is demonstrated that the suggested feedback controller exhibits properties of global stability based on a rigorous Lyapunov theoretical analysis.

(4)

Sufficient numerical experimental results verify the viability and efficiency of the proposed approach.

The rest of this paper is organized as follows: In Section 2, the dynamics of an IMM is presented. The differential flatness properties of the injection hydraulic system are verified. The optimal tracking control problem of injection velocity is established. In Section 3, the dynamic model of the IMM is approximately linearized by Taylor series expansion and the optimal control problem is solved. In Section 4, the global asymptotic stability of the controller is demonstrated. In Section 5, numerical simulations are conducted to further verify the accuracy of the proposed controller. Finally, a summary and prospect of the current work are given.

2. Problem Formulation

2.1. Mathematical Model of the IMM

Figure 2 shows an organizational layout of the control hydraulic system used in a typical IMM. The entire system consists of a signal measurement control system and a hydraulic system. The hydraulic system is composed of a motor system and a loading system. The output control voltage of the signal measurement control system regulates the speed of the permanent magnet synchronous servo motor (PMSM) through the servo driver. The tiny time constant of the PMSM can typically be described as a first-order inertial element. As a result, the PMSM is reduced to a first-order inertial chain, which can be expressed as

$$G\left(s\right)=\frac{K_v}{T_{d}s+1},$$

(1)

where $K_v$ is the speed gain determined by the characteristics of the servo drive, and $T_d$ is a given small constant. The PMSM has a low moment of inertia and quick acceleration and deceleration response times. In the majority of industrial operations, servo motors have been shown to be aperiodic and overdamped. Consequently, the servo motor model can be denoted as:

$$\frac{\mathrm{d}n\left(t\right)}{\mathrm{d}t}=\frac{K_{v}u\left(t\right)-n\left(t\right)}{T_d},$$

(2)

where $n\left(t\right)$ is the motor speed value, and $u\left(t\right)$ is the input signal of the servo drive.

The gear pump is rotated by the PMSM, and the output of the gear pump is controlled by the servo motor speed. The existence of a safety valve can prevent high motor speed wear gear pump. Moreover, the input voltage signal $u\left(t\right)$ complies with the following bound restrictions

$$u_{min}\le u\left(t\right)\le u_{max},$$

(3)

where $u_{min}$ and $u_{max}$ are given constants due to the real physical conditions.

Furthermore, the output flow of the gear pump can be formulated as:

$$q\left(t\right)=D_{p}n\left(t\right)-\frac{C_{ip}{F}_p\left(t\right)}{\eta }-\frac{n\left(t\right)F_p\left(t\right)D_p}{{\beta }_e},$$

(4)

where $q\left(t\right)$ denotes the output flow, and $D_p$ and $C_{ip}$ denote the displacement and leakage coefficient of the quantitative pump, respectively. $F_p$ denotes the output pressure, $\eta$ denotes the viscosity of the oil, and ${\beta }_e$ denotes the elastic modulus of the oil volume.

The pressure sensor may collect the drive system pressure $F_p$ and transmit that information to the signal measurement and the control system. The pressure drop of the high-pressure pipeline can also be disregarded because the hydraulic pipeline is composed of stainless steel. As a result, the flow change of the wheelless chamber is formulated as:

$$q\left(t\right)=A_1\dot{y}\left(t\right)+\frac{C_{ep}{F}_p\left(t\right)}{\eta }+\frac{(V_g+A_{1}y\left(t\right)){\dot{F}}_p\left(t\right)}{{\beta }_e},$$

(5)

where $A_1$ denotes the effective area of the rodless cavity of the hydraulic cylinder, $y\left(t\right)$ denotes the displacement, $C_{ep}$ denotes the total leakage coefficient, $V_g$ denotes the total volume of the high-pressure chamber. The displacement sensor measures the displacement $y\left(t\right)$ and the corresponding speed $\dot{y}\left(t\right)$ and transmits them to the signal measurement and control system.

The loading system that consists of a three-phase motor and an Atos proportional relief valve is an exact replica of the drive system. The electro-hydraulic loading device, which mimics the linear motion of the hydraulic cylinder, controls the output force of the loading cylinder. As a result, the hydraulic cylinder’s motion force balance can be formulated as:

$$F_p\left(t\right)A_1=m_t\ddot{y}\left(t\right)+B_p\dot{y}\left(t\right)+Ky+F_L,$$

(6)

where $m_t$ denotes the equivalent mass of the piston rod and load, $B_p$ denotes the viscous damping coefficient of the drive cylinder, K denotes the elastic coefficient of the load, and $F_L$ denotes the external load.

The hydraulic control system under consideration utilizes sensors to gather signals related to pressure, displacement, and velocity. The collected signals are then transmitted to a control system for signal measurement and analysis. The system compares the speed signal in conjunction with the required driving cylinder’s speed signal and generates a control signal accordingly. This control signal is employed to regulate the speed function of the servo driver and the PMSM, based on the input voltage. Eventually, indirect flow control for the hydraulic cylinder and the complete control of the driving hydraulic cylinder are provided by adjusting the electric motor’s rotational speed.

To summarize, we have constructed the evolution process of the speed servo system of the variable speed pump controlling the hydraulic cylinder in an IMM. Based on the above analysis, it can be deduced that the dynamic system is a complex coupled dynamics model with nonlinear characteristics. In order to simplify the subsequent optimal control problem establishment and controller design, we define $[x_1\left(t\right),x_2\left(t\right),x_3\left(t\right),x_4\left(t\right)]=[n\left(t\right),F_p\left(t\right),y\left(t\right),\dot{y}\left(t\right)]$ as new state variables of the underlying hydraulic system. Then, the mathematical model of the variable speed pump-controlled hydraulic cylinder speed servo system can be formulated as:

$$\{\begin{array}{ll}{\dot{x}}_1(t)=\frac{K_{v}u-x_1(t)}{T_d},& \text{(7a)}\\ \left.{\dot{x}}_2(t)=\frac{{\beta }_e}{V_g+A_1{x}_3(t)}[D_p{x}_1(t)(1-\frac{x_2(t)}{{\beta }_e}))-(C_{ip}+C_{ep})\eta x_2(t)-A_1{x}_4(t)\right],& \text{(7b)}\\ {\dot{x}}_3(t)=x_4(t),& \text{(7c)}\\ {\dot{x}}_4(t)=\frac{1}{m_t}\left(A_1{x}_2(t)-B_p{x}_4(t)-K{x}_3(t)-F_L\right),& \text{(7d)}\end{array}$$

Alternatively, the state-space model (7) can be also expressed as

$$\left(\begin{array}{c}{\dot{x}}_1\left(t\right)\\ {\dot{x}}_2\left(t\right)\\ {\dot{x}}_3\left(t\right)\\ {\dot{x}}_4\left(t\right)\end{array}\right)=\left(\begin{array}{c}-\frac{x_1\left(t\right)}{T_d}\\ \frac{{\beta }_e}{V_g+A_1{x}_3\left(t\right)}\left[D_p{x}_1\left(t\right)(1-\frac{x_2\left(t\right)}{{\beta }_e}))-(C_{ip}+C_{ep})\eta x_2\left(t\right)-A_1{x}_4\left(t\right)\right]\\ x_4\left(t\right)\\ \frac{1}{m_t}\left(A_1{x}_2\left(t\right)-B_p{x}_4\left(t\right)-K{x}_3\left(t\right)-F_L\right)\end{array}\right)+\left(\begin{array}{c}\frac{K_v}{T_d}\\ 0\\ 0\\ 0\end{array}\right)u\left(t\right)$$

(8)

As a result, the dynamic model (8) can be expressed in the following compact form:

$$\dot{\mathit{x}}\left(t\right)={\mathit{f}}_{\mathbf{1}}\left(\mathit{x}\left(\mathit{t}\right)\right)+{\mathit{f}}_{\mathbf{2}}\left(\mathit{x}\left(\mathit{t}\right)\right)u\left(t\right),$$

(9)

where $\mathit{x}\left(t\right)\in {\mathbb{R}}^{4\times 1}$, ${\mathit{f}}_{\mathbf{1}}\left(\mathit{x}\left(\mathit{t}\right)\right)\in {\mathbb{R}}^{4\times 1}$, ${\mathit{f}}_{\mathbf{2}}\left(\mathit{x}\left(\mathit{t}\right)\right)\in {\mathbb{R}}^{4\times 1}$ and $u\left(t\right)\in \mathbb{R}$.

2.2. Objective Function

The quality of the final injection-molded products depends on the IMMs’ ability to accurately track the target injection velocity within a specific time T. Therefore, the main aim of this paper is to construct an optimal control signal $u\left(t\right)$ that enables fast tracking of the target injection velocity while consuming the least amount of energy possible. As a result, the following performance cost function is defined in this study to be minimized:

$$\begin{array}{cc}\hfill \underset{u\left(t\right)}{min}:J\left(u\left(t\right)\right)& =\frac{1}{2}{\int }_0^T\left\{{\left[v\left(t\right)-v_d\left(t\right)\right]}^2+u^2\left(t\right)\right\}dt,\hfill \end{array}$$

(10)

where $v_d\left(t\right)$ denotes desired injection velocity during injection molding process; it is a time-dependent state trajectory variable, which can be set in advance according to the actual system operation requirements. As a result, we propose the following Problem P${}_0$ in the IMM.

Problem 1. 

Given a dynamic system (8) of an injection molding hydraulic system with strong nonlinear characteristics, the main aim is to design an optimal robust controller $u\left(t\right)$ to minimize the objective function (10) to make the speed of the injecting molding $v\left(t\right)$ track the desired injection velocity output trajectory $v_d\left(t\right)$ within a given time T.

3. Optimal Robust Controller Design

This section aims to devise an optimal robust controller to tackle Problem P${}_0$. The first step in this process involves a comprehensive analysis of the differential flatness characteristics of system (7). Following this, the linearization procedure is executed using the Taylor series expansion technique to streamline the original dynamic model. The last step entails designing an optimal feedback robust controller that takes into account model uncertainty and external disturbances.

3.1. Differential Flatness Properties of System (7)

In order to design the optimal controller rigorously in the subsequent section, we firstly need to prove that the hydraulic system defined in (7) is differentially flat. In dynamic model (7), note that the position of the driving hydraulic cylinder is selected as the flat output, that is, $y\left(t\right)=x_3\left(t\right)$. We have

$${\dot{x}}_3\left(t\right)=x_4\left(t\right)\Rightarrow x_4\left(t\right)=\dot{y}\left(t\right),$$

(11)

which means that $x_4\left(t\right)$ denotes a differential function. Then, we note

$${\dot{x}}_4\left(t\right)=\frac{1}{m_t}\left(A_1{x}_2\left(t\right)-B_p{x}_4\left(t\right)-K{x}_3\left(t\right)-F_L\right)\Rightarrow \ddot{y}\left(t\right)=\frac{1}{m_t}\left(A_1{x}_2\left(t\right)-B_p\dot{y}-Ky\left(t\right)-F_L\right).$$

(12)

Next, from the dynamic model (7), one obtains that

$${\dot{x}}_2\left(t\right)=\frac{{\beta }_e}{V_g+A_1{x}_3\left(t\right)}\left[D_p{x}_1\left(t\right)(1-\frac{x_2\left(t\right)}{{\beta }_e}))-(C_{ip}+C_{ep})\eta x_2\left(t\right)-A_1{x}_4\left(t\right)\right].$$

(13)

Note that (13) can be solved with respect to $x_1\left(t\right)$, indicating that $x_1\left(t\right)$ is ultimately a differential function. Finally, from model (7), one has

$$u\left(t\right)=\frac{{\dot{x}}_1\left(t\right)T_d+x_1\left(t\right)}{K_v}.$$

(14)

This implies that $u\left(t\right)$ is also a differential function. As a result, we complete the demonstration of the hydraulic system’s differential flatness qualities. The hydraulic system’s control loop setpoints can be also calculated using the differential flatness property.

3.2. Taylor Series Expansion

In our work, in order to efficiently design the feedback controller for the original nonlinear system (8), we first use the first-order Taylor series expansion method [35] to linearize and approximate the original nonlinear system (8) in this section. The linearization process is mainly based on the first-order Taylor expansion and the computation of the associated Jacobian matrices. The nonlinear system (8) undergoes an approximate linearization around the temporary operating point $({\mathit{x}}^{*},u^{*})$, where ${\mathit{x}}^{*}$ is the current value and $u^{*}$ is the last sampled value. The modeling error due to the omission of higher order terms from the Taylor series expansion can also be seen as a perturbation. Therefore, the linearization process results in the following form:

$$\dot{\mathit{x}}\left(\mathit{t}\right)=\mathit{A}\mathit{x}\left(\mathit{t}\right)+\mathit{B}u\left(t\right)+\tilde{\mathit{d}},$$

(15)

where $\tilde{\mathit{d}}$ represents the modeling error due to the linearization process. $\mathit{A}$ and $\mathit{B}$ are Jacobian expansions that can be computed by the Taylor series expansion:

$$\begin{array}{cc}\hfill \mathit{A}& =\frac{\partial [{\mathit{f}}_{\mathbf{1}}\left(\mathit{x}\left(\mathit{t}\right)\right)+{\mathit{f}}_{\mathbf{2}}\left(\mathit{x}\left(\mathit{t}\right)\right)u\left(t\right)]}{\partial \mathit{x}}{\mid }_{(x^{*},u^{*})}\hfill \\ \hfill & =\frac{\partial {\mathit{f}}_{\mathbf{1}}\left(\mathit{x}\left(\mathit{t}\right)\right)}{\partial \mathit{x}}{\mid }_{(x^{*},u^{*})}+\frac{\partial {\mathit{f}}_{\mathbf{2}}\left(\mathit{x}\left(\mathit{t}\right)\right)u\left(t\right)}{\partial \mathit{x}}{\mid }_{(x^{*},u^{*})}\hfill \\ \hfill & =\frac{\partial {\mathit{f}}_{\mathbf{1}}\left(\mathit{x}\left(\mathit{t}\right)\right)}{\partial \mathit{x}}{\mid }_{(x^{*},u^{*})},\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill \mathit{B}& =\frac{\partial [{\mathit{f}}_{\mathbf{1}}\left(\mathit{x}\left(\mathit{t}\right)\right)+{\mathit{f}}_{\mathbf{2}}\left(\mathit{x}\left(\mathit{t}\right)\right)u\left(t\right)]}{\partial \mathit{u}}{\mid }_{(x^{*},u^{*})}\hfill \\ & =\frac{\partial {\mathit{f}}_{\mathbf{2}}\left(\mathit{x}\left(\mathit{t}\right)\right)}{\partial u}{\mid }_{(x^{*},u^{*})},\hfill \end{array}$$

(16b)

where $\frac{\partial {\mathit{f}}_{\mathbf{1}}\left(\mathit{x}\left(\mathit{t}\right)\right)}{\partial \mathit{x}}{\mid }_{(x^{*},u^{*})}$ is calculated by

$$\frac{\partial {\mathit{f}}_{\mathbf{1}}\left(\mathit{x}\left(\mathit{t}\right)\right)}{\partial \mathit{x}}{\mid }_{(x^{*},u^{*})}=\left(\begin{array}{cccc}\frac{-1}{T_d}& 0& 0& 0\\ \frac{D_p({\beta }_e-x_2)}{(V_g+A_1{x}_3)}& \frac{D_p{x}_1-(C_{ip}+C_{ep}){\beta }_e\eta }{V_g+A_1{x}_3}& \frac{-A_1{\beta }_e}{{(V_g+A_1{x}_3)}^2}(D_p{x}_1(1-\frac{x_2}{{\beta }_e})-(C_{ip}+C_{ep})\eta x_2-A_1{x}_4)& \frac{-A_1{\beta }_e}{V_g+A_1{x}_3}\\ 0& 0& 0& 1\\ 0& \frac{A}{m_t}& \frac{-k}{m_t}& \frac{B_p}{m_t}\end{array}\right),$$

and $\frac{\partial {\mathit{f}}_{\mathbf{2}}\left(\mathit{x}\left(\mathit{t}\right)\right)}{\partial u}{\mid }_{(x^{*},u^{*})}$ is computed as

$$\frac{\partial {\mathit{f}}_{\mathbf{2}}\left(\mathit{x}\left(\mathit{t}\right)\right)}{\partial u}{\mid }_{(x^{*},u^{*})}=\left(\begin{array}{c}\frac{K_v}{T_d}\\ 0\\ 0\\ 0\end{array}\right).$$

As a result, using approximate linearization through first-order Taylor series expansion, one can avoid global linearization transformations and apply the optimal controller directly to the original nonlinear state-space system model.

Remark 1. 

The approximation system (15) is a linearized version of the original nonlinear system (8) around an equilibrium point. The relationship between the approximation system (15) and the original nonlinear system (8) is that the first approximation system approximates the behavior of the original nonlinear system near an equilibrium point. The first approximation system can also be used to analyze the stability of the original nonlinear system.

3.3. Optimal Robust Controller Design

After linearization around $({\mathit{x}}^{*},u^{*})$ by first-order Taylor series expansion, the original nonlinear dynamic system (8) can be written as follows:

$$\dot{\mathit{x}}\left(t\right)=\mathit{A}\mathit{x}\left(t\right)+\mathit{B}u\left(t\right)+{\tilde{\mathit{d}}}_1,$$

(17)

where ${\tilde{\mathit{d}}}_1$ denotes the modeling error due to the linearization process of the system (8). Now, the main aim is to find a set of optimal inputs $u^{*}\left(t\right)$ that can derive the injection molding’s output $\mathit{x}\left(t\right)$ to track the desired output ${\mathit{x}}_d\left(t\right)={[x_{1d},\dots ,x_{4d}]}^{\top }$ within a specified period T. Suppose the difference between the optimal control input $u^{*}\left(t\right)$ and the current control input $u\left(t\right)$ is $\Delta u\left(t\right)$, that is,

$$u^{*}\left(t\right)=u\left(t\right)+\Delta u\left(t\right),$$

(18)

and we have

$${\dot{\mathit{x}}}_d\left(t\right)=\mathit{A}{\mathit{x}}_d\left(t\right)+\mathit{B}{u}^{*}\left(t\right)+{\tilde{\mathit{d}}}_2.$$

(19)

Then, the regulated system (17) can be formulated as

$$\dot{\mathit{x}}\left(t\right)=\mathit{A}\mathit{x}\left(t\right)+\mathit{B}u\left(t\right)+\mathit{B}{u}^{*}\left(t\right)-\mathit{B}{u}^{*}\left(t\right)+{\tilde{\mathit{d}}}_1.$$

(20)

Assuming that the aggregate disturbance term in (20) is ${\tilde{\mathit{d}}}_3={\tilde{\mathit{d}}}_1-\mathit{B}{u}^{*}\left(t\right)$, then one obtains

$$\dot{\mathit{x}}\left(t\right)=\mathit{A}\mathit{x}\left(t\right)+\mathit{B}u\left(t\right)+\mathit{B}{u}^{*}\left(t\right)+{\tilde{\mathit{d}}}_3.$$

(21)

Denote the tracking error dynamics as $\mathit{E}\left(t\right)=\mathit{x}\left(t\right)-{\mathit{x}}_d\left(t\right)$; subtracting (19) from (21) obtains

$$\dot{\mathit{E}}\left(t\right)=\mathit{A}\mathit{E}\left(t\right)+\mathit{B}u\left(t\right)+\tilde{\mathit{d}},$$

(22)

where $\tilde{\mathit{d}}={\tilde{\mathit{d}}}_3-{\tilde{\mathit{d}}}_2$. According to (22), the objective performance function (10) can be formulated as

$$\underset{u\left(t\right)}{min}\underset{\tilde{\mathit{d}}}{max}:J\left(t\right)=\frac{1}{2}{\int }_0^T\left\{{\mathit{E}}^T\left(t\right)\mathit{Q}\mathit{E}\left(t\right)+u^T\left(t\right)ru\left(t\right)-{\rho }^2{\tilde{\mathit{d}}}^T\tilde{\mathit{d}}\right\}dt,r,\rho >0,$$

(23)

where $\mathit{Q}$ denotes a positive semi-definite symmetric matrix, and r and $\rho$ denote the control signal and perturbation signal weighting factors, respectively. Therefore, the original Problem P${}_0$ has been successfully transformed into the following Problem 1.

Problem 2. 

Given dynamic of the linearized injection hydraulic system (17) and the tracking error dynamics (22), in the case of minimum energy consumption, the aim is to find an optimal signal $u\left(t\right)$ that minimizes objective function (23) assuming the largest disturbance $\tilde{\mathit{d}}$.

Assumption 1. 

It is assumed that (i) The energy transmitted by the disturbance signal $\tilde{\mathit{d}}\left(t\right)$ is bounded, i.e., ${\int }_0^{\infty }{\tilde{\mathit{d}}}^T\left(t\right)\tilde{\mathit{d}}\left(t\right)dt<\infty$, and (ii) Matrices $[\mathit{A},\mathit{B}]$ are stabilizable.

Lemma 1. 

For the linearized system (22) and the cost function (23), the optimal feedback control law is given by

$$u\left(t\right)=-\mathit{M}\mathit{E}\left(t\right),$$

(24)

with $\mathit{M}=\frac{1}{r}{\mathit{B}}^T\mathit{H}$, where $\mathit{H}$ denotes a positive definite symmetric matrix that can be solved by the following Riccati equation

$${\mathit{A}}^T\mathit{H}+\mathit{HA}+\mathit{Q}-\mathit{H}(\frac{2}{r}\mathit{B}{\mathit{B}}^T-\frac{1}{{\rho }^2}\mathit{N}{\mathit{N}}^T)\mathit{H}=0.$$

(25)

Proof. 

The optimal control problem in closed form can be solved in the case of linear continuous-time systems with a quadratic cost function. For a linear system

$$\dot{\mathit{E}}\left(t\right)=\mathit{A}\left(t\right)\mathit{E}\left(t\right)+\mathit{B}\left(t\right)u\left(t\right),$$

(26)

with a cost function that comprises quadratic terms in the form:

$$J\left(t\right)=\frac{1}{2}{\int }_0^T\{{\mathit{E}}^T\left(t\right)\mathit{Q}\left(t\right)\mathit{E}\left(t\right)+u^T\left(t\right)ru\left(t\right)\}dt,$$

(27)

then the optimal value of the cost function is

$$J^0\left(t\right)=\frac{1}{2}{\mathit{E}}^T\left(t\right)\mathit{H}\left(t\right)\mathit{E}\left(t\right)$$

(28)

with $\mathit{H}\left(t\right)$ being a symmetric positive definite matrix.

For the system mentioned above, the Hamiltonian function is defined as

$$\mathit{G}=\frac{1}{2}{\mathit{E}}^T\mathit{Q}\mathit{E}+\frac{1}{2}{u}^{T}ru+\frac{1}{2}{\mathit{E}}^T\mathit{H}(\mathit{A}\mathit{E}+\mathit{B}u)+\frac{1}{2}{(\mathit{A}\mathit{E}+\mathit{B}u)}^T\mathit{H}\mathit{E}$$

(29)

By taking the derivative of (29) with respect to the control input u and applying its extremum condition, one can obtain the following result:

$$\frac{\partial \mathit{G}}{\partial u}=ru+{\mathit{B}}^T\mathit{H}\mathit{E}=0,$$

(30)

Solving the above equation for $u\left(t\right)$ yields the optimal control input

$$u^0\left(t\right)=-\frac{1}{r}{\mathit{B}}^T\left(t\right)\mathit{H}\left(t\right)\mathit{E}\left(t\right).$$

(31)

Substituting the optimal control input into the Hamiltonian function (29) yields the following result:

$$\begin{array}{cc}\hfill {\mathit{G}}^0=\underset{u\in [0,T]}{min}\mathit{G}& =\frac{1}{2}{\mathit{E}}^T\mathit{Q}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{HB}{r}^{-1}{\mathit{B}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T{\mathit{A}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{A}\mathit{E}-{\mathit{E}}^T\mathit{HB}{r}^{-1}{\mathit{B}}^T\mathit{H}\mathit{E}\hfill \\ \hfill & =\frac{1}{2}{\mathit{E}}^T(\mathit{Q}+{\mathit{A}}^T\mathit{H}+\mathit{H}\mathit{A}-\mathit{HB}{r}^{-1}{\mathit{B}}^T\mathit{H})\mathit{E}.\hfill \end{array}$$

(32)

Next, differentiating the cost function of Equation (28) yields

$$\frac{\partial J^0}{\partial t}=\frac{1}{2}{\mathit{E}}^T\left(t\right)\frac{\mathrm{d}\mathit{H}\left(t\right)}{\mathrm{d}t}\mathit{E}\left(t\right).$$

(33)

Equating (32) to (28) results in the following formulation of the Hamilton–Jacobi–Bellman:

$$\begin{array}{cc}\hfill -\frac{1}{2}{\mathit{E}}^T\left(t\right)\frac{\mathrm{d}\mathit{H}\left(t\right)}{\mathrm{d}t}\mathit{E}\left(t\right)=\underset{u\in [0,T]}{min}\mathit{G}& =\frac{1}{2}{\mathit{E}}^T\mathit{Q}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{HB}{r}^{-1}{\mathit{B}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T{\mathit{A}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{A}\mathit{E}-{\mathit{E}}^T\mathit{HB}{r}^{-1}{\mathit{B}}^T\mathit{H}\mathit{E}\hfill \\ \hfill & =\frac{1}{2}{\mathit{E}}^T(\mathit{Q}+{\mathit{A}}^T\mathit{H}+\mathit{H}\mathit{A}-\mathit{HB}{r}^{-1}{\mathit{B}}^T\mathit{H})\mathit{E}.\hfill \end{array}$$

(34)

After performing intermediate computations, one arrives at the following differential Riccati equation:

$$-\frac{\mathrm{d}\mathit{H}\left(t\right)}{\mathrm{d}t}={\mathit{A}}^T\mathit{H}+\mathit{H}\mathit{A}+\mathit{Q}-\mathit{HB}{r}^{-1}{\mathit{B}}^T\mathit{H}$$

(35)

The boundary condition for solving differential Equation (35) is derived from the following relation:

$$J^0\left(T\right)=\frac{1}{2}{\mathit{E}}^T\left(T\right)\mathit{H}\left(T\right)\mathit{E}\left(T\right)$$

(36)

with $\mathit{H}\left(T\right)=0$. By integrating (35) from T to 0, one can find the matrix $\mathit{H}\left(t\right):t\in [0,T]$. Additionally, using (31), one can determine the optimal control input to be applied to the system. Furthermore, using (27), one can find the minimum value of the system’s cost function.

The above procedure for solving the optimal control problem of a linear dynamical system results in the design of a Linear Quadratic Regulator. If matrices A and B in the state-space model of the system in (26) are time-invariant and the weight matrices Q and r in the quadratic cost function of Equation (27) are also time-invariant, and if the solution of the differential Riccati equation $\mathit{H}\left(t\right)$ reaches a steady-state value (i.e., $\frac{\mathrm{d}\mathit{H}\left(t\right)}{\mathrm{d}t}=0$), then (35) becomes

$${\mathit{A}}^T\mathit{H}+\mathit{H}\mathit{A}+\mathit{Q}-\mathit{HB}{r}^{-1}{\mathit{B}}^T\mathit{H}=0.$$

(37)

In this case, the optimal feedback control is given by

$$u\left(t\right)=-\frac{1}{r}{\mathit{B}}^T\mathit{H}\mathit{E}\left(t\right),$$

(38)

where $\mathit{H}$ is now the solution of (37). As a result, the optimized cost function becomes $J^0=\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{E}$. Note that the superposition principle of Bellman optimality states that $u\left(t\right)=-\frac{1}{r}{\mathit{B}}^T\mathit{H}\mathit{E}\left(t\right)$ can be used to solve for the optimal control u, which represents the minimal change in control input required to eliminate the tracking error of the state vector. Similarly, finding the worst-case disturbance by solving the optimal control problem for $\tilde{\mathit{d}}$ yields $\tilde{\mathit{d}}=\frac{1}{{\rho }^2}{\mathit{N}}^T\mathit{H}\mathit{E}\left(t\right)$. This completes the proof. □

4. Lyapunov Stability Analysis

This part provides a comprehensive theoretical analysis of Lyapunov stability, which proves the stability of the closed-loop system under our proposed optimal feedback controller. It is proved that the system based on the proposed controller (24) can achieve asymptotic convergence (global stability) to the desired output curve under reasonable conditions and guarantee the tracking performance of the injection velocity during IM.

Theorem 1 

([36]). The dynamic system described by $\dot{x}\left(t\right)=f\left(x\left(t\right)\right)$ is asymptotically stable in the vicinity of the equilibrium $x_0=0$ if there exists a function $\mathcal{V}\left(x\right)$ satisfying:

(i)

$\mathcal{V}\left(x\right(t\left)\right)$ to be continuous and to have a continuous first order derivative at $x_0=0$.

(ii)

$\mathcal{V}\left(x\right(t\left)\right)>0$, if $x\ne 0$ and $\mathcal{V}\left(0\right)=0$.

(iii)

$\dot{\mathcal{V}}\left(x\left(t\right)\right)<0$, $\forall x\ne 0$.

Theorem 2 

([37]). Suppose that $f\left(t\right):[0,\infty )⟶\mathbb{R}$ is uniformly continuous and that ${lim}_{t\to +\infty }{\int }_0^{t}f\left(\tau \right)d\tau$ exists. Then ${lim}_{t\to +\infty }f\left(t\right)=0$ holds.

As previously demonstrated, the tracking error of the injection velocity are stated as

$$\dot{\mathit{E}}\left(t\right)=\mathit{A}\mathit{E}\left(t\right)+\mathit{B}u\left(t\right)+\mathit{N}\tilde{\mathit{d}},$$

(39)

where $\mathit{N}=\mathit{I}\in {\mathbb{R}}^{4\times 4}$, $\mathit{I}$ is an identity matrix. The injection errors of the dynamic model’s uncertainty are represented by variable $\tilde{\mathit{d}}$. Now, we propose the following Lyapunov function

$$\mathcal{V}\left(t\right)=\frac{1}{2}{\mathit{E}}^T\left(t\right)\mathit{H}\mathit{E}\left(t\right).$$

(40)

Differentiating (40) with respect to t, one obtains

$$\begin{array}{cc}\hfill \dot{\mathcal{V}}\left(t\right)& =\frac{1}{2}{\dot{\mathit{E}}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\dot{\mathit{E}}\hfill \\ \hfill & =\frac{1}{2}{\left[\mathit{A}\mathit{E}+\mathit{B}u+\mathit{N}\tilde{\mathit{d}}\right]}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\left[\mathit{A}\mathit{E}+\mathit{B}u+\mathit{N}\tilde{\mathit{d}}\right]\hfill \\ \hfill & =\frac{1}{2}{\left[{\mathit{E}}^T{\mathit{A}}^T+u^T{\mathit{B}}^T+{\tilde{\mathit{d}}}^T{\mathit{N}}^T\right]}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\left[\mathit{A}\mathit{E}+\mathit{B}u+\mathit{N}\tilde{\mathit{d}}\right]\hfill \\ \hfill & =\frac{1}{2}{\mathit{E}}^T{\mathit{A}}^T\mathit{H}\mathit{E}+\frac{1}{2}{u}^T{\mathit{B}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\tilde{\mathit{d}}}^T{\mathit{N}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{A}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{B}u+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{N}\tilde{\mathit{d}}\hfill \\ \hfill & =\frac{1}{2}{\mathit{E}}^T({\mathit{A}}^T\mathit{H}+\mathit{H}\mathit{A})\mathit{E}+(\frac{1}{2}{u}^T{\mathit{B}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{B}u)+(\frac{1}{2}{\tilde{\mathit{d}}}^T{\mathit{N}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{N}\tilde{\mathit{d}})\hfill \end{array}$$

(41)

Assumption 2. 

For a given positive definite matrix $\mathit{Q}$ and coefficients r and ρ, there exists a positive definite matrix $\mathit{H}$ that is the solution of the matrix problem shown below:

$${\mathit{A}}^T\mathit{H}+\mathit{H}\mathit{A}=-\mathit{Q}+\mathit{H}(\frac{2}{r}\mathit{B}{\mathit{B}}^T-\frac{1}{{\rho }^2}\mathit{N}{\mathit{N}}^T)\mathit{H},$$

(42)

Note that the system is governed by the following state feedback law

$$u\left(t\right)=-\frac{1}{r}{\mathit{B}}^T\mathit{H}\mathit{E}\left(t\right).$$

(43)

Based on (42) and (43), (41) can be rewritten as

$$\begin{array}{cc}\hfill \dot{\mathcal{V}}\left(t\right)& =\frac{1}{2}{\mathit{E}}^T(-\mathit{Q}+\mathit{H}(\frac{2}{r}\mathit{B}{\mathit{B}}^T-\frac{1}{{\rho }^2}\mathit{N}{\mathit{N}}^T)\mathit{H})\mathit{E}+{\mathit{E}}^T\mathit{H}\mathit{B}(-\frac{1}{r}{\mathit{B}}^T\mathit{H}\mathit{E})+(\frac{1}{2}{\tilde{\mathit{d}}}^T{\mathit{N}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{N}\tilde{\mathit{d}})\hfill \\ \hfill & =-\frac{1}{2}{\mathit{E}}^T\mathit{Q}\mathit{E}+\frac{1}{r}{\mathit{E}}^T\mathit{H}\mathit{B}{\mathit{B}}^T\mathit{H}\mathit{E}-\frac{1}{2{\rho }^2}{\mathit{E}}^T\mathit{H}\mathit{N}{\mathit{N}}^T\mathit{H}\mathit{E}-\frac{1}{r}{\mathit{E}}^T\mathit{H}\mathit{B}{\mathit{B}}^T\mathit{H}\mathit{E}+(\frac{1}{2}{\tilde{\mathit{d}}}^T{\mathit{N}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{N}\tilde{\mathit{d}})\hfill \\ \hfill & =-\frac{1}{2}{\mathit{E}}^T\mathit{Q}\mathit{E}-\frac{1}{2{\rho }^2}{\mathit{E}}^T\mathit{H}\mathit{N}{\mathit{N}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\tilde{\mathit{d}}}^T{\mathit{N}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{N}\tilde{\mathit{d}}.\hfill \end{array}$$

(44)

Lemma 2. 

The following inequality exists

$$-\frac{1}{2{\rho }^2}{\mathit{E}}^T\mathit{H}\mathit{N}{\mathit{N}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\tilde{\mathit{d}}}^T{\mathit{N}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{N}\tilde{\mathit{d}}\le \frac{1}{2}{\rho }^2{\tilde{\mathit{d}}}^T\tilde{\mathit{d}}$$

(45)

Proof. 

Considering the term ${(\rho a-\frac{1}{\rho }b)}^2$, one can obtain

$$\begin{array}{cc}\hfill {\rho }^2{a}^2+\frac{1}{{\rho }^2}{b}^2-2ab& \ge 0,\hfill \end{array}$$

(46a)

$$\begin{array}{cc}\hfill \frac{1}{2}{\rho }^2{a}^2+\frac{1}{2{\rho }^2}{b}^2-ab& \ge 0,\hfill \end{array}$$

(46b)

$$\begin{array}{cc}\hfill ab-\frac{1}{2{\rho }^2}{b}^2& \le \frac{1}{2}{\rho }^2{a}^2,\hfill \end{array}$$

(46c)

$$\begin{array}{cc}\hfill \frac{1}{2}ab+\frac{1}{2}ab-\frac{1}{2{\rho }^2}{b}^2& \le \frac{1}{2}{\rho }^2{a}^2.\hfill \end{array}$$

(46d)

Make the following substitutions: $a=\tilde{\mathit{d}}$ and $b={\mathit{E}}^T\mathit{H}\mathit{N}$. Equation (46) becomes

$$\frac{1}{2}{\tilde{\mathit{d}}}^T{\mathit{N}}^T\mathit{H}\mathit{E}+\frac{1}{2}{\mathit{E}}^T\mathit{H}\mathit{N}\tilde{\mathit{d}}-\frac{1}{2{\rho }^2}{\mathit{E}}^T\mathit{H}\mathit{N}{\mathit{N}}^T\mathit{H}\mathit{E}\le \frac{1}{2}{\rho }^2{\tilde{\mathit{d}}}^T\tilde{\mathit{d}}$$

(47)

Then, we complete the proof. □

Now, substituting (47) into (44) can obtain

$$\dot{\mathcal{V}}\left(t\right)\le -\frac{1}{2}{\mathit{E}}^T\mathit{Q}\mathit{E}+\frac{1}{2}{\rho }^2{\tilde{\mathit{d}}}^T\tilde{\mathit{d}}.$$

(48)

Integrating $\mathcal{V}\left(t\right)$ from 0 to T gives

$$\begin{array}{c}\hfill {\int }_0^T\dot{\mathcal{V}}\left(t\right)dt\le -\frac{1}{2}{\int }_0^T{∥\mathit{E}∥}_Q^{2}dt+\frac{1}{2}{\rho }^2{\int }_0^T{∥\tilde{\mathit{d}}∥}^{2}dt\\ \hfill 2\mathcal{V}\left(T\right)+{\int }_0^T{∥\mathit{E}∥}_Q^{2}dt\le 2\mathcal{V}\left(0\right)+{\rho }^2{\int }_0^T{∥\tilde{\mathit{d}}∥}^{2}dt,\end{array}$$

(49)

Additionally, if there is a constant $M_p>0$ that

$${\int }_0^{\infty }{∥\tilde{\mathit{d}}∥}^{2}dt\le M_p,$$

(50)

then

$${\int }_0^T{∥\mathit{E}∥}_Q^{2}dt\le 2\mathcal{V}\left(0\right)+{\rho }^2{M}_p,$$

(51)

that is

$$\underset{T\to +\infty }{lim}{\int }_0^T{∥\mathit{E}∥}_Q^{2}dt=2\mathcal{V}\left(0\right)+{\rho }^2{M}_p.$$

(52)

Based on Theorem 2, we can obtain

$$\underset{t\to +\infty }{lim}{\mathit{E}}^T\left(t\right)\mathit{Q}\mathit{E}\left(t\right)=0.$$

(53)

where $\mathit{Q}$ is the positive definite matrix given above; due to $\mathit{H}$ also being a positive definite matrix, the following formula can be derived

$$\underset{t\to +\infty }{lim}{\mathit{E}}^T\left(t\right)\mathit{H}\mathit{E}\left(t\right)=0.$$

(54)

According to (54), we can obtain

$$\underset{t\to +\infty }{lim}\mathcal{V}\left(t\right)=0,$$

(55)

and

$$\underset{t\to +\infty }{lim}\dot{\mathcal{V}}\left(t\right)=0.$$

(56)

As a result, based on Theorem 1, it can be proven that the control scheme is globally asymptotically stable. As the number of iterations of the control algorithm increases, the tracking error tends to zero.

5. Numerical Simulations

In this section, the control strategy proposed in the previous sections is tested for its feasibility and effectiveness. In numerical experiments, all simulation experiments are performed on the platform of Matlab R2019a. The computer hardware platform is configured as Intel(R) Core i7-6820H CPU 2.7GHz, 16GB RAM, and 64-bit Windows 10 operating system.

Table 1. Main parameters in the dynamic system.

Variable	Variable Symbol	Value
Speed gain	$K_v$	100
Time constant	$T_d$	0.005
Oil viscosity	$\eta$	$4.6\times {10}^{-3}$
Elastic modulus of oil volume	${\beta }_e$	$1.6\times {10}^9$
Total volume of high pressure chamber	$V_g$	$3.9\times {10}^{-3}$
Effective area of rodless chamber	$A_1$	$3.1\times {10}^{-3}$
Displacement of quantitative pump	$D_p$	$6.0\times {10}^{-6}$
Leakage coefficient of quantitative pump	$C_{ip}$	$4.5\times {10}^{-11}$

shows some main characteristic parameters of the IMM model.

The initial experiment involves evaluating the tracking control of the injection velocity and other states within the IMM utilizing the optimal controller we designed. The corresponding numerical experimental outcomes are presented in Figure 3 and Figure 4. These illustrate that the optimal control scheme we developed demonstrates excellent performance in the speed-tracking control of the IMM. Note that the feedback control gain is determined at each control strategy iteration by repeatedly solving the algebraic Riccati Equation (25). Figure 3 depicts that the control input converges quickly and remains stable. Similarly, Figure 4 shows that all state variables in the IMM swiftly and precisely converge to the reference set points, enabling the desired curves to be tracked. In addition, another injection velocity tracking signal within the IMM is also evaluated, and the corresponding numerical results are presented in Figure 5 and Figure 6. Similarly, the results show that the control input converges rapidly and remains stable, and all states in the IMM converge swiftly and accurately to the preset references, further validating the effectiveness of the controller we designed.

Furthermore, during our numerical process, we also examine the developed nonlinear control method’s tracking accuracy at various reference set points.

Table 2. Tracking the RMSE of the desired speed $v_{d1}$ in the disturbance-free case.

	${\mathit{RMSE}}_{{\mathit{x}}_1}$	${\mathit{RMSE}}_{{\mathit{x}}_2}$	${\mathit{RMSE}}_{{\mathit{x}}_3}$	${\mathit{RMSE}}_{{\mathit{x}}_4}$
$setpoin{t}_1$	$0.0236$	102.1911	$8.6393\times {10}^{-5}$	$1.0533\times {10}^{-4}$
$setpoin{t}_2$	$0.0847$	147.2880	$2.7525\times {10}^{-4}$	$1.5215\times {10}^{-4}$
$setpoin{t}_3$	$0.0991$	180.0929	$5.2280\times {10}^{-4}$	$1.8598\times {10}^{-4}$
$setpoin{t}_4$	$0.3138$	417.7483	$9.5517\times {10}^{-4}$	$4.3165\times {10}^{-4}$
$setpoin{t}_5$	$0.2297$	464.5643	$1.5000\times {10}^{-3}$	$4.7959\times {10}^{-4}$
$setpoin{t}_6$	$0.2979$	509.3806	$2.2000\times {10}^{-3}$	$5.2590\times {10}^{-4}$

and

Table 3. Tracking the RMSE of the desired speed $v_{d2}$ in the disturbance-free case.

	${\mathit{RMSE}}_{{\mathit{x}}_1}$	${\mathit{RMSE}}_{{\mathit{x}}_2}$	${\mathit{RMSE}}_{{\mathit{x}}_3}$	${\mathit{RMSE}}_{{\mathit{x}}_4}$
$setpoin{t}_1$	$0.0236$	102.1911	$8.6393\times {10}^{-5}$	$1.0533\times {10}^{-4}$
$setpoin{t}_2$	$0.0833$	147.2576	$2.7526\times {10}^{-4}$	$1.5211\times {10}^{-4}$
$setpoin{t}_3$	$0.3484$	541.8267	$7.4757\times {10}^{-4}$	$5.5983\times {10}^{-4}$
$setpoin{t}_4$	$0.3458$	625.1940	$1.5000\times {10}^{-4}$	$6.4563\times {10}^{-4}$
$setpoin{t}_5$	$0.5635$	471.6619	$2.3000\times {10}^{-4}$	$4.8771\times {10}^{-4}$
$setpoin{t}_6$	$0.2884$	508.2908	$3.1000\times {10}^{-4}$	$5.2452\times {10}^{-4}$

show the achieved results, respectively. The control method applies a change equal to $\Delta \alpha \%$ to $m_t$ in (8) for the IMM model and the tracking performance under disturbances, as shown in

Table 4. Tracking the RMSE of the desired speed $v_{d1}$ in the case of disturbances.

$\Delta \alpha \%$	${\mathit{RMSE}}_{{\mathit{x}}_1}$	${\mathit{RMSE}}_{{\mathit{x}}_2}$	${\mathit{RMSE}}_{{\mathit{x}}_3}$	${\mathit{RMSE}}_{{\mathit{x}}_4}$
$0\%$	$0.2160$	464.2767	$0.0015$	$4.5740\times {10}^{-4}$
$10\%$	$0.2188$	464.8364	$0.0022$	$4.6235\times {10}^{-4}$
$20\%$	$0.2215$	465.3996	$0.0029$	$4.6731\times {10}^{-4}$
$30\%$	$0.2269$	466.5362	$0.0035$	$4.7725\times {10}^{-4}$
$40\%$	$0.2296$	467.1095	$0.0042$	$4.8222\times {10}^{-4}$
$50\%$	$0.2350$	468.2659	$0.0049$	$4.9217\times {10}^{-4}$

, respectively. It can be noticed in Table 2 that the tracking accuracy is satisfactory despite the model perturbations that exist. As a result, the control approach suggested in this study performs satisfactorily and can precisely track the reference set points even when there are disturbances.

It is important to note that the selection of parameters r, Q, and $\rho$ in (25) determines the transient performance of the control algorithm. The parameter r represents the control output weight factor in the objective function. A small value of r can eliminate tracking errors in the states. The parameter Q represents the state variable weight matrix in the objective function. A large value of Q allows state variables to converge quickly to their reference set points. The choice of decay coefficient $\rho$ affects the resilience of the control strategy. By selecting a value of $\rho$ small enough to satisfy the tracking performance criterion in (25), the global asymptotic stability of the control loop is ensured and tracking errors in state variables are eliminated.

6. Conclusions

In this paper, we propose an efficient optimal robust control strategy for the dynamic model of a variable speed pump-controlled hydraulic cylinder’s speed servo system within an IMM. The dynamic system model is augmented and approximately linearized using the first-order Taylor series. A reliable feedback controller is then designed. At each time step of the control scheme, the corresponding Riccati equation is solved iteratively to determine the reliable feedback gain of the feedback controller. The global asymptotic stability of the control strategy is demonstrated through Lyapunov analysis. Numerical experiments are conducted to validate the feasibility of the control strategy. The proposed approach can be easily adapted to other similar types of nonlinear optimal control problems that arise in discrete manufacturing processes.