A Machine Proof System of Point Geometry Based on Coq

Abstract

An important development in geometric algebra in recent years is the new system known as point geometry, which treats points as direct objects of operations and considerably simplifies the process of geometric reasoning. In this paper, we provide a complete formal description of the point geometry theory architecture and give a rigorous and reliable formal verification of the point geometry theory based on the theorem prover Coq. Simultaneously, a series of tactics are also designed to assist in the proof of geometric propositions. Based on the theoretical architecture and proof tactics, a universal and scalable interactive point geometry machine proof system, PointGeo, is built. In this system, any arbitrary point-geometry-solvable geometric statement may be proven, along with readable information about the solution’s procedure. Additionally, users may augment the rule base by adding trustworthy rules as needed for certain issues. The implementation of the system expands the library of Coq resources on geometric algebra, which will become a significant research foundation for the fields of geometric algebra, computer science, mathematics education, and other related fields.

1. Introduction

The proof of geometric theorems is one of mathematics’ fundamental and most challenging tasks. In recent years, reasoning and proof have gradually moved away from the traditional paper-and-pencil model. The higher thinking activities of the human brain can be mechanized, and machines can perform tedious and complex verification. Machine proofs of geometric theorems have also played an important role in mathematical research and intelligence education, with a wide range of variations and applications. Early work on machine proofs of geometric theorems was represented by Wu’s method [1] as an algebraic proof method. Algebraic methods other than Wu’s method include the Gröbner basis method [2] and the numerical parallelism method [3], etc. In order to support automation, these methods often have different degrees of limitations, and the polynomial transformations that transform the reasoning of geometric problems into algebra [4] also lose the geometric meaning of the proof process, which greatly reduces the readability. Subsequently, database-based search methods have also made great progress and search methods can produce traditional mathematical proofs and discover new theorems, and these are considered to be the first choice for intelligent educational software development [5]. However, the search method is not a complete method and still suffers from difficulties in composition and a lack of auxiliary quantities in reasoning, which represent major limitations.

For the proof of geometric theorems, the number of terms that need to be expressed using coordinate-based algebraic methods is often large, so there are various problems, such as high computational complexity and difficulty in understanding complex geometric propositions. The geometric algebraic method is a method that can directly calculate geometric objects (such as points, lines, etc.) as terms, which has the characteristics of a simple expression and strong geometric meaning, so the method of geometric theorem proof based on geometric algebraic principles can overcome the above difficulties to a certain extent. In particular, the advanced invariant methods of geometric algebraic methods significantly reduce the number of terms that need to be used using coordinate-based algebraic methods, but strong expertise is also required to read the proofs [6]. In addition, the combination of physics and mathematics, prime geometry, has obvious geometric significance and advances the development of geometric algebra. In 2018, Zhang proposed an intuitive new geometric algebraic system called “point geometry”, which has a simple theoretical system, easy-to-understand laws and properties, and geometric algebraic methods such as prime geometry, the coordinate method, and the vector method [7,8]. For example, the proof of the triangle median theorem can be completed with only one line of proof, as in Example 1.

Example 1

(The triangle median theorem). As shown in Figure 1, the three midlines $AM,BN,CP$ of triangle $ABC$ intersect to a point. To prove this, we assume point A is the origin O, and we let point G be the intersection of midline $BN$ and midline $CP$. Firstly, given that $B=2P$ and $C=2N$, it follows that $2M=B+C=2P+C=2N+B=3G$. Then, we can conclude that point G is on the line $AM$ and that $3AG=2AM$.

Theorem proving is a powerful technique in computer science and mathematics that expresses and verifies systems in a machine-readable form, providing significant advantages in terms of correctness and precision, particularly for complex problems. Theorem proving can reduce errors and tedious reasoning processes and provides mathematicians and computer scientists with a more intuitive and reliable means of verification, playing a crucial role in computer science and mathematics [9,10,11,12]. However, for sufficiently complex problems, complete automation is often challenging, and for complicated proof procedures, relying solely on pen and paper is no longer reliable. Therefore, interactive theorem proving has become a more reliable and efficient means of proof. There are many advanced interactive theorem provers available, such as Coq [13,14], Isabelle [15], HOL [16], etc. Among them, Coq, based on the calculus of inductive constructions, is a powerful theorem prover with strong expressive power, covering multiple domains, including program verification and mathematical theorem proving. It provides an efficient, reliable, and automated proof environment. In the field of computer science, Coq has been widely used for program verification, language design, formal semantics, security protocol analysis, program repair, and many other applications, as documented in various research studies [17,18,19,20,21]. Coq is also widely used in mathematics to formalize [22,23] and verify theorems and lemmas. A comparative study by Narboux et al. [24] in 2022 explored traditional pencil-and-paper proofs versus formal proof methods in high school geometry, revealing potential challenges in formalization due to different formulas and proofs. Fortunately, however, recent research has shown that Coq’s advantages in terms of verifiability and interactivity have made it widely adopted for the verification of mathematical theorems. Notably, Boldo et al. [25] fully formalized the Beppo Levi theorem and Fatou’s lemma using the Coq proof assistant in 2021. Additionally, Fu et al. [26] proposed a Coq-based formalization of infinitesimal calculus, utilizing it to formally verify important results such as the Newton–Leibniz formula and Taylor’s theorem. Coq has also been employed to formalize various other mathematical theorems, including the topology space relation model [27], Tonelli’s theorem [28], and so on. In the field of automated theorem proving for geometry, the geometry library of Coq provides a rich set of geometric concepts and theorems, covering areas such as Euclidean geometry, non-Euclidean geometry, and vector spaces, offering strong support for the automated proving of geometric theorems, as well as new possibilities for teaching and research in geometry. For instance, Julien Narboux et al. used Coq to implement the process of the area method and proposed GeoCoq, a formalized geometry theory based on the Tarski axiom system [29,30,31,32]. Furthermore, Pedro Quaresma et al. proposed a new readability criterion for formal proofs produced by automated theorem provers for geometry, inspired by their modernization of Lemoine’s Geometrography, to enhance the readability of automated proofs in geometry [33]. These works have not only promoted the development of geometry but also demonstrated the importance of interactive proofs in automated theorem proving for geometry.

Our work presents a formal description and verification of a new algebraic system for point geometry using the Coq theorem prover. The result is a reliable, versatile, and extensible machine proof system for point geometry called PointGeo. The paper is divided into three main parts. The first part provides the formalization and verification of the knowledge base of point geometry, allowing geometric theorems, properties, and problems to be expressed in the Coq language and verified by the Coq kernel to ensure the validity of every step (Section 2 and Section 3). The second part describes the design of the automatic proof tactics in the system. The third part discusses the overall structure and proof methods of PointGeo (Section 4).

2. The Formal Description of Definitions

The theory of point geometry provides a more straightforward notation and advanced logic that permits direct operations on geometric points as objects. This makes it easier to solve geometric issues and provides richer geometric meaning. However, due to the complexity of geometry, it is challenging to develop a complete algorithm to solve all geometry problems automatically. For this reason, it is crucial to develop an interactive and scalable system to solve geometric problems. In this section, we will first introduce the formal description of definitions in point geometry that the Coq kernel can understand.

2.1. Type and Proof

In Coq, every item has a type, and each type is also an item. There are many different types—for example, atomic types such as the natural number type $nat$, the integer type Z, and the real number type R, and arrow types such as $A\to B$. An arrow type can also be expressed as the type of a function. If the type of a function f is $A\to B$, i.e., f: $A\to B$, then f maps any variable of type A to a value of type B. In addition, the type operator can also construct a binary group $(a,b)$ of type $A\times B$, where a is of type A and b is of type B.

The description of a geometric problem includes the hypotheses and the conclusion, and its initial proof state is formed as $E_p,\mathsf{\Gamma }{⊢}^{?}g$. $E_p$ denotes the point geometry theoretical environment of PointGeo. $\mathsf{\Gamma }$ is the context, a sequence of statements such as $\left[x_1:T_1;x_2:T_2;\cdots ;x_n:T_n\right]$, which generally includes all hypotheses of the geometric proposition. g denotes the conclusion. The proof of the geometric problem needs to be advanced by applying the tactics interactively, and the process of proof may generate multiple subgoals $g_i$. The proof is completed if all the goals are proven, i.e., $g_i=\left[\right]$.

In fact, CIC is a higher-order typed lambda calculus with natural support for inductive data types based on the Curry–Howard isomorphism, which ties lambda-term-type inference to natural deductive proofs in complete intuitionistic predicate logic. In other words, judgment is type reasoning. Specifically, intuitionism holds that a logical judgment is valid if and only if the constructing subject can verify it. This corresponds to what is represented in Coq: if t exists such that $E,\mathsf{\Gamma }⊢t:g$, then t is said to be a proof of g, where t is a lambda term of type g. In other words, the proof of g is to build a lambda item of type g. This is consistent with geometric algebra concepts such as Wu’s method and the identity-based method for point geometry. The main idea is that if the conclusion polynomial can be constructed from the conditional polynomial, then the conclusion is proven. However, the identity-based method is incomplete for more sophisticated constraints, such as those of higher order or with quantifiers. Fortunately, PointGeo’s platform, Coq, supports dependent types, which means that there is sufficient descriptive power here to describe geometric problems or rules and implement proofs of these problems.

2.2. Basic Definition of Point Geometry and Its Formal Description

To precisely describe points in point geometry theory, they are uniquely specified here by pairs of real number information regarding the point’s position,

$$Point\in Set\triangleq R\times RR\_R\_to\_Point:R\to R\to Point\left(r_1,r_2\right):Point,$$

where $Point$ is the type of point; $Set$ is the type of $Point$. $R\_R\_to\_point$ is a function that maps pairs of real numbers to points. “( _ , _) ” is the Coq notion of $R\_R\_to\_point$, i.e., if $r_1$, $r_2$ belong to R, then ($r_1$, $r_2$) is a point. Specifically, the origin O is described as $R\_R\_to\_point(0,0)$, i.e., $O=(0,0)$. In addition, functions $Px$ and $Py$ are designed to extract the first and second components of the point, respectively, and they indicate that if $P=(r_1,r_2)$, then $Px\left(P\right)=r_1$, $Py\left(P\right)=r_2$; in other words, for any point P, we have $P=\left(Px\right(P),Py(P\left)\right)$.

The basic operations of point geometry depend on the choice of the origin. The relationship between the coordinates of the points relative to the origin represents the relationship between the points. The definition of addition and scalar multiplication in point geometry is as follows.

Definition 1

(Addition of points). If $A=(x_A,y_A)$, $B=(x_B,y_B)$, and $C=(x_A+x_B,x_A+y_B)$, then the addition of A and B is C, which is denoted by $A+B=C$.

Definition 2

(Scalar multiplication). If $A=(x,y),B=(\lambda x,\lambda y)$, then the scalar multiplication of A is denoted by $B=\lambda A$.

Corresponding to the addition and scalar multiplication of points in PointGeo are the binary functions Pplus and Pmults:

$$\begin{array}{c}Pplus((p_1:Point),(p_2:Point))\triangleq \left(\left(Px\left(p_1\right)+Px\left(p_2\right)\right),\left(Py\left(p_1\right)+Py\left(p_2\right)\right)\right)\\ Pmults(\lambda :R),(p:Point)\triangleq \left(\right(\lambda \ast Px\left(p\right)),(\lambda \ast Py\left(p\right)\left)\right)\end{array}$$

$Pplus$ and $Pmults$ are defined by applying the addition and multiplication operations, respectively, to the position coordinates of the point, $Px$ and $Py$, through the R_R_to_Point function. In the scope of points, the function symbols for the addition and scalar multiplication of points are ‘+’ and ‘*’, respectively, written ‘$p_1+p_2$’ and ‘$\lambda \ast p$’, where p, $p_1$, and $p_2$ are of type $Point$ and $\lambda$ is of type R. The addition and scalar multiplication of points inherit the relevant laws of the real numbers, such as the law of union and distribution, and these laws have been verified in Coq. The source code of basic rules is given in the file Basics.v (the components of this work will be discussed in Section 5). In addition, the source code for this work can be obtained from https://github.com/RanranL/Pointgeo (accessed on 6 May 2023).

Additionally, the monomial function Pneg, defined as ‘If $P=(x,y)$, then $Pneg\left(P\right)=(-x,-y)$’, represents the point’s negative form. Based on the Pneg, the subtraction of points is defined as follows:

$$Pminus(P_1,P_2)\triangleq Pplus(\left(P_1\right),Pneg\left(P_2\right))$$

The function symbol for Pminus is ‘−’, written ‘$p_1-p_2$’. For instance, for points $p_1$ and $p_2$, the expression ‘$p_1-p_2$’ can be considered equivalent to ‘$p_1+(-p_2)$’. In vector geometry, $\overrightarrow{AB}$ is equivalent to $\overrightarrow{OB}-\overrightarrow{OA}$, where O is the origin, $\overrightarrow{OB}$ is equivalent to B in point geometry, and $\overrightarrow{OA}$ is equal to point A in point geometry, so vector $\overrightarrow{AB}$ is equivalent to ‘$B-A$’ in point geometry. It follows that vector geometry and point geometry are interconvertible.

The outer product of the points is also defined by subtraction.

Definition 3

(Outer product). The outer product of the two points of the convention is $AB=B-A$.

The functions Vec and OutP represent vectors and two-point outer products, respectively, of type ‘$Point\to Point\to Point$’:

$$Vec(P_1,P_2)\triangleq Pminus(P_2,P_1)OutP(P_1,P_2)\triangleq Pminus(P_2,P_1)$$

The outer product of points also satisfies the law of union and distribution, and its function symbol is ‘×’, written ‘$p_1\times p_2$’. Furthermore, it is clear from the definition that the outer product of two points and the subtraction of points, vectors, and points are equivalent:

$$Pminus(P_1,P_2)\iff Vec(P_2,P_1)\iff Out(P_2,P_1)$$

Definition 4

(Outer product of three points). If $A=\left(x_A,y_A\right),B=\left(x_B,y_B\right),C=\left(x_C,y_C\right)$, then $ABC=x_A{y}_B+x_B{y}_C+x_C{y}_A-x_A{y}_C-x_B{y}_A-x_C{y}_B$.

The outer product of three points is also the area of the triangle formed by the three points with the sign, and its intuitive geometric meaning is as follows: ‘In the right-handed coordinate system, if the triangle vertices A, B, and C are in anti-clockwise order, then $ABC>0$; otherwise, $ABC<0$. If A, B, and C are collinear, then $ABC=0$’. The outer product of three points is expressed using the ternary function ‘s’:

$$\begin{gathered} s\left(p_1:\right.Point)\left(p_2:\right.Point\left)\left(p_3:\right.Point\right)\in \mathbb{R}\triangleq Px\left(p_1\right)\ast Py\left(p_2\right)+Px\left(p_2\right)\ast Py\left(p_3\right)+ \\ Px\left(p_3\right)\ast Py\left(p_1\right)-Px\left(p_1\right)\ast Py\left(p_3\right)-Px\left(p_2\right)\ast Py\left(p_1\right)-Px\left(p_3\right)\ast Py\left(p_2\right) \end{gathered}$$

For addition in point geometry, not only the scalar multiplication and the outer product but also the inner product is an operation that satisfies the distributive law, which is defined as follows.

Definition 5

(Scalar product). If $A=(x,y),B=(u,v)$ then $A·B=ux+vy$.

The binary function Scalarprod represents the scalar product of two points; the function symbol is ‘·’.

$$Scalarprod\left(\left(p_1:\right.\right.Point),\left(p_2:\right.Point\left.)\right)\in \mathbb{R}\triangleq Px\left(p_1\right)\ast Px\left(p_2\right)+Py\left(p_1\right)\ast Py\left(p_2\right)$$

For a given point P, the square of P is defined using the scalar product of the point with itself, denoted as $Scalarprod(P,P)$. We represent the square of point P as $Pnorm\_sqr\left(P\right)$, which is later expressed as $\sqrt{P^2}$ for simplicity of description; $Pnorm\left(P\right)$ means, i.e., $\left|P\right|$; $distance(P_1,P_2)$ means the length of the line segment $P_1{P}_2$. The point square, the modulus, and the length of the line segment at two points are defined formally as

$$Pnorm\_sqr\left(P\right)\triangleq Scalarprod(P,P)$$

$$Pnorm\left(P\right)\triangleq Sqrt(Pnorm\_sqr(P\left)\right)$$

$$distance(P_1,P_2)\triangleq Sqrt(Pnorm\_sqr\left(Pminus(P_2,P_1)\right))$$

One innovative approach to solving difficulties with angles is to multiply points with complex numbers; the definition of the multiplication of complex and point is as follows.

Definition 6

(Multiplication of complex and point). If $A=(x,y)$ in the Cartesian coordinate system and the complex $\alpha =u+vi,$ then define $\alpha A=uA+i\left(uA\right)$.

For a complex number, $z=u+iv$, where ‘$+i$’ is a binary function of type $R\to R\to C$. Similar to $Px$ and $Py$, there is $Cre\left(z\right)=u$ and $Cim\left(z\right)=v$. CPmult denotes the complex number multiplied by a point:

$$CPmult(z,p)\triangleq \left(\right(Cre\left(z\right)\ast Px\left(p\right)-Cim\left(z\right)\ast Px\left(y\right)),(Cre\left(z\right)\ast Py\left(p\right)+Cim\left(z\right)\ast Px\left(y\right)\left)\right)$$

3. Formal Description and Proof of Geometric Propositions

This section will give a brief introduction to the proof model. We start by describing the geometric construction, a set of geometric predicates used to describe a geometric proposition.We then continue with a group of rules for proofs and finally show how to complete a proof for a geometric proposition.

3.1. Geometric Predicates

Geometric objects come first, followed by the relationships between them. Geometric predicates are intuitive predicates used to express static relations. Complex geometries are often constructed from simple geometries, and in order to describe geometric propositions, this subsection describes the construction of the main geometric predicates in point geometry.

Starting from the collinearity of three points, if there exists a real number $\lambda$ such that $\overrightarrow{P_1{P}_2}=\lambda \overrightarrow{P_1{P}_3}$, then, in vector geometry, it can be concluded that the three points $P_1$, $P_2$, and $P_3$ are collinear, so the formal representation of vector collinearity is $Vcollin$.

Predicate 1

(Vcollin). $\exists \lambda :R,Vec\left(P_1,P_2\right)=\lambda \ast Vec\left(P_1,P_3\right).$

Since $Vec(P_1,P_2)$ is equivalent to $Pminus(P_2,P_1)$, the collinear formalism of three points in point geometry is described as $collin$.

Predicate 2

(Collin). $\exists \lambda :R,P_2-P_1=\lambda \ast \left(P_3-P_1\right).$

Note that if $P_1$ is the origin O, then clearly O, $P_2$, and $P_3$ are collinear if and only if there exists a $\lambda$ with $P_2=\lambda \ast P_3$.

If two lines $AB$ and $CD$ intersect, as long as there is the equation $u+v=r+s$ such that $u{P}_1+v{P}_2=r{P}_3+s{P}_4$, there is $P_F$, $P_G$ satisfying $(u+v)P_F=u{P}_1+v{P}_2=r{P}_3+s{P}_4=(r+s)P_G$. In fact, it is easy to see from the above linear combination of two points that as long as $u+v=r+s\ne 0$, the points $P_F$ and $P_G$ are on the lines $P_1{P}_2$ and $P_3{P}_4$, which also implies $P_F=P_G$. Therefore, $P_F$($P_G$) is the intersection point of $P_1{P}_2$ and $P_3{P}_4$. In conclusion, the information of the intersection point $P_F$ of two lines can be derived from the linear combination of four points, such as ‘$P_F=(u/(u+v))P_1+(v/(u+v))P_2$’. $Xcollin$ is a geometric predicate describing the intersection point of two lines.

Predicate 3

(Xcollin). $u+v=r+s\to u\ast P_1+v\ast P_2=r\ast P_3+s\ast P_4\to (r+s)\ast P_X=r\ast P_3+s\ast P_4$.

Consider the geometric meaning of the point geometry equation $P_1+P_2={\lambda P}_3$ when $\lambda =1,2,3$ as $P_{1}O{P}_2{P}_3$ as a parallelogram, $P_3$ as the midpoint of $P_1{P}_2$, and $P_3$ as the center of gravity of triangle $O{P}_1{P}_2$, respectively; then, the parallelogram ($Parall$), the midpoint ($Midpoint$), and the center of gravity of triangle ($Ptr\_median$) can be constructed.

Predicate 4

(Parall). $P_1+P_3=P_2+P_4$.

Predicate 5

(Midpoint). $P_1+P_2=2\ast P_3$.

Predicate 6

(Tra_median). $3\ast P_{\mathrm{G}}=P_1+P_2+P_3$.

Now, we can specify the geometric proposition that we wish to verify using geometric predicates. Geometric figures and propositions contain a great deal of information, so it is only necessary to add the relevant information to the context. The relevant hypothesis and conclusion in Example 1 are shown as follows.

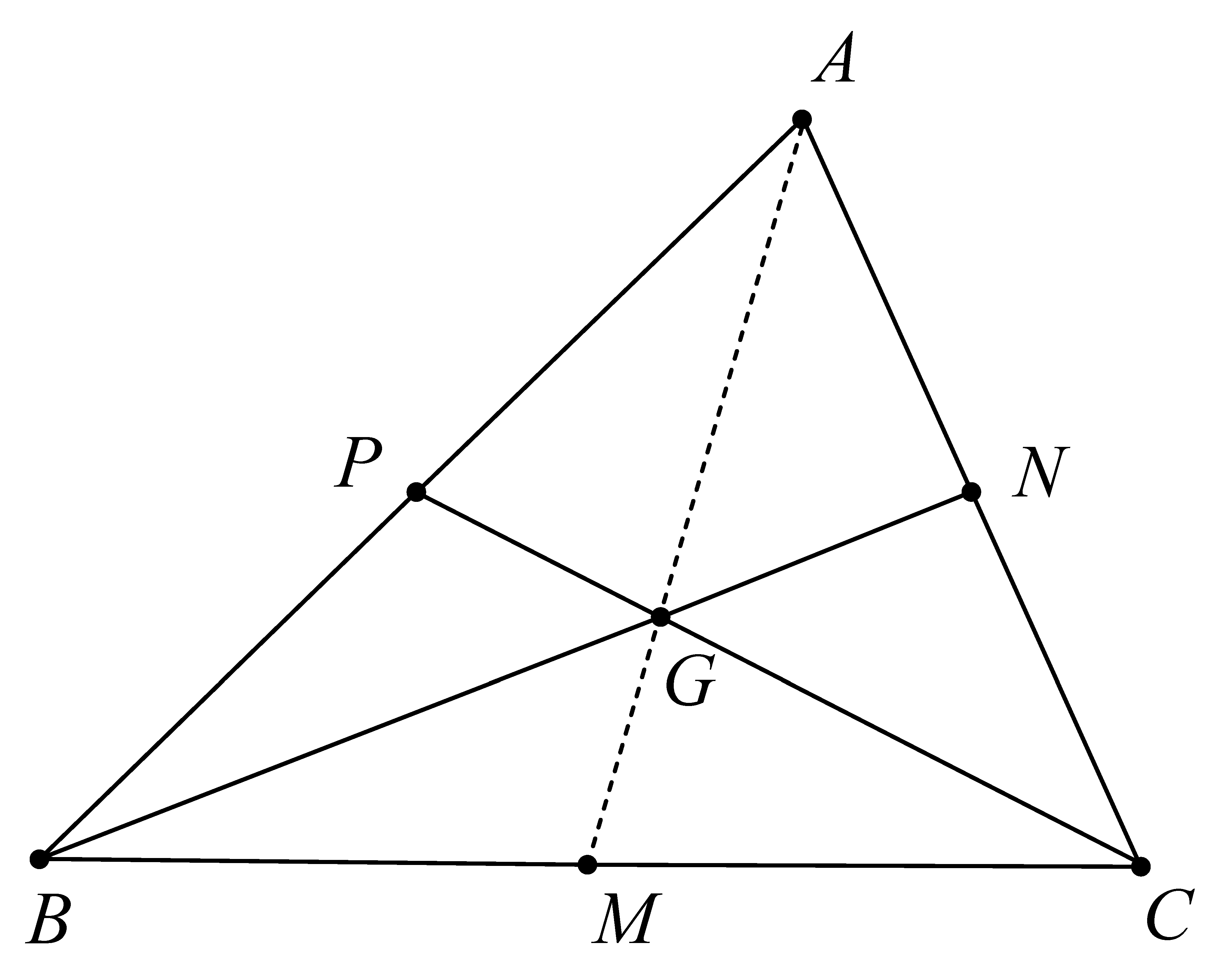
• Hypothesis: Point P is midpoint of segment $AB$.
• Hypothesis: Point N is the midpoint of segment $AC$.
• Hypothesis: Point M is the midpoint of segment $BC$.
• Hypothesis: $BN$ and $CP$ intersect at point G.
• Conclusion: Three points, A, B, and C, are collinear.

The conclusion in Example 1 is equivalent to proving that the points A, G, and M are collinear, i.e., they satisfy the ‘collin (A, G, M)’ relation. The description of Example 1 is as follows.

Example First_exam: ∀ A B C M N P G : Point,
   A = O → Midpoint P A B → Midpoint N A C → Midpoint M B C → Xcollin
	N B P C G → collin A G M.
		

3.2. Rules and Proof Mode

Thus far, we have seen how to describe geometric propositions in Coq based on the definition of point geometry and geometric predicates. However, this is insufficient to prove a geometric proposition. Additional reliable proof rules and proof tactics are required. We will show how to prove a geometric proposition after giving some typical rules.

3.2.1. Rules

Let us first consider the rule $Peq$ for determining the equality of two points.

Rule 1

(Peq). $\forall P_1{P}_2:\mathrm{Point},P_1=P_2\leftrightarrow Px\left(P_1\right)=Px\left(P_2\right)\wedge Py\left(P_1\right)=Py\left(P_2\right).$

The Peq rule, which expands the equality in point geometry to the equality of the corresponding real coordinates, is used to verify the validity of fundamental rules. Take the verification of the exchange law of the addition of points (Rule 2) as an example.

Rule 2

(Padd_comm). $\forall P_1{P}_2:\mathrm{Point},P_1+P_2=P_2+P_1.$

Proof of Rule 2.

According to the rule Peq, proving that the equation $P_1+P_2=P_2+P_1$ holds is equivalent to proving that $Px(P_1+P_2)=Px(P_2+P_1)\wedge Py(P_1+P_2)=Py(P_2+P_1)$.    □

Furthermore, the origin in point geometry is a rather particular point, and there are several rules about the origin that are easily verified by Peq’s rule.

$$Pneg\_0:-O=OPmult\_0:n\ast O=OPplus\_0\_l:O+P=P$$

$$Pplus\_0\_r:P+O=PPminus\_0\_l:O-P=-PPminus\_0\_r:P-O=P$$

With the basic rules of point geometry as a basis, some more complex geometric propositions can be proven directly based on points, without expanding the coordinates of the points. For example, the co-side theorem, expressed by the product of three points, bridges point geometry and the area method by converting the ratio of triangle areas into the ratio of sides. A variation of the co-side theorem is offered here to simplify the demonstration of the pertinent geometric propositions.

Rule 3

(CommonEdg). If F is the intersection of lines $AB$ and $CD$ and $F\ne B$, then we have $\frac{\left|ACD\right|}{\left|BCD\right|}=\frac{\left|AF\right|}{\left|BF\right|}$.

Proof of Rule 3 

If F is the intersection of lines $AB$ and $CD$, and $F\ne B$, then for all u, v, r, s, as long as $u+v=r+s$, we have $(u+v)F=uA+vB=rC+sD$. We also have the equation $uACD+vBCD=0$ when we use $CD$ as the outer product. Furthermore, since $(u+v)F=uA+vB$, it follows that $u(F-A)+v(F-B)=0$. Therefore, we can conclude that $\frac{\left|ACD\right|}{\left|BCD\right|}=\frac{\left|AF\right|}{\left|BF\right|}$ based on the previous deductions.    □

Other laws, such as the laws of addition, scalar multiplication, outer products, the complex multiplication of points, and the logical relationships between geometric predicates, are already established in Coq. Moreover, the user may add rules as needed, and when the rules are verified in point geometry theory, they can be used to prove more geometric propositions.

3.2.2. Proof Mode

This part aims to elaborate on a proof mode for a geometric proposition, which can be accomplished by interacting with tactics. The reliability of this proof process is guaranteed by Coq, an interactive proof assistant tool whose kernel ensures the correctness of tactics. To assist with the development of proofs, Coq offers a robust decision process and a library of automated proof tactics. Several proof tactics commonly used in interactive proof development are listed below.

• intros: Adds assumptions to the current context.
• apply H: Applies the hypothesis or rule H.
• rewrite: A tactic for replacement.
• unfold$def$: Used to expand the definition.
• destruct: For discussion by the situation.

Now, consider the proof of Example 1; the state before the start of the proof is shown below.

1 goal
---------------------------------------------------------------------------
∀ A B N C P G M : Point, A = O → Midpoint P A B → Midpoint N A C →
    Midpoint M B C → Xcollin N B P C G → collin A G M.
         

The area above the dashed line represents the context $\mathsf{\Gamma }$, where $\mathsf{\Gamma }=\left[\right]$ at this point, and the area below the dashed line represents the geometric proposition to be proven. Firstly, with the exception of the conclusion ‘collin A G M’, which remains to be proven, all other statements will be introduced into the context through the tactic ‘intros’. The left-hand side of the proof state presented below is the result of using the ‘intros’, and this state is the initial proof state. Then, with the following tactics, the geometric predicate will be expanded, and the origin will be eliminated according to the following rules.

unfold Midpoint, Xcollin, collin in *;

rewrite H, Pplus_0_l in *;

do 2 rewrite Pminus_0_r.   

The proof state enters the geometric-algebraic state, as in the right-hand side of the proof state presented below.

	- A, B, N, C, P, G, M: Point
- A, B, N, C, P, G, M :	- H : A = O
Point	- H0: B = 2 * P
- H : A = O	- H1: C = 2 * N
- H0: Midpoint P A B	- H2: B + C = 2 * M
- H1: Midpoint N A C	- H3: ∀ u v r s: R, (u + v) = (r + s) → u * N
- H2: Midpoint M B C	+ v * B = r * P + s * C →  (r + s) * G = r
- H3: Xcollin N B P C G	* P + s * C
--------------------------	-----------------------------------------------
collin A G M	∃ m, G = m * M

For example, the equation corresponding to hypothesis $H_0$ is $2P=A+B$. Using the rewrite tactic, according to hypothesis H, replacing the origin A with O, there is $2P=O+B$. Moreover, using the Pplus_0_l rule, the rewrite tactic can replace $O+B$ with B, yielding $H_0$.

The current goal is to introduce a term of G as a proof according to the context. From the geometric proposition, it is clear that point G is the intersection of the lines $NB$ and $PC$. However, there is no expression in the context that directly expresses the relationship between G and M. It is necessary to establish the equidistant relationships among points N, B, P, and C in order to deduce the expression for point G based on $H_3$. From assumptions $H_0$, $H_1$, and $H_2$, we know that N, B, P, and C satisfy the equation $HX:2N+B=2P+C$. The addition of this equation is performed by the tactic assert below.

    assert HX: 2 * N +1 * B = 2 * P + 1 * C). {rewrite <- H1, H0. Psolver. }

The content in “{ }” is proof of HX, and the tactic ’Psolver’ is a decision procedure that can solve linear arithmetic problems with points, which will be introduced in detail in Section 4. From $HX$ and $H_3$, we know that $3G=2P+C$, and from $H_0$ and $H_2$, we know that $B+C=2M$, so it is easy to determine that $m=2/3$; the conclusion can be proven, and this part of the proof is realized by the following tactics.

    apply H3 in HX; auto. exists (2/3); Psolver.

The preceding proof is similar to a step-by-step proof and is hence time-consuming. In the next part, we will introduce numerous automatic tactics to make proofs easier.

4. Proof Tactics

The previous sections focused on the formal description and verification of point geometry theory, including definitions, geometric predicates, rules, and proof models for geometric propositions. We can also design automatic solving and programmable tactics to prove specific types of complicated geometric problems. This section details the functions and methods of several essential geometric proof tactics.

4.1. Oelim

4.1.1. Origin

In point geometry, any point can be chosen as the origin, and the geometric relations between points can be constructed with reference to the origin, which is the cleverness of point geometry. For example, $Parall\left(P_1{P}_2{P}_3{P}_4\right)$ means parallelogram $P_1{P}_2{P}_3{P}_4$, which means that wherever the origin is, as long as the four points $P_1$, $P_2$, $P_3$, and $P_4$ satisfy $P_1+P_2=P_3+P_4$, it means that the quadrilateral $P_1{P}_2{P}_3{P}_4$ is a parallelogram. In particular, if $P_1$ is taken as the origin, then $P_2=P_3+P_4$. The flexibility in the choice of origin makes the point geometry solution process more concise.

For a geometric proposition, once the origin is determined, all points set as the origin in this proposition can be eliminated by the six rules about the origin in Section 3.2.1.

Example 2.

Below is an example of origin elimination.

$$P_1=O,Parall{P}_1{P}_2{P}_3{P}_4⊢P_2=P_3+P_4$$

$$\begin{array}{ccc}1\hfill & P_1=O\hfill & Premise\hfill \\ 2\hfill & Parall{P}_1{P}_2{P}_3{P}_4\hfill & Premise\hfill \\ 3\hfill & P_1+P_2=P_3+P_4\hfill & unfoldParall,2\hfill \\ 4\hfill & O+P_2=P_3+P_4\hfill & rewrite1,3\hfill \\ 5\hfill & P_2=P_3+P_4\hfill & rewritePplus\_0\_l,4\hfill \end{array}$$

4.1.2. Method of Eliminating the Origin

Oelim is a tactic that automates a process similarly to the elimination of the origin in Example 2. If the current proof state is $st$, Oelim unfolds the geometric predicate’s definition, introduces the conditions and assumptions into the context, and then eliminates the origin. The proof state after the elimination of the origin by the Oelim tactic is denoted as $s{t}^{eO}$. The method is as in Algorithm 1.

Algorithm 1Oelim
Input: Current proof state $st$.
Output: Algebraic proof state $s{t}^{eO}$
1: Expand the geometric predicate and introduce the hypothesis into the context.
2: if $\mathsf{\Gamma }⊢(H:?P=O)$ then
3:     for $eachi\in \{1,\dots ,m+1\}$do	▹m is the number of hypotheses
4:         if $P\in V\left(H{p}_i\right)$then	▹ Conclusion g is $H{p}_{m+1}$
5:            $term\left(H{p}_i\right):=term\left(H{p}_i\right)(P/O)$;
6:            Elim O with rules of O; return;
7:         end if
8:     end for
9: else
10:     Elim O with rules of O; return;
11: end if

If the current proof state is denoted as $st$, with $\mathsf{\Gamma }$ as the current context and the geometric proposition $P:\forall \left(v_1:T_1\right)\left(v_2:T_2\right)\cdots \left(v_n:T_n\right),\left(H{p}_1\to H{p}_2\to \cdots \to H{p}_{m+1}\right)$ as the current goal, then the current state is denoted as

$$st=E_p,\mathsf{\Gamma }{⊢}^{?}\forall \left(v_1:T_1\right)\left(v_2:T_2\right)\cdots \left(v_n:T_n\right),\left(H{p}_1\to H{p}_2\to \cdots \to H{p}_{m+1}\right)$$

where $H{p}_{m+1}$ is the proof goal g of the geometric proposition. First, let ${\widetilde{Hp}}_i$ denote the point geometric algebraic state of each ${Hp}_i$ after unfolding the geometric predicate, where ${\widetilde{Hp}}_{m+1}$ denotes the point geometric algebraic form $\tilde{g}$ of conclusion g; then, step 1 unfolds the geometric predicate by applying the ‘unfold’ and introduces the hypothesis into the context by using the ‘intros’, so that the proof state becomes

$$\widetilde{st}:E_p,\mathsf{\Gamma }::{\left[(v_i:T_i)\right]}_{i=1}^n::{\left[(H_j:{\widetilde{Hp}}_j)\right]}_{j=1}^m{⊢}^{?}\tilde{g}$$

If a point is given as the origin in the hypothesis, i.e., there is an item “$H:?P=0$” in the context, then we use the rewrite tactic to replace all occurrences of point P in the context with point O and apply origin elimination rules to remove the origin. If not, then we apply the rule to eliminate the origin directly. At this point, if we use ${{Hp}_i}^{eO}$ to denote the hypothesis and $g^{eO}$ to denote the conclusion, then we have ${\mathsf{\Gamma }}^{eO}={\left[(v_i:T_i)\right]}_{i=1}^n::{\left[(H_j:{{\widetilde{Hp}}_j}^{eO})\right]}_{j=1}^m$, and the proof state after applying the Oelim tactic is as follows:

$$s{t}^{eO}=E_p,\mathsf{\Gamma }::{\mathsf{\Gamma }}^{eO}{⊢}^{?}{g}^{eO}$$

It is easy to see that the origin of all terms in the algebraic state of ${st}^{eO}$ has been eliminated. Oelim uses tactics such as $intros$, $unfold$, and $rewrite$ to introduce the hypothesis into the context, expand the geometric predicate, and apply the origin-related rules to replace the eliminated origin so that the proof of the topic enters the simplified algebraic state, i.e., $st⟹{st}^{eO}$.

4.2. Linear Point Geometry Decision Procedures Based on Real Numbers

Positivstellensatz generalizes Hilbert’s zero theorems for a finite set S of polynomials, and it searches for the refutation of $Cone\left(S\right)$ to prove a nonlinear arithmetic problem [34]. Psolver is a tactic used to solve point geometry problems using a Positivstellensatz-based decision procedure on linear algebra over the field of real and rational numbers, where the transformation of real numbers to points is implemented by $Peq$ (Rule 1).

The method of Psolver is implemented by Algorithm 2. Firstly, the method unfolds all not (¬) in the current state, and its resultant state is represented by ${\mathrm{UF}}_{not}\left(st\right)$. Then, Pfactor initiates the recursive expansion of the formula structure. Firstly, if the goal to be proven, g, has the pattern ‘$(\_\to \_)$’, the ‘intros’ tactic is used to introduce a new declaration into the context, resulting in a new proof state denoted as ‘$Intro\left(st\right)$’ in this context. Let $\mathrm{APPL}Peq\left(st\right)$ denote the application of the Peq rule to expand all point geometric equalities in the proof state $st$. Therefore, the new proof state obtained by applying the Peq rule to the current state is ‘$\mathrm{APPL}Peq\left(Intro\right(st\left)\right)$’. For the context $\mathsf{\Gamma }$ in the current proof state, for all declarations with type pattern ‘$(\_\wedge \_)$’, ‘$(\_\vee \_)$’ or ‘$(\_\leftrightarrow \_)$’ that need to be discussed on a case-by-case basis, the method uses the destruct tactic, such that $i{d}^{\sim }$ denotes the new sequence of declarations generated after applying the destruct tactic. The state obtained by applying the Peq rule is represented as ${\mathrm{APPL}}_{Peq}(Intro\left(st\right))$. In the same way, the problem is solved by deconstructing and transforming the goal to be proven with patterns ‘$(\_\leftrightarrow \_)$’, ‘$(\_\wedge \_)$’ and ‘$(\_\vee \_)$’, and the proof state obtained is a real algebraic state.

Algorithm 2Psolver

Input: Current proof state $st$. Output: If $st=E_p,\mathsf{\Gamma }{⊢}^{?}\left[\right]$, then the goal is proven; otherwise, do nothing 1: Procedure Pfactor ($st$) 2: $st={\mathrm{UF}}_{not}\left(st\right)$; 3: ifg in pattern of $\left({}_{-}\to {}_{-}\right)$ then 4:     $st={\mathrm{APPL}}_{Peq}(Intro\left(st\right))$; 5:     Pfactor ($st$); 6: else 7:     for each $id$ that $\mathsf{\Gamma }⊢id:Point$ or $id:(\_\wedge \_)$ or $id:(\_\vee \_)$ or $(\_\leftrightarrow \_)$ do 8:         $i{d}^{\sim }=Destr\left(id\right)$; 9:         if g is in pattern of (_ ↔ _) or $(\_\wedge \_)$ then 10:            $g_i=SP{\left(g\right)}_i$; 11:            $st=APP{L}_{Peq}\left(st\left(g/g_i\right)\right)$; 12:            Pfactor ($st$); 13:         else if g is in pattern of $(\_\vee \_)$ then; 14:            $st=st(g/LAR(g\left)\right)$; 15:            Pfactor $\left(APP{L}_{Peq}\left(st\right)\right)$; 16:         end if 17:     end forreturn; 18: end if 19: Procedure Psolver ($st$) 20: Psolver(Pfactor($st$));

4.3. A Proof Method for a Hilbert Intersection Problem

One of the proofs of Example 1 mentioned in Section 3 is tedious. In fact, PointGeo can use only one tactic, HilbertX, to complete the proof and return the solution process. Designing automatic proof tactics such as this can enhance the readability of machine proofs and improve the efficiency in solving them.

4.3.1. Framework of HilbertX

HilbertX is an incomplete Hilbert intersection class proof method as in Algorithm 3. For a Hilbert intersection class problem P, the HilbertX tactic deduces the hidden intersection information and returns the solution process information to efficiently assist in solving the geometric problem. The proof method of the HilbertX tactic is shown in Figure 2.

HilbertX solves the problem with intersections and returns the solution information, which is output on lines 1 and 8, respectively. The tactic accepts four optional parameters, a, b, c, and d. The four parameters are entered if and only if there are two intersections in the problem. For a geometric proposition, Oelim is first invoked to eliminate the origin and transform the proof state into a geometric algebraic state. Then, the hidden information term is obtained by HilXcol_K (Section 4.3.2) and automatically solved by the point geometric linear arithmetic decision process. If the geometric proposition is not solved, the $s{t}^{eO}$ proof state is retained.

Algorithm 3 Framework of HilbertX
Input: Current proof state $st$ and optional parameters a b c d.
Output: “Done” if the goal is proven, $s{t}^{eO}$ otherwise
1: $s{t}^{eO}:=Oelim\left(st\right)$;	▹ return information
2: if type of $a=ltac\_No\_arg$ then
3:     $s{t}^P:=$ Psolver $\left(s{t}^{eO}\right)$;
4:     if $s{t}^P=E_p,\mathsf{\Gamma }{⊢}^{?}\left[\right]$ then return “Done”;
5:     else return;
6:     end if
7: else
8:     $s{t}^K:=$Hilxcol_K$(s{t}^{eo},a,b,c,d)$;
9:     $s{t}^{P^{\prime }}:=Psolver\left(s{t}^K\right)$;
10:     if $s{t}^{P^{\prime }}=E_p,\mathsf{\Gamma }{⊢}^{?}\left[\right]$ then return “Done”;	▹ return information
11:     else return;
12:     end if
13: end if

4.3.2. Generation of Intersection Information Items

If the line $AB$ intersects the line $CD$, then their intersection K is unique and fixed, and the $Xcollin$ rule can be obtained from the algebraic relations of A, B, C, and D to their algebraic relations with K, i.e., the information term ${term}_k$ of the intersection K of $AB$ and $CD$. The algebraic relation of the four points here means finding a set of values of u, v, r, and s such that $u+v=r+s\to u\ast A+v\ast B=r\ast C+s\ast D$ holds and the information term ${term}_k$ is the equation $(r+s)K=r\ast C+s\ast D$ or $\left(u+v\right)K=u\ast A+v\ast B$ obtained by $Xcollin$.

4.3.3. Step-by-Step Proof and Proof by Tactic

Example 3.

In parallelogram $ABCD$, M is the midpoint of $AB$ and P is the intersection of $AC$ and $BD$. Then, $\overrightarrow{AC}=3\overrightarrow{AP}$. The predicates corresponding to the conditions and conclusions are represented as follows.

• parallelogram ABCD: $ParallelABCD$.
• M is the midpoint of AB: $MidpointMAB$.
• P is the intersection of AC and BD: $XcollinACMDP$.
• $\overrightarrow{AC}=3\overrightarrow{AP}$: $VecAC=3\ast VecAP$

Since Example 3 is a Hilbert intersection class problem, HilbertX can prove this proposition. The proposition description, proof, and proof process information of Example 3 are as follows.

• Lemma Para_exam: ∀ A B C D M P : Point,
• A=O → Parall A B C D → Midpoint M A B → Xcollin A C M D P → Vec A C = 3 * Vec A P.
• Proof. HilbertX 2 1 2 1. Qed.
• ------------------------------------
• After unfolding predictions and eliminating the 0, we obtain the following hypotheses:
• H: A = O.
• H0: C = B + D.
• H1: B = 2 * M.
• H2: ∀ u v r s : R,
• u + v = r + s → u * O + v * C = r * M + s * D → (r + s ) * P = r * M + s * D.
• We begin to prove the goal: C = 3 * P.
• Firstly, we construct the equation Hx: 2 * O + 1 * C = 2 * M + 1 * D.
• By the rule of Xcollin, we obtain the equation of P: Hx: (2 + 1) * P = 2 * M + 1 * D.
• Finally, the proposition can be proven by the algebraic operations of points. Done.

The proof of Example 1 mentioned in Section 3.2.2 is tedious and is equivalent to a step-by-step proof. In fact, it is also a Hilbert intersection class problem, which can be proven using only one tactic, HilbertX, which can also return information about the solution process.

Table 1. The number of proof lines required for a step-by-step proof using the rule is 14, and the proof can be completed in only one line using the tactic, which also returns information about the solution process.

Geometry Propositions	Proof Mode Line Numbers	Tactic Line Numbers
First_exam	7	1
Para_exam	14	1

compares the code lengths of the step-by-step proof and the tactic proof for Example 1 and Example 3, and it is clear that the number of proof lines required for the step-by-step proof using the rule is 14, while the tactic requires only one line, which is more convenient and faster.

Consider the comparison of the lengths of the step-by-step proofs and the tactic proofs for the two proof topics, as shown in the following table.

5. Proof System

We propose a point geometric machine proof system, PointGeo, which is capable of integrating multiple geometric-theorem-proving methods and allowing users to add content as needed. Based on a verified point-based geometric theory framework, PointGeo can prove any solvable geometric proposition in point geometry. The design of this system aims to provide an efficient and accurate method of proof, and it provides a new tool and perspective for research in the field of point geometry.

5.1. Structure of the System

PointGeo consists of five main parts, namely basic definitions, fundamental properties, and common rules of point geometry; geometric predicates; proof tactics; and propositional proofs, which are distributed as shown in

Table 2. The content of PointGeo.

PointGeo	Content	Line Numbers	Outline
PF.v	Basic definition	95	32
Pbasics.v	Properties	304	67
Plemma.v	Rules	273	61
Pconstruct.v	Predicates	76	26
PTactic.v	Proof tactics	316	41
Proj.v	Machine proof	1783	188

.

5.2. Proof Method

PointGeo is a scalable proof system that accepts a variety of methods. It is possible to prove geometric propositions based on the basic theory of point geometry, such as Hilbert-intersection-like problems and geometric problems on angular rotations, similar to Morley’s theorem.

Example 4

(Morley’s theorem).

In $\Delta ABC$, let P, Q, and R be the intersection points of the trisection of two angles of the triangle. Then, triangle $\Delta PQR$ is an equilateral triangle.

In order to prove the conclusion of Morley’s Theorem, which states that $e^{\frac{i\pi }{3}}(Q-P)=R-P$, we can introduce the notation $e^{\frac{i\pi }{3}}=\omega$. The objective is then to demonstrate that $\omega Q-R={\omega }^{2}P$. The description of Morley’s theorem is presented as follows, and its proof is also completed in PointGeo.

• Theorem Morley:
• ∀ (A B C’ P Q R’ : Point) (a b r : R) (w u v : C),
• A = O → triangle0 A B C’ (3 * a) (3 * b) → triangle0 A B R’ a b → triangle0 A Q C’ a (PI - a - r) → triangle0 B C’ P b r → w = Cexp (0 +i (PI / 3) → u = Cexp (0 +i (- 2 * a) → v = Cexp (0 +i (- 2 * b) → r = (PI / 3 - a - b)  → (CPmult w Q) - R’ = CPmult (w ^ 2) P.
• Proof.... Qed.

The definition of the outer product of three points in point geometry theory relates the area to the points. This leads to the co-side theorem, an essential theorem in the area method, in point geometry theory. Therefore, PointGeo supports the use of the area method to prove geometric propositions. Solving geometric propositions using the area method has higher readability and can avoid complex parameters. This feature is well illustrated in the proof of Pappus’s theorem, as shown in Example 5.

Example 5

(Pappus’ theorem). Let points A, B, and C be collinear; D, E, and F be collinear; the lines AE and BD intersect at P; AF and CD intersect at Q; and CE and BF intersect at R. Then, P, Q, and R are collinear, as in Figure 3.

The CommEdg rule derived from the properties of the outer product provides a proof rule for the area-based proof of Pappus’s theorem. For example, as shown in Figure 3b, if $RC$ and $EQ$ intersect at point E, i.e., if the condition $Xcollin\left(RCEQ\right)$ is satisfied, then applying the CommEdg rule yields the equation $\frac{Rabs\left(sREQ\right)}{Rabs\left(sCEQ\right)}=\frac{distanceER}{distanceEC}$, i.e.,

$$\frac{\left|REQ\right|}{\left|CEQ\right|}=\frac{\left|RE\right|}{\left|CE\right|}:XcollinRCEQE\to sCEQ\ne 0\to \frac{\mathrm{Rabs}(\mathrm{s}\mathrm{REQ})}{\mathrm{Rabs}\left(sCEQ\right)}=\frac{\mathrm{distance}ER}{\mathrm{distance}EC}.$$

Similarly, the new problem-solving information for (c)~(n) in Figure 3 can be inferred through CommEdg. The formal description and a more detailed formal proof of the Pappus theorem have been completed in PointGeo.

Propositional descriptions and proofs based on point geometry theory can also be converted into vectors and proven using the vector method. However, the rules related to vectors are not yet complete. Fortunately, it can be solved quickly by the Psolver using the real-related decision process.

6. Conclusions

We formalized and verified the new algebraic geometry system, point geometry, and constructed an interactive geometry-theorem-proving system based on point geometry theory. The system guarantees the reliability of proofs and supports user-generated content with scalability. Moreover, we designed automatic proof tactics to enhance the automation level of interactive proof and enabled the automatic presentation of the proof process by recording the proof status, providing readability. The system also supports multiple geometric-theorem-proving methods. Our next step is to improve various automatic proof methods in PointGeo, such as the point elimination algorithm based on the area method, to make the system more versatile, efficient, and readable.