Self-Similarity Principle and the General Theory of Fractal Elements: How to Fit a Random Curve with a Clearly Expressed Trend?

Abstract

The well-known power-law fractal element was determined to need several important revisions by the authors of this work. It is now possible to demonstrate that any scaling equation associated with a fractal element is actually K-fold degenerated and includes previously unknown but crucial adjustments. These new discoveries have the potential to significantly alter the preexisting theory and create new connections between it and its experimental support, particularly when it comes to measurements of the impedances of diverse metamaterials. It is now easy to demonstrate that any random curve with a clearly stated tendency in a specific range of scales is self-similar using the method involving reduction to three invariant points (Ymx, Ymn, and Ymin). This useful procedure indicates that the chosen random curve, even after being compressed a certain number of times, still resembles the original curve. Based on this common peculiarity, it is now possible to derive “a universal” fitting function that can be used in a variety of applied sciences, particularly those that deal with complex systems, to parametrize many initial curves when a model fitting function derived from a simple model is not present. This self-similarity principle-derived function demonstrates its effectiveness in data linked to photodiode noise and the smoothed integral curves produced from well-known transcendental numbers E and Pi, which are considered in the paper as an example.

1. Introduction and Formulation of the Problem

Whether there is another principle that can generate power-law dependencies without the use of non-integer operators, or whether power-law dependencies follow from the models that have non-integer operators are important questions that require a solution. Fractional calculus is now the most advanced area in mathematics. The characteristics of non-integer operators are the subject of many excellent monographs. These operators make it possible to resolve some difficult mathematical physical properties. Here, we would like to draw attention to Yu. I. Babenko’s monograph [1], in which he first employed a unique technique for splitting (extraction of the square root) from diffusion equation containing integer operators and nonhomogeneous coefficients. Thanks to this original technique, he was able to find analytical solutions that were not known earlier. It is also appropriate to mention the monographs of Prof. V.V. Uchaikin [2] and the capital monograph of Prof. S.G. Samko with co-authors [3], which open a door in new mathematics to young researches. Specialized journals, such as Fractional Calculus and Applied Analysis (FCAA), have determined the basic trend in the development of this field of mathematics. The development of materials has made it possible to implement non-integer operations such as differentiation and integration in a range of fractional elements [4]. However, there is currently a weakness in this area of mathematics: there is no justification for the physical/geometrical meaning of these operators in comparison to integer operators, such as the area under the curve and the slope value produced by the first derivative. One should recall the attempts made by RRN, one of the authors of this study, to design a method for averaging a smoothed function over a Cantor (fractal) set. This results in the Riemann–Liouville-type fractional integral [5,6]; however, the interpretation of the significance of the various fractional integral types [7] is far from an explicit and justified interpretation.

Another problem is related to the question formulated above. This problem was formulated also in the papers of J. Sabatier [8,9,10], who noticed that it is necessary to generate a difference between the fractal models generated by non-integer operators and the power-law dependencies that exist irrespective of these proposed models. In a book [11] written by one of the authors, the way in which the fractional calculus could be naturally associated with fractional-order signal processing was shown.

This study aims to demonstrate that the self-similar principle does in fact produce power-law dependencies and complex conjugated addings. We only have the complex-conjugated addings for the unit root. We also wish to demonstrate that any randomly generated curve with a clearly defined trend that is compressed in ξ times maintains its self-invariance. This finding enables the fitting function to be derived, and it actually creates a new “information space” or platform, in addition to the Fourier transformation and the z-transform, two operations that are frequently applied in the field of current signal processing. When the fitting function produced from a simple model is absent, this self-similarity principle enables the fitting of a large variety of random functions.

The content of the paper is organized as follows. In the second chapter, we develop the general theory of the fractional power-law elements when some roots are degenerated. In Section 3, we show the algorithm for the treatment of the functions that exhibit the self-similar property. Two examples are considered. In the conclusion of the final section, we discuss the obtained results and outline the perspectives of further research.

2. General Theory of the Fractional Power-Law Elements, The Influence of the Degenerated Terms

It is well known from the grounds of fractal geometry [12] that the Weierstrass–Mandelbrot function for different values of scales and the range of the fractal dimension 1 < D < 2 is self-similar. This function W(t) for further purposes is convenient to generalize and represent in the following form:

$$\begin{array}{l}W(t)={\displaystyle \sum _{n=-N}^N{\left(b^{D-2}{e}^{i\phi }\right)}^n\left(1-\exp \left(it{\xi }^n\right)\right)\stackrel{b^{D-2}{e}^{i\phi }\to b{e}^{i\phi }}{=}}\\ \to S\left(z\right)={\displaystyle \sum _{n=-N}^N{b}^{n}f\left(z{\xi }^n\right)}\end{array}$$

(1)

Here, $b=\left|b\right|e^{i\phi }$ is a complex value and the newly defined parameter b in the second line can accept any arbitrary value (positive, negative or even complex). Parameter ξ defines a scaling parameter and ϕ is the phase of a complex value, t is a temporal variable. Here, the sum S(z) is defined for any variable, including time, frequency, etc. The complex function f(z) figuring in (1) has the following asymptotic decompositions:

$$f(z)=\left(\begin{array}{l}{c}_1\left|z\right|+c_2{\left|z\right|}^2+\dots \hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}\hspace{0.17em}\left|z\right|<<1,\\ \frac{A_1}{\left|z\right|}+\frac{A_2}{{\left|z\right|}^2}+\dots \hspace{0.17em}at\hspace{0.17em}\hspace{0.17em}\left|z\right|>>1.\end{array}\right.$$

(2)

Considering the conditions imposed above, one can obtain the following relationship from (1):

$$S(z\xi )=\frac{1}{b}S\left(z\right)+b^{N}f\left(z{\xi }^{N+1}\right)-b^{-N-1}f\left(z{\xi }^{-N}\right).$$

(3)

This sum was analyzed in paper [13]. Four cases (when the two last terms in (3) become negligible) are possible:

Case (a) when b, ξ > 1. The contribution of the two terms in (3) becomes negligible when ξ > b.

Case (b) when b, ξ < 1. The contribution of the two terms in (3) becomes negligible when ξ < b.

Case (c) when b > 1, ξ < 1. For this case, it is necessary that bξ < 1.

Case (d) when b < 1, ξ > 1. For this case, it is necessary that bξ > 1.

For b = 1, the contribution of the last two terms is valid also, if the function f(z) keeps its limiting values in accordance with the decompositions (2). The numerical verification of the real part of the function S(z) was realized also in paper [13]. Therefore, one can approximately write the following:

$$\begin{array}{l}S(z\xi )\cong rS(z),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}r=b^{-1},\\ for\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left|\frac{A_2}{A_1}\right|<<\hspace{0.17em}\left|z\right|<<\hspace{0.17em}\left|\frac{c_1}{c_2}\right|.\end{array}$$

(4)

Let us highlight the case in which b = 1. In this case, we obtain the simplest functional equation using the solution expressed in the form of log-periodic decomposition:

$$S(z)\equiv \mathrm{Pr}\left(\ln z\pm \ln \xi \right)={\displaystyle \sum _{k=0}^{K>>1}\left[A{c}_k\cos \left(2\pi k\frac{\ln z}{\ln \xi }\right)+\sin \left(2\pi k\frac{\ln z}{\ln \xi }\right)\right].}$$

(5)

Here, Pr(lnz) determines the solution of the functional Equation (4) expressed in the form of a log-periodic function at b = 1.

Attentive analysis shows that scaling Equation (4) is the K-th fold degenerated. Let us write this equation in the following form:

$$\begin{array}{l}\left(D_{\xi }^2-r{D}_{\xi }\right)S\left(z\right)\cong {\epsilon }_2,\hspace{0.17em}\hspace{0.17em}\left(r{D}_{\xi }-r^2\right)S\left(z\right)\cong {\epsilon }_2,\\ D_{\xi }S(z)\stackrel{def}{\equiv }S\left(z\xi \right)\end{array}$$

(6)

Here, for convenience, we introduce the scaling operator D_ξ. Let us explain the meaning of Equation (6).

If we neglect the existing error between both sides of (4), then it implies that the error of the first order ε₁ equals zero. What happens if we take into account the error of the first order (ε₁ ≠ 0) and neglect the error of the second order ε₂ = 0? In this case, we have to continue the scaling property and write two equations in the first line of (6). If these small remnant values ε₂ in (6) equal each other, then one can write the following scaling equation for the sum S(z)

$$\begin{array}{l}S\left(z{\xi }^2\right)=2rS\left(z\xi \right)-r^{2}S(z),\\ or\hspace{0.17em}\hspace{0.17em}{\left(D_{\xi }-r\right)}^{2}S(z)=\left(D_{\xi }-r\right){\epsilon }_1\cong {\epsilon }_2=0.\end{array}$$

(7)

Continuing these scaling manipulations in Equation (6), one can conclude that the simple Equation (4) is equivalent to the scaling equation

$$\begin{array}{l}\left(D_{\xi }-r\right){\epsilon }_{K-1}={\epsilon }_k\cong 0\\ or\hspace{0.17em}\hspace{0.17em}\\ {\left(D_{\xi }-1\right)}^{K}S(z)\cong {\epsilon }_K=0,\end{array}$$

(8)

and that, therefore, it is the K-th fold degenerated. Here, we introduce the fluctuations in the K-th-order ε_K. Usually, many researchers, in attempts to detect the power-law fractal element, limit themselves by the simplest case (4) and take into account the fluctuations in the first-order ε₁. However, the solution of the functional Equation (8) prompts some essential corrections. The solution of the functional Equation (8) for the K-th-fold degenerated case can be written in the following form [14]:

$$S(z)=z^{\nu }\left({\displaystyle \sum _{q=0}^{K-1}{\left(\frac{\ln (z)}{\ln \xi }\right)}^q}\right)\mathrm{Pr}\left(\ln z\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\nu =\frac{\ln r}{\ln \xi },\hspace{0.17em}\hspace{0.17em}{z}^{\nu }\equiv r^{\ln z/\ln \xi }.$$

(9)

For practical purposes, it is sufficient to take into account at least the case K = 2 and the fluctuations in the second-order ε₂. Log-periodic function Pr(lnz) is defined by Equation (5).

$$S(z)=z^{\nu }\left(1+\frac{\ln z}{\ln \xi }\right)\mathrm{Pr}\left(\ln z\right).$$

(10)

Equation (10) determines an important correction for the single power-law fractal element that has not been taken into account by many researchers working in this area. Attentive analysis shows that solution (10) admits further generalization. Let us rewrite (10) in the following form:

$$\begin{array}{l}S(z)=z^{\nu }\left({\mathrm{Pr}}_1\left(\ln z\right)+b_1\left(\frac{\ln z}{\ln \xi }\right){\mathrm{Pr}}_2\left(\ln z\right)\right),\\ {\mathrm{Pr}}_{1,2}\left(\ln z\right)={\displaystyle \sum _{k=0}^{K>>1}\left[A{c}_k^{\left(1,2\right)}\cos \left(2\pi k\left(\frac{\ln z}{\ln \xi }\right)\right)+A{s}_k^{\left(1,2\right)}\sin \left(2\pi k\left(\frac{\ln z}{\ln \xi }\right)\right)\right]}.\end{array}$$

(11)

The substitution of this solution into Equation (7) and the requirement that there is only one root equal to r = ν leads to the following condition:

$$1+2b_1=d,$$

(12)

where d coincides with any arbitrary number d ≠ 0. Equation (10) represents a partial case when b₁ = 1 and d = 3. Condition (12) for any K looks cumbersome and, therefore, is not given. Solution (11) for the root ν ≠ 1 and K = 2 can be used as the generalized fitting function for the detection of possible corrections in the fitting of measured data related to the detection of the power-law fractal element, when the fluctuations in the second-order ε₂ become important. Below, this function will be used for the case of ν = 1 for the fitting of a wide class of random functions that have a clearly expressed trend. These preliminary evaluations allow other important steps to be undertaken and more complex cases to be considered. Let us consider now two independent sums similar to those written in (1). We suppose also that the similar evaluations made above allow the following combinations to be written:

$$\begin{array}{l}S(z)=S_1(z)+S_2(z),\\ S(z\xi )=r_1{S}_1(z\xi )+r_2{S}_2(z\xi ),\\ S_{1,2}(z)={\displaystyle \sum _{n=-N}^N{b}_{1,2}^n{f}_{1,2}\left(z\xi \right),\hspace{0.17em}\hspace{0.17em}{r}_{1,2}=b_{1,2}^{-1}}.\end{array}$$

(13)

By excluding unknown sums S_1,2(z) from the first two lines and substituting them into equation

$$S\left(z{\xi }^2\right)=r_1^2{S}_1\left(z\right)+r_2^2{S}_2\left(z\right),$$

(14)

we obtain the following functional equation:

$$\begin{array}{l}S\left(z{\xi }^2\right)=w_{1}S\left(z\xi \right)+w_{0}S(z),\\ w_1=r_1+r_2,\hspace{0.17em}\hspace{0.17em}{w}_2=-r_1{r}_2.\end{array}$$

(15)

Using the scaling operator D_ξ defined above, one can represent the functional Equation (15) in a more compact form with the corresponding solution:

$$\begin{array}{l}\left(D_{\xi }-r_1\right)\cdot \left(D_{\xi }-r_2\right)S\left(z\right)={\epsilon }_1\cong 0\\ S(z)=z^{{\nu }_1}{\mathrm{Pr}}_1\left(\ln z\right)+z^{{\nu }_2}{\mathrm{Pr}}_2\left(\ln z\right),\hspace{0.17em}\hspace{0.17em}{\nu }_{1,2}=\ln \left(r_{1,2}\right)/\ln \xi \end{array}$$

(16)

However, the calculations show clearly that solution (16) is not complete. This solution does not take into account the degeneration of the corresponding roots r_1,2. With the help of scaling operator D_ξ, it is very easy to take into account the influence of the degeneration effect and the corresponding fluctuations/corrections ${\epsilon }_{K_1+K_2}$ of the (K₁ + K₂) order. Because of the linearity of the corresponding functional equations, one can write a more general functional equation:

$$\begin{array}{l}{\left(D_{\xi }-r_1\right)}^{K_1}\cdot {\left(D_{\xi }-r_2\right)}^{K_2}S\left(z\right)=0\\ S(z)=z^{{\nu }_1}\left({\displaystyle \sum _{l=0}^{K_1-1}{\left(\frac{\ln z}{\ln \xi }\right)}^l}\right){\mathrm{Pr}}_1\left(\ln z\right)+z^{{\nu }_2}\left({\displaystyle \sum _{l=0}^{K_2-1}{\left(\frac{\ln z}{\ln \xi }\right)}^l}\right){\mathrm{Pr}}_2\left(\ln z\right),\hspace{0.17em}\hspace{0.17em}\\ {\nu }_{1,2}=\ln \left(r_{1,2}\right)/\ln \xi .\end{array}$$

(17)

This solution takes into account the degeneration effect that has a place for two roots ν₁ and ν₂. For practical purposes, it is useful to write down the case K_1,2 = 2. Taking into account Equation (11), one can approximately write the following:

$$\begin{array}{l}{\left(D_{\xi }-r_1\right)}^2{\left(D_{\xi }-r_2\right)}^{2}S\left(z\right)=0,\\ S(z)\cong z^{{\nu }_1}\left(1+b_1\left(\frac{\ln z}{\ln \xi }\right)\right){\mathrm{Pr}}_1\left(\ln z\right)+z^{{\nu }_2}\left(1+b_2\left(\frac{\ln z}{\ln \xi }\right)\right){\mathrm{Pr}}_2\left(\ln z\right).\end{array}$$

(18)

Solution (18) takes into account the fluctuations in the second order and can be used for fitting purposes related to the detection of a linear combination of a couple of power-law exponents. These calculations allow the general expressions to be written for a combination of the roots r₁, r₂, …, r_s, which have different degeneration degrees. Collecting all the calculations made above for different partial cases, one can write the following and homogeneous (when the right-hand of this equation equals zero) functional equation:

$${\displaystyle \prod _{l=1}^s{\left(D_{\xi }-r_l\right)}^{K_l}S(z)=0}.$$

(19)

This is written for the case in which each root r_l (l = 1, 2, …, s) has its own degree of degeneration K_l. The solution of the functional equation for the degeneration case can be written in the complete analogy using Equation (17), as follows:

$$S(z)\cong {\displaystyle \sum _{l=1}^s{z}^{{\nu }_l}\left({\displaystyle \sum _{q=0}^{K_l-1}{\left(\frac{\ln z}{\ln \xi }\right)}^q}\right){\mathrm{Pr}}_l\left(\ln z\right)},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\nu }_l=\ln \left(r_l\right)/\ln \xi .$$

(20)

In the conclusion of this section, one can notice the tight analogy between the sums figuring in (1) and the product:

$$P\left(z\right)={\displaystyle \prod _{n=-N}^{N}f\left(z{\xi }^n\right)}.$$

(21)

In the contrast of the previous asymptotic behavior (2), we suppose that the function f(z) has the following decompositions for small and large values of z:

$$f(z)=\left(\begin{array}{l}{c}_0+c_1\left|z\right|+c_2{\left|z\right|}^2+\dots \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}\hspace{0.17em}\left|z\right|<<1,\\ A_0+\frac{A_1}{\left|z\right|}+\frac{A_2}{{\left|z\right|}^2}+\dots \hspace{0.17em}at\hspace{0.17em}\hspace{0.17em}\left|z\right|>>1.\end{array}\right.$$

(22)

Therefore, for different values of ξ, we obtain the following from (21):

$$\begin{array}{l}P\left(z\xi \right)=\frac{f\left(z{\xi }^{N+1}\right)}{f\left(z{\xi }^{-N}\right)}P\left(z\right)\cong \left\{\begin{array}{l}g\cdot P(z),\hspace{0.17em}\hspace{0.17em}g=A_0/c_0,\hspace{0.17em}\hspace{0.17em}\xi >1\\ g^{-1}P(z),\hspace{0.17em}\hspace{0.17em}\xi <1\end{array}\right.,\\ for\hspace{0.17em}\hspace{0.17em}\left|\frac{A_1}{A_0}\right|<<\left|z\right|<<\left|\frac{c_0}{c_1}\right|.\end{array}$$

(23)

Equation (23) is similar to Equation (4), and, therefore, all mathematical manipulations applied earlier to (4) are valid also to Equation (23). A more detailed consideration of the product (21), especially the linear combination of similar products, such as (13), merits separate research. Unfortunately, we do not have real experimental data related to the verification of the proposed theory that is outlined in this section.

The tentative results obtained in this theoretical section enable more general conclusions that can be propagated for any fitting purposes to be made. Let us represent the conventional regression problem in the following form:

$$\begin{array}{l}y(x)-f(x)={\epsilon }_1\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}or\\ \left(\widehat{y}-\widehat{f}\right)(x)={\epsilon }_1.\end{array}$$

(24)

Following the roots of quantum mechanics, the second line in (24) is represented in the operator form.

On the right-hand side, we define again ε₁ as the errors/remnants of the first order. If we want to take into account the errors of the second order, it is necessary to apply the left-side operator twice, taking into account the fact that operators y and f do not commute with each other. It is easy to see that the commutator [y,f](x) = y(f(x)) − f(y(x) ≠ 0. Therefore, we obtain the following:

$${\left(\widehat{y}-\widehat{f}\right)}^{2}x=\left(\widehat{y}-\widehat{f}\right){\epsilon }_1={\epsilon }_2\cong 0$$

(25)

Opening these operators, one can present (25) in the conventional form:

$$y\left[y(x)\right]-y\left[f(x)\right]-f\left[y(x)\right]+f\left[f(x)\right]=0$$

(26)

Therefore, in order to take into account more accurate fluctuations in the second order, it is necessary to make measurements presented by two terms in (26), while the other two terms can be evaluated theoretically. This new Formula (25) allows the remnant fluctuations in the K-th order to be taken into account if one rewrites (25) in the following form:

$$\begin{array}{l}{\left(\widehat{y}-\widehat{f}\right)}^k(x)\cong 0,\hspace{0.17em}\hspace{0.17em}k=1,2\dots ,K,\hspace{0.17em}\\ \left[\widehat{y},\widehat{f}\right]\ne 0\hspace{0.17em}\hspace{0.17em}or\hspace{0.17em}\hspace{0.17em}y\left[f(x)\right]-f\left[y(x\right]\ne 0.\end{array}$$

(27)

The authors do hope that this new and important aspect of regression analysis can find wide application in attempts to fit important experiments when the remnant functions or errors of the second, third, etc., play an important role.

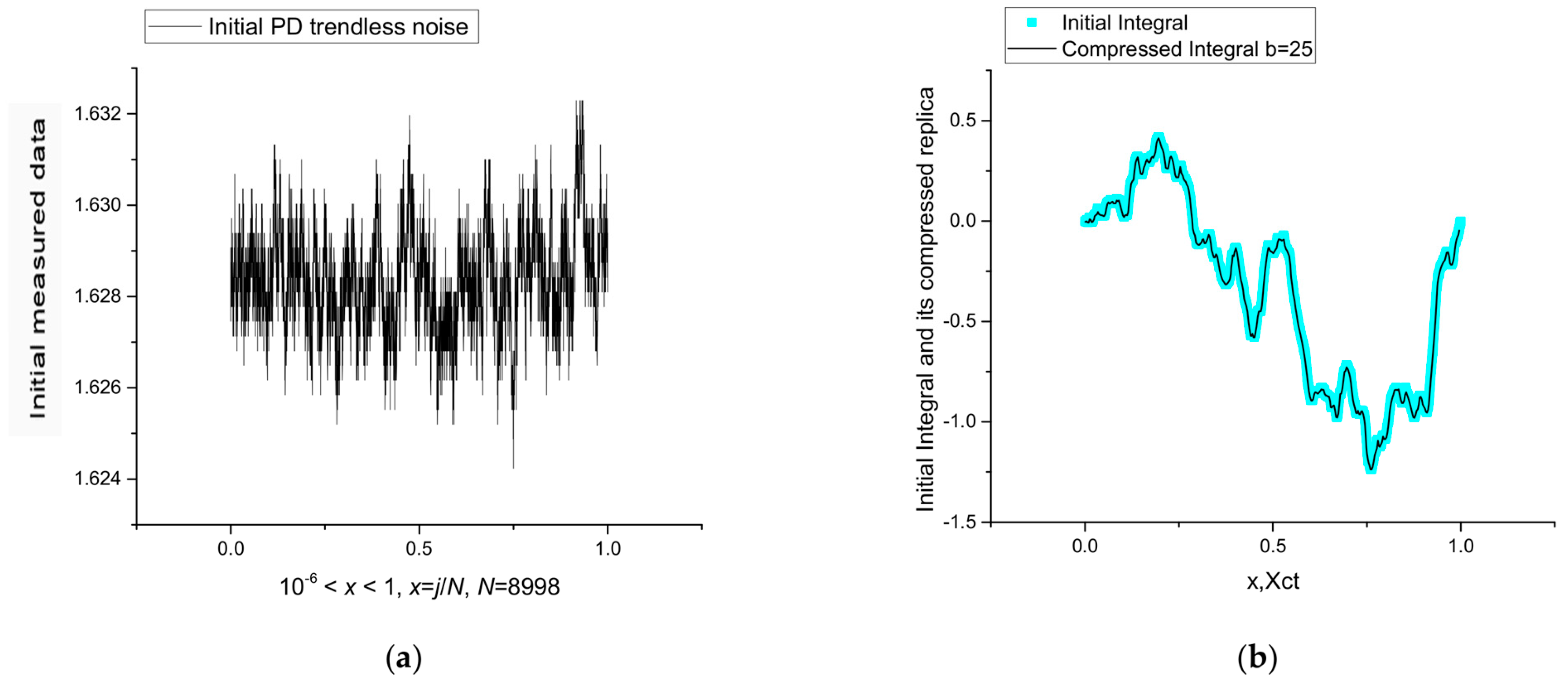
In the next section, we want to prove that many random curves (do not have the proposed model for their fitting) with, however, a clearly expressed trend are self-similar and that they can be accurately fitted using the fitting Function (11), when the influence of the degeneration terms, at least for K = 2, becomes essential.

3. The Proposed Algorithm and Description of the Data Processing Procedure

3.1. The Verification of the Self-Similar Principle

By considering any “noisy” component that does not have a clearly expressed trend, one can create a clearly expressed trend with the help of an integration procedure:

$$\begin{array}{l}J{y}_j=J{y}_{j-1}+\frac{1}{2}\left(x_j-x_{j-1}\right)\cdot \left(D{y}_j+D{y}_{j-1}\right),\hspace{0.17em}\hspace{0.17em}D{y}_j=y_j-mean(y),\\ mean(y)=\frac{1}{N}{\displaystyle \sum _{j=1}^N{y}_j},\hspace{0.17em}\hspace{0.17em}j=1,2,\dots ,N.\end{array}$$

(28)

One can notice that a reduction to three incident/invariant points (maximal, mean and minimal), as explained in detail in paper [15], in the fixed interval that has N_b successive data points is equivalent to a compression procedure. One can notice that the distribution of these points inside the remaining points [N/N_b] (where […] defines the operation of taking the integer value) is similar to the initial curve. In practice, if the initial data curve has 5·10³–10⁴ data points, then b is taken from the interval (10–25). This means that the initial curve remains self-similar and only 250–1000 data points are sufficient for the fitting purposes. It is obvious that further distortions of b become useless because it can lead to the essential distortions of the initial random curve. This statement was tested empirically on different data. Therefore, this observation can be expressed mathematically as follows:

$$Jy\left(x\xi \right)\cong a\cdot Jy(x),\hspace{0.17em}\hspace{0.17em}\xi \hspace{0.17em}=1/b,\hspace{0.17em}\hspace{0.17em}a\cong 1.$$

(29)

Based on the expressions obtained in the previous section, one can conclude that any random curve is self-similar and can satisfy the scaling equation, which takes into account the fluctuations in the K-th order:

$$\begin{array}{l}{\left(D_{\xi }-1\right)}^{K}J{y}_K(x)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}K=1,2,\dots ,\\ or\hspace{0.17em}\hspace{0.17em}Jy(x{\xi }^K)={\displaystyle \sum _{l=0}^{K-1}{w}_{l}Jy\left(x{\xi }^l\right)},\hspace{0.17em}\hspace{0.17em}{w}_l=C_K^l=\frac{K!}{l!\left(K-l\right)!},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\displaystyle \sum _{l=0}^{K-1}{w}_l}=1.\end{array}$$

(30)

The solution of this functional equation can be expressed as follows:

$$J{y}_K(x)=\left({\displaystyle \sum _{k=0}^{K-1}{\left(\frac{\ln (x)}{\ln \left(\xi \right)}\right)}^k}\right)\mathrm{Pr}\left(\frac{\ln (x)}{\ln \left(\xi \right)}\right).$$

(31)

Here, again, the log-periodic function Pr(lnz) is defined in (5). In practice, the verification of solution (30) on real data shows that the case of K = 1 does not provide an acceptable fit (because it is relatively crude and takes into account only the errors of the zeroth order), while the case of K = 2 is proven to be sufficient for fitting purposes. For K = 2, one can write the solution in the following equivalent form that follows from solution (11) and can be used as the fitting function for random curves that have a clearly expressed trend:

$$\begin{array}{l}J{y}_2(x)=\left(A_0+{\mathrm{Pr}}_1\left(\ln z\right)+\left(\frac{\ln z}{\ln \xi }\right){\mathrm{Pr}}_2\left(\ln z\right)\right),\\ {\mathrm{Pr}}_{1,2}\left(\ln z\right)={\displaystyle \sum _{k=1}^{K>>1}\left[A{c}_k^{\left(1,2\right)}\cos \left(2\pi k\left(\frac{\ln z}{\ln \xi }\right)\right)+A{s}_k^{\left(1,2\right)}\sin \left(2\pi k\left(\frac{\ln z}{\ln \xi }\right)\right)\right]}.\end{array}$$

(32)

One can notice that the parameter b₁ in (32) is omitted because it modifies the constants Ac_k⁽²⁾ and As_k⁽²⁾. The constant A₀ in (32) is proportional to Ac₀⁽¹⁾. If the initial integral curve can be expressed in terms of Expression (32), then the fitting parameters are expressed by parameters $\xi ,\hspace{0.17em}\hspace{0.17em}{A}_0,\hspace{0.17em}\hspace{0.17em}A{c}_k^{(s)},\hspace{0.17em}\hspace{0.17em}A{s}_k^{(s)},\hspace{0.17em}\hspace{0.17em}k=1,2,\dots ,K,s=1,2.$ Another important remark is related to the value of the nonlinear scaling parameter ξ. This parameter accepts the arbitrary value and can be located presumably inside the interval Rg(ln(x)) = max(lnx) − min(lnx), i.e., lnξ < Rg(lnx), or can exceed it. If the first condition is satisfied, then this case is determined as “internal fractality or self-similarity”. Meanwhile, in the opposite case, when lnξ > Rg(lnx), we have “external fractality”. These two inequalities determine the limits of the parameter lnξ. A possible interval for lnξ, in which the hidden optimal scaling can be located, is determined approximately from the inequality for K = 2:

$$L{\xi }_{\min }\cong \left(\frac{1}{2}\right)Rg(\ln x)\hspace{0.17em}\le \hspace{0.17em}\ln \xi \hspace{0.17em}\le \hspace{0.17em}Rg(\ln x)\cong L{\xi }_{\max }$$

(33)

How can the optimal values of lnξ in the analysis of the available data be defined? The evaluation of the true value of lnξ is determined from the minimization of the minimal fitting error value. Another question that can be posed is the following: is the linear functional equation of (30) optimal or not? Let us make the next step and consider the nonlinear functional equation of the type

$${\left[Jy\left(x\cdot {\xi }^K\right)\right]}^s={\displaystyle \sum _{l=0}^{K-1}{w}_l{\left[Jy\left(x\cdot {\xi }^l\right)\right]}^s}$$

(34)

where the nonlinear parameter s is located presumably in the interval $\left|s\right|\le 1$ and covers the well-known mean values for s = −1 (harmonic mean), s = 0 (geometric mean) and s = 1 (arithmetic mean). We also assume that all the functions figuring in (11) are positive. The case of s = 0 is considered as the limiting case:

$$\begin{array}{l}\left[Jy\left(x{\xi }^K\right)\right]=\underset{s\to 0}{\lim }{\left[{\displaystyle \sum _{l=0}^{K-1}{w}_{l}J{y}^s\left(x{\xi }^l\right)}\right]}^{\frac{1}{s}}\cong \\ \cong \underset{s\to 0}{\lim }\exp \left(\frac{1}{s}\right)\ln \left[{\displaystyle \sum _{l=0}^{K-1}{w}_l\left(1+s\cdot \ln \left(Jy\left(x{\xi }^l\right)\right)\right)}\right]=\\ =\exp \left({\displaystyle \sum _{l=0}^{K-1}{w}_l\ln \left(Jy\left(x{\xi }^l\right)\right)}\right)={\displaystyle \prod _{l=0}^{K-1}{\left[Jy\left(x{\xi }^l\right)\right]}^{w_l}}.\end{array}$$

(35)

Taking into account the Bellman’s inequality [16], which is valid for any set of positive values, including positive functions, that are located in the first and second quarters of the OXY axes, one can conclude that

$$\begin{array}{l}{\displaystyle \prod _{l=0}^{K-1}{\left[F\left(x{\xi }^l\right)\right]}^{w_l}}\le \hspace{0.17em}{\displaystyle \sum _{l=0}^{K-1}{w}_{l}F\left(x{\xi }^l\right),\hspace{0.17em}\hspace{0.17em}}\\ for\hspace{0.17em}\hspace{0.17em}all\hspace{0.17em}\hspace{0.17em}F\left(x{\xi }^l\right)\hspace{0.17em}>0.\end{array}$$

(36)

This means that for the case of K = 2, the generalized geometric mean (GGM) is expressed in the following form:

$$J{y}_2(x{\xi }^2)={\left[J{y}_2\left(x\xi \right)\right]}^2{\left[J{y}_2\left(x\right)\right]}^{-1}$$

(37)

which corresponds to the global fitting minimum. For fitting purposes, it is necessary to take the natural logarithm from (37) and consider the fitting function Ly₂(x) = ln(y₂(x)). Taking into account Bellman’s inequality (36), it is necessary to shift the initial function into the positive region:

$$\begin{array}{l}J{Y}_2(x)=\frac{\left[J{y}_2(x)-\min (J{y}_2(x))\right]+1}{Range\left[J{y}_2(x)-\min (J{y}_2(x))\right]},\hspace{0.17em}\hspace{0.17em}\\ Range(F(x))=\max (F(x))-\min \left(F(x)\right).\end{array}$$

(38)

Therefore, all fitting functions should be prepared in accordance with Expression (39) and simultaneous fitting functions, similar to Jy₂(x) and its natural logarithm:

$$LJ{y}_2(x{\xi }^2)=2LJ{y}_2(x\xi )-LJ{y}_2(x)$$

(39)

For input variable x, we choose a “universal” uniform and normalize the following scale to the unit value:

$$x{n}_j=\frac{x_j-x_0}{x_N-x_0},\hspace{0.17em}\hspace{0.17em}or\hspace{0.17em}\hspace{0.17em}{x}_j=x_0+x{n}_j\left(x_N-x_0\right)$$

(40)

The presentation of the input data vs. the dimensionless x_j is very convenient because it is easy to restore any required scale by identifying the initial x₀ and final x_N parameters, only. Below, we illustrate some of the key figures of the proposed algorithm.

3.2. The Verification on Real Data

3.2.1. The Photodiode Data

Now, the algorithm described in Section 3.1 is “tuned” for verification on the available data. As the first example, we consider the photodiode noisy data. The experimental details are described in paper [17]. Therefore, we omit this part and use only the recorded data presented in the form of trendless sequences. We are not going to demonstrate the fit of all measurements. For us, it is important to show the flexibility of the proposed algorithm, which can be applied to a wide variety of random curves with trends. In Figure 1a we show the initial noise for one of the tested photodiodes. Figure 1b demonstrates the self-similar property.

Figure 2a demonstrates the self-similar property associated with three curves Ymx(Xct), Ymn(Xct) and Ymin(Xct) that are coincides practically with each other. The situation is changed essentially if the compression value b becomes large. This case is shown in Figure 2b.

Figure 3a shows the curves prepared for the fitting in accordance with Expressions (38) and (39). Figure 3b demonstrates the minimization of the fitting error. It allows to find the optimal value of the nonlinear fitting parameter ln(ξ_min).

Figure 4a shows the fit of the curves shown initially on the previous Figure 3a. The distribution of the module values Amd_k is shown in Figure 4b.

Figure 5a shows the distribution of the phases φ_k. Figure 5b demonstrates the validity of Bellman’s inequality. The global minimum corresponds to the generalized geometric mean at s = 0.

3.2.2. The Self-Similar Data Obtained from Transcendental Numbers

Any transcendental or irrational sequence is endless, as is common knowledge. As a consequence, if one chooses the finite segment of the selected number (N = 60,000), then this sequence is combined into triple combinations (Nc = N/3) and, finally, these combinations are normalized to the unit value; as a result of this transformation, we receive an “ideal” noise. For instance, we obtain the following “pseudo-random” sequences for two “renowned” trans-numbers, Pi and the Euler constant (E) (the integer parts 3.2 of these numbers are omitted):

Pi

→ 0.141, 0.592, 0.653, 0.589, 0.793, ….

E

→ 0.718, 0.281, 0.828, 0.459, 0. 452, ….

The normalized triple combinations (Nc = 20,000) formed from trans-number Pi is shown in Figure 6a. Distribution of the triple combinations for transcendental number E is shown in Figure 6b.

Figure 6b demonstrates the same correlations for the Euler constant E.

One can differentiate these triple distributions and see the desired differences with the help of integration procedure (28).

Figure 7a,b show again the self-similarity property of the curves with the clearly expressed trend.

The Figure 8a shows how to find the optimal value of the nonlinear parameter ln(ξ_opt) for both the trans-numbers, Pi (blue curve) and E (red curve). Figure 8b and Figure 9a demonstrate the quality of the fitting procedure. The distribution of the fitting parameters for the two trans-numbers are shown in Figure 9a,b and Figure 10, correspondingly.

The Figure 9a demonstrates the fit of the compressed integral corresponding to the trans-number E. Figure 9b shows the distributions of the modules and phases (shown in the small figure above) for the trans-number Pi.

Figure 10 shows the distributions of the modules and phases (shown in the small figure) for the trans-number E.

4. Main Results and Their Discussion

The brief findings presented in this research allow for the following interpretations. The theory described in Section 2 should be used to analyze impedances in various materials with clearly specified self-similar structures, in which it is possible to anticipate impedance/admittance in the form of various power-law fractal elements. Although the authors lack compelling data for the validation of the suggested theory, many researchers working in this field will be eager to test it using their own measured data.

An attentive reader should pay attention to general Expressions (24)–(27), which enable the influence of the second-order fluctuations/remnants of ε₂ or even higher fluctuations in ε_K to be taken into account if one can apply the regression analysis to the fluctuations of the previous order

$$\begin{array}{l}\left(\widehat{y}-\widehat{f}\right){\epsilon }_{K-1}={\epsilon }_K\cong 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\epsilon }_0\equiv (x)\hspace{0.17em}\hspace{0.17em}\\ or\hspace{0.17em}\hspace{0.17em}{\left(\widehat{y}-\widehat{f}\right)}^K(x)\cong \hspace{0.17em}0.\end{array}$$

(41)

Expressions (24)–(27) and (41) generalize traditional regression analysis and have broad applicability in the field of contemporary signal processing. Another finding from this study is also significant. When the power-law exponent equals one, it follows from Section 2.

Any random curve with a clearly stated trend will produce three distributions when the technique is applied and the incident points are reduced to three (Ymax, Ymean, and Ymin). These distributions are demonstrated to be comparable to the initial curve with a high number of data points at specific ranges of the compression value b. The number of initial data points affects parameter b’s value. The initial number of data points in the scenarios above for the study of photodiodes is Nb = 8998. As seen in Figure 2, the initial curve is invariant to its compressed counterpart after this curve has been compressed in b = 25 times. Nb = 20,000 and b = 50 in the case of the transcendental integers Pi and E. Figure 8a and Figure 9a demonstrate the self-similar feature and the corresponding fit of these curves realized in the frame of the proposed method.

For these two different types of data obtained from different sources, we can obtain the common fitting platform associated with the fitting parameters. In total, for the cases considered above, we have $\xi ,\hspace{0.17em}\hspace{0.17em}{A}_0,\hspace{0.17em}\hspace{0.17em}A{c}_k^{(s)},\hspace{0.17em}\hspace{0.17em}A{s}_k^{(s)},\hspace{0.17em}\hspace{0.17em}k=1,2,\dots ,K,s=1,2$, 2K + 4 fitting parameters in total. The final value of K depends on the value of the fitting error. With a clearly specified trend, these fitting parameters can be used to compare various random curves. The “universal” fit suggested in this study will undoubtedly be used in data compression, their transmission, cryptography, medical diagnosis, the proper training of artificial intelligence, and other fields in which data compression and their fit are important procedures. Indeed, anyone reading this paper should understand that any random curve with a clearly expressed trend can be fitted within the frame of the concept based on the self-similar principle. In conclusion, we should also state that the relationship between the possible non-integer operators and power-law dependencies that follow from the self-similar principle is considered in detail in a recent paper [18].