Transfer of Quantum States and Stationary Quantum Correlations in a Hybrid Optomechanical Network

Abstract

We present a systematic study on the effects of dynamical transfer and steady-state synchronization of quantum states in a hybrid optomechanical network consisting of two cavities, which carry atoms inside and interact via a common moving mirror such as the mechanical oscillator. It is found that a high fidelity transfer of Schrödinger’s cat and squeezed states between two cavities modes is possible. On the other hand, we demonstrate the synchronization effect of the cavity modes in a steady squeezed state with its high fidelity realized by the mechanical oscillator that intermediates the generation, transfer and stabilization of the squeezing. In this framework, we also study the generation and evolution of bipartite and tripartite entanglement and find its connection to the effects of quantum state transfer and synchronization. Particularly, when the transfer occurs at the maximal fidelity, any entanglement is almost zero, so the different cavity modes are disentangled. However, these modes become entangled when the two bosonic modes are synchronized in a stationary squeezed state. The results provided by the current study may find applications in quantum information technologies, in addition to the setups for metrology, where squeezed states are essential.

1. Introduction

The protocols of generation, protection and transfer of coherent and non-classical states in quantum systems are considered of great importance in the era of the third quantum revolution [1]. For example, the concept of quantum internet [2] may become a focus of development in the future. To distribute quantum states over a network, the mapping or transfer of a quantum state to another system or a different degree of freedom is demanded as an essential element. The realization of such a function was proposed and experimentally tested by means of atomic ensembles [3], single atoms [4], solid qubits [5,6] and even pure optics [7,8]. More efficient and flexible methods of performing high-fidelity quantum state transfer always attract high interest from almost all directions of research on quantum technology.

In many applications such as metrology [9,10,11,12], sensing [13,14] (e.g., gravitational-wave detection [15]), and continuous-variable information processing [16,17], squeezed states of light, spins or mechanical oscillator (MO) motion are indispensable ingredients. Nowadays, squeezing is often produced and controlled in spin/opto-mechanical systems, generally known as hybrid systems, and generating and transferring the squeezing of different degrees of freedom such as photons, phonons and spins [18,19,20,21,22] become more and more meaningful to the potential applications. The transfer of the non-classical states (such as squeezed states) between separate systems can be very useful to the formation of a quantum network. Recently, there have been several studies proposing the protocols of quantum state transfer in optomechanical configurations [23,24,25]. As an alternative to quantum state transfer, one can perform a quantum dynamical synchronization of the degrees of freedom in the hybrid system, and even for the entire network in some particular cases. Synchronization here refers to those between the dynamical stabilization of a target steady-state of several degrees of freedom; see, e.g., [21,26]. Generally, such a protocol is not trivial to realize in the quantum systems [27]. Moreover, for a real system, it is crucial to protect the target quantum states from the intrinsic decoherence effects.

In the present work, we propose a kind of quantum stable synchronization protocol, i.e., synchronization between the photonic mode and phononic mode in high-fidelity squeezed states for a hybrid optomechanical system that carries the driven three-level atoms. We show that such synchronization can be realized by a coherent pump of squeezed phonons or photons in order to initialize squeezing in one of the modes, i.e., MO or the mode of one of the cavities. The mechanism of the squeezing initialization applied by us is inspired by a milestone work of Walls [28]. Additionally, to the synchronization of the stationary squeezed states of a pair of modes, it is of particular interest to study the quantum correlations between these modes. About two decades ago some studies showed how the multipartite entanglement within the continuous variables is related to a joint quadrature squeezing [29,30,31,32]. For example, in a recent work [33], the authors propose an experimental verification of the quadripartite entanglement by measuring squeezing in joint amplitude and phase quadratures. In this context, it is appealing to study and understand the correlation effect between the multipartite entanglement and squeezing in the hybrid optomechanical systems.

We highlight the increasing interest in the systems of optomechanical networks due to their wide spectrum of applications [34,35,36,37,38]. For example, the double-cavity, also known as a mirror-in-the-middle optomechanical system, can be considered the simplest type of network and was studied in various proposals [22,39,40,41,42,43,44]. In the present work, we will consider a kind of double-cavity optomechanical system with its movable middle mirror (the mechanical oscillator), but there is no transmission of the light field through the mirror. The concerned system contains a three-level atom placed on each side of the movable mirror. This hybrid optomechanical system carrying three-level atoms can be of particular interest because of its important role in different protocols such as entanglement formation, mechanical cooling, sensing, and others. For example, in Ref. [45], a quantum repeater protocol based on an arrangement of QED-optomechanical hybrid is proposed to distribute the entanglement between two distant three-level atoms. Another work [46] considers a hybrid optomechanical cooling with a three-level atomic ensemble fixed in a strongly excited optical cavity. One more scheme [47] proposes to apply three-level cascade atoms to entangle two optomechanical oscillators as well as two-mode fields. In our present work, the role of driven three-level atoms and MO is to stimulate and control the quantum protocols as the state transfer and stable synchronization of the squeezing in photonic and phononic modes. In view of the results of high-efficiency state transfer and squeezing synchronization in our simplest model of two-mode double-cavity optomechanics, it is possible to generalize the model to a network with several mechanical oscillators and many cavity modes. This kind of optomechanical network is expected to be highly relevant to quantum technologies such as sensing, metrology, the transmission of quantum states and correlations and many others.

This work is organized as follows. In Section 2, we present the conceptual model of the hybrid optomechanical network and a brief analysis of the role of the driving fields that stimulate the three-level atoms. In Section 3, we evaluate the dynamical transfer of the quantum states between the cavities. Here, using two different quantum states as initial conditions in the first cavity, we show how these states are transferred to the second cavity. Next, in Section 4, we show how the bipartite and tripartite correlations are generated and evolved for the lossless dynamics. We analyze the dynamical effect of the correlations as compared to the transfer of quantum states between the cavities. Section 5 is devoted to the study of the stationary synchronization of squeezing between two bosonic modes as a function of the optomechanical and Jaynes–Cummings couplings. Moreover, a comprehensive analysis of the entanglement generation as a consequence of the squeezing synchronization effect is presented. Finally, we discuss and conclude our findings in Section 6 and Section 7.

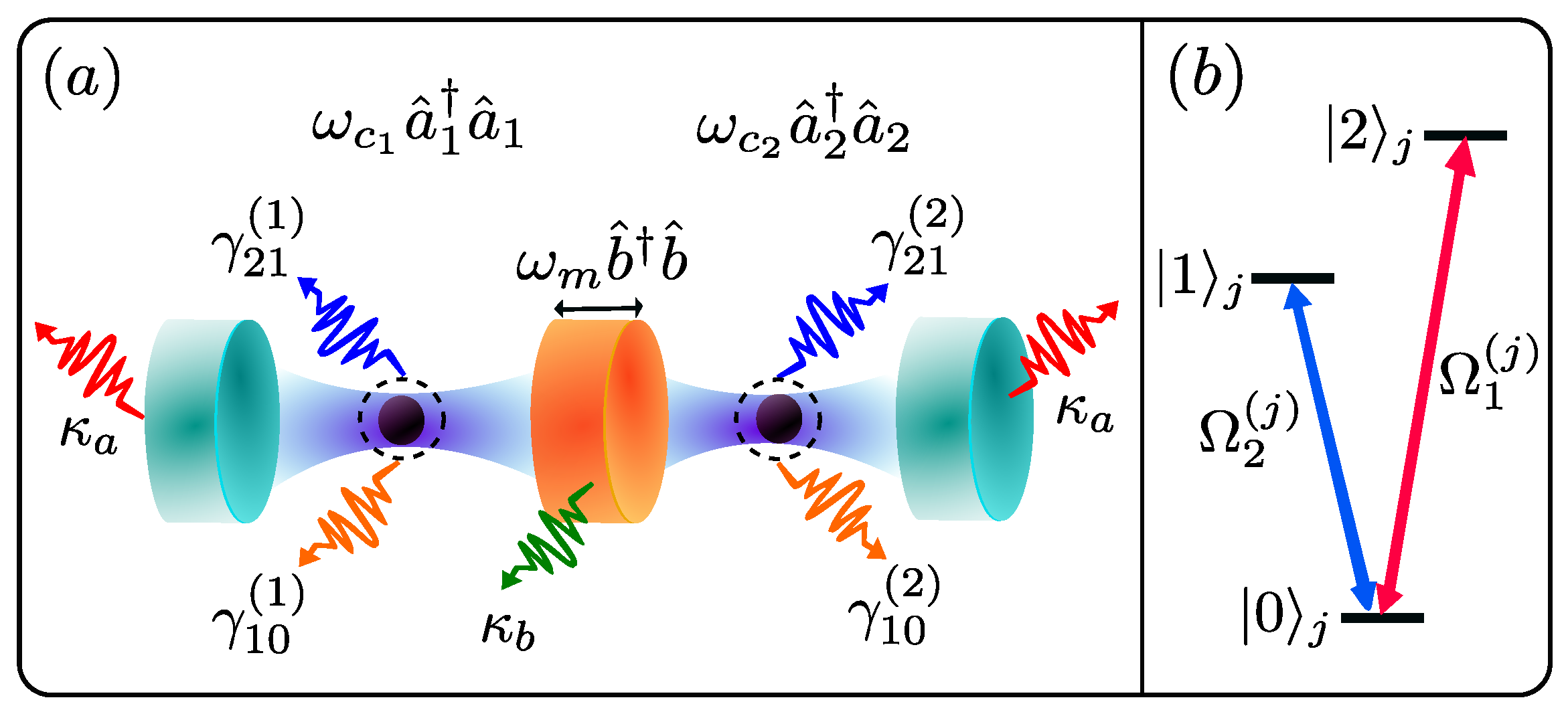
2. Hybrid Optomechanical System

Our concerned hybrid atom-cavity-mechanics system is illustrated in Figure 1. The hybrid system is composed of two optical cavities coupled to the same mechanical oscillator (MO) through non-linear optomechanical interaction, similar to setups such as [22,41], with an addition that each cavity is coupled to the upper two levels of a three-level atom. The total system Hamiltonian is ($\hslash =1$)

$$\begin{array}{c}\hfill \mathcal{H}={\omega }_m{b}^{†}b+\sum _{j=1}^2\left[{\omega }_{c_j}{a}_j^{†}{a}_j+\sum _{i=0}^2{\omega }_{i,j}{\sigma }_{ii,j}+g_j\left(a_j{\sigma }_{21,j}^{+}+a_j^{†}{\sigma }_{21,j}^{-}\right)+{\left(-1\right)}^j\lambda a_j^{†}{a}_j\left(b+b^{†}\right)\right],\end{array}$$

(1)

where ${\omega }_{i,j}$ are the energy levels of the three-level j-atom, $a_j\left(a_j^{†}\right)$ and $b\left(b^{†}\right)$ the annihilation (creation) operators of the j-th cavity and MO, respectively. The Jaynes–Cummings type interaction between the two upper levels of the three-level j-atom and the j-mode of the cavity field of frequency ${\omega }_{c_j}$ is quantified by the coupling constant $g_j$, and the interaction between the cavities and the MO of frequency ${\omega }_m$ corresponds to the standard optomechanical coupling quantified by the constant $\lambda$. The atomic operators of lowering (raising) denoted as ${\sigma }_{kl,j}^{-}\left({\sigma }_{kl,j}^{+}\right)={|k\rangle }_j\langle l|{\left(\right|l\rangle }_j\langle k\left|\right)$ obey the standard anti-commutation relations.

2.1. Effective Atom–Photon–Phonon Interaction

An essential step to see the mutual couplings between the different elements in the hybrid system is to derive the following effective Hamiltonian in an interaction picture (see the details in Appendix A):

$$\begin{array}{c}\hfill {\mathcal{H}}_1=\sum _{j=1}^2{g}_j{a}_j{\sigma }_{21,j}^{+}\exp \left\{ı\left({\Delta }_{j}t+{(-1)}^{j+1}F\left(t\right)\right)\right\}+H.c.,\end{array}$$

(2)

here we have defined the Hermitian operator $F\left(t\right)\equiv ı\frac{\lambda }{{\omega }_m}\left(b{\eta }^{*}-b^{†}\eta \right)$, with $\eta \equiv e^{ı{\omega }_{m}t}-1$, and the detuning ${\Delta }_j\equiv {\omega }_{2,j}-{\omega }_{1,j}-{\omega }_{c_j}$.

In what follows, we detail the conditions and parameter regimes where the concerned effects exist. We choose the regime with ${\Delta }_j=-{\omega }_m$, where a further simplified effective Hamiltonian

$$\begin{array}{c}\hfill {\mathcal{H}}_2=\sum _{j=1}^2{(-1)}^{j+1}{\Lambda }_j{a}_j{\sigma }_{21,j}^{+}{b}^{†}+H.c.,\end{array}$$

(3)

where ${\Lambda }_j\equiv g_j·\lambda /{\omega }_m$ is a tripartite atom–photon–phonon interaction strength, which exists after neglecting the fast oscillations of the mechanical frequency in the weak coupling regime $\lambda \ll {\omega }_m$ [36,48,49] (for more details see Equations (A11)–(A13) in Appendix A). It is possible to realize such an effective Hamiltonian according to the current experimental results that the optomechanical coupling covers a wide spectrum of values [34], but the choice ${\Delta }_j=-{\omega }_m$ is crucial to its realization (other choices, e.g., ${\Delta }_j={\omega }_m$, will give rise to another effective Hamiltonian consisting of the terms proportional to $a_j{\sigma }_{21,j}^{+}b+H.c.$).

We highlight that the Hamiltonian in Equation (3) quantifies the effective tripartite interaction in our hybrid system and plays a key role in realizing the protocols of quantum state transfer and squeezing synchronization, which will be studied in the following sections. It enables the quantum states in the first cavity to be transferred to the MO, later from MO to the second cavity, and vice-versa (a reversible process for the unitary dynamics). The role of the tripartite coupling in the squeezing transfer process is described in detail in Section 6.1. This approach of realizing an effective Hamiltonian for the transfer of quantum states between optical cavities distinguishes from many other approaches such as adiabatic passages [50,51], shortcuts to adiabaticity [52,53,54,55], composite pulses [56,57,58] and others.

2.2. Atomic Driving

In order to realize the transfer and synchronization of the quantum states between two cavities, we apply the laser pumps of the strengths ${\Omega }_1^{\left(j\right)}$ and ${\Omega }_2^{\left(j\right)}$ to the atoms $j=\{1,2\}$, respectively. As shown in Figure 1b, these lasers are resonant with the transitions ${|2\rangle }_j⟷{|0\rangle }_j$ and ${|1\rangle }_j⟷{|0\rangle }_j$. In the interaction picture, the coherent drives are described by the Hamiltonian

$$\begin{array}{c}\hfill {\mathcal{H}}_L=\sum _{j=1}^2\left\{{\Omega }_1^{\left(j\right)}\left({\sigma }_{20,j}^{-}+{\sigma }_{20,j}^{+}\right)+{\Omega }_2^{\left(j\right)}\left({\sigma }_{10,j}^{-}+{\sigma }_{10,j}^{+}\right)\right\}.\end{array}$$

(4)

Assuming that the ${|1\rangle }_j⟷{|0\rangle }_j$ transition (coupled to the classical field ${\Omega }_2^{\left(j\right)}$) and the ${|2\rangle }_j⟷{|1\rangle }_j$ transition (coupled to the quantum cavity field) are dipole allowed, i.e., the involved states are of opposite parity, then the driving field ${\Omega }_1^{\left(j\right)}$ for the ${|2\rangle }_j⟷{|0\rangle }_j$ transition will couple the states with the same parity so that it is dipole forbidden. To achieve such coupling, we can use a non-linear process as an effective coherent pump from a Raman-like configuration resonant to the carrier transition where a fourth level is present and adiabatically eliminated. Moreover, for a better understanding of the role of driving fields, we have a discussion in Section 6.

3. Dynamical Transfer of Quantum States between Cavities

3.1. Initialization of the Cavities, Mechanical Oscillator and Atoms

In this section, we start with the initial states of the two cavities, MO and the two atoms. Particularly, we consider two different non-classical initial states for the first cavity:

(I) Squeezed state given by

$${|\psi \left(0\right)\rangle }_{c_1}=\exp \left[\frac{1}{2}\left({\xi }^{*}{a}_1^2-\xi a_1^{†2}\right)\right]|0\rangle ,$$

(5)

where $\xi =r\exp (ı\theta )$ is the squeezing parameter.

(II) Schrödinger’s cat state of the form

$${|\psi \left(0\right)\rangle }_{c_1}=\mathcal{N}\left(|\alpha \rangle +|-\alpha \rangle \right),$$

(6)

where $\mathcal{N}$ is a normalization constant and $|\alpha \rangle$ is a common coherent state.

Our purpose is to transfer the quantum states in Equations (5) and (6) to the second cavity, which is initially in a thermal state, similar to the mechanical oscillator. On a coherent basis, the state of the second cavity can be written as

$${\rho }_{c_2}\left(0\right)=\frac{1}{\pi {\overline{n}}_{c_2}}\int |\alpha \rangle \langle \alpha |\exp (-|\alpha {|}^2/{\overline{n}}_{c_2})d^2\alpha ,$$

(7)

and the mechanical oscillator as

$${\rho }_m\left(0\right)=\frac{1}{\pi {\overline{n}}_m}\int |\beta \rangle \langle \beta |\exp (-|\beta {|}^2/{\overline{n}}_m)d^2\beta ,$$

(8)

where $\alpha$ and $\beta$ are in general complex numbers. Here, ${\overline{n}}_{m\left(c\right)}={\left(\exp \left[\hslash {\omega }_{m\left(c\right)}/\left({\kappa }_{B}T\right)\right]-1\right)}^{-1}$ is the average value of phonon (photons) occupation number initially in the thermal equilibrium with their reservoirs at a temperature T, and ${\kappa }_B$ is the Boltzmann’s constant. In addition, the two three-level atoms are initialized in the ground state

$${\rho }_{a_1}\left(0\right)={\rho }_{a_2}\left(0\right)=|0\rangle \langle 0|.$$

(9)

3.2. Dissipative Dynamics under the Markovian Master Equation

If we include the dissipation caused by the system–environment coupling, the dissipative dynamics of the hybrid quantum system are described by the Markovian master equation (ME) for the density matrix:

$$\begin{array}{c}\hfill \frac{d\rho }{dt}=-ı[{\mathcal{H}}_2+{\mathcal{H}}_L,\rho ]+\sum _{j=1}^2\frac{{\gamma }_{21}^{\left(j\right)}}{2}\left(1+{\overline{n}}_{a_j}\right)\mathcal{L}\left[{\sigma }_{21,j}^{-}\right]+\frac{{\gamma }_{21}^{\left(j\right)}}{2}{\overline{n}}_{a_j}\mathcal{L}\left[{\sigma }_{21,j}^{+}\right]+\frac{{\gamma }_{10}^{\left(j\right)}}{2}\left(1+{\overline{n}}_{a_j}\right)\mathcal{L}\left[{\sigma }_{10,j}^{-}\right]\\ \hfill +\frac{{\gamma }_{10}^{\left(j\right)}}{2}{\overline{n}}_{a_j}\mathcal{L}\left[{\sigma }_{10,j}^{+}\right]+\frac{{\kappa }_a^{\left(j\right)}}{2}\left(1+{\overline{n}}_{c_j}\right)\mathcal{L}\left[a_j\right]\\ \hfill +\frac{{\kappa }_a^{\left(j\right)}}{2}{\overline{n}}_{c_j}\mathcal{L}\left[a_j^{†}\right]+\frac{{\kappa }_b}{2}\left(1+{\overline{n}}_m\right)\mathcal{L}\left[b\right]+\frac{{\kappa }_b}{2}{\overline{n}}_m\mathcal{L}\left[b^{†}\right],\end{array}$$

(10)

where the common Lindblad dissipative terms are defined by: $\mathcal{L}\left[\mathcal{O}\right]=2\mathcal{O}\rho {\mathcal{O}}^{†}-{\mathcal{O}}^{†}\mathcal{O}\rho -\rho {\mathcal{O}}^{†}\mathcal{O}$. Here, ${\overline{n}}_{a_j}$, ${\overline{n}}_{c_j}$ and ${\overline{n}}_m$ are the average occupation number for the reservoirs of atoms, photons and phonons, respectively, and ${\gamma }_{21}^{\left(j\right)}$$\left({\gamma }_{10}^{\left(j\right)}\right)$ are the spontaneous emission rate from level ${|2\rangle }_j$ to ${|1\rangle }_j$ (level ${|1\rangle }_j$ to ${|0\rangle }_j$), and ${\kappa }_a^{\left(j\right)}$$\left({\kappa }_b\right)$ is the decay rate of the j-th cavity (mechanical) mode.

In the following sections, we will numerically calculate some figures-of-merit and other quantities such as the fidelity, entanglement and quadrature fluctuations (QF), under the approximation of ${\overline{n}}_a={\overline{n}}_c={\overline{n}}_m\ll 1$. This choice is realistic considering some recent experiments; for example, a hybrid system with the MO in the regime of microwave frequencies as in Refs. [59,60] where the mechanical mode has ${\omega }_m/2\pi \approx 2$ GHz, and one will also have ${\overline{n}}_{th}\approx {10}^{-4}$ by cooling the system to the temperatures $T\sim 10$ mK.

3.3. Fidelity of the Transfer Protocol

Now, let us use the fidelity defined as

$$F({\rho }_{c_1}\left(0\right),\rho \left(t\right))\equiv Tr\sqrt{\sqrt{{\rho }_{c_1}\left(0\right)}\rho \left(t\right)\sqrt{{\rho }_{c_1}\left(0\right)}}$$

(11)

as a figure of merit to quantify the state transfer during their evolution. In the above equation, $\rho \left(t\right)\equiv \left\{{\rho }_{c_1}\left(t\right),{\rho }_{c_2}\left(t\right),{\rho }_m\left(t\right)\right\}$ define the states of first cavity, second cavity and MO, respectively. The above definition shows that the comparison is made between the initial state of the first cavity and the state of any involved bosonic mode during its evolution.

In what follows, we evaluate the fidelity according to the definition in Equation (11) in the lossless case; see Figure 2. First, the numerical calculations indicate that, when there is no atomic pump, i.e., ${\Omega }_1^{\left(j\right)}={\Omega }_2^{\left(j\right)}=0$, the fidelity for each bosonic mode remains constant during the time evolution, implying that the concerned quantum states are almost unchanged (see Figure 2a,d). On the other hand, in Figure 2b,e, we see how the presence of atomic pumps, e.g., ${\Omega }_1^{\left(j\right)}={\Omega }_2^{\left(j\right)}=10$, begin to facilitate the transfer of a quantum state from the first to the second cavity. In this case, one finds that all involved boson modes increase their transfer probability under the action of the atomic pumps, but this pump intensity is not enough to achieve high fidelity for the state transfer to the second cavity. Finally, when a sufficiently high optimal atomic pump intensity is used, e.g., ${\Omega }_1^{\left(j\right)}={\Omega }_2^{\left(j\right)}=80$, it allows at certain times a high fidelity closed to one; see Figure 2c,f. We point out that high fidelity is possible only in the first cycles of the time evolution, while one observes that the fidelity will decrease with time because the three modes become more and more entangled and such an effect destroys the periodic transfer (see Figure 5 and the corresponding analysis in the next section). One way to offset the negative effect is to increase the pump intensities (${\Omega }_1$ and ${\Omega }_2$), and then a high fidelity can be preserved for more cycles during the time evolution.

Driving the atomic system by an external pump can realize the transfer of a quantum state between cavities with a fidelity close to one. The results in Figure 2 correspond to an ideal situation, i.e., for unitary dynamics, but the realistic systems are exposed to dissipation and decoherence, so we also performed a study considering how the dissipation rates of atoms, cavities and MO influence the fidelity of the state transfer between the cavities. The effect of dissipation will impair good fidelity. In Figure 3, we evaluate the fidelity between the first and second cavity field at the dimensionless time $t_2$ (see Figure 2c) as a function of the atomic driving strength (${\Omega }_1^{\left(j\right)}={\Omega }_2^{\left(j\right)}$) and the cavity damping rates ${\kappa }_a^{\left(j\right)}$, while fixing the dissipation rate for the atoms and the MO. We observe that the optimal fidelity only exists when the driving field is well enhanced and the cavity losses are decreased, which are possibly achievable by the available means.

4. Quantum Entanglement

In this section, we will study the bipartite and tripartite quantum entanglement for our hybrid system. We will also analyze the relation between the entanglement and the transfer effect we have studied in the previous section.

In general, for subsystems A and B and their associated density matrix ${\widehat{\rho }}_{AB}$, the negativity [61] is defined as

$$\mathcal{N}\left({\widehat{\rho }}_{AB}\right)=\sum _i\frac{|{\zeta }_i|-{\zeta }_i}{2},$$

(12)

where ${\zeta }_i$ are the eigenvalues of the partial transpose of the density matrix ${\widehat{\rho }}_{AB}$ with respect to one of the subsystems. Here, we also employ the measure of genuine tripartite entanglement, as the minimum residual contangle [62], defined as

$$E_l^{A\left|B\right|C}=\underset{A,B,C}{min}\left[E_l^{A\left|\right(BC)}-E_l^{A|B}-E_l^{A|C}\right],$$

(13)

where the contangles $\left\{E_l^{A\left|\right(BC)},E_l^{A|B},E_l^{A|C}\right\}$ are defined as the quadratic logarithm of $\left\{\parallel {\widehat{\rho }}^{T_A}\parallel ,\parallel {\widehat{\rho }}_{AB}^{T_A}\parallel ,\parallel {\widehat{\rho }}_{AC}^{T_A}\parallel \right\}$ with the trace norm $(\parallel ·\parallel )$, partial transpose (superscript), and partial trace (subscript), respectively.

In stage I of Figure 4, we see that the initially bipartite entanglement is generated between cavity 1 and MO (see the green curve), and later in time, MO will be entangled with the second cavity (see the blue curve). On the other hand, a minor bipartite entanglement is generated between the cavities (see the magenta curve). Its maximum value occurs when the other bipartite entanglements are equal. Meanwhile, the tripartite entanglement is also generated, which becomes the maximum at the same time (see the black curve). In this first stage, we conclude that when the bipartite entanglements $\{\mathcal{N}\left({\rho }_{C_1,MO}\right),\mathcal{N}\left({\rho }_{C_2,MO}\right)\}$ vanish, the transfer of states between the cavities occurs with the maximal fidelity (see the red curve). As the entanglement between the MO and cavity 2 is generated, the initial state of cavity 1 can be transferred to the second cavity.

In stage II, we observe that the entanglement between cavity 2 and the MO increases again. This fact reduces the transfer fidelity that finally falls when the entanglement between cavity 1 and the MO reaches a new maximum. Here, the tripartite entanglement takes a higher maximum value than the one in stage I. This maximal value will increase with time as the three subsystems become more and more entangled. Therefore, one obtains a different quantum resource in our model, the generation of tripartite entanglement, which increases while the transfer efficiency and the bipartite correlations decrease. Finally, at the beginning of stage III, cavity 1 returns to its initial state to repeat the cycle of stage I.

Concerning the case of Schrödinger’s cat transfer, we use an even cat state (Equation (6)) containing only even Fock state terms:

$$|\psi \left(0\right)\rangle \propto 2\exp \left\{-{\left|\alpha \right|}^2/2\right\}\sum _{n=0}^{\infty }\frac{{\alpha }^{2n}}{\sqrt{2n!}}|2n\rangle .$$

(14)

Since the form of the above state is proportional to pairs of excitations similar to a squeezed state, we conclude that the evolution of the quantum correlations as the bipartite and tripartite entanglement will result in an effect analogous to those shown in Figure 4, so we omit their detailed numerical results.

5. Stationary Synchronization of Squeezing in Hybrid Network

The effect studied in the previous section occurs periodically, i.e., there are definite moments when the transfer occurs. Therefore, the transfer of the quantum states is a reversible effect. On the other hand, in this section, we study the possibility of the steady-state squeezing synchronization in several modes, which we call the ‘quantum state synchronization’ effect for the cavities and MO mode. This effect is irreversible as compared to the transfer, principally because in this case the tripartite system reaches an equilibrium between the pump and dissipation mechanisms, which is similar to a laser/maser model.

In order to realize a steady-state squeezing in various bosonic modes (cavities and MO), one should initiate the squeezing of any of these modes. As it is observed in our recent study [21], one can make a squeezing by connecting the hybrid system to a squeezed bath. On the other hand, it is also possible to induce a squeezing by a coherent driving of a photonic or phononic mode similar to the proposal in Ref. [28]. For example, a phonon-squeezing pump is described by the Hamiltonian

$${\mathcal{H}}_q=q(b^{†2}+b^2)$$

(15)

in an interaction picture, where q is proportional to the driving field strength. As a result, the mechanical resonator can be prepared dynamically in a squeezed state. The dissipative dynamics of the hybrid quantum system are described by the following Markovian master equation in a Lindblad form

$$\begin{array}{ccc}\hfill \frac{d\rho }{dt}& =& -ı[{\mathcal{H}}_2+{\mathcal{H}}_q+{\mathcal{H}}_L,\rho ]+\widehat{L}\left(\rho \right),\hfill \end{array}$$

(16)

where $\widehat{L}\left(\rho \right)$ is a part as appearing in Equation (10).

5.1. Definition of Quantum Fluctuations

In what follows, we will calculate the degree of squeezing for the states of the cavity and mechanical oscillator. For this purpose, we rely on the numerical methods according to [63] to solve Equation (16) in the steady states, i.e., $\dot{\rho }=0$, and calculate the quantum fluctuations (QF) defined by

$$\begin{array}{c}\hfill \langle {\left(\Delta {\mathcal{X}}_{\mathcal{O}}\right)}^2\rangle =\langle {\mathcal{X}}^2\rangle -{\langle \mathcal{X}\rangle }^2,\langle {\left(\Delta {\mathcal{Y}}_{\mathcal{O}}\right)}^2\rangle =\langle {\mathcal{Y}}^2\rangle -{\langle \mathcal{Y}\rangle }^2,\end{array}$$

(17)

with the quadratures $\mathcal{X}=\left(\mathcal{O}{e}^{ı{\varphi }_{\mathcal{O}}}+{\mathcal{O}}^{†}{e}^{ı{\varphi }_{\mathcal{O}}}\right)/2$ and $\mathcal{Y}=\left(\mathcal{O}{e}^{-ı{\varphi }_{\mathcal{O}}}-{\mathcal{O}}^{†}{e}^{ı{\varphi }_{\mathcal{O}}}\right)/2ı$. Here, $\mathcal{O}$ can be a photon or phonon operator and the angle ${\varphi }_{\mathcal{O}}$ permits the generalization of the direction of the QF, i.e., to indicate the squeezing along any pair of axes $(x^{\prime },y^{\prime })$ in the phase space. Then, the squeezing condition for the quadrature, e.g., $\mathcal{X}$, corresponds to the relation $\langle {\left(\Delta {\mathcal{X}}_{\mathcal{O}}\right)}^2\rangle <0.25$.

5.2. Influence of the Squeezing Pump Strength and Tripartite Hybrid Interaction

In this part, we study the influence of the squeezing driving of the first cavity and MO modes on the squeezing synchronization effect and how this result is related to the bipartite and tripartite quantum entanglement between the bosonic modes. Moreover, the importance of the tripartite coupling to these resources will be studied.

Case 1: 

Squeezing Pump of the Mechanical Mode

To understand the mechanism of a squeezing driving of the mechanical oscillator mode and analyze the stationary states of the bosonic modes in the presence of the dissipation channels, we numerically evaluate the influence of the tripartite interaction coupling, ${\Lambda }_i$ and the MO’s squeezing pump strength q on the time evolution of the QF for all bosonic modes in the hybrid system. For example, in Figure 5a one observes that, in the absence of the tripartite coupling for the second cavity, i.e., ${\Lambda }_2=0$, the second cavity initially in a thermal state with very low excitation number (${\overline{n}}_{c_2}={10}^{-3}$) (close to an almost vacuum state) will maintain the value of vacuum fluctuations $\langle {(\Delta {\mathcal{X}}_{a_2})}^2\rangle \approx 0.25$ throughout the dynamical process (see the magenta line). In this case, squeezing is generated only in MO and first cavity with ${\Lambda }_1=1$; see the green and blue lines, respectively. Therefore, a bipartite entanglement between the first cavity and MO, $\mathcal{N}({\widehat{\rho }}_{c_1},{\widehat{\rho }}_m)$, is realized while other kinds of entanglement are absent as seen from Figure 5d.

In order to generate the squeezing in the second cavity, it is necessary to activate the tripartite interaction coupling, i.e., ${\Lambda }_2>0$ as in Figure 5b,c. As a consequence, the squeezing in the second cavity is generated while the squeezing in the first cavity is lost when ${\Lambda }_1=0$. In this case, a bipartite entanglement between the second cavity and MO, i.e., $\mathcal{N}({\widehat{\rho }}_{c_2},{\widehat{\rho }}_m)$, manifests as shown in Figure 5e. On the other hand, when both tripartite interaction couplings are equal (${\Lambda }_1/{\omega }_m={\Lambda }_2/{\omega }_m=1$), one observes in Figure 5c the perfect synchronization between the modes of both cavity fields in steady states. In this situation shown in Figure 5f, where the bipartite entanglement between cavity 1/cavity 2 and MO is equally distributed throughout the dynamics, the bipartite entanglement between the cavities, which is quantified by $\mathcal{N}({\widehat{\rho }}_{c_1},{\widehat{\rho }}_{c_2})$, reaches a higher value, implying a stronger stationary correlation between the cavity fields.

Case 2: 

Squeezing Pump of the First Cavity Mode

As an alternative configuration, we can induce the squeezing in the first cavity by the pump Hamiltonian

$${\mathcal{H}}_{q^{\prime }}=q^{\prime }(a_1^{†2}+a_1^2).$$

(18)

As in the previous case, we vary both tripartite interaction couplings ${\Lambda }_j$ and find how all these mechanisms control the squeezing stabilization of the two cavity fields and MO modes. Similar to case 1, in the absence of the tripartite coupling (${\Lambda }_2=0$), one observes that there is no squeezing for the second cavity mode; see Figure 6a. A squeezing evolves only in the first cavity and MO. In addition, to generate a squeezing synchronization between the MO and the cavities, it is necessary to choose the phase of QF, such that ${\varphi }_{c_1}={\varphi }_{c_2}=\pi /4$ and ${\varphi }_m=-\pi /4$. Then, the squeezed fields of the cavities and MO (on the orthogonal axis) can be efficiently synchronized in the steady states.

In general, the effect of squeezing evolution behaves similarly to Case 1; in order to induce a squeezing in the second cavity, it is necessary to activate the tripartite interaction couplings, i.e., ${\Lambda }_j>0$. Therefore, one can reach a squeezing synchronization between the MO and second cavity by controlling the tripartite interaction couplings and phase $\varphi$, which appears in the definition in Equation (17), without changing the rest parameters. Similar to Case 1, the entanglement is distributed among all bosonic modes. However, in this situation, the bipartite entanglement between a cavity field and MO becomes stronger than the entanglement between the cavity fields, as compared to Case 1 where the squeezing is pumped initially in the MO; see the green curves in Figure 5f and Figure 6f.

It is important to mention that for both cases of squeezing synchronization studied in this section, the tripartite entanglement is not generated in the hybrid network as shown by the black curves in Figure 5 and Figure 6. The mentioned tripartite entanglement, $E_1^{C_1\left|C_2\right|m}$, is rather sensitive to the losses. The losses of the cavities and MO can destroy the tripartite entanglement and some bipartite ones totally, though these losses synchronize a stationary squeezing between the bosonic modes of the concerned system. The complete results presented in this section are summarized in

Table 1. Relationship between the necessary parameters for the generation of squeezing synchronization and bipartite entanglement between bosonic modes. Here, C${}_1$ (C${}_2$) means cavity 1 (cavity 2), respectively, and MO—mechanical oscillator.

	Strength		Phase QF ($\mathit{\pi }/4$)			Synchronization			Entanglement
Pump	${\mathbf{\Lambda }}_{\mathbf{1}}$	${\mathbf{\Lambda }}_{\mathbf{2}}$	${\mathit{\varphi }}_{{\mathit{c}}_{\mathbf{1}}}$	${\mathit{\varphi }}_{{\mathit{c}}_{\mathbf{2}}}$	${\mathit{\varphi }}_{\mathit{m}}$	${\mathit{C}}_{\mathbf{1}}$/${\mathit{C}}_{\mathbf{2}}$	${\mathit{C}}_{\mathbf{1}}$/MO	${\mathit{C}}_{\mathbf{2}}$/MO	${\mathit{C}}_{\mathbf{1}}$/${\mathit{C}}_{\mathbf{2}}$	${\mathit{C}}_{\mathbf{1}}$/MO	${\mathit{C}}_{\mathbf{2}}$/MO
	1	0	+	+	−		✓			✓
MO	0	1	+	+	−			✓			✓
	1	1	+	+	−	✓			✓	✓	✓
	1	0	+	+	−		✓			✓
$C_1$	0	1	+	+	−
	1	1.1	+	+	−	✓			✓	✓	✓

.

6. Discussion and Outlook

6.1. Effects of Driving the Three-Level Atoms and Tripartite Hybrid Interaction

The roles of externally driving the atoms and of the effective atom–photon–phonon interaction are important in the dynamical transfer of the quantum states between two cavities. Here, we perform a qualitative description of how the squeezing is transferred from the first to the second cavity by defining an arbitrary state as $|n_{a_1},n_{a_2},n_{c_1},n_b,n_{c_2}\rangle$, where $n_{a_{1\left(2\right)}},n_{c_{1\left(2\right)}},n_b$ are the excitation numbers in the first (second) atom, first (second) cavity and mechanical oscillator, respectively. An initial state $|00200\rangle$, for example, approximates that the first cavity is prepared in a squeezed state with its average photon numbers as 2, while the rest subsystems are in their ground states. The Hamiltonian $H_2+H_L$ including the effective interaction and driving can transfer the state from the first to the second cavity by the following dynamical procedure:

$$\begin{array}{cc}\hfill & |00200\rangle \underset{{\Omega }_2^{\left(1\right)}}{\to }|10200\rangle \underset{{\sigma }_{21,1}^{+}{a}_1{b}^{†}}{\to }|20110\rangle \underset{{\Omega }_1^{\left(2\right)}}{\to }|22110\rangle \underset{{\sigma }_{21,2}^{-}{a}_2^{†}b}{\to }|21101\rangle \underset{{\Omega }_1^{\left(1\right)}}{\to }|01101\rangle \stackrel{}{\to }\\ & \underset{{\Omega }_2^{\left(1\right)}}{\to }|11101\rangle \underset{{\sigma }_{21,1}^{+}{a}_1{b}^{†}}{\to }|21011\rangle \underset{{\Omega }_2^{\left(2\right)}}{\to }|20011\rangle \underset{{\Omega }_1^{\left(2\right)}}{\to }|22011\rangle \underset{{\sigma }_{21,2}^{-}{a}_2^{†}b}{\to }|21002\rangle .\end{array}$$

(19)

In this evolution process, one finds that the driving process ${\Omega }_2^{\left(1\right)}$ of the atom in the first cavity, together with the effective tripartite coupling ${\sigma }_{21,1}^{+}{a}_1{b}^{†}$, allows the transfer of one excitation from the first cavity field to MO, so the system evolves to the state $|20110\rangle$. Next, by driving the atom in the second cavity by ${\Omega }_1^{\left(2\right)}$ to its level $|2\rangle$, it is possible to transfer the excitation from the MO to the second cavity field by the effective tripartite coupling ${\sigma }_{21,2}^{-}{a}_2^{†}b$, thus ending in the state $|21101\rangle$. Until this stage we have one excitation transferred from the first to the second cavity. Now, to transfer the second excitation from the first cavity field, one should again create the excitation in MO, and then the driving processes with ${\Omega }_1^{\left(1\right)}$ and ${\Omega }_2^{\left(1\right)}$ allow the possibility of transferring this excitation to the MO by using the same tripartite coupling ${\sigma }_{21,1}^{+}{a}_1{b}^{†}$, ending in the state $|21011\rangle$. Finally, the transfer of the MO’s excitation to the second cavity is possible using the process ${\sigma }_{21,2}^{-}{a}_2^{†}b$ under the condition that the atom in the second cavity must be prepared in the level $|2\rangle$ through the level $|1\rangle$, respectively, by the driving processes with ${\Omega }_2^{\left(2\right)}$ and ${\Omega }_1^{\left(2\right)}$; see Figure 1b. As a result, the system ends up in the state $|21002\rangle$, thus transferring the illustrated state from the first to the second cavity as observed in Figure 2c at $t=t_2$. The protocol of transferring a state from cavity 1 to cavity 2 is sketched in Figure 7.

6.2. Experimental Feasibility

In our numerical calculations, we have considered the optomechanical coupling within a range $\lambda \le 0.01{\omega }_m$ and, if taking ${\omega }_m/\left(2\pi \right)\approx 2$ GHz to have a low number of thermal excitations (as explained in Section 3), we will obtain the top limit value $\lambda /\left(2\pi \right)\approx 20$ MHz. This is considered a strong optomechanical coupling but it is experimentally feasible, particularly considering the very recent experiment [64], where the optomechanical coupling $\propto 40$ MHz was reached. Alternatively, the optomechanical coupling can be increased in the setups such as those discussed in [65,66,67]. For the squeezing synchronization protocol, we consider a strong dissipation situation with the cavity damping rate as ${\kappa }_a/\left(2\pi \right)=400$ MHz and MO damping rate as ${\kappa }_b/\left(2\pi \right)=4$ MHz (see Figure 4), which are compatible with the recent experiments in the optomechanics [34,59,60].

7. Conclusions

We have proposed a hybrid optomechanical network consisting of two cavities with a three-level atom in each one and a movable mirror (mechanical oscillator) in the middle. This hybrid system naturally realizes an effective tripartite coupling for a number of quantum dynamical processes. In addition to quantum state transfer, our setup can also generate a bipartite entanglement between the bosonic modes and prepare the stationary squeezed states of mechanical and cavity modes. We find that when two external fields independently drive each atom, the squeezed state and Schrödinger’s cat state can be transferred with extremely high fidelity between the cavities, and the increase in the pump intensities can improve the transfer fidelity further. In this framework, we are able to achieve the dynamical generation and distribution of bipartite and tripartite entanglement. As the hybrid system evolves with time, the cavity–cavity transfer protocol is weakened by the fact that the tripartite interaction between the bosonic modes (two photonic and one phononic) becomes stronger to create a tripartite entanglement. However, at the instants when the transfer of quantum state is feasible, the bipartite and tripartite entanglement will almost vanish. Additionally, considering the highly dissipative dynamics of the hybrid optomechanical system with the driven atoms and coherent pumping of squeezed phonons/photons at the initial stage, one can synchronize a pair of bosonic modes in squeezed steady states for the pairs of bipartite systems, i.e., cavity 1-cavity 2, cavity 1-MO, and cavity 2-MO. The squeezing synchronization of the cavity modes and mechanical modes can be achieved regardless of the discussed pump mechanisms. This result facilitates the experimental performance by choosing a proper pumping mechanism as detailed in Table 1. We hope that the present study will provide more understandings that are helpful to the development of optomechanical networks, which combine the processes of quantum state generation and transfer, as well as the distribution of quantum correlations. Especially, those quantum information protocols involving distributed squeezing may evolve from the presented model or its variations.