The NBRULC Reliability Class: Mathematical Theory and Goodness-of-Fit Testing with Applications to Asymmetric Censored and Uncensored Data
Abstract
:1. Introduction
- (i)
- ‘New better than renewal used’, denoted by , if
- (ii)
- ‘New better (worse) than renewal used’ in the Laplace transform order, denoted by , iforwhere
- (iii)
- ‘New better than renewal used’ in the Laplace transform in increasing convex order, denoted by , iforthis could be rewritten aswhere . It is clear that
2. Testing against NBRULC Alternatives
- (a)
- As is asymptotically normal, having a mean of 0 and variance where is determined by
- (b)
- Under the variance is
3. Pitman’s Asymptotic Efficiency of
- (i)
- The Weibull distribution:
- (ii)
- The LFR distribution:
- (iii)
- The Makeham distribution:
4. The Monte Carlo Method
4.1. Critical Points
4.2. The Power Estimates of the Test
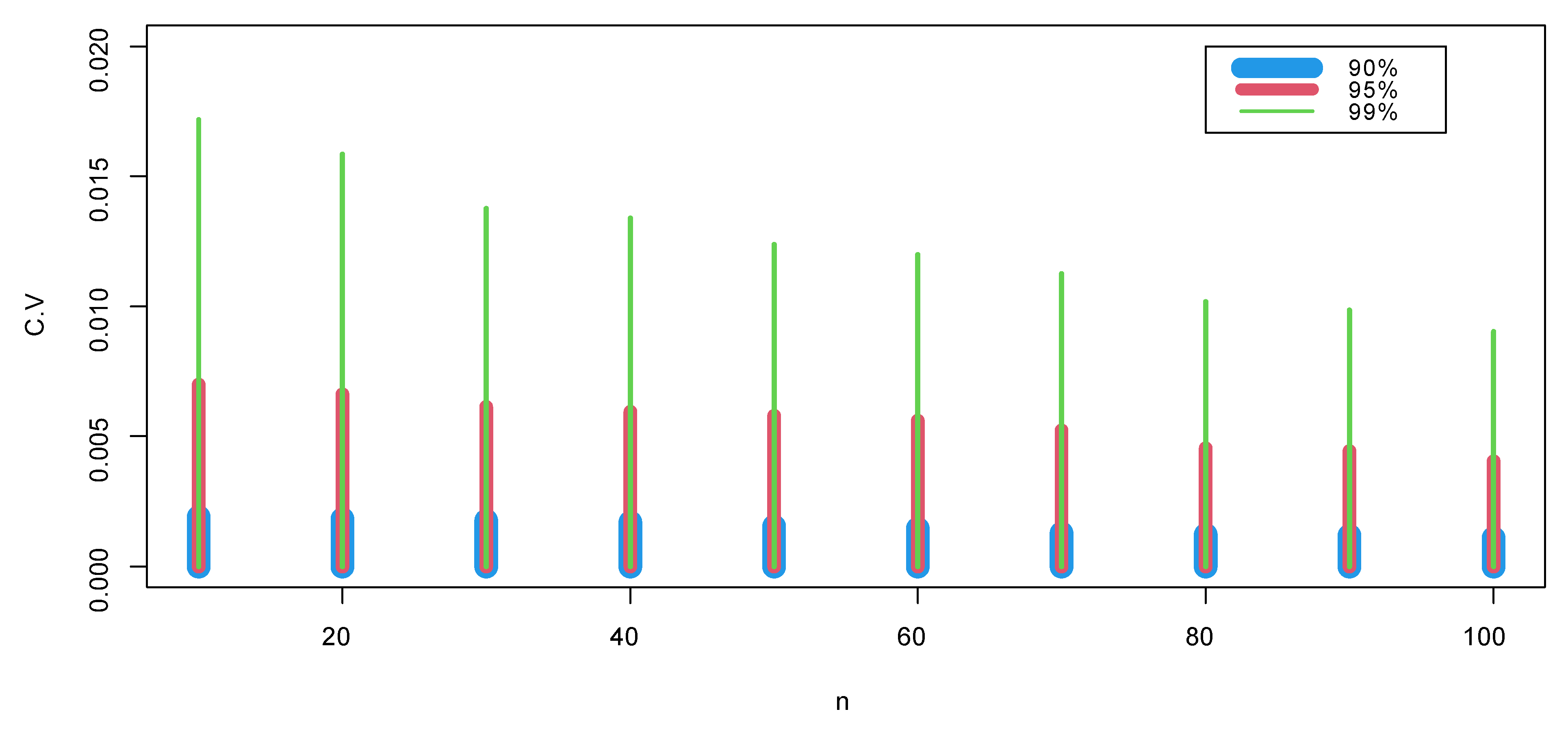
5. Testing for Censored Data
Estimates of the Test Power
6. Censored and Uncensored Observations in Applications to Real Data
6.1. Non-Censored Data
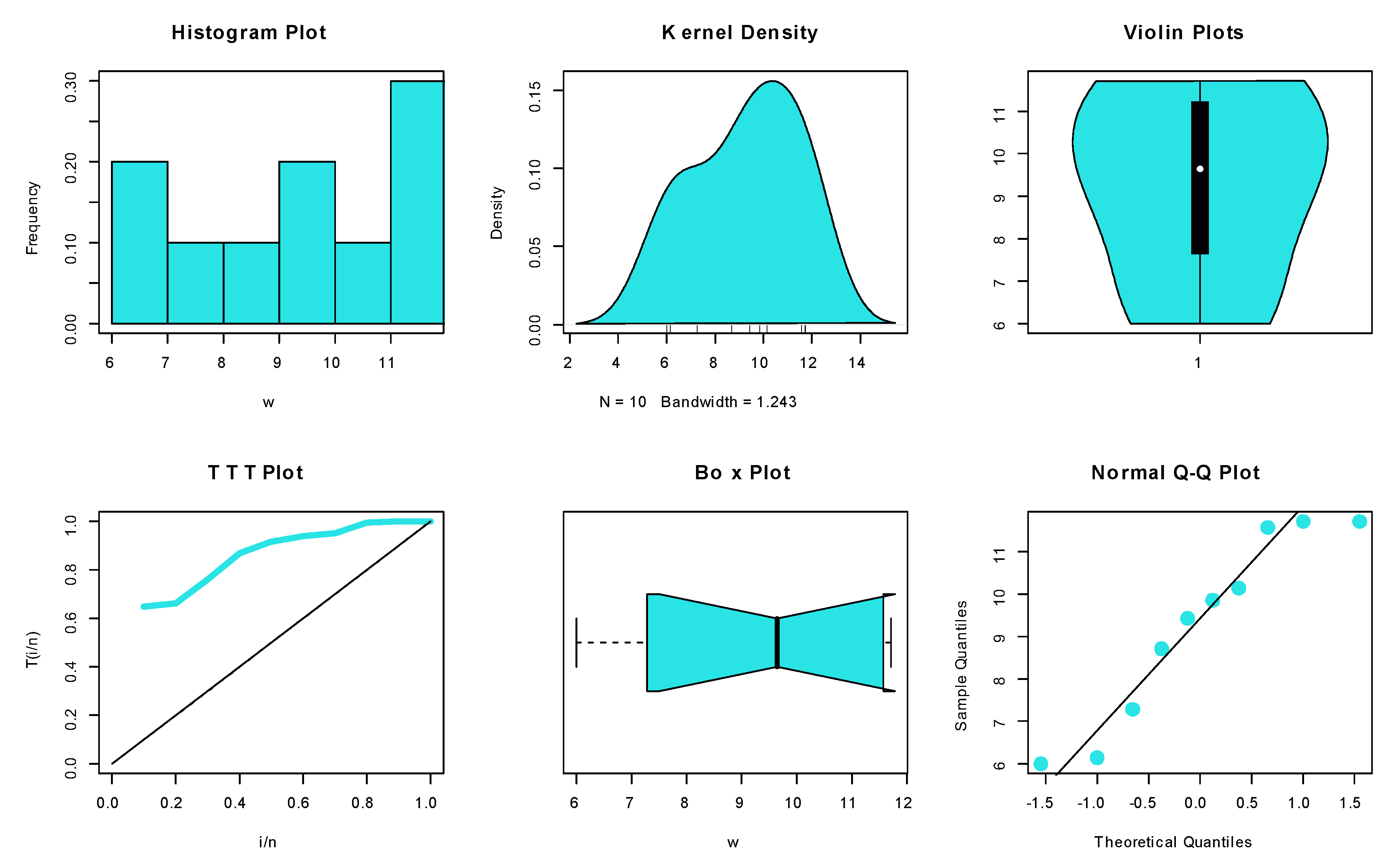
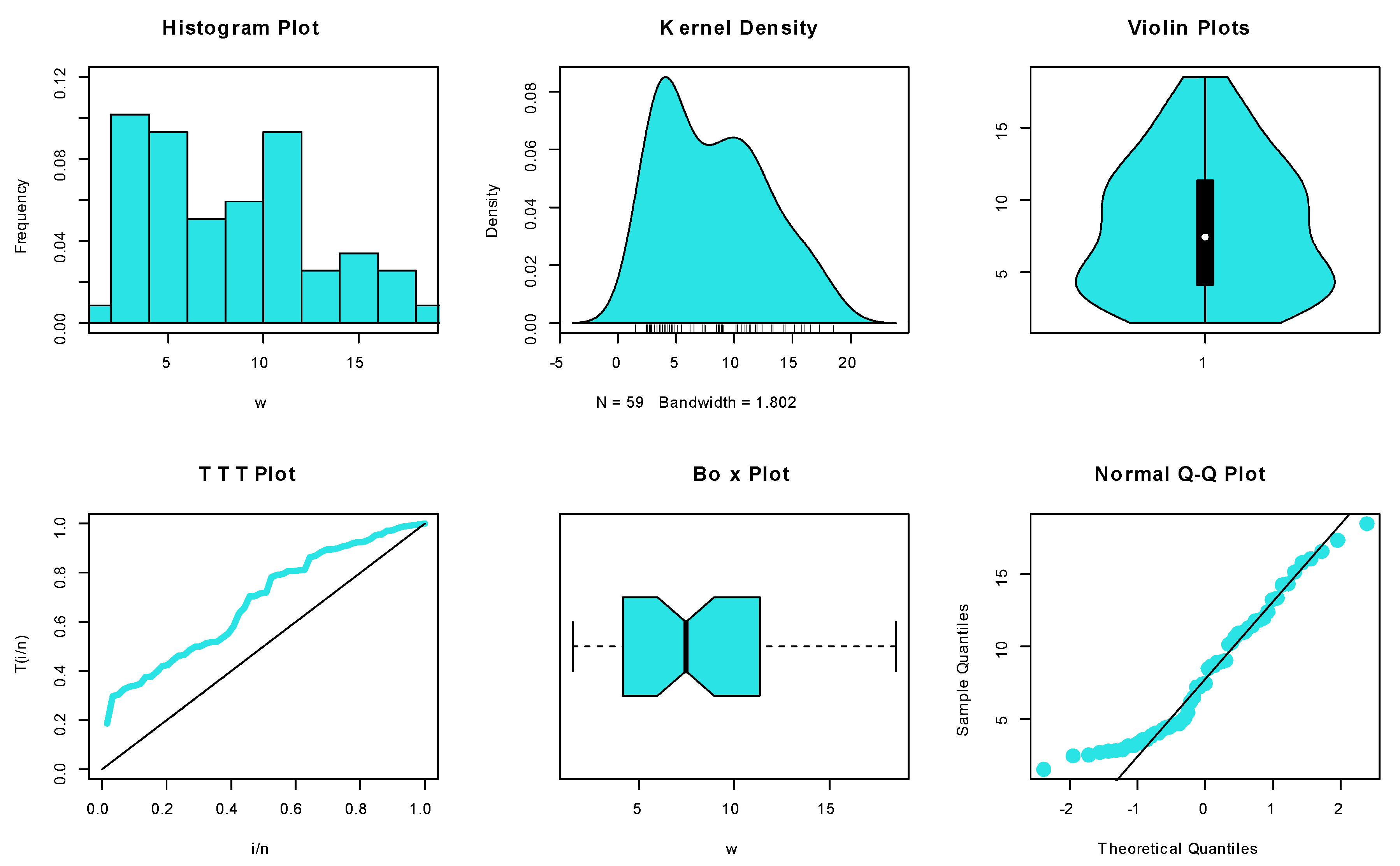
6.1.1. Dataset I: Methylmercury Poisoning
6.1.2. Dataset II: Endurance of Ball Bearings
6.1.3. Dataset III: Leukaemia
6.1.4. Dataset IV: Leukaemia
6.1.5. Dataset V: Carbon Fibers
| Dataset A: | ||||||||
| Dataset B: | ||||||||
6.1.6. Dataset VI: COVID-19
6.1.7. Dataset VII: COVID-19
6.1.8. Dataset VIII: Wind Speed
| Dataset A: | |||||||
| Dataset B: | ||||||||
6.2. Censored Data
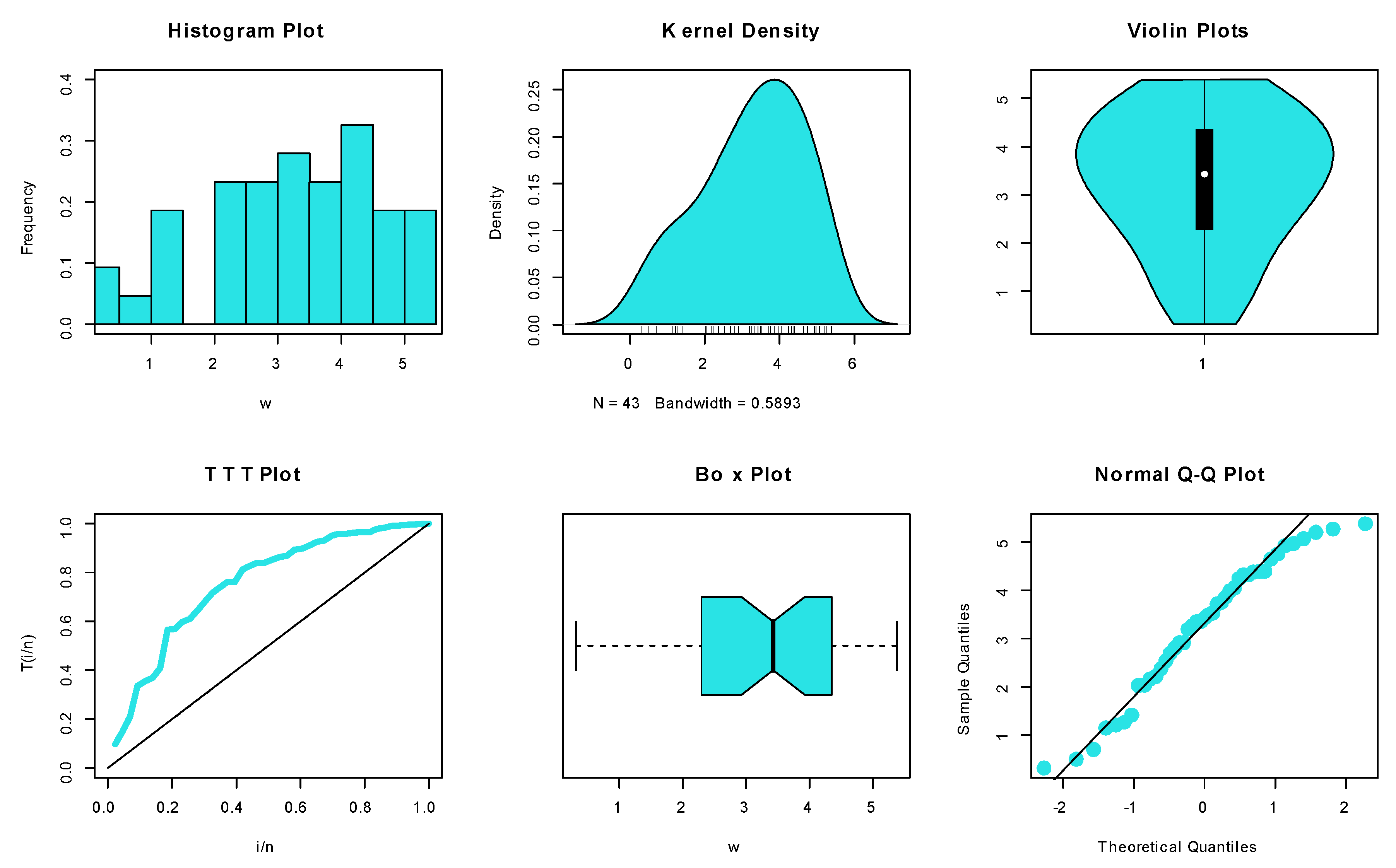
6.2.1. Dataset IX: Lung Cancer
- Censored observations:
| 0.14 | 0.14 | 0.29 | 0.43 | 0.57 | 0.57 | 1.86 | 3.00 | 3.00 | 3.29 |
| 3.29 | 6.00 | 6.00 | 6.14 | 8.71 | 10.57 | 11.86 | 15.57 | 16.57 | 17.29 |
| 18.71 | 21.29 | 23.86 | 26.00 | 27.57 | 32.14 | 33.14 | 47.29 | ||
- Uncensored observations:
| 0.43 | 2.86 | 3.14 | 3.14 | 3.43 | 3.43 | 3.71 | 3.86 | 6.14 | 6.86 | 9.00 |
| 9.43 | 10.71 | 10.86 | 11.14 | 13.00 | 14.43 | 15.71 | 18.43 | 18.57 | 20.71 | 29.14 |
| 29.71 | 40.57 | 48.57 | 49.43 | 53.86 | 61.86 | 66.57 | 68.71 | 68.96 | 72.86 | 72.86 |
6.2.2. Dataset XI: Melanoma
| 13 | 14 | 19 | 19 | 20 | 21 | 23 | 23 | 25 | 26 |
| 26 | 27 | 27 | 31 | 32 | 34 | 34 | 37 | 38 | 38 |
| 40 | 46 | 50 | 53 | 54 | 57 | 58 | 59 | 60 | 65 |
| 65 | 66 | 70 | 85 | 90 | 98 | 102 | 103 | 110 | 118 |
| 124 | 130 | 136 | 138 | 141 | 234 |
| 16 | 21 | 44 | 50 | 55 | 67 | 73 | 76 | 80 | 81 |
| 86 | 93 | 100 | 108 | 114 | 120 | 124 | 125 | 129 | 130 |
| 132 | 134 | 140 | 147 | 148 | 151 | 152 | 152 | 158 | 181 |
| 190 | 193 | 194 | 213 | 215 |
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Bryson, M.C.; Siddiqui, M.M. Some criteria for aging. J. Am. Stat. Assoc. 1969, 64, 1472–1483. [Google Scholar] [CrossRef]
- Bhattacharyya, D.; Khan, R.A.; Mitra, M. A test of exponentiality against DMTTF alternatives via L-statistics. Stat. Probab. Lett. 2020, 165, 108853. [Google Scholar] [CrossRef]
- Barlow, R.E.; Proschan, F. Statistical Theory of Reliability and Life Testing; To Begin With: Silver Spring, MD, USA, 1981. [Google Scholar]
- Klefsjo, B. The HNBUE and HNWUE classes of life distributions. Nav. Res. Logist. 1982, 29, 331–344. [Google Scholar] [CrossRef]
- Khan, R.A.; Bhattacharyya, D.; Mitra, M. Exact and asymptotic tests of exponentiality against nonmonotonic mean time to failure type alternatives. Stat. Pap. 2021, 62, 3015–3045. [Google Scholar] [CrossRef]
- Kumazawa, Y. A class of tests statistics for testing whether new is better than used. Commun. Stat. Theory Methods 1983, 12, 311–321. [Google Scholar] [CrossRef]
- Mahmoud, M.A.W.; EL-Sagheer, R.M.; Etman, W.B.H. Testing exponentiality against new better than renewal used in Laplace transform order. J. Stat. Appl. Probab. 2016, 5, 279–285. [Google Scholar] [CrossRef]
- Mahmoud, M.A.W.; EL-Sagheer, R.M.; Etman, W. B H. Moments inequalities for NBRUL distributions with hypotheses testing applications. Austrian J. Stat. 2018, 47, 95–104. [Google Scholar]
- Majumder, P.; Mitra, M. A test for detecting Laplace order dominance and related Bahadur efficiency issues. Stat. Pap. 2019, 60, 1921–1937. [Google Scholar] [CrossRef]
- Bhattacharyya, D.; Khan, R.A.; Mitra, M. Tests for Laplace order dominance with applications to insurance data. Insur. Math. Econ. 2021, 99, 163–173. [Google Scholar] [CrossRef]
- Navarro, J. Preservation of DMRL and IMRL aging classes under the formation of order statistics and coherent systems. Stat. Probab. Lett. 2018, 137, 264–268. [Google Scholar] [CrossRef]
- Abu-Youssef, S.E.; Hassan, E.M.A.; Gerges, S.T. A new nonparametric class of life distributions based on ordering moment generating approach. J. Stat. Appl. Probab. Lett. 2020, 7, 151–162. [Google Scholar]
- Ghosh, S.; Mitra, M. A new test for exponentiality against HNBUE alternatives. Commun. Stat. Theory Methods 2020, 49, 27–43. [Google Scholar] [CrossRef]
- Navarro, J.; Pellerey, F. Preservation of ILR and IFR aging classes in sums of dependent random variables. Appl. Stoch. Model. Bus. Ind. 2022, 38, 240–261. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Al-Bossly, A.; EL-Sagheer, R.M.; Almohaimeed, B.; Etman, W.B.H.; Eliwa, M.S. A moment inequality for the NBRULC class: Statistical properties with applications to model asymmetric data. Symmetry 2022, 14, 2353. [Google Scholar] [CrossRef]
- EL-Sagheer, R.M.; Abu-Youssef, S.E.; Sadek, A.; Omar, K.M.; Etman, W.B.H. Characterrization and testing NBRUL class of life distributions based on Laplace transform technique. J. Stat. Appl. Probab. 2022, 11, 1–14. [Google Scholar]
- Gadallah, A.M.; Mohammed, B.I.; Al-Babtain, A.A.; Khosa, S.K.; Kilai, M.; Yusuf, M.; Bakr, M.E. Modeling various survival distributions using a nonparametric hypothesis testing based on Laplace transform approach with some real applications. Comput. Math. Methods Med. 2022, 2022, 5075716. [Google Scholar] [CrossRef]
- Mansour, M.M.M. Assessing treatment methods via testing exponential property for clinical data. J. Stat. Appl. Probab. 2022, 11, 109–113. [Google Scholar]
- Ghosh, S.; Mitra, M. A weighted integral approach to testing against HNBUE alternatives. Stat. Probab. Lett. 2017, 129, 58–64. [Google Scholar] [CrossRef]
- Majumder, P.; Mitra, M. A test of exponentiality against alternatives. J. Nonparametr. Stat. 2019, 31, 794–812. [Google Scholar] [CrossRef]
- Lai, C.D.; Xie, M. Stochastic Ageing and Dependence for Reliability; Springer: New York, NY, USA, 2006. [Google Scholar]
- Etman, W.B.H.; EL-Sagheer, R.M.; Abu-Youssef, S.E.; Sadek, A. On some characterizations to NBRULC class with hypotheses testing application. Appl. Math. Inf. Sci. 2022, 16, 139–148. [Google Scholar]
- Ghosh, S.; Majumder, P. A moment inequality for decreasing mean time to failure distributions with hypothesis testing application. J. Stat. Comput. Simul. 2022, 92, 2875–2890. [Google Scholar] [CrossRef]
- Bakr, M.E.; Al-Babtain, A.A. Non-parametric hypothesis testing for unknown aged class of life distribution using real medical data. Axioms 2023, 12, 369. [Google Scholar] [CrossRef]
- Ghosh, S.; Mitra, M. On the exact distribution of generalized Hollander-Proschan type statistics. Commun. Stat. Simul. Comput. 2022, 51, 5051–5067. [Google Scholar] [CrossRef]
- Alqifar, H.; Eliwa, M.S.; Etman, W.B.H.; El-Morshedy, M.; Al-Essa, L.A.; EL-Sagheer, R.M. Reliability class testing and hypothesis specification: NBRULC-t∘ characterizations with applications for medical and engineering data modeling. Axioms 2023, 12, 414. [Google Scholar] [CrossRef]
- Mahmoud, M.A.W.; Abdul Alim, N.A. A goodness of fit approach to NBURFR and NBARFR classes. Econ. Qual. Control 2006, 21, 59–75. [Google Scholar] [CrossRef]
- Kayid, M.; Diab, L.S.; Alzughaibi, A. Testing NBU (2) class of life distribution based on goodness of fit approach. J. King Saud-Univ.-Sci. 2010, 22, 241–245. [Google Scholar] [CrossRef] [Green Version]
- Bera, S.; Bhattacharyya, D.; Khan, R.A.; Mitra, M. Test for harmonic mean residual life function: A goodness of fit approach. Math. Comput. Simul. 2023, 203, 58–70. [Google Scholar] [CrossRef]
- Mahmoud, M.A.W.; Diab, L.S.; Radi, D.M. Testing exponentiality against RNBUL class of life distribution based on goodness of fit. J. Stat. Appl. Probab. 2019, 8, 57–66. [Google Scholar] [CrossRef]
- Abu-Youssef, S.E.; Ali, N.S.A.; Bakr, M.E. Used better than aged in mgf ordering class of life distribution with application of hypothesis testing. J. Stat. Appl. Probab. Lett. 2020, 7, 23–32. [Google Scholar]
- Bakr, M.E.; Nagy, M.; Al-Babtain, A.A. Non-parametric hypothesis testing to model some cancers based on goodness of fit. AIMS Math. 2022, 7, 13733–13745. [Google Scholar] [CrossRef]
- Abu-Youssef, S.E.; El-Toony, A.A. A new class of life distribution based on Laplace transform and It’s applications. Inf. Sci. Lett. 2022, 11, 355–362. [Google Scholar]
- Abu-Youssef, S.E.; Gerges, S.T. Based on the goodness of fit approach, a new test statistics for testing NBUCmgf class of life distributions. Pak. J. Stat. 2022, 38, 129–144. [Google Scholar]
- Etman, W.B.H.; El-Morshedy, M.; Eliwa, M.S.; Almohaimeed, A.; EL-Sagheer, R.M. A new reliability class-test statistic for life distributions under convolution, mixture and homogeneous shock model: Characterizations and applications in engineering and medical fields. Axioms 2023, 12, 331. [Google Scholar] [CrossRef]
- Lee, A.J. U-Statistics-Theorem and Practice. In Statistics Textbooks Monographs; Marcel Dekker: New York, NY, USA, 1990; p. 110. [Google Scholar]
- Mugdadi, A.R.; Ahmad, I.A. Moment inequalities derived from comparing life with its equilibrium form. J. Stat. Plan. Inference 2005, 134, 303–317. [Google Scholar] [CrossRef]
- Kango, A.I. Testing for new is better than used. Commun. Stat. Theory Methods 1993, 12, 311–321. [Google Scholar]
- Abdel Aziz, A.A. On testing exponentiality against RNBRUE alternatives. Appl. Math. Sci. 2007, 35, 1725–1736. [Google Scholar]
- Kaplan, E.L.; Meier, P. Nonparametric estimation from incomplete observation. J. Am. Stat. Assoc. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Kocha, S.C. Testing exponenttality against monotone failure rate average. Commun. Stat. Theory Methods 1985, 14, 381–392. [Google Scholar] [CrossRef]
- Pavur, R.J.; Edgeman, R.L.; Scott, R.C. Quadratic statistics for the goodness-of-fit test of the inverse Gaussian distribution. IEEE Trans. Reliab. 1992, 41, 118–123. [Google Scholar] [CrossRef]
- Abouammoh, A.M.; Abdulghani, S.A.; Qamber, I.S. On partial orderings and testing of new better than renewal used classes. Reliab. Eng. Syst. Saf. 1994, 43, 37–41. [Google Scholar] [CrossRef]
- Kotz, S.; Johnson, N.L. Encyclopedia of Statistical Sciences; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Bader, M.G.; Priest, A.M. Statistical aspects of fibre and bundle strength in hybrid composites. In Progress in Science and Engineering of Composites; Hayashi, T., Kawata, K., Umekawa, S., Eds.; ICCM-IV: Tokyo, Japan, 1982; pp. 1129–1136. [Google Scholar]
- Kundu, D.; Gupta, R.D. Estimation of P[Y<X] for Weibull Distributions. IEEE Trans. Reliab. 2006, 55, 270–280. [Google Scholar]
- EL-Sagheer, R.M.; Eliwa, M.S.; Alqahtani, K.M.; EL-Morshedy, M. Asymmetric randomly censored mortality distribution: Bayesian framework and parametric bootstrap with application to COVID-19 data. J. Math. 2022, 2022, 8300753. [Google Scholar] [CrossRef]
- Almongy, H.M.; Almetwally, E.M.; Aljohani, H.M.; Alghamdi, A.S.; Hafez, E.H. A new extended rayleigh distribution with applications of COVID-19 data. Results Phys. 2021, 23, 104012. [Google Scholar] [CrossRef] [PubMed]
- Ghazal, M.G.M.; EL-Sagheer, R.M.; Mahmoud, M.A.W.; Al-Babtain, A.A.; Bakr, M.E.; Hasaballah, M.M. Inference for two populations 3-Burr-XII in presence of joint progressive censoring. Hindawi Complex. 2022, 2022, 6171714. [Google Scholar]
- Lagakos, S.W.; Williams, J.S. Models for censored survival analysis: A cone class of variable-sum models. Biometrika 1978, 65, 181–189. [Google Scholar] [CrossRef]
- Lee, S.Y.; Wolfe, R.A. A simple test for independent censoring under the proportional hazards model. Biometrics 1998, 54, 1176–1182. [Google Scholar] [CrossRef]
- Susarla, V.; Vanryzin, J. Empirical Bayes estimations of a survival function right censored observation. Ann. Stat. 1978, 6, 710–755. [Google Scholar] [CrossRef]
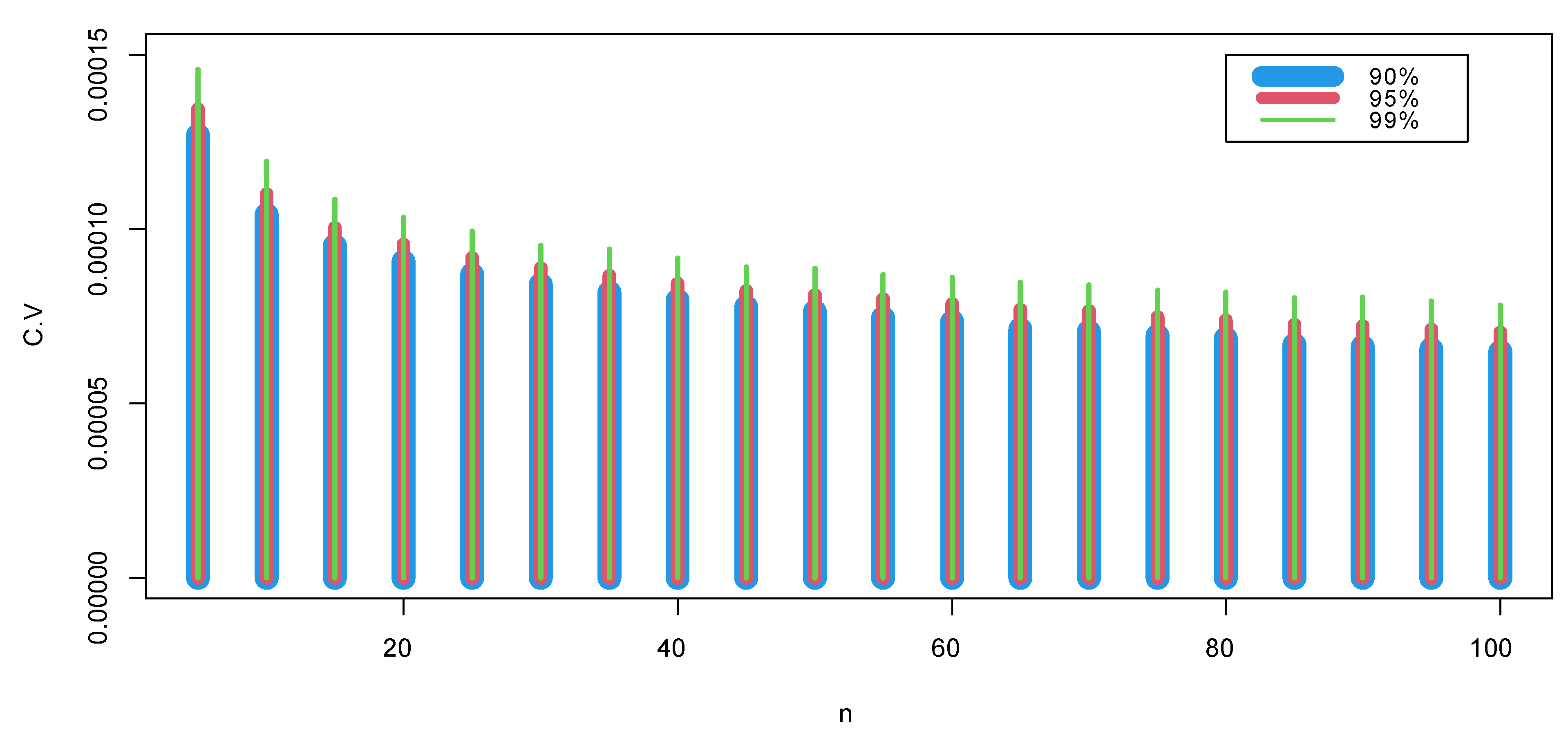

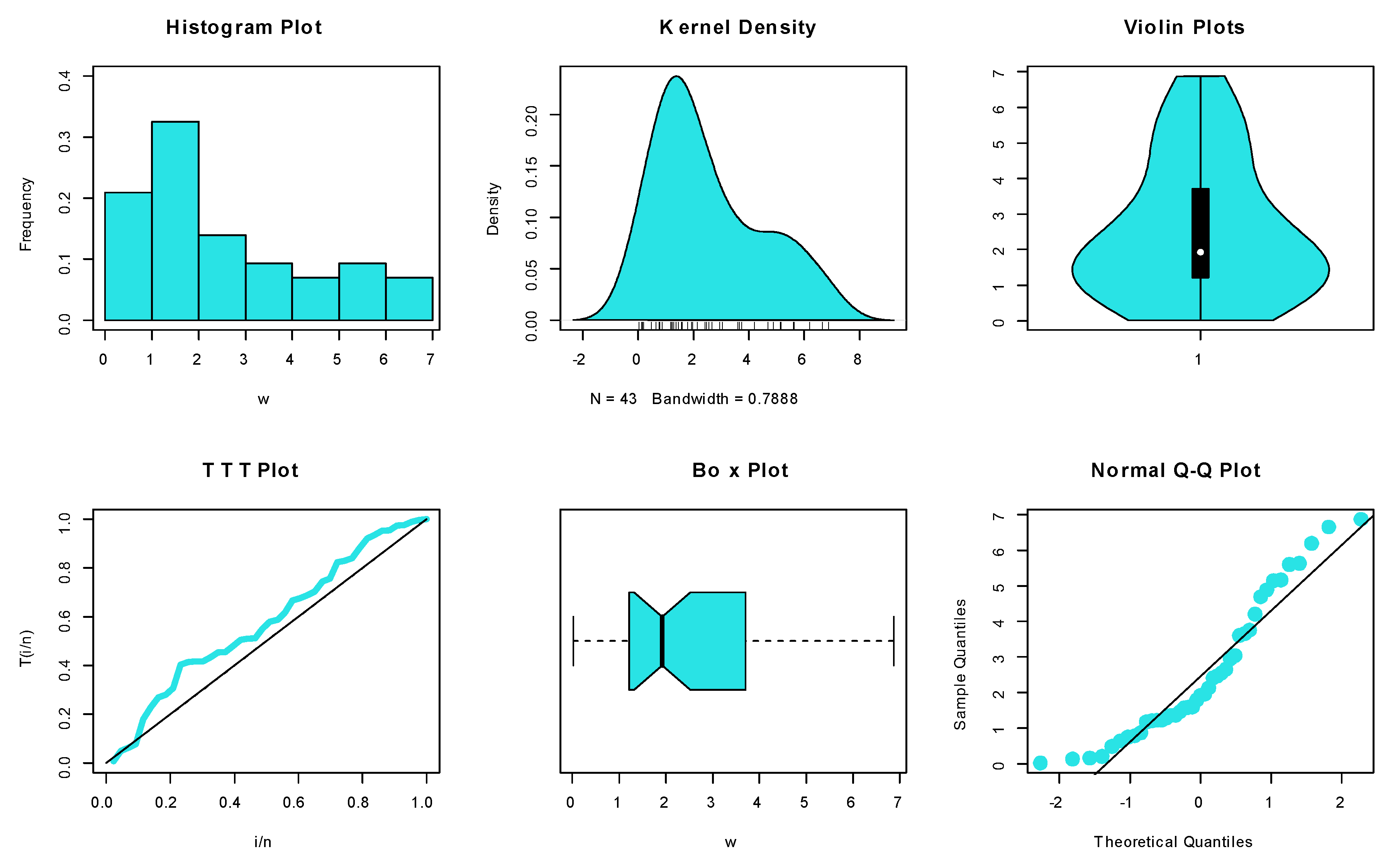

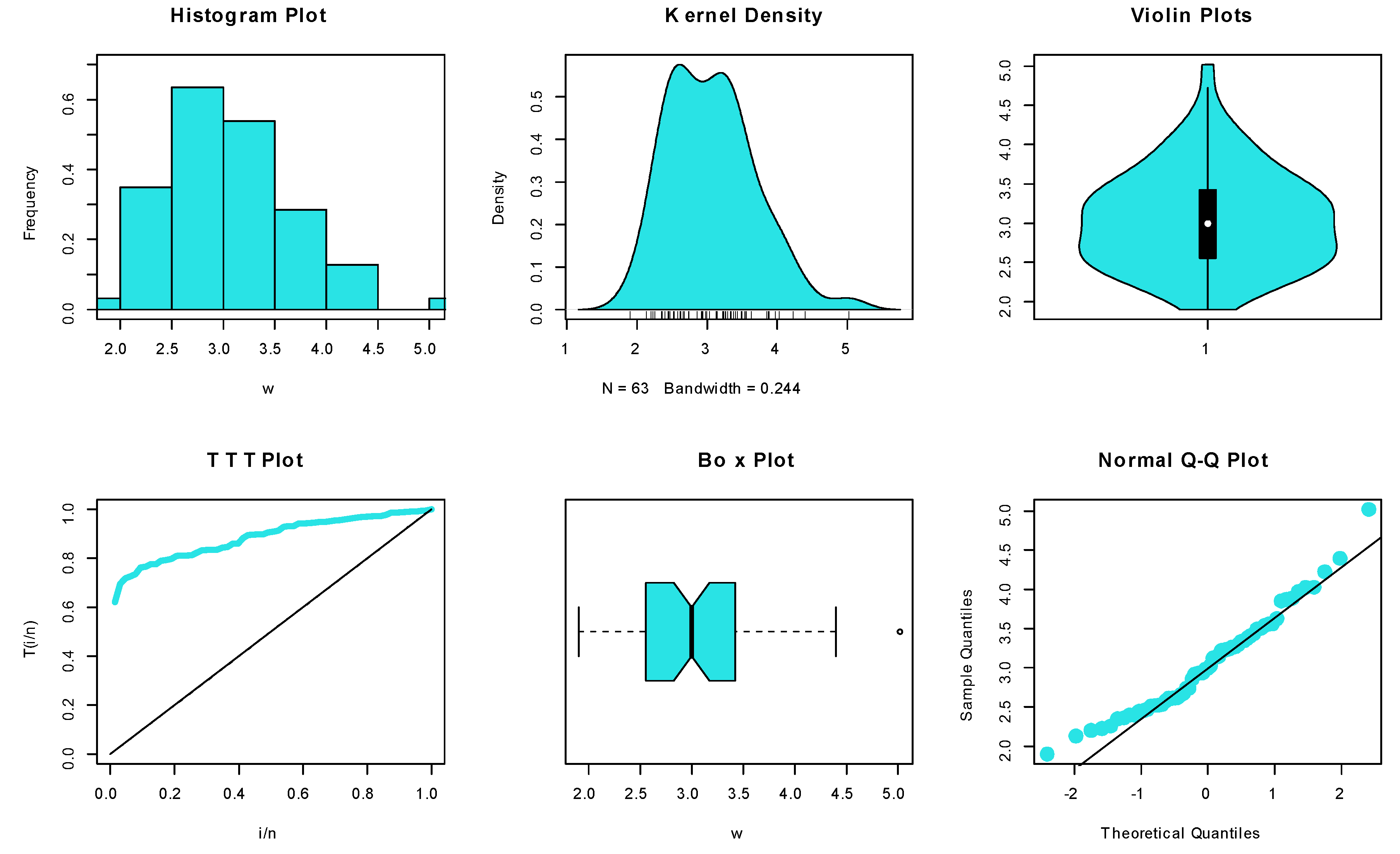
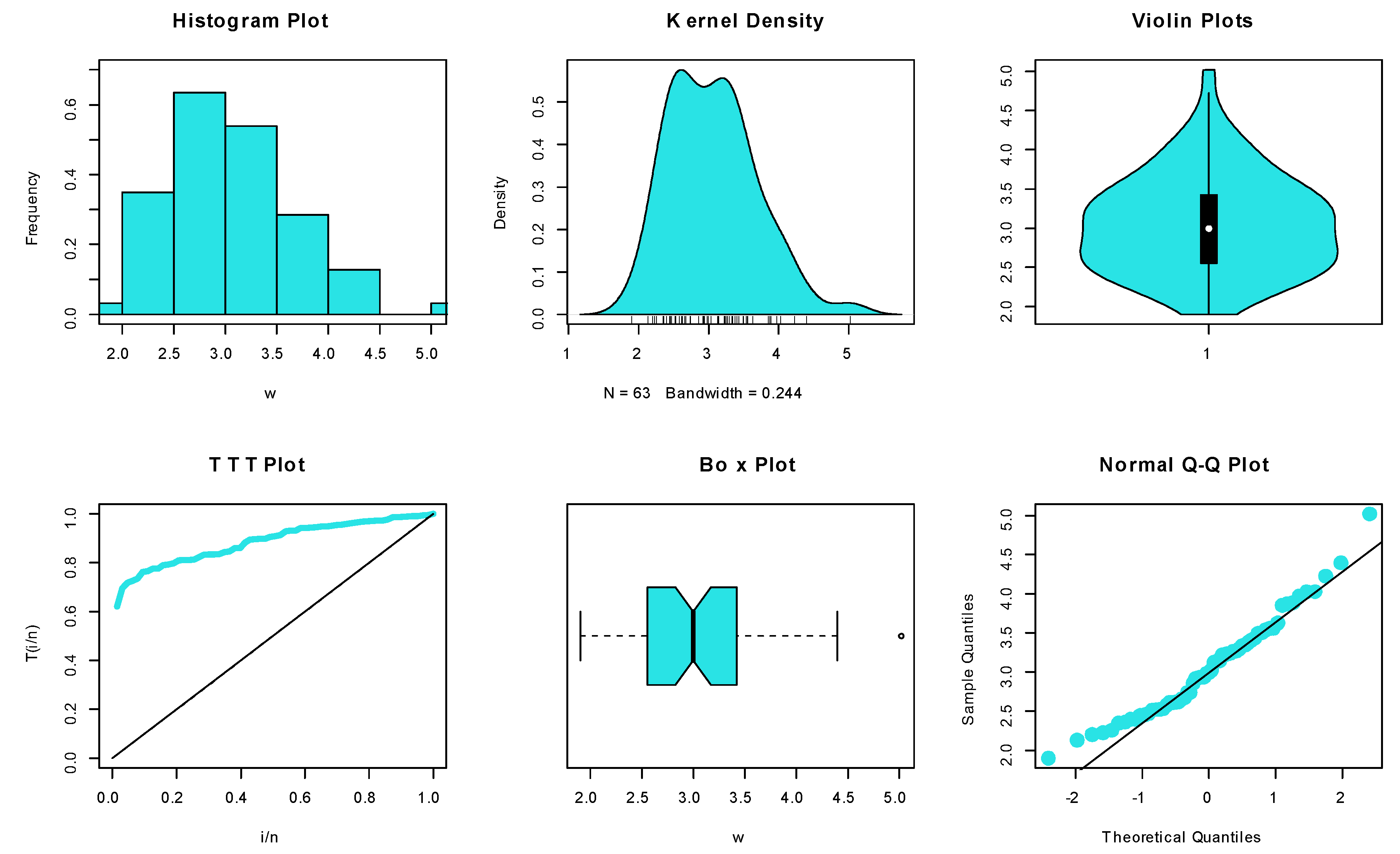
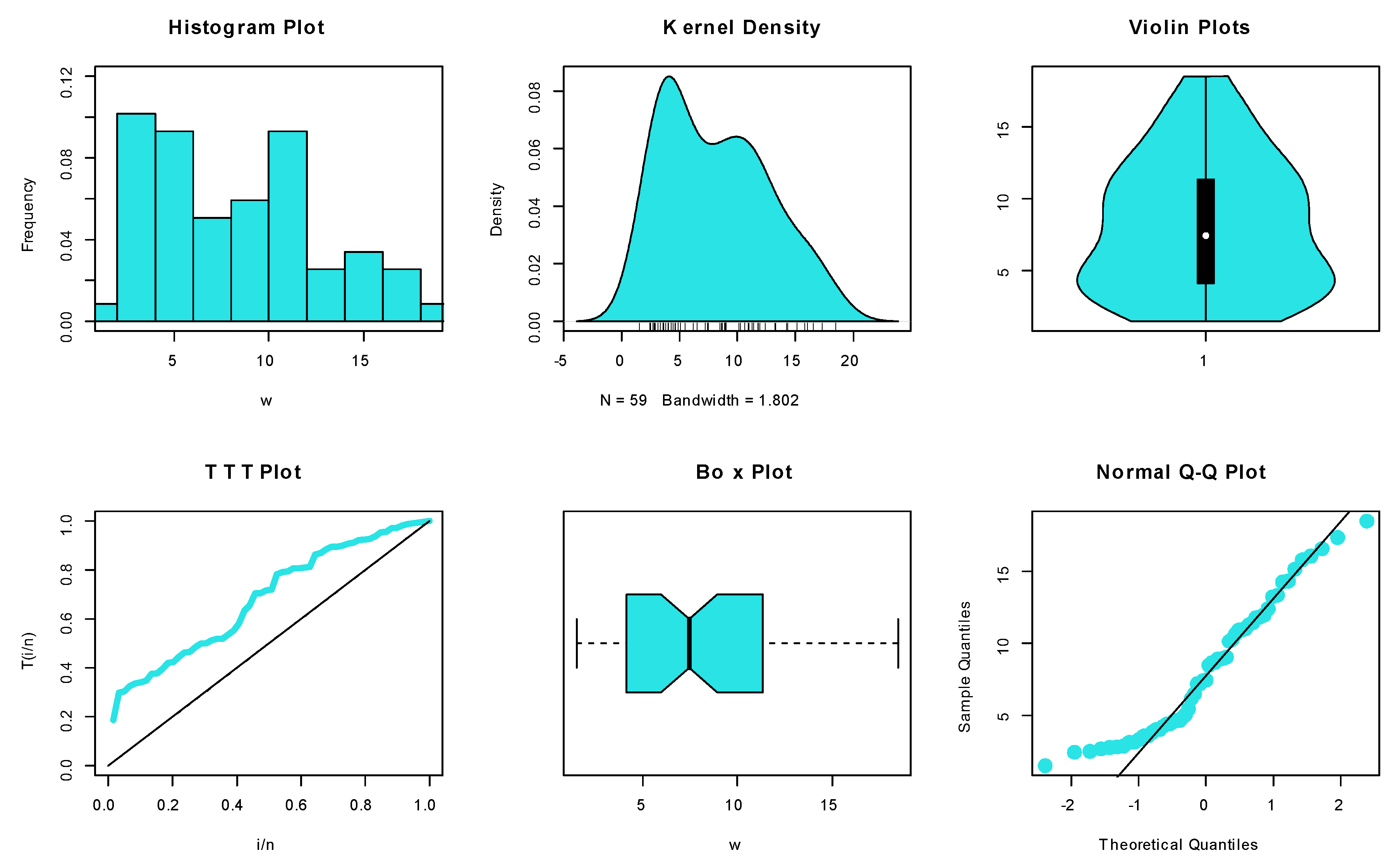

| Distribution | Our Test | |||||
|---|---|---|---|---|---|---|
| Weibull | 0.170 | 0.132 | 0.223 | 0.597 | 0.851 | 1.023 |
| LFR | 0.408 | 0.433 | 0.535 | 0.851 | 0.974 | 0.996 |
| Makeham | 0.039 | 0.144 | 0.184 | 0.148 | 0.213 | 0.249 |
| n | |||
|---|---|---|---|
| 5 | |||
| 10 | |||
| 15 | |||
| 20 | |||
| 25 | |||
| 30 | |||
| 35 | |||
| 40 | |||
| 45 | |||
| 50 | |||
| 55 | |||
| 60 | |||
| 65 | |||
| 70 | |||
| 75 | |||
| 80 | |||
| 85 | |||
| 90 | |||
| 95 | |||
| 100 |
| n | Weibull | Gamma | |
|---|---|---|---|
| 10 | 2 | ||
| 3 | |||
| 4 | |||
| 20 | 2 | ||
| 3 | |||
| 4 | |||
| 30 | 2 | ||
| 3 | |||
| 4 |
| n | |||
|---|---|---|---|
| 10 | |||
| 20 | |||
| 30 | |||
| 40 | |||
| 50 | |||
| 60 | |||
| 70 | |||
| 80 | |||
| 90 | |||
| 100 |
| n | Weibull | LFR | Gamma | |
|---|---|---|---|---|
| 10 | 2 | |||
| 3 | ||||
| 4 | ||||
| 20 | 2 | |||
| 3 | ||||
| 4 | ||||
| 30 | 2 | |||
| 3 | ||||
| 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Etman, W.B.H.; Eliwa, M.S.; Alqifari, H.N.; El-Morshedy, M.; Al-Essa, L.A.; EL-Sagheer, R.M. The NBRULC Reliability Class: Mathematical Theory and Goodness-of-Fit Testing with Applications to Asymmetric Censored and Uncensored Data. Mathematics 2023, 11, 2805. https://doi.org/10.3390/math11132805
Etman WBH, Eliwa MS, Alqifari HN, El-Morshedy M, Al-Essa LA, EL-Sagheer RM. The NBRULC Reliability Class: Mathematical Theory and Goodness-of-Fit Testing with Applications to Asymmetric Censored and Uncensored Data. Mathematics. 2023; 11(13):2805. https://doi.org/10.3390/math11132805
Chicago/Turabian StyleEtman, Walid B. H., Mohamed S. Eliwa, Hana N. Alqifari, Mahmoud El-Morshedy, Laila A. Al-Essa, and Rashad M. EL-Sagheer. 2023. "The NBRULC Reliability Class: Mathematical Theory and Goodness-of-Fit Testing with Applications to Asymmetric Censored and Uncensored Data" Mathematics 11, no. 13: 2805. https://doi.org/10.3390/math11132805






