Mixture Basis Function Approximation and Neural Network Embedding Control for Nonlinear Uncertain Systems with Disturbances
Abstract
:1. Introduction
- (1)
- A novel approximation method is proposed that allows an approximate nonlinear function of the system globally rather than existing methods that are only local. Hence, in the practical application, when some state oversteps the limited range, the RBF will fail to approximate, whereas MBF will have not have this problem.
- (2)
- An improved disturbance observer is designed for the disturbance estimation problem that relaxes the restriction condition about the rate of disturbance changing and thus expands the practical application range of the disturbance observer. Meanwhile, the simulation results show that our method has superior estimation performance.
- (3)
- The proposed neural network embedding controller is able to improve control performance without impacting the Lyapunov stability of the base controller. In the practice, it can be regarded as a “hot plug” module, that is to say, it is capable of being embedded in any existing control scheme as long as the base controller is Lyapunov stable, and of optimizing the control performance by updating weight parameters according to a specific objective function.
2. Problem Formulation and Preliminaries
2.1. System Statements
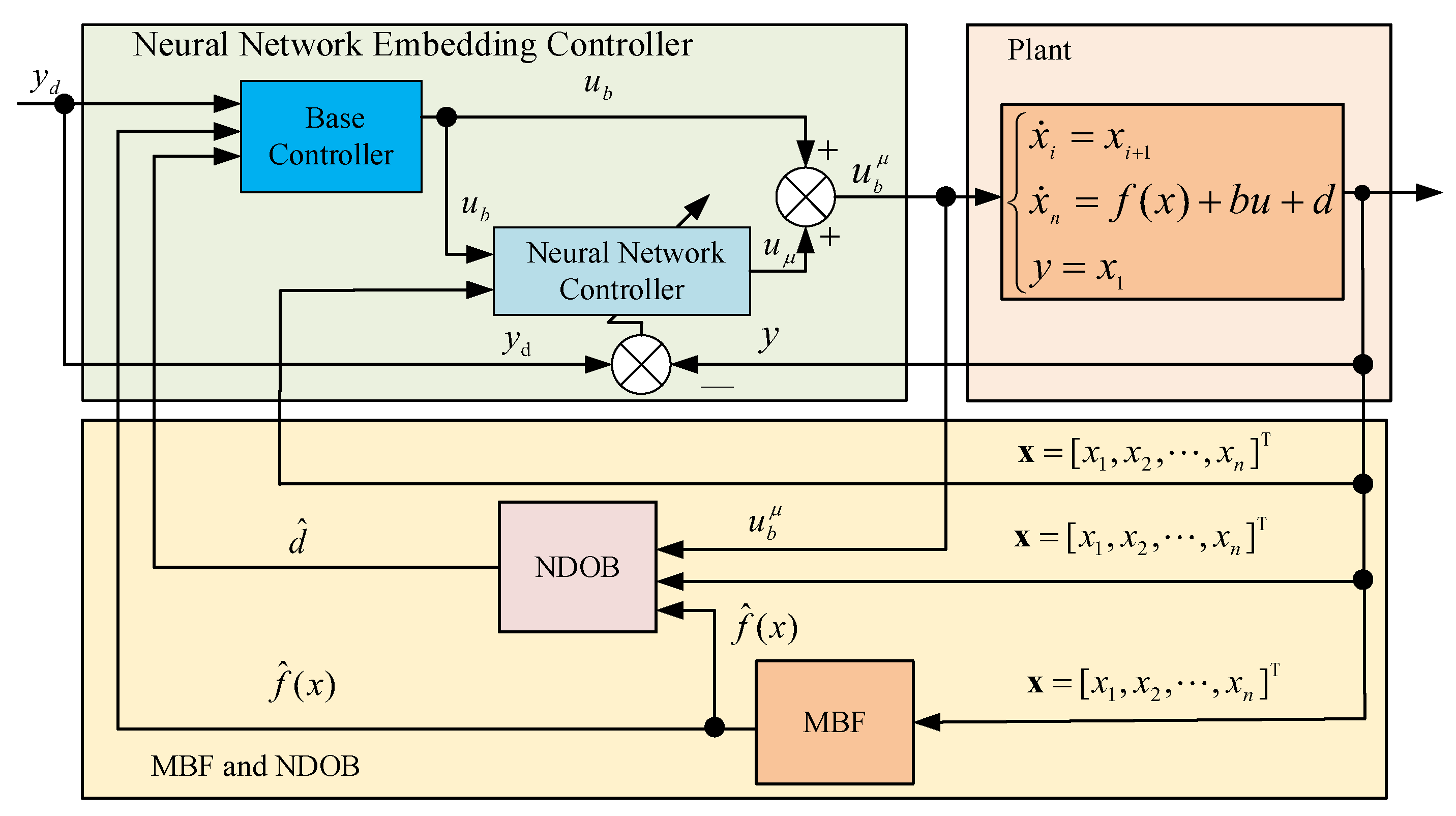
2.2. Controller Description
3. Base Controller Design
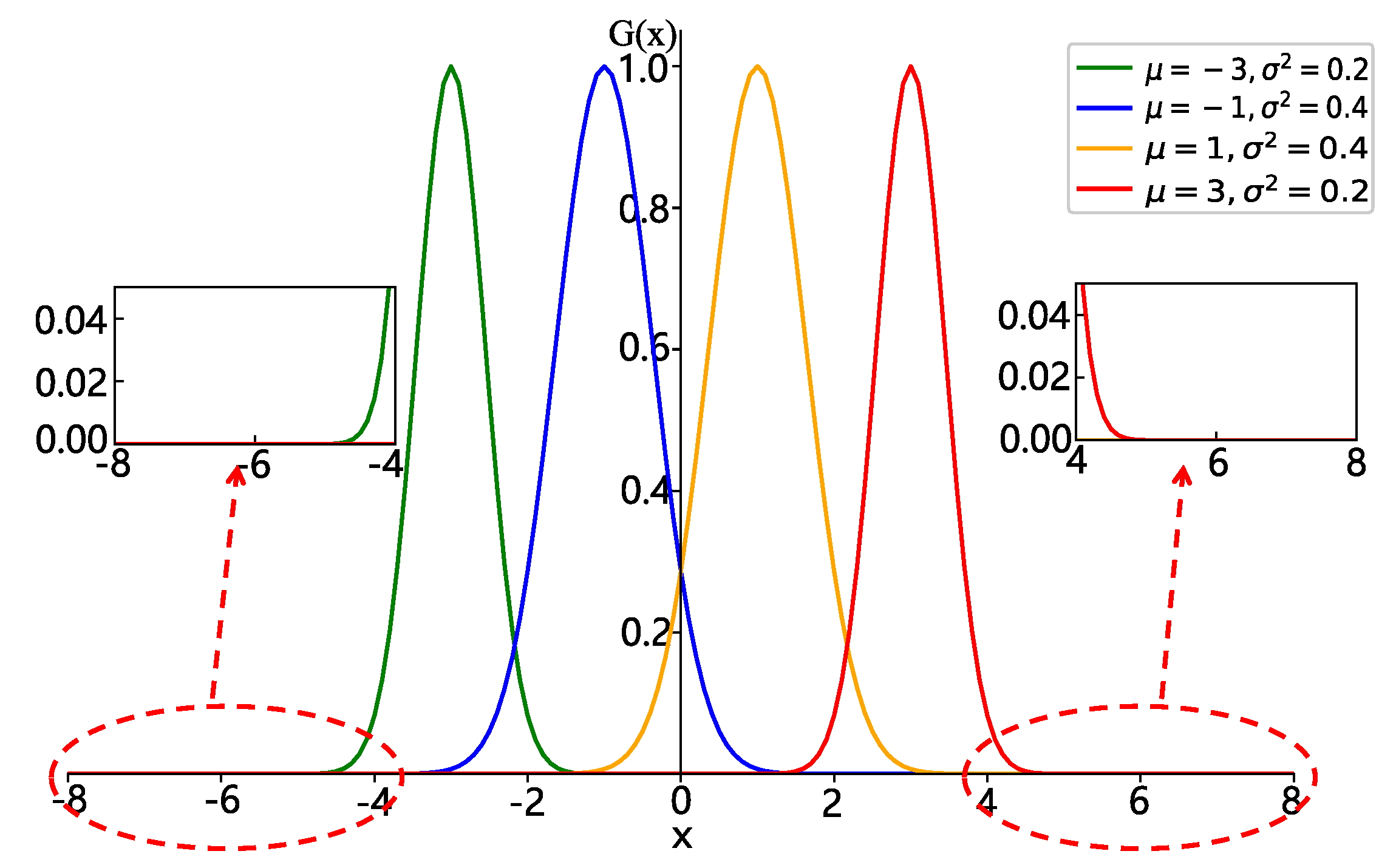
3.1. Mixture Basic Functions (MBF) Approximator Design
3.2. Disturbance Observer Design
3.3. Base Controller Design and Stability Analysis
4. Neural Network Embedding and Control Performance Optimization
4.1. Neural Network Embedding
4.2. Control Performance Optimization
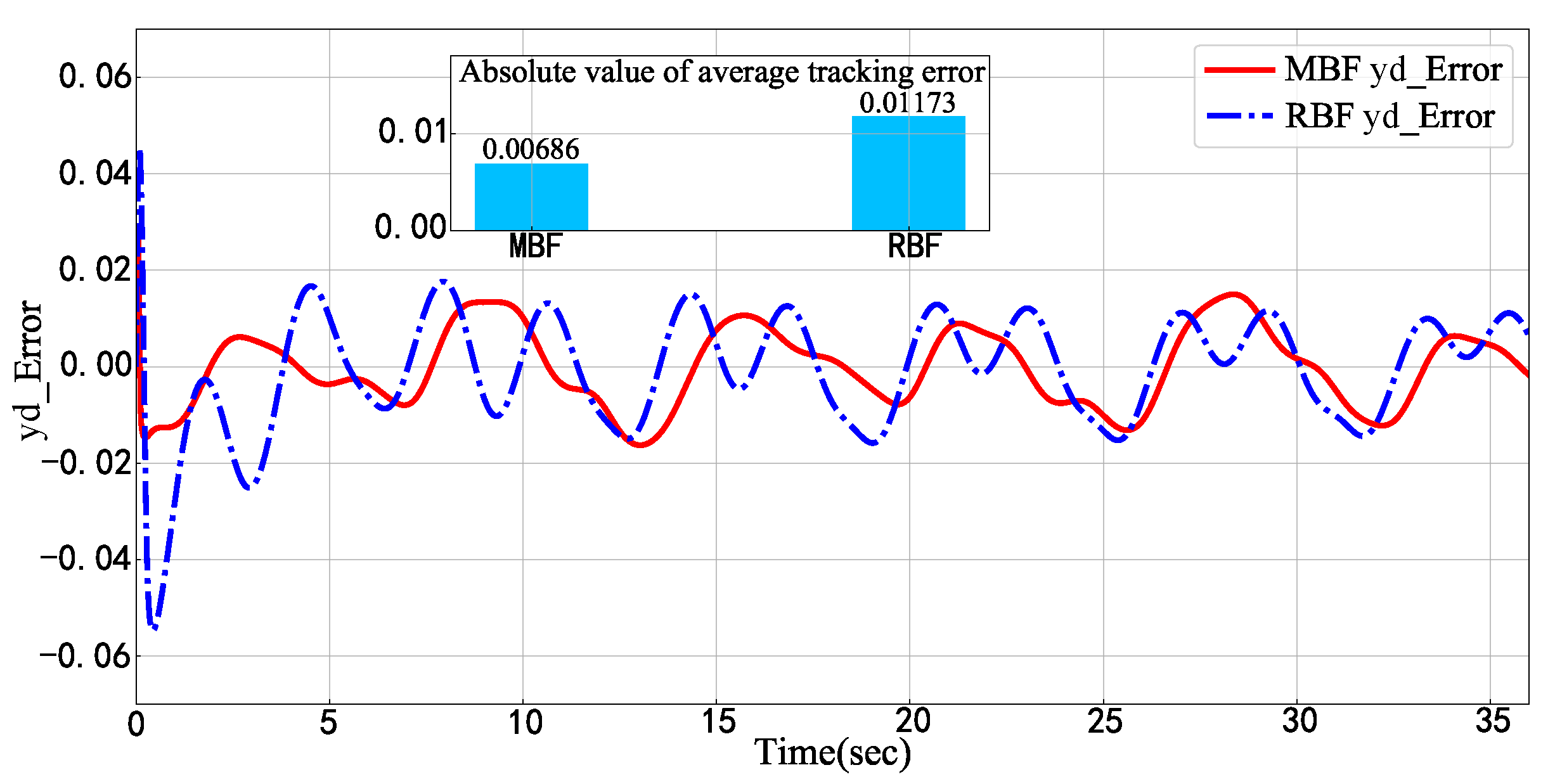
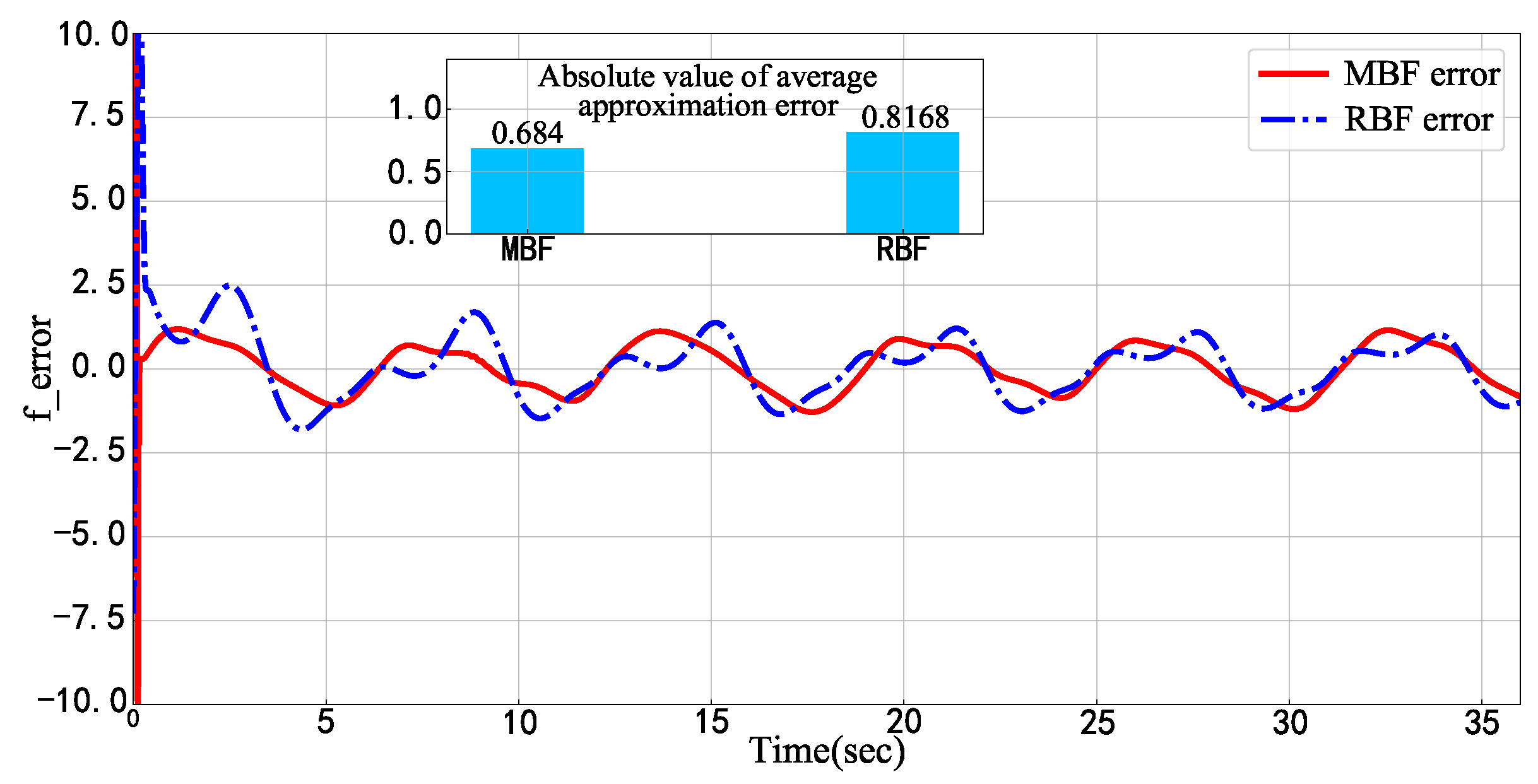
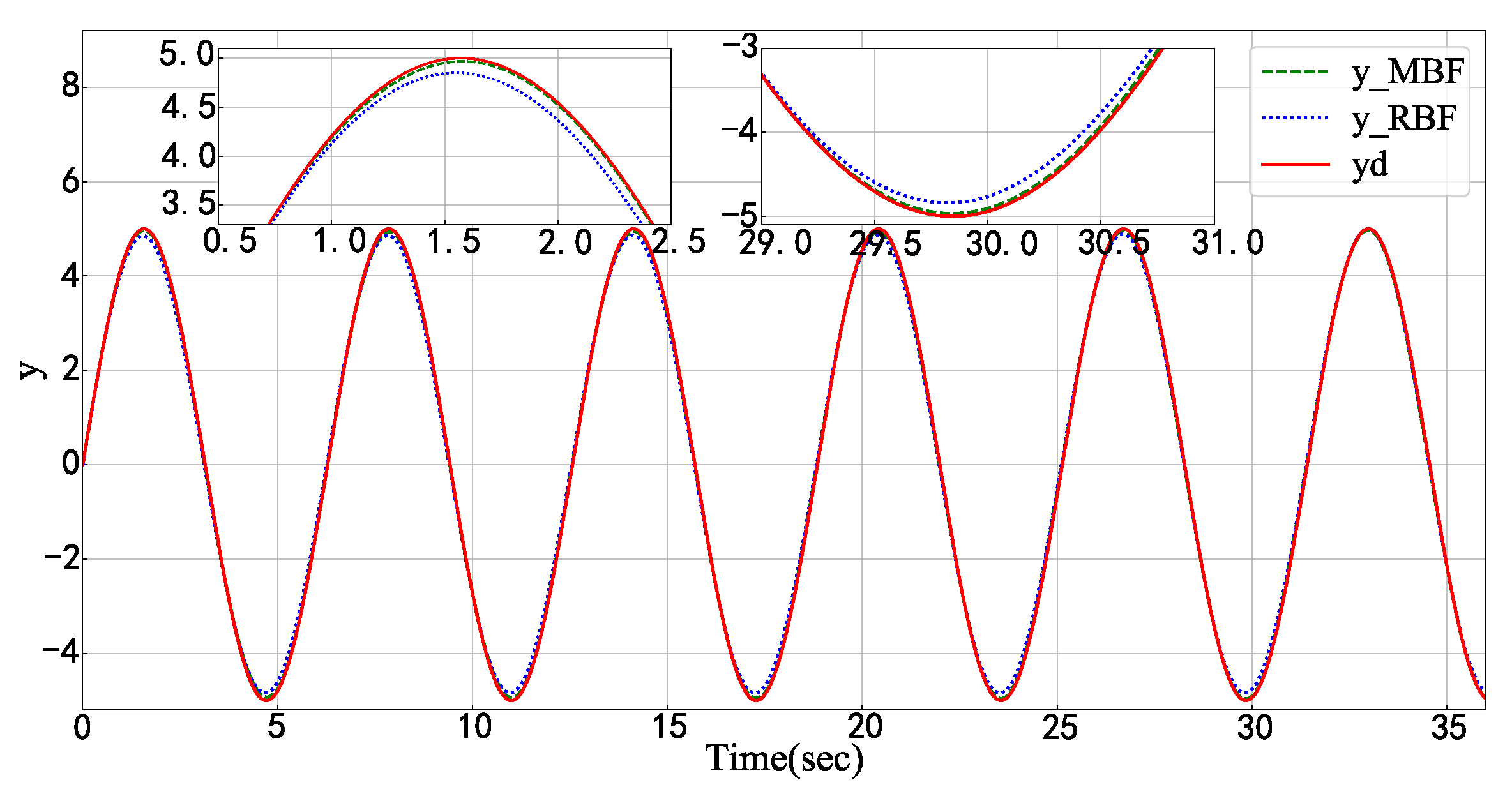
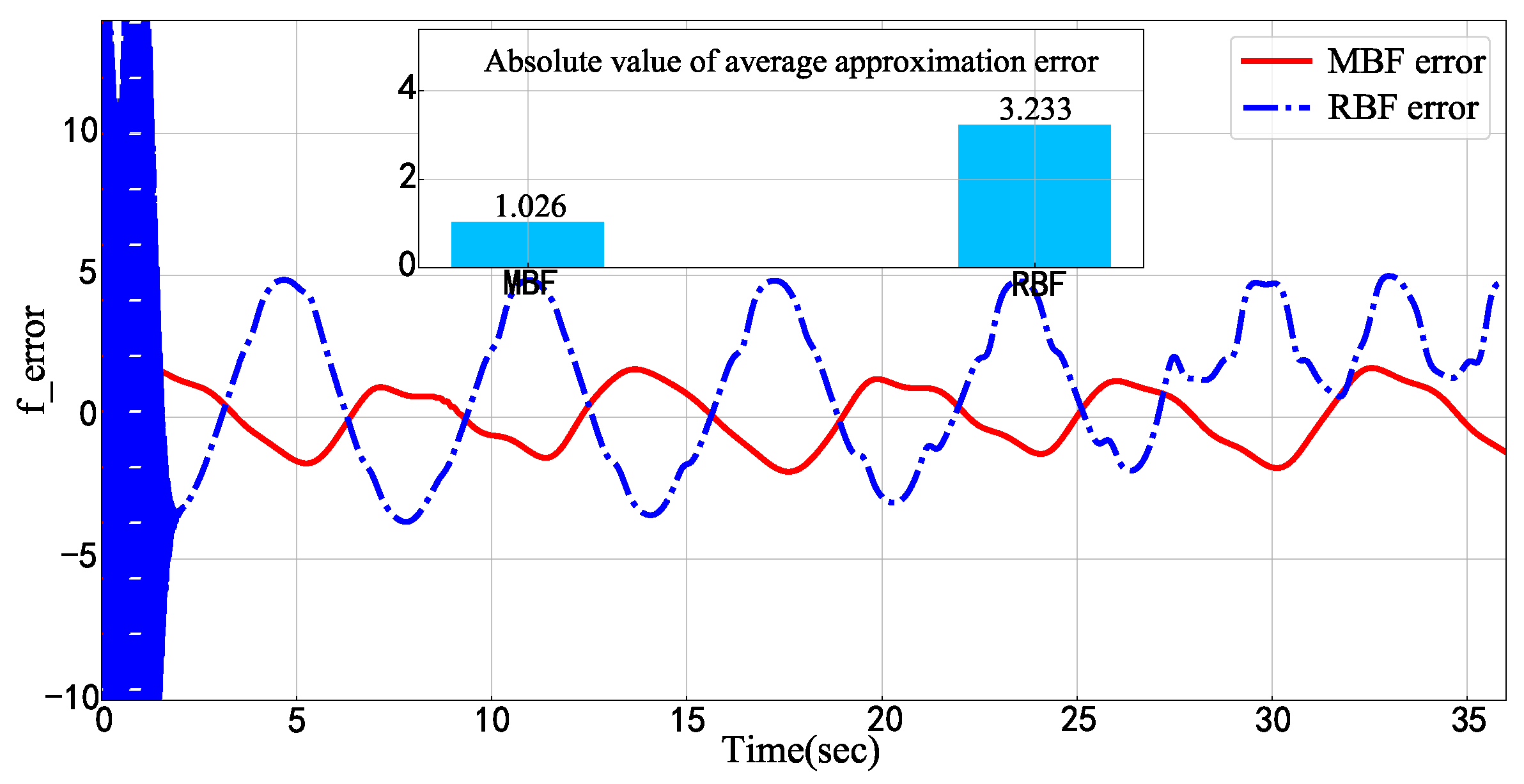
5. Simulations
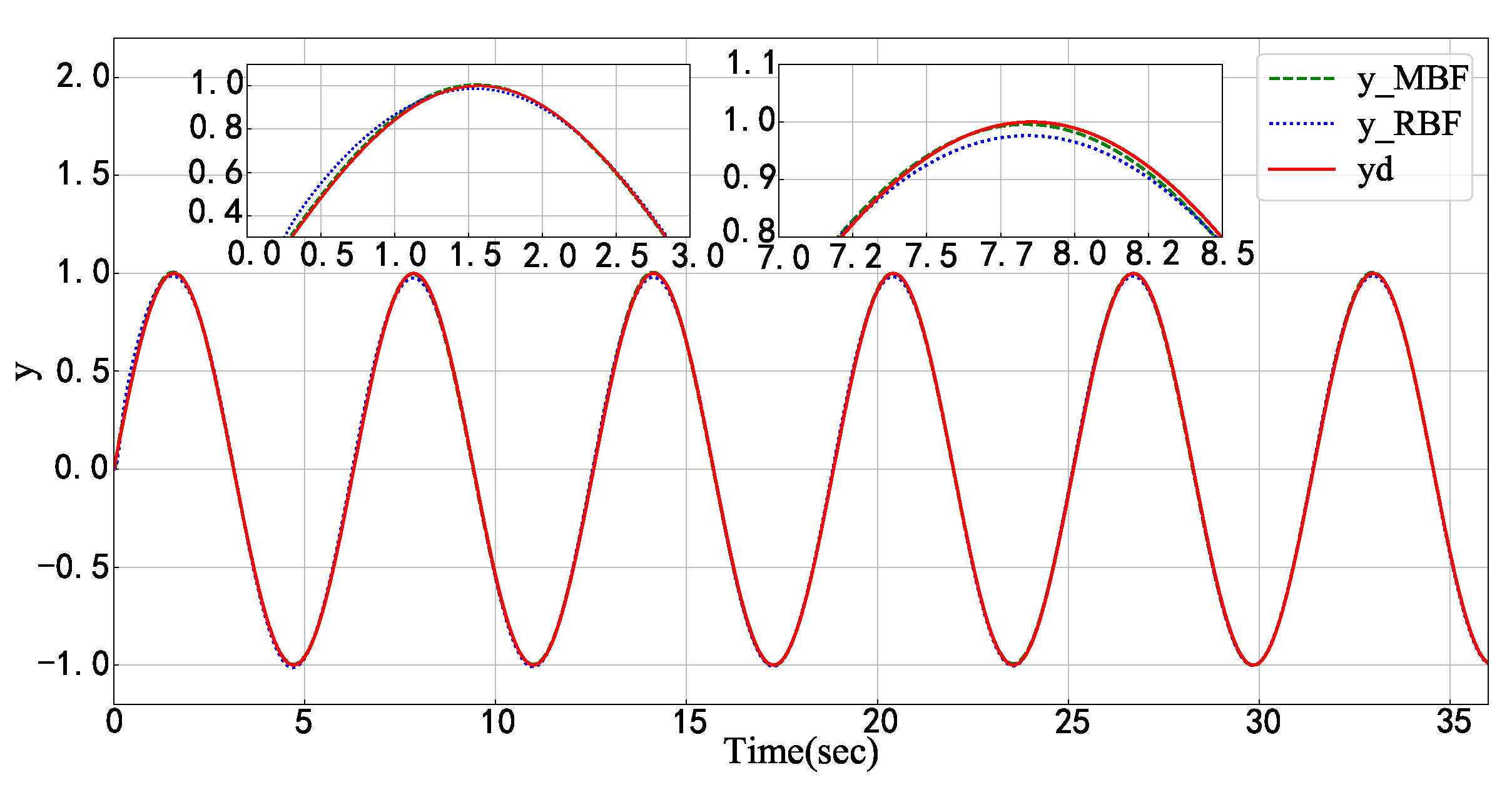
5.1. Numerical Model Examples
5.2. Physical Model Simulation
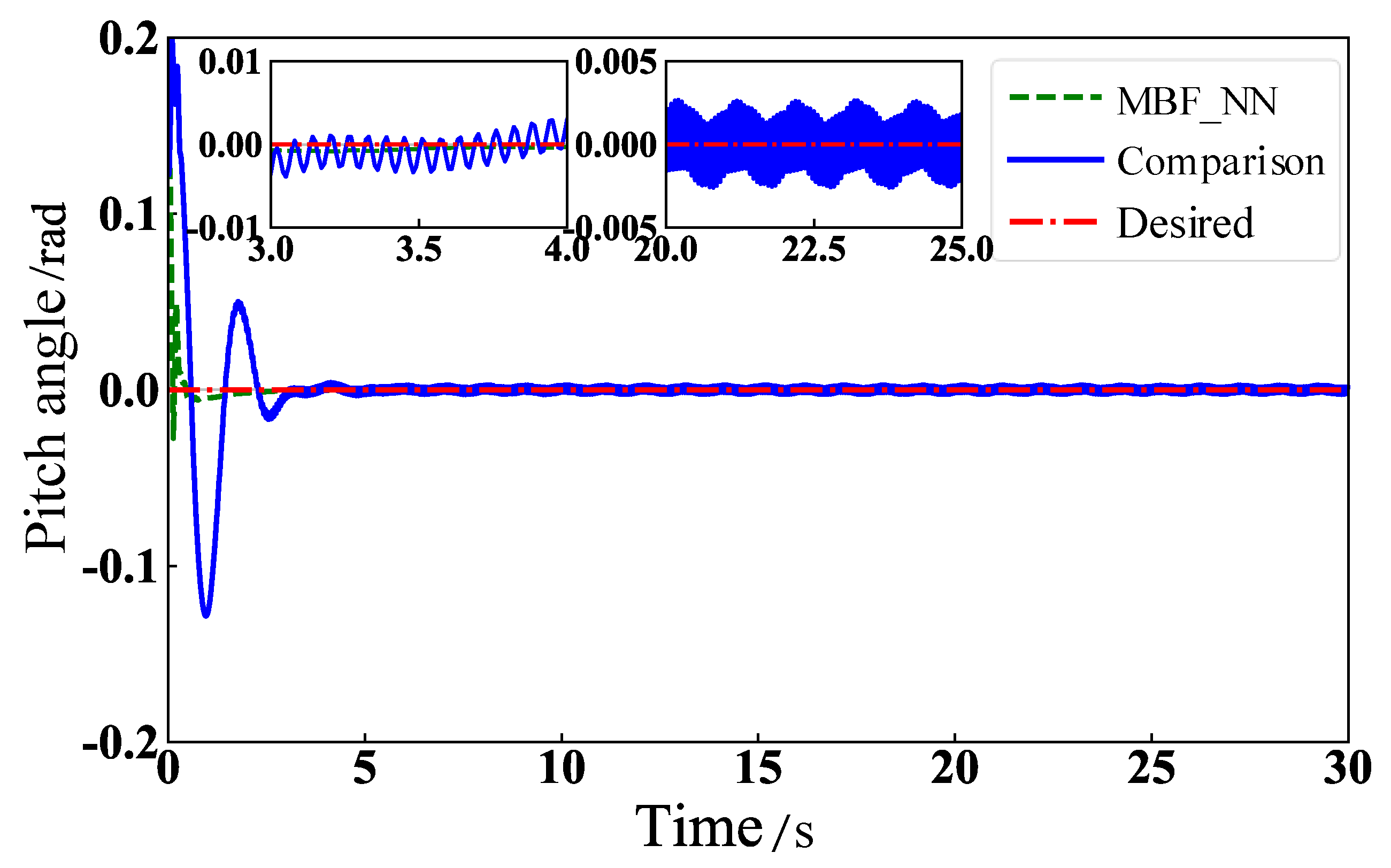
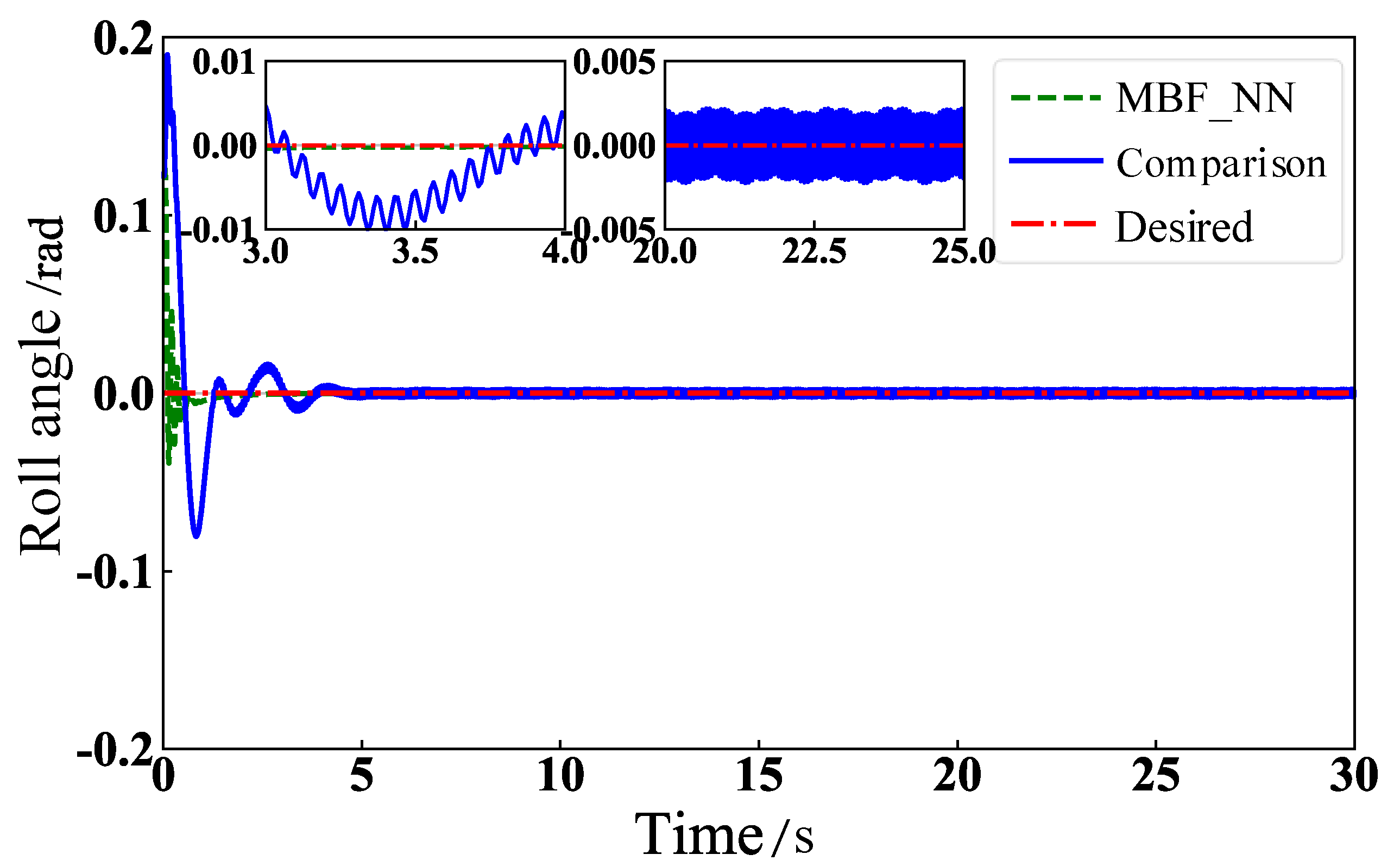
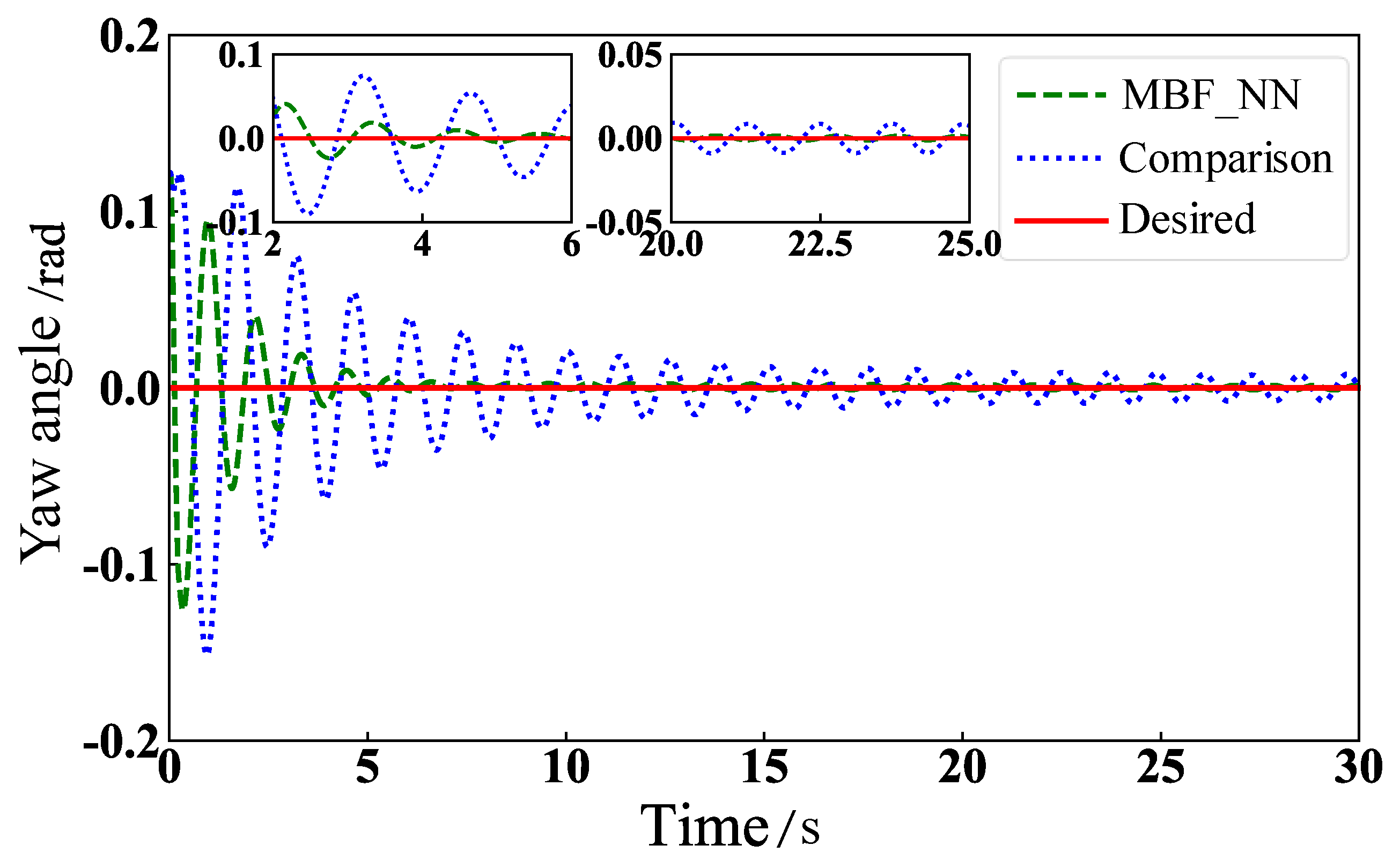
6. Virtual Experiments
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yeam, T.I.; Lee, D.C. Design of sliding-mode speed controller with active damping control for single-inverter dual-PMSM drive systems. IEEE Trans. Power Electron. 2021, 36, 5794–5801. [Google Scholar] [CrossRef]
- Ding, L.; Liu, C.; Liu, X.; Zheng, X.; Wu, H. Kinematic stability analysis of the tethered unmanned aerial vehicle quadrotor during take-off and landing. Chin. J. Sci. Instrum. 2020, 41, 70–78. [Google Scholar]
- Hu, Y.; Benallegue, M.; Venture, G.; Yoshida, E. Interact with me: An exploratory study on interaction factors for active physical human-robot interaction. IEEE Robot. Autom. Lett. 2020, 5, 6764–6771. [Google Scholar] [CrossRef]
- Wang, H.Q.; Liu, P.X.; Li, S.; Wang, D. Adaptive neural output-feedback control for a class of nonlower triangular nonlinear systems with unmodeled dynamics. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3658–3668. [Google Scholar] [PubMed]
- Chen, C.; Modares, H.; Xie, K.; Lewis, F.L.; Wan, Y.; Xie, S. Reinforcement learning based adaptive optimal exponential tracking control of linear systems with unknown dynamics. IEEE Trans. Autom. Control 2019, 64, 4423–4438. [Google Scholar] [CrossRef]
- Yang, W.; Guo, J.; Liu, Y.; Zhai, G. Multi-objective optimization of contactor’s characteristics based on RBF neural networks and hybrid method. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Meng, X.; Rozycki, P.; Qiao, J.F.; Wilamowski, B.M. Nonlinear System Modeling Using RBF Networks for Industrial Application. IEEE Trans. Ind. Inform. 2018, 14, 931–940. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, F.; Sun, W.; Gu, J.; Yao, B. RBF Neural Network Based Adaptive Robust Control for Nonlinear Bilateral Teleoperation Manipulators With Uncertainty and Time Delay. IEEE/ASME Trans. Mechatron. 2019, 25, 906–918. [Google Scholar] [CrossRef]
- Shojaei, K. Coordinated Saturated Output-Feedback Control of an Autonomous Tractor-Trailer and a Combine Harvester in Crop-Harvesting Operation. IEEE Trans. Veh. Technol. 2021, 71, 1224–1236. [Google Scholar] [CrossRef]
- Wang, A.; Liu, L.; Qiu, J.; Feng, G. Event-Triggered Robust Adaptive Fuzzy Control for a Class of Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2019, 27, 1648–1658. [Google Scholar] [CrossRef]
- Chen, B.; Lin, C.; Liu, X.; Liu, K. Adaptive fuzzy tracking control for a class of MIMO nonlinear systems in nonstrict-feedback form. IEEE Trans. Cybern. 2017, 45, 2744–2755. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.B. Adaptive sliding mode robust control based on multi-dimensional Taylor network for trajectory tracking of quadrotor UAV. IET Control Theory Appl. 2020, 14, 1855–1866. [Google Scholar] [CrossRef]
- Das, S.; Subudhi, B. A two-degree-of-freedom internal model-based active disturbance rejection controller for a wind energy conversion system. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 2664–2671. [Google Scholar] [CrossRef]
- Zhou, R.; Fu, C.; Tan, W. Implementation of Linear Controllers via Active Disturbance Rejection Control Structure. IEEE Trans. Ind. Electron. 2021, 68, 6217–6226. [Google Scholar] [CrossRef]
- He, T.; Wu, Z. Iterative learning disturbance observer based attitude stabilization of flexible spacecraft subject to complex disturbances and measurement noises. IEEE/CAA J. Autom. Sin. 2021, 8, 1576–1587. [Google Scholar] [CrossRef]
- Lu, Y.S. Sliding-mode disturbance observer with switching-gain adaptation and its application to optical disk drives. IEEE Trans. Ind. Electron. 2009, 56, 3743–3750. [Google Scholar]
- Yan, Y.; Yang, J.; Sun, Z.; Zhang, C.; Li, S.; Yu, H. Robust speed regulation for PMSM servo system with multiple sources of disturbances via an augmented disturbance observer. IEEE/ASME Trans. Mechatron. 2018, 23, 769–780. [Google Scholar] [CrossRef]
- Cui, Y.; Qiao, J.; Zhu, Y.; Yu, X.; Guo, L. Velocity-tracking control based on refined disturbance observer for gimbal servo system with multiple disturbances. IEEE Trans. Ind. Electron. 2021, 69, 10311–10321. [Google Scholar] [CrossRef]
- Tang, L.; Ding, B.; He, Y. An efficient 3D model retrieval method based on convolutional neural network. Acta Electron. Sin. 2021, 49, 64–71. [Google Scholar]
- Luo, H.L.; Yuan, P.; Kang, T. Review of the methods for salient object detection based on deep learning. Acta Electron. Sin. 2021, 49, 1417–1427. [Google Scholar]
- Yin, X.; Zhao, X. Deep neural learning based distributed predictive control for offshore wind farm using high-fidelity LES data. IEEE Trans. Ind. Electron. 2020, 68, 3251–3261. [Google Scholar] [CrossRef]
- Kang, Y.; Chen, S.; Wang, X.; Cao, Y. Deep convolutional identifier for dynamic modeling and adaptive control of unmanned helicopter. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 524–538. [Google Scholar] [CrossRef]
- Li, K.; Li, Y.M.; Hu, X.M.; Shao, F. A robust and accurate object tracking algorithm based on convolutional neural network. Acta Electron. Sin. 2018, 46, 2087–2093. [Google Scholar]
- Guo, X.G.; Wang, J.L.; Liao, F.; Teo, R.S. CNN-based distributed adaptive control for vehicle-following platoon with input saturation. IEEE Trans. Intell. Transp. Syst. 2017, 19, 3121–3132. [Google Scholar] [CrossRef]
- Xu, H.; Jagannathan, S. Neural network-based finite horizon stochastic optimal control design for nonlinear networked control systems. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 472–485. [Google Scholar] [CrossRef] [PubMed]
- Wen, G.; Chen, C.P.; Ge, S.S.; Yang, H.; Liu, X. Optimized adaptive nonlinear tracking control using actor–critic reinforcement learning strategy. IEEE Trans. Ind. Inform. 2019, 15, 4969–4977. [Google Scholar] [CrossRef]
- Tan, L.N.; Cong, T.P.; Cong, D.P. Neural network observers and sensorless robust optimal control for partially unknown PMSM with disturbances and saturating voltages. IEEE Trans. Power Electron. 2021, 36, 12045–12056. [Google Scholar] [CrossRef]
- Han, H.G.; Zhang, L.; Hou, Y.; Qiao, J.F. Nonlinear model predictive control based on a self-organizing recurrent neural network. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 402–415. [Google Scholar] [CrossRef]
- Le, M.; Yan, Y.-M.; Xu, D.-F.; Li, Z.-W.; Sun, L.-F. Neural Network Embedded Learning Control for Nonlinear System with Unknown Dynamics and Disturbance. Acta Autom. Sin. 2020, 47, 2016–2028. [Google Scholar]
- Zhang, X.; Chen, X.; Zhu, G.; Su, C.Y. Output Feedback Adaptive Motion Control and Its Experimental Verification for Time-Delay Nonlinear Systems With Asymmetric Hysteresis. IEEE Trans. Ind. Electron. 2019, 67, 6824–6834. [Google Scholar] [CrossRef]
- Powell, M.J.D. Approximation Theory and Methods; Cambridge University Press: Cambridge, UK, 1981. [Google Scholar]
- Chen, W.H. Nonlinear disturbance observer-enhanced dynamic inversion control of missiles. J. Guid. Control. Dyn. 2003, 26, 161–166. [Google Scholar] [CrossRef]
- He, Y.; Zhou, Y.; Cai, Y.; Yuan, C.; Shen, J. DSC-based RBF neural network control for nonlinear time-delay systems with time-varying full state constraints. ISA Trans. 2021, 129, 79–90. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Yang, C.; Pan, Y.; Cheng, L. Composite learning enhanced neural control for robot manipulator with output error constraints. IEEE Trans. Ind. Inform. 2019, 17, 209–218. [Google Scholar] [CrossRef]
- Yang, T.; Gao, X. Adaptive Neural Sliding-Mode Controller for Alternative Control Strategies in Lower Limb Rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 28, 238–247. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Hu, Y. Trajectory Control of Quadrotor With Cable-Suspended Load via Dynamic Feedback Linearization. Acta Autom. Sin. 2020, 46, 1993–2002. [Google Scholar]
- Huang, H.; Yang, C.; Chen, C.P. Optimal robot- environment interaction under broad fuzzy neural adaptive control. IEEE Trans. Cybern. 2021, 51, 3824–3835. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Yan, Y.; Li, Z.; Liu, J. Neural-embedded learning control for fully-actuated flying platform of aerial manipulation system. Neurocomputing 2022, 482, 212–223. [Google Scholar] [CrossRef]
- Le, M.; Yanxun, C.; Zhiwei, L.; Dongfu, X.; Yulong, Z. A framework of learning controller with Lyapunov-based constraint and application. Chin. J. Sci. Instrum. 2019, 40, 189–198. [Google Scholar]
- Shao, S.; Chen, M.; Zhao, Q. Discrete-time fault tolerant control for quadrotor UAV based on disturbance observer. Acta Aeronaut. Et Astronaut. Sin. 2020, 41, 89–97. [Google Scholar]
- Fu, C.; Tian, Y.; Huang, H.; Zhang, L.; Peng, C. Finite-time trajectory tracking control for a 12-rotor unmanned aerial vehicle with input saturation. ISA Trans. 2018, 81, 52–62. [Google Scholar] [CrossRef]




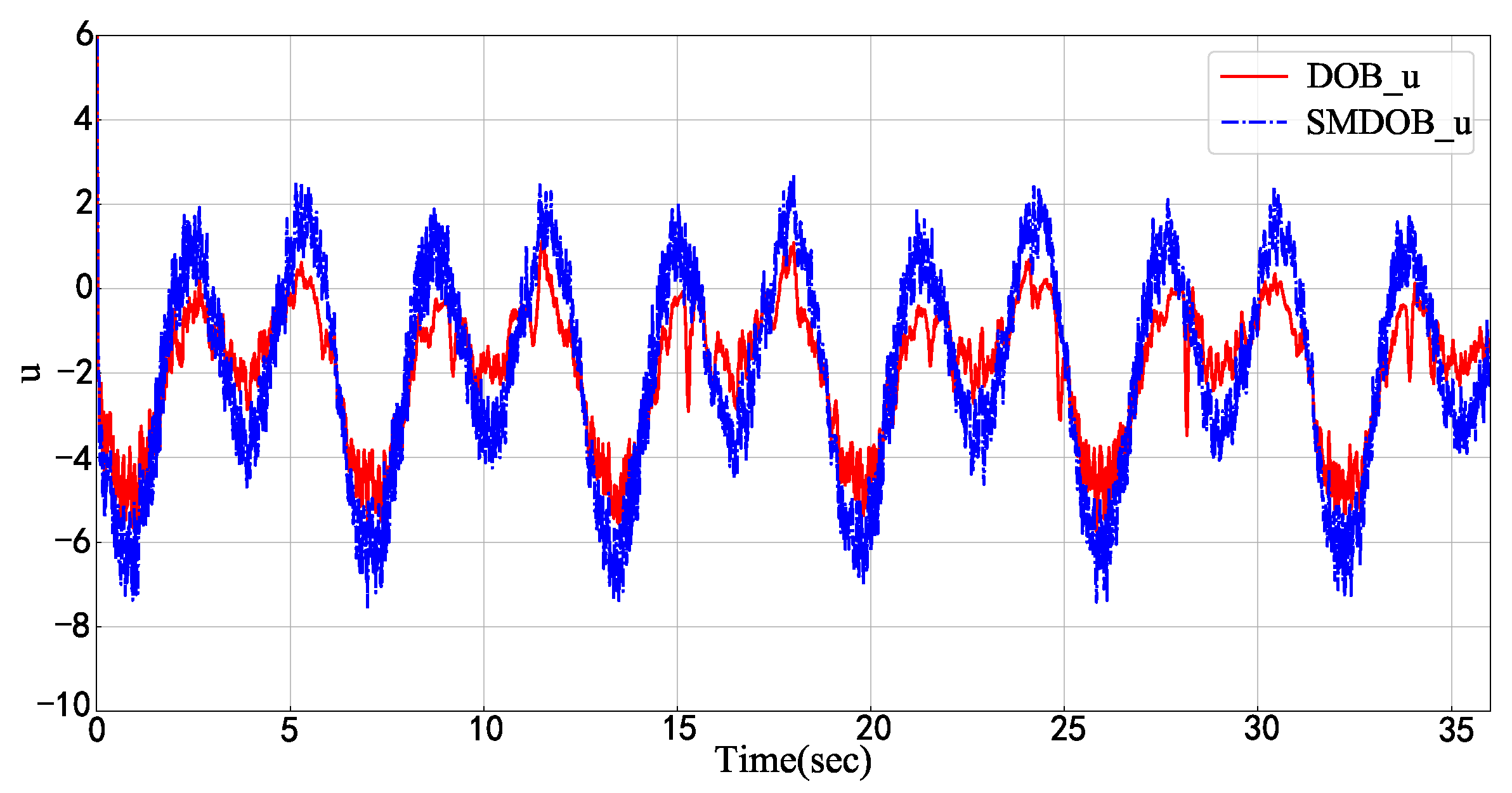
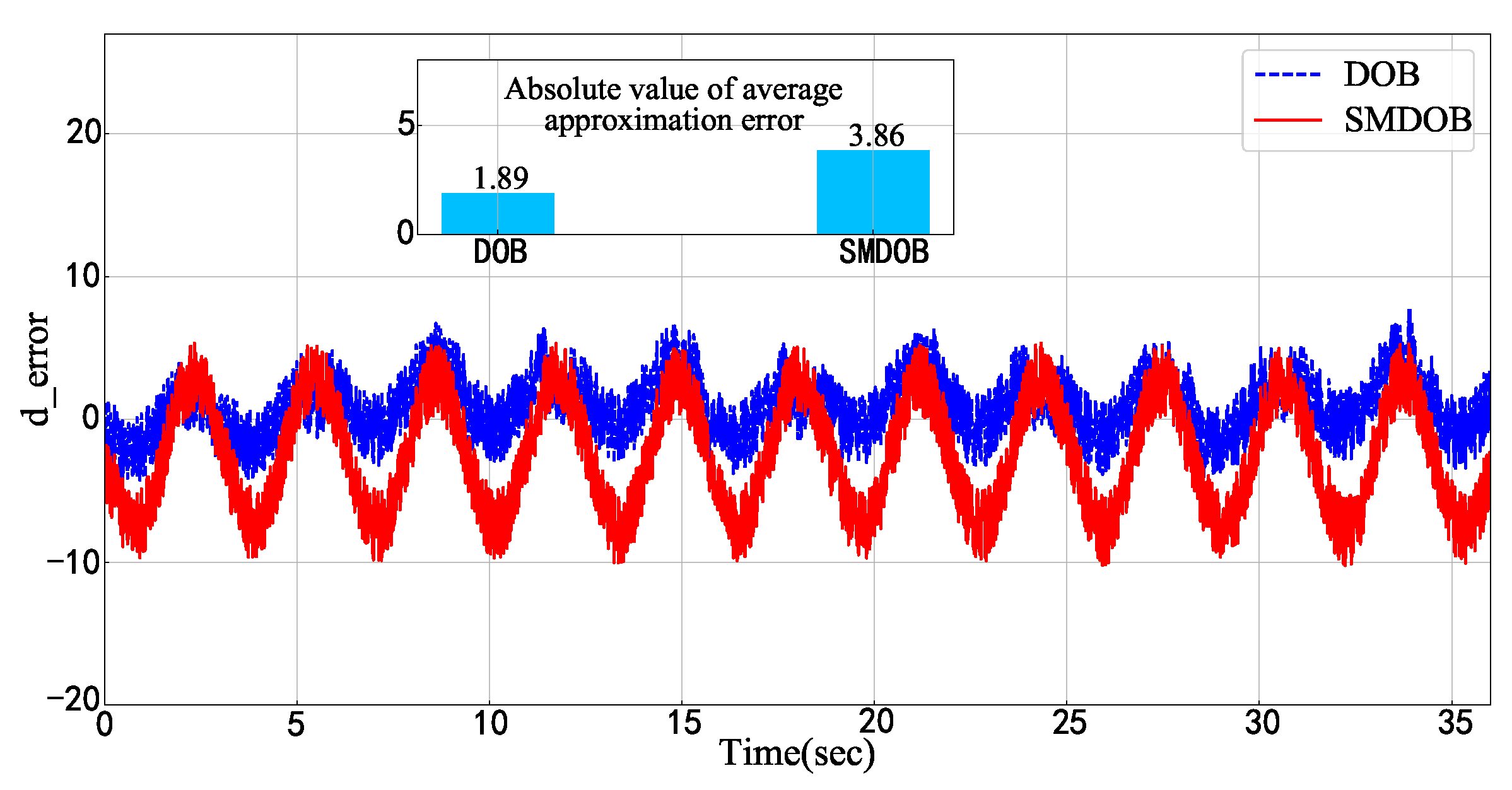
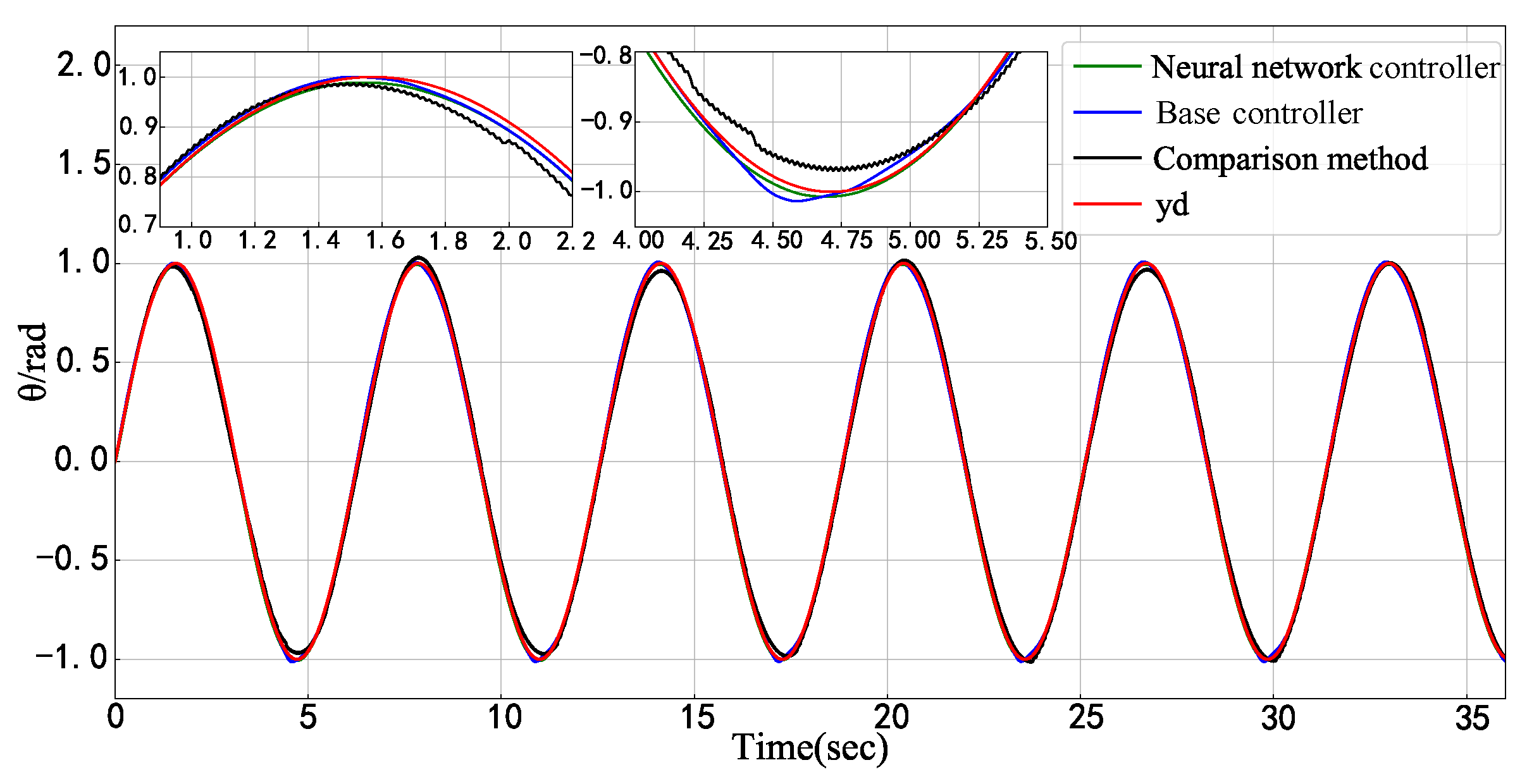
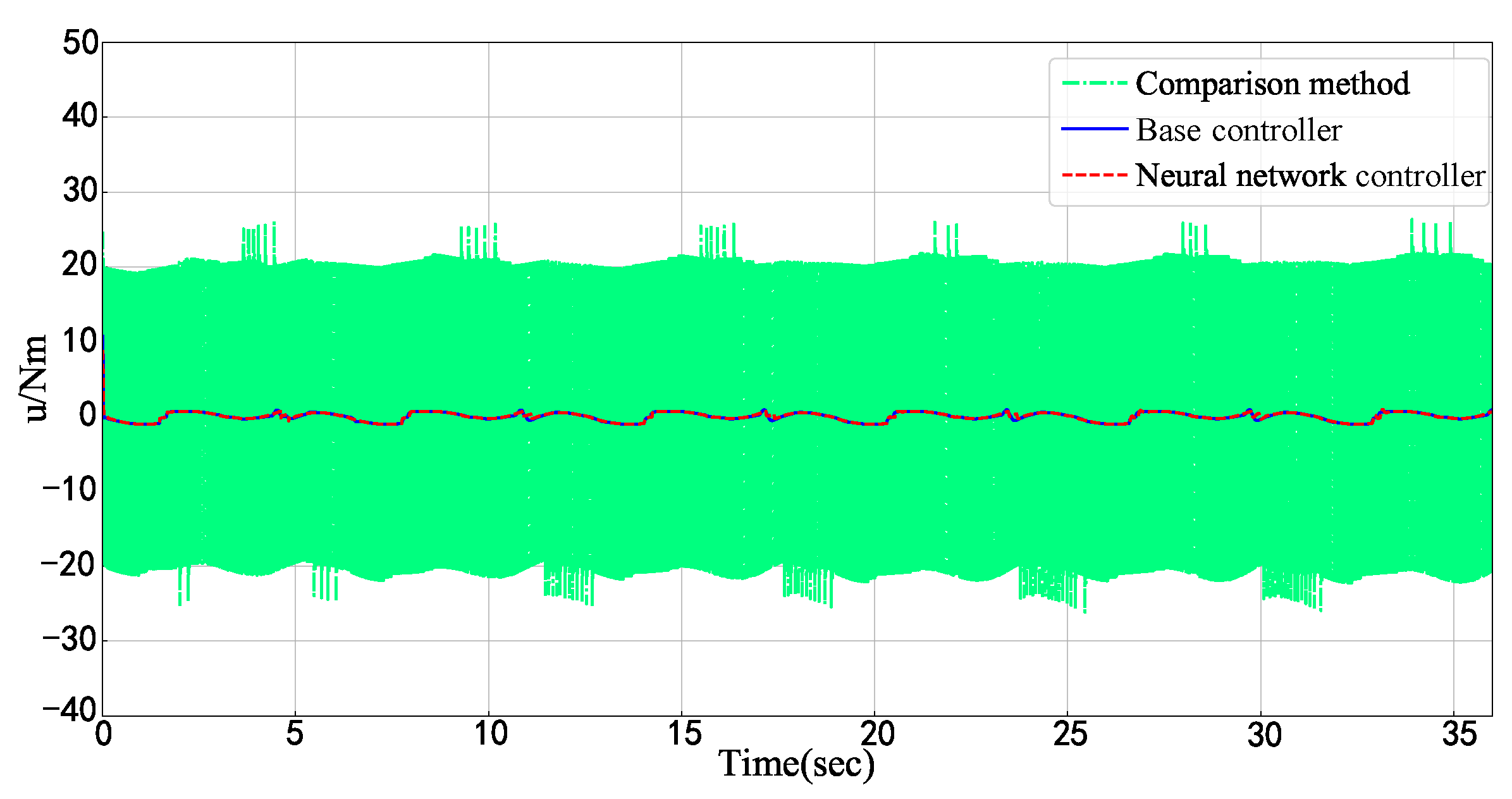



| Control Flow | |
|---|---|
| Nonlinear Function Approximation: | |
| Disturbance Estimation: | |
| Base Controller: | |
| Neural Network Embedding Controller: | |
| Parameters Update: | |
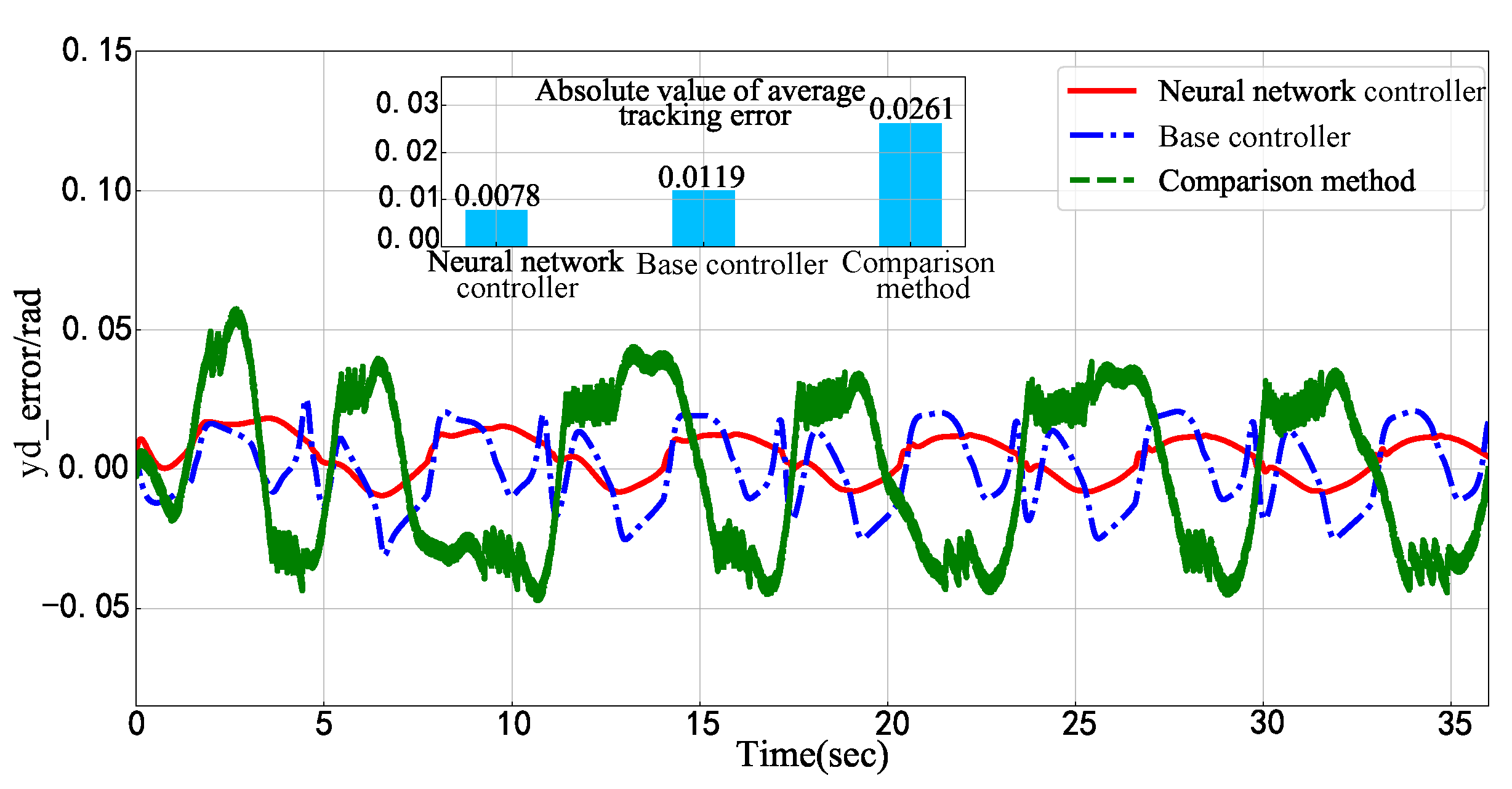
| Methods | Max | Mean | Max | Mean |
|---|---|---|---|---|
| Comparison method | ||||
| Base controller | ||||
| Neural network controller |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Zhang, Q.; Wang, T.; Wu, X.; Liu, J.; Jiang, W. Mixture Basis Function Approximation and Neural Network Embedding Control for Nonlinear Uncertain Systems with Disturbances. Mathematics 2023, 11, 2823. https://doi.org/10.3390/math11132823
Ma L, Zhang Q, Wang T, Wu X, Liu J, Jiang W. Mixture Basis Function Approximation and Neural Network Embedding Control for Nonlinear Uncertain Systems with Disturbances. Mathematics. 2023; 11(13):2823. https://doi.org/10.3390/math11132823
Chicago/Turabian StyleMa, Le, Qiaoyu Zhang, Tianmiao Wang, Xiaofeng Wu, Jie Liu, and Wenjuan Jiang. 2023. "Mixture Basis Function Approximation and Neural Network Embedding Control for Nonlinear Uncertain Systems with Disturbances" Mathematics 11, no. 13: 2823. https://doi.org/10.3390/math11132823
APA StyleMa, L., Zhang, Q., Wang, T., Wu, X., Liu, J., & Jiang, W. (2023). Mixture Basis Function Approximation and Neural Network Embedding Control for Nonlinear Uncertain Systems with Disturbances. Mathematics, 11(13), 2823. https://doi.org/10.3390/math11132823






