Planning Allocation for GTO-GEO Transfer Spacecraft with Triple Orthogonal Gimbaled Thruster Boom
Abstract
:1. Introduction
2. Mathematical Preliminaries
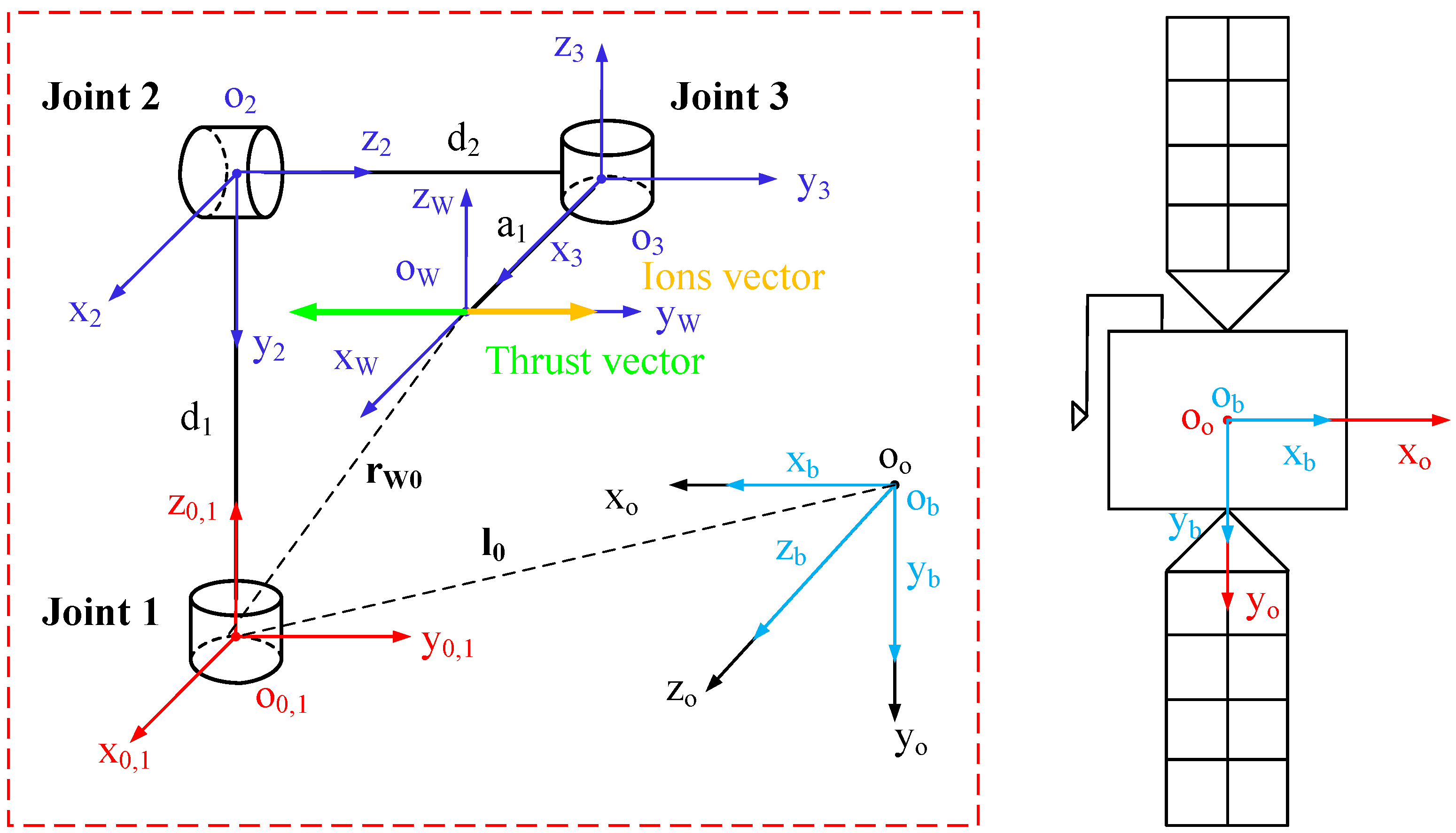
2.1. Modeling of GTO-GEO Transfer Satellite Based on Triple Orthogonal Configuration
2.1.1. Preparation
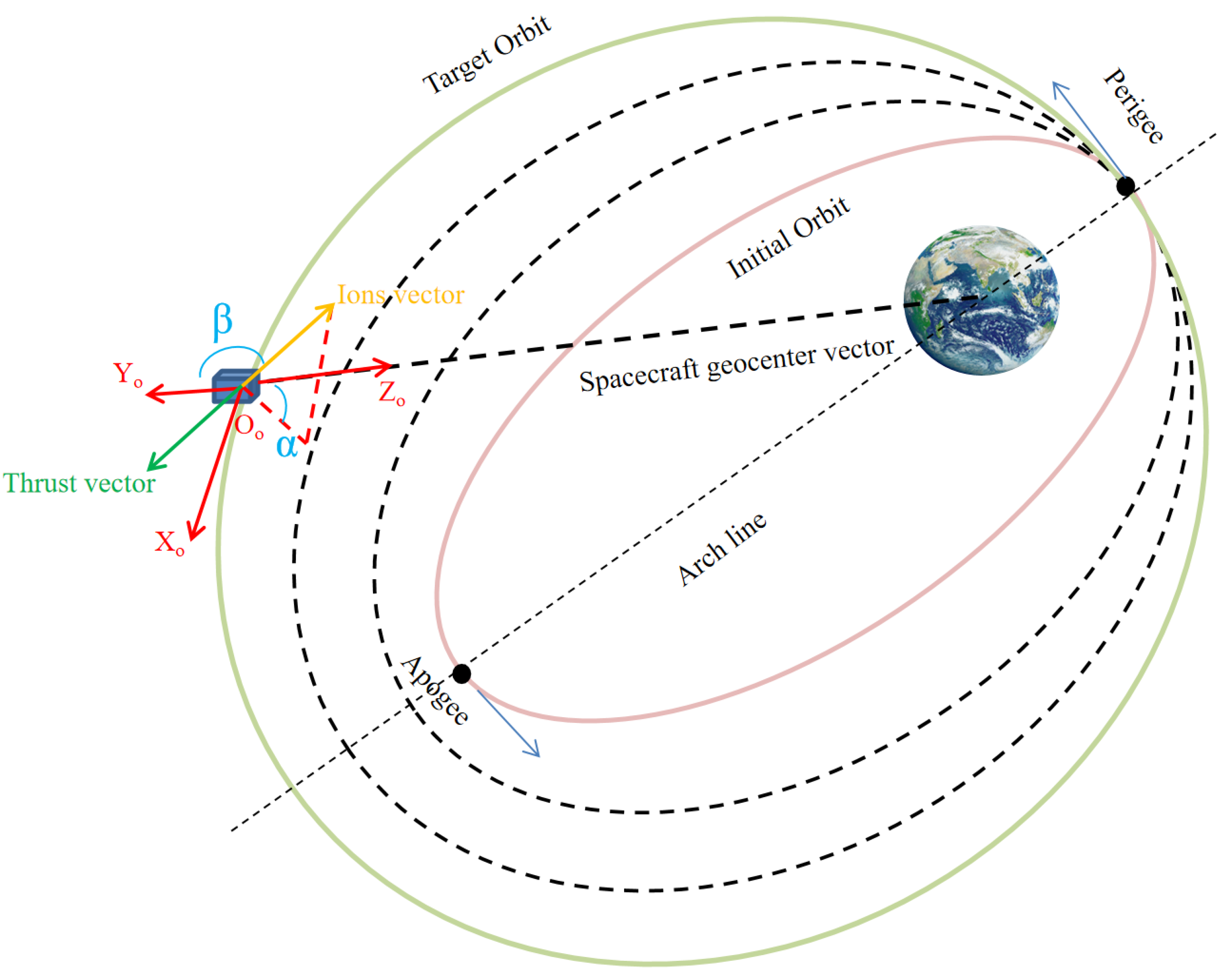
2.1.2. GTO-GEO Transfer Spacecraft Kinematics and Dynamics
2.2. Gimbaled Thruster Boom Dynamics
2.2.1. Kinematics of the Thrust Vector-Regulated Gimbaled Thruster Boom
2.2.2. Thrust Vector Adjustment Dynamics
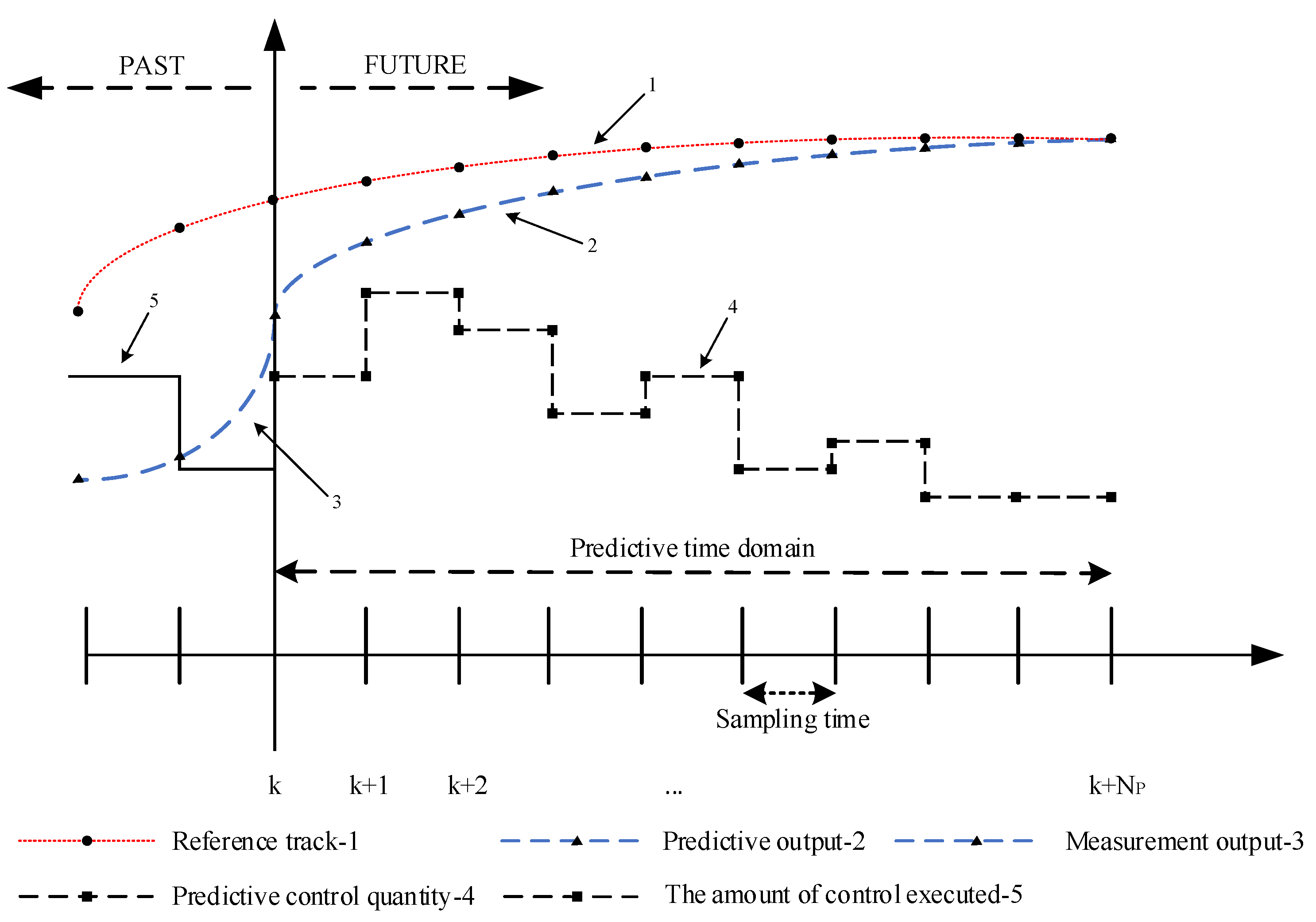
3. Planning Algorithm Design
3.1. Controller Description
3.2. Stability Analysis
4. Planning Algorithm Design
4.1. Simulation Condition Configuration
4.2. Result and Discussion
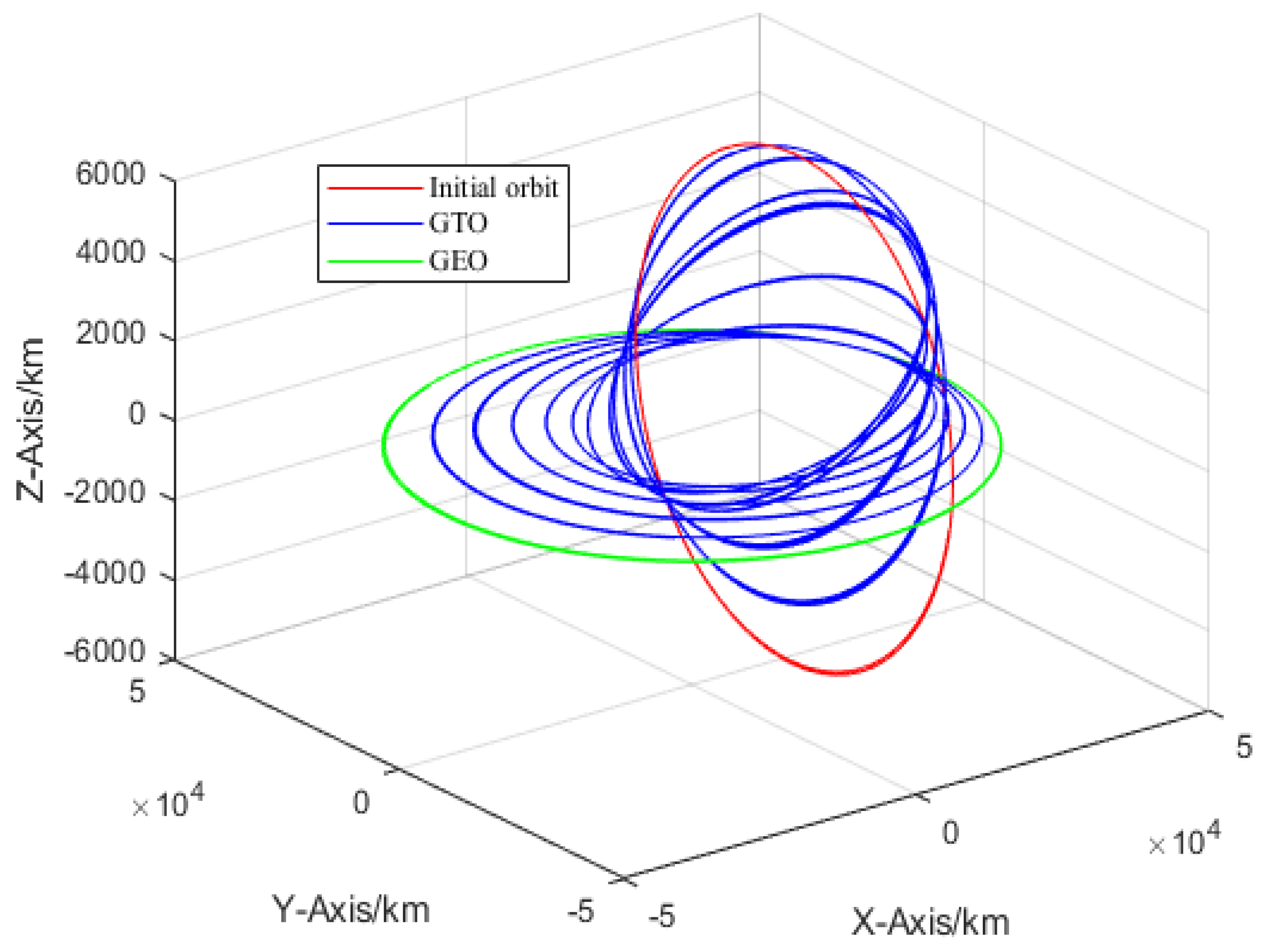
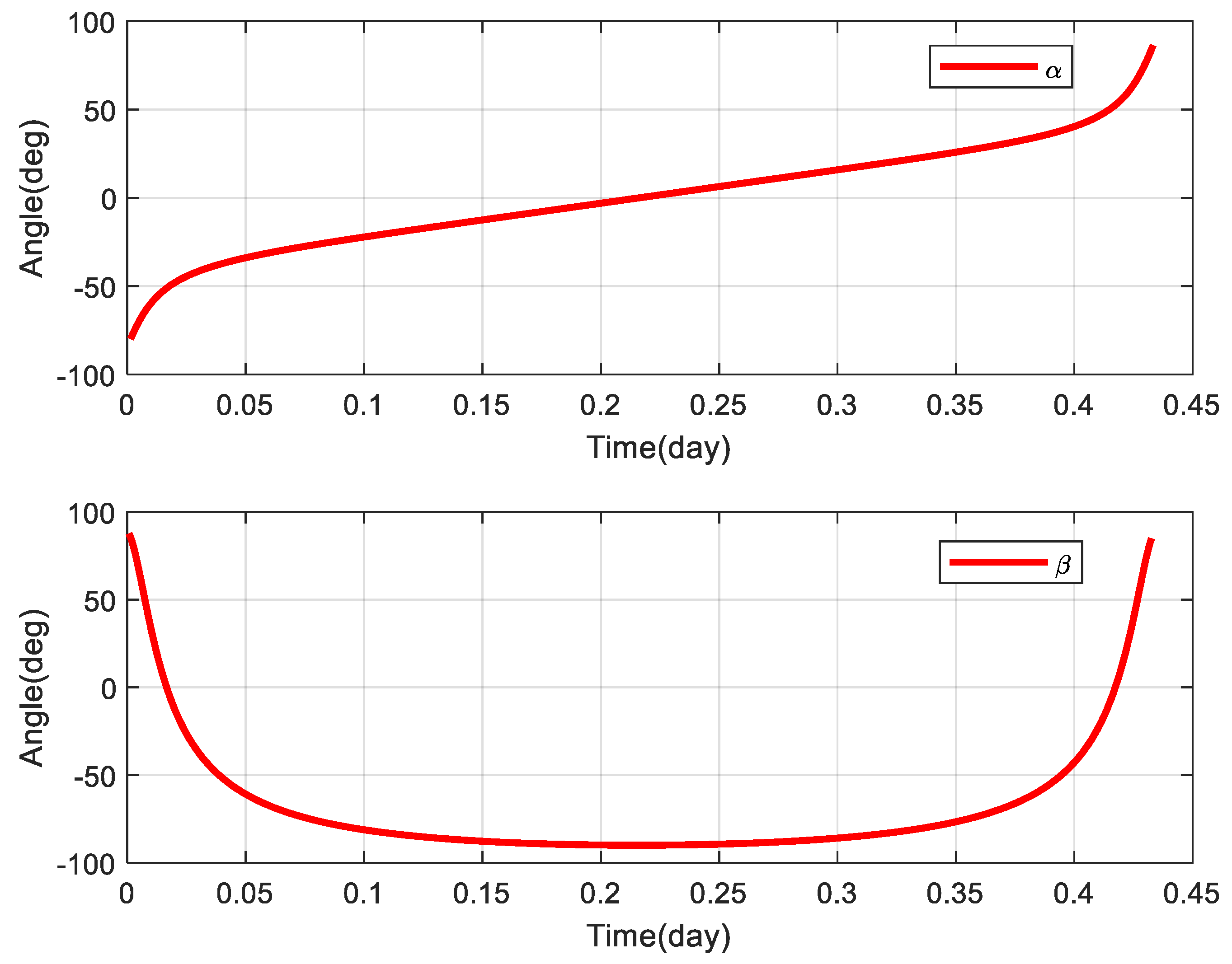
4.2.1. GTO-GEO Orbital Transfer Simulation Result and Discussion
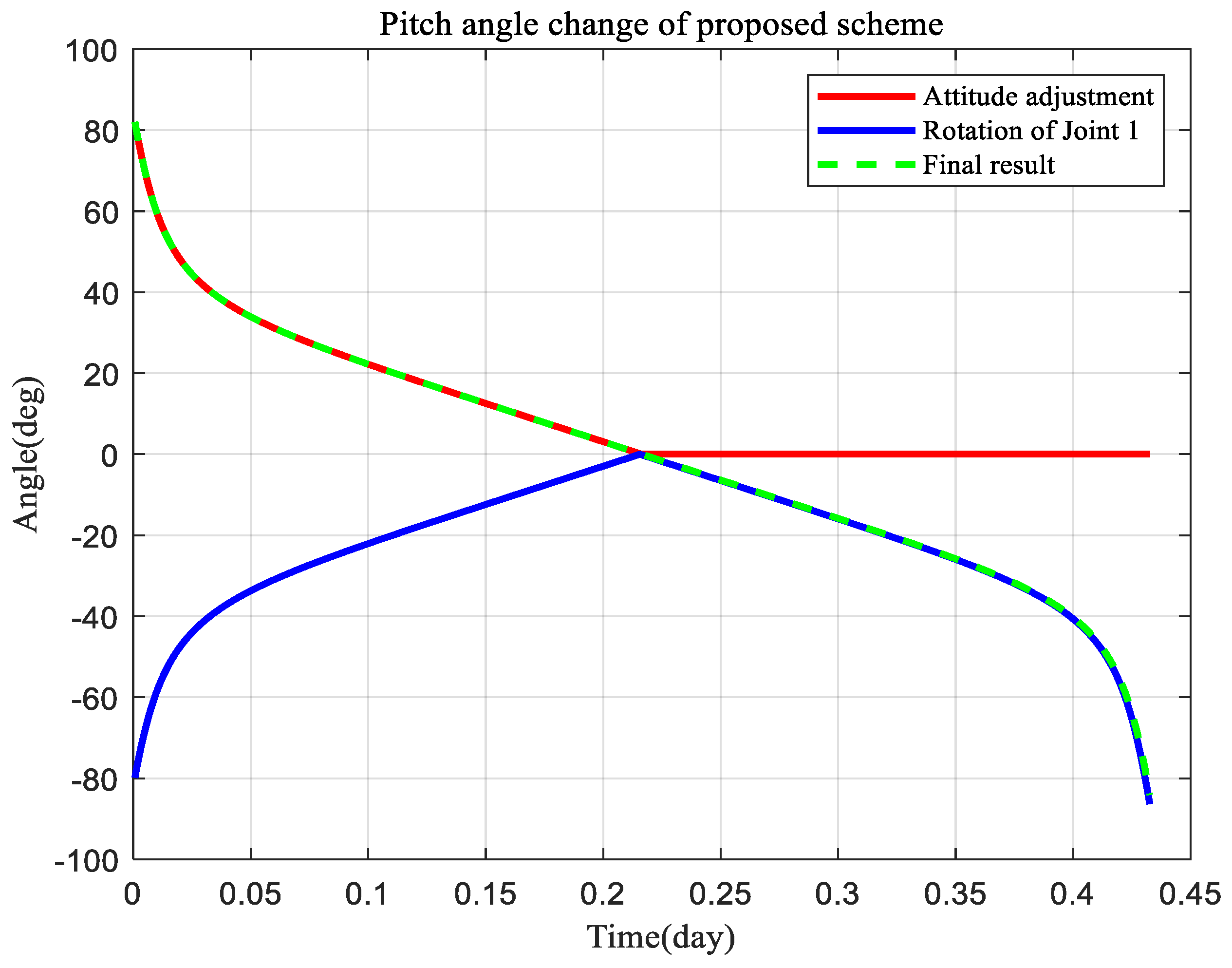
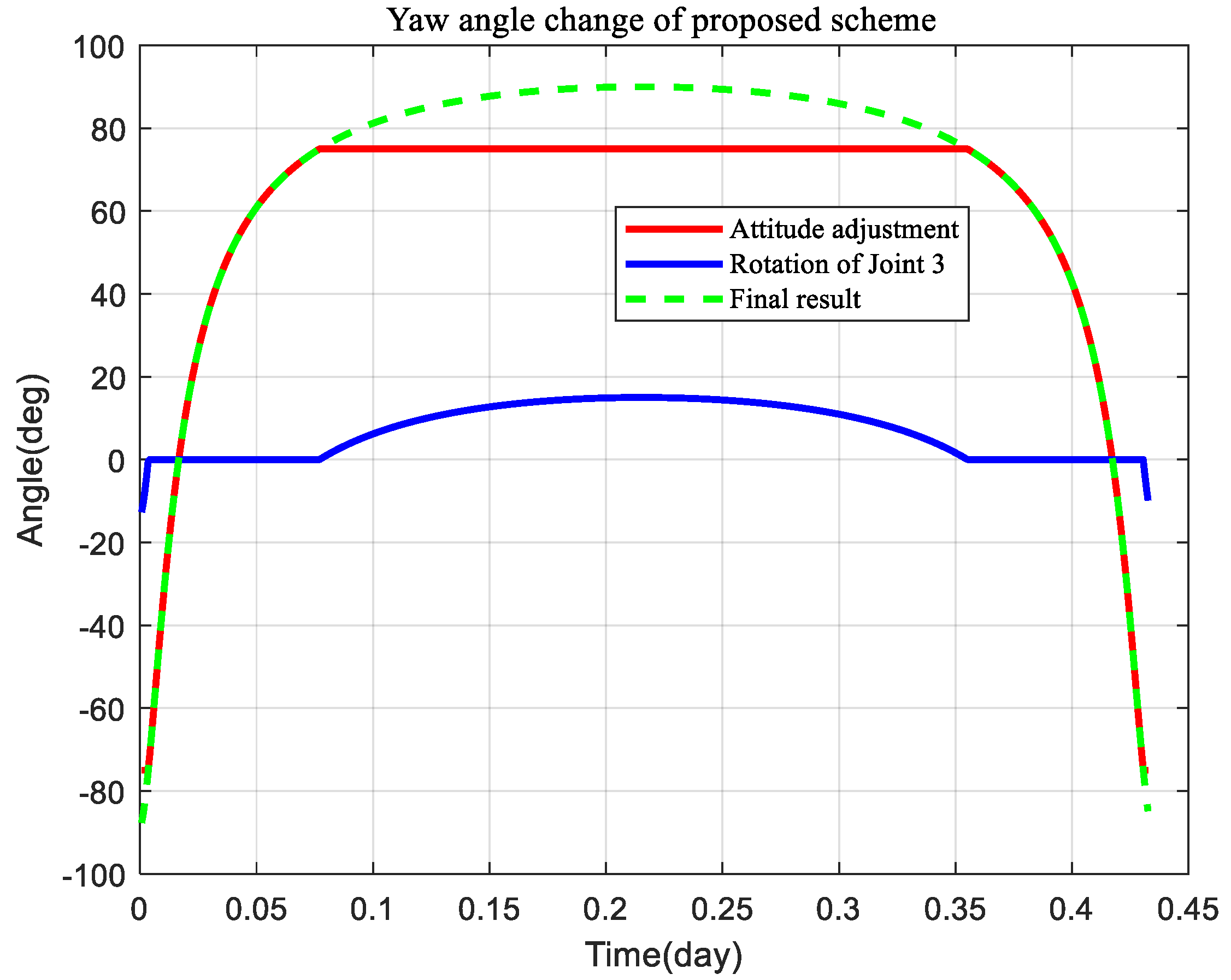
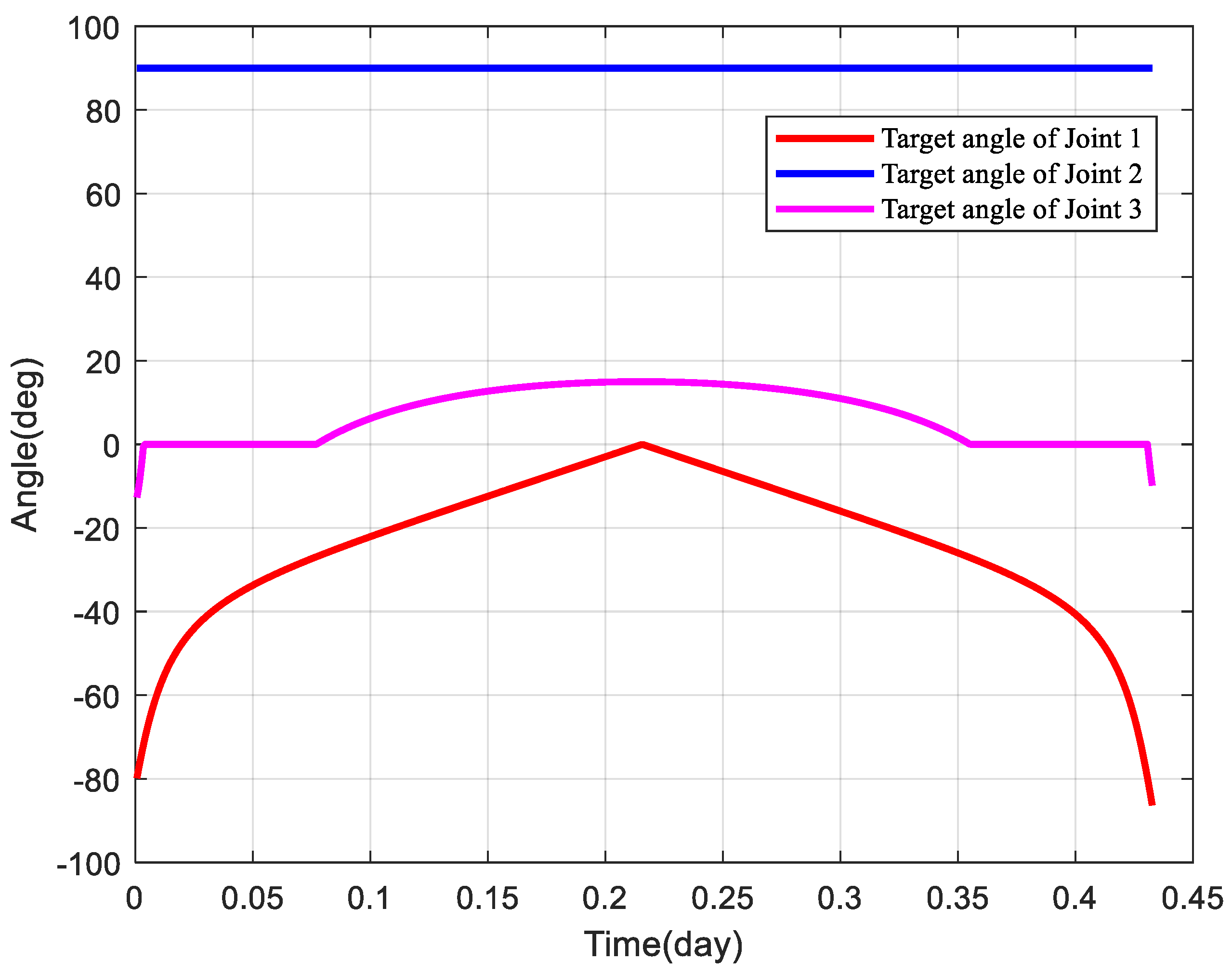
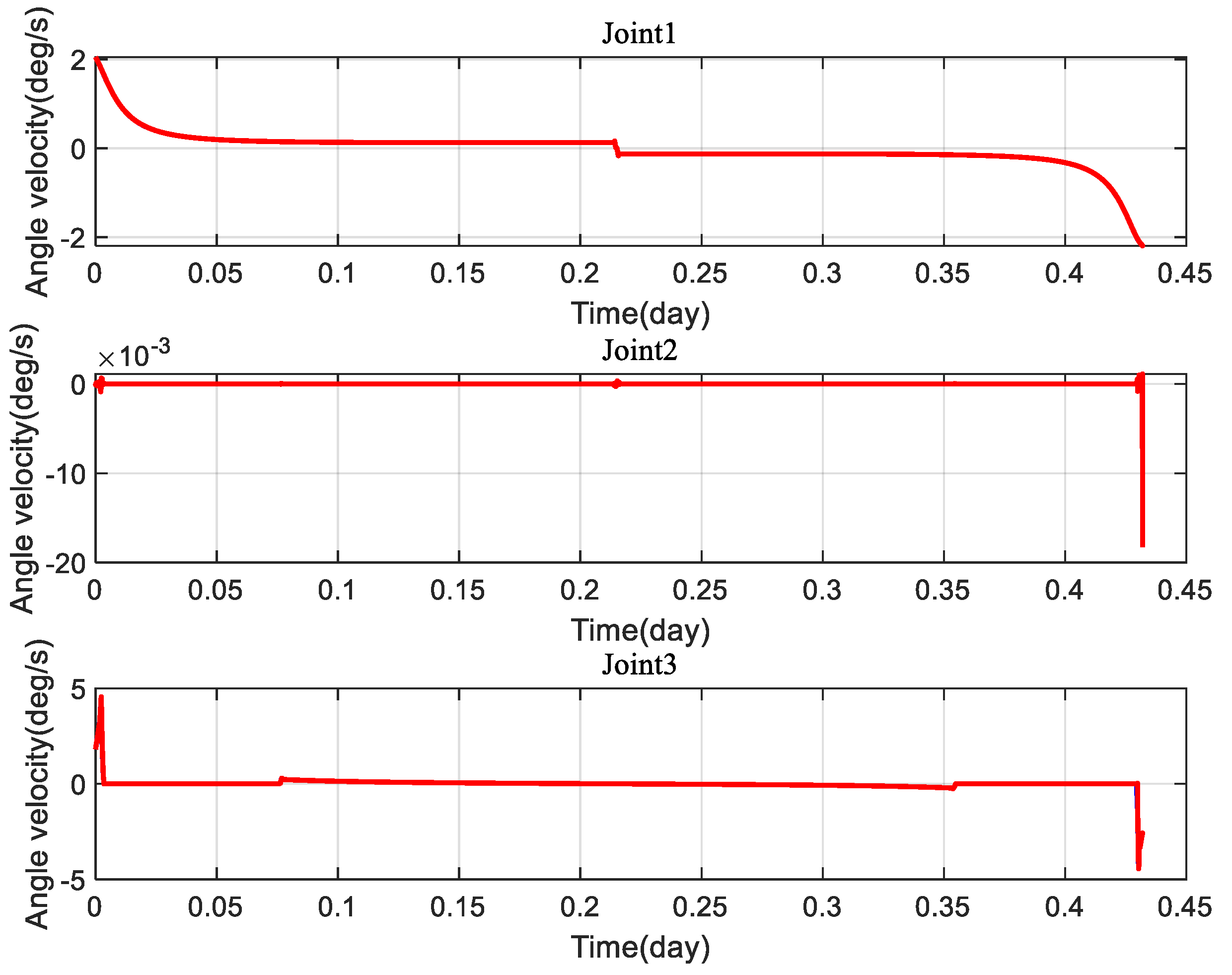
4.2.2. Gimbaled Thruster Boom Simulation Result and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lijun, Y.; Chunyang, L.; Wenshan, Z. North/South Station Keeping of the GEO Spacecrafts in Asymmetric Configuration by Electric Propulsion with Manipulator. Mathematics 2022, 10, 2340. [Google Scholar]
- Hu, Z.; Wang, M.; Yuan, J.G. Development and enlightenment of foreign all-EP satellite platforms. Spacecr. Environ. Eng. 2015, 32, 566–570. [Google Scholar]
- Giulio, C.; Kiyoshi, K.; Daisuke, N.C. Design and testing of additively manufactured high-efficiency resistojet on hydrogen propellant. Acta Astronaut. 2021, 181, 14–27. [Google Scholar]
- Wang, Z.; Grant, M.J. Minimum-fuel low-thrust transfers for spacecraft: A convex approach. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2274–2290. [Google Scholar] [CrossRef]
- Roth, M. Strategies for Geostationary Spacecraft Orbit SK Using Electrical Propulsion Only. Ph.D. Thesis, Czech Technical University, Prague, Czech Republic, 2020. [Google Scholar]
- Wang, Z.; Grant, M.J. Optimization of minimum-time low-thrust transfers using convex programming. J. Spacecr. Rocket. 2018, 55, 586–598. [Google Scholar] [CrossRef]
- Gazzino, C.; Louembet, C.; Arzelier, D.; Jozefowiez, N.; Losa, D.; Pittet, C.; Cerri, L. Interger Programming for Optimal Control of Geostationary SK of Low-thrust Satellites. IFAC-Pap. OnLine 2017, 50, 8169–8174. [Google Scholar] [CrossRef]
- Dalin, Y.; Bo, X.; Youtao, G. Optimal strategy for low-thrust spiral trajectories using Lyapunov-based guidance. Adv. Space Res. 2015, 56, 865–878. [Google Scholar] [CrossRef]
- Gazzino, C.; Arzelier, D.; Louembet, C.; Cerri, L.; Pittet, C.; Losa, D. Long-Term Electric-Propulsion Geostationary Station-Keeping via Integer Programming. J. Guid. Control Dyn. 2019, 42, 976–991. [Google Scholar] [CrossRef]
- Yang, D.; Xu, B.; Zhang, L. Optimal low-thrust spiral trajectories using Lyapunov-based guidance. Acta Astronaut. 2016, 126, 275–285. [Google Scholar] [CrossRef]
- Feuerbornl, S.A.; Neary, D.A. Finding a Way: Boeing’s All Electric Propulsion Spacecraft. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013; pp. 1–5. [Google Scholar]
- Li, C.; Xu, B.; Zhou, W.; Peng, Q. Geostationary Station-Keeping of Electric-Propulsion Satellite Equipped with Robotic Arms. Aerospace 2022, 9, 182. [Google Scholar] [CrossRef]
- Deremetz, M.; Grunwald, G.; Cavenago, F.; Roa, M.A.; De Stefano, M.; Mishra, H.; Reiner, M.; Govindaraj, S.; But, A.; Sanz Nieto, I.; et al. Concept of operations and preliminary design of a modular multi-arm robot using standard interconnects for on-orbit large assembly. In Proceedings of the 72nd International Astronautical Congress, Dubai, United Arab Emirates, 25 October 2021. [Google Scholar]
- Zhihong, J.; Cao, X.; Huang, X.; Li, H.; Ceccarelli, M. Progress and development trend of space intelligent robot technology. Space Sci. Technol. 2022, 2022, 11. [Google Scholar]
- Min, W.; Qiang, L.; Xingang, L.; Ran, A. Electric Thrusters Confifiguration Strategy Study on Station-Keeping and Momentum Dumping of GEO Satellite. In Proceedings of the 2019 5th International Conference on Control Science and Systems Engineering (ICCSSE), Shanghai, China, 14–16 August 2019; pp. 115–121. [Google Scholar]
- Uzo-Okoro, E.; Erkel, D.; Manandhar, P.; Dahl, M.; Kiley, E.; Cahoy, K.; De Weck, O.L. Optimization of On-Orbit Robotic Assembly of Small Satellites. ASCEND 2020, 2020, 4195. [Google Scholar]
- Sembély, X.; Wartelski, M.; Doubrère, P.; Deltour, B.; Cau, P.; Rochard, F. Design and Development of an Electric Propulsion Deployable Arm for Airbus Eurostar E3000 ComSat Platform. In Proceedings of the 35th International Electric Propulsion Conference, Atlanta, GA, USA, 8–12 October 2017; pp. 8–12. [Google Scholar]
- Liu, H.; Dongyu, L.; Zaian, J. Review and prospect of space manipulator technology. AAAS 2021, 42, 14. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J.; Zhao, S.; Qi, R.; Li, Y. Autonomous onboard estimation of mean orbital elements for geostationary electric-propulsion satellites. Aerosp. Sci. Technol. 2019, 94, 105369. [Google Scholar] [CrossRef]
- Liu, F.; Ye, L.; Liu, C.; Wang, J.; Yin, H. Micro-Thrust, Low-Fuel Consumption, and High-Precision East/West Station Keeping Control for GEO Satellites Based on Synovial Variable Structure Control. Mathematics 2023, 11, 705. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, S. Non-equatorial equilibrium points around an asteroid with gravitational orbit-attitude coupling perturbation. Astrodynamics 2020, 4, 1–16. [Google Scholar] [CrossRef]
- Yan’gang, L.; Zheng, Q. A decision support system for satellite layout integrating multi-objective optimization and multi-attribute decision making. J. Syst. Eng. Electron. 2019, 30, 535–544. [Google Scholar]
- Patiño, J.; Encalada-Dávila, Á.; Sampietro, J.; Tutivén, C.; Saldarriaga, C.; Kao, I. Damping Ratio Prediction for Redundant Cartesian Impedance-ControlledRobots Using Machine Learning Techniques. Mathematics 2023, 11, 1021. [Google Scholar] [CrossRef]
- Wang, H.; Liu, B.; Ping, X.; An, Q. Path Tracking Control for Autonomous Vehicles Based on an Improved MPC. IEEE Access 2019, 7, 161064–161073. [Google Scholar] [CrossRef]
- Caverly, R.; Di Cairano, S.; Weiss, A. Control Allocation and Quantization of a GEO Satellite with 4DOF Gimbaled Thruster Booms. In Proceedings of the AIAA Scitech 2020 Forum, Online, 24–28 August 2020. [Google Scholar]
- Kuai, Z. Research on GEO Satellite Orbit Maintenance and Orbit Transfer Strategy under Pulse and EP. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2017. [Google Scholar]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]





| Parameter | Value | |
|---|---|---|
| Initial orbit | Perigee height | 964 km |
| Apogee height | 35,741 km | |
| Orbital inclination | 20.8 deg | |
| Gimbaled thruster boom | Movement range of Joint 1 | −90~0 deg |
| Movement range of Joint 2 | +75~+105 deg | |
| Movement range of Joint 3 | −15~+15 deg | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, G.; Kong, X. Planning Allocation for GTO-GEO Transfer Spacecraft with Triple Orthogonal Gimbaled Thruster Boom. Mathematics 2023, 11, 2844. https://doi.org/10.3390/math11132844
Ma G, Kong X. Planning Allocation for GTO-GEO Transfer Spacecraft with Triple Orthogonal Gimbaled Thruster Boom. Mathematics. 2023; 11(13):2844. https://doi.org/10.3390/math11132844
Chicago/Turabian StyleMa, Guangfu, and Xianglong Kong. 2023. "Planning Allocation for GTO-GEO Transfer Spacecraft with Triple Orthogonal Gimbaled Thruster Boom" Mathematics 11, no. 13: 2844. https://doi.org/10.3390/math11132844
APA StyleMa, G., & Kong, X. (2023). Planning Allocation for GTO-GEO Transfer Spacecraft with Triple Orthogonal Gimbaled Thruster Boom. Mathematics, 11(13), 2844. https://doi.org/10.3390/math11132844










