Observer-Based Dynamic Event-Triggered Tracking Consensus for Switched Multi-Agent Systems

Abstract

This article discusses the event-triggered consensus problem for a switched multi-agent system (MASs) with switching topologies. An observer-based dynamic event-triggered (DET) controller with a discontinuous nonlinear term is designed to reduce arduous communication. With the designed approach, the error system can reach a tracking consensus. Then, a continuous observer-based DET protocol is created using the boundary layer method to prevent chattering effects. Moreover, by employing the Riccati equation and the switched Lyapunov function method, some sufficient criteria are put forward to guarantee the tracking consensus of the systems. The suggested observer-based DET protocol can also exclude the Zeno behavior. Finally, two examples verify the validity of the analysis.

1. Introduction

In recent decades, MASs have been widely studied in the engineering field such as spacecraft formation, sensor networks, mobile robots, and so on [1,2,3]. Particularly, the extensive application of the consensus control problems for MASs has attracted great interest among scholars [4]. To achieve system consensus, it is necessary to design effective control protocols or algorithms, so that each agent in MASs can continuously adjust its behavior based on the information sent by its neighbors.

Event-triggered control, as an effective control method, has attracted increasing attention in the past decade (see [5,6,7,8] and references therein). Unlike time-triggered control, which operates based on a fixed time schedule, event-triggered control adjusts system actions based on specific events or changes in the system’s state. It aims to activate control actions only when necessary, minimizing the utilization of system resources and improving efficiency. In the early work [9], the researchers introduced static event-triggered control into the study of MASs, which proved to be successful in extending the sampling period. After that, the static event-triggered control was combined with the observer. To name a few, a static event-triggered adaptive distributed observer was designed for studying the cooperative issue for heterogeneous linear MASs [10], and it was found that the rate of executing the operation in the processor can be enormously decreased. Recently, a data reduction and transmission method based on awareness is proposed to design asynchronous communication and event-triggered control scheme, which can avoid continuous communication between agents of both communication and control parties [11]. Different from the classical periodic sampling control [12], the above static event-triggered strategy can significantly prevent needless sampling and improve the utilization of restricted bandwidth resources. Nevertheless, when the threshold value in the triggering condition remains constant, some unnecessary communication is still going on. This results in a waste of sampling resources and computing resources. Thus, it is necessary to adjust the triggering threshold in the existing event-triggered strategy to further reduce the communication cost.

Considering the shortage of static event-triggered control, many scholars have studied the DET control method and reported corresponding results [13,14,15,16,17,18]. The core of this method is to introduce an auxiliary dynamic threshold in the triggering condition, so compared to the static threshold, the average time between events in the DET mechanism is longer. Therefore, it has the advantage of greatly reducing communication frequency in the implementation of the control process. For example, Ref. [13] provided a DET scheme to decrease the communication frequency. In detail, the total number of triggers determined by the DET strategy is less than the static one. Two independent DET strategies are designed to deal with the leader-following bounded consensus in MASs [14], which can avert frequent updates of the sensors and controllers simultaneously. Later, under the adaptive DET strategy, Ref. [15] extended the undirected graph to the directed graph and discussed the bounded consensus of MASs. In the present works on the DET method, most of them assume that the communication topology is fixed [14,15,17]. However, for most realistic circumstances, the fixed communication topologies are not adequate to characterize the interaction between agents. That is to say, the topologies may change in different time periods. In view of this, analysis of consensus for MASs with switching topologies is crucial, and substantial relevant systems (such as smart grid systems [19], general linear systems [20], and Euler–Lagrange systems [21]) have been reported.

It should be also pointed out that in some practical situations, many complex processes encompass switched modes, for example, traffic lights switch among different colors. Therefore, modeling each agent as a switched system is more general [22,23,24]. By introducing the idea of the switching method, a switching complex dynamic network describing a physical system more accurately is established. Recently, switched MASs with event-triggered control have drawn a large amount of attention [25,26,27,28,29,30,31,32]. For example, in [25], the event-triggered strategy is first used to investigate the tracking consensus of nonlinear switched MASs with unknown parameters, and an adaptive law is devised by utilizing the backstepping technique to analyze the unknown parameters. Ref. [27] discusses the security consensus problems for time-varying multi-agent systems with denial-of-service attacks and parameter uncertainty, updating the control input signal by adopting a new event-driven mechanism with a state-dependent threshold within a given limited range. A bumpless transfer control and event-triggered communication were discussed in [31] to handle the output consensus issue of a class of switched multi-agent systems. The cooperative output regulation for switched heterogeneous MASs under a switching strategy was proposed in [32]. The above references have proved that the consensus of switched MASs is affected by the subsystems and the switching rule. Moreover, in practical engineering applications, due to economic and technical limitations of measurement methods, it is difficult to obtain all state information, which makes implementing state feedback control challenging. The introduction of observers solves the contradiction between the performance superiority of state feedback and the physical difficulty of its realization. Thus, it is essential to consider observer-based control strategies for available measurement outputs. Unfortunately, the above literature [25,26,27,28,29,30,31,32] assumed that full state information can be obtained directly, and the control mechanisms only considered the static event-triggered mechanism. At present, there is little research on observer-based DET tracking consensus issues for switched MASs with a leader of nonzero control inputs, which inspired this research.

The above work inspired us to investigate tracking consensus for switched MASs where the leader system involves nonzero control inputs. In other words, we propose an observer-based DET protocol that includes a discontinuous nonlinear term and a continuous nonlinear term to ensure the stability of the switched MASs. The contributions are concluded below.

• Different from the existing results in [33,34,35] which focus on fixed network topology, this paper investigates the consensus for switched MASs with arbitrarily switching communication topologies.
• A more general observer-based DET consensus protocol with a variable threshold is provided, where the controller includes discontinuous function and continuous function. Compared with most relative works that handle the consensus of switched MASs adopting static event-triggered strategies [25,26,28,29], this paper can further reduce the expenses associated with system resource usage.
• Compared to the minimum switching law proposed in [30], this paper allows multiple modes of switching within an event interval, and the minimum dwell time of each subsystem is unlimited. The result obtained in this way is more general than the result in [30].

The rest of this paper is organized as follows. In Section 2, the preliminaries are described. Section 3 gives the tracking consensus criteria for switched MASs. In Section 4, some examples are shown to explain the validity of the provided approach. Section 5 concludes this paper.

Notations: $\mathbb{N}$ represents the set of natural numbers. ${\mathbb{R}}^n$ and ${\mathbb{R}}^{n\times n}$ are the n-dimensional Euclidean space and $n\times n$ real matrices, respectively. ${\lambda }_{max}(·)$ and ${\lambda }_{min}(·)$ are the maximal and minimal eigenvalues of a real matrix, respectively. $\parallel ·\parallel$ represents the Euclidean norm for vertices or matrices. The n-dimensional identity matrix is denoted as $I_n$. ⊗ stands for the Kronecker product.

2. Preliminaries

2.1. Graph Theory

Denote $\sigma :[0,\infty )\to \mathcal{S}$, where $\mathcal{S}=\{1,2,\cdots ,s\}$ is the switching signal. The switching instant sequence ${\left\{r_q\right\}}_{q=1}^{\infty }$, $q\in {\mathbb{Z}}^{+}$ satisfies $0=r_0<r_1<r_2<\cdots <r_q\to +\infty$. The interconnection topology among agents is described by an undigraph ${\widehat{\mathcal{G}}}_{\sigma \left(t\right)}=(\widehat{\mathcal{V}},{\widehat{\mathcal{E}}}_{\sigma \left(t\right)})$, where $\widehat{\mathcal{V}}=\{0,1,\cdots ,N\}$ represents the set of all agents. ${\mathcal{G}}_{\sigma \left(t\right)}=(\mathcal{V},{\mathcal{E}}_{\sigma \left(t\right)},{\mathcal{A}}_{\sigma \left(t\right)})$ stands for the induced subgraph of ${\widehat{\mathcal{G}}}_{\sigma \left(t\right)}$, where $\mathcal{V}=\{1,2,\cdots ,N\}$, ${\mathcal{E}}_{\sigma \left(t\right)}\subseteq \mathcal{V}\times \mathcal{V}$. ${\mathcal{A}}_{\sigma \left(t\right)}=\left[a_{vj}^{\sigma \left(t\right)}\right]\in {\mathbb{R}}^{N\times N}$ denotes the adjacency matrix of graph ${\mathcal{G}}_{\sigma \left(t\right)}$, where $a_{vj}^{\sigma \left(t\right)}$ is the weight of the edge $(j,v)$, and $a_{vj}^{\sigma \left(t\right)}=0\iff (j,v)\notin {\mathcal{E}}_{\sigma \left(t\right)}$ means agent v cannot receive any information from agent j, otherwise, $a_{vj}^{\sigma \left(t\right)}>0\iff (j,v)\in {\mathcal{E}}_{\sigma \left(t\right)}$. $a_{vj}^{\sigma \left(t\right)}=0\iff (j,v)\notin {\mathcal{E}}_{\sigma \left(t\right)}$, otherwise, $a_{vj}^{\sigma \left(t\right)}>0\iff (j,v)\in {\mathcal{E}}_{\sigma \left(t\right)}$. The Laplacian matrix ${\mathcal{L}}_{\sigma \left(t\right)}=\left[l_{vj}^{\sigma \left(t\right)}\right]\in {\mathbb{R}}^{N\times N}$ of a graph ${\mathcal{G}}_{\sigma \left(t\right)}$ is defined as $l_{vv}^{\sigma \left(t\right)}={\sum }_{j=1,j\ne v}^N{a}_{vj}^{\sigma \left(t\right)}$ and $l_{vj}^{\sigma \left(t\right)}=-a_{vj}^{\sigma \left(t\right)}$ with $v\ne j$. Define the matrix ${\mathcal{M}}_{\sigma \left(t\right)}=\mathrm{diag}\{m_1^{\sigma \left(t\right)},m_2^{\sigma \left(t\right)},\cdots ,m_N^{\sigma \left(t\right)}\}$ as the connection relationship between the followers and the leader. If the v-th follower can receive information from the leader, $m_v^{\sigma \left(t\right)}>0$, otherwise, $m_v^{\sigma \left(t\right)}=0$. Let ${\mathcal{H}}_{\sigma \left(t\right)}={\mathcal{L}}_{\sigma \left(t\right)}+{\mathcal{M}}_{\sigma \left(t\right)}$.

2.2. Problem Statement

Consider switched MASs containing N followers and one leader. The dynamics of the vth follower is expressed as

$$\begin{array}{cc}\hfill {\dot{z}}_v\left(t\right)=& F_{\sigma \left(t\right)}{z}_v\left(t\right)+E_{\sigma \left(t\right)}{u}_v\left(t\right),\hfill \\ \hfill y_v\left(t\right)=& C_{\sigma \left(t\right)}{z}_v\left(t\right),\hfill \end{array}$$

(1)

where $z_v\left(t\right)\in {\mathbb{R}}^n$ ($v=1,2,\cdots ,N$) represents the system state, $u_v\left(t\right)\in {\mathbb{R}}^m$ denotes the control input, and $y_v\left(t\right)\in {\mathbb{R}}^r$ is the sensor output of v-th agent. $F_{\sigma \left(t\right)}$, $E_{\sigma \left(t\right)}$, and $C_{\sigma \left(t\right)}$ are constant system matrices.

The leader’s dynamics is expressed as

$${\dot{z}}_0\left(t\right)=F_{\sigma \left(t\right)}{z}_0\left(t\right)+E_{\sigma \left(t\right)}{u}_0\left(t\right),$$

(2)

where $z_0\left(t\right)\in {\mathbb{R}}^n$ and $u_0\left(t\right)\in {\mathbb{R}}^m$ are the state and nonzero input, respectively. Suppose that $\parallel u_0\left(t\right)\parallel \le \epsilon$, where $\epsilon >0$.

To facilitate our major works, the following assumptions are presented.

Assumption 1. 

The pairs $(F_{\sigma \left(t\right)},E_{\sigma \left(t\right)})$ are stabilizable. That is, for given $Q_{\sigma \left(t\right)}>0$, ${\lambda }_0>0$, the Riccati equation

$$F_{\sigma \left(t\right)}^T{P}_{\sigma \left(t\right)}+P_{\sigma \left(t\right)}{F}_{\sigma \left(t\right)}-{\lambda }_{\sigma \left(t\right)}{P}_{\sigma \left(t\right)}{E}_{\sigma \left(t\right)}{E}_{\sigma \left(t\right)}^T{P}_{\sigma \left(t\right)}+Q_{\sigma \left(t\right)}=0,$$

has a solution $P_{\sigma \left(t\right)}>0$. ${\lambda }_{\sigma \left(t\right)}={\lambda }_{max}\left({\mathcal{H}}_{\sigma \left(t\right)}\right)$.

Assumption 2. 

The pairs $(F_{\sigma \left(t\right)},C_{\sigma \left(t\right)})$ are observable.

Assumption 3. 

${\widehat{\mathcal{G}}}_{\sigma \left(t\right)}$ is connected, and at least one follower can obtain information from the leader.

To facilitate the discussion in next section, we introduce the following definition.

Definition 1 

([36]). For all $t>r_0=0$, $N_{\sigma }[0,t)$ denotes number of switches of $\sigma \left(t\right)$ within the interval $[0,t)$. If

$$\begin{array}{c}\hfill N_{\sigma }[0,t)\le N_0+\frac{t}{{\tau }_a}\end{array}$$

holds for positive numbers $N_0$ and ${\tau }_a$, then $N_0$ is called the chatter bound and ${\tau }_a$ is the average dwell time (ADT).

The following lemma is also useful for the analysis.

Lemma 1 

([37]). If the ADT ${\tau }_a>\frac{ln\mu }{\varrho }$ and $W_i(·)\ge 0$ satisfies

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{W}}_i\left(t\right)\le -\vartheta W_i\left(t\right)+\delta ,t\in [r_q,r_{q+1})\hfill \\ W_i\left(r_q\right)\le \mu W_i\left(r_q^{-}\right),q=1,2,\cdots \hfill \end{array}\right.\end{array}$$

then $W_i\left(t\right)$ is bounded and converges into the residual set:

$$\begin{array}{c}\hfill \mathcal{B}=\left\{W_i:W_i\le \frac{\delta {\mu }^{N_0}}{\varrho -\frac{ln\mu }{{\tau }_a}},i\in \mathcal{S}\right\},\end{array}$$

where $\varrho >0$, $\mu \ge 1$, $\vartheta >0$, $\delta \ge 0$, $W_i\left(r_q^{-}\right)={lim}_{t\to r_q^{-}}{W}_i\left(t\right)$.

In engineering applications, the state information of the system (1) may not be fully achievable due to implementation costs. Therefore, utilizing an observer-based approach, the following state observer is designed:

$$\begin{array}{cc}\hfill {\dot{\widehat{z}}}_v\left(t\right)=& F_{\sigma \left(t\right)}{\widehat{z}}_v\left(t\right)+E_{\sigma \left(t\right)}{u}_v\left(t\right)+G_{\sigma \left(t\right)}(y_v\left(t\right)-{\widehat{y}}_v\left(t\right)),\hfill \end{array}$$

(3)

where ${\widehat{z}}_v\left(t\right)$ denotes the observer state vector, $G_{\sigma \left(t\right)}\in {\mathbb{R}}^{n\times r}$ denotes the observer gain to be determined later.

In the following, the DET control schemes are proposed to reduce communication costs. Define $e_v^{t_k}\left(t\right)={\widehat{z}}_v\left(t\right)-{\widehat{z}}_v\left(t_k\right)$ as the measurement error. The trigger sequence $\{t_k,k\in \mathbb{N}\}$ is generated by

$$\begin{array}{c}\hfill t_{k+1}=inf\{t>t_k:\theta \parallel (I\otimes E_{\sigma \left(t\right)}^T{P}_{\sigma \left(t\right)})e_{t_k}\left(t\right){\parallel }^2\ge \eta \left(t\right)\},\end{array}$$

(4)

where $\theta >0$, $e_{t_k}\left(t\right)={[{\left(e_1^{t_k}\left(t\right)\right)}^T,{\left(e_2^{t_k}\left(t\right)\right)}^T,\cdots ,{\left(e_N^{t_k}\left(t\right)\right)}^T]}^T$, $\eta \left(t\right)$ is a variable, which satisfies

$$\dot{\eta }\left(t\right)=-\rho \eta \left(t\right)-\gamma {\parallel (I\otimes E_{\sigma \left(t\right)}^T{P}_{\sigma \left(t\right)})e_{t_k}\left(t\right)\parallel }^2,$$

where $\rho >0$, $\gamma >0$.

Next, we will give an important lemma to ensure that it remains Zeno-free.

Lemma 2 

([16]). For prescribed scalars $\eta \left(0\right)>0$, $\rho >0$, $\theta >0$ and $\gamma >0$, $\eta \left(t\right)$ meets

$$\eta \left(t\right)>\eta \left(0\right)e^{-(\rho +\frac{\gamma }{\theta })t}>0.$$

Let ${\overline{z}}_v\left(t\right)={\widehat{z}}_v\left(t_k\right),t\in [t_k,t_{k+1})$. For each follower, the following event-based tracking control protocol is designed:

$$\begin{array}{cc}\hfill u_v\left(t\right)=& K_{\sigma \left(t\right)}\left[\sum _{j=1}^N{a}_{vj}^{\sigma \left(t\right)}({\overline{z}}_j\left(t\right)-{\overline{z}}_v\left(t\right))+m_v^{\sigma \left(t\right)}(z_0\left(t\right)-{\overline{z}}_v\left(t\right))\right]-\pi {\psi }_v\left(K_{\sigma \left(t\right)}{\tilde{e}}_v\left(t\right)\right),\hfill \end{array}$$

(5)

where $K_{\sigma \left(t\right)}=E_{\sigma \left(t\right)}^T{P}_{\sigma \left(t\right)}\in {\mathbb{R}}^{m\times n}$ represents the feedback gain matrix, $\pi >0$. ${\tilde{e}}_v\left(t\right)$ and nonlinear function ${\psi }_v(·):{\mathbb{R}}^m\to {\mathbb{R}}^m$ will be designed later.

Remark 1. 

Unlike the classical time-triggered control mechanism that periodically samples system states, our study introduces a DET control scheme. This scheme determines the interval $[t_k,t_{k+1})$ based on specific triggering conditions proposed in our research.

Remark 2. 

It is important to remember that some crucial results for event-triggered control have already been published [8,9,10]. These results are different from our DET control scheme in two ways. First, the insertion of the dynamic threshold $\eta \left(t\right)$ makes DET conditions (4) dynamic for the measurement error. Second, this research takes switched systems into account as opposed to the current DET control approaches for deterministic systems.

According to (1), (3) and (5), we may obtain

$$\begin{array}{cc}\hfill {\dot{z}}_v\left(t\right)=& F_{\sigma \left(t\right)}{z}_v\left(t\right)+E_{\sigma \left(t\right)}{K}_{\sigma \left(t\right)}[\sum _{j=1}^N{a}_{vj}^{\sigma \left(t\right)}({\overline{z}}_j\left(t\right)-{\overline{z}}_v\left(t\right))\hfill \\ \hfill & +m_v^{\sigma \left(t\right)}(z_0\left(t\right)-{\overline{z}}_v\left(t\right))]-\gamma E_{\sigma \left(t\right)}{\psi }_v\left(K_{\sigma \left(t\right)}{\tilde{e}}_v\left(t\right)\right).\hfill \\ \hfill {\dot{\widehat{z}}}_v\left(t\right)=& F_{\sigma \left(t\right)}{\widehat{z}}_v\left(t\right)+E_{\sigma \left(t\right)}{K}_{\sigma \left(t\right)}[\sum _{j=1}^N{a}_{vj}^{\sigma \left(t\right)}({\widehat{z}}_j\left(t\right)-e_j^{t_k}\left(t\right)\hfill \\ \hfill & -{\widehat{z}}_v\left(t\right)+e_v^{t_k}\left(t\right))+m_v^{\sigma \left(t\right)}(z_0\left(t\right)-{\widehat{z}}_v\left(t\right)+e_v^{t_k}\left(t\right))]\hfill \\ \hfill & -\gamma E_{\sigma \left(t\right)}{\psi }_v\left(K_{\sigma \left(t\right)}{\tilde{e}}_v\left(t\right)\right)+G_{\sigma \left(t\right)}{C}_{\sigma \left(t\right)}{\widehat{e}}_v\left(t\right).\hfill \end{array}$$

Let ${\tilde{e}}_v\left(t\right)={\widehat{z}}_v\left(t\right)-z_0\left(t\right)$ as the tracking error and ${\widehat{e}}_v\left(t\right)=z_v\left(t\right)-{\widehat{z}}_v\left(t\right)$ as the observation error. Based on the above discussion, it is easy to get

$$\begin{array}{cc}\hfill {\dot{\tilde{e}}}_v\left(t\right)=& F_{\sigma \left(t\right)}{\tilde{e}}_v\left(t\right)+E_{\sigma \left(t\right)}{K}_{\sigma \left(t\right)}\left[\sum _{j=1}^N{a}_{vj}^{\sigma \left(t\right)}({\tilde{e}}_j\left(t\right)-e_j^{t_k}\left(t\right)-{\tilde{e}}_v\left(t\right)+e_v^{t_k}\left(t\right))-m_v^{\sigma \left(t\right)}({\tilde{e}}_v\left(t\right)-e_v^{t_k}\left(t\right))\right]\hfill \\ \hfill & -\gamma E_{\sigma \left(t\right)}{\psi }_v\left(K_{\sigma \left(t\right)}{\tilde{e}}_v\left(t\right)\right)-E_{\sigma \left(t\right)}{u}_0\left(t\right)+G_{\sigma \left(t\right)}{C}_{\sigma \left(t\right)}{\widehat{e}}_v\left(t\right).\hfill \\ \hfill {\dot{\widehat{e}}}_v\left(t\right)=& (F_{\sigma \left(t\right)}-G_{\sigma \left(t\right)}{C}_{\sigma \left(t\right)}){\widehat{e}}_v\left(t\right).\hfill \end{array}$$

Incorporating the Kronecker product, the above error systems are further characterized as compact representation

$$\begin{array}{cc}\hfill \dot{\tilde{e}}\left(t\right)=& (I\otimes F_{\sigma \left(t\right)}-{\mathcal{H}}_{\sigma \left(t\right)}\otimes E_{\sigma \left(t\right)}{K}_{\sigma \left(t\right)})\tilde{e}\left(t\right)+({\mathcal{H}}_{\sigma \left(t\right)}\otimes E_{\sigma \left(t\right)}{K}_{\sigma \left(t\right)})e_{t_k}\left(t\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & -\gamma (I\otimes E_{\sigma \left(t\right)})\Psi \left[\tilde{e}\left(t\right)\right]-\left[{\mathbf{1}}_N\otimes E_{\sigma \left(t\right)}{u}_0\left(t\right)\right]+(I\otimes G_{\sigma \left(t\right)}{C}_{\sigma \left(t\right)})\widehat{e}\left(t\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \dot{\widehat{e}}\left(t\right)=& \left[I\otimes (F_{\sigma \left(t\right)}-G_{\sigma \left(t\right)}{C}_{\sigma \left(t\right)})\right]\widehat{e}\left(t\right),\hfill \end{array}$$

(7)

where

$$\begin{array}{cc}\hfill & \tilde{e}\left(t\right)={[{\tilde{e}}_1^T\left(t\right),{\tilde{e}}_2^T\left(t\right),\cdots ,{\tilde{e}}_N^T\left(t\right)]}^T,\widehat{e}\left(t\right)={[{\widehat{e}}_1^T\left(t\right),{\widehat{e}}_2^T\left(t\right),\cdots ,{\widehat{e}}_N^T\left(t\right)]}^T,\hfill \\ \hfill & \Psi \left[\tilde{e}\left(t\right)\right]={[{\psi }_1{\left(K_{\sigma \left(t\right)}{\tilde{e}}_1\left(t\right)\right)}^T,{\psi }_2{\left(K_{\sigma \left(t\right)}{\tilde{e}}_2\left(t\right)\right)}^T,\cdots ,{\psi }_N{\left(K_{\sigma \left(t\right)}{\tilde{e}}_N\left(t\right)\right)}^T]}^T.\hfill \end{array}$$

The tracking consensus problem of the switched MASs (1) and (2) has been converted to the stability of the corresponding error systems (6) and (7). By providing the system formula, we will introduce the main results in the next section.

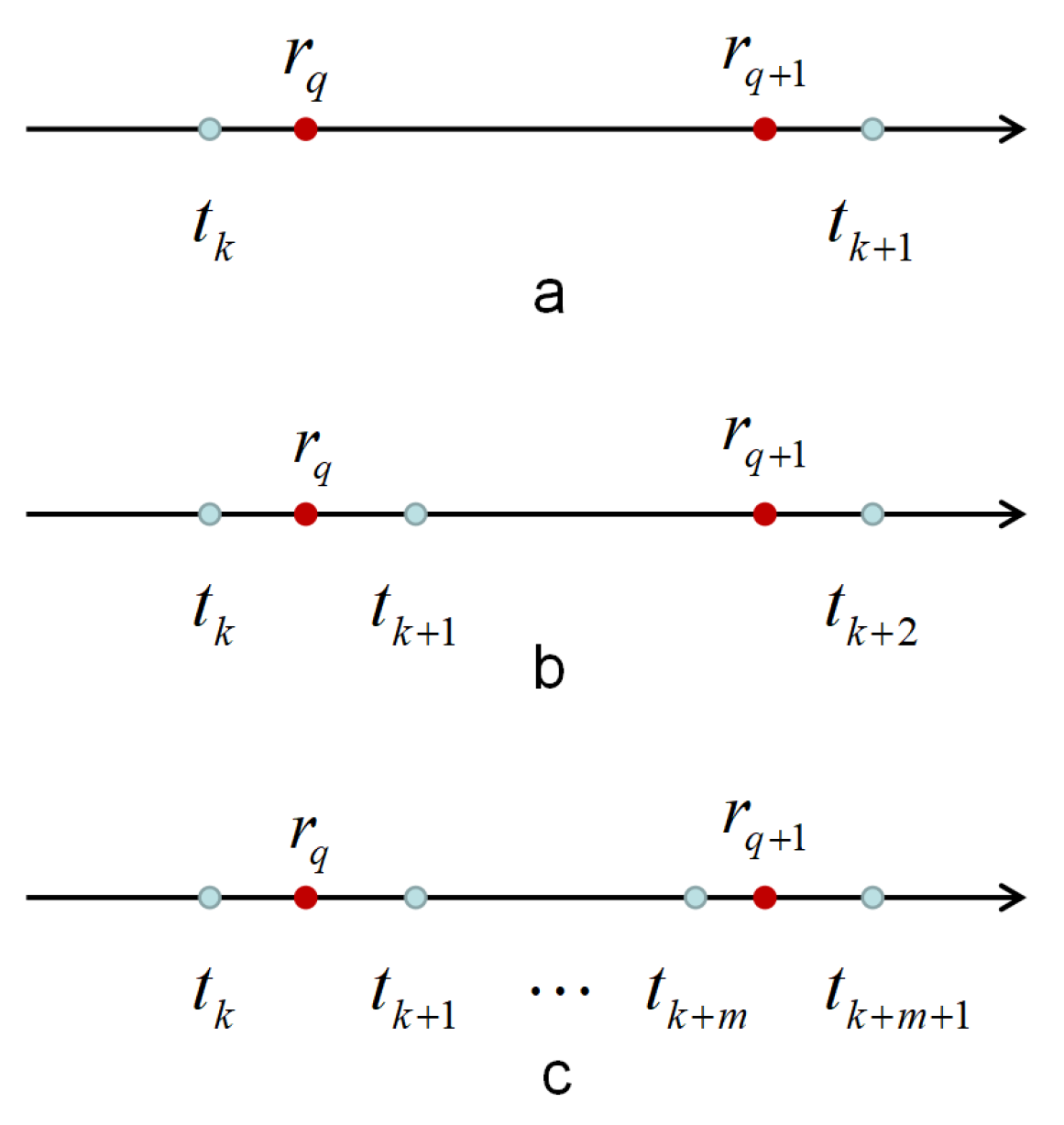
3. Main Results

The major works that appeared are twofold. In Section 3.1, the DET protocol with a discontinuous term ${\psi }_v(·)$ is considered. Under the proposed DET protocol, the Zeno behavior will be eliminated. On the other hand, a continuous observer-based DET protocol is designed by using the boundary layer method in Section 3.2.

3.1. DET Protocol with Discontinuous Term ${\psi }_v(·)$

Define the nonlinear function ${\psi }_v(·)$ as

$$\begin{array}{c}\hfill {\psi }_v\left({\varpi }_v\right)=\left\{\begin{array}{c}\frac{{\varpi }_v}{\parallel {\varpi }_v\parallel },\parallel {\varpi }_v\parallel >0\hfill \\ {\mathbf{0}}_m,\parallel {\varpi }_v\parallel =0\hfill \end{array}\right.{\varpi }_v\in {\mathbb{R}}^m.\end{array}$$

(8)

In what follows, we put forward an algorithm (Algorithm 1) to design the nonsmooth DET protocol.

Algorithm 1 An algorithm to design the nonsmooth DET protocol

If Assumptions 1–3 hold, the DET protocol can be taken into consideration in the following steps. For any $i,\in \mathcal{S}$. Choose $Q_i>0$, $K_i=-E_i{P}_i^T$, the Riccati equation: $$F_i^T{P}_i+P_i{F}_i-{\lambda }_i{P}_i{E}_i{E}_i^T{P}_i+Q_i=0$$ has a solution $P_i>0$. Choose the feedback matrix $G_i$, such that $F_i-G_i{C}_i$ is Huriwitz, then there exists a $R_i>0$, such that $$R_i(F_i-G_i{C}_i)+{(F_i-G_i{C}_i)}^T{R}_i+{\omega }_{i}I=0,$$ where ${\omega }_i$ is a positive constant. Choose positive constants $\gamma$, $\theta$, $\rho$, $\varrho$, $\epsilon$, ${\tau }_a$ and $\mu >1$, such that $$Q_i<\mu Q_j,P_i<\mu P_j,{\tau }_a>\frac{ln\mu }{\varrho },{\lambda }_0>\gamma >\epsilon ,\rho -\frac{{\lambda }_0-\gamma }{\theta }>0.$$

Theorem 1. 

If Assumptions 1–3 hold, under the event-based tracking control protocols (5) with the DET condition (4), and Algorithm 1, then systems (6) and (7) can asymptotically approach zero and the switched MASs (1) can track the leader (2).

Proof. 

We introduce the following Lyapunov function:

$$\begin{array}{c}\hfill V_{\sigma \left(t\right)}\left(t\right)={\tilde{e}}^T\left(t\right)(I\otimes P_{\sigma \left(t\right)})\tilde{e}\left(t\right)+{\varsigma }_{\sigma \left(t\right)}{\widehat{e}}^T\left(t\right)(I\otimes R_{\sigma \left(t\right)})\widehat{e}\left(t\right)\end{array}$$

and

$$\begin{array}{c}\hfill W_{\sigma \left(t\right)}\left(t\right)=V_{\sigma \left(t\right)}\left(t\right)+\eta \left(t\right),\end{array}$$

(9)

where ${\varsigma }_{\sigma \left(t\right)}$ will be given later.

Assume $\sigma \left(t\right)=i$ for $t\in [r_q,r_{q+1})$. According to the above discussion, the stability will be analyzed from the following two cases.

Case 1. If there is no trigger moment in the interval $[r_q,r_{q+1})$, i.e., $t_k\le r_q<r_{q+1}\le t_{k+1}$, The DET condition is not satisfied, and the last sampling system state is maintained. Define $\zeta \left(t\right)$ as

$$\begin{array}{c}\hfill \zeta \left(t\right)=e_{t_k}\left(t\right),t\in [r_q,r_{q+1}).\end{array}$$

Calculating the derivative of $V_i(\tilde{e}\left(t\right),\widehat{e}\left(t\right))$ along with (6) and (7) yields

$$\begin{array}{cc}\hfill {\dot{V}}_i\left(t\right)=& {\tilde{e}}^T\left(t\right)[I\otimes (P_i{F}_i+F_i^T{P}_i)]\tilde{e}\left(t\right)-2{\tilde{e}}^T\left(t\right)({\mathcal{H}}_i\otimes P_i{E}_i{E}_i^T{P}_i)\tilde{e}\left(t\right)\hfill \\ \hfill & +2{\tilde{e}}^T\left(t\right)({\mathcal{H}}_i\otimes P_i{E}_i{E}_i^T{P}_i)\zeta \left(t\right)-2{\tilde{e}}^T\left(t\right)({\mathbf{1}}_N\otimes P_i{E}_i)u_0\left(t\right)\hfill \\ \hfill & -2\gamma {\tilde{e}}^T\left(t\right)(I\otimes P_i{E}_i)\Psi \left[\tilde{e}\left(t\right)\right]+2{\tilde{e}}^T\left(t\right)(I\otimes P_i{G}_i{C}_i)\widehat{e}\left(t\right)\hfill \\ \hfill & +{\varsigma }_i{\widehat{e}}^T\left(t\right)\left[I\otimes [R_i(F_i-G_i{C}_i)+{(F_i-G_i{C}_i)}^T{R}_i]\right]\widehat{e}\left(t\right).\hfill \end{array}$$

(10)

By virtue of the Cauchy inequality, we can obtain

$$\begin{array}{c}\hfill 2{\tilde{e}}^T\left(t\right)({\mathcal{H}}_i\otimes P_i{E}_i{E}_i^T{P}_i)e_{ET}\left(t\right)\le {\tilde{e}}^T\left(t\right)({\mathcal{H}}_i\otimes P_i{E}_i{E}_i^T{P}_i)\tilde{e}\left(t\right)+{\zeta }^T\left(t\right)({\mathcal{H}}_i\otimes P_i{E}_i{E}_i^T{P}_i)\zeta \left(t\right).\end{array}$$

(11)

using the Young’s inequality gives

$$\begin{array}{c}\hfill 2{\tilde{e}}^T\left(t\right)(I\otimes P_i{G}_i{C}_i)\widehat{e}\left(t\right)\le \frac{1}{2}{\tilde{e}}^T\left(t\right)(I\otimes Q_i)\tilde{e}\left(t\right)+\frac{\parallel P_i{G}_i{C}_i{\parallel }^2}{{\lambda }_{min}\left(Q_i\right)}{\widehat{e}}^T\left(t\right)\widehat{e}\left(t\right).\end{array}$$

(12)

According to the fact $x^{T}y\le \parallel x\parallel \parallel y\parallel$, it is easy to obtain

$$\begin{array}{cc}\hfill -2{\tilde{e}}^T\left(t\right)({\mathbf{1}}_N\otimes P_i{E}_i)u_0\left(t\right)& =-2\sum _{v=1}^N{\tilde{e}}_v^T\left(t\right)P_i{E}_i{u}_0\left(t\right)\hfill \\ \hfill & \le 2\sum _{v=1}^N\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel \parallel u_0\left(t\right)\parallel \hfill \\ \hfill & \le 2\epsilon \sum _{v=1}^N\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel .\hfill \end{array}$$

(13)

Then, from (8), one has

$$\begin{array}{cc}\hfill -2\gamma {\tilde{e}}^T\left(t\right)(I\otimes P_i{E}_i)\Psi \left[\tilde{e}\left(t\right)\right]& =-2\gamma \sum _{v=1}^N{\tilde{e}}_v^T\left(t\right)P_i{E}_i{\psi }_i\left[E_i^T{P}_i{\tilde{e}}_v\left(t\right)\right]\hfill \\ \hfill & =-2\gamma \sum _{v=1}^N{\left[E_i^T{P}_i{\tilde{e}}_v\left(t\right)\right]}^T\frac{E_i^T{P}_i{\tilde{e}}_v\left(t\right)}{\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel }\hfill \\ \hfill & =-2\gamma \sum _{v=1}^N\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel .\hfill \end{array}$$

(14)

Since $F_i-G_i{C}_i$ is Hurwitz, it is well known that there exists a $R_i>0$ such that $R_i(F_i-G_i{C}_i)+{(F_i-G_i{C}_i)}^T{R}_i+{\omega }_{i}I=0$, where ${\omega }_i>0$. Then we can obtain

$$\begin{array}{cc}\hfill & {\widehat{e}}^T\left(t\right)\left[I\otimes [R_i(F_i-G_i{C}_i)+{(F_i-G_i{C}_i)}^T{R}_i]\right]\widehat{e}\left(t\right)\le -{\omega }_i{\widehat{e}}^T\left(t\right)\widehat{e}\left(t\right).\hfill \end{array}$$

(15)

Let ${\varsigma }_i=\frac{2\parallel P_i{G}_i{C}_i{\parallel }^2}{{\omega }_i{\lambda }_{min}\left(Q_i\right)}$, substituting (11)–(15) into (10), it yields that

$$\begin{array}{cc}\hfill {\dot{V}}_i\left(t\right)\le & {\tilde{e}}^T\left(t\right)\left[I\otimes (P_i{F}_i+F_i^T{P}_i-{\lambda }_i{P}_i{E}_i{E}_i^T{P}_i\right]\tilde{e}\left(t\right)+\frac{1}{2}{\tilde{e}}^T\left(t\right)(I\otimes Q_i)\tilde{e}\left(t\right)\hfill \\ \hfill & +\frac{\parallel P_i{G}_i{C}_i{\parallel }^2}{{\lambda }_{min}\left(Q_i\right)}{\widehat{e}}^T\left(t\right)\widehat{e}\left(t\right)+e_{ET}^T\left(t\right)({\mathcal{H}}_i\otimes P_i{E}_i{E}_i^T{P}_i)e_{ET}\left(t\right)\hfill \\ \hfill & -2\frac{\parallel P_i{G}_i{C}_i{\parallel }^2}{{\lambda }_{min}\left(Q_i\right)}{\widehat{e}}^T\left(t\right)\widehat{e}\left(t\right)+2\epsilon \sum _{v=1}^N\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel -2\gamma \sum _{v=1}^N\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel .\hfill \end{array}$$

(16)

From the DET condition (4), for all $t\in [0,+\infty )$

$${\zeta }^T\left(t\right)(I\otimes P_i{E}_i{E}_i^T{P}_i)\zeta \left(t\right)\le \frac{\eta \left(t\right)}{\theta }.$$

then, by using $\gamma \ge \epsilon$ and Assumption 1, one has

$$\begin{array}{cc}\hfill {\dot{W}}_i\left(t\right)\le & -\frac{1}{2}{\tilde{e}}^T\left(t\right)(I\otimes Q_i)\tilde{e}\left(t\right)-\frac{\parallel P_i{G}_i{C}_i{\parallel }^2}{{\lambda }_{min}\left(Q_i\right)}{\widehat{e}}^T\left(t\right)\widehat{e}\left(t\right)\hfill \\ \hfill & +{\zeta }^T\left(t\right)({\mathcal{H}}_i\otimes P_i{E}_i{E}_i^T{P}_i)\zeta \left(t\right)-\rho \eta \left(t\right)-\gamma {\zeta }^T\left(t\right)(I\otimes P_i{E}_i{E}_i^T{P}_i)\zeta \left(t\right)\hfill \\ \hfill \le & -{\alpha }_{1i}{\tilde{e}}^T\left(t\right)(I\otimes P_i)\tilde{e}\left(t\right)-{\alpha }_3\eta \left(t\right)-{\alpha }_{2i}\frac{2\parallel P_i{G}_i{C}_i{\parallel }^2}{{\omega }_i{\lambda }_{min}\left(R_i\right)}{\widehat{e}}^T\left(t\right)\widehat{e}\left(t\right)\hfill \\ \hfill \le & -\varrho W_i\left(t\right),\hfill \end{array}$$

(17)

where ${\alpha }_{1i}=\frac{{\lambda }_{min(I_N\otimes Q_i)}}{{\lambda }_{max}\left(P_i\right)}$, ${\alpha }_{2i}=\frac{2}{{\lambda }_{max}(I_N\otimes R_i)}$, ${\alpha }_{3i}=\rho -\frac{{\lambda }_i-\gamma }{\theta }$ and $\varrho ={min}_{i\in \mathcal{S}}\{{\alpha }_{1i},{\alpha }_{2i},{\alpha }_{3i}\}$. Then one obtains

$$\begin{array}{c}\hfill W_i\left(t\right)\le e^{-\varrho (t-r_q)}{W}_i\left(r_q\right).\end{array}$$

(18)

Case 2. If there are $m(\in {\mathbb{N}}^{+})$ trigger moments in the interval $[r_q,r_{q+1})$, i.e., $t_k<r_q\le t_{k+1}<\cdots <t_{k+m}\le r_{q+1}<t_{k+m+1}$, then one can have

$$\begin{array}{c}\hfill \zeta \left(t\right)=\left\{\begin{array}{c}{e}_{t_k}\left(t\right),t\in [r_q,t_{k+1})\hfill \\ e_{t_{k+1}}\left(t\right),t\in [t_{k+1},t_{k+2})\hfill \\ ⋮\hfill \\ e_{t_{k+m}}\left(t\right),t\in [t_{k+m},r_{q+1}).\hfill \end{array}\right.\end{array}$$

Similarly, Equation (10) is also true on subintervals $[r_q,t_{k+1})$, $[t_{k+1},t_{k+2})$, ⋯,$[t_{k+m},r_{q+1})$, which renders (17) holding on these subintervals. Thus we can obtain that

$$W_i\left(t\right)\le \left\{\begin{array}{c}{e}^{-\varrho (t-r_q)}{W}_i\left(r_q\right),t\in [r_q,t_{k+1})\hfill \\ e^{-\varrho (t-t_{k+1})}{W}_i\left(t_{k+1}\right),t\in [t_{k+1},t_{k+2})\hfill \\ ⋮\hfill \\ e^{-\varrho (t-t_{k+m})}{W}_i\left(t_{k+m}\right),t\in [t_{k+m},r_{q+1}).\hfill \end{array}\right.$$

(19)

It should be pointed out that since the Lyapunov function $W_i\left(t\right)$ is continuous, then (18) can be derived from (19) on the interval $[r_q,r_{q+1})$.

Executing the similar steps in Case 1 and utilizing condition (3) in Algorithm 1, we have

$$\begin{array}{c}\hfill W_{\sigma \left(r_q\right)}\left(r_q\right)\le \mu W_{\sigma \left(r_q^{-}\right)}\left(r_q^{-}\right).\end{array}$$

(20)

Suppose that $0=r_0<r_1<r_2<\cdots <r_q=t_{N_{\sigma }(0,t)}<t$. Then, from (18) and (20), one has

$$\begin{array}{cc}\hfill W_{\sigma \left(t\right)}\left(t\right)\le & \mu e^{-\varrho (t-r_q)}{W}_{\sigma \left(r_q^{-}\right)}\left(r_q^{-}\right)\hfill \\ \hfill \le & \mu e^{-\varrho (t-r_q)}{e}^{-\varrho (r_q-r_{q-1})}{W}_{\sigma \left(r_{q-1}\right)}\left(r_{q-1}\right)\hfill \\ \hfill \le & {\mu }^2{e}^{-\varrho (t-r_{q-1})}{W}_{\sigma \left(r_{q-1}^{-}\right)}\left(r_{q-1}^{-}\right)\hfill \\ \hfill ⋮& \hfill \\ \hfill \le & {\mu }^{N_{\sigma }(r_0,t)}{e}^{-\varrho (t-r_0)}{W}_{\sigma \left(r_0\right)}\left(r_0\right)\hfill \\ \hfill \le & {\mu }^{N_0}{e}^{-(\varrho -\frac{ln\mu }{{\tau }_a})(t-r_0)}{W}_{\sigma \left(r_0\right)}\left(r_0\right).\hfill \end{array}$$

Then, from ${\tau }_a>\frac{ln\mu }{\varrho }$ that ${lim}_{t\to \infty }{W}_{\sigma \left(t\right)}\left(t\right)=0$. Since $W_i\left(t\right)\ge V_i\left(t\right)$, $V_i\left(t\right)$ is bounded and ${lim}_{t\to \infty }{V}_i\left(t\right)=0$, which denotes that ${\tilde{e}}_v$ and ${\widehat{e}}_v$ can asymptotically approach zero, ${lim}_{t\to \infty }\parallel {\tilde{e}}_v\parallel =0$ and ${lim}_{t\to \infty }\parallel {\widehat{e}}_v\parallel =0$, thus ${lim}_{t\to \infty }\parallel z_v\left(t\right)-z_0\left(t\right)\parallel ={lim}_{t\to \infty }\parallel e_v\parallel =0$, where $e_v={\tilde{e}}_v-{\widehat{e}}_v=z_v\left(t\right)-z_0\left(t\right)$. The proof is completed. □

Remark 3. 

According to Theorem 1, multiple switching instances or no switching instance can occur within event intervals $[t_k,t_{k+1})$. The relationship between triggering instant and switching instant is given in Figure 1. This study introduces a more general scenario compared to the assumption of at most one switch each event interval [30] and synchronized switching and sampling within a fixed period [38]. It is important to note that $\zeta \left(t\right)$ is piecewise continuous and bounded, ensuring the continuity of $W_{\sigma \left(t\right)}\left(t\right)$ [39], thus validating the conclusion (18).

Next, Theorem 2 is developed to prove Zeno-free. The so-called Zeno behavior refers to the event-triggered scheme we designed being excited infinitely within a limited time in the event-triggered control. Our purpose is to prove that any two adjacent triggering intervals are greater than zero.

Theorem 2. 

Under consensus conditions in Algorithm 1, there is Zeno-free in the proposed DET protocol.

Proof. 

The systems contain switching signals and event-triggered signals, respectively. Therefore, it is indispensable to clarify their relationship. Suppose that in the interval $[r_q,r_{q+1})$, $\sigma \left(t\right)=i$. After that, the following two cases will be taken into account. □

Case 1. There is no switch on the interval $[t_k,t_{k+1})$. Then

$$\begin{array}{cc}\hfill D^{+}\parallel e_{t_k}\left(t\right)\parallel & \le \parallel \widehat{z}\left(t\right)\parallel \hfill \\ \hfill & = \parallel (I\otimes F_i)\widehat{z}\left(t\right)-(H_i\otimes E_i{K}_i)(\widehat{z}\left(t_k\right)-z_0\left(t\right))-\pi (I\otimes E_i)\Psi \left[\tilde{e}\left(t\right)\right]\parallel \hfill \\ \hfill & \le \parallel (I\otimes F_i)e_{t_k}\left(t\right)\parallel +\parallel (H_i\otimes E_i{K}_i)\parallel [\parallel (\widehat{z}\left(t_k\right)-z\left(t\right)\parallel \hfill \\ \hfill & +\parallel z\left(t\right)-z_0\left(t\right)\parallel ]+\pi \parallel E_i\parallel +\parallel (I\otimes F_i)\widehat{z}\left(t_k\right)\parallel .\hfill \end{array}$$

(21)

From Theorem 1, we can know that the $\tilde{e}\left(t\right)$ and $\widehat{e}\left(t\right)$ are bounded for any finite time. Thus, let $\Delta$ be the upper bound of $\parallel (H_i\otimes E_i{K}_i)\parallel \left[\parallel (\widehat{z}\left(t_k\right)-z\left(t\right)\parallel +\parallel z\left(t\right)-z_0\left(t\right)\parallel \right]$, we obtain

$$\begin{array}{cc}\hfill D^{+}\parallel e_{t_k}\left(t\right)\parallel & \le \parallel F_i\parallel \parallel e_{t_k}\left(t\right)\parallel +\Delta +\pi \parallel E_i\parallel +\parallel (I\otimes F_i)\widehat{z}\left(t_k\right)\parallel \hfill \\ \hfill & \le {\phi }_1\parallel e_{t_k}\left(t\right)\parallel +{\Lambda }_k,\hfill \end{array}$$

where ${\phi }_1={max}_{i\in \mathcal{S}}\{\parallel F_i\parallel \}$, ${\Lambda }_k={max}_{i\in \mathcal{S}}\{\Delta +\pi \parallel E_i\parallel +\parallel (I\otimes F_i)\widehat{z}\left(t_k\right)\parallel \}$. Then we have

$$\parallel e_{t_k}\left(t\right)\parallel \le \frac{{\Lambda }_k}{{\phi }_1}\left(e^{{\phi }_1(t-t_k)}-1\right).$$

thus

$$\begin{array}{c}\hfill \parallel (I\otimes E_i^T{P}_i)e_{t_k}\left(t\right)\parallel \le \frac{{\Lambda }_k{\phi }_2}{{\phi }_1}\left(e^{{\phi }_1(t-t_k)}-1\right),\end{array}$$

(22)

where ${\phi }_2={max}_{i\in \mathcal{S}}\{\parallel E_i^T{P}_i\parallel \}$.

According to the DET condition (4), the next triggering moment $t_{k+1}$ satisfies

$$\parallel (I\otimes E_i^T{P}_i)e_{t_k}\left(t_{k+1}\right)\parallel \ge \eta \left(t_{k+1}\right)\ge \frac{\eta \left(0\right)}{\theta }{e}^{-(\rho +\frac{1}{\theta })t_{k+1}},$$

from (22), we can obtain

$$\frac{{\Lambda }_k{\phi }_2}{{\phi }_1}\left(e^{{\phi }_1(t_{k+1}-t_k)}-1\right)\ge \frac{\eta \left(0\right)}{\theta }{e}^{-(\rho +\frac{1}{\theta })t_{k+1}}.$$

Through calculation, we can further obtain

$$t_{k+1}-t_k\ge \frac{1}{{\phi }_1}ln\left(1+\frac{{\phi }_1}{{\phi }_2{\Lambda }_k}\frac{\eta \left(0\right)}{\theta }{e}^{-(\rho +\frac{1}{\theta })t_{k+1}}\right).$$

Case 2. There exist some switches on the triggering interval $[t_k,t_{k+1})$, i.e., $t_k\le r_q<r_{q+1}<\cdots <r_{q+l}<t<t_{k+1}$, where $l\in {\mathbb{Z}}^{+}$. If system (1) has infinite triggering within a limited time interval, it is said that system (1) has Zeno behavior. Assume that M stands for the Zeno time, and $t_{k+1}\to M$, $t_k\to M$, thus $t_{k+1}-t_k\to 0$. Nevertheless, $t_k<r_q<\cdots <r_{q+l}<t_{k+1}$, there are some ${\xi }_{n^{\ast }}>0$, $n^{\ast }=0,1,\cdots ,l$, such that $t_{k+1}-r_{q+l}\ge {\xi }_0$, $r_{q+l}-r_{q+l-1}\ge {\xi }_1$, ⋯, $r_q-t_k\ge {\xi }_{l+1}$. Then $t_{k+1}-r_{q+l}+r_{q+l}\cdots -t_k\ge {\xi }_0+{\xi }_1+\cdots +{\xi }_{l+1}={\xi }^{\ast }>0$, in other words, $t_{k+1}-t_k>{\xi }^{\ast }$, which is contrary to $t_{k+1}-t_k\to 0$ converges to 0. Thus, it is Zeno free.

Remark 4. 

The proof of Theorem 2 is inspired by [40] but different from [40]. In this paper, it is formidable to prohibit Zeno behavior since Theorem 2 needs to take into account how the triggering instants and switching instants are related.

One disadvantage of the DET protocol with the discontinuous term ${\psi }_v(·)$ is that it produces the undesirable chattering effect in real implementation. To avoid the chattering effect, the next section will adopt the boundary layer technique to design a DET protocol with a continuous term ${\psi }_v(·)$.

3.2. DET Protocol with Continuous Term ${\psi }_v(·)$

Define the nonlinear function ${\psi }_v(·):{\mathbb{R}}^m\to {\mathbb{R}}^m$ as

$$\begin{array}{c}\hfill {\psi }_v\left({\varpi }_v\right)=\left\{\begin{array}{c}\frac{{\varpi }_v}{\parallel {\varpi }_v\parallel },\parallel {\varpi }_v\parallel \ge {\varphi }_v\hfill \\ \frac{{\varpi }_v}{{\varphi }_v},\parallel {\varpi }_v\parallel <{\varphi }_v\hfill \end{array}\right.{\varpi }_v\in {\mathbb{R}}^m,\end{array}$$

(23)

where ${\varphi }_v>0$ represents the widths of the boundary layers.

Theorem 3 will clarify that the bounded consensus of switched MASs can be obtained under Algorithm 1, DET condition (4) and event-based tracking control protocols (5).

Theorem 3. 

If Assumptions 1–3 hold, under the event-based tracking control protocols (5) with the DET condition (4), and Algorithm 1, then the switched MASs (1) and (2) will reach bounded consensus.

Proof. 

Suppose $V_{\sigma \left(t\right)}\left(t\right)$ is the Lyapunov function provided by (9). Combination Theorem 1, we obtain

$$\begin{array}{cc}\hfill & -2{\tilde{e}}^T\left(t\right)({\mathbf{1}}_N\otimes P_i{E}_i)u_0\left(t\right)-2\gamma {\tilde{e}}^T\left(t\right)(I\otimes P_i{E}_i)\Psi \left[\tilde{e}\left(t\right)\right].\hfill \end{array}$$

Next, we consider the following three cases.

(1) $\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel \ge {\varphi }_v$, $v=1,\cdots ,N$. Using the analysis method in Section 3.1, by introducing the auxiliary Lyapunov function $W_i\left(t\right)$, one obtains that

$$\begin{array}{c}\hfill {\dot{W}}_i\left(t\right)\le -\varrho W_i\left(t\right).\end{array}$$

(24)

(2) $\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel <{\varphi }_v$, $v=1,\cdots ,N$. From (13) and (14), one has

$$\begin{array}{cc}\hfill -2{\tilde{e}}^T\left(t\right)({\mathbf{1}}_N\otimes P_i{E}_i)u_0\left(t\right)& \le 2\epsilon \sum _{v=1}^N\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel \hfill \\ \hfill & \le 2\epsilon N\overline{\varphi }-2\gamma {\tilde{e}}^T\left(t\right)(I\otimes P_i{E}_i)\Psi \left[\tilde{e}\left(t\right)\right]\hfill \\ \hfill & =-2\gamma \sum _{v=1}^N{\left[E_i^T{P}_i{\tilde{e}}_v\left(t\right)\right]}^T\frac{E_i^T{P}_i{\tilde{e}}_v\left(t\right)}{{\varphi }_v}\hfill \\ \hfill & \le 2\gamma N\overline{\varphi },\hfill \end{array}$$

where $\overline{\varphi }={max}_{v=1,\cdots ,N}{\varphi }_v$. In light of Theorem 1, yields

$$\begin{array}{c}\hfill {\dot{W}}_i\left(t\right)\le -\varrho W_i\left(t\right)+2N\overline{\varphi }(\epsilon +\gamma ).\end{array}$$

(25)

(3) $\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel \ge {\varphi }_v$ for $v=1,\cdots ,N_1$, and $\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel <{\varphi }_v$ for $v=N_1+1,\cdots ,N$, where $1\le N_1\le N-1$. Then

$$\begin{array}{cc}\hfill & -2{\tilde{e}}^T\left(t\right)({\mathbf{1}}_N\otimes P_i{E}_i)u_0\left(t\right)\hfill \\ \hfill \le & 2\epsilon \left(\sum _{v=1}^{N_1}\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel +\sum _{v=N_1+1}^N\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel \right)\hfill \\ \hfill \le & 2\epsilon \sum _{v=1}^{N_1}\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel +2\epsilon (N-N_1)\overline{\varphi }-2\gamma {\tilde{e}}^T\left(t\right)(I\otimes P_i{E}_i)\Psi \left[\tilde{e}\left(t\right)\right]\hfill \\ \hfill =& -2\gamma \left(\sum _{v=1}^{N_1}{\left[E_i^T{P}_i{\tilde{e}}_v\left(t\right)\right]}^T\frac{E_i^T{P}_i{\tilde{e}}_v\left(t\right)}{\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel }+\sum _{v=N_1+1}^N{\left[E_i^T{P}_i{\tilde{e}}_v\left(t\right)\right]}^T\frac{E_i^T{P}_i{\tilde{e}}_v\left(t\right)}{{\varphi }_v}\right)\hfill \\ \hfill =& -2\gamma \sum _{v=1}^N\parallel E_i^T{P}_i{\tilde{e}}_v\left(t\right)\parallel +2\gamma (N-N_1)\overline{\varphi }.\hfill \end{array}$$

Since $\gamma \ge \epsilon$, one has

$$\begin{array}{c}\hfill {\dot{W}}_i\left(t\right)\le -\varrho W_i\left(t\right)+2(N-N_1)\overline{\varphi }(\epsilon +\gamma ).\end{array}$$

(26)

Further, it can be seen from (24)–(26) that

$$\begin{array}{c}\hfill {\dot{W}}_i\left(t\right)\le -\varrho W_i\left(t\right)+2N\overline{\varphi }(\epsilon +\gamma ).\end{array}$$

According to Lemma 1, we obtain

$$\begin{array}{c}\hfill W_i\left(t\right)\le 2N\overline{\varphi }(\epsilon +\gamma )\frac{{\mu }^{N_0}}{\varrho -\frac{ln\mu }{{\tau }_a}},t\to \infty .\end{array}$$

Obviously, $V_i\left(t\right)\le 2N\overline{\varphi }(\epsilon +\gamma )\frac{{\mu }^{N_0}}{\varrho -\frac{ln\mu }{{\tau }_a}},t\to \infty$. Further, from (9) and the fact $\parallel e\left(t\right)\parallel \le \parallel \tilde{e}\left(t\right)\parallel + \parallel \widehat{e}\left(t\right)\parallel$, we have

$$\begin{array}{c}\hfill \parallel e\left(t\right)\parallel \le (\frac{1}{\sqrt{\underline{\kappa }}}+\frac{1}{\sqrt{\underline{\varsigma }\underline{\pi }}})\sqrt{\frac{2N\overline{\varphi }(\epsilon +\gamma ){\mu }^{N_0}}{\varrho -\frac{ln\mu }{{\tau }_a}}},t\to \infty \end{array}$$

(27)

where $\underline{\kappa }={min}_{i\in \mathcal{S}}{\lambda }_{min}\left(P_i\right)$, $\underline{\pi }={min}_{i\in \mathcal{S}}{\lambda }_{min}\left(R_i\right)$, $\underline{\varsigma }={min}_{i\in \mathcal{S}}\left\{{\varsigma }_i\right\}$. Then, the switched MASs (1) and (2) can reach bounded consensus. The proof is completed. □

Remark 5. 

Although complete consensus can not be ensured by applying the continuous protocol (23), the chattering effect can be prevented. Keep in mind that the intrinsic shortcoming of the discontinuous controller is the unfavorable chattering effect in real-world application (8) [41]. From (27), we know that the bound of $e\left(t\right)$ is decided by the nonzero control inputs and the maximum width ${\varphi }_v$, the number of followers, and the ADT. It can be noted that the smaller the $\overline{\varphi }$, the smaller the bound of $e\left(t\right)$.

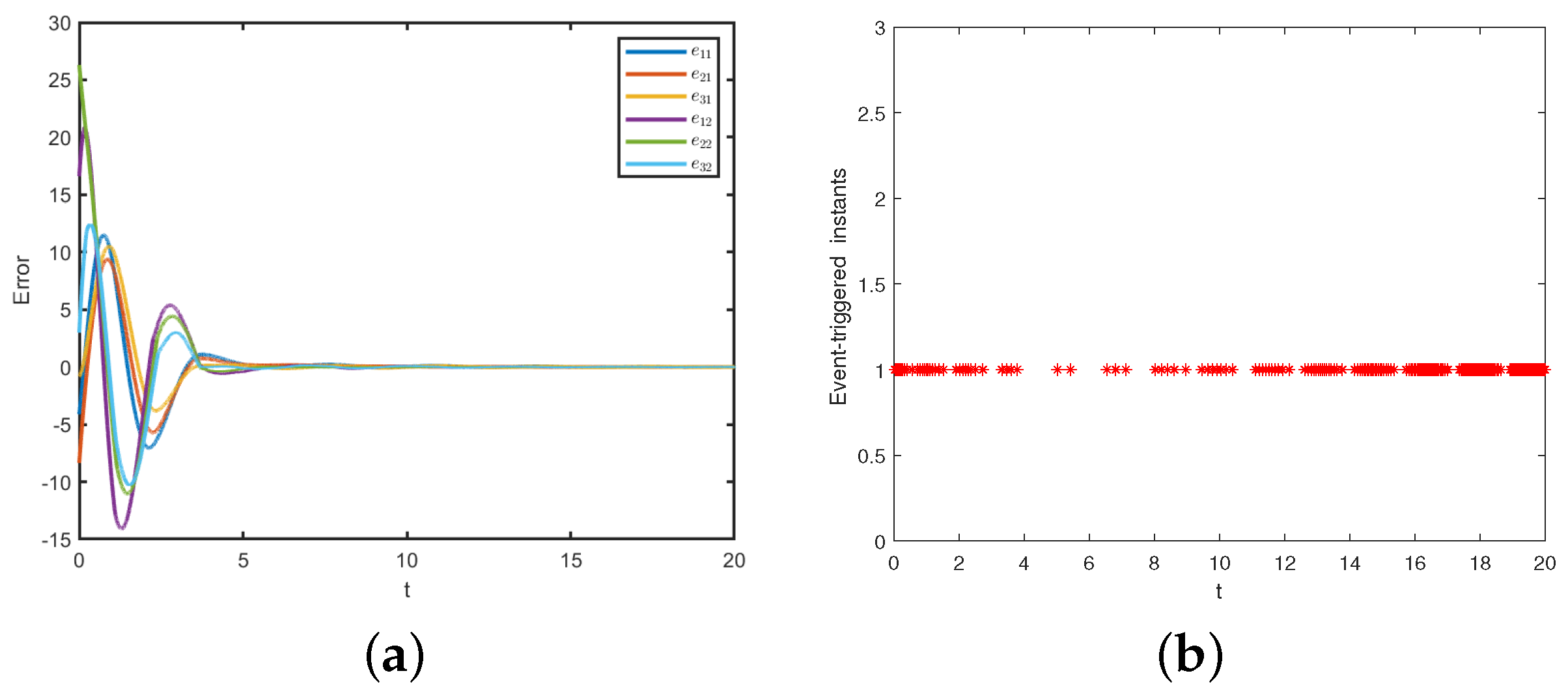
4. Numerical Simulation

Two numerical simulations verify the validity of the above results and the effectiveness of the proposed DET mechanism for switched MASs.

Assume that the topology switches between the graphs ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ are depicted by Figure 2a,b, where the switching signals are 1 and 2, respectively. The leader is

$${\dot{z}}_0\left(t\right)=F_{\sigma \left(t\right)}{z}_0\left(t\right)+E_{\sigma \left(t\right)}{u}_0\left(t\right)$$

and the v-th followers are described by

$$\begin{array}{cc}\hfill {\dot{z}}_v\left(t\right)=& F_{\sigma \left(t\right)}{z}_v\left(t\right)+E_{\sigma \left(t\right)}{u}_v\left(t\right)\hfill \\ \hfill y_v\left(t\right)=& C_{\sigma \left(t\right)}{z}_v\left(t\right)\hfill \end{array}$$

(28)

with $z_v\left(t\right)={[z_{v1}\left(t\right),z_{v2}\left(t\right)]}^T,v=1,2,3$, $\sigma \left(t\right)\in \{1,2\}$ and

$$\begin{array}{c}{F}_1=\left[\begin{array}{cc}0& 2\\ -3& 0\end{array}\right]F_2=\left[\begin{array}{cc}0& 1\\ -2& 0\end{array}\right]E_1={\left[\begin{array}{cc}0& 1.5\end{array}\right]}^T{E}_2={\left[\begin{array}{cc}0& 2\end{array}\right]}^T\hfill \\ C_1=\left[\begin{array}{cc}1& 0\end{array}\right]C_2=\left[\begin{array}{cc}1& 1\end{array}\right]\hfill \\ {\mathcal{H}}_1=\left[\begin{array}{ccc}1& 0& -0.5\\ 0& 1& -1\\ -0.5& -1& 1.5\end{array}\right]{\mathcal{H}}_2=\left[\begin{array}{ccc}1& -0.5& 0\\ -0.5& 1& -0.5\\ 0& -0.5& 1.5\end{array}\right]\hfill \\ {\mathcal{M}}_1=\left[\begin{array}{ccc}0.5& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]{\mathcal{M}}_2=\left[\begin{array}{ccc}0.5& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right].\hfill \end{array}$$

Then, ${\lambda }_1=2.3956$, ${\lambda }_2=1.9010$. Let $u_0\left(t\right)=0.3cos\left(t\right)$.

Example 1. 

Choose $\theta =5.2$, $\gamma =0.6$, $\rho =0.4$, solving conditions (1) and (2) in Algorithm 1, we have

$$\begin{array}{cccc}\hfill & P_1=\left[\begin{array}{cc}1.1442& 0.1514\\ 0.1514& 0.6336\end{array}\right]\hfill & \hfill & P_2=\left[\begin{array}{cc}2.0031& 0.2222\\ 0.2222& 0.8012\end{array}\right]\hfill \\ \hfill & K_1=\left[\begin{array}{cc}0.3028& 1.2671\end{array}\right]\hfill & \hfill & K_2=\left[\begin{array}{cc}0.3333& 1.2019\end{array}\right].\hfill \end{array}$$

Through calculation, $\epsilon =0.3$, we select $\pi =3$, $\theta =5.2$, $\rho =0.4$ and $\gamma =0.6$. Next, set $N_0=1$ and ${\tau }_a=0.5$ s. Then the trajectories of $z_{v1}\left(t\right)$ and $z_{v2}\left(t\right)$ are shown in Figure 2a,b, respectively. Then the trajectories of $z_{v1}\left(t\right)$ and $z_{v2}\left(t\right)$ are shown in Figure 3a,b, respectively. Figure 4a illustrates the consensus of the switched MASs. Meanwhile, Figure 4b is the sampling moments. The above simulation results verify the effectiveness of the proposed DET control strategy.

Example 2. 

Consider the same parameters as those in Example 1. According to Theorem 3, switched MASs (1) and (2) will realize bounded consensus. The consensus error signal $e_v\left(t\right)$ is displayed in Figure 5a,b. Assuming that Err(t)$=\parallel e\left(t\right)\parallel =\sqrt{{\sum }_{v=1}^3{\parallel e_v\left(t\right)\parallel }^2}$. ${\psi }_v(·)$ is determined by Theorem 3. Additionally, under any ${\varphi }_v$, Err (t) can achieve bounded consensus. Without losing generality, we select $\varphi =0.5,0.7,1$, the trajectories of Err(t) are illustrated in Figure 6a. In addition, the switching signal with two modes is given in Figure 6b.

5. Conclusions

The tracking consensus control of switched MASs was discussed in this paper, where the system and communication topology were switched simultaneously and the leader system had nonzero control inputs. The proposed observer-based DET protocols include two nonlinear terms to handle the effect of nonzero control inputs. Moreover, the Zeno behavior for MASs under the observer-based DET protocols can be excluded. In addition, by employing the switched Lyapunov function method and Riccati equation, some sufficient criteria are put forward to ensure that all followers can track the leader. Compared with the existing works in the literature, the designed observer-based DET protocols can successfully limit the frequency of data transfer across agents while maintaining MASs consensus. Finally, two numerical examples show that the designed control protocol can reduce controller updates. In the future, the method suggested in this paper will be used to discuss the consensus problem of switched stochastic MASs with delay impulsive effects.