Numerical Method for Geometrical Feature Extraction and Identification of Patient-Specific Aorta Models in Pediatric Congenital Heart Disease
Abstract
:1. Introduction
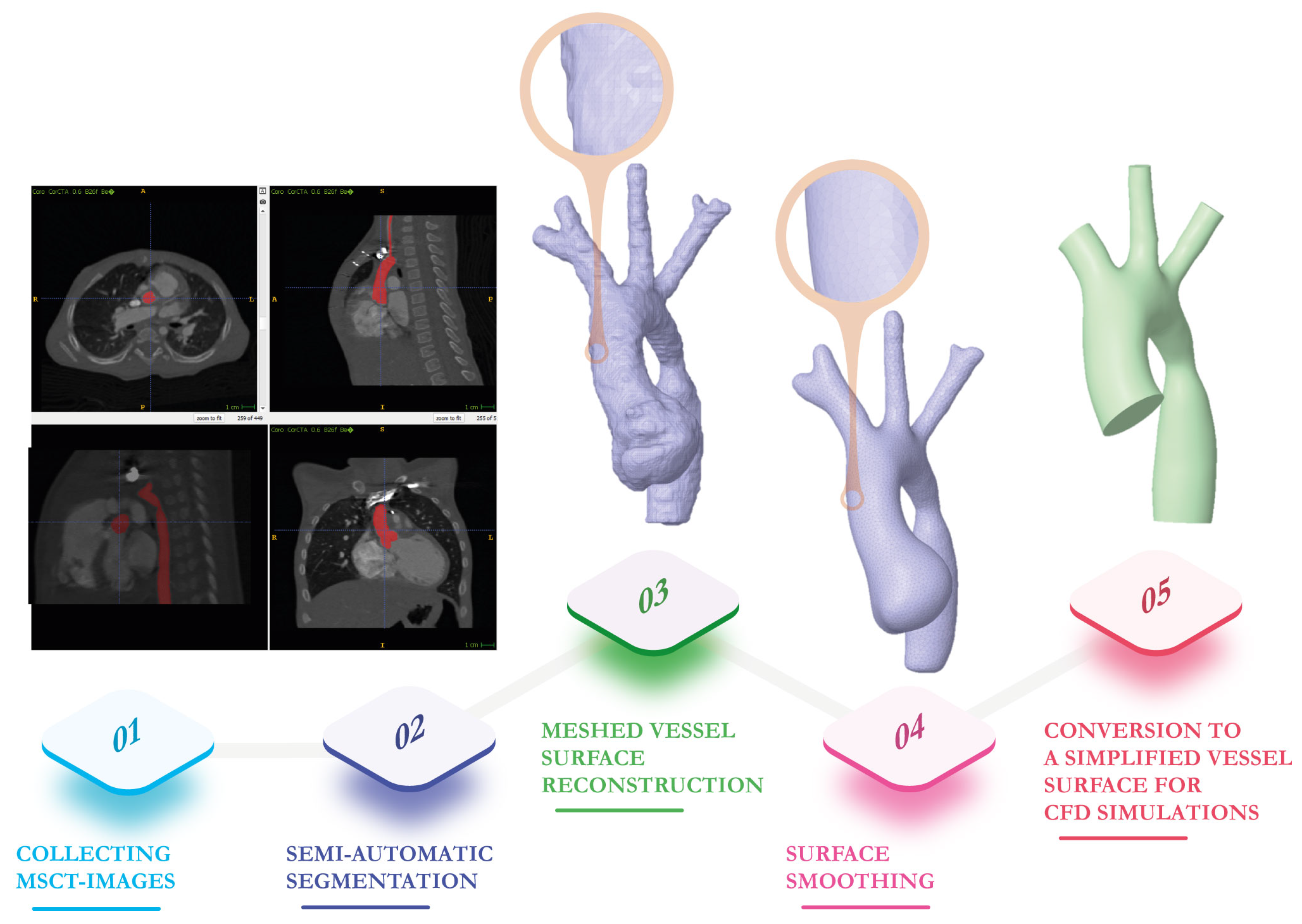
2. Vessel Surface Determination from Multi-Slice Computed Tomography Images
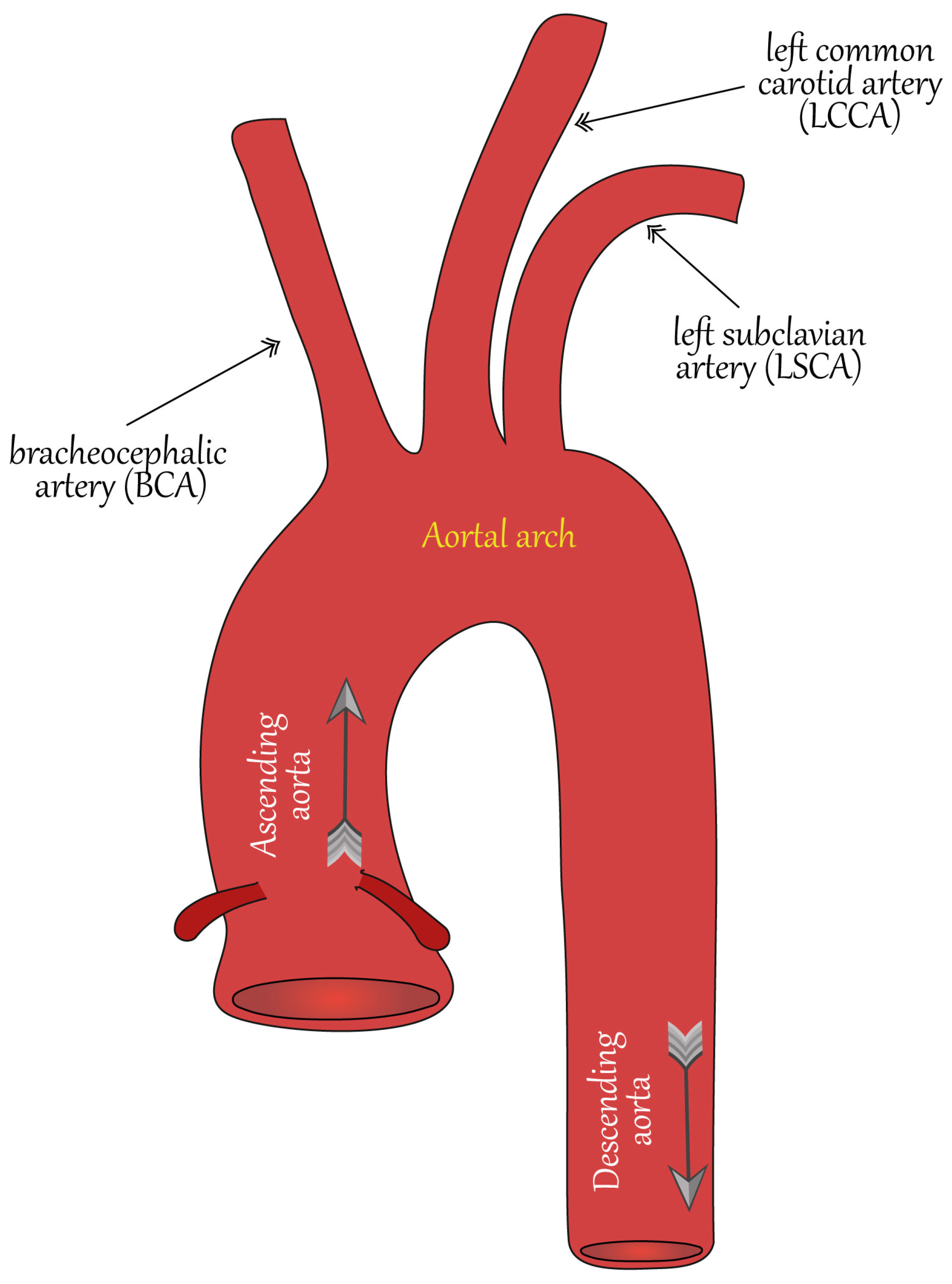
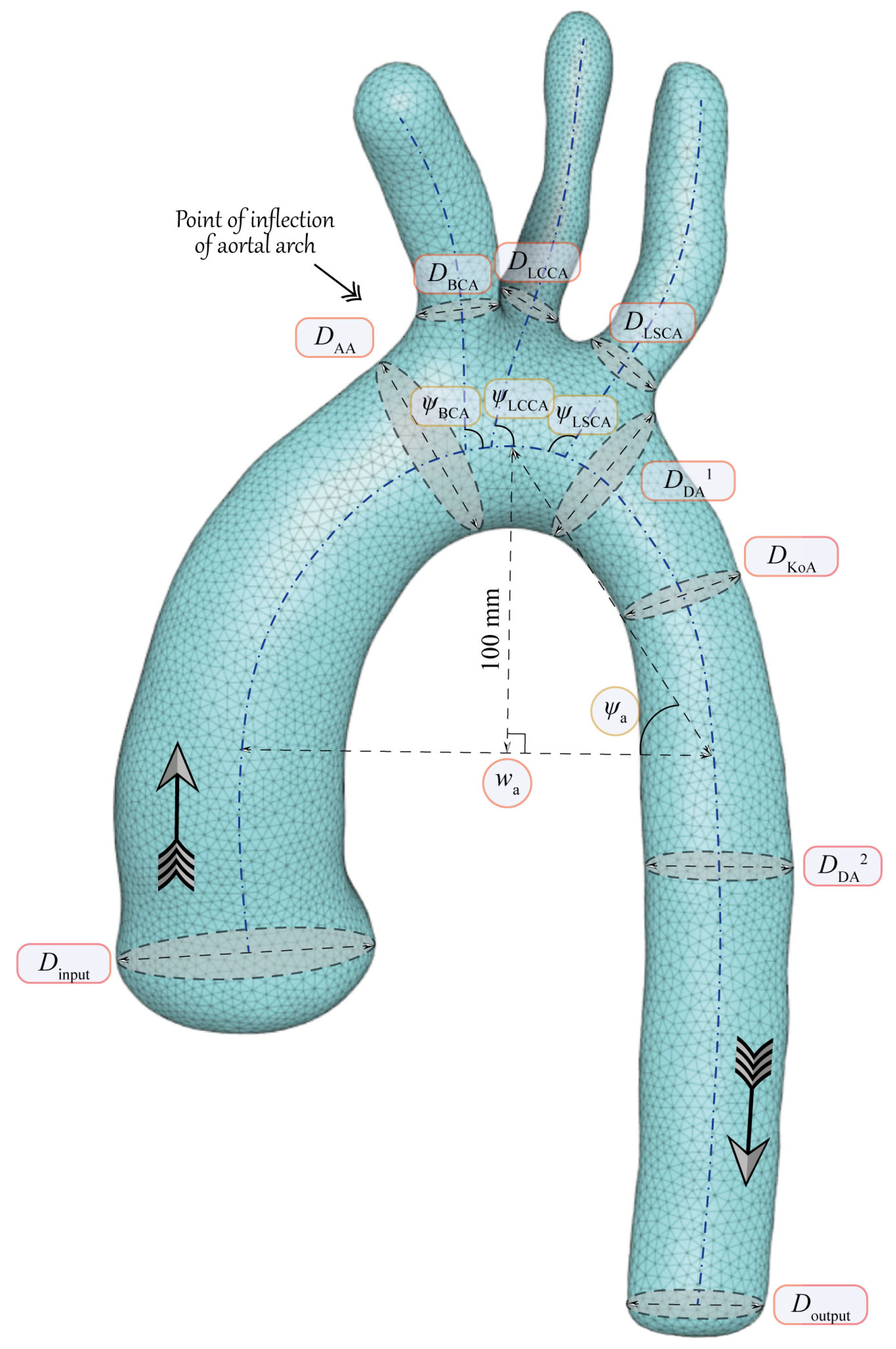
3. Main Geometrical Characteristics of Aorta
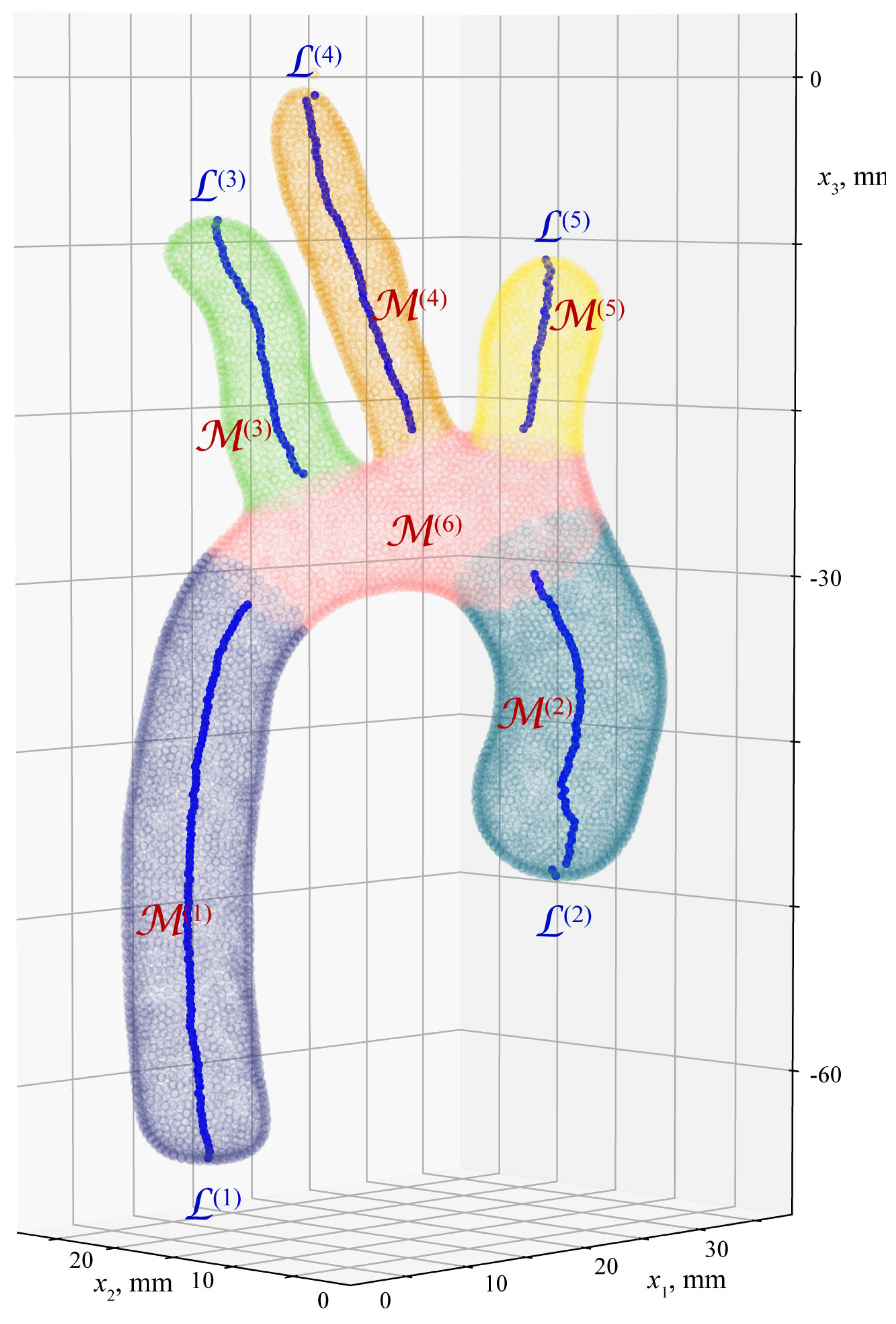
4. Algorithm for Extraction of Geometrical Characteristics of Aorta
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Midgett, M.; Rugonyi, S. Congenital heart malformations induced by hemodynamic altering surgical interventions. Front. Physiol. 2014, 5, 287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verheugt, C.L.; Uiterwaal, C.S.; Grobbee, D.E.; Mulder, B.J. Long-term prognosis of congenital heart defects: A systematic review. Int. J. Cardiol. 2008, 131, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Chen, R.; Juan, Y.H.; Li, H.; Wang, J.; Yu, Z.; Liu, H. Clinical validation and assessment of aortic hemodynamics using computational fluid dynamics simulations from computed tomography angiography. Biomed. Eng. Online 2018, 17, 53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsang, V.; Haapanen, H.; Neijenhuis, R. Aortic Coarctation/Arch Hypoplasia Repair: How Small Is Too Small. Semin. Thorac. Cardiovasc. Surg. Pediatr. Card. Surg. Annu. 2019, 22, 10–13. [Google Scholar] [CrossRef]
- Taebi, A. Deep Learning for Computational Hemodynamics: A Brief Review of Recent Advances. Fluids 2022, 7, 197. [Google Scholar] [CrossRef]
- Oster, M.E.; McCracken, C.; Kiener, A.; Aylward, B.; Cory, M.; Hunting, J.; Kochilas, L.K. Long-Term Survival of Patients With Coarctation Repaired During Infancy (from the Pediatric Cardiac Care Consortium). Am. J. Cardiol. 2019, 124, 795–802. [Google Scholar] [CrossRef]
- Alkashkari, W.; Albugami, S.; Hijazi, Z.M. Management of Coarctation of The Aorta in Adult Patients: State of The Art. Korean Circ. J. 2019, 49, 298. [Google Scholar] [CrossRef]
- Cao, H.; Li, Y.; Zhao, Y.; Xiong, T.; Liu, Z.; Zheng, T.; Chen, M. Hemodynamic Characteristics of Patients With Suspected Coronary Heart Disease at Their Initial Visit. Front. Physiol. 2021, 12, 714438. [Google Scholar] [CrossRef]
- Kuchumov, A.G.; Kamaltdinov, M.R.; Khairulin, A.R.; Kochergin, M.V.; Shmurak, M.I. Patient-Specific 0D–3D Modeling of Blood Flow in Newborns To Predict Risks of Complications After Surgery. Health Risk Anal. 2022, 2022, 159–167. [Google Scholar] [CrossRef]
- Kuchumov, A.G.; Khairulin, A.; Shmurak, M.; Porodikov, A.; Merzlyakov, A. The Effects of the Mechanical Properties of Vascular Grafts and an Anisotropic Hyperelastic Aortic Model on Local Hemodynamics during Modified Blalock–Taussig Shunt Operation, Assessed Using FSI Simulation. Materials 2022, 15, 2719. [Google Scholar] [CrossRef]
- Pil, N.; Kuchumov, A.G.; Kadyraliev, B.; Arutunyan, V. Influence of Aortic Valve Leaflet Material Model on Hemodynamic Features in Healthy and Pathological States. Mathematics 2023, 11, 428. [Google Scholar] [CrossRef]
- Totorean, A.F.; Totorean, I.C.; Bernad, S.I.; Ciocan, T.; Malita, D.C.; Gaita, D.; Bernad, E.S. Patient-Specific Image-Based Computational Fluid Dynamics Analysis of Abdominal Aorta and Branches. J. Pers. Med. 2022, 12, 1502. [Google Scholar] [CrossRef] [PubMed]
- Thamsen, B.; Yevtushenko, P.; Gundelwein, L.; Lamecker, H.; Kühne, T.; Goubergrits, L. Unsupervised Learning and Statistical Shape Modeling of the Morphometry and Hemodynamics of Coarctation of the Aorta; Springer International Publishing: Cham, Switzerland, 2020; Volume 12264 LNCS, pp. 776–785. [Google Scholar] [CrossRef]
- Yang, F.; Zhai, B.; Hou, L.G.; Zhang, Q.; Wang, J. Computational fluid dynamics in the numerical simulation analysis of end-to-side anastomosis for coarctation of the aorta. J. Thorac. Dis. 2018, 10, 6578–6584. [Google Scholar] [CrossRef] [PubMed]
- Manchester, E.L.; Pirola, S.; Salmasi, M.Y.; O’Regan, D.P.; Athanasiou, T.; Xu, X.Y. Analysis of Turbulence Effects in a Patient-Specific Aorta with Aortic Valve Stenosis. Cardiovasc. Eng. Technol. 2021, 12, 438–453. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Guo, X.; Stäb, D.; Jin, N.; Poon, E.K.; Lim, R.P.; Ooi, A. Computational fluid dynamic simulations informed by CT and 4D flow MRI for post-surgery aortic dissection—A case study. Int. J. Heat Fluid Flow 2022, 96, 108986. [Google Scholar] [CrossRef]
- Hassanein, W.; Albert, A.; Florath, I.; Hegazy, Y.Y.; Rosendahl, U.; Bauer, S.; Ennker, J. Concomitant aortic valve replacement and coronary bypass: The effect of valve type on the blood flow in bypass grafts. Eur. J. Cardio-Thorac. Surg. 2007, 31, 391–396. [Google Scholar] [CrossRef] [Green Version]
- Deyranlou, A.; Miller, C.A.; Revell, A.; Keshmiri, A. Effects of Ageing on Aortic Circulation During Atrial Fibrillation; a Numerical Study on Different Aortic Morphologies. Ann. Biomed. Eng. 2021, 49, 2196–2213. [Google Scholar] [CrossRef]
- Liang, L.; Mao, W.; Sun, W. A feasibility study of deep learning for predicting hemodynamics of human thoracic aorta. J. Biomech. 2020, 99, 109544. [Google Scholar] [CrossRef]
- Yevtushenko, P.; Goubergrits, L.; Gundelwein, L.; Setio, A.; Ramm, H.; Lamecker, H.; Heimann, T.; Meyer, A.; Kuehne, T.; Schafstedde, M. Deep Learning Based Centerline-Aggregated Aortic Hemodynamics: An Efficient Alternative to Numerical Modeling of Hemodynamics. IEEE J. Biomed. Health Inform. 2022, 26, 1815–1825. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, C.; Zhang, P.; Golub, M.V.; Yu, B. Enriched physics-informed neural networks for 2D in-plane crack analysis: Theory and MATLAB code. Int. J. Solids Struct. 2023, 276, 112321. [Google Scholar] [CrossRef]
- Bruse, J.L.; McLeod, K.; Biglino, G.; Ntsinjana, H.N.; Capelli, C.; Hsia, T.Y.; Sermesant, M.; Pennec, X.; Taylor, A.M.; Schievano, S.; et al. A statistical shape modelling framework to extract 3D shape biomarkers from medical imaging data: Assessing arch morphology of repaired coarctation of the aorta. BMC Med. Imaging 2016, 16, 40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, L.; Liu, M.; Martin, C.; Elefteriades, J.A.; Sun, W. A machine learning approach to investigate the relationship between shape features and numerically predicted risk of ascending aortic aneurysm. Biomech. Model. Mechanobiol. 2017, 16, 1519–1533. [Google Scholar] [CrossRef]
- Hahn, L.D.; Baeumler, K.; Hsiao, A. Artificial intelligence and machine learning in aortic disease. Curr. Opin. Cardiol. 2021, 36, 695–703. [Google Scholar] [CrossRef]
- Song, M.H.; Sato, M.; Ueda, Y. Three-dimensional simulation of the Blalock-Taussig shunt using computational fluid dynamics. Surg. Today 2001, 31, 688–694. [Google Scholar] [CrossRef] [PubMed]
- Lagana, K.; Balossino, R.; Migliavacca, F.; Pennati, G.; Bove, E.L.; de Leval, M.R.; Dubini, G. Multiscale modeling of the cardiovascular system: Application to the study of pulmonary and coronary perfusions in the univentricular circulation. J. Biomech. 2005, 38, 1129–1141. [Google Scholar] [CrossRef]
- Arnaz, A.; Piskin, S.; Oguz, G.N.; Yusuf, Y.; Pekkan, K.; Sarioglu, T. Effect of modified Blalock-Taussig shunt anastomosis angle and pulmonary artery diameter on pulmonary flow. Anatol. J. Cardiol. 2018, 20, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Yuan, H.; Chen, X.; Liu, J.; Zhou, C.; Huang, M.; Jian, Q.; Zhuang, J. Hemodynamic of the patent ductus arteriosus in neonates with modified Blalock-Taussig shunts. Comput. Methods Programs Biomed. 2020, 186, 105223. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Q.; Qian, Y.; Hong, H.; Liu, J. Numerical simulation and hemodynamic analysis of the modified Blalock-Taussig shunt. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 707–710. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y.; Ding, J.; Ren, X.; Bai, F.; Zhang, M.; Ma, L.; Wang, W.; Xie, J.; Qiao, A. Hemodynamic effects of the anastomoses in the modified blalock-taussig shunt: A numerical study using a 0D/3D coupling method. J. Mech. Med. Biol. 2015, 15, 1550017. [Google Scholar] [CrossRef]
- Geronzi, L.; Haigron, P.; Martinez, A.; Yan, K.; Rochette, M.; Bel-Brunon, A.; Porterie, J.; Lin, S.; Marin-Castrillon, D.M.; Lalande, A.; et al. Assessment of shape-based features ability to predict the ascending aortic aneurysm growth. Front. Physiol. 2023, 14, 378. [Google Scholar] [CrossRef]
- Saitta, S.; Sturla, F.; Caimi, A.; Riva, A.; Palumbo, M.C.; Nano, G.; Votta, E.; Corte, A.D.; Glauber, M.; Chiappino, D.; et al. A Deep Learning-Based and Fully Automated Pipeline for Thoracic Aorta Geometric Analysis and Planning for Endovascular Repair from Computed Tomography. J. Digit. Imaging 2022, 35, 226–239. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clustersin Large Spatial Databases with Noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Piccinelli, M.; Veneziani, A.; Steinman, D.A.; Remuzzi, A.; Antiga, L. A Framework for Geometric Analysis of Vascular Structures: Application to Cerebral Aneurysms. IEEE Trans. Med. Imaging 2009, 28, 1141–1155. [Google Scholar] [CrossRef]
- Dirks, V.; Prêtre, R.; Knirsch, W.; Valsangiacomo Buechel, E.R.; Seifert, B.; Schweiger, M.; Hübler, M.; Dave, H. Modified Blalock Taussig shunt: A not-so-simple palliative procedure. Eur. J. Cardio-Thorac. Surg. 2013, 44, 1096–1102. [Google Scholar] [CrossRef]
- Kuchumov, A.; Khairulin, A.; Biyanov, A.; Porodikov, A.; Arutyunyan, V.; Sinelnikov, Y. Effectiveness of Blalock-Taussig shunt performance in the congenital heart disease children. Russ. J. Biomech. 2020, 24, 65–83. [Google Scholar] [CrossRef]
- Shaikh, S.; Al-Mukhaini, K.S.; Al-Rawahi, A.H.; Al-Dafie, O. Outcomes of Infants Undergoing Modified Blalock-Taussig Shunt Procedures in Oman: A retrospective study. Sultan Qaboos Univ. Med. J. 2021, 21, 457–464. [Google Scholar] [CrossRef] [PubMed]
- Sahuquillo, J.; Rosas, K.; Calvo, H.; Alcina, A.; Gándara, D.; López-Bermeo, D.; Poca, M.A. How to Choose a Shunt for Patients with Normal Pressure Hydrocephalus: A Short Guide to Selecting the Best Shunt Assembly. J. Clin. Med. 2021, 10, 1210. [Google Scholar] [CrossRef] [PubMed]
- Kamaltdinov, M.; Kuchumov, A. Application of a mathematical model of systemic circulation for determination of blood flow parameters after modified Blalock-Taussig shunt operation in newborns. Russ. J. Biomech. 2021, 25, 268–284. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuchumov, A.G.; Doroshenko, O.V.; Golub, M.V.; Saychenko, N.D.; Rakisheva, I.O.; Shekhmametyev, R.M. Numerical Method for Geometrical Feature Extraction and Identification of Patient-Specific Aorta Models in Pediatric Congenital Heart Disease. Mathematics 2023, 11, 2871. https://doi.org/10.3390/math11132871
Kuchumov AG, Doroshenko OV, Golub MV, Saychenko ND, Rakisheva IO, Shekhmametyev RM. Numerical Method for Geometrical Feature Extraction and Identification of Patient-Specific Aorta Models in Pediatric Congenital Heart Disease. Mathematics. 2023; 11(13):2871. https://doi.org/10.3390/math11132871
Chicago/Turabian StyleKuchumov, Alex G., Olga V. Doroshenko, Mikhail V. Golub, Nikita D. Saychenko, Irina O. Rakisheva, and Roman M. Shekhmametyev. 2023. "Numerical Method for Geometrical Feature Extraction and Identification of Patient-Specific Aorta Models in Pediatric Congenital Heart Disease" Mathematics 11, no. 13: 2871. https://doi.org/10.3390/math11132871
APA StyleKuchumov, A. G., Doroshenko, O. V., Golub, M. V., Saychenko, N. D., Rakisheva, I. O., & Shekhmametyev, R. M. (2023). Numerical Method for Geometrical Feature Extraction and Identification of Patient-Specific Aorta Models in Pediatric Congenital Heart Disease. Mathematics, 11(13), 2871. https://doi.org/10.3390/math11132871







