Inference Based on the Stochastic Expectation Maximization Algorithm in a Kumaraswamy Model with an Application to COVID-19 Cases in Chile
Abstract
:1. Introduction
2. Background
2.1. Trapezoidal Kumaraswamy Distribution
2.2. EM Algorithm
3. Bayesian Estimation for the Trapezoidal Kumaraswamy Model
3.1. The Model
3.2. SEM Algorithm
- (i)
- Generate candidates fromwhere is a hyperparameter and denotes the log-normal distribution. Here, we know thatThen, with probability provided bywe accept or reject the new values of the parameters (both of them).
- (ii)
- For a value generated from , that is, uniform in [0, 1], consider
- (i)
- [Initialization] Set arbitrary initial values for the parameter vector .
- (ii)
- [E-step] Compute from (4).
- (iii)
- [S-step] Simulate a sample from for each .
- (iv)
- [M-step]
- (a)
- Establish the weights from .
- (b)
- (c)
- (v)
- [Iteration] Repeat E-step, S-step, and M-step until a convergence criterion is achieved.
4. Simulation Study
4.1. Simulation Scenario
4.2. Results of the Simulations
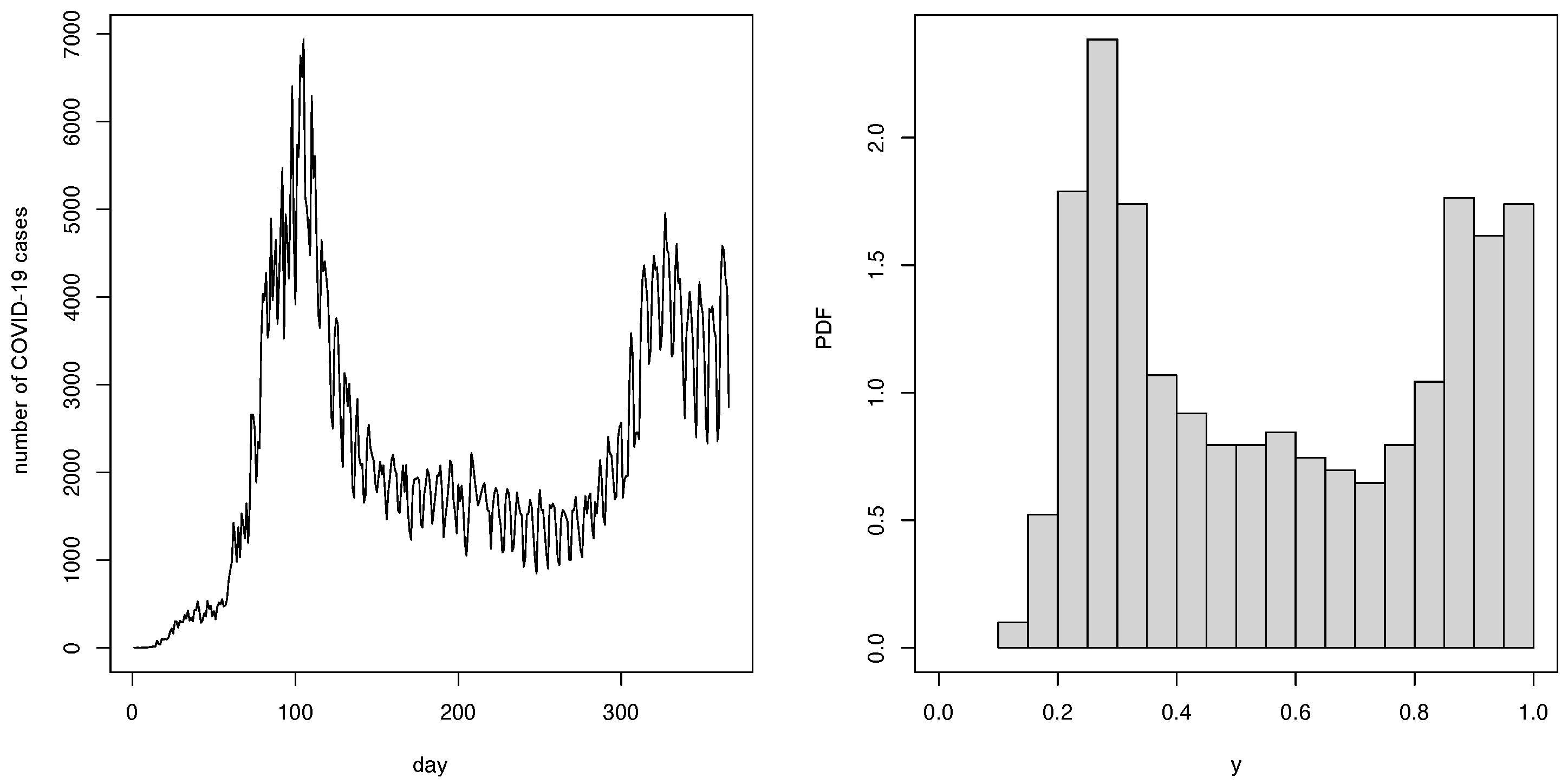
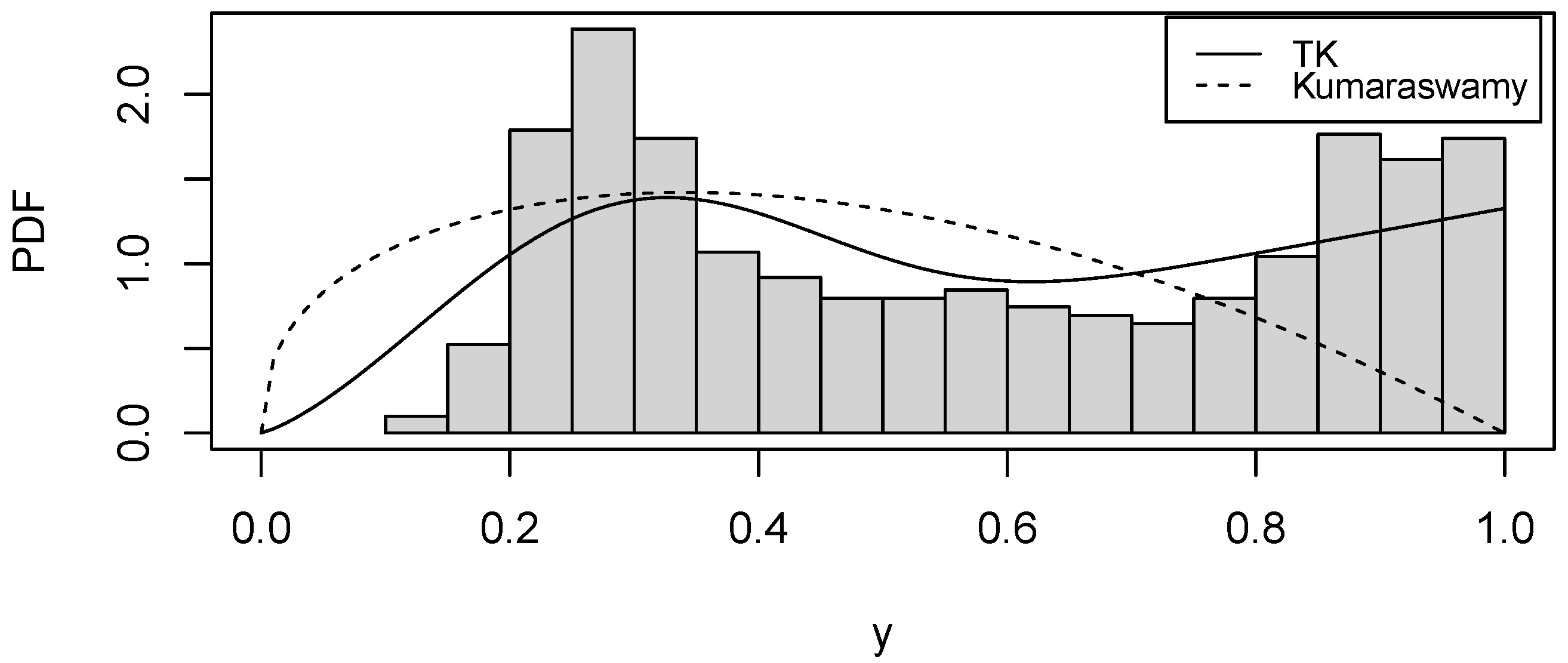
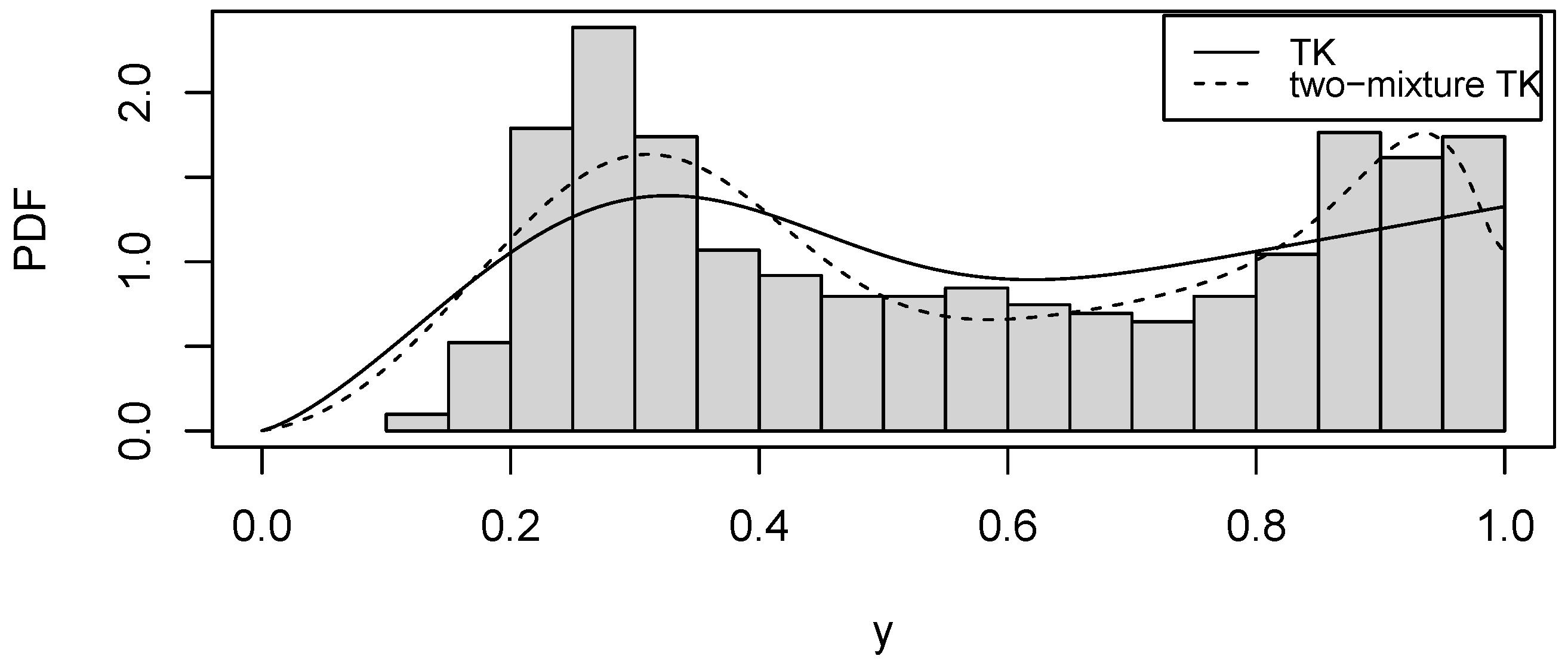
5. Empirical Illustration Using Real-World Data
COVID-19 Data
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumaraswamy, P. A generalized probability density function for double-bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Jones, M.C. Kumaraswamy distribution: A beta-type distribution with some tractability advantages. Stat. Methodol. 2009, 6, 70–81. [Google Scholar] [CrossRef]
- Bayer, F.M.; Cribari-Neto, F.; Santos, J. Inflated Kumaraswamy regressions with application to water supply and sanitation in Brazil. Stat. Neerl. 2021, 75, 453–481. [Google Scholar] [CrossRef]
- Tian, W.; Pang, L.; Tian, C.; Ning, W. Change point analysis for Kumaraswamy distribution. Mathematics 2023, 11, 553. [Google Scholar] [CrossRef]
- Nagy, H.; Al-Omari, A.I.; Hassan, A.S.; Alomani, G.A. Improved estimation of the inverted Kumaraswamy distribution parameters based on ranked set sampling with an application to real data. Mathematics 2022, 10, 4102. [Google Scholar] [CrossRef]
- Akinsete, A.; Famoye, F.; Lee, C. The Kumaraswamy-geometric distribution. J. Stat. Distrib. Appl. 2014, 1, 17. [Google Scholar] [CrossRef] [Green Version]
- Akinsete, A.; Famoye, F. The beta-Pareto distribution. Statistics 2008, 42, 547–563. [Google Scholar] [CrossRef]
- Figueroa-Zuniga, J.; Niklitschek, S.; Leiva, V.; Liu, S. Modeling heavy-tailed bounded data by the trapezoidal beta distribution with applications. REVSTAT-Stat. J. 2022, 20, 387–404. [Google Scholar]
- Cordeiro, G.; dos Santos, B. The beta power distribution. Braz. J. Probab. Stat. 2012, 26, 88–112. [Google Scholar]
- Cordeiro, G.; de Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2011, 81, 883–898. [Google Scholar] [CrossRef]
- Cordeiro, G.; Nadarajah, S.; Ortega, E. The Kumaraswamy Gumbel distribution. Stat. Methods Appl. 2012, 21, 139–168. [Google Scholar] [CrossRef]
- De Santana, T.; Ortega, E.; Cordeiro, G.; Silva, G. The Kumaraswamy-log-logistic distribution. J. Stat. Theory Appl. 2012, 11, 265–291. [Google Scholar]
- Eugene, N.; Lee, C.; Famoye, F. Beta-normal distribution and its applications. Commun. Stat. Theory Methods 2002, 3, 497–512. [Google Scholar] [CrossRef]
- Liang, Y.; Sun, D.; He, C.; Schootman, M. Modeling bounded outcome scores using the binomial-logit-normal distribution. Chil. J. Stat. 2014, 5, 3–14. [Google Scholar]
- Nadarajah, S.; Kotz, S. The beta-Gumbel distribution. Math. Probl. Eng. 2004, 10, 323–332. [Google Scholar] [CrossRef] [Green Version]
- Nadarajah, S.; Kotz, S. The beta exponential distribution. Reliab. Eng. Syst. Saf. 2006, 91, 689–697. [Google Scholar] [CrossRef]
- Figueroa, J.; Sanhueza, R.; Lagos, B.; Ibacache, G. Modeling bounded data with the trapezoidal Kumaraswamy distribution and applications to education and engineering. Chil. J. Stat. 2020, 11, 163–176. [Google Scholar]
- Cordeiro, G.; Ortega, M.; Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Frankl. Inst. 2010, 347, 1399–1429. [Google Scholar] [CrossRef]
- Mead, M.; Abd-Eltawab, A. A Note on Kumaraswamy-Fréchet Distribution. Aust. J. Basic Appl. Sci. 2014, 8, 294–300. [Google Scholar]
- de Pascoa, M.; Ortega, E.; Cordeiro, G. The Kumaraswamy generalized gamma distribution with application in survival analysis. Stat. Methodol. 2011, 8, 411–433. [Google Scholar] [CrossRef]
- García, C.B.; Pérez, J.G.; van Dorp, J.R. Modeling heavy-tailed, skewed and peaked uncertainty phenomena with bounded support. Stat. Methods Appl. 2011, 20, 463–486. [Google Scholar] [CrossRef]
- Hahn, E.D. Mixture densities for project management activity times: A robust approach to PERT. Eur. J. Oper. Res. 2008, 188, 450–459. [Google Scholar] [CrossRef]
- McLachlan, G.; Peel, D. Finite Mixture Models; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Dempster, A.; Laird, N.; Rubin, D. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. B 1977, 39, 1–38. [Google Scholar]
- Anil Meera, A.; Wisse, M. Dynamic expectation maximization algorithm for estimation of linear systems with colored noise. Entropy 2021, 23, 1306. [Google Scholar] [CrossRef] [PubMed]
- Lucini, M.M.; Van Leeuwen, P.J.; Pulido, M. Model error estimation using the expectation maximization algorithm and a particle flow filter. SIAM/ASA J. Uncertain. Quantif. 2021, 9, 681–707. [Google Scholar] [CrossRef]
- Han, M.; Wang, Z.; Zhang, X. An approach to data acquisition for urban building energy modeling using a gaussian mixture model and expectation-maximization algorithm. Buildings 2021, 11, 30. [Google Scholar] [CrossRef]
- Okamura, H.; Dohi, T. Application of EM algorithm to NHPP-based software reliability assessment with generalized failure count data. Mathematics 2021, 9, 985. [Google Scholar] [CrossRef]
- Massa, P.; Benvenuto, F. Predictive risk estimation for the expectation maximization algorithm with Poisson data. Inverse Probl. 2021, 37, 045013. [Google Scholar] [CrossRef]
- Mahdizadeh, M.; Zamanzade, E. On estimating the area under the ROC curve in ranked set sampling. Stat. Methods Med. Res. 2022, 31, 1500–1514. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Leiva, V.; Sanhueza, A.; Vilca, F. Estimation in the Birnbaum-Saunders distribution based on scale-mixture of normals and the EM-algorithm. Stat. Oper. Res. Trans. 2009, 33, 171–192. [Google Scholar]
- Couri, L.; Ospina, R.; da Silva, G.; Leiva, V.; Figueroa-Zuniga, J. A study on computational algorithms in the estimation of parameters for a class of beta regression models. Mathematics 2022, 10, 299. [Google Scholar] [CrossRef]
- Marchant, C.; Leiva, V.; Cysneiros, F.J.A. A multivariate log-linear model for Birnbaum-Saunders distributions. IEEE Trans. Reliab. 2016, 65, 816–827. [Google Scholar] [CrossRef]
- Celeux, G.; Govaert, G. A classification EM algorithm for clustering and two stochastic versions. Comput. Stat. Data Anal. 1992, 14, 315–332. [Google Scholar] [CrossRef] [Green Version]
- Celeux, G.; Diebolt, J. The SEM algorithm: A probabilistic teacher algorithm derived from the EM algorithm for the mixture problem. Comput. Stat. Q. 1985, 2, 73–82. [Google Scholar]
- Leiva, V.; Mazucheli, M.; Alves, B. A novel regression model for fractiles: Formulation, computational aspects, and applications to medical data. Fractal Fract. 2023, 7, 169. [Google Scholar] [CrossRef]
- Worldometers. COVID-19 Coronavirus Pandemic. Available online: www.worldometers.info/coronavirus (accessed on 21 June 2023).
- Mazucheli, M.; Alves, B.; Menezes, A.F.B.; Leiva, V. An overview on parametric quantile regression models and their computational implementation with applications to biomedical problems including COVID-19 data. Comput. Methods Programs Biomed. 2022, 221, 106816. [Google Scholar] [CrossRef]
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Chakraborty, T.; Ghosh, I. Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: A data-driven analysis. Chaos Solitons Fractals 2020, 135, 109850. [Google Scholar] [CrossRef]
- De la Fuente-Mella, H.; Rubilar, R.; Chahuán-Jiménez, K.; Leiva, V. Modeling COVID-19 cases statistically and evaluating their effect on the economy of countries. Mathematics 2021, 9, 1558. [Google Scholar] [CrossRef]
- Ospina, R.; Leite, A.; Ferraz, C.; Magalhaes, A.; Leiva, V. Data-driven tools for assessing and combating COVID-19 out-breaks based on analytics and statistical methods in Brazil. Signa Vitae 2022, 18, 18–32. [Google Scholar]
- Jerez-Lillo, N.; Álvarez, B.L.; Gutiérrez, J.M.; Figueroa-Zúñiga, J.; Leiva, V. A statistical analysis for the epidemiological surveillance of COVID-19 in Chile. Signa Vitae 2022, 18, 19–30. [Google Scholar]
- Boselli, P.M.; Soriano, J.M. COVID-19 in Italy: Is the mortality analysis a way to estimate how the epidemic lasts? Biology 2023, 12, 584. [Google Scholar] [CrossRef]
- Da Silva, C.C.; De Lima, C.L.; Da Silva, A.C.G.; Silva, E.L.; Marques, G.S.; De Araújo, L.J.B.; De Santana, M.A. COVID-19 dynamic monitoring and real-time spatio-temporal forecasting. Front. Public Health 2021, 9, 641253. [Google Scholar] [CrossRef]
- Sardar, I.; Akbar, M.A.; Leiva, V.; Alsanad, A.; Mishra, P. Machine learning and automatic ARIMA/Prophet models-based forecasting of COVID-19, Methodology, evaluation, and case study in SAARC countries. Stoch. Environ. Res. Risk Assess. 2022, 37, 345–359. [Google Scholar] [CrossRef]
- Heredia Cacha, I.; Sáinz-Pardo Díaz, J.; Castrillo, M.; García, Á.L. Forecasting COVID-19 spreading through an ensemble of classical and machine learning models: Spain’s case study. Sci. Rep. 2023, 13, 6750. [Google Scholar] [CrossRef]
- Gondim, J.A.M. Preventing epidemics by wearing masks: An application to COVID-19. Chaos Solitons Fractals 2021, 143, 110599. [Google Scholar] [CrossRef] [PubMed]
- Vasconcelos, G.L.; Brum, A.A.; Almeida, F.A.G.; Macêdo, A.M.S.; Duarte-Filho, G.C.; Ospina, R. Standard and Anomalous Waves of COVID-19, A Multiple-Wave Growth Model for Epidemics. Braz. J. Phys. 2021, 51, 1867–1883. [Google Scholar] [CrossRef]
- Vasconcelos, G.L.; Macêdo, A.M.S.; Duarte-Filho, G.C.; Brum, A.A.; Ospina, R.; Almeida, F.A.G. Power law behaviour in the saturation regime of fatality curves of the COVID-19 pandemic. Sci. Rep. 2021, 11, 4619. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Darcet, D.; Wang, Q.; Sornette, D. Generalized logistic growth modeling of the COVID-19 outbreak: Comparing the dynamics in provinces in China and in the rest of the world. Nonlinear Dyn. 2020, 101, 1561–1581. [Google Scholar] [CrossRef]
- Pérez-Ortega, J.; Almanza-Ortega, N.N.; Torres-Poveda, K.; Martínez-González, G.; Zavala-Díaz, J.C.; Pazos-Rangel, R. Application of data science for cluster analysis of COVID-19 mortality according to sociodemographic factors at municipal level in Mexico. Mathematics 2022, 10, 2167. [Google Scholar] [CrossRef]
- Alkady, W.; ElBahnasy, K.; Leiva, V.; Gad, W. Classifying COVID-19 based on amino acids encoding with machine learning algorithms. Chemom. Intell. Lab. Syst. 2022, 224, 104535. [Google Scholar] [CrossRef] [PubMed]
- De Araújo Morais, L.R.; Da Silva Gomes, G.S. Forecasting daily COVID-19 cases in the world with a hybrid ARIMA and neural network model. Appl. Soft Comput. 2022, 126, 109315. [Google Scholar] [CrossRef]
- Yousaf, M.; Zahir, S.; Riaz, M.; Hussain, S.M.; Shah, K. Statistical analysis of forecasting COVID-19 for upcoming month in Pakistan. Chaos Solitons Fractals 2020, 138, 109926. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165. [Google Scholar] [CrossRef] [PubMed]
- Martin-Barreiro, C.; Ramirez-Figueroa, J.A.; Cabezas, X.; Leiva, V.; Galindo-Villardón, M.P. Disjoint and functional principal component analysis for infected cases and deaths due to COVID-19 in South American countries with sensor-related data. Sensors 2021, 21, 4094. [Google Scholar] [CrossRef] [PubMed]
- Chimmula, V.K.R.; Zhang, L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 2020, 135, 109864. [Google Scholar] [CrossRef]
- ArunKumar, K.E.; Kalaga, D.V.; Sai Kumar, C.M.; Chilkoor, G.; Kawaji, M.; Brenza, T.M. Forecasting the dynamics of cumulative COVID-19 cases (confirmed, recovered and deaths) for top-16 countries using statistical machine learning models: Auto-regressive integrated moving average (ARIMA) and seasonal auto-regressive integrated moving average (SARIMA). Appl. Soft Comput. 2021, 103, 107161. [Google Scholar] [CrossRef]
- Verma, H.; Mandal, S.; Gupta, A. Temporal deep learning architecture for prediction of COVID-19 cases in India. Expert Syst. Appl. 2022, 195, 116611. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna. 2022. Available online: www.r-project.org (accessed on 21 June 2023).
- Bouguila, Z.; Monga, E.; Ziou, D. Practical Bayesian estimation of a finite beta mixture through Gibbs sampling and its applications. Stat. Comput. 2006, 16, 215–225. [Google Scholar] [CrossRef]
- Casella, G.; Robert, C. Introducing Monte Carlo Methods with R; Springer: New York, NY, USA, 2010. [Google Scholar]
- Diebolt, J.; Robert, C. Estimation of finite mixture distributions through Bayesian sampling. J. R. Stat. Soc. B 1994, 56, 363–375. [Google Scholar] [CrossRef]
- Spiegelhalter, D.; Best, N.; Carlin, B.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. B 2002, 64, 583–639. [Google Scholar] [CrossRef] [Green Version]
- Brooks, S.P. Discussion on the paper by Spiegelhalter, Best, Carlin, and van der Linde. J. R. Stat. Soc. B 2002, 64, 616–618. [Google Scholar]
- Carlin, B.; Louis, T. Bayes and Empirical Bayes Methods for Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Smithson, M.; Verkuilen, J. A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. Psychol. Methods 2006, 11, 54–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Distribution | Mean DIC | Mean EAIC | Mean EBIC | |
|---|---|---|---|---|
| TK | (0.5, 0.1) | −802.301 | −794.466 | −774.835 |
| (0.5, 1) | −801.519 | −794.616 | −774.985 | |
| (1, 0.1) | −780.712 | −782.756 | −763.125 | |
| (1, 1) | −783.543 | −783.138 | −763.507 | |
| Kumaraswamy | −526.796 | −604.993 | −595.177 |
| Distribution | Parameter | True Value | Mean | Standard Deviation | Median | 95% CI |
|---|---|---|---|---|---|---|
| TK | a | 0.1 | 0.098 | 0.018 | 0.095 | (0.077, 0.117) |
| b | 0.3 | 0.300 | 0.027 | 0.298 | (0.263, 0.335) | |
| 5 | 4.944 | 0.271 | 4.933 | (4.637, 5.237) | ||
| 10 | 9.932 | 1.234 | 9.646 | (8.303, 11.233) | ||
| Kumaraswamy | - | 3.006 | 0.154 | 2.996 | (2.828, 3.170) | |
| - | 3.139 | 0.327 | 3.097 | (2.825, 3.398) |
| Indicator | a | b | ||
|---|---|---|---|---|
| RelBias | −0.0041 | −0.0283 | −0.0174 | −0.0231 |
| 0.0139 | 0.0212 | 0.2170 | 0.9884 |
| Distribution | ( | Mean DIC | Mean EAIC | Mean EBIC |
|---|---|---|---|---|
| TK | (0.5, 0.1) | −1257.515 | −1321.922 | −1302.291 |
| (0.5, 1) | −1232.631 | −1311.324 | −1291.693 | |
| Kumaraswamy | −1257.887 | −1326.381 | −1316.566 |
| Distribution | Parameter | True Value | Mean | Standard Deviation | Median | 95% CI |
|---|---|---|---|---|---|---|
| TK | a | 0 | ||||
| b | 0 | |||||
| 5 | 4.980 | 0.149 | 4.970 | (4.715, 5.249) | ||
| 10 | 10.054 | 0.715 | 9.839 | (8.666, 11.272) | ||
| Kumaraswamy | 5 | 4.971 | 0.152 | 4.963 | (4.709, 5.239) | |
| 10 | 10.009 | 0.728 | 9.804 | (8.641, 11.214) |
| Distribution | Mean DIC | Mean EAIC | Mean EBIC |
|---|---|---|---|
| TK | 876.3951 | −207.6895 | −188.9261 |
| Kumaraswamy | 424.0051 | 428.0051 | 437.3868 |
| Distribution | Parameter | Mean | Standard Deviation | Median | 95% CI |
|---|---|---|---|---|---|
| TK | a | 0.0009 | 0.0030 | 0 | (0, 0.0050) |
| b | 1.3264 | 0.0487 | 1.3267 | (1.2373, 1.4211) | |
| 2.4929 | 0.5118 | 2.4966 | (1.4474, 3.4459) | ||
| 12.9142 | 8.4907 | 10.7872 | (1.5407, 29.9875) | ||
| Kumaraswamy | 1.4027 | 0.5590 | 1.2789 | (0.6033, 2.4522) | |
| 2.0127 | 7.5916 | 0.8599 | (0.4080, 2.1823) |
| Distribution | Mean DIC | Mean EAIC | Mean EBIC |
|---|---|---|---|
| Two-mixture TK | −603.6924 | −585.6924 | −543.4748 |
| TK | 876.3951 | −207.6895 | −188.9261 |
| Parameter | Mean | Standard Deviation | Median | 95% CI |
|---|---|---|---|---|
| 0.0013 | 0.0043 | 0 | (0, 0.0081) | |
| 1.6641 | 0.1651 | 1.6680 | (1.3678, 2) | |
| 15.8136 | 6.8317 | 15.4616 | (2.2682, 27.8903) | |
| 2.9145 | 2.5286 | 2.2340 | (0.0589, 8.1871) | |
| 0.0026 | 0.0097 | 0 | (0, 0.0162) | |
| 0.0938 | 0.01952 | 0 | (0, 0.6082) | |
| 3.0370 | 0.4966 | 3.065 | (2.0029, 3.9354 | |
| 26.4600 | 15.5967 | 22.7700 | (4.3897, 59.6894) | |
| p | 0.6120 | 0.0601 | 0.6248 | (0.4671, 0.6994) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Figueroa-Zúñiga, J.; Toledo, J.G.; Lagos-Alvarez, B.; Leiva, V.; Navarrete, J.P. Inference Based on the Stochastic Expectation Maximization Algorithm in a Kumaraswamy Model with an Application to COVID-19 Cases in Chile. Mathematics 2023, 11, 2894. https://doi.org/10.3390/math11132894
Figueroa-Zúñiga J, Toledo JG, Lagos-Alvarez B, Leiva V, Navarrete JP. Inference Based on the Stochastic Expectation Maximization Algorithm in a Kumaraswamy Model with an Application to COVID-19 Cases in Chile. Mathematics. 2023; 11(13):2894. https://doi.org/10.3390/math11132894
Chicago/Turabian StyleFigueroa-Zúñiga, Jorge, Juan G. Toledo, Bernardo Lagos-Alvarez, Víctor Leiva, and Jean P. Navarrete. 2023. "Inference Based on the Stochastic Expectation Maximization Algorithm in a Kumaraswamy Model with an Application to COVID-19 Cases in Chile" Mathematics 11, no. 13: 2894. https://doi.org/10.3390/math11132894
APA StyleFigueroa-Zúñiga, J., Toledo, J. G., Lagos-Alvarez, B., Leiva, V., & Navarrete, J. P. (2023). Inference Based on the Stochastic Expectation Maximization Algorithm in a Kumaraswamy Model with an Application to COVID-19 Cases in Chile. Mathematics, 11(13), 2894. https://doi.org/10.3390/math11132894







