Three-Part Composite Pareto Modelling for Income Distribution in Malaysia
Abstract
1. Introduction
2. Methodologies
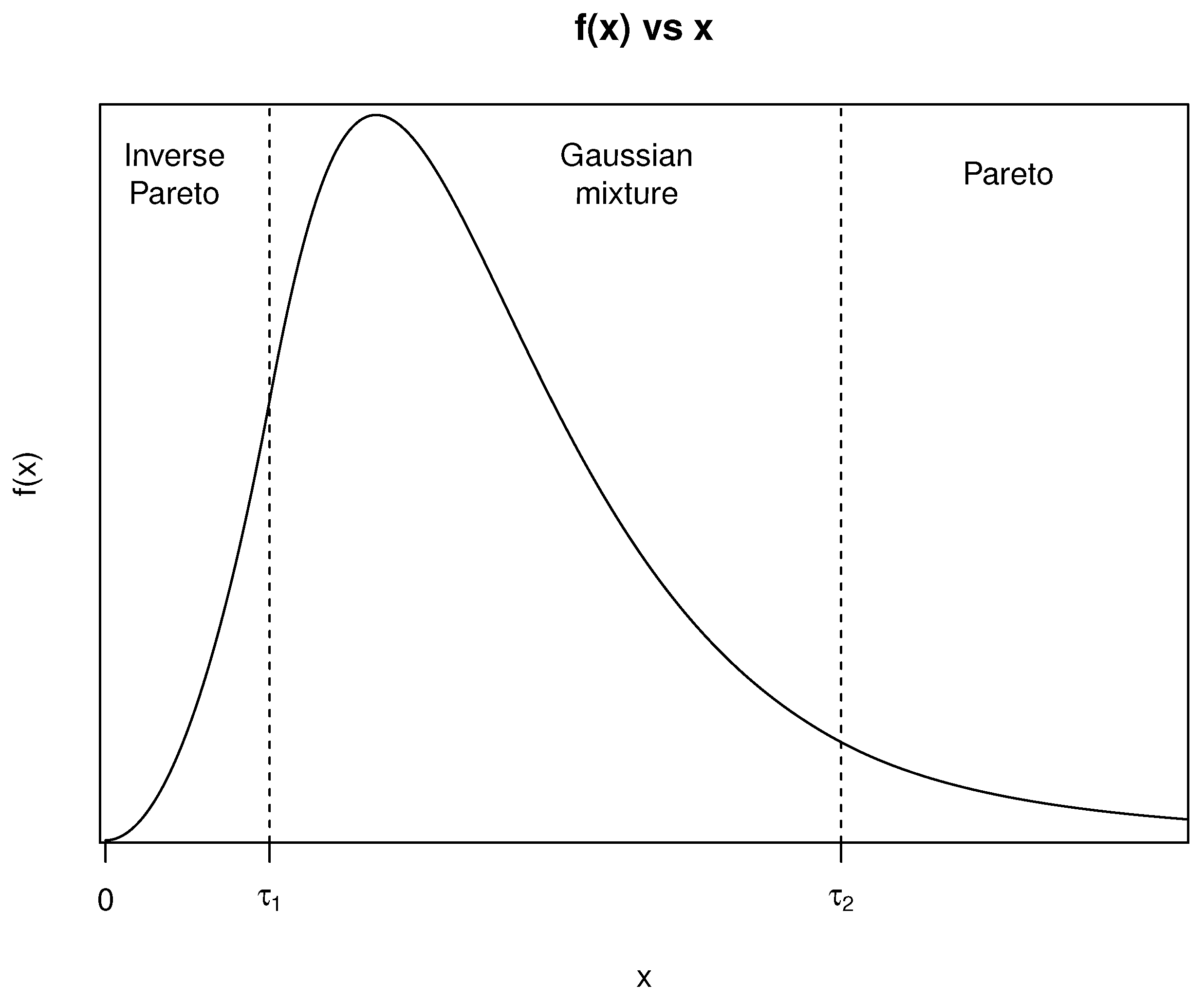
2.1. Three-Part Composite Pareto Model
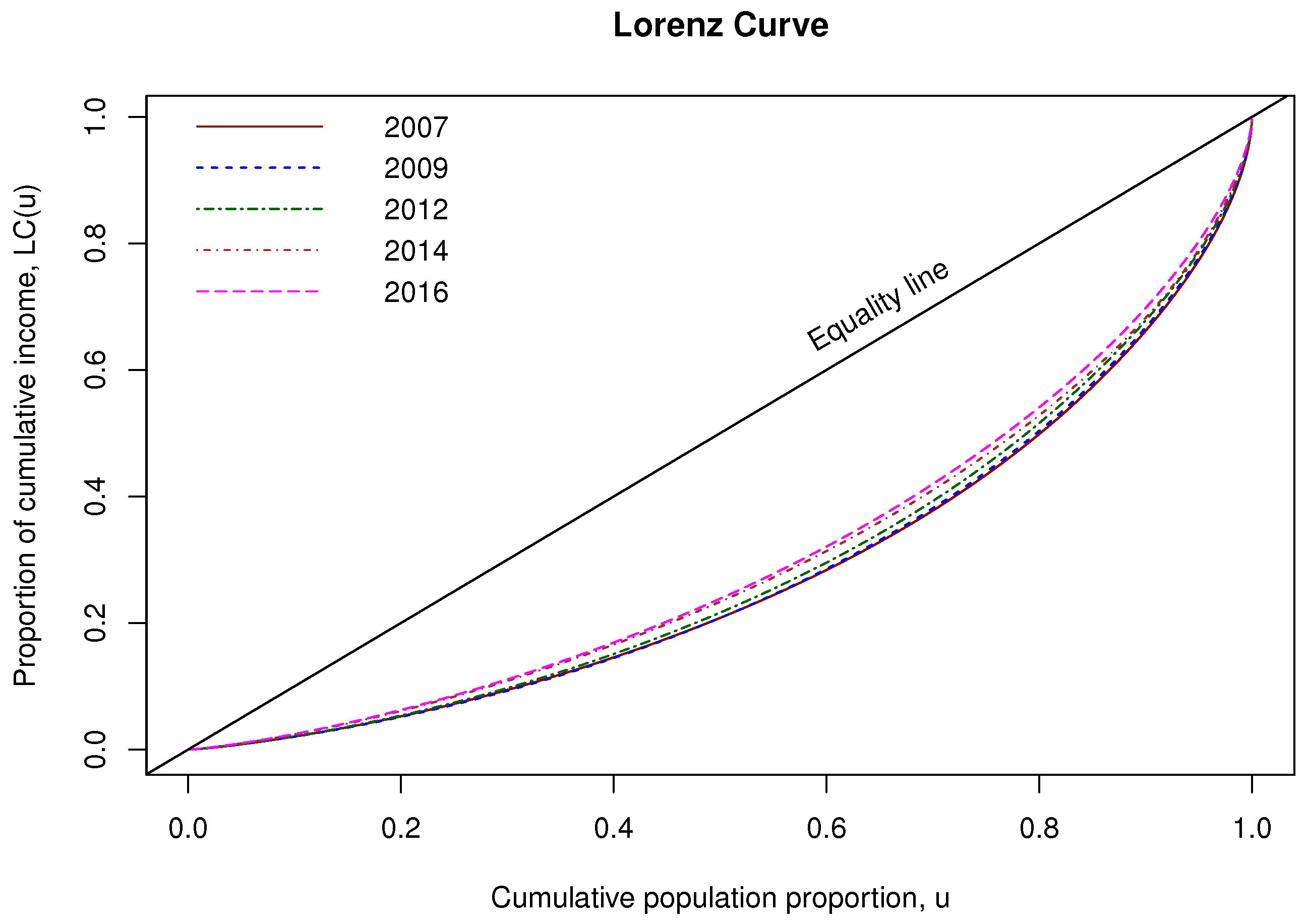
2.2. Lorenz Curve and Gini Index
2.3. Semi-Parametric Three-Part Composite Pareto Model
2.4. Statistical Methods for Complex Survey Data
3. Application to Income Distribution in Malaysia
3.1. Household Income Survey
3.2. Application of the Model
3.3. Income Inequality Using IP-GM-P Model
3.4. Comparison with Official Poverty Rate
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3PCP | Three-part composite Pareto model |
| BIC | Bayesian information criterion |
| CDF | Cumulative distribution function |
| HIS | Household income survey |
| IP-GM-P | Inverse Pareto-Gaussian mixture-Pareto |
| KS | Kolmogorov–Smirnov |
| Probability density function |
References
- Latimaha, R.; Bahari, Z.; Ismail, N.A. Examining the linkages between street crime and selected state economic variables in Malaysia: A panel data analysis. J. Ekon. Malays. 2019, 53, 59–72. [Google Scholar]
- Wang, S. Hate Crime Analysis based on Artificial Intelligence Methods. E3S Web Conf. 2021, 251, 01062. [Google Scholar] [CrossRef]
- Wilkinson, R.G.; Pickett, K.E. Income inequality and population health: A review and explanation of the evidence. Soc. Sci. Med. 2006, 62, 1768–1784. [Google Scholar] [CrossRef]
- Babones, S.J. Income inequality and population health: Correlation and causality. Soc. Sci. Med. 2008, 66, 1614–1626. [Google Scholar] [CrossRef]
- Patel, V.; Burns, J.K.; Dhingra, M.; Tarver, L.; Kohrt, B.A.; Lund, C. Income inequality and depression: A systematic review and meta-analysis of the association and a scoping review of mechanisms. World Psychiatry 2018, 17, 76–89. [Google Scholar] [CrossRef]
- Dewan, P.; Rørth, R.; Jhund, P.S.; Ferreira, J.P.; Zannad, F.; Shen, L.; Køber, L.; Abraham, W.T.; Desai, A.S.; Dickstein, K.; et al. Income Inequality and Outcomes in Heart Failure. JACC Heart Fail. 2019, 7, 336–346. [Google Scholar] [CrossRef]
- Posner, R.A. Equality, Wealth, and Political Stability. J. Law Econ. Organ. 1997, 13, 344–365. [Google Scholar] [CrossRef]
- Ravallion, M. Ethnic inequality and poverty in Malaysia since May 1969. Part 1: Inequality. World Dev. 2020, 134, 105040. [Google Scholar] [CrossRef]
- Dagum, C. A New Model of Personal Income Distribution: Specification and Estimation, Economie Appliquee. 1977; 413–437.
- Singh, S.K.; Maddala, G.S. A Function for Size Distribution of Incomes. Econometrica 1976, 44, 963–970. [Google Scholar] [CrossRef]
- Drăgulescu, A.; Yakovenko, V.M. Exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States. Phys. A Stat. Mech. Appl. 2001, 299, 213–221. [Google Scholar] [CrossRef]
- Fujiwara, Y.; Souma, W.; Aoyama, H.; Kaizoji, T.; Aoki, M. Growth and fluctuations of personal income. Phys. A Stat. Mech. Appl. 2003, 321, 598–604. [Google Scholar] [CrossRef]
- Jenkins, S.P. Pareto Models, Top Incomes and Recent Trends in UK Income Inequality. Economica 2017, 84, 261–289. [Google Scholar] [CrossRef]
- Oancea, B.; Andrei, T.; Pirjol, D. Income inequality in Romania: The exponential-Pareto distribution. Phys. A Stat. Mech. Appl. 2017, 469, 486–498. [Google Scholar] [CrossRef]
- Oancea, B.; Pirjol, D.; Andrei, T. A Pareto upper tail for capital income distribution. Phys. A Stat. Mech. Appl. 2018, 492, 403–417. [Google Scholar] [CrossRef]
- Reed, W.J. The Pareto, Zipf and other power laws. Econ. Lett. 2001, 74, 15–19. [Google Scholar] [CrossRef]
- Reed, W.J. The Pareto law of incomes—An explanation and an extension. Phys. A Stat. Mech. Appl. 2003, 319, 469–486. [Google Scholar] [CrossRef]
- Chakrabarti, B.K.; Chakraborti, A.; Chakravarty, S.R.; Chatterjee, A. Income and wealth distribution data for different countries. In Econophysics of Income and Wealth Distributions; Cambridge University Press: Cambridge, UK, 2013; pp. 7–34. [Google Scholar] [CrossRef]
- Razak, F.A.; Shahabuddin, F.A. Malaysian Household Income Distribution: A Fractal Point of View. Sains Malays. 2018, 47, 2187–2194. [Google Scholar] [CrossRef]
- Safari, M.A.M.; Masseran, N.; Ibrahim, K. Optimal threshold for Pareto tail modelling in the presence of outliers. Phys. A Stat. Mech. Appl. 2018, 509, 169–180. [Google Scholar] [CrossRef]
- Safari, M.A.M.; Masseran, N.; Ibrahim, K. A robust semi-parametric approach for measuring income inequality in Malaysia. Phys. A Stat. Mech. Appl. 2018, 512, 1–13. [Google Scholar] [CrossRef]
- Safari, M.A.M.; Masseran, N.; Ibrahim, K. On the identification of extreme outliers and dragon-kings mechanisms in the upper tail of income distribution. J. Appl. Stat. 2019, 46, 1886–1902. [Google Scholar] [CrossRef]
- Safari, M.A.M.; Masseran, N.; Ibrahim, K.; AL-Dhurafi, N.A. The power-law distribution for the income of poor households. Phys. A Stat. Mech. Appl. 2020, 557, 124893. [Google Scholar] [CrossRef]
- Cooray, K.; Ananda, M. Modeling actuarial data with a composite lognormal-Pareto model. Scand. Actuar. J. 2005, 2005, 321–334. [Google Scholar] [CrossRef]
- Albrecher, H.; Beirlant, J.; Teugels, J.L. Reinsurance: Actuarial and Statistical Aspects; Statistics in Practice; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Klugman, S.A.; Panjer, H.H.; Willmot, G.E. Loss Models: From Data to Decisions, 5th ed.; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Preda, V.; Ciumara, R. On composite models: Weibull-Pareto and Lognormal-Pareto. A comparative study. Rom. J. Econ. Forecast. 2006, 3, 32–46. [Google Scholar]
- Scollnik, D.P.M. On composite lognormal-Pareto models. Scand. Actuar. J. 2007, 2007, 20–33. [Google Scholar] [CrossRef]
- Cooray, K. The Weibull–Pareto Composite Family with Applications to the Analysis of Unimodal Failure Rate Data. Commun. Stat. Theory Methods 2009, 38, 1901–1915. [Google Scholar] [CrossRef]
- Teodorescu, S.; Vernic, R. On composite Pareto models. Math. Rep. 2013, 15, 11–29. [Google Scholar]
- Bakar, S.; Hamzah, N.; Maghsoudi, M.; Nadarajah, S. Modeling loss data using composite models. Insur. Math. Econ. 2015, 61, 146–154. [Google Scholar] [CrossRef]
- Calderín-Ojeda, E. A Note on Parameter Estimation in the Composite Weibull–Pareto Distribution. Risks 2018, 6, 11. [Google Scholar] [CrossRef]
- Aminzadeh, M.S.; Deng, M. Bayesian predictive modeling for Inverse Gamma-Pareto composite distribution. Commun. Stat. Theory Methods 2019, 48, 1938–1954. [Google Scholar] [CrossRef]
- Benatmane, C.; Zeghdoudi, H.; Shanker, R.; Lazri, N. Composite Rayleigh-Pareto distribution: Application to real fire insurance losses data set. J. Stat. Manag. Syst. 2021, 24, 545–557. [Google Scholar] [CrossRef]
- Mendes, B.V.d.M.; Lopes, H.F. Data driven estimates for mixtures. Comput. Stat. Data Anal. 2004, 47, 583–598. [Google Scholar] [CrossRef]
- Luckstead, J.; Devadoss, S. Pareto tails and lognormal body of US cities size distribution. Phys. A Stat. Mech. Appl. 2017, 465, 573–578. [Google Scholar] [CrossRef]
- Luckstead, J.; Devadoss, S.; Danforth, D. The size distributions of all Indian cities. Phys. A Stat. Mech. Appl. 2017, 474, 237–249. [Google Scholar] [CrossRef]
- Wiegand, M.; Nadarajah, S. New composite distributions for modeling industrial income and wealth per employee. Phys. A Stat. Mech. Appl. 2018, 492, 1901–1908. [Google Scholar] [CrossRef]
- Majid, M.H.A.; Ibrahim, K. Composite Pareto Distributions for Modelling Household Income Distribution in Malaysia. Sains Malays. 2021, 50, 2047–2058. [Google Scholar] [CrossRef]
- Clementi, F.; Gallegati, M. Pareto’s Law of Income Distribution: Evidence for Germany, the United Kingdom, and the United States. In Econophysics of Wealth Distributions: Econophys-Kolkata I; Chatterjee, A., Yarlagadda, S., Chakrabarti, B.K., Eds.; Springer: Milano, Italy, 2005; pp. 3–14. [Google Scholar] [CrossRef]
- Banerjee, A.; Yakovenko, V.M.; Di Matteo, T. A study of the personal income distribution in Australia. Phys. A Stat. Mech. Appl. 2006, 370, 54–59. [Google Scholar] [CrossRef]
- Cowell, F.A.; Victoria-Feser, M.P. Robust stochastic dominance: A semi-parametric approach. J. Econ. Inequal. 2007, 5, 21–37. [Google Scholar] [CrossRef]
- Kleiber, C.; Kotz, S. Statistical Size Distributions in Economics and Actuarial Sciences; Wiley Series in Probability and Statistics; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Kakwani, N.C.; Podder, N. Efficient Estimation of the Lorenz Curve and Associated Inequality Measures from Grouped Observations. In Modeling Income Distributions and Lorenz Curves; Chotikapanich, D., Ed.; Springer: New York, NY, USA, 2008; pp. 57–70. [Google Scholar] [CrossRef]
- Gastwirth, J.L. A General Definition of the Lorenz Curve. Econometrica 1971, 39, 1037. [Google Scholar] [CrossRef]
- Jorda, V.; Sarabia, J.M.; Jäntti, M. Inequality Measurement with Grouped Data: Parametric and Non-Parametric Methods. J. R. Stat. Soc. Ser. A Stat. Soc. 2021, 184, 964–984. [Google Scholar] [CrossRef]
- Schneider, M.P.A.; Scharfenaker, E. Mixing it up: The case for finite mixture models to study the distribution of income. Eur. Phys. J. Spec. Top. 2020, 229, 1685–1704. [Google Scholar] [CrossRef]
- Anderson, G.; Farcomeni, A.; Pittau, M.G.; Zelli, R. A new approach to measuring and studying the characteristics of class membership: Examining poverty, inequality and polarization in urban China. J. Econom. 2016, 191, 348–359. [Google Scholar] [CrossRef]
- Anderson, G.; Pittau, M.; Zelli, R.; Thomas, J. Income Inequality, Cohesiveness and Commonality in the Euro Area: A Semi-Parametric Boundary-Free Analysis. Econometrics 2018, 6, 15. [Google Scholar] [CrossRef]
- Chotikapanich, D.; Griffiths, W.E. Estimating Income Distributions Using a Mixture of Gamma Densities. In Modeling Income Distributions and Lorenz Curves; Chotikapanich, D., Ed.; Springer: New York, NY, USA, 2008; pp. 285–302. [Google Scholar] [CrossRef]
- Lubrano, M.; Ndoye, A.A.J. Income inequality decomposition using a finite mixture of log-normal distributions: A Bayesian approach. Comput. Stat. Data Anal. 2016, 100, 830–846. [Google Scholar] [CrossRef]
- Marron, J.S.; Wand, M.P. Exact Mean Integrated Squared Error. Ann. Stat. 1992, 20, 712–736. [Google Scholar] [CrossRef]
- Pfeffermann, D. The Role of Sampling Weights When Modeling Survey Data. Int. Stat. Rev. Rev. Int. De Stat. 1993, 61, 317. [Google Scholar] [CrossRef]
- Chambers, R.L.; Skinner, C.J. Analysis of Survey Data; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Janczura, J.; Weron, R. Goodness-of-Fit Testing for Regime-Switching Models, Working Paper. 2010.
- Janczura, J.; Weron, R. Goodness-of-fit testing for the marginal distribution of regime-switching models with an application to electricity spot prices. AStA Adv. Stat. Anal. 2013, 97, 239–270. [Google Scholar] [CrossRef]
- Xu, C.; Chen, J.; Mantel, H. Pseudo-likelihood-based Bayesian information criterion for variable selection in survey data. Surv. Methodol. 2013, 39, 303–321. [Google Scholar]
- OECD. It Together: Why Less Inequality Benefits All; OECD Publishing: Paris, France, 2015. [Google Scholar] [CrossRef]
- Congressional Budget Office. Projected Changes in the Distribution of Household Income, 2016 to 2021; Congressional Budget Office: Washington, DC, USA, 2019.
- Department of Statistics Malaysia. Estimates of Household Income and Poverty Incidence in Malaysia 2020; Technical Report; Department of Statistics Malaysia: Putrajaya, Malaysia, 2021.
- Department of Statistics Malaysia. Household Income and Basic Amenities Survey Report 2016; Technical Report; Department of Statistics Malaysia: Putrajaya, Malaysia, 2017; ISSN 2232-1012.


| Year | p-Value | ||||||
|---|---|---|---|---|---|---|---|
| 2007 | 3.2515 | 2.3674 | 0.0781 | 0.0757 | 464 | 4074 | 0.9782 |
| 2009 | 3.7424 | 2.3995 | 0.0615 | 0.0819 | 475 | 4431 | 0.9115 |
| 2012 | 4.4722 | 2.4513 | 0.0361 | 0.0996 | 518 | 4956 | 0.7948 |
| 2014 | 4.4227 | 2.6125 | 0.0296 | 0.0287 | 681 | 10179 | 0.9919 |
| 2016 | 4.5953 | 2.6405 | 0.0245 | 0.0597 | 759 | 8261 | 0.9306 |
| Year | IP-GM-P | Absolute Poverty Incidence | Relative Poverty Incidence |
|---|---|---|---|
| 2007 | 7.81 | 3.6 | 17.4 |
| 2009 | 6.15 | 3.8 | 19.3 |
| 2012 | 3.61 | 1.7 | 19.2 |
| 2014 | 2.96 | 0.6 | 15.6 |
| 2016 | 2.45 | 0.4 1 | 15.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majid, M.H.A.; Ibrahim, K.; Masseran, N. Three-Part Composite Pareto Modelling for Income Distribution in Malaysia. Mathematics 2023, 11, 2899. https://doi.org/10.3390/math11132899
Majid MHA, Ibrahim K, Masseran N. Three-Part Composite Pareto Modelling for Income Distribution in Malaysia. Mathematics. 2023; 11(13):2899. https://doi.org/10.3390/math11132899
Chicago/Turabian StyleMajid, Muhammad Hilmi Abdul, Kamarulzaman Ibrahim, and Nurulkamal Masseran. 2023. "Three-Part Composite Pareto Modelling for Income Distribution in Malaysia" Mathematics 11, no. 13: 2899. https://doi.org/10.3390/math11132899
APA StyleMajid, M. H. A., Ibrahim, K., & Masseran, N. (2023). Three-Part Composite Pareto Modelling for Income Distribution in Malaysia. Mathematics, 11(13), 2899. https://doi.org/10.3390/math11132899








