Crossing Numbers of Join Product with Discrete Graphs: A Study on 6-Vertex Graphs

Abstract

Reducing the number of crossings on graph edges can be useful in various applications, including network visualization, circuit design, graph theory, cartography or social choice theory. This paper aims to determine the crossing number of the join product $G^{*}+D_n$, where $G^{*}$ is a connected graph isomorphic to $K_{2,2,2}\setminus \{e_1,e_2\}$ obtained by removing two edges $e_1,e_2$ with a common vertex and a second vertex from the different partitions of the complete tripartite graph $K_{2,2,2}$, and $D_n$ is a discrete graph composed of n isolated vertices. The proofs utilize known exact crossing number values for join products of specific subgraphs $H_k$ of $G^{*}$ with discrete graphs in combination with the separating cycles. Similar approaches can potentially estimate unknown crossing numbers of other six-vertex graphs with a larger number of edges in join products with discrete graphs, paths or cycles.

1. Introduction

The crossing number is an important parameter of a graph as it provides information about the complexity of the graph and the difficulty of visualizing it [1]. In addition, the crossing number is related to many other graph parameters and algorithms, such as planarity testing, graph coloring and graph embedding. Graphs are widely used to represent complex networks, such as social, communication and transportation networks. Reducing the number of edge crossings in network visualizations can help to understand the network’s underlying structure and identify important nodes and connections [2]. In electronic circuit design, minimizing the number of edge crossings is important for reducing signal interference and improving circuit performance. Graph drawings with fewer crossings can lead to more efficient and reliable circuit designs [3]. In graph theory, reducing the number of edge crossings is a fundamental problem in planar graph theory. Many important graph algorithms and optimization problems are defined for planar graphs, where the graphs have no edge crossings [4]. In cartography, graphs are used to represent geographic features, such as roads, rivers and political boundaries. Reducing the number of edge crossings in such graphs can lead to clearer and more readable maps [5]. In social choice theory, the problem of drawing election maps with minimal edge crossings has been studied extensively. The goal is to create fair and unbiased election districts while minimizing the number of edge crossings [6]. Overall, reducing the number of crossings on graph edges can help in visualizing and understanding complex data, improving system performance and optimizing graph algorithms and optimizations [7].

Examining the number of crossings of simple graphs is a classic but still challenging problem. Garey and Johnson [8] proved that determining the crossing number $\mathrm{cr}\left(G\right)$ of a graph G belongs between NP-complete problems. Clancy’s work [9] provides a comprehensive collection of precise crossing number values for particular graphs or groups of graphs. The primary objective of his survey is to consolidate the published outcomes on crossing numbers and provide references, while also acknowledging the original authors who first reported these results. One of his chapters focuses specifically on the crossing numbers of join products involving simple graphs with at most six vertices (Chapter 4 in [9]). Let $D_n$ denote the discrete graph (sometimes called empty graph) on n vertices, and let $G+D_n$ be the join product of two graphs, G and $D_n$. The exact values for crossing numbers of $G+D_n$ for all graphs G of order at most four are given by Klešč and Schrötter [10], and, for some connected graphs G of order five and six, they are also listed in [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Additionally, it is worth noting that $\mathrm{cr}(G+D_n)$ are only available for certain disconnected graphs G [37,38,39,40].

The objective of this paper is to broaden the existing findings related to the outlined topic by applying them to new connected graphs. To achieve this, we introduce an innovative approach that leverages information from subgraphs with known crossing numbers. It will be shown that it is appropriate to combine this idea with the possibility of an existence of a separating cycle in some particular drawings of the investigated graph. In order to properly explain the given procedure, in the next chapter, we will define the necessary basic mathematical apparatus. Consequently, we will deal with cyclic permutations and possible drawings of graph $G^{*}$, which is a connected graph of order six isomorphic to the complete tripartite graph $K_{2,2,2}\setminus \{e_1,e_2\}$ obtained by removing two edges $e_1,e_2$ with one common vertex and a second vertex from $K_{2,2,2}$ different partitions. Finally, the crossing number of $G^{*}+D_n$ will be determined and proofed in the last chapter.

2. Basic Mathematical Apparatus

In graph theory, the crossing number $\mathrm{cr}\left(G\right)$ of a graph is the minimum number of crossings that a drawing of the graph in the plane must have. In other words, it is the smallest number of intersections between pairs of edges in any drawing of the graph in the plane. More formally, given a simple graph G, a drawing of G in the plane is a representation of the graph where the vertices from the vertex set $V\left(G\right)$ are represented by points and the edges from the edge set $E\left(G\right)$ are represented by curves connecting the points. A crossing occurs when two edges intersect at a point that is not an endpoint of either edge. It is evident that a drawing characterized by a minimal number of crossings, known as an optimal drawing, inherently possesses the desirable qualities of a good drawing. In such a drawing, the edges do not intersect themselves, no two edges cross multiple times and there are no instances where two edges connected to the same vertex intersect [11].

Let D be a good drawing of the graph G. We denote the number of crossings in D by ${\mathrm{cr}}_D\left(G\right)$. Let $G_i$ and $G_j$ be edge-disjoint subgraphs of G. We denote the number of crossings between edges of $G_i$ and edges of $G_j$ by ${\mathrm{cr}}_D(G_i,G_j)$, and the number of crossings among edges of $G_i$ in D by ${\mathrm{cr}}_D\left(G_i\right)$. It is readily apparent that, for any three subgraphs $G_i$, $G_j$ and $G_k$ of G that do not share any common edges, the following equations are valid:

$${\mathrm{cr}}_D(G_i\cup G_j)={\mathrm{cr}}_D\left(G_i\right)+{\mathrm{cr}}_D\left(G_j\right)+{\mathrm{cr}}_D(G_i,G_j),$$

(1)

$${\mathrm{cr}}_D(G_i\cup G_j,G_k)={\mathrm{cr}}_D(G_i,G_k)+{\mathrm{cr}}_D(G_j,G_k).$$

(2)

Throughout this paper, some parts of proofs will be based on Kleitman’s result [41] on crossing numbers for some complete bipartite graphs $K_{m,n}$ on $m+n$ vertices with a partition $V\left(K_{m,n}\right)=V_1\cup V_2$ and $V_1\cap V_2=Ø$ containing an edge between every pair of vertices from $V_1$ and $V_2$ of sizes m and n, respectively. He showed that

$$\mathrm{cr}\left(K_{m,n}\right)=⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋,\mathrm{if}min\{m,n\}\le 6.$$

(3)

The composite graph obtained by combining two graphs, $G_i$ and $G_j$, known as their join product $G_i+G_j$, is constructed by incorporating separate copies of $G_i$ and $G_j$ with no shared vertices. This combination is achieved by adding all possible edges between the vertex sets $V\left(G_i\right)$ and $V\left(G_j\right)$. In the case where $\left|V\right(G_i\left)\right|=m$ and $\left|V\right(G_j\left)\right|=n$, the edge set of $G_i+G_j$ is composed of the disjoint sets of edges from $G_i$, $G_j$ and the complete bipartite graph $K_{m,n}$.

In a good drawing D of some graph G, we say that a cycle C separates some two different vertices of the subgraph $G\setminus C$ if they are contained in different components of ${\mathbb{R}}^2\setminus C$, where ${\mathbb{R}}^2$ means a two-dimensional space. This considered cycle C is said to be a separating cycle of graph G in D.

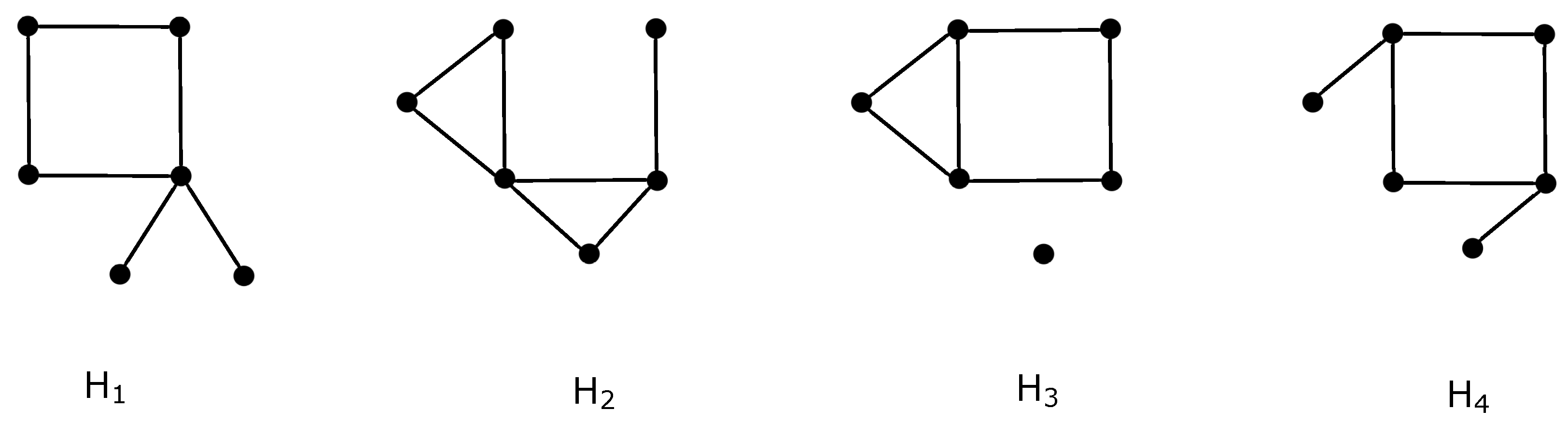
Let $G^{*}=(V\left(G^{*}\right),E\left(G^{*}\right))$ be the connected graph of order six isomorphic to $K_{2,2,2}\setminus \{e_1,e_2\}$, and let $V\left(G^{*}\right)=\{v_1,v_2,\cdots ,v_6\}$. A lot of possible drawings of the graph $G^{*}$ are partially solved using the existence of a separating cycle on its edges together with the already known exact values of $\mathrm{cr}(H_k+D_n)$ for four subgraphs $H_k$ of $G^{*}$, presented in Theorems 1, 2, 3 and 4 in the next chapter. The considered specific subgraphs $H_k$, $k=1,2,3,4$ are depicted in Figure 1.

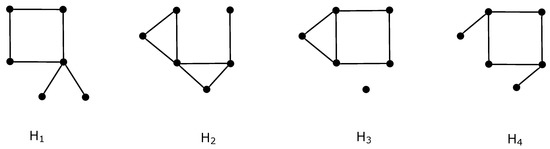
Figure 1. Four graphs $H_k$ on six vertices with well-known values of $\mathrm{cr}(H_k+D_n)$, where $k=1,2,3,4$.

3. Cyclic Permutations and Possible Drawings of ${\mathbf{G}}^{*}$

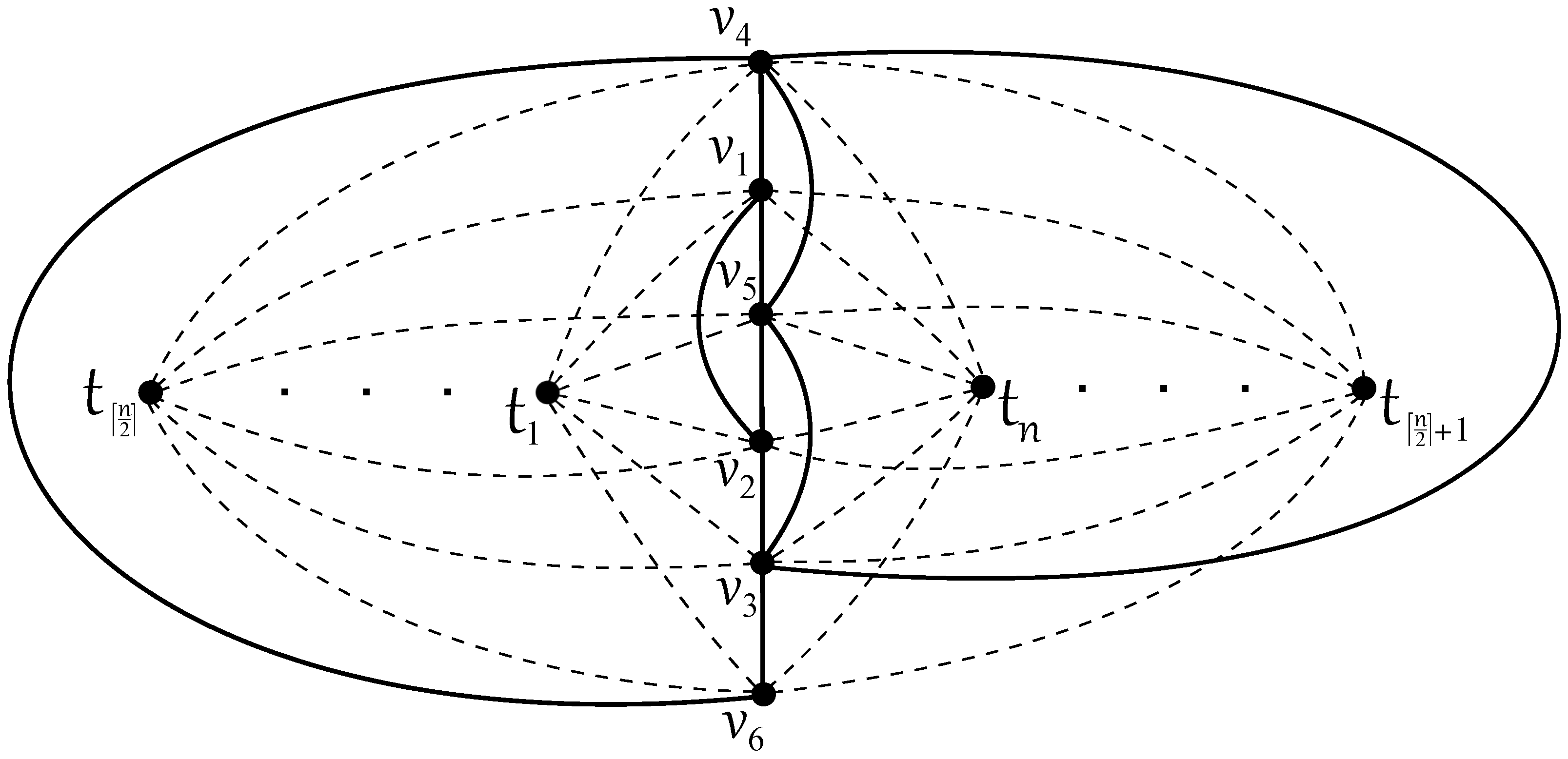
The join product, denoted as $G^{*}+D_n$ (or sometimes $G^{*}+n{K}_1$), is formed by combining a copy of the graph $G^{*}$ with n additional vertices, labeled as $t_1,\cdots ,t_n$. Each of these newly added vertices $t_i$ is connected to every vertex in the original graph $G^{*}$. We define the subgraph $T^i$ as the collection of six edges incident to the fixed vertex $t_i$. This arrangement leads to the following result:

$$G^{*}+D_n=G^{*}\cup K_{6,n}=G^{*}\cup \left(\bigcup _{i=1}^n{T}^i\right).$$

(4)

Let us consider a good drawing D of $G^{*}+D_n$. The rotation, ${\mathrm{rot}}_D\left(t_i\right)$, of a vertex $t_i$ in D is defined as the cyclic permutation that documents the counterclockwise order, in which the edges departing from $t_i$ appear. This rotation, introduced by Hernández-Vélez et al. [42] or Woodall [43], employs a notation $\left(123456\right)$ to represent the counter-clockwise order of edges incident to the vertex $t_i$, such as $t_i{v}_1$, $t_i{v}_2$, $t_i{v}_3$, $t_i{v}_4$, $t_i{v}_5$ and $t_i{v}_6$. It is important to note that the rotation signifies a cyclic permutation. In the given drawing D, it is highly advantageous to categorize the n subgraphs $T^i$ into three distinct subsets based on the number of times they intersect edges of $G^{*}$. Let $R_D$ represent the set of subgraphs where ${\mathrm{cr}}_D(G^{*},T^i)=0$ (indicating zero crossings), and let $S_D$ represent the set of subgraphs where ${\mathrm{cr}}_D(G^{*},T^i)=1$ (indicating one crossing). All remaining subgraphs $T^i$, which cross edges of $G^{*}$ at least twice in D, fall into the third subset.

It is easy to see that, if D is a good drawing of $G^{*}+D_n$ with the empty set $R_D\cup S_D$, then ${\sum }_{i=1}^n{\mathrm{cr}}_D(G^{*},T^i)\ge 2n$ enforces at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ crossings in D provided by

$$\begin{array}{ccc}\hfill {\mathrm{cr}}_D(G^{*}+D_n)& =& {\mathrm{cr}}_D\left(G^{*}\right)+{\mathrm{cr}}_D\left(K_{6,n}\right)+{\mathrm{cr}}_D(G^{*},K_{6,n})\hfill \\ & \ge & 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋.\hfill \end{array}$$

(5)

According to the expected result of main Theorem 5, this leads to a consideration of the nonempty set $R_D\cup S_D$ in all good drawings of $G^{*}+D_n$.

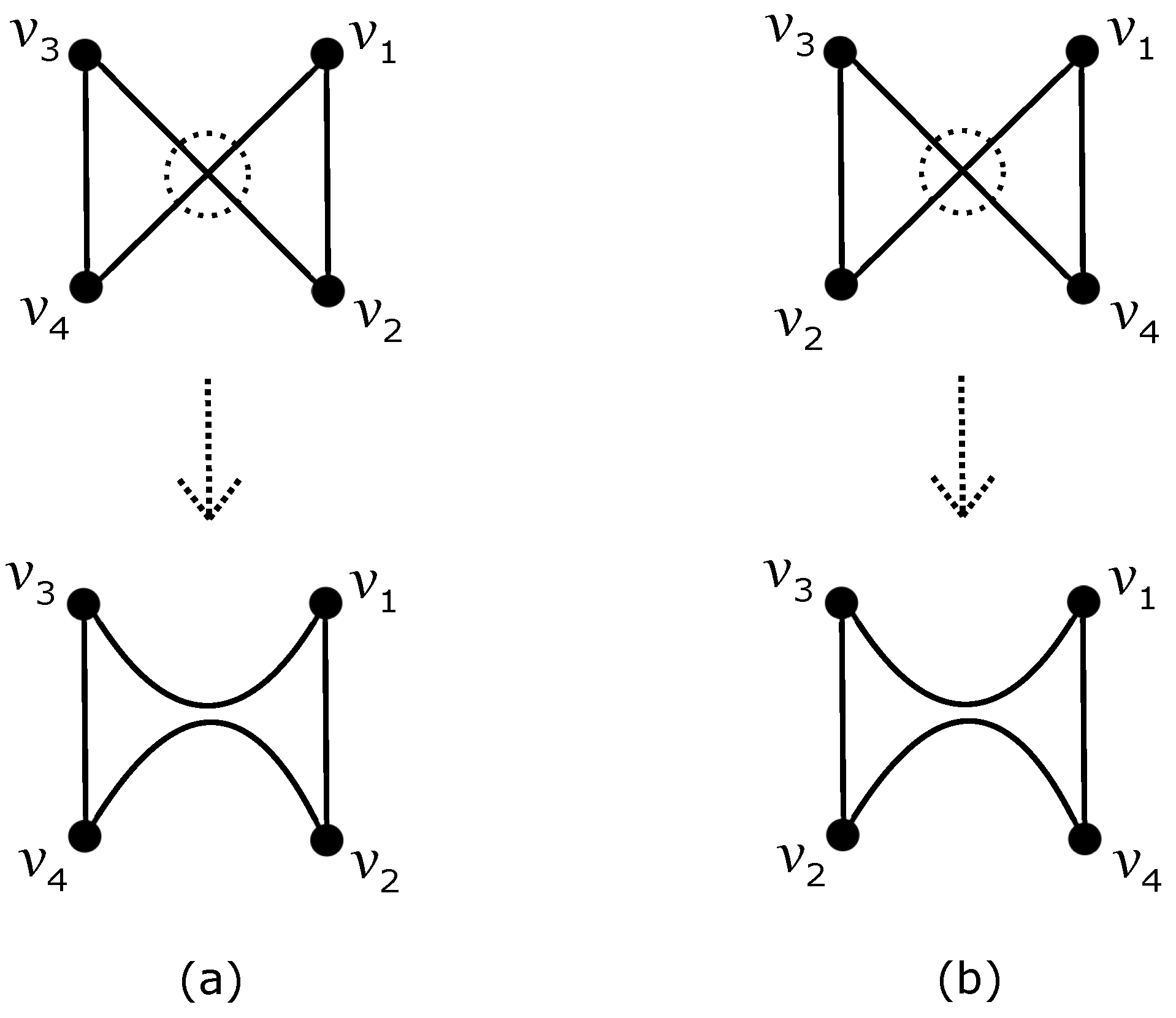
Let us explore the various potential drawings of $G^{*}$ induced by D with the degree sequence $(2,3,3,4,4,4)$. In the rest of the paper, suppose that $\mathrm{deg}\left(v_6\right)=2$, and also $\mathrm{deg}\left(v_5\right)=4$ if $v_5{v}_6\notin E\left(G^{*}\right)$. The graph $G^{*}$ contains a cycle $C_4$ induced on four remaining vertices of degrees 3, 3, 4 and 4 as a subgraph (for brevity, we write $C_4^{★}$), and let $v_1$, $v_2$, $v_3$ and $v_4$ be their vertex notation in the appropriate order of the cycle $C_4^{★}$. In Figure 2a, we show the ability to redraw a crossing of two edges of $C_4^{★}$ to obtain a new drawing of $G^{*}$ induced by D with fewer edge crossings (the vertex notation is now in a different order). The redrawing of $C_4^{★}$ in Figure 2b produces a drawing of another graph containing the complete bipartite graph $K_{2,4}$ as a subgraph, but Ho [17] knows that $\mathrm{cr}(K_{2,4}+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n$. Clearly, $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+1$ (obtained by adding one crossing by a return back to the original graph) is greater than our expected result of $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$.

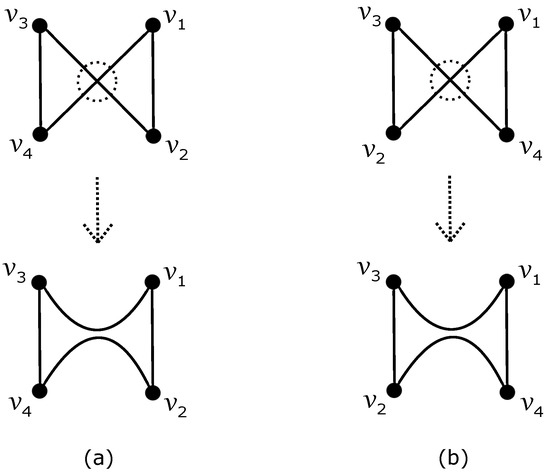
Figure 2. Elimination of a crossing on the edges of $C_4^{★}$: (a) redrawing of graph $G^{*}$ with vertex notation in a different order; (b) redrawing of cycle $C_4^{★}$, which causes a drawing of a new graph containing $K_{2,4}$ as a subgraph.

Both considered redrawings of cycle $C_4^{★}$ allow us to suppose that edges of $C_4^{★}$ do not cross each other in all discussed good drawings of $G^{*}$. In an effort to reach less than $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ crossings, two remaining vertices $v_5$ and $v_6$ of graph $G^{*}$ must be placed in the same region of the considered good subdrawing $D\left(C_4^{★}\right)$. The reason is that removing all edges of $C_4^{★}$ results in a good drawing of $H_1+D_n$ with at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋$ crossings by [31] (Theorem 1), where the graph $H_1$ on six vertices consists of one 4 cycle and two leaves adjacent to the same vertex of the 4 cycle (see Figure 1).

Theorem 1

([31], Theorem 3.4). $\mathrm{cr}(H_1+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋$ for $n\ge 1$.

Note that $C_4^{★}$ would be a separating cycle in this drawing and thus would be crossed at least n times. Based on that, in the rest of the paper, let both vertices $v_5$ and $v_6$ be placed in the common outer region of $D\left(C_4^{★}\right)$.

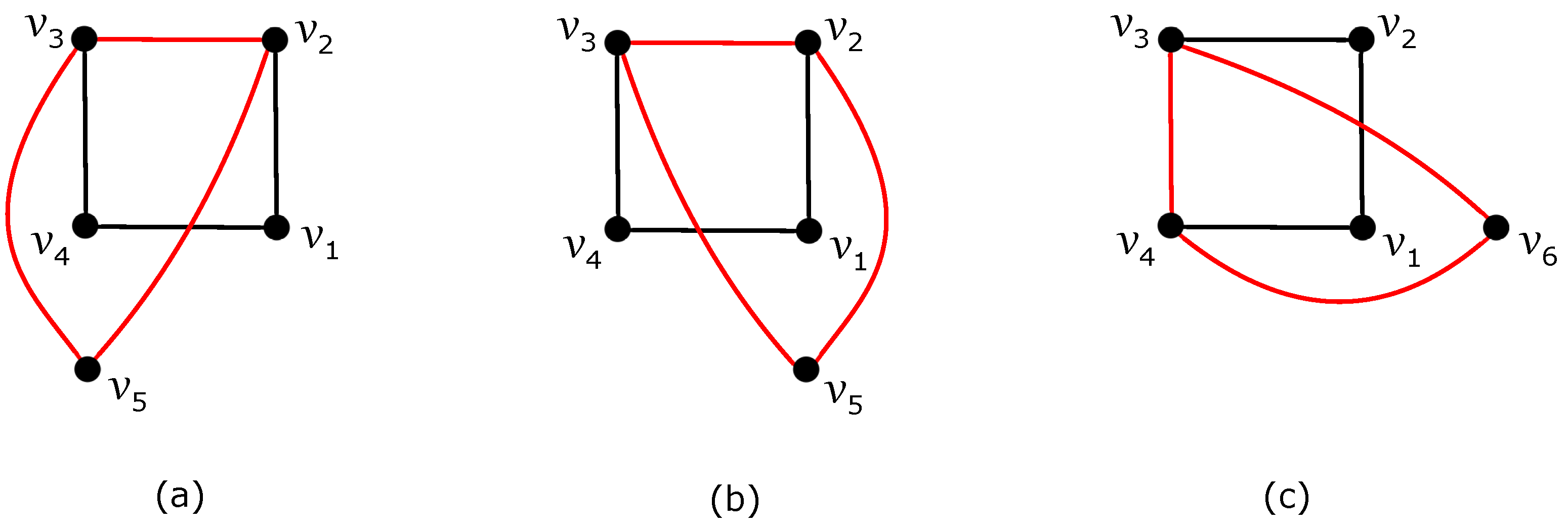
Using the idea of a separating cycle, if we consider some subdrawing of the graph $G^{*}$ presented in Figure 3a or Figure 3b, then the value of $\mathrm{cr}(H_2+D_n)$ proofed in [33] (Theorem 2) enforces at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋+n+1$ crossings on edges of $G^{*}+D_n$.

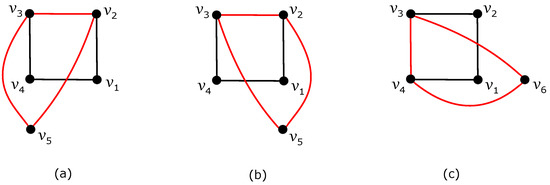
Figure 3. Three separating cycles on the edges of $G^{*}$: (a) a subdrawing of $G^{*}$ with the separating cycle $v_2{v}_3{v}_5{v}_2$ and the vertex $v_4$ located inside it; (b) a subdrawing of $G^{*}$ with the separating cycle $v_2{v}_3{v}_5{v}_2$ and the vertex $v_1$ located inside it; (c) a subdrawing of $G^{*}$ with the separating cycle $v_3{v}_4{v}_6{v}_3$.

Theorem 2

([33], Corollary 2). $\mathrm{cr}(H_2+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋$ for $n\ge 1$.

Removing all edges of the separating cycle $v_3{v}_4{v}_6{v}_3$ in Figure 3c produces a good drawing that includes $H_3+D_n$ as a subgraph. Consequently, the result of Theorem 3 also implies at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋+n+1$ crossings on the edges of $G^{*}+D_n$.

Theorem 3

([38], Theorem 3.4). $\mathrm{cr}(H_3+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋$ for $n\ge 1$.

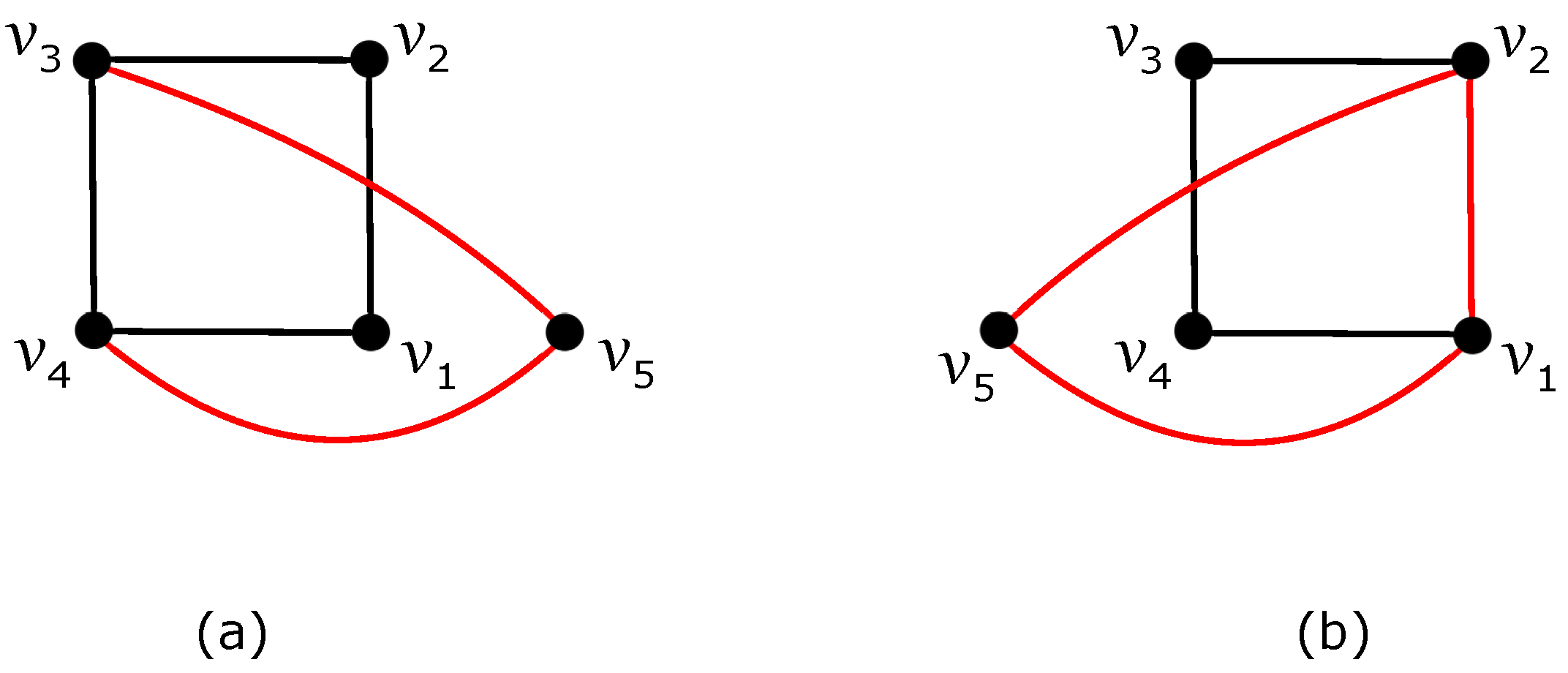
In the next, let $v_3{v}_4{v}_6{v}_3$ not be a separating cycle in $D\left(G^{*}\right)$. In the case of the subdrawing of $G^{*}$ in Figure 4a, the good drawing of $H_3+D_n$ with at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋$ crossings is obtained by removing all edges of the separating cycle $v_3{v}_5{v}_4{v}_3$ by Theorem 3. Finally, removing all edges of the separating cycle $v_1{v}_5{v}_2{v}_1$ in Figure 4b results in a good drawing, including $H_4+D_n$ as a subgraph, which yields at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋+n+1$ crossings at edges of $G^{*}+D_n$ according to Theorem 4.

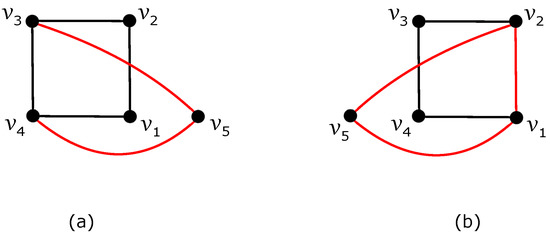
Figure 4. Two separating cycles on the edges of $G^{*}$: (a) a subdrawing of $G^{*}$ with the separating cycle $v_3{v}_4{v}_5{v}_3$; (b) a subdrawing of $G^{*}$ with the separating cycle $v_1{v}_2{v}_5{v}_1$.

Theorem 4

([13], Theorem 3.1). $\mathrm{cr}(H_4+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋$ for $n\ge 1$.

The proof of following Lemma 1 can be omitted based on all the above observations.

Lemma 1.

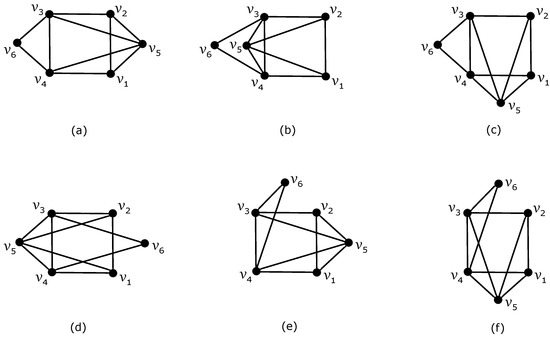
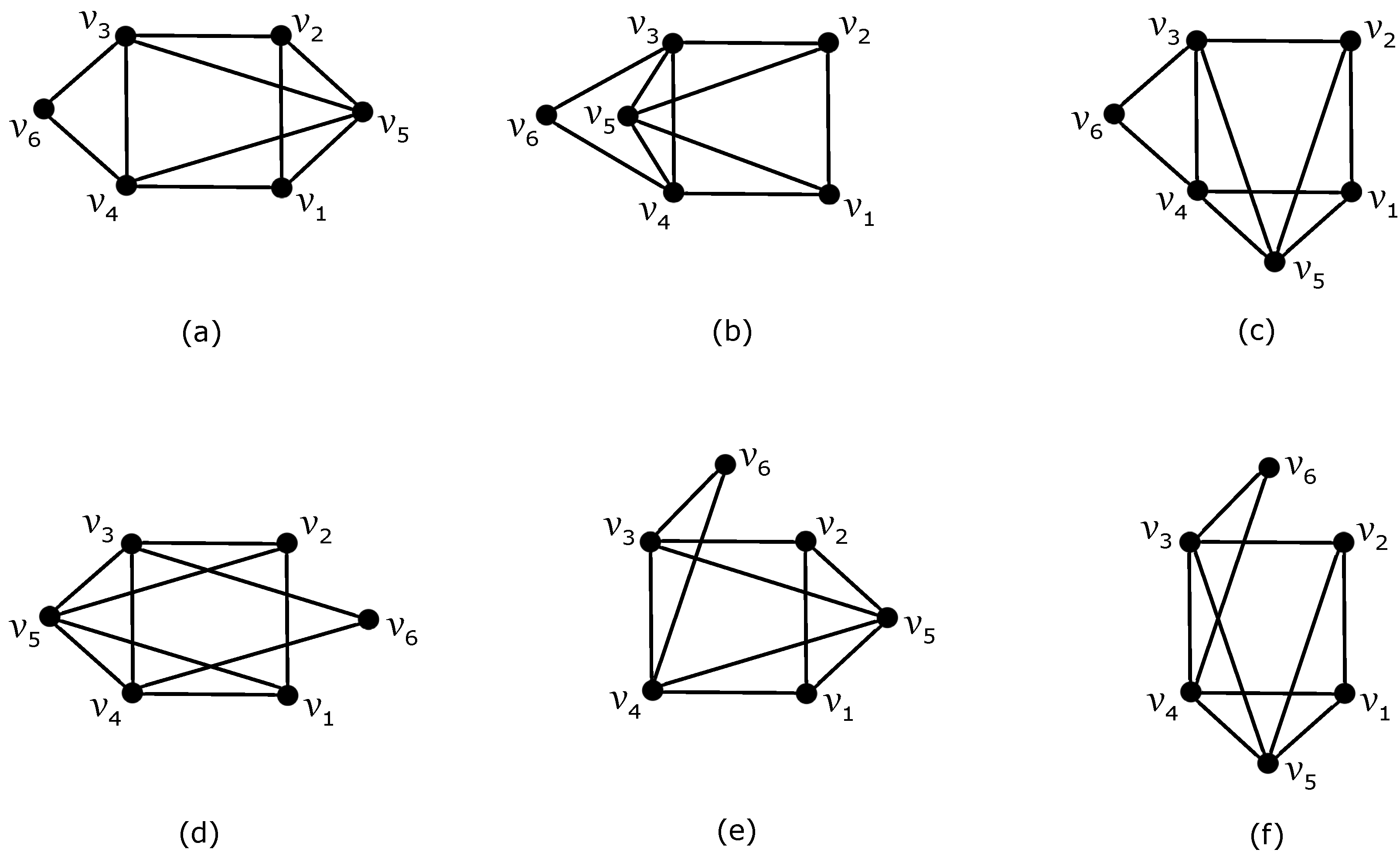
In any optimal drawing D of the join product $G^{*}+D_n$, the edges of $C_4^{★}$ do not cross each other. Moreover, if both vertices $v_5$ and $v_6$ are placed in a common region of $D\left(C_4^{★}\right)$, then the drawing of $G^{*}$ induced by D is isomorphic to one of the six drawings depicted in Figure 5.

Figure 5. Six considered nonplanar drawings of graph $G^{*}$ with a possibility of obtaining a subgraph $T^i$ by which edges of $G^{*}$ can be crossed at most once: (a) the drawing of $G^{*}$ with ${\mathrm{cr}}_D\left(G^{*}\right)=2$ and two crossings on edge $v_1{v}_2$; (b) the drawing of $G^{*}$ with ${\mathrm{cr}}_D\left(G^{*}\right)=2$ and two crossings on edge $v_3{v}_4$; (c) the drawing of $G^{*}$ with ${\mathrm{cr}}_D\left(G^{*}\right)=2$ and two crossings on edge $v_1{v}_4$; (d) the drawing of $G^{*}$ with two crossings on both edges $v_1{v}_2$ and $v_3{v}_4$; (e) the drawing of $G^{*}$ with ${\mathrm{cr}}_D\left(G^{*}\right)=4$ and two crossings on edge $v_1{v}_2$; (f) the drawing of $G^{*}$ with ${\mathrm{cr}}_D\left(G^{*}\right)=4$ and two crossings on edge $v_1{v}_4$.

In the proof of Theorem 5, Lemma 2 related to some restricted subdrawings of the graph $G^{*}+D_n$ is also required. The meaning of Lemma 2 is actually wider since it can be generalised for any graph G on six vertices fulfilling the conditions.

Lemma 2.

For $n\ge 2$, let D be a good drawing of $G^{*}+D_n$ in which, for some i, $i\in \{1,\cdots ,n\}$ and for all $j=1,\cdots ,n$, $j\ne i$, ${\mathrm{cr}}_D(G^{*}\cup T^i,T^j)\ge 5$. If ${\mathrm{cr}}_D(G^{*}\cup T^i,T^j)>5$ for p different subgraphs $T^j$, then D has at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+4⌊\frac{n}{2}⌋+p+{\mathrm{cr}}_D(G^{*}\cup T^i)$ crossings.

Proof. 

Let $F^i$ denote the subgraph $G^{*}\cup T^i$ for $T^i\in R_D$, where $i\in \{1,\cdots ,n\}$. Thus, for a given subdrawing of $G^{*}$ in D, any subgraph $F^i$ is exactly represented by ${\mathrm{rot}}_D\left(t_i\right)$. Assume, without loss of generality, that the edges of $F^n=G^{*}\cup T^n$ are crossed in D at least five times by the edges of every subgraph $T^j$, $j=1,\cdots ,n-1$ and that p of subgraph $T^j$ crosses the edges of $F^n$ more than five times. As $G^{*}+D_n=K_{6,n-1}\cup F^n$, we have

$$\begin{array}{ccc}\hfill {\mathrm{cr}}_D(G^{*}+D_n)& =& {\mathrm{cr}}_D\left(K_{6,n-1}\right)+{\mathrm{cr}}_D(K_{6,n-1},F^n)+{\mathrm{cr}}_D\left(F^n\right)\hfill \\ & \ge & 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+5(n-1)+p+{\mathrm{cr}}_D(G^{*}\cup T^n)\hfill \\ \hfill & \ge & 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+4⌊\frac{n}{2}⌋+p+{\mathrm{cr}}_D(G^{*},T^n)+{\mathrm{cr}}_D\left(G^{*}\right).\hfill \end{array}$$

(6)

□

Note that the last estimate used in the proof of Lemma 2 does not offer at least $6\lfloor \frac{n}{2}\rfloor \lfloor \frac{n-1}{2}\rfloor +n+2\lfloor \frac{n}{2}\rfloor$ crossings only for n odd with $p=0$ and $T^n\in R_D$ in some planar drawing of $G^{*}$.

A final lemma that we will use in the proof of Theorem 5 is labelled Lemma 3:

Lemma 3.

$\mathrm{cr}(G^{*}+D_1)=1$.

Proof. 

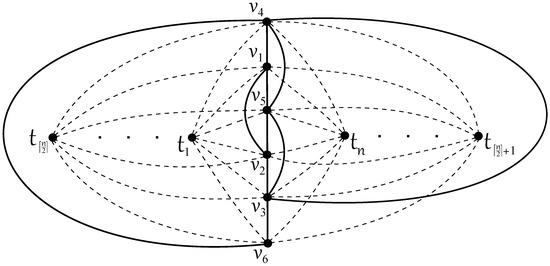
Figure 6 offers the subdrawing of $G^{*}+D_1$ with 1 crossing, so $\mathrm{cr}(G^{*}+D_1)\le 1$. Graph $G^{*}+D_1$ contains a subgraph isomorphic to $K_{3,3}$, and it is well-known by Kleitman [41] that $\mathrm{cr}\left(K_{3,3}\right)=1$. As $\mathrm{cr}(G^{*}+D_1)\ge \mathrm{cr}\left(K_{3,3}\right)=1$, the proof of Lemma 3 is complete. □

Figure 6. The good drawing of $G^{*}+D_n$ with $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ crossings.

4. Crossing Number of the Join Product ${\mathbf{G}}^{*}+{\mathbf{D}}_{\mathbf{n}}$

Based on the previous sections, we have prepared all the lemmas for determining and proving the resulting value of the crossing number for investigated graph $G^{*}+D_n$.

Theorem 5.

$\mathrm{cr}(G^{*}+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ for $n\ge 1$.

Proof. 

The result is justified for $n=1$ using Lemma 3. In Figure 6, the edges of the complete bipartite graph $K_{6,n}$ cross each other exactly

$$6\left(\genfrac{}{}{0pt}{}{\lceil \frac{n}{2}\rceil }{2}\right)+6\left(\genfrac{}{}{0pt}{}{\lfloor \frac{n}{2}\rfloor }{2}\right)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$$

(7)

times, edges of any subgraph $T^i$, $i=1,\cdots ,⌈\frac{n}{2}⌉$ produce one crossing on edges of $G^{*}$ and edges of any subgraph $T^i$, $i=⌈\frac{n}{2}⌉+1,\cdots ,n$ create just three crossings on edges of $G^{*}$. Thus, such an obtained number of crossings in Figure 6 gives us an upper bound for our Theorem 5. Suppose now that, for $n\ge 2$, there is a drawing D of $G^{*}+D_n$ with

$${\mathrm{cr}}_D(G^{*}+D_n)<6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋,$$

(8)

and let

$$\mathrm{cr}(G^{*}+D_m)=6⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋+m+2⌊\frac{m}{2}⌋\mathrm{for}\mathrm{any}\mathrm{integer}m<n.$$

(9)

For easier reading, if $r=|R_D|$ and $s=|S_D|$, then assumption (8) together with ${\mathrm{cr}}_D\left(K_{6,n}\right)\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$ using (3) imply the following relation with respect to edge crossings of $G^{*}$ in D:

$${\mathrm{cr}}_D\left(G^{*}\right)+\sum _{T^i\in R_D}{\mathrm{cr}}_D(G^{*},T^i)+\sum _{T^i\in S_D}{\mathrm{cr}}_D(G^{*},T^i)+\sum _{T^i\notin R_D\cup S_D}{\mathrm{cr}}_D(G^{*},T^i)<n+2⌊\frac{n}{2}⌋,$$

(10)

i.e.,

$${\mathrm{cr}}_D\left(G^{*}\right)+0r+1s+2(n-r-s)<n+2⌊\frac{n}{2}⌋.$$

(11)

Using the last inequality (11), we obtain $r+s\ge 1$, which ensures the existence of at least one subgraph $T^i$ whose edges could cross edges of $G^{*}$ at most once in D. In the following, it will be our aim to show a contradiction with (8) in all the considered subcases.

We suppose the drawing with the vertex notation of $G^{*}$ in such a way as shown in Figure 5a. Since the set $R_D\cup S_D$ is not empty, two possible subcases may occur:

(a)

Let $R_D$ be the non-empty set; that is, there is a subgraph $T^i\in R_D$. The reader can easily see that subgraph $F^i=G^{*}\cup T^i$ is uniquely represented by ${\mathrm{rot}}_D\left(t_i\right)=\left(146325\right)$. If edges of $F^i$ are crossed by any other subgraph $T^j$ at least five times, Lemma 2 contradicts assumption (8) in D. If there is a $T^j$ such that ${\mathrm{cr}}_D(G^{*}\cup T^i,T^j)<5$, then the vertex $t_j$ must be placed in the quadrangular region of subdrawing $D\left(G^{*}\right)$ with two vertices $v_3$ and $v_4$ of $G^{*}$ on its boundary, and ${\mathrm{cr}}_D(G^{*}\cup T^i,T^j)=4$ enforces ${\mathrm{cr}}_D(T^i,T^j)=0$. Thus, by fixing subgraph $T^i\cup T^j$, we have

$$\begin{array}{ccc}\hfill & & {\mathrm{cr}}_D(G^{*}+D_{n-2})+{\mathrm{cr}}_D(T^i\cup T^j)+{\mathrm{cr}}_D(K_{6,n-2},T^i\cup T^j)+{\mathrm{cr}}_D(G^{*},T^i\cup T^j)\hfill \\ & \ge & 6⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+n-2+2⌊\frac{n-2}{2}⌋+0+6(n-2)+4\hfill \\ \hfill & =& 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋,\hfill \end{array}$$

(12)

where the edges of $T^i\cup T^j$ are crossed by each other subgraph $T^k$ at least six times using ${\mathrm{cr}}_D\left(K_{6,3}\right)\ge 6$ again due to (3).

(b)

Let $R_D$ be the empty set; that is, there is a subgraph $T^i\in S_D$. There are only two ways of obtaining the subdrawing of $G^{*}\cup T^i$ depending on which of the two edges $v_3{v}_6$ or $v_4{v}_6$ of $G^{*}$ is crossed by $t_i{v}_4$ or $t_i{v}_3$, respectively. For both such possibilities, Lemma 2 also confirms a contradiction with (8) because it is not difficult to verify that ${\mathrm{cr}}_D(G^{*}\cup T^i,T^j)\ge 5$ is fulfilled for any $T^j$, $j\ne i$ in all possible regions of $D(G^{*}\cup T^i)$.

The verification proceeds in a similar way also for all five remaining drawings of graph $G^{*}$ in Figure 5. We have shown that there are at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ crossings in each good drawing D of $G^{*}+D_n$, and this completes the proof of Theorem 5. □

5. Conclusions

One of the first steps in finding the crossing number of a simple graph $G=\left(V\right(G),E(G\left)\right)$ in the join product with the discrete graphs $D_n$ is the analysis of its possible drawings. Such analysis becomes more complicated as the number of edges increases, especially if $3V\left(G\right)\le 2E\left(G\right)$. The large number of possible non-isomorphic drawings of the investigated graph $G^{*}$ was a major problem for determining $\mathrm{cr}(G^{*}+D_n)$. We found over 25 of them. As mentioned in the introduction, this problem is partially solved using two redrawings of $G^{*}$ in Figure 2 and separating cycles in Figure 3 and Figure 4, thanks to which it is not necessary to deal with all the drawings of $G^{*}$. The crossing number of $G^{*}+D_n$ equals to $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ is determined in Theorem 5 with the proof that is strongly based on Lemma 2. This lemma in a very special form can be used to establish crossing numbers of different graphs on six vertices too. The proofs are also created with the help of four subgraphs $H_k$ of our considered graph $G^{*}$. We anticipate that similar types of methodologies can be applied to determine the unknown crossing numbers of other graphs that have six vertices but more edges. Of course, this also applies to graphs of order six that contain graph $G^{*}$ as a subgraph. Such discussions involve combining the graphs with discrete graphs, as well as with paths and cycles.