Neuroadaptive Asymptotic Tracking Control of Nonlinear Systems with Multiple Uncertainties

Abstract

In this work, several innovative robust neuroadaptive control algorithms are integrated via the command filtered backstepping approach for a class of mismatched uncertain nonlinear systems. They utilize neural network adaptive control to achieve an enhanced model compensation effect. In addition, different robust terms with a positive time-varying integral expression are synthesized for each of the algorithms to address external disturbances. Each of the synthesized control algorithms has a continuous control input and cannot only remove the adverse effects of the “explosion of complexity” inherent in the traditional backstepping technology but also produce an asymptotic tracking result for the closed-loop system via strict theoretical analysis. Comparative simulation verifications are implemented to check the feasibility and practicability of the presented controllers.

1. Introduction

Modeling uncertainties caused by hard-to-model factors, for example system parameters varying with working conditions, unexpected external disturbances and so on, which widely exist in various practical applications [1,2]. The existence of these uncertainties becomes a major obstacle to developing high-performance closed-loop controllers. Over the past few years, the control of plants with modeling uncertainties has received considerable appeal, and many advanced control schemes such as adaptive robust control [3], robust adaptive control (RAC) [4,5], disturbance-observer-based adaptive control [6,7,8,9,10,11], fuzzy control [12] and so on, have been integrated. However, in general, the abovementioned control strategies can only guarantee that the final tracking error converges to residual bounded sets with the magnitude of the disturbance [13]. How to acquire an asymptotic tracking result [14] that is of considerable theoretical as well as practical significance has attracted more and more interest from scholars.

Recently, several novel algorithms have been constructed to address the asymptotic tracking issue for the control of systems with modeling uncertainties. In [15], the authors proposed a systematic adaptive sliding mode scheme for systems with external disturbance and parametric uncertainties. Notably, a discontinuous term appears in the constructed control input, which may give rise to high-frequency oscillation and even instability. To overcome these drawbacks, some control schemes with continuous control inputs that combine sliding mode control (SMC) and adaptive control (AC) have been proposed [16,17,18]. In addition, by merging AC with the integral robust control [19], P. M. Patre et al. have achieved asymptotic tracking control for systems with unstructured uncertainties and structured uncertainties [20]. It should be pointed out that the bounds of the first-order and second-order time derivatives of the disturbance are required to be known a priori in [20], which makes it quite conservative since it is almost impossible to actually obtain these bounds. Without knowing any bound of disturbance in advance, Zhengqiang Zhang et al. [21,22] and Yong-Hua Liu et al. [23,24] have, respectively, constructed different RAC control schemes with integrable time-varying functions for uncertain nonlinear systems and, meanwhile, yielded asymptotic tracking results. Furthermore, other remarkable control approaches can be found in [25,26,27,28]. However, the abovementioned control techniques cannot effectively handle mismatched model uncertainties and maintain asymptotic tracking performance at the same time.

Based on above detailed analyses, we try to develop the exact tracking control for nonlinear systems to handle matched and mismatched modeling uncertainties simultaneously. However, depending on the design framework within the traditional backstepping technique makes it complex and difficult, since repetitive derivatives of virtual control functions involving robust terms need to be calculated and the adverse influence of the “explosion of complexity” will be inevitably caused [29]. Fortunately, with the development of dynamic surface control (DSC) [30] and command filtered backstepping (CFB) technology [31,32], the adverse effects of traditional backstepping technology can be avoided. More importantly, compared with DSC, the CFB technology introduces a nonlinear command filter (CF) to estimate the virtual control law and introduces a compensation signal to remove the estimation error at each step. Therefore, we intend to employ the CFB technology to design the control strategy. However, it is difficult and changeling to achieve asymptotic tracking performance because the introduced compensation signal itself will be affected by the filtering error. Therefore, by combing with neural networks (NNs), we will develop several novel RAC control schemes that introduce nonlinear robust terms into the dynamics of the compensation signal and the virtual control function at each step to handle the filtering error as well as the external disturbance, respectively. It should be pointed out that the main difference between these strategies lies in the nonlinear robust term.

The main innovations and contributions of this paper are presented as:

(1)

Without requiring definite bounds of exogenous disturbances, several novel control schemes that can reject matched uncertainties and, meanwhile, mismatched uncertainties are put forward;

(2)

By constructing a set of asymptotic filters, the asymptotic stability can be acquired without an “explosion of complexity”;

(3)

The synthesized controllers with simple control schemes can be easily applied to extensive plants without much complexity.

Notation: n is the system order; i = 1, …, n; l = 2, …, n − 1; j = 1, …, n − 1; $\widehat{\ast }$ is the estimate of $\ast$; $\tilde{\ast }=\ast -\widehat{\ast }$ is the estimation error with regard to $\ast$; p_j(t) > 0, q_i(t) > 0 and satisfy ${\displaystyle {\int }_0^t{p}_j(\tau ) }d\tau \le {\omega }_j<\infty$, ${\displaystyle {\int }_0^t{q}_i(\tau ) }d\tau \le {\varpi }_i<\infty$, $\forall t$ ≥ 0 with the constants ${\omega }_j,{\varpi }_i$ > 0 [21]; in addition, tanh$(\ast )$ is a hyperbolic tangent function of $\ast$.

2. General Control Issue Formulation

We consider the uncertain nonlinear system as

$$\begin{array}{l}{\dot{x}}_j=x_{j+1}+{\psi }_j({\overline{x}}_j)+D_j(t)\\ {\dot{x}}_n=h(x)u+{\psi }_n({\overline{x}}_n)+D_n(t)\\ y=x_1\end{array}$$

(1)

where x = [x₁, …, x_n]^T ∈ Rⁿ is the system state vector and ${\overline{x}}_i$ = [x₁, …, x_i]^T ∈ Rⁱ can be measurable; ${\psi }_i({\overline{x}}_i)$ are unknown smooth functions with respect to ${\overline{x}}_i$; the function h(x) ∈ R⁺ is known; u ∈ R is the actual control input added to (1); y ∈ R is the system output; and D_i(t) are unexpected time-varying disturbances.

Given the smooth desired trajectory y_r = x_1d(t) ∈ C¹, we expect to integrate a continuously bounded u such that x₁ can follow x_1d (t) asymptotically.

Assumption 1. 

There exists a positive constant d_i so that:

$$d_i={\sup }_{t\ge 0}\left|D_i(t)\right|$$

(2)

Lemma 1 

([21,33]). For any variables ξ, ζ ∈ R, as well as μ > 0

$$0\le \left|\xi \right|-\xi \tanh \left(\xi /\mu \right)\le \varsigma \mu ,0\le \left|\zeta \right|-\frac{{\zeta }^2}{\sqrt{{\zeta }^2+{\mu }^2}}<\mu$$

(3)

where ς = 0.2785.

Remark 1. 

Notably, the considered system model (1) here takes matched and mismatched uncertainties into account, which is universal for practical plants.

Remark 2. 

Only the first derivative of the instruction is needed, which makes the assumption more relaxed compared with that of the time derivatives of y_r up to the nth order that are required by most controller designs.

3. Command Filtered Robust Adaptive Controller Design

3.1. NN Adaptation

Based on [34], ${\psi }_i({\overline{x}}_i)$ can be expressed as

$${\psi }_i({\overline{x}}_i)=W_i^T{\varphi }_i({\overline{x}}_i)+f_i({\overline{x}}_i)$$

(4)

where W_i and ${\varphi }_i({\overline{x}}_i)$ are NN weights and radial basis functions, respectively, and $f_i({\overline{x}}_i)$ are residual errors.

Moreover, ${\psi }_i({\overline{x}}_i)$ can be approximated by

$${\widehat{\psi }}_i({\overline{x}}_i)={\widehat{W}}_i^T{\varphi }_i({\overline{x}}_i)$$

(5)

Remark 3. 

There exists a positive constant α_i such that:

$${\alpha }_i={\sup }_{t\ge 0}{\displaystyle |}{D}_i(t)+f_i({\overline{x}}_i)|$$

(6)

3.2. Control Schemes Design

In this section, we intend to propose several different control schemes.

A set of tracking errors e_i and error compensations z_i is given as follows [31]:

$$\begin{array}{l}{e}_1=x_1-y_r,e_{j+1}=x_{j+1}-{\beta }_{j,c}\\ z_1=e_1-{\eta }_1,z_{j+1}=e_{j+1}-{\eta }_{j+1}\end{array}$$

(7)

where β_j,c denote the outputs of the CFs with the virtual control functions β_j being the inputs and η_i being the compensating signal to be presented later.

A set of compensating signals for the filtering errors is introduced as [31]

$$\begin{array}{l}{\dot{\eta }}_j=-{\gamma }_j{\eta }_j+{\eta }_{j+1}-{\epsilon }_j\\ {\dot{\eta }}_n=-{\gamma }_n{\eta }_n\end{array}$$

(8)

where γ_j are adjustable positive gains and ε_j = β_j − β_j,c indicate the filtering errors.

Control scheme I:

Inspired by [35], a set of filters with exact filtering performance can be designed as

$$\begin{array}{l}{\omega }_{cj}{\dot{\beta }}_{j,c}={\epsilon }_j-{\phi }_{js},{\beta }_{j,c}(0):={\beta }_j(0)\\ {\phi }_{js}=-\frac{{\omega }_{cj}{\epsilon }_j{\widehat{\Delta }}_j}{{\epsilon }_j\tanh [{\epsilon }_j{p}_j^{-1}(t)]+p_j(t)}\end{array}$$

(9)

where ω_cj are adjustable parameters for the filters. Then, Δ_j = sup_t≥0|${\dot{\beta }}_j$| and ${\widehat{\Delta }}_j$ can be updated as

$${\dot{\widehat{\Delta }}}_j=\frac{{\kappa }_j{\epsilon }_j^2}{{\epsilon }_j\tanh [{\epsilon }_j{p}_j^{-1}(t)]+p_j(t)}$$

(10)

where κ_j are positive adaptation gains. It should be pointed out that η_js denotes a robust term to suppress the disturbance caused by the deviation between β_s−1,c and β_s−1.

Moreover, the error dynamics of the CFs are

$${\dot{\epsilon }}_j=-\frac{1}{{\omega }_{cj}}{\epsilon }_j+{\dot{\beta }}_j+\frac{1}{{\omega }_{cj}}{\phi }_{js}$$

(11)

Step 1:

Based on (1), (7) and (8), ${\dot{z}}_1$ can be produced as

$${\dot{z}}_1={\beta }_1+{\gamma }_1{\eta }_1+z_2+W_1^T{\varphi }_1({\overline{x}}_1)+f_1({\overline{x}}_1)+D_1(t)-{\dot{y}}_r$$

(12)

Hence, β₁ can be constructed as

$$\begin{array}{l}{\beta }_1=-{\gamma }_1{e}_1-{\widehat{W}}_1^T{\varphi }_1({\overline{x}}_1)+{\beta }_{1s}+{\dot{y}}_r\\ {\beta }_{1s}=-\frac{z_1{\widehat{\alpha }}_1}{z_1\tanh [z_1{q}_1^{-1}(t)]+q_1(t)}\end{array}$$

(13)

where β_1s denotes a nonlinear robust control law exploited to reject the lumped disturbance; ${\widehat{\alpha }}_1$ is updated by

$${\dot{\widehat{\alpha }}}_1=\frac{k_1{z}_1^2}{z_1\tanh [z_1{q}_1^{-1}(t)]+q_1(t)}$$

(14)

where k₁ is a positive adaptation gain.

After substituting (13) into (12), one yields

$${\dot{z}}_1=-{\gamma }_1{z}_1+z_2+{\tilde{W}}_1^T{\varphi }_1({\overline{x}}_1)+{\beta }_{1s}+f_1({\overline{x}}_1)+D_1(t)$$

(15)

Step l:

With (1), (7) and (8), one has

$${\dot{z}}_l={\beta }_l+z_{l+1}+{\gamma }_l{\eta }_l+W_l^T{\varphi }_l({\overline{x}}_l)+f_l({\overline{x}}_l)+D_l(t)-{\dot{\beta }}_{l-1,c}$$

(16)

Along with (16), β_l can be devised as

$$\begin{array}{l}{\beta }_l=-{\gamma }_l{e}_l-z_{l-1}-{\widehat{W}}_l^T{\varphi }_l({\overline{x}}_l)+{\beta }_{ls}+{\dot{\beta }}_{l-1,c}\\ {\beta }_{ls}=-\frac{z_l{\widehat{\alpha }}_l}{z_l\tanh [z_l{q}_l^{-1}(t)]+q_l(t)}\end{array}$$

(17)

where β_ls are nonlinear robust control laws utilized to handle the external disturbances D_l(t); ${\widehat{\alpha }}_l$ can be updated by

$${\dot{\widehat{\alpha }}}_l=\frac{k_l{z}_l^2}{z_l\tanh [z_l{q}_l^{-1}(t)]+q_l(t)}$$

(18)

where k_l are positive adaptation gains.

According to (16) and (17), ${\dot{z}}_l$ can be arranged as

$${\dot{z}}_l=-{\gamma }_l{z}_l+z_{l+1}-z_{l-1}+{\tilde{W}}_l^T{\varphi }_l({\overline{x}}_l)+{\beta }_{ls}+f_l({\overline{x}}_l)+D_l(t)$$

(19)

Step n:

Depending on (1), (7) and (8), we can achieve ${\dot{z}}_n$ as

$${\dot{z}}_n=h(x)u+W_n^T{\varphi }_n({\overline{x}}_n)+f_n({\overline{x}}_n)+D_n(t)-{\dot{\beta }}_{n-1,c}+{\gamma }_n{\eta }_n$$

(20)

In viewing (20), we can construct the actual control function u as:

$$\begin{array}{l}u=\frac{1}{h(x)}\left[-{\gamma }_n{e}_n-z_{n-1}-{\widehat{W}}_n^T{\varphi }_n({\overline{x}}_n)+{\dot{\beta }}_{n-1,c}+u_s\right]\\ u_s=-\frac{z_n{\widehat{\alpha }}_n}{z_n\tanh [z_n{q}_n^{-1}(t)]+q_n(t)}\end{array}$$

(21)

where u_s denotes a nonlinear robust term to handle D_n(t); ${\alpha }_n$ can be estimated by

$${\dot{\widehat{\alpha }}}_n=\frac{k_n{z}_n^2}{z_n\tanh [z_n{q}_n^{-1}(t)]+q_n(t)}$$

(22)

where k_n > 0 is an adjustable adaptation gain.

Based on (20) and (21), we have

$${\dot{z}}_n=-{\gamma }_n{z}_n-z_{n-1}+{\tilde{W}}_n^T{\varphi }_n({\overline{x}}_n)+f_n({\overline{x}}_n)+{\beta }_{ns}+D_n(t)$$

(23)

Control scheme II:

Furthermore, an alternative control scheme that is different from control scheme I will be proposed.

Inspired by [21,36,37,38,39], the novel robust terms of φ_js in CFs can be constructed as

$${\phi }_{js}=-\frac{{\omega }_{cj}{\epsilon }_j{\widehat{\Delta }}_j^2}{{\epsilon }_j\tanh [{\epsilon }_j{p}_j^{-1}(t)]{\widehat{\Delta }}_j+p_j(t)},{\dot{\widehat{\Delta }}}_j=\frac{{\kappa }_j{\epsilon }_j^2}{\sqrt{{\epsilon }_j^2+p_j^2(t)}}$$

(24)

Comparing (24) with (9), it is easy to find that this scheme is different.

Moreover, the novel robust terms β_js and u_s in virtual and actual control schemes can be integrated by [21,36,37,38,39]

$$\begin{array}{l}{\beta }_{js}=-\frac{z_j{\widehat{\alpha }}_j^2}{z_j\tanh [z_j{q}_j^{-1}(t)]{\widehat{\alpha }}_j+q_j(t)},{\dot{\widehat{\alpha }}}_j=\frac{k_j{z}_j^2}{\sqrt{z_j^2+q_j^2(t)}}\\ u_s=-\frac{z_n{\widehat{\alpha }}_n^2}{z_n\tanh [z_n{q}_n^{-1}(t)]{\widehat{\alpha }}_n+q_n(t)},{\dot{\widehat{\alpha }}}_n=\frac{k_n{z}_n^2}{\sqrt{z_n^2+q_n^2(t)}}\end{array}$$

(25)

Control scheme III:

In addition, an alternative control scheme that is different from the above control schemes will be proposed.

According to [21,36,37,38,39], the robust terms of φ_js in CFs can be constructed as

$${\phi }_{js}=-\frac{{\omega }_{cj}{\epsilon }_j{\widehat{\Delta }}_j^2}{\sqrt{{\epsilon }_j^2{\widehat{\Delta }}_j^2+p_j^2(t)}},{\dot{\widehat{\Delta }}}_j=\frac{{\kappa }_j{\epsilon }_j^2}{{\epsilon }_j\tanh [{\epsilon }_j{p}_j^{-1}(t)]+p_j(t)}$$

(26)

Comparing (26) with (9) and (24), it is easy to find that this is different.

Additionally, the novel robust terms β_js and u_s in virtual and actual control schemes can be integrated by [21,36,37,38,39]

$$\begin{array}{l}{\beta }_{js}=-\frac{z_j{\widehat{\alpha }}_j^2}{\sqrt{z_j^2{\widehat{\alpha }}_j^2+q_j^2(t)}},{\dot{\widehat{\alpha }}}_j=\frac{k_j{z}_j^2}{z_j\tanh [z_j{q}_j^{-1}(t)]+q_j(t)}\\ u_s=-\frac{z_n{\widehat{\alpha }}_n^2}{\sqrt{z_n^2{\widehat{\alpha }}_n^2+q_n^2(t)}},{\dot{\widehat{\alpha }}}_n=\frac{k_n{z}_n^2}{z_n\tanh [z_n{q}_n^{-1}(t)]+q_n(t)}\end{array}$$

(27)

3.3. Main Results

Theorem 1. 

With the NN weight adaptation function synthesized as

$${\dot{\widehat{W}}}_i=\mathrm{Proj}\left\{{\Gamma }_i{\varphi }_i({\overline{x}}_i)z_i\right\}$$

(28)

and by adjusting design parameters felicitously, then the integrated control schemes can guarantee that all states within the considered system are bounded. In particular, asymptotic tracking can be eventually obtained.

Proof. 

See Appendix A. □

Remark 4. 

As performed in [40], in order to avoid parameter overestimation, the continuous projection mapping function can be utilized to constraint ${\widehat{\Delta }}_j$ and ${\widehat{\alpha }}_i$.

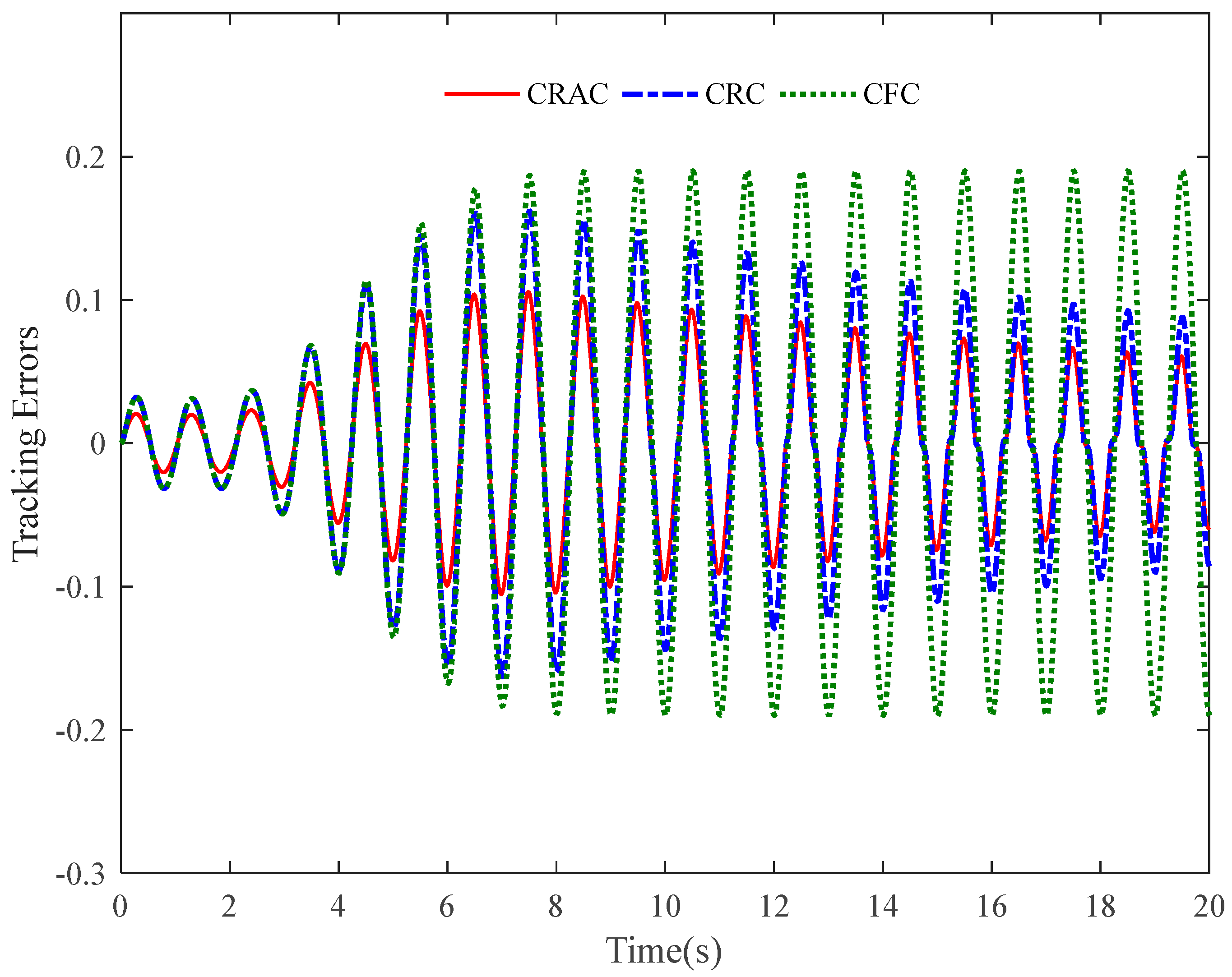
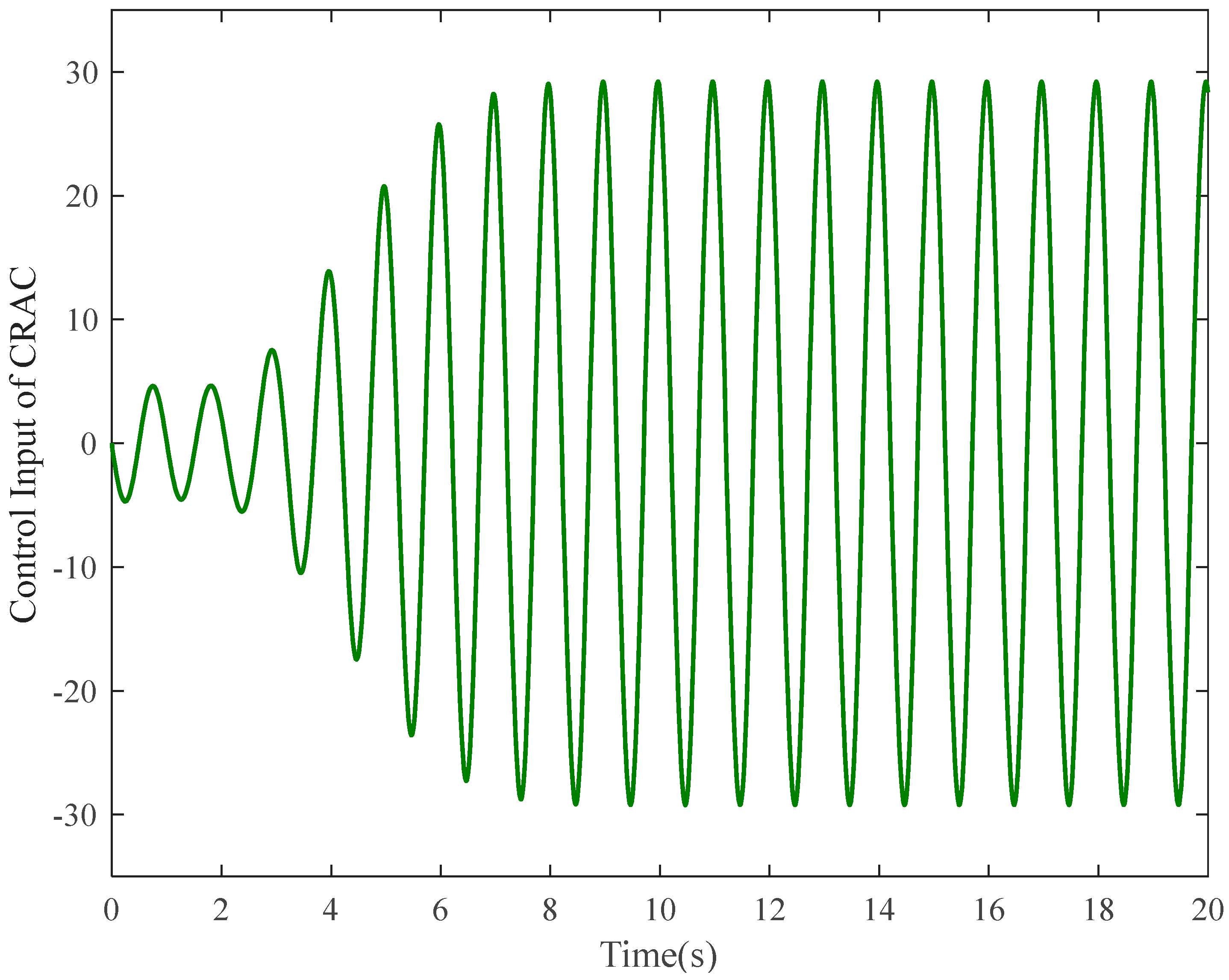
4. Verification Case

A numerical example is employed as:

$$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3+{\psi }_2({\overline{x}}_2)+D_2(t)\\ {\dot{x}}_3=h(x)u+{\psi }_3({\overline{x}}_3)+D_3(t)\end{array}$$

(29)

where ${\psi }_2({\overline{x}}_2)$ = −(25/6)x₁ − (1125/12)x₂, D₂(t) = (625/3)sin(2πt), h(x) = 39,775/16, ${\psi }_3({\overline{x}}_3)$ = −(925/4)x₁ − (23,125/16)x₂ − (600/13)x₃ and D₃(t) = (4625/2)sin(2πt).

To check the effectiveness of the synthesized strategies, the following controllers will be compared by tracking the desired trajectory x_1d = 2sin(2πt)[1 − exp(−0.01t³)].

(1)

CRAC: This is the presented command filtered robust neuroadaptive controller with control scheme I. The control gains are adjusted as: γ₁ = 100, γ₂ = 100 and γ₃ = 100. The adaptation gains are chosen as: κ₁ = 5, κ₂ = 1 and k₂ = 10, k₃ = 1. The design parameters of CFs are tuned as: w_c1 = w_c2 = 1.0 × 10⁻³. In addition, p₁(t) = p₂(t) = q₂(t) = q₃(t) = 100/(t² + 0.1). The NN adaptation rate matrices are selected as Γ₂ = 5.0 × 10⁻²I_11×11 and 2.0 × 10³I_11×11. For ${\psi }_2({\overline{x}}_2)$, the center vector is evenly spaced in [−1, 1] × [−2, 2] and the widths for x₁ and x₂ are both 1. For ${\psi }_3({\overline{x}}_3)$, the center vector is evenly spaced in [−1, 1] × [−2, 2] × [−600, 600] and the widths for x₁, x₂ and x₃ are 500, 500 and 1000, respectively.

(2)

CRC: This is the control scheme that is the same as CRAC but without NN compensation.

(3)

CFC: This is the control scheme that is same as CRAC but without NN compensation and the robust terms φ_1s, φ_2s, β_2s and u_s.

For fair comparison, all parameters for CRC and FC are chosen as same as those of CRAC.

The tracking result of CRAC is given in Figure 1, which indicates that the x₁ can track x_1d closely. Additionally, the contrastive tracking errors of the employed three algorithms are exhibited on Figure 2. It is seen from them that the developed algorithm exhibits a better performance than others in aspects of transient as well as steady errors. It is worth noting that the proposed scheme performs the asymptotic tracking phenomenon since the tracking error gradually converges to zero. By comparing the performances of CRAC and CRC, the superiority of the NN compensations is indicated. Moreover, the robust performance of CRAC can be verified by observing the tracking results of CRC and CFC. In addition, the estimated performance of unknown functions with the CRAC algorithm can be seen from Figure 3, which shows that they are regular with bounded values. Moreover, the control input of CRAC is presented in Figure 4, which is smooth and bounded.

5. Conclusions

In this paper, several different robust neuroadaptive controllers that incorporate neuroadaptive control and nonlinear robust terms with a positive time-varying integral term have been integrated for the high-performance tracking of uncertain systems. Furthermore, the “explosion of complexity” caused by the traditional backstepping technology has been removed by utilizing the CFB design procedure. Specially, for each of the proposed controllers, an asymptotic tracking result for mismatched uncertain systems has been achieved. Comparative simulation verifications are achieved for an uncertain nonlinear system. The numerical results indicate the high-performance features of the presented controllers.