Oscillatory Behavior of Heat Transfer and Magnetic Flux of Electrically Conductive Fluid Flow along Magnetized Cylinder with Variable Surface Temperature
Abstract
:1. Introduction
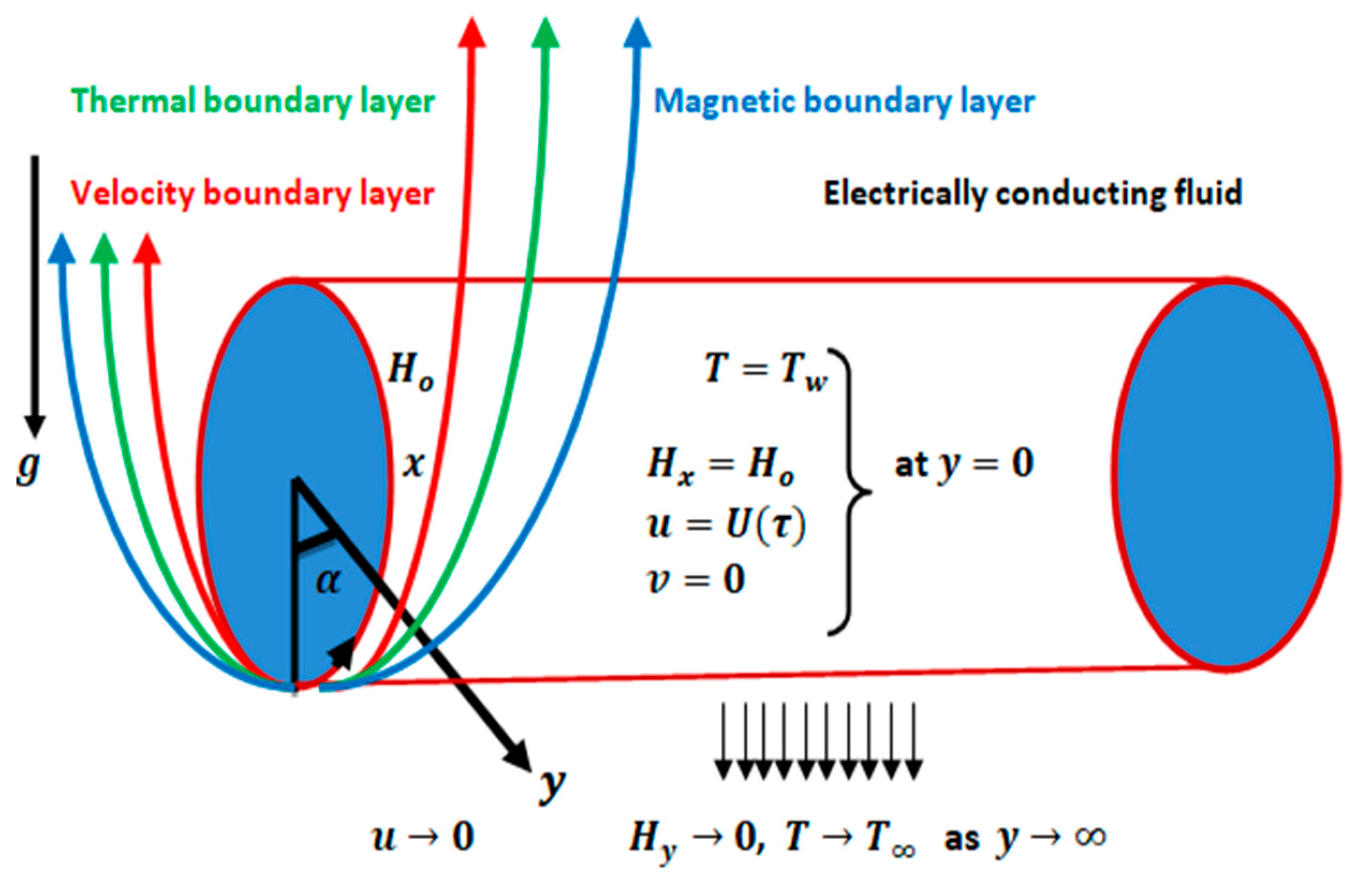
2. Problem Statement and Mathematical Formulation
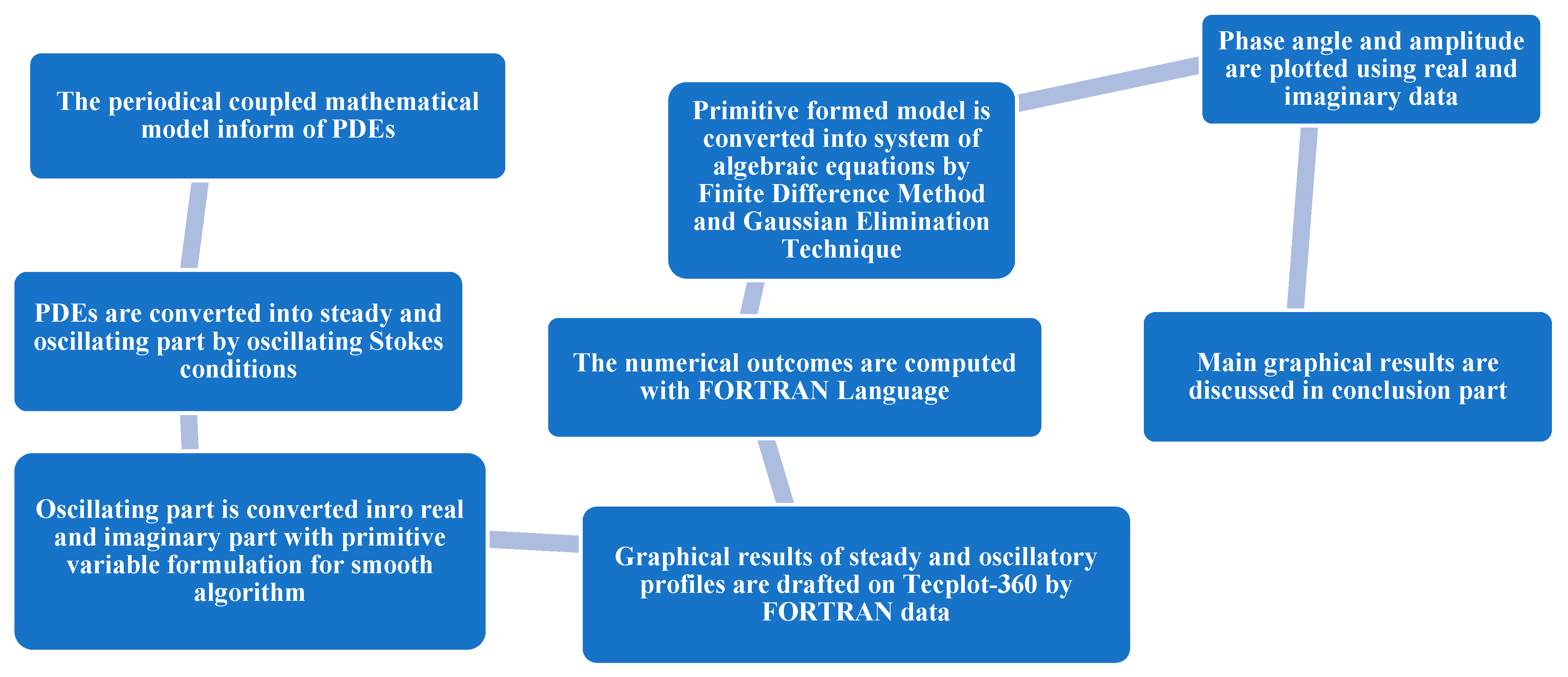
3. Computational Scheme
4. Results and Discussions
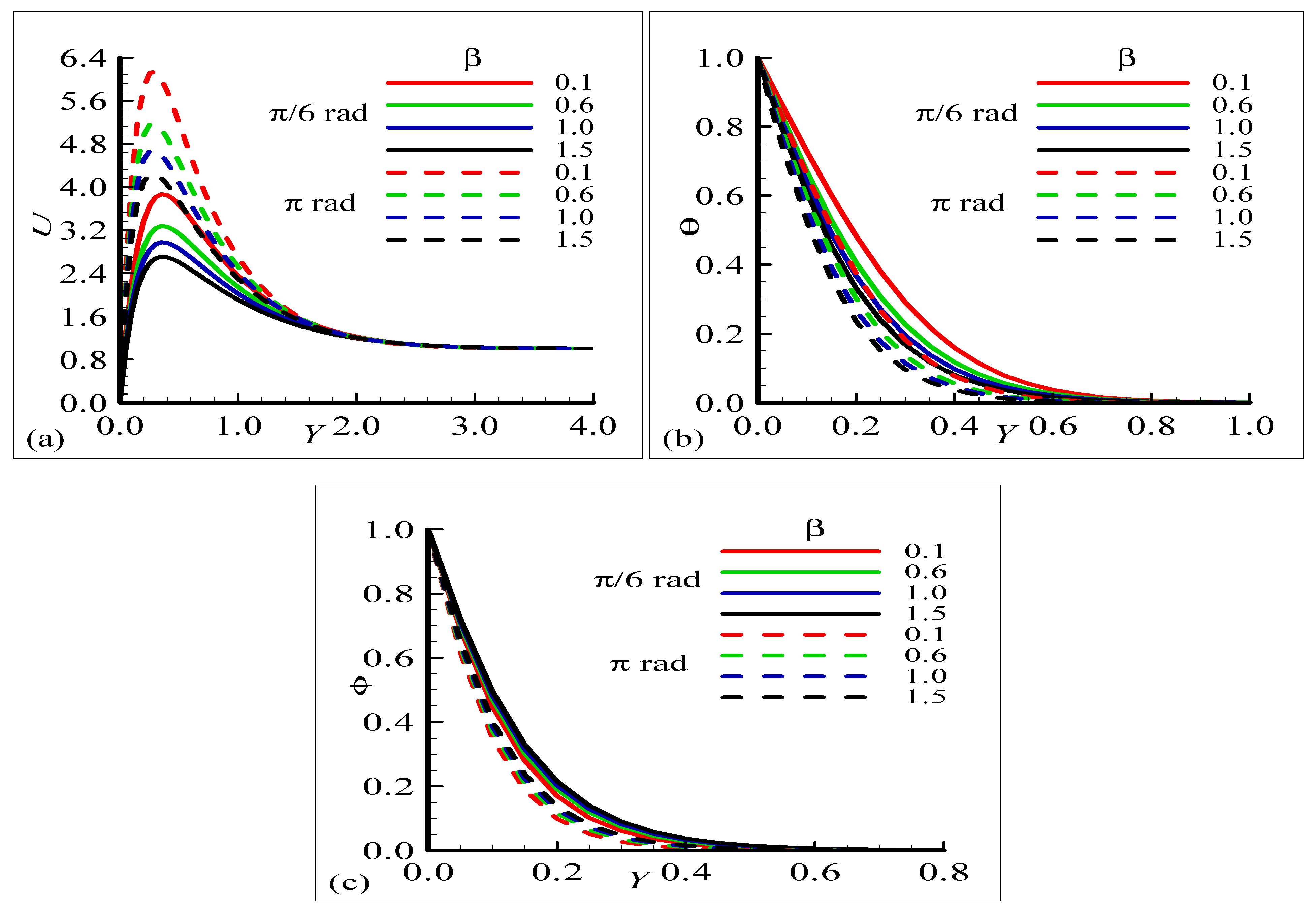
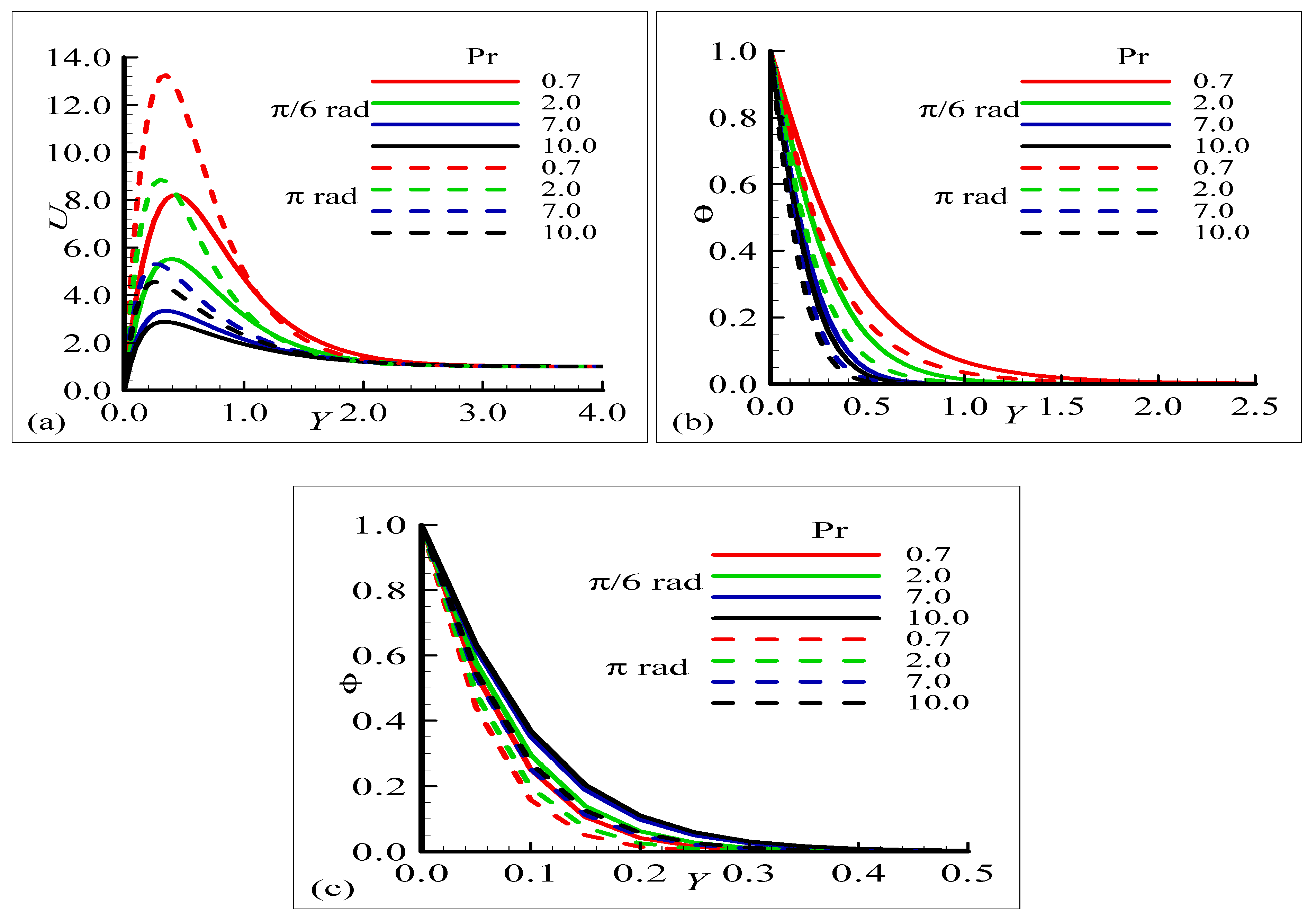
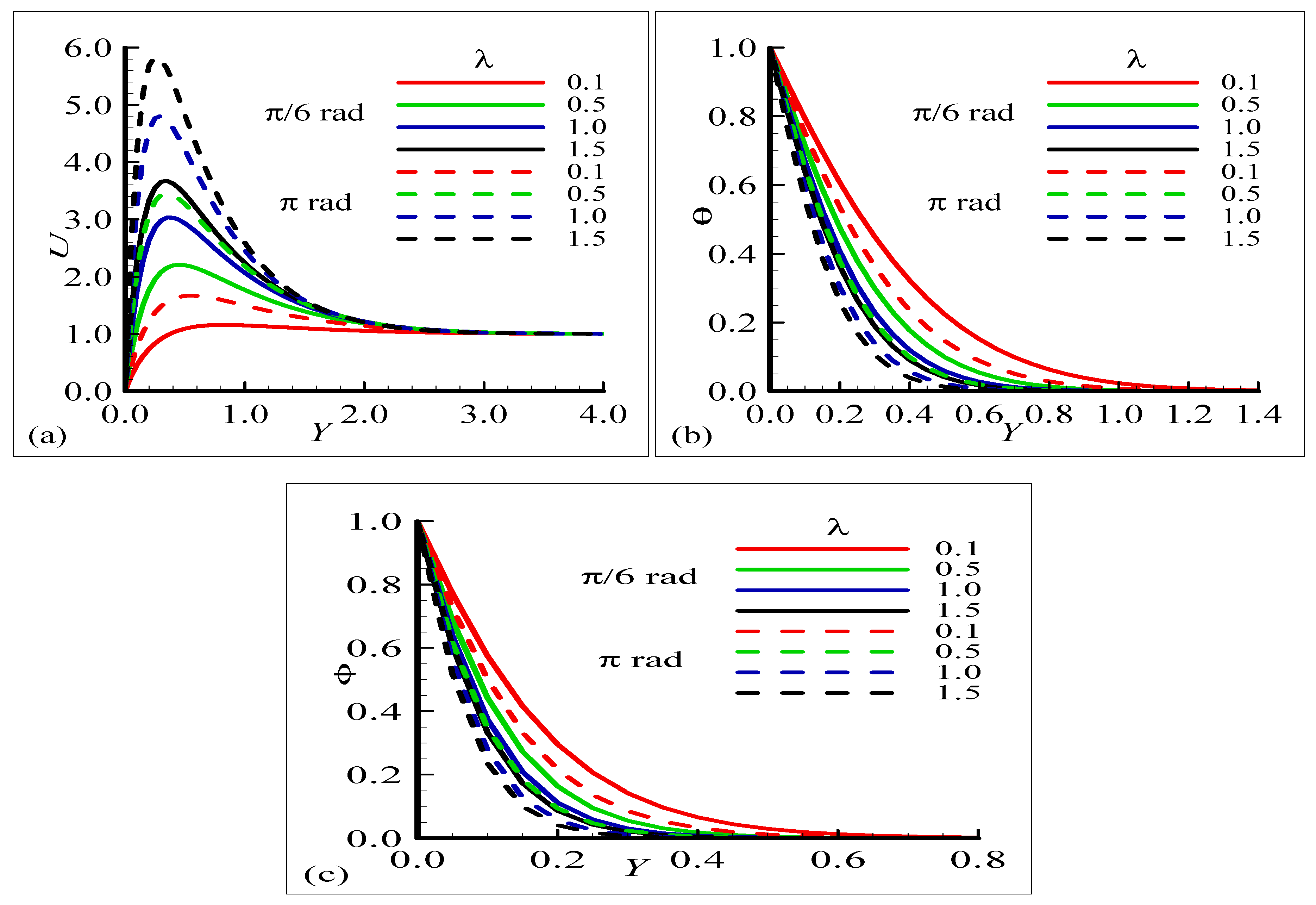
4.1. Steady Profiles of Velocity , Temperature , and Magnetic Field Graph
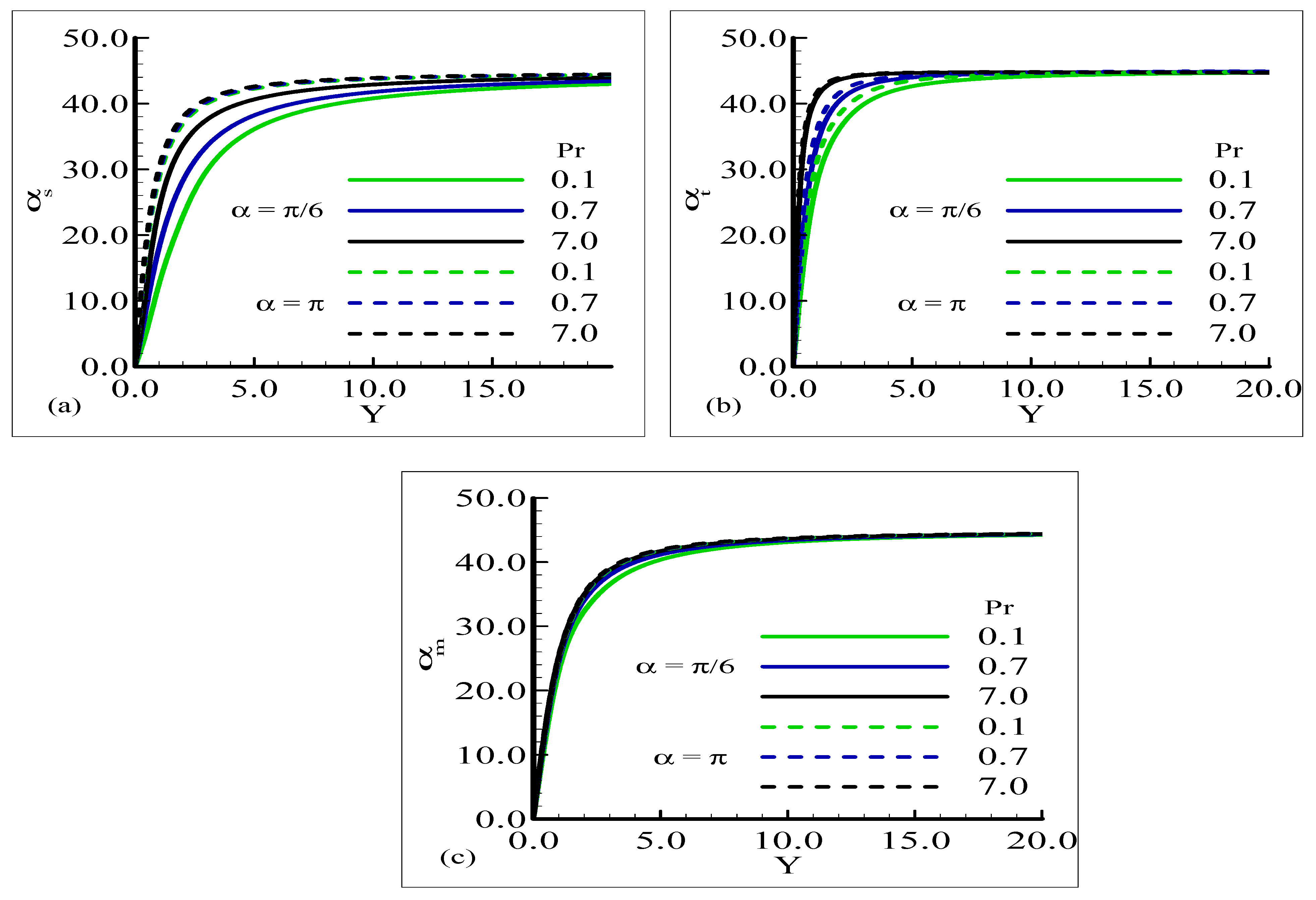
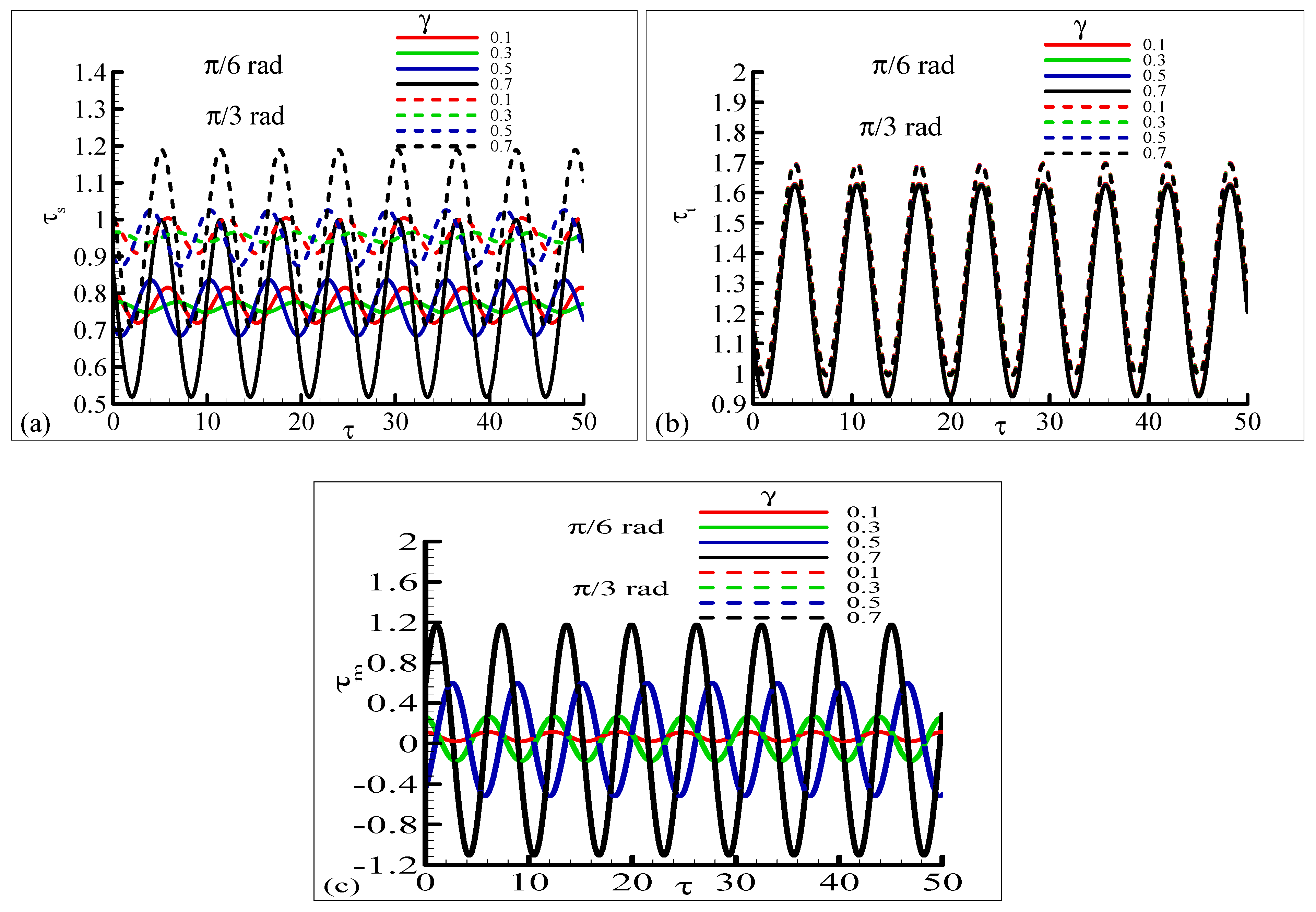
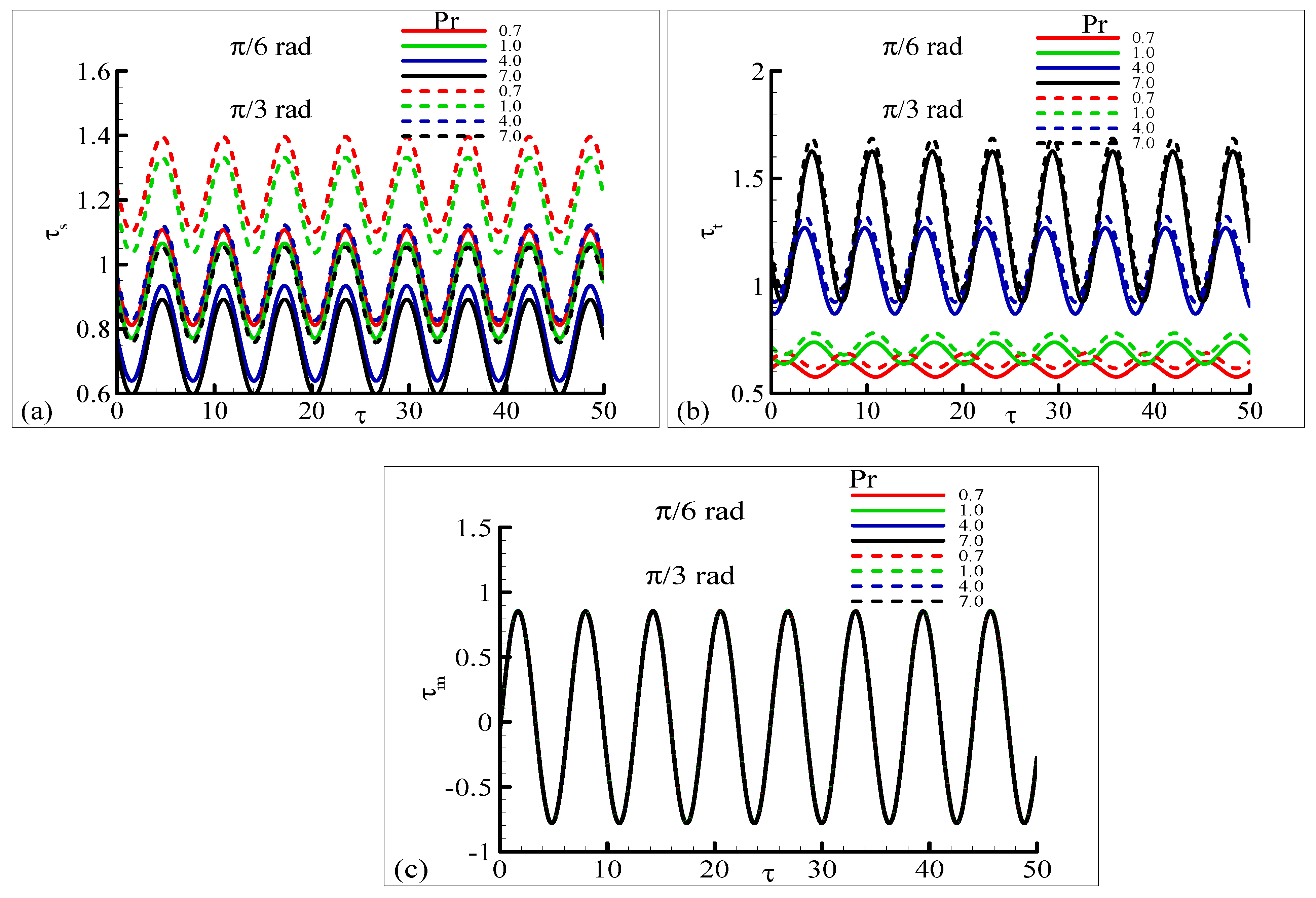
4.2. Phase Angle Behavior of Periodic Shear Stress , Heat Rate , and Magnetic Flux
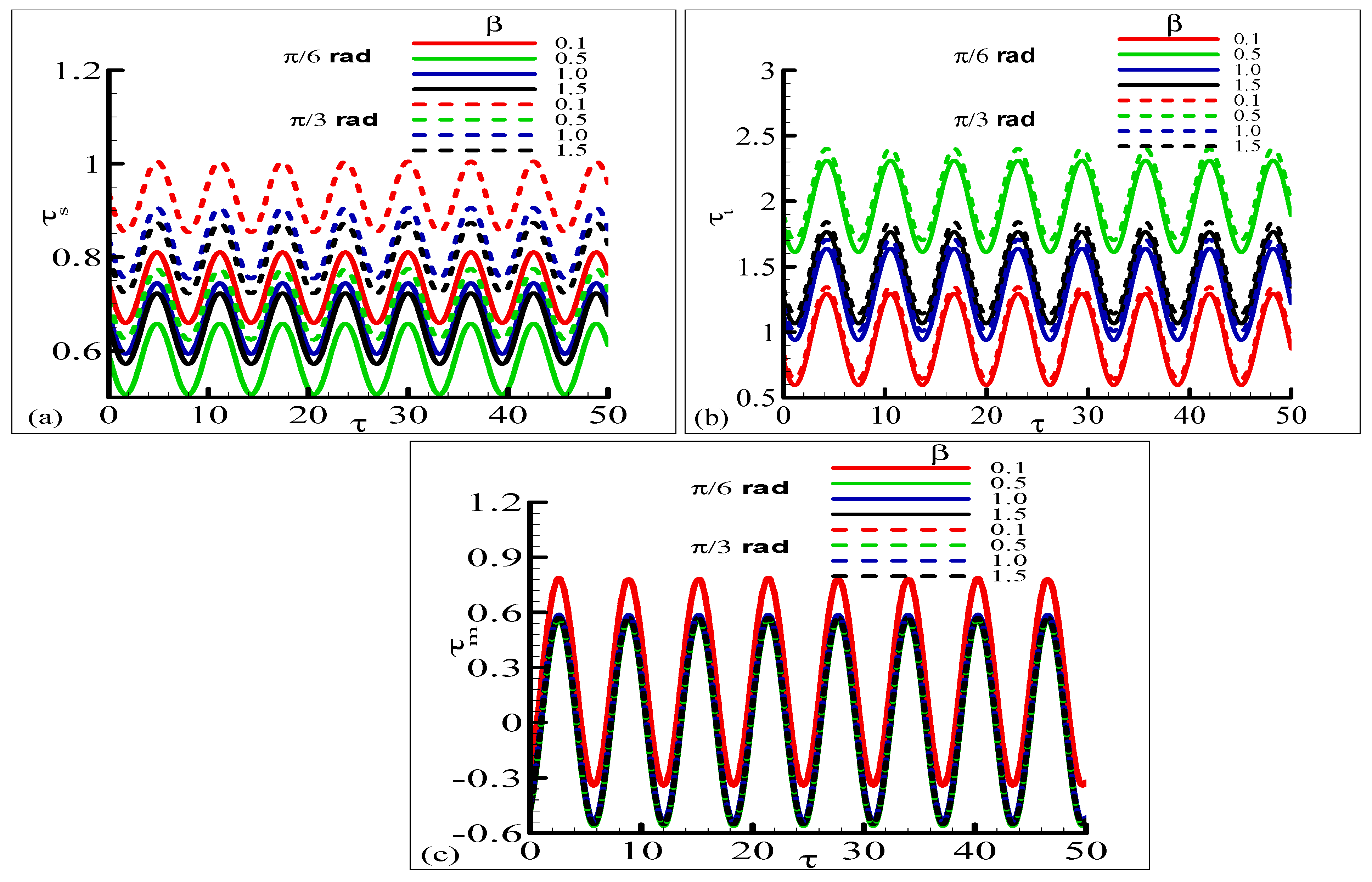
4.3. Oscillatory Profiles of Skin Friction , Heat Rate , and Magnetic Flux
5. Conclusions
- •
- The highest velocities occur for lower values at , but the temperature increases with , and the highest values occur at .
- •
- The increase in Prandtl number leads to a more important induced magnetic flux.
- •
- The fluid temperature increases by increasing the surface temperature due to the enhancement of the buoyancy forces.
- •
- The oscillation amplitude of , , and becomes more important with the increase in surface temperature number .
- •
- Induced magnetic flux is increased with the increase in magnetic Prandtl number.
- •
- The skin friction oscillation has higher amplitude for higher Pr values.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Farid, S.K.; Billah, M.M.; Rahman, M.M.; Sharif, U.M. Numerical study of fluid flow on magneto-hydrodynamic mixed convection in a lid driven cavity having a heated circular hollow cylinder. Procedia Eng. 2013, 56, 474–479. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.Y.; Kleinstreuer, C.; Chiang, H. Mixed convection from a rotating cone with variable surface temperature. Numer. Heat Transf. Part A Appl. 1994, 25, 75–83. [Google Scholar] [CrossRef]
- Dinarvand, S.; Nademi Rostami, M.; Dinarvand, R.; Pop, I. Improvement of drug delivery micro-circulatory system with a novel pattern of CuO-Cu/blood hybrid nanofluid flow towards a porous stretching sheet. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4408–4429. [Google Scholar] [CrossRef]
- Reddy, M.G. Radiation effects on MHD natural convection flow along a vertical cylinder embedded in a porous medium with variable surface temperature and concentration. Front. Heat Mass Transf. 2014, 5, 013004. [Google Scholar] [CrossRef]
- Javaherdeh, K.; Nejad, M.M.; Moslemi, M. Natural convection heat and mass transfer in MHD fluid flow past a moving vertical plate with variable surface temperature and concentration in a porous medium. Eng. Sci. Technol. Int. J. 2015, 18, 423–431. [Google Scholar] [CrossRef] [Green Version]
- Mahdy, A. Simultaneous impacts of MHD and variable wall temperature on transient mixed Casson nanofluid flow in the stagnation point of rotating sphere. Appl. Math. Mech. 2018, 39, 1327–1340. [Google Scholar] [CrossRef]
- Mokaddes Ali, M.; Rushd, S.; Akhter, R.; Alim, M.A. Magneto-hydrodynamic mixed convective heat transfer in a nanofluid filled wavy conduit having rotating cylinders. Sci. Iran. 2022, 29, 486–501. [Google Scholar]
- Bég, O.A.; Zueco, J.; Norouzi, M.; Davoodi, M.; Joneidi, A.A.; Elsayed, A.F. Network and Nakamura tridiagonal computational simulation of electrically-conducting biopolymer micro-morphic transport phenomena. Comput. Biol. Med. 2014, 44, 44–56. [Google Scholar]
- Al-Farhany, K.; Al-Muhja, B.; Loganathan, K.; Periyasamy, U.; Ali, F.; Sarris, I.E. Analysis of Convection Phenomenon in Enclosure Utilizing Nanofluids with Baffle Effects. Energies 2022, 15, 6615. [Google Scholar] [CrossRef]
- Al-Mdallal, Q.; Prasad, V.R.; Basha, H.T.; Sarris, I.; Akkurt, N. Keller box simulation of magnetic pseudoplastic nano-polymer coating flow over a circular cylinder with entropy optimisation. Comput. Math. Appl. 2022, 118, 132–158. [Google Scholar] [CrossRef]
- Sofiadis, G.; Sarris, I. Reynolds number effect of the turbulent micropolar channel flow. Phys. Fluids 2022, 34, 075126. [Google Scholar] [CrossRef]
- Heckel, J.J.; Chen, T.S.; Armaly, B.F. Mixed convection along slender vertical cylinders with variable surface temperature. Int. J. Heat Mass Transf. 1989, 32, 1431–1442. [Google Scholar] [CrossRef]
- Chen, T.S.; Tien, H.C.; Armaly, B.F. Natural convection on horizontal, inclined, and vertical plates with variable surface temperature or heat flux. Int. J. Heat Mass Transf. 1986, 29, 1465–1478. [Google Scholar] [CrossRef]
- Mushtaq, M.; Asghar, S.; Hossain, M.A. Mixed convection flow of second grade fluid along a vertical stretching flat surface with variable surface temperature. Heat Mass Transf. 2007, 43, 1049–1061. [Google Scholar] [CrossRef]
- Hossain, M.A.; Bhowmick, S.; Gorla, R.S.R. Unsteady mixed-convection boundary layer flow along a symmetric wedge with variable surface temperature. Int. J. Eng. Sci. 2006, 44, 607–620. [Google Scholar] [CrossRef]
- Koh, J.C.Y.; Hartnett, J.P. Skin friction and heat transfer for incompressible laminar flow over porous wedges with suction and variable wall temperature. Int. J. Heat Mass Transf. 1961, 2, 185–198. [Google Scholar] [CrossRef]
- Lim, A.E.; Lam, Y.C. Electroosmotic Flow Hysteresis for Fluids with Dissimilar pH and Ionic Species. Micromachines 2021, 12, 1031. [Google Scholar] [CrossRef]
- Sodeifian, G.; Nikooamal, H.R.; Yousefi, A.A. Molecular dynamics study of epoxy/clay nanocomposites: Rheology and molecular confinement. J. Polym. Res. 2012, 19, 9897. [Google Scholar] [CrossRef]
- Sodeifian, G. Non-linear rheology of polymer melts: Constitutive equations, rheological properties of polymer blends, shear flow, sliding plate rheometers. LAP Lambert Acad. Publ. 2011. [Google Scholar]
- Alharbi, K.A.M.; Ullah, Z.; Jabeen, N.; Ashraf, M. Magnetohydrodynamic and Thermal Performance of Electrically Conducting Fluid along the Symmetrical and Vertical Magnetic Plate with Thermal Slip and Velocity Slip Effects. Symmetry 2023, 15, 1148. [Google Scholar] [CrossRef]
- Ullah, Z.; Ahmad, H.; Khan, A.A.; Aldhabani, M.S.; Alsulami, S.H. Thermal conductivity effects on mixed convection flow of electrically conducting fluid along vertical magnetized plate embedded in porous medium with convective boundary condition. Mater. Today Commun. 2023, 35, 105892. [Google Scholar] [CrossRef]
- Hossain, M.A.; Roy, N.C.; Siddiqa, S. Unsteady mixed convection dusty fluid flow past a vertical wedge due to small fluctuation in free stream and surface temperature. Appl. Math. Comput. 2017, 293, 480–492. [Google Scholar] [CrossRef]
- Maranna, T.; Sneha, K.N.; Mahabaleshwar, U.S.; Sarris, I.E.; Karakasidis, T.E. An Effect of Radiation and MHD Newtonian Fluid over a Stretching/Shrinking Sheet with CNTs and Mass Transpiration. Appl. Sci. 2022, 12, 5466. [Google Scholar] [CrossRef]
- Mabood, F.; Fatunmbi, E.O.; Benos, L.; Sarris, I.E. Entropy Generation in the Magnetohydrodynamic Jeffrey Nanofluid Flow Over a Stretching Sheet with Wide Range of Engineering Application Parameters. Int. J. Appl. Comput. Math. 2022, 8, 1–18. [Google Scholar] [CrossRef]
- Chawla, S.S. Magnetohydrodynamic oscillatory flow past a semi-infinite flat plate. Int. J. Non-Linear Mech. 1971, 6, 117–134. [Google Scholar] [CrossRef]
- Mahmood, M.; Asghar, S.; Hossain, M.A. Hydromagnetic flow of viscous incompressible fluid past a wedge with permeable surface. ZAMM J. Appl. Math. Mech. Z. Angew. Mech. Appl. Math. Mech. 2009, 89, 174–188. [Google Scholar] [CrossRef]
- Ullah, Z.; Jabeen, N.; Khan, M.U. Amplitude and Phase Angle of Oscillatory Heat Transfer and Current Density along a Nonconducting Cylinder with Reduced Gravity and Thermal Stratification Effects. Mathematics 2023, 11, 2134. [Google Scholar] [CrossRef]
- Khan, M.N.; Ullah, Z.; Wang, Z.; Gamaoun, F.; Eldin, S.M.; Ahmad, H. Analysis of fluctuating heat and current density of mixed convection flow with viscosity and thermal conductivity effects along horizontal nonconducting cylinder. Case Stud. Therm. Eng. 2023, 46, 103023. [Google Scholar] [CrossRef]
- Ullah, Z.; Ehsan, M.; Ahmad, H.; Ilyas, A. Combined effects of MHD and slip velocity on oscillatory mixed convective flow around a non-conducting circular cylinder embedded in a porous medium. Case Stud. Therm. Eng. 2022, 38, 102341. [Google Scholar] [CrossRef]
- Cheng, P.; Minkowycz, W.J. Free convection about a vertical flat plate embedded in a porous medium with application to heat transfer from a dike. J. Geophys. Res. 1977, 82, 2040–2044. [Google Scholar] [CrossRef]

| Chawla [25] | Mahmood et al. [26] | Present Results | |
|---|---|---|---|
| 1.0 | 0.3204 | 0.3148 | 0.3162 |
| 10.0 | 0.3210 | 0.3151 | 0.3181 |
| 100.0 | 0.3244 | 0.3156 | 0.3207 |
| Cheng [30] | Javaherdeh et al. [5] | Present Results | |
|---|---|---|---|
| 1 | 1.0000 | 0.99978 | 0.9998 |
| 1/3 | 0.6776 | 0.67773 | 0.6774 |
| 0.0 | 0.3371 | 1.1503 | 1.0921 | 5.6912 |
| 0.2 | 0.3837 | 1.2246 | 1.2131 | 6.0830 |
| 0.4 | 0.3891 | 1.2356 | 1.2403 | 6.1716 |
| 0.6 | 0.3913 | 1.2420 | 1.2567 | 6.2263 |
| 0.8 | 0.3925 | 1.2464 | 1.2680 | 6.2643 |
| 1.0 | 0.3932 | 1.2494 | 1.2758 | 6.2910 |
| 1.2 | 0.3936 | 1.2513 | 1.2810 | 6.3087 |
| 1.4 | 0.3938 | 1.2524 | 1.2839 | 6.3186 |
| 1.6 | 0.3939 | 1.2527 | 1.2846 | 6.3212 |
| 1.8 | 0.3938 | 1.2521 | 1.2832 | 6.3165 |
| 2.0 | 0.3935 | 1.2508 | 1.2797 | 6.3044 |
| 2.2 | 0.3931 | 1.2486 | 1.2738 | 6.2842 |
| 2.4 | 0.3923 | 1.2453 | 1.2651 | 6.2545 |
| 2.6 | 0.3908 | 1.2404 | 1.2526 | 6.2125 |
| 2.8 | 0.3880 | 1.2331 | 1.2339 | 6.1507 |
| 3.0 | 0.3805 | 1.2192 | 1.2004 | 6.0422 |
| 0.3359 | 1.1486 | 1.0897 | 5.6761 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, Z.; Altaweel, N.H.; Aldhabani, M.S.; Ghachem, K.; Alhadri, M.; Kolsi, L. Oscillatory Behavior of Heat Transfer and Magnetic Flux of Electrically Conductive Fluid Flow along Magnetized Cylinder with Variable Surface Temperature. Mathematics 2023, 11, 3045. https://doi.org/10.3390/math11143045
Ullah Z, Altaweel NH, Aldhabani MS, Ghachem K, Alhadri M, Kolsi L. Oscillatory Behavior of Heat Transfer and Magnetic Flux of Electrically Conductive Fluid Flow along Magnetized Cylinder with Variable Surface Temperature. Mathematics. 2023; 11(14):3045. https://doi.org/10.3390/math11143045
Chicago/Turabian StyleUllah, Zia, Nifeen H. Altaweel, Musaad S. Aldhabani, Kaouther Ghachem, Muapper Alhadri, and Lioua Kolsi. 2023. "Oscillatory Behavior of Heat Transfer and Magnetic Flux of Electrically Conductive Fluid Flow along Magnetized Cylinder with Variable Surface Temperature" Mathematics 11, no. 14: 3045. https://doi.org/10.3390/math11143045
APA StyleUllah, Z., Altaweel, N. H., Aldhabani, M. S., Ghachem, K., Alhadri, M., & Kolsi, L. (2023). Oscillatory Behavior of Heat Transfer and Magnetic Flux of Electrically Conductive Fluid Flow along Magnetized Cylinder with Variable Surface Temperature. Mathematics, 11(14), 3045. https://doi.org/10.3390/math11143045









