Variational Solution and Numerical Simulation of Bimodular Functionally Graded Thin Circular Plates under Large Deformation
Abstract
:1. Introduction
2. Method and Problem
2.1. Displacement Variational Method
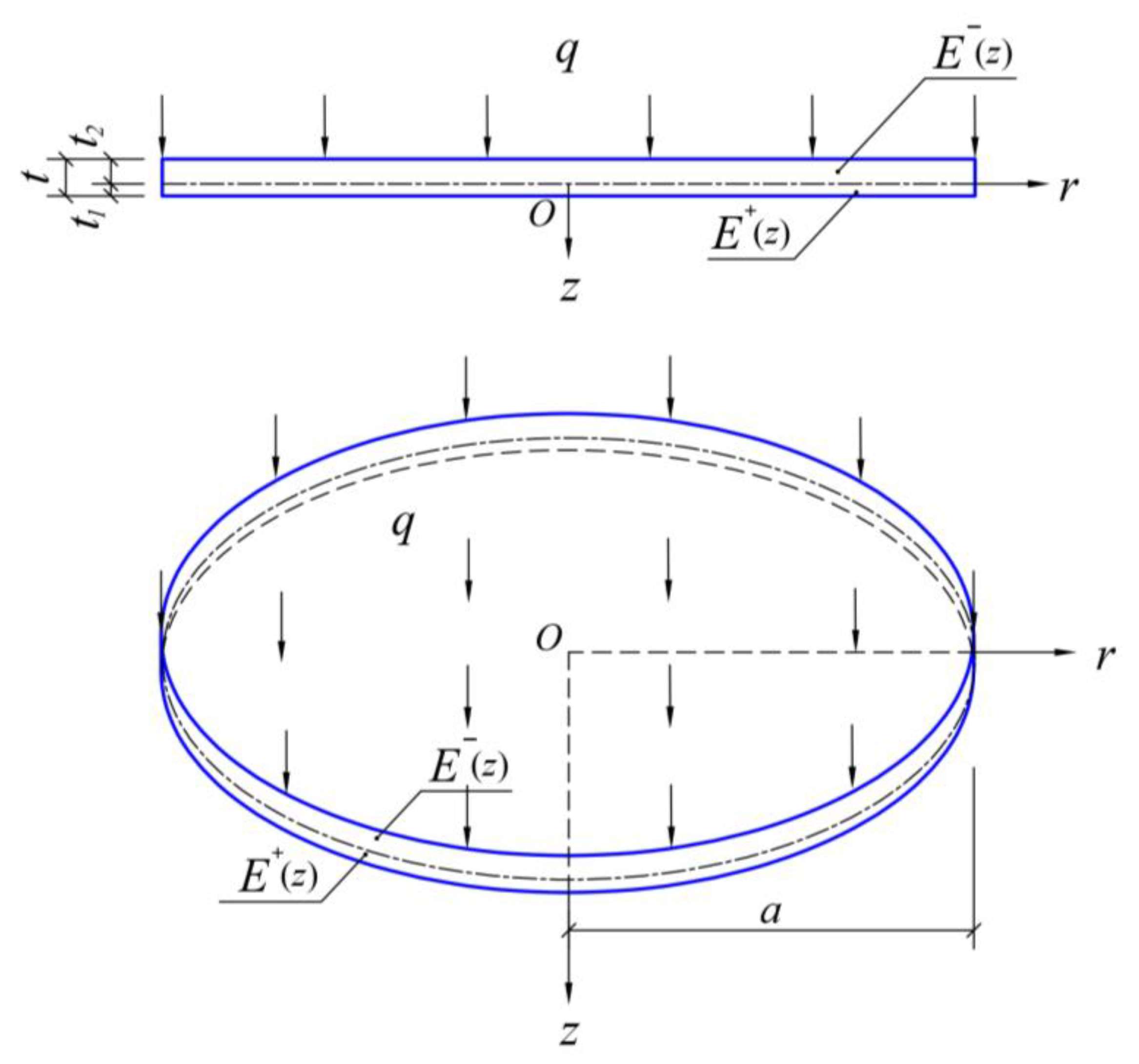
2.2. Description of Problem
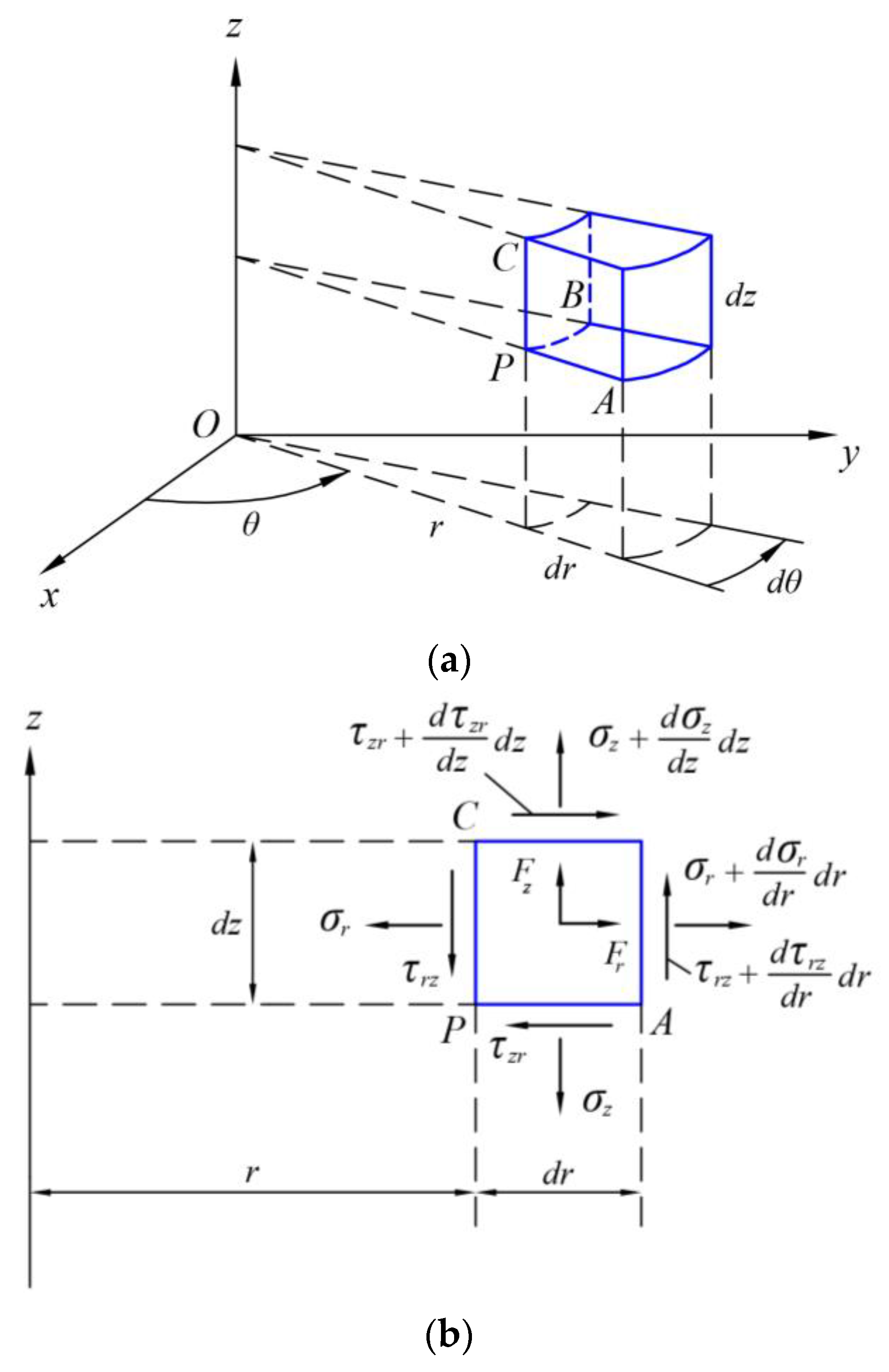
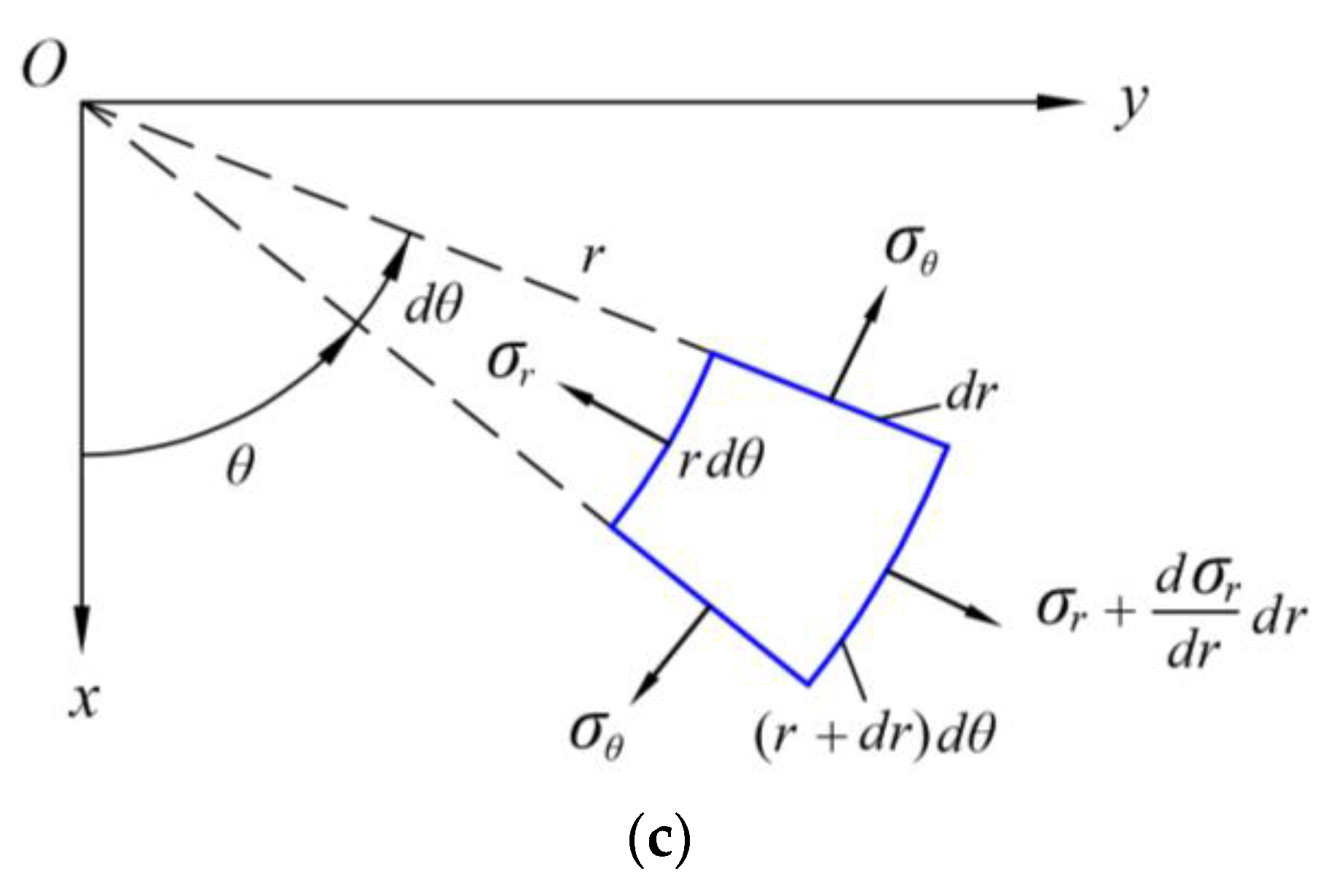
3. Geometrical and Physical Equations of Thin Circular Plates
3.1. Geometrical Equations under Large Deformation
3.2. Physical Equations
4. Displacement Variational Method
4.1. Total Strain Energy
4.2. Ritz Method
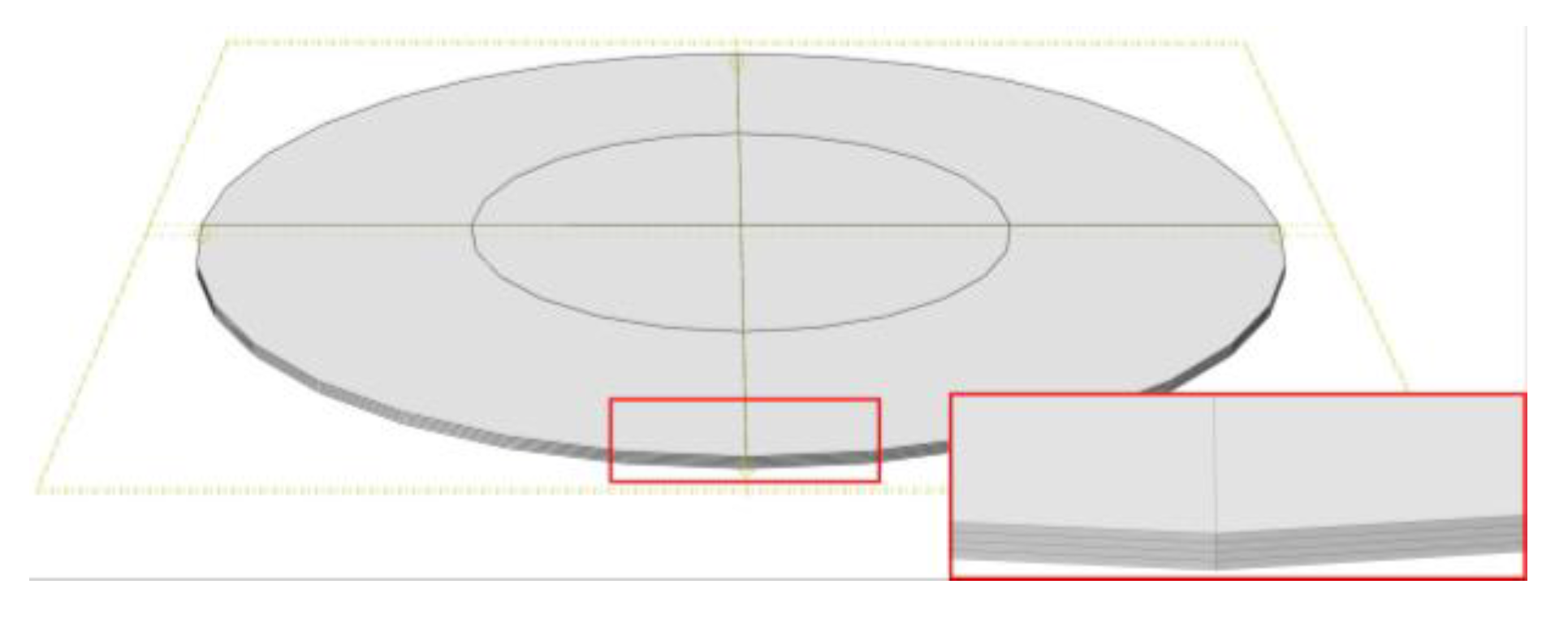
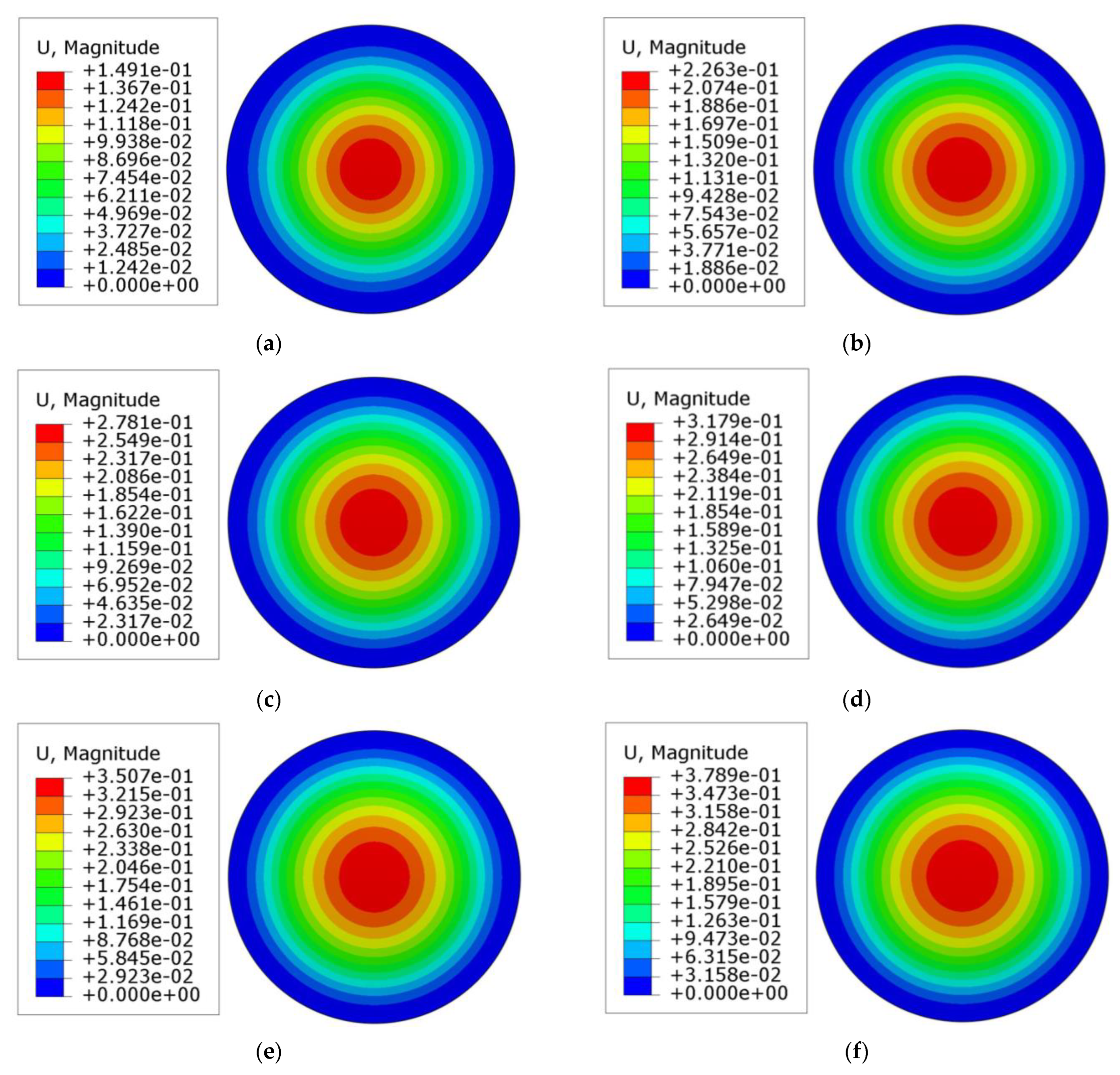
5. Numerical Simulation and Comparison with Variational Solution
6. Results and Discussion
6.1. Numerical Comparision of Three Solutions
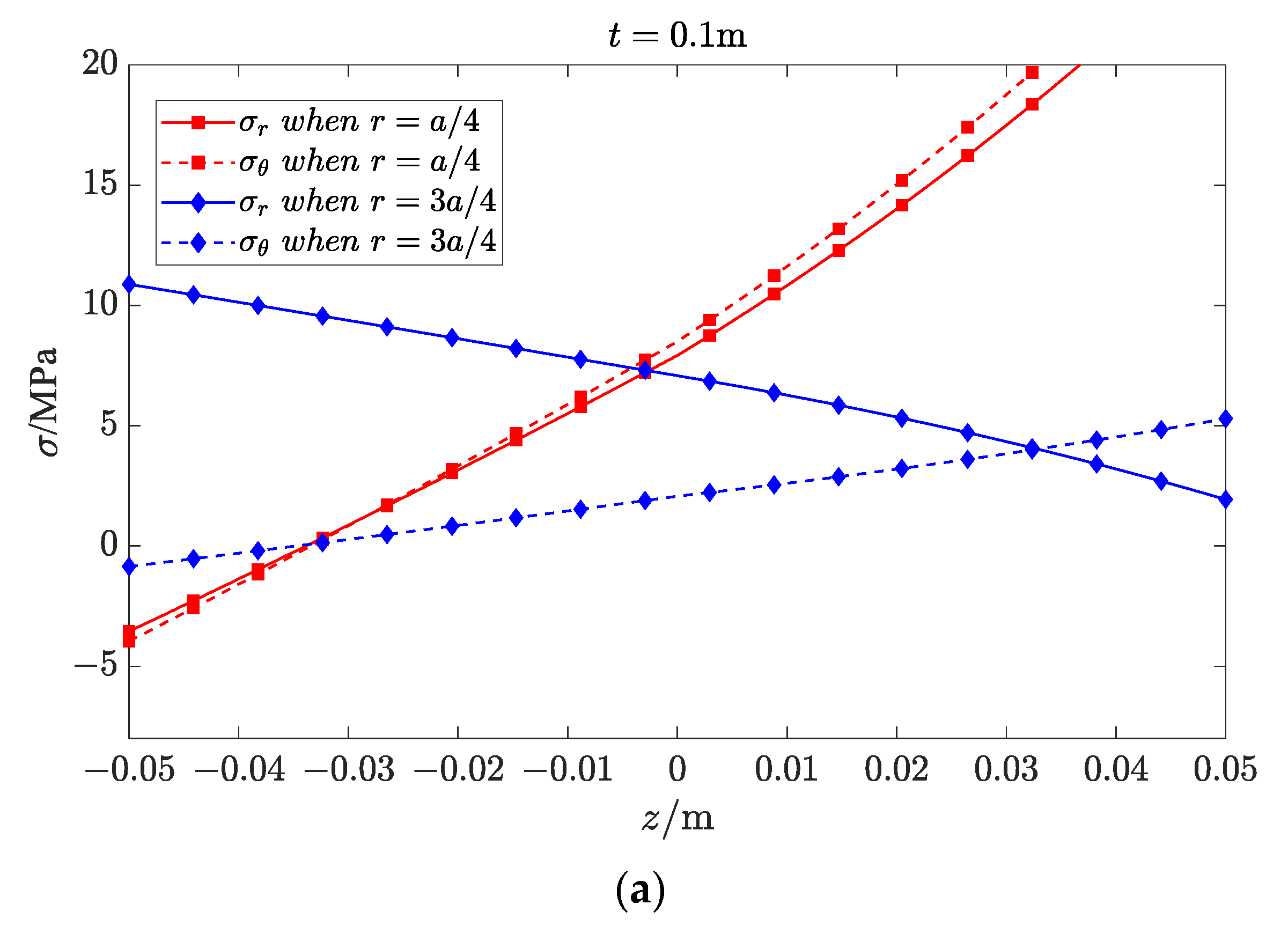
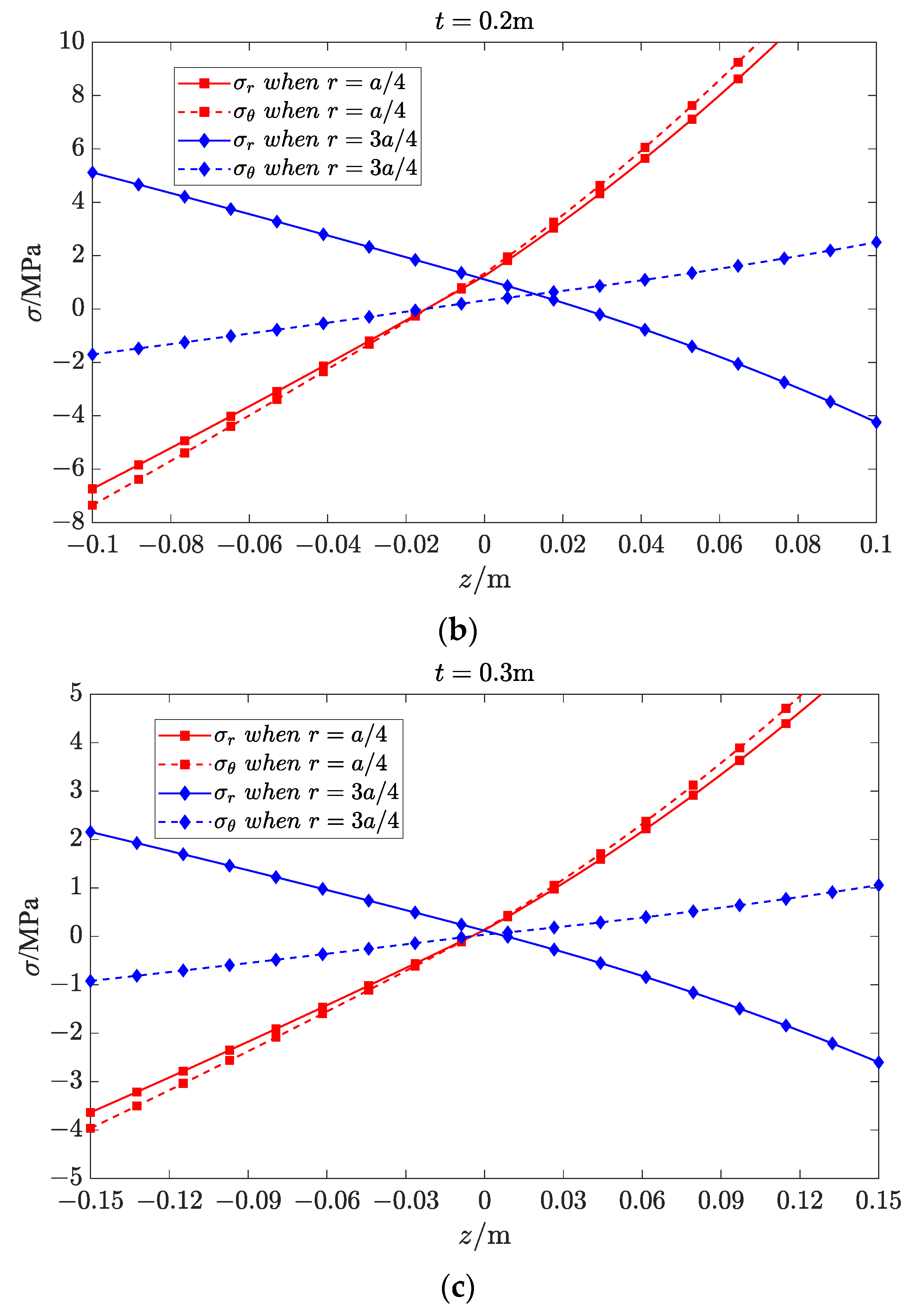
6.2. Stress Variation along Plate Thickness
7. Conclusions
- (i)
- The numerical simulation results verify the validity of the perturbation solution obtained in our previous study and the variational solution presented in this study.
- (ii)
- The perturbation method and variational method are both, in terms of nature, theoretical, being able to give useful analytical expressions that are convenient for use in the analysis and design. However, the variational method based on the energy principle avoids the establishment of an equation of equilibrium, which is necessary in the perturbation method yet.
- (iii)
- Compared with the traditional variational method, the improvement on this method in this study lies mainly in such a fact that the derivation of total strain energy is somewhat complicated due to the introduction of bimodular functionally graded materials and structural large deformation. In addition, the bending stiffness of the bimodular FGM plate may also be obtained from the derivation of total strain energy, but not necessarily from the conditions of equilibrium.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Jones, R.M. Stress-strain relations for materials with different moduli in tension and compression. AIAA J. 1977, 15, 16–23. [Google Scholar] [CrossRef]
- Koizumi, M. Functionally gradient materials the concept of FGM. Ceram. Trans. 1993, 34, 3–10. [Google Scholar]
- Gong, Y.; Mei, Y.; Liu, J. Capillary adhesion of a circular plate to solid: Large deformation and movable boundary condition. Int. J. Sci. Mech. 2017, 126, 222–228. [Google Scholar] [CrossRef]
- Huang, X.; Wang, M.; Feng, Y.; Wang, X.; Qiu, X. Finite deformation analysis of the elastic circular plates under pressure loading. Thin-Walled Struct. 2023, 188, 110864. [Google Scholar] [CrossRef]
- Barak, M.M.; Currey, J.D.; Weiner, S.; Shahar, R. Are tensile and compressive Young’s moduli of compact bone different. J. Mech. Behav. Biomed. Mater. 2009, 2, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Destrade, M.; Gilchrist, M.D.; Motherway, J.A.; Murphy, J.G. Bimodular rubber buckles early in bending. Mech. Mater. 2010, 42, 469–476. [Google Scholar] [CrossRef] [Green Version]
- Jones, R.M. Apparent flexural modulus and strength of multimodulus materials. J. Compos. Mater. 1976, 10, 342–354. [Google Scholar] [CrossRef]
- Bert, C.W. Models for fibrous composites with different properties in tension and compression. ASME J. Eng. Mater. Technol. 1977, 99, 344–349. [Google Scholar] [CrossRef]
- Ambartsumyan, S.A. Elasticity Theory of Different Moduli; Wu, R.F.; Zhang, Y.Z., Translators; China Railway Publishing House: Beijing, China, 1986. [Google Scholar]
- Reddy, J.N.; Chao, W.C. Nonlinear bending of bimodular material plates. Int. J. Solids Struct. 1983, 19, 229–237. [Google Scholar] [CrossRef]
- Zinno, R.; Greco, F. Damage evolution in bimodular laminated composite under cyclic loading. Compos. Struct. 2001, 53, 381–402. [Google Scholar] [CrossRef]
- Khan, A.H.; Patel, B.P. Nonlinear periodic response of bimodular laminated composite annular sector plates. Compos. Part B-Eng. 2019, 169, 96–108. [Google Scholar] [CrossRef]
- Yao, W.J.; Ye, Z.M. Analytical solution for bending beam subject to lateral force with different modulus. Appl. Math. Mech. (Engl. Ed.) 2004, 25, 1107–1117. [Google Scholar]
- Zhao, H.L.; Ye, Z.M. Analytic elasticity solution of bi-modulus beams under combined loads. Appl. Math. Mech. (Engl. Ed.) 2015, 36, 427–438. [Google Scholar] [CrossRef]
- He, X.T.; Cao, L.; Wang, Y.Z.; Sun, J.Y.; Zheng, Z.L. A biparametric perturbation method for the Föppl-von Kármán equations of bimodular thin plates. J. Math. Anal. Appl. 2017, 455, 1688–1705. [Google Scholar] [CrossRef]
- Ye, Z.M.; Chen, T.; Yao, W.J. Progresses in elasticity theory with different moduli in tension and compression and related FEM. Mech. Eng. 2004, 26, 9–14. [Google Scholar]
- Du, Z.L.; Zhang, Y.P.; Zhang, W.S.; Guo, X. A new computational framework for materials with different mechanical responses in tension and compression and its applications. Int. J. Solids Struct. 2016, 100–101, 54–73. [Google Scholar] [CrossRef]
- Ma, J.W.; Fang, T.C.; Yao, W.J. Nonlinear large deflection buckling analysis of compression rod with different moduli. Mech. Adv. Mater. Struct. 2019, 26, 539–551. [Google Scholar] [CrossRef]
- Almajid, A.; Taya, M.; Hudnut, S. Analysis of out-of-plane displacement and stress field in a piezocomposite plate with functionally graded microstructure. Int. J. Solids Struct. 2001, 38, 3377–3391. [Google Scholar] [CrossRef]
- Kumar, S.; Murthy Reddy, K.V.V.S.; Kumar, A.; Rohini Devi, G. Development and characterization of polymer–ceramic continuous fiber reinforced functionally graded composites for aerospace application. Aerosp. Sci. Technol. 2013, 26, 185–191. [Google Scholar] [CrossRef]
- Maalej, M.; Ahmed, S.F.U.; Paramasivam, P. Corrosion durability and structural response of functionally-graded concrete beams. J. Adv. Concr. Technol. 2003, 1, 307–316. [Google Scholar] [CrossRef] [Green Version]
- Rabbani, V.; Hodaei, M.; Deng, X.; Lu, H.; Hui, D.; Wu, N. Sound transmission through a thick-walled FGM piezo-laminated cylindrical shell filled with and submerged in compressible fluids. Eng. Struct. 2019, 197, 109323. [Google Scholar] [CrossRef]
- Van Vinh, P.; Van Chinh, N.; Tounsi, A. Static bending and buckling analysis of bi-directional functionally graded porous plates using an improved first-order shear deformation theory and FEM. Eur. J. Mech. Solid. 2022, 96, 104743. [Google Scholar] [CrossRef]
- Xue, X.-Y.; Wen, S.-R.; Sun, J.-Y.; He, X.-T. One- and two-dimensional analytical solutions of thermal stress for bimodular functionally graded beams under arbitrary temperature rise modes. Mathematics 2022, 10, 1756. [Google Scholar] [CrossRef]
- He, X.T.; Pei, X.X.; Sun, J.Y.; Zheng, Z.L. Simplified theory and analytical solution for functionally graded thin plates with different moduli in tension and compression. Mech. Res. Commun. 2016, 74, 72–80. [Google Scholar] [CrossRef]
- He, X.-T.; Li, X.; Yang, Z.-X.; Liu, G.-H.; Sun, J.-Y. Application of biparametric perturbation method to functionally graded thin plates with different moduli in tension and compression. Z. Angew. Math. Mech. 2019, 99, e201800213. [Google Scholar] [CrossRef]
- Li, X.; He, X.-T.; Ai, J.-C.; Sun, J.-Y. Large deformation problem of bimodular functionally-graded thin circular plates subjected to transversely uniformly-distributed load: Perturbation solution without small-rotation-angle assumption. Mathematics 2021, 9, 2317. [Google Scholar] [CrossRef]
- He, X.-T.; Pang, B.; Ai, J.-C.; Sun, J.-Y. Functionally graded thin circular plates with different moduli in tension and compression: Improved Föppl–von Kármán equations and its biparametric perturbation solution. Mathematics 2022, 10, 3459. [Google Scholar] [CrossRef]
- Chien, W.Z. Large deflection of a circular clamped plate under uniform pressure. Chin. J. Phys. 1947, 7, 102–113. [Google Scholar]
- Xu, Z.L. Elasticity, 5th ed.; Higher Education Press: Beijing, China, 2016. [Google Scholar]
- Xue, X.-Y.; Du, D.-W.; Sun, J.-Y.; He, X.-T. Application of variational method to stability analysis of cantilever vertical plates with bimodular effect. Materials 2021, 14, 6129. [Google Scholar] [CrossRef]
- He, X.-T.; Chang, H.; Sun, J.-Y. Axisymmetric large deformation problems of thin shallow shells with different moduli in tension and compression. Thin-Walled Struct. 2023, 182, 110297. [Google Scholar] [CrossRef]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Volmir, A.C. Flexible Plates and Shells; Lu, W.D.; Huang, Z.Y.; Lu, D.H., Translators; Science Press: Beijing, China, 1959. [Google Scholar]
- He, X.-T.; Li, W.-M.; Sun, J.-Y.; Wang, Z.-X. An elasticity solution of functionally graded beams with different moduli in tension and compression. Mech. Adv. Mater. Struct. 2018, 25, 143–154. [Google Scholar] [CrossRef]

| Physical Quantities | Taken Values |
|---|---|
| plate radius a | 10 m |
| plate thickness t | 0.2 m |
| neutral layer modulus E0 | 2 × 1010 Pa |
| load magnitudes q | 10 kPa to 200 kPa |
| tensile grade index α1 | 0.5 |
| compressive grade index α2 | 0.1 |
| tensile Poisson’s ratio μ+ | 0.35 |
| compressive Poisson’s ratio μ− | 0.25 |
| Distance from Plate Top (m) | Modulus of Elasticity (×1010 Pa) | Poisson’s Ratio |
|---|---|---|
| 0.0625t | 1.913 | 0.25 |
| 0.1875t | 1.937 | 0.25 |
| 0.3125t | 1.961 | 0.25 |
| 0.4375t | 1.986 | 0.25 |
| 0.5625t | 2.055 | 0.35 |
| 0.6875t | 2.186 | 0.35 |
| 0.8125t | 2.326 | 0.35 |
| 0.9375t | 2.475 | 0.35 |
| q (kPa) | Central Deflection w0 (m) | |||
|---|---|---|---|---|
| Result from Analytical Calculations | Result from [26] | Result from FEM | ||
| 10 | 0.0898 1 | 0.0897 2 | 0.0895 | 0.0885 |
| 20 | 0.1538 | 0.1514 | 0.1516 | 0.1491 |
| 30 | 0.2003 | 0.1953 | 0.1963 | 0.1925 |
| 40 | 0.2368 | 0.2293 | 0.2311 | 0.2263 |
| 50 | 0.2670 | 0.2571 | 0.2602 | 0.2542 |
| 60 | 0.2931 | 0.2808 | 0.2851 | 0.2781 |
| 70 | 0.3160 | 0.3015 | 0.3070 | 0.2991 |
| 80 | 0.3366 | 0.3200 | 0.3268 | 0.3179 |
| 90 | 0.3554 | 0.3367 | 0.3447 | 0.3350 |
| 100 | 0.3727 | 0.3519 | 0.3613 | 0.3507 |
| 110 | 0.3887 | 0.3660 | 0.3766 | 0.3653 |
| 120 | 0.4037 | 0.3790 | 0.3910 | 0.3789 |
| 130 | 0.4178 | 0.3913 | 0.4045 | 0.3917 |
| 140 | 0.4312 | 0.4028 | 0.4173 | 0.4038 |
| 150 | 0.4438 | 0.4137 | 0.4294 | 0.4152 |
| 160 | 0.4558 | 0.4240 | 0.4409 | 0.4262 |
| 170 | 0.4674 | 0.4338 | 0.4519 | 0.4366 |
| 180 | 0.4784 | 0.4432 | 0.4625 | 0.4466 |
| 190 | 0.4890 | 0.4522 | 0.4726 | 0.4562 |
| 200 | 0.4992 | 0.4608 | 0.4824 | 0.4654 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.-T.; Wang, X.-G.; Pang, B.; Ai, J.-C.; Sun, J.-Y. Variational Solution and Numerical Simulation of Bimodular Functionally Graded Thin Circular Plates under Large Deformation. Mathematics 2023, 11, 3083. https://doi.org/10.3390/math11143083
He X-T, Wang X-G, Pang B, Ai J-C, Sun J-Y. Variational Solution and Numerical Simulation of Bimodular Functionally Graded Thin Circular Plates under Large Deformation. Mathematics. 2023; 11(14):3083. https://doi.org/10.3390/math11143083
Chicago/Turabian StyleHe, Xiao-Ting, Xiao-Guang Wang, Bo Pang, Jie-Chuan Ai, and Jun-Yi Sun. 2023. "Variational Solution and Numerical Simulation of Bimodular Functionally Graded Thin Circular Plates under Large Deformation" Mathematics 11, no. 14: 3083. https://doi.org/10.3390/math11143083





