Study on the Influence of an Under-Crossing Parallel Double-Line Shield Tunnel on the Existing Tunnel Structure
Abstract
1. Introduction
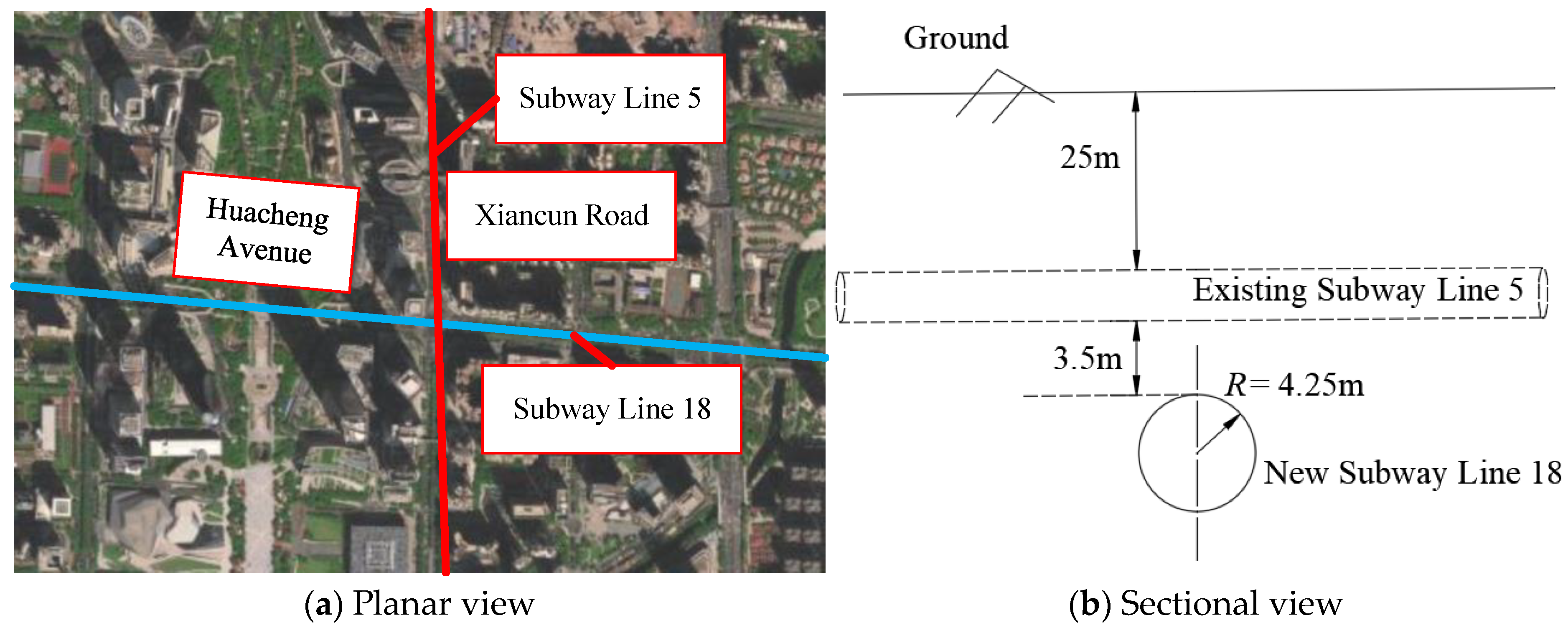
2. Engineering Background
3. Analysis of Influence of Tunnel Construction on Overlying Strata Deformation
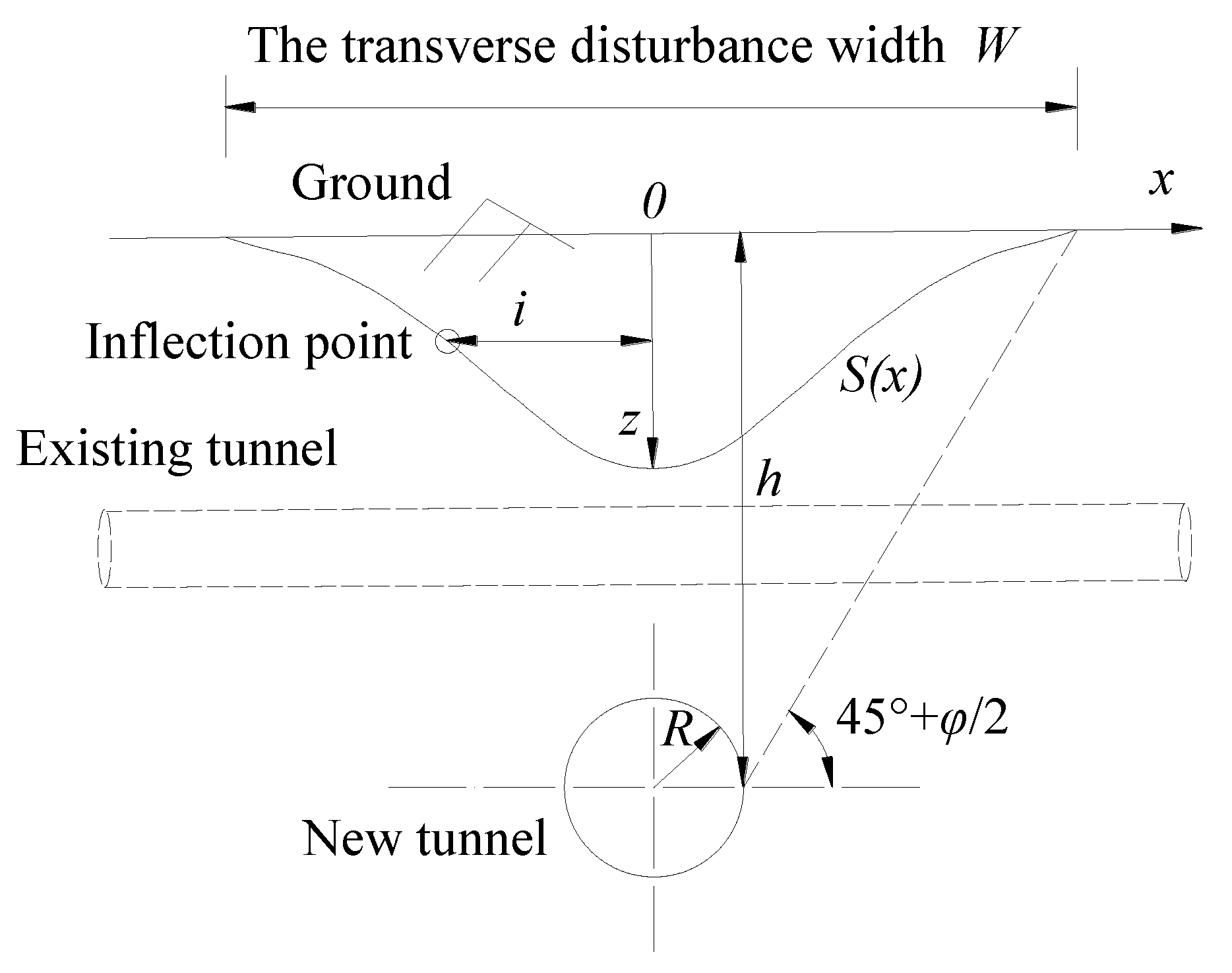
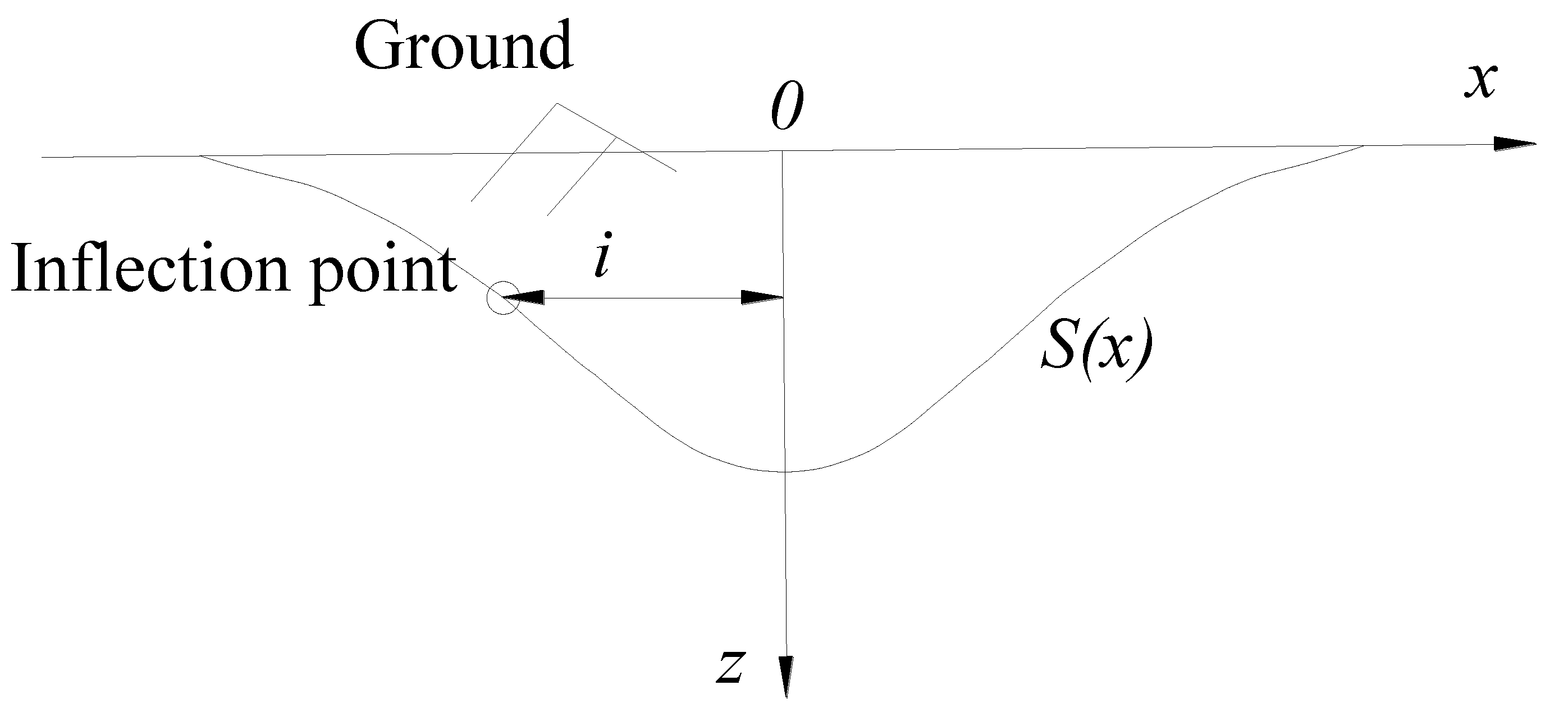
3.1. Empirical Formula for Surface Transverse Settlement
3.2. Empirical Formula of Surface Longitudinal Settlement
4. Three-Dimensional Numerical Analysis of the Influence of an Under-Crossing Parallel Double-Line Shield Tunnel on the Existing Tunnel Structure
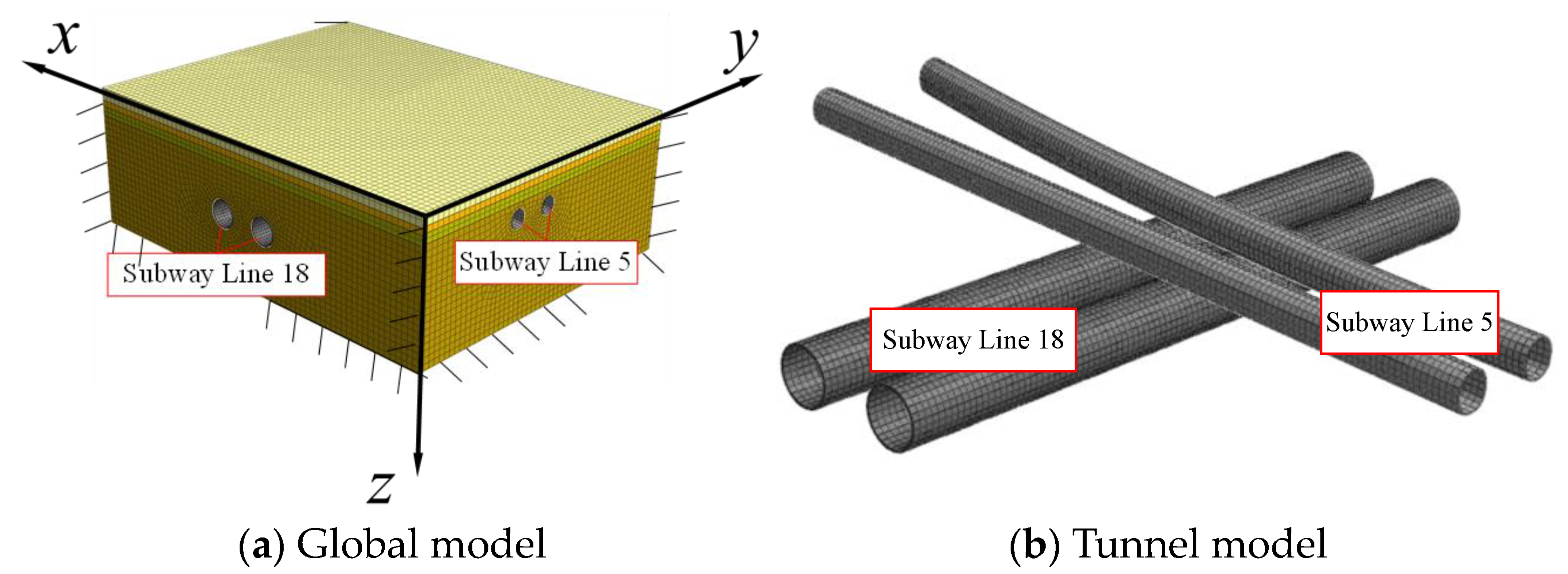
4.1. Three-Dimensional Numerical Model
4.2. Analysis and Conclusion of Three-Dimensional Numerical Results
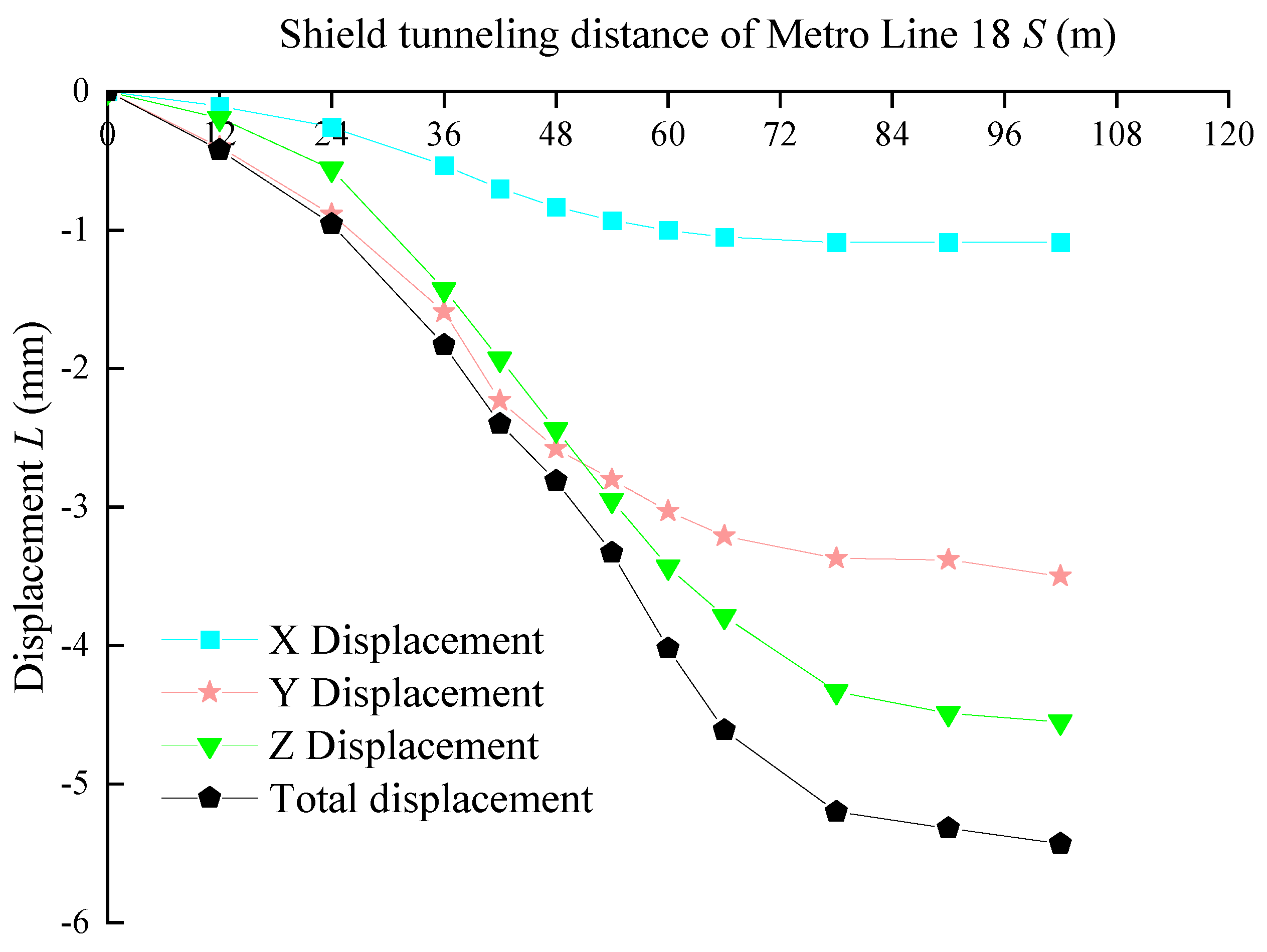
4.2.1. Displacement Analysis of Existing Subway Tunnels
4.2.2. Internal Forces Analysis of Existing Subway Tunnels Caused by New Tunnel Installation
4.2.3. Comparison between Calculated Values and Theoretical Values of Loose Soil Pressure
4.2.4. Comparison of Field Monitoring Results with Numerical Simulation
4.2.5. Conclusion of Three-Dimensional Numerical Simulation and Field Monitoring Results
5. Safety Measures and Suggestions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, Z.; Zuo, J.; Zhu, F.; Liu, H.; Xu, C. Non-orthogonal Failure Behavior of Roadway Surrounding Rock Subjected to Deep Complicated Stress. Rock Mech. Rock Eng. 2023. [Google Scholar] [CrossRef]
- Choi, J.; Lee, S. Influence of existing tunnel on mechanical behavior of new tunnel. KSCE J. Civ. Eng. 2010, 14, 773–783. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M. Geotechnical influence on existing subway tunnels induced by multiline tunneling in Shanghai soft soil. Comput. Geotech. 2014, 56, 121–132. [Google Scholar] [CrossRef]
- Huang, L.; Ma, J.; Lei, M.; Liu, L.; Lin, Y.; Zhang, Z. Soil-water inrush induced shield tunnel lining damage and its stabilization: A case study. Tunn. Undergr. Space Technol. 2020, 97, 103290. [Google Scholar] [CrossRef]
- Lin, Y.; Ma, J.; Lai, Z.; Huang, L.; Lei, M. A FDEM approach to study mechanical and fracturing responses of geo-materials with high inclusion contents using a novel reconstruction strategy. Eng. Fract. Mech. 2023, 282, 109171. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, X.; Ma, J.; Huang, L. A finite-discrete element based appoach for modelling the hydraulic fracturing of rocks with irregular inclusions. Eng. Fract. Mech. 2022, 261, 108209. [Google Scholar] [CrossRef]
- Xu, Q.; Zhu, H.; Ma, X.; Ma, Z.; Li, X.; Tang, Z.; Zhuo, K. A case history of shield tunnel crossing through group pile foundation of a road bridge with pile underpinning technologies in Shanghai. Tunn. Undergr. Space Technol. 2015, 45, 20–33. [Google Scholar] [CrossRef]
- Esen Sze, Y.; Jim Yee, T.; Henry Kim, I.; Osborne, N.; Chang, K.; Siew, R. Tunnelling undercrossing existing live MRT tunnels. Tunn. Undergr. Space Technol. 2016, 57, 241–256. [Google Scholar] [CrossRef]
- Lin, Y.; Yin, Z.; Wang, X.; Huang, L. A systematic 3D simulation method for geomaterials with block inclusions from image recognition to fracturing modelling. Theor. Appl. Fract. Mech. 2022, 117, 103194. [Google Scholar] [CrossRef]
- Liu, H.; Small, J.; Carter, J.; Williams, D. Effects of tunnelling on existing support systems of perpendicularly crossing tunnels. Comput. Geotech. 2009, 36, 880–894. [Google Scholar] [CrossRef]
- Ng, C.; Fong, K.; Liu, H. The effects of existing horseshoe-shaped tunnel sizes on circular crossing tunnel interactions: Three-dimensional numerical analyses. Tunn. Undergr. Space Technol. 2018, 77, 68–79. [Google Scholar] [CrossRef]
- Yang, F.; Liu, J.; Liu, Y.; Zhang, L. Research on Spacing Effect of The Construction of Shield Tunnels undercrossed Existing Tunnels at Close Distance. IOP Conf. Ser. Earth Environ. Sci. 2018, 189, 022086. [Google Scholar] [CrossRef]
- Cao, R.; Peng, L.; Zhao, Y. Control of Strata Deformation in Subway Interval Tunnels Crossing a High-Speed Rail Shield Tunnel at a Short Distance. Arab. J. Sci. Eng. 2021, 46, 5013–5022. [Google Scholar] [CrossRef]
- Chen, F.; Wang, L.; Zhang, W. Reliability assessment on stability of tunnelling perpendicularly beneath an existing tunnel considering spatial variabilities of rock mass properties. Tunn. Undergr. Space Technol. 2019, 88, 276–289. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, C.; Fu, H.; Deng, H.; Ma, S.; Fu, J. Numerical Study on the Disturbance Effect of Short-Distance Parallel Shield Tunnelling Undercrossing Existing Tunnels. Adv. Civ. Eng. 2020, 2020, 8810658. [Google Scholar] [CrossRef]
- Liang, J.; Tang, X.; Wang, T.; Lin, W.; Yan, J.; Fu, C. Analysis for Ground Deformation Induced by Undercrossed Shield Tunnels at a Small Proximity Based on Equivalent Layer Method. Sustainability 2022, 14, 9972. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, W. Numerical Simulation of Dynamic Response Law of Intersecting Metro Tunnels in Upper and Lower Strata. Geotech. Geol. Eng. 2020, 38, 3773–3785. [Google Scholar] [CrossRef]
- Fang, Q.; Du, J.; Li, J.; Zhang, D.; Cao, L. Settlement characteristics of large-diameter shield excavation below existing subway in close vicinity. J. Cent. South Univ. 2021, 28, 882–897. [Google Scholar] [CrossRef]
- Islam, M.; Iskander, M. Twin tunnelling induced ground settlements: A review. Tunn. Undergr. Space Technol. 2021, 110, 103614. [Google Scholar] [CrossRef]
- Hasan, M.; Husaini; Abdullah, N. Deformation and crack analysis of tunnel structure subjected to static distributed load using Pseudoshell model. IOP Conf. Ser. Mater. Sci. Eng. 2019, 523, 012034. [Google Scholar] [CrossRef]
- Luo, C.; Cheng, Y.; Bai, Z.; Shen, T.; Wu, X.; Wang, Q. Study on Deformation Law of Subway Construction under Passing Existing Line in Short Distance. Adv. Civ. Eng. 2021, 2021, 6626927. [Google Scholar] [CrossRef]
- Weng, X.; Yu, H.; Niu, H.; Hu, J.; Han, W.; Huang, X. Interactive effects of crossing tunnel construction on existing tunnel: Three-dimensional centrifugal test and numerical analyses. Transp. Geotech. 2022, 35, 100789. [Google Scholar] [CrossRef]
- Lai, H.; Zhao, X.; Kang, Z.; Chen, R. A new method for predicting ground settlement caused by twin-tunneling under-crossing an existing tunnel. Environ. Earth Sci. 2017, 76, 726. [Google Scholar] [CrossRef]
- Yin, M.; Jiang, H.; Jiang, Y.; Sun, Z.; Wu, Q. Effect of the excavation clearance of an under-crossing shield tunnel on existing shield tunnels. Tunn. Undergr. Space Technol. 2018, 78, 245–258. [Google Scholar] [CrossRef]
- Lin, X.; Chen, R.; Wu, H.; Cheng, H. Deformation behaviors of existing tunnels caused by shield tunneling undercrossing with oblique angle. Tunn. Undergr. Space Technol. 2019, 89, 78–90. [Google Scholar] [CrossRef]
- Gan, X.; Yu, J.; Gong, X.; Liu, N.; Zheng, D. Behaviours of existing shield tunnels due to tunnelling underneath considering asymmetric ground settlements. Undergr. Space 2022, 7, 882–897. [Google Scholar] [CrossRef]
- Peck, R. Deep excavations and tunnelling in soft ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 25–31 August 1969; pp. 225–290. [Google Scholar]
- Attewell, P.; Woodman, J. Predicting the dynamics of ground settlement and its derivatives caused by tunneling in soil. Ground Eng. 1982, 15, 13–22, 36. [Google Scholar]
- New, B.; O’ReilIy, M. Tunnelling induced ground movements: Predicting their magnitude and effects (invited review paper). In Proceedings of the 4th International Conference on Ground Movements and Structures, Cardiff, UK, 8–11 July 1991; Pentech Press: London, UK, 1991; pp. 671–690. [Google Scholar]
- Liu, J.; Hou, X. Shield Tunnel; China Railway Publishing House: Beijing, China, 1991. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons: New York, NY, USA, 1943. [Google Scholar]









| Layer No. | Rock and Soil Layer Name | Layer Thickness (m) | Volume Weight γ (kN/m3) | Young’s Modulus E (MPa) | Poisson’s Ratio μ | Cohesion c (kPa) | Internal Friction Angle φ (°) |
|---|---|---|---|---|---|---|---|
| ① | miscellaneous fill | 4.00 | 19.5 | 10.0 | 0.38 | 10.0 | 15.0 |
| ② | silty clay | 3.50 | 18.5 | 15.0 | 0.36 | 15.0 | 17.0 |
| ③ | strongly weathered argillaceous siltstone | 4.50 | 21.0 | 70.0 | 0.28 | 30.0 | 22.0 |
| ④ | slightly weathered argillaceous siltstone | 8.00 | 25.0 | 5000.0 | 0.19 | 500.0 | 30.0 |
| Simulated Working Condition | Maximum Displacement (mm) | |||
|---|---|---|---|---|
| Horizontal X Displacement | Horizontal Y Displacement | Vertical Z Displacement | Total Displacement | |
| Analysis of initial ground stress field of site | 0.000 | 0.000 | 0.000 | 0.000 |
| Construction of subway Line 5 has been completed | 0.000 | 0.000 | 0.000 | 0.000 |
| Subway Line 18 tunnel excavation 12 m | −0.105 | −0.401 | −0.191 | −0.421 |
| Subway Line 18 tunnel excavation 24 m | −0.256 | −0.887 | −0.561 | −0.956 |
| Subway Line 18 tunnel excavation 36 m | −0.533 | −1.59 | −1.43 | −1.83 |
| Subway Line 18 tunnel excavation 42 m | −0.701 | −2.23 | −1.93 | −2.40 |
| Subway Line 18 tunnel excavation 48 m | −0.833 | −2.58 | −2.44 | −2.81 |
| Subway Line 18 tunnel excavation 54 m | −0.931 | −2.80 | −2.95 | −3.33 |
| Subway Line 18 tunnel excavation 60 m | −1.00 | −3.03 | −3.43 | −4.02 |
| Subway Line 18 tunnel excavation 66 m | −1.05 | −3.21 | −3.79 | −4.61 |
| Subway Line 18 tunnel excavation 78 m | −1.09 | −3.37 | −4.33 | −5.20 |
| Subway Line 18 tunnel excavation 90 m | −1.09 | −3.38 | −4.49 | −5.32 |
| Subway Line 18 tunnel excavation 102 m | −1.09 | −3.50 | −4.55 | −5.43 |
| Simulated Working Condition | Internal Forces (kN/m) | |
|---|---|---|
| the Axial Force of Unit Width in the X Direction | the Axial Force of Unit Width in the Y Direction | |
| Construction of subway Line 5 has been completed | 1688.77 | 914.07 |
| Subway Line 18 tunnel excavation 12 m | 1720.92 | 939.71 |
| Subway Line 18 tunnel excavation 24 m | 1769.92 | 981.11 |
| Subway Line 18 tunnel excavation 36 m | 1852.52 | 1052.14 |
| Subway Line 18 tunnel excavation 42 m | 1902.04 | 1094.79 |
| Subway Line 18 tunnel excavation 48 m | 1939.99 | 1126.64 |
| Subway Line 18 tunnel excavation 54 m | 1965.26 | 1147.56 |
| Subway Line 18 tunnel excavation 60 m | 1980.09 | 1160.14 |
| Subway Line 18 tunnel excavation 66 m | 1987.24 | 1166.98 |
| Subway Line 18 tunnel excavation 78 m | 1988.23 | 1171.35 |
| Subway Line 18 tunnel excavation 90 m | 1981.16 | 1170.17 |
| Subway Line 18 tunnel excavation 102 m | 1976.62 | 1171.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Zhang, D.; Lian, C.; Zhang, J.; Yin, H. Study on the Influence of an Under-Crossing Parallel Double-Line Shield Tunnel on the Existing Tunnel Structure. Mathematics 2023, 11, 3125. https://doi.org/10.3390/math11143125
Zeng L, Zhang D, Lian C, Zhang J, Yin H. Study on the Influence of an Under-Crossing Parallel Double-Line Shield Tunnel on the Existing Tunnel Structure. Mathematics. 2023; 11(14):3125. https://doi.org/10.3390/math11143125
Chicago/Turabian StyleZeng, Linhai, Daobing Zhang, Changjiang Lian, Jiahua Zhang, and Huadong Yin. 2023. "Study on the Influence of an Under-Crossing Parallel Double-Line Shield Tunnel on the Existing Tunnel Structure" Mathematics 11, no. 14: 3125. https://doi.org/10.3390/math11143125
APA StyleZeng, L., Zhang, D., Lian, C., Zhang, J., & Yin, H. (2023). Study on the Influence of an Under-Crossing Parallel Double-Line Shield Tunnel on the Existing Tunnel Structure. Mathematics, 11(14), 3125. https://doi.org/10.3390/math11143125









