Optimal Train Platforming with Shunting Operations for Multidirectional Passenger Stations: A Case Study of Guangzhou Station
Abstract
1. Introduction
2. Literature Review
- (1)
- Current research focuses on train routes that include inbound and outbound routes. On this basis, in this paper, we extend the TPP to include shunting routes in the arrival–departure depot. This addition makes the constraints for route conflict-free conditions more complex but also more realistic.
- (2)
- Our proposed TPP model addresses the challenges encountered in multidirectional busy and complex stations with diverse train types. Additionally, our TPP model accounts for the interconnections of railroad car between different directions or lines.
- (3)
- In terms of algorithmic methodology, we employ a customized algorithm that suits different train operation types. It establishes an initial population that supports iterative optimization and offers adaptability. The main objective is to increase the likelihood of achieving a feasible solution for the TPP model with shunting operations in multidirectional passenger stations using an improved genetic algorithm.
- (4)
- By analyzing the buffer time occupied by switch groups, we show that the shunting operation plays an important role in the operation of multidirectional passenger stations and confirm the efficacy of the model and algorithm presented in this paper, which caters to the requirements of specialized operations and the adaptable shunting maneuvers of locomotives.
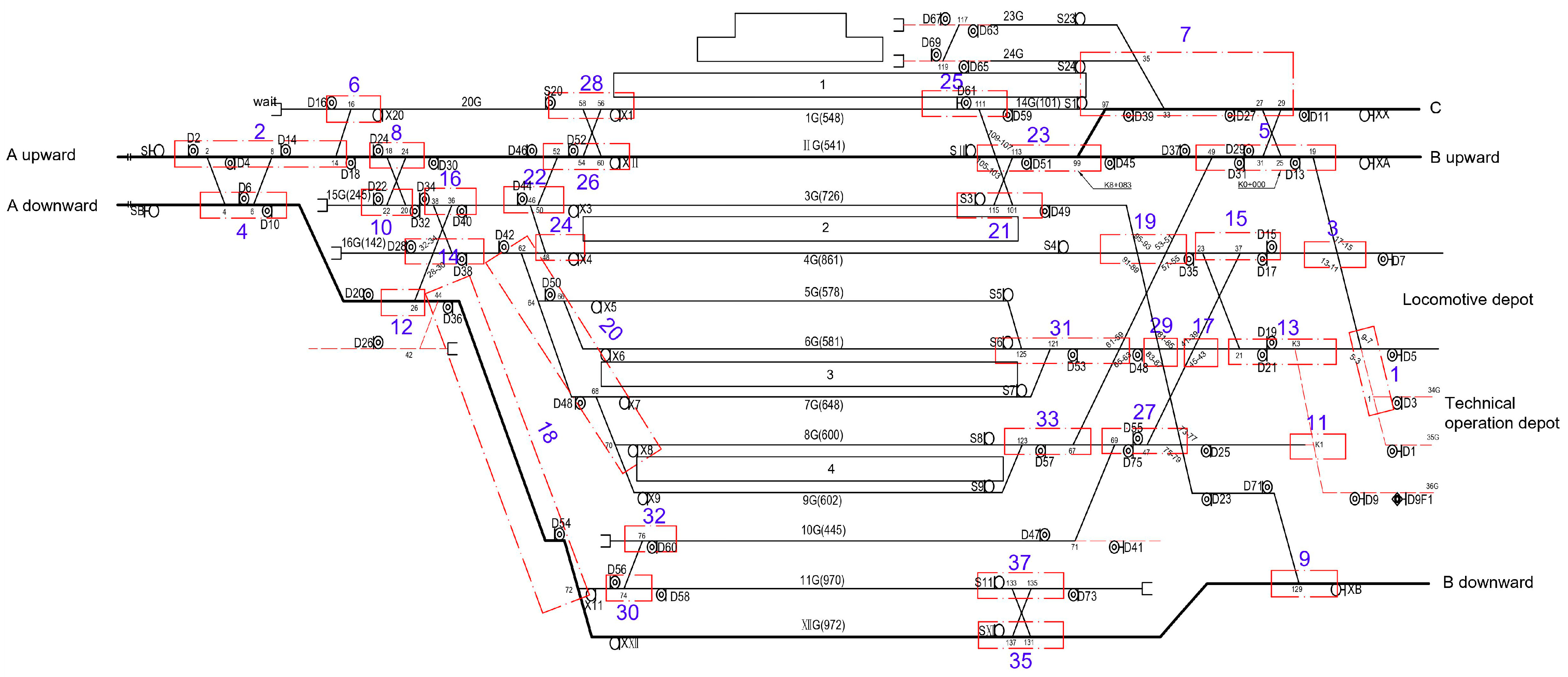
3. Analysis of VCTS Operating Conditions
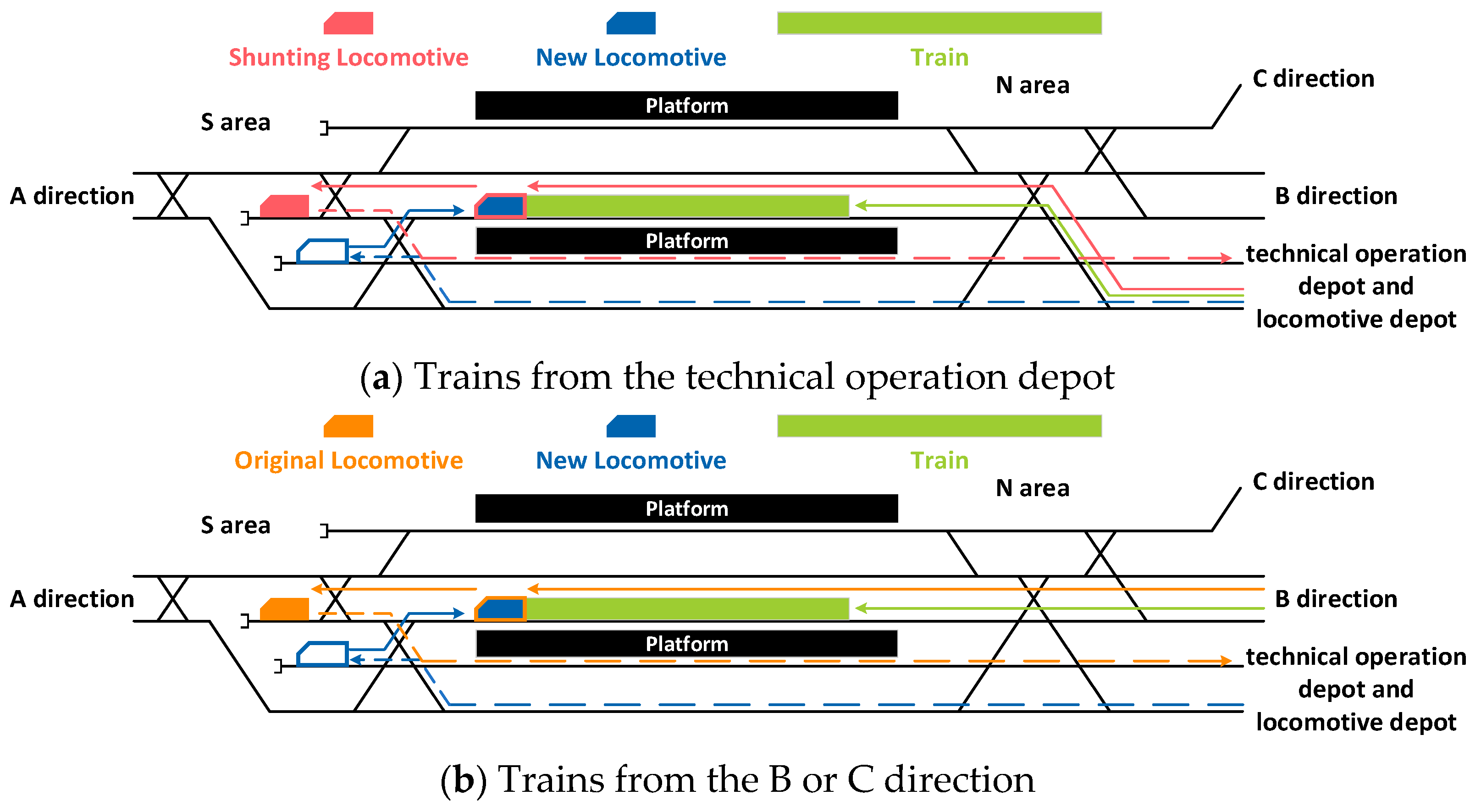
3.1. Train Types Based on Directions and Shunting Operation Chains
3.2. Assumptions
- (1)
- The shunting capacity of locomotives is sufficient for many railroad car shunting operations in this station. The operations that each track can provide are definite. The running times of arrival, departure, and shunting routes in the throat areas can be collected from daily operations. Moreover, the fixed track utilization rule analyzed in Zeng et al. [35] is also used in this paper.
- (2)
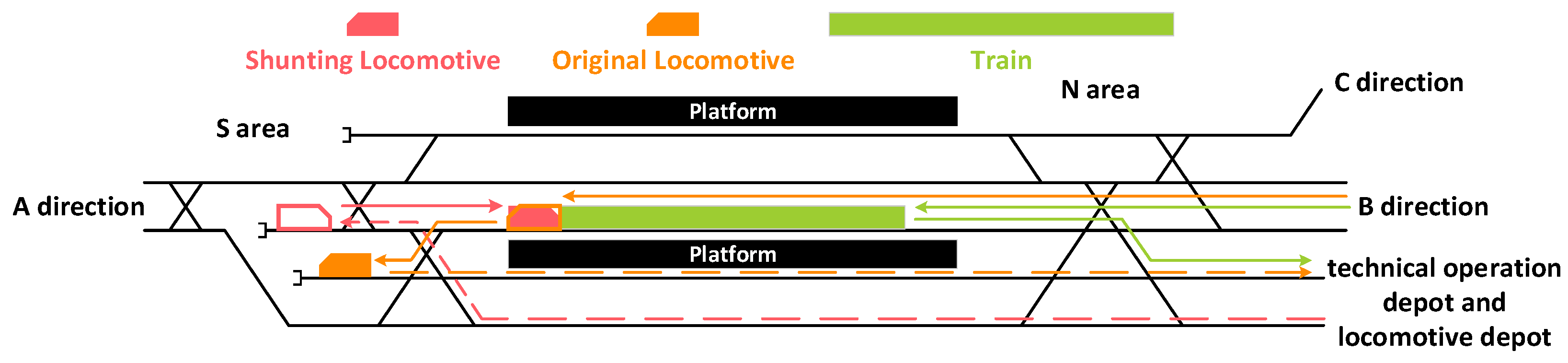
- There is a locomotive walking track (e.g., track 5G in Figure 1) in a multidirectional complex passenger station. To simplify the problem, we disregard the impact of flexible shunting operations on arrival–departure routes in the throat area.
- (3)
- The timetables and railroad car plans of two trains using the same railroad cars will be used as the inputs of the algorithm. The train preparation time criterion, locomotive replacement operation time standard, and shunting operation time standard are stipulated in the station documents.
4. Model Formulation
4.1. Constraints
4.2. Objectives
5. An Improved Genetic Algorithm for the TPP with Shunting Operations
6. Experimental Results and Discussion
6.1. Occupation Time Analysis
6.2. Shunting Occupation Time Analysis
7. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Zhu, X.; Wang, L. Track allocation optimization in multi-directional high-speed railway stations. Symmetry 2019, 11, 459. [Google Scholar] [CrossRef]
- Lusby, R.M.; Larsen, J.; Ehrgott, M.; Ryan, D. Railway track allocation: Models and methods. OR Spectr. 2011, 33, 843–883. [Google Scholar] [CrossRef]
- Caprara, A.; Galli, L.; Toth, P. Solution of the train platforming problem. Transp. Sci. 2011, 45, 246–257. [Google Scholar] [CrossRef]
- Lu, G.; Ning, J.; Liu, X.; Nie, Y. Train platforming and rescheduling with flexible interlocking mechanisms: An aggregate approach. Transp. Res. Part E Logist. Transp. Rev. 2022, 159, 102622. [Google Scholar] [CrossRef]
- Cacchiani, V.; Galli, L.; Toth, P. A tutorial on non-periodic train timetabling and platforming problems. Euro. J. Transp. Logist. 2015, 4, 285–320. [Google Scholar] [CrossRef]
- Zhang, Y.; Umar, A.M.; An, M. Overview of optimization models and algorithms for train platforming problem. In Proceedings of the 4th International Conference on Electrical and Information Technologies for Rail Transportation (EITRT) 2019, Rail Transportation System Safety and Maintenance Technologies; Springer: Singapore, 2019; pp. 707–716. [Google Scholar]
- Zhang, Q.; Lusby, R.; Shang, P.; Zhu, X. Simultaneously re-optimizing timetables and platform schedules under planned track maintenance for a high-speed railway network. Transp. Res. Part C 2020, 121, 102823. [Google Scholar] [CrossRef]
- Zwaneveld, P.J.; Kroon, L.G.; Romeijn, H.E.; Salomon, M.; Dauzère-Pérès, S.; Van Hoesel, S.P.M.; Ambergen, H.W. Routing trains through railway stations: Model formulation and algorithms. Transp. Sci. 1996, 30, 181–194. [Google Scholar] [CrossRef]
- Billionnet, A. Using integer programming to solve the train-platforming problem. Transp. Sci. 2003, 37, 213–222. [Google Scholar] [CrossRef]
- Sels, P.; Vansteenwegen, P.; Dewilde, T.; Cattrysse, D.; Waquet, B.; Joubert, A. The train platforming problem: The infrastructure management company perspective. Transp. Res. Part B Methodol. 2014, 61, 55–72. [Google Scholar] [CrossRef]
- Dewilde, T.; Sels, P.; Cattrysse, D.; Vansteenwegen, P. Robust railway station planning: An interaction between routing, timetabling and platforming. J. Rail Transp. Plan. Manag. 2013, 3, 68–77. [Google Scholar] [CrossRef]
- Dewilde, T.; Sels, P.; Cattrysse, D.; Vansteenwegen, P. Improving the robustness in railway station areas. Eur. J. Oper. Res. 2014, 235, 276–286. [Google Scholar] [CrossRef]
- Corman, F.; Goverde RM, P.; D’Ariano, A. Rescheduling dense train traffic over complex station interlocking areas. In Robust and Online Large-Scale Optimization; Springer: Berlin/Heidelberg, Germany, 2009; pp. 369–386. [Google Scholar]
- Lusby, R.M.; Larsen, J.; Ehrgott, M.; Ryan, D.M. A set packing inspired method for real-time junction train routing. Comput. Oper. Res. 2013, 40, 713–724. [Google Scholar] [CrossRef]
- Pellegrini, P.; Marlière, G.; Rodriguez, J. Optimal train routing and scheduling for managing traffic perturbations in complex junctions. Transp. Res. Part B Methodol. 2014, 59, 58–80. [Google Scholar] [CrossRef]
- Pellegrini, P.; Pesenti, R.; Rodriguez, J. Efficient train re-routing and rescheduling: Valid inequalities and reformulation of RECIFE-MILP. Transp. Res. Part B Methodol. 2019, 120, 33–48. [Google Scholar] [CrossRef]
- Sels, P.; Cattrysse, D.; Vansteenwegen, P. Automated platforming & routing of trains in all Belgian railway stations. Expert Syst. Appl. 2016, 62, 302–316. [Google Scholar]
- Matteo, F.; Michele, M. Using a general-purpose Mixed-Integer Linear Programming solver for the practical solution of real-time train rescheduling. Eur. J. Oper. Res. 2017, 263, 258–264. [Google Scholar]
- Meng, X.; Wang, Y.; Xiang, W.; Jia, L. An integrated model for train rescheduling and station track assignment. IET Intell. Transp. Syst. 2020, 15, 17–30. [Google Scholar] [CrossRef]
- Neeraj, K.; Abhishek, M. An efficient method of disturbance analysis and train rescheduling using MWDLNN and BMW-SSO algorithms. Soft Comput. 2021, 25, 12031–12041. [Google Scholar]
- Wang, Y.; Song, R.; He, S.; Song, Z. Train Routing and Track Allocation Optimization Model of Multi-Station High-Speed Railway Hub. Sustainability 2022, 14, 7292. [Google Scholar] [CrossRef]
- García-Ródenas, R.; López-García, M.L.; Cadarso, L.; Codina, E. A Mixed-integer Linear Program for Real-time Train Platforming Management. Transp. Res. Procedia 2022, 62, 815–823. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhang, Y.; Su, H.; Hu, R. Robustness-Oriented Optimization of Train Platforming Problem in Busy Complex Railway Station. Math. Probl. Eng. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Li, H.; Jin, M.; He, S.; Ye, Z.; Song, J. Optimal track utilization in electric multiple unit maintenance depots. Comput. Ind. Eng. 2017, 108, 81–87. [Google Scholar] [CrossRef]
- Haahr, J.T.; Lusby, R.M.; Wagenaar, J.C. Optimization methods for the train unit shunting problem. Eur. J. Oper. Res. 2017, 262, 981–995. [Google Scholar] [CrossRef]
- Guo, B.; Wu, W.; Zhu, X. Analysis and model the rolling stock shunting plan safety optimization problem in the hub type high-speed railway station. In Proceedings of the 2020 International Conference on Urban Engineering and Management Science (ICUEMS), Zhuhai, China, 24–26 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 472–475. [Google Scholar]
- Wang, J.; Lin, B.; Jin, J. Optimizing the shunting schedule of electric multiple units depot using an enhanced particle swarm optimization algorithm. Comput. Intell. Neurosci. 2016, 2016, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Miranda, P.L.; Cordeau, J.F.; Frejinger, E. A time–space formulation for the locomotive routing problem at the Canadian National Railways. Comput. Oper. Res. 2022, 139, 105629. [Google Scholar] [CrossRef]
- Chen, W.; Yang, W.; Zhang, G. Track Utilization Optimization Method for Arrival Yard of Marshalling Station Considering Arrival and Break-Up Coordination Operation. Mathematics 2022, 10, 3289. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, R.; He, S.; Li, H.; Guo, X. Optimization of Classification Track Assignment Considering Block Sequence at Train Marshaling Yard. J. Adv. Transp. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Schasfoort, B.; Gkiotsalitis, K.; Eikenbroek, O.; van Berkum, E. A dynamic model for real-time track assignment at railway yards. J. Rail Transp. Plan. Manag. 2020, 14, 100198. [Google Scholar] [CrossRef]
- Shi, J.; Li, H. Optimization of the Shunting Operation Plan at Electric Multiple Units Depots. J. Adv. Transp. 2019, 2019. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, X.; Kang, L. Real-time track reallocation for emergency incidents at large railway stations. Mathematical Problems in Engineering 2019, 2019, 1–15. [Google Scholar] [CrossRef]
- Wang, H.; Yue, Y. Optimizing train-platforming plans at arrival-departure tracks of high-speed railway stations. In Proceedings of the 2020 IEEE 5th International Conference on Intelligent Transportation Engineering (ICITE), Beijing, China, 11–13 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 461–466. [Google Scholar]
- Zeng, Q.; Hu, R.; Zhang, Y.; Su, H.; Liu, Y. A Genetic Simulated Annealing Algorithm for Real-Time Track Reallocation in Busy Complex Railway Station. Math. Probl. Eng. 2022, 2022, 1–13. [Google Scholar] [CrossRef]
- Carey, M.; Carville, S. Scheduling and Platforming Trains at Busy Complex Stations. Transp. Res. Part A Policy Pract. 2003, 37, 195–224. [Google Scholar] [CrossRef]




| Reference | Routes of Arr./Dep. | Routes of Shunting Operations | Multiple Directions | Fixed Track Utilization Rules | Occupation Time Analysis |
|---|---|---|---|---|---|
| Billionnet et al. [9] | - | - | - | - | - |
| Dewilde et al. [12] | - | - | - | - | - |
| Zwaneveld et al. [8] | √ | - | - | - | - |
| Liu et al. [33] | √ | - | - | - | - |
| Lu et al. [4] | √ | - | √ | - | - |
| Sels et al. [10] | √ | - | - | - | √ |
| Wang et al. [34] | √ | - | √ | - | - |
| Zhang et al. [1] | √ | - | √ | √ | √ |
| This paper | √ | √ | √ | √ | √ |
| Train Type | From | To | Nswitch | Sswitch | Nreplace | Sreplace | Nshunting | Sshunting |
|---|---|---|---|---|---|---|---|---|
| NSTs | • | • | √ | √ | - | - | - | - |
| STs | • | • | √ | √ | - | - | - | - |
| STs | A | A | - | √ | - | - | - | - |
| STs | B or C | B or C | √ | - | - | - | - | - |
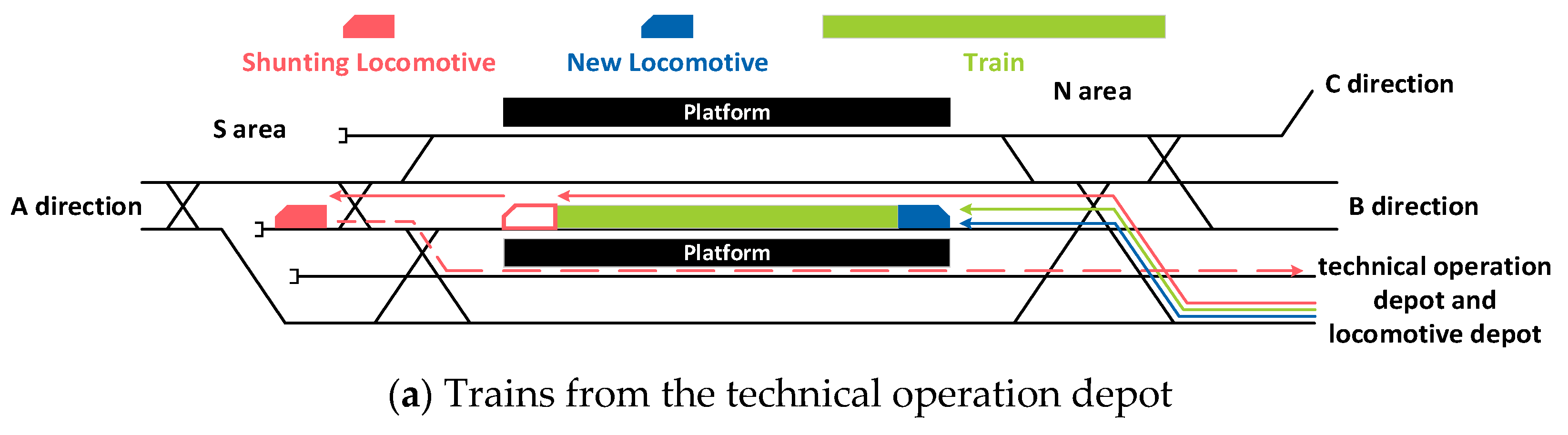
| STLSs | D | A | √ | √ | - | √ | √ | √ |
| STLSs | B or C | A | √ | √ | - | √ | √ | √ |
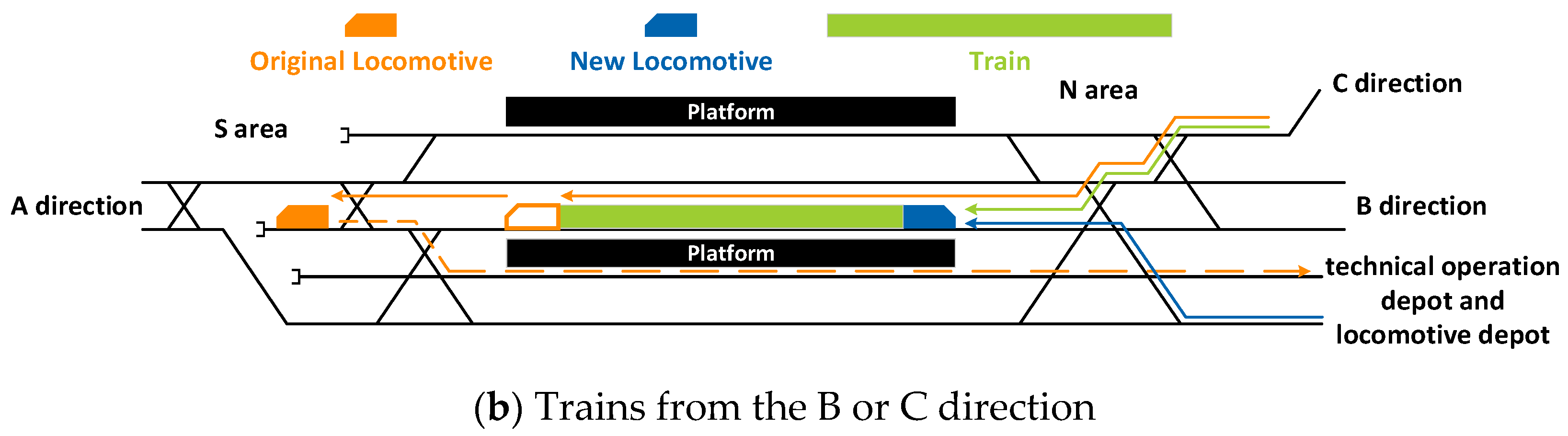
| STLNSs | D | B or C | √ | √ | - | - | √ | √ |
| STLNSs | B | C | √ | √ | - | - | √ | √ |
| STLNSs | C | B | √ | √ | - | - | √ | √ |
| TASs | A | D | √ | √ | - | - | √ | √ |
| TBCSs | B or C | D | √ | √ | - | √ | √ | √ |
| Symbol | Description |
|---|---|
| . | |
| . | |
| when it first occupies station resources. | |
| when it no longer occupies station resources. | |
| . | |
| . | |
| Time horizon of the station operation daily plan. | |
| Standard arrival operation time of terminal trains. | |
| Standard departure operation time of original trains. | |
| Standard operation time of original locomotive separation or new locomotive attachment operations in the south throat area. | |
| Standard operation time of original locomotive separation or new locomotive attachment operations in the north throat area. | |
| Standard operation time of locomotive replacement operations, including both original locomotive separation and new locomotive attachment operations. | |
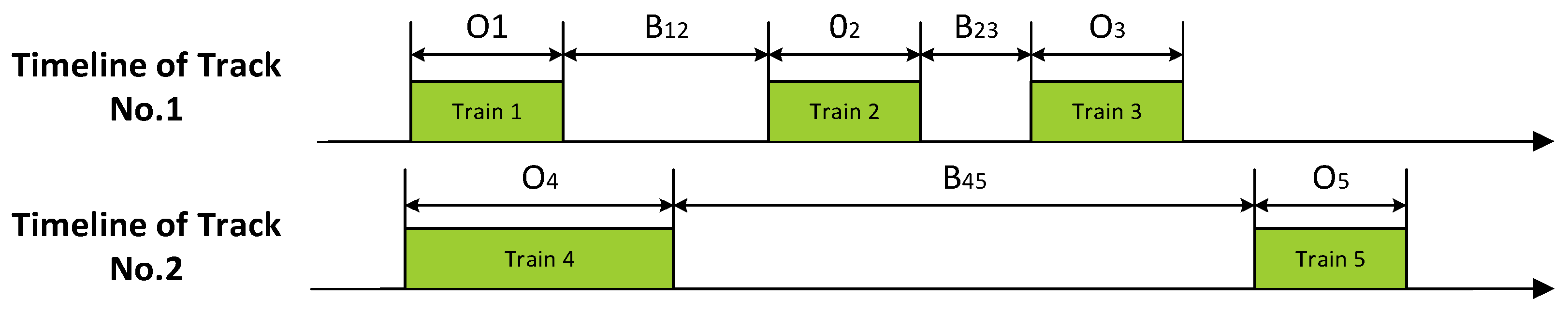
| Safety time interval for platform track occupation. | |
| is the total number of tracks. | |
| is the total number of arrival–departure tracks. | |
| is the total number of special operation tracks. | |
| Set of main tracks. | |
| ; denotes the total number of through passenger trains. | |
| ; denotes the total number of through passenger trains. | |
| Set of trains whose operation type belongs to Ts | |
| Set of trains whose operation type belongs to STLSs | |
| Set of trains whose operation type belongs to STLNSs | |
| Set of trains whose operation type belongs to TASs | |
| Set of trains whose operation type belongs to TBCSs | |
| Set of all switch groups within the train operating route in the S throat area | |
| Set of all switch groups within the locomotive operating route in the S throat area | |
| Set of all switch groups within the train operating route in the N throat area | |
| Set of all switch groups within the train inbound route in the N throat area | |
| Set of all switch groups within the train outbound route in the N throat area | |
| Set of all switch groups within the locomotive operating route in the N throat area |
| Symbol | Description |
|---|---|
| , 0 otherwise. | |
| , and 0 otherwise. | |
| , and 0 otherwise. | |
| , and 0 otherwise. | |
| , and 0 otherwise. | |
| , and 0 otherwise. | |
| , and 0 otherwise. | |
| , and 0 otherwise. |
| Arrival or Departure Direction | Receiving Routes | Departure Routes | Passing-Through Routes in an Upwards Direction | Passing-Through Routes in a Downwards Direction |
|---|---|---|---|---|
| B | 6 | 6 | 4 | 5 |
| C (D/H/P/T) | 5 | 6 | 4 | 4 |
| A (D/H/P/T) | 6 | 6 | 5 | 4 |
| C (M) | 4 | 4 | - | - |
| A (M) | 5 | 5 | - | - |
| 180 s | 240 s | 300 s | 20 min | 35 min |
| No. | Type | Arr | Dep | From | To | Original Track | Optimized Track | No. | Type | Arr | Dep | From | To | Original Track | Optimized Track |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | D | 10:40 | 10:46 | C | A | 1 | 1 | 26 | D | 13:22 | 13:30 | A | C | 1 | 3 |
| 2 | H | 10:44 | 11:18 | A | B | II | II | 27 | D | 13:23 | 13:48 | C | C | 3 | 4 |
| 3 | T | 10:46 | —— | B | D | 8 | 6 | 28 | T | 13:26 | —— | B | D | 9 | 8 |
| 4 | T | 10:57 | —— | B | D | 9 | 7 | 29 | T | 13:41 | —— | B | D | 7 | 9 |
| 5 | D | 10:58 | 11:04 | A | C | 3 | 3 | 30 | D | 13:44 | 13:52 | C | A | 1 | 1 |
| 6 | D | 11:03 | 11:20 | C | C | 1 | 4 | 31 | T | —— | 14:20 | D | B | 8 | 6 |
| 7 | T | —— | 11:40 | D | B | 6 | 8 | 32 | P | 13:47 | 13:47 | B | A | Ⅻ | Ⅻ |
| 8 | T | 11:12 | 11:32 | A | C | 4 | 1 | 33 | D | 14:02 | 14:17 | A | A | 3 | 4 |
| 9 | T | 11:18 | 11:38 | C | A | 3 | 3 | 34 | T | 14:04 | —— | B | D | 6 | 7 |
| 10 | D | 11:30 | 11:44 | A | A | 7 | 9 | 35 | M | 14:08 | 16:12 | C | C | 23 | 23 |
| 11 | T | 11:43 | —— | B | D | 8 | 3 | 36 | T | 14:13 | —— | B | D | 9 | 8 |
| 12 | D | 11:44 | 11:50 | A | C | 3 | 1 | 37 | T | —— | 14:56 | D | B | 4 | 9 |
| 13 | T | 11:50 | 12:11 | A | B | 6 | 4 | 38 | D | 14:24 | 14:30 | A | C | 3 | 3 |
| 14 | T | 11:52 | —— | B | D | 9 | 6 | 39 | T | —— | 15:09 | D | B | 1 | 7 |
| 15 | T | 12:06 | 13:06 | B | B | 7 | 7 | 40 | H | 14:37 | 14:39 | A | B | II | II |
| 16 | D | 12:13 | 12:32 | C | C | 3 | 3 | 41 | D | 14:50 | 14:55 | C | A | 3 | 1 |
| 17 | T | —— | 13:00 | D | B | 6 | 8 | 42 | P | 14:52 | 15:02 | A | B | II | II |
| 18 | T | 12:30 | —— | B | D | 9 | 9 | 43 | D | 15:08 | 15:11 | C | A | 3 | 4 |
| 19 | T | 12:32 | 12:52 | A | B | 4 | 1 | 44 | D | 15:15 | 15:41 | A | A | 7 | 1 |
| 20 | P | 12:42 | 12:46 | A | B | II | II | 45 | T | —— | 15:50 | D | B | 8 | 6 |
| 21 | T | 12:44 | 13:40 | B | B | 8 | 6 | 46 | D | 15:25 | 15:29 | C | A | 3 | 3 |
| 22 | P | 12:51 | 13:12 | B | A | Ⅻ | Ⅻ | 47 | T | 15:25 | 15:35 | B | A | 9 | 9 |
| 23 | D | 13:01 | 13:06 | C | A | 1 | 4 | 48 | T | —— | 16:06 | D | B | 1 | 8 |
| 24 | D | 13:02 | 13:08 | A | C | 4 | 3 | 49 | T | 15:37 | 15:47 | B | A | 3 | 7 |
| 25 | T | 13:13 | 13:33 | A | B | 6 | 7 |
| Time Parameter | Original Plan | Optimized Plan |
|---|---|---|
| Maximum buffer time (min) | 101 | 58 |
| Minimum buffer time (min) | 5 | 5 |
| Quadratic difference in buffer times | 584.82 | 406.13 |
| Quadratic difference in track utilization times | 5.14 | 1.14 |
| Number of trains that have buffer times between [0, 20] (min) | 17 | 12 |
| Number of trains that have buffer times between [20, 40] (min) | 9 | 9 |
| Number of trains that have buffer times between [40, 60] (min) | 6 | 14 |
| Number of trains that have buffer times between [60, ∞] (min) | 4 | 0 |
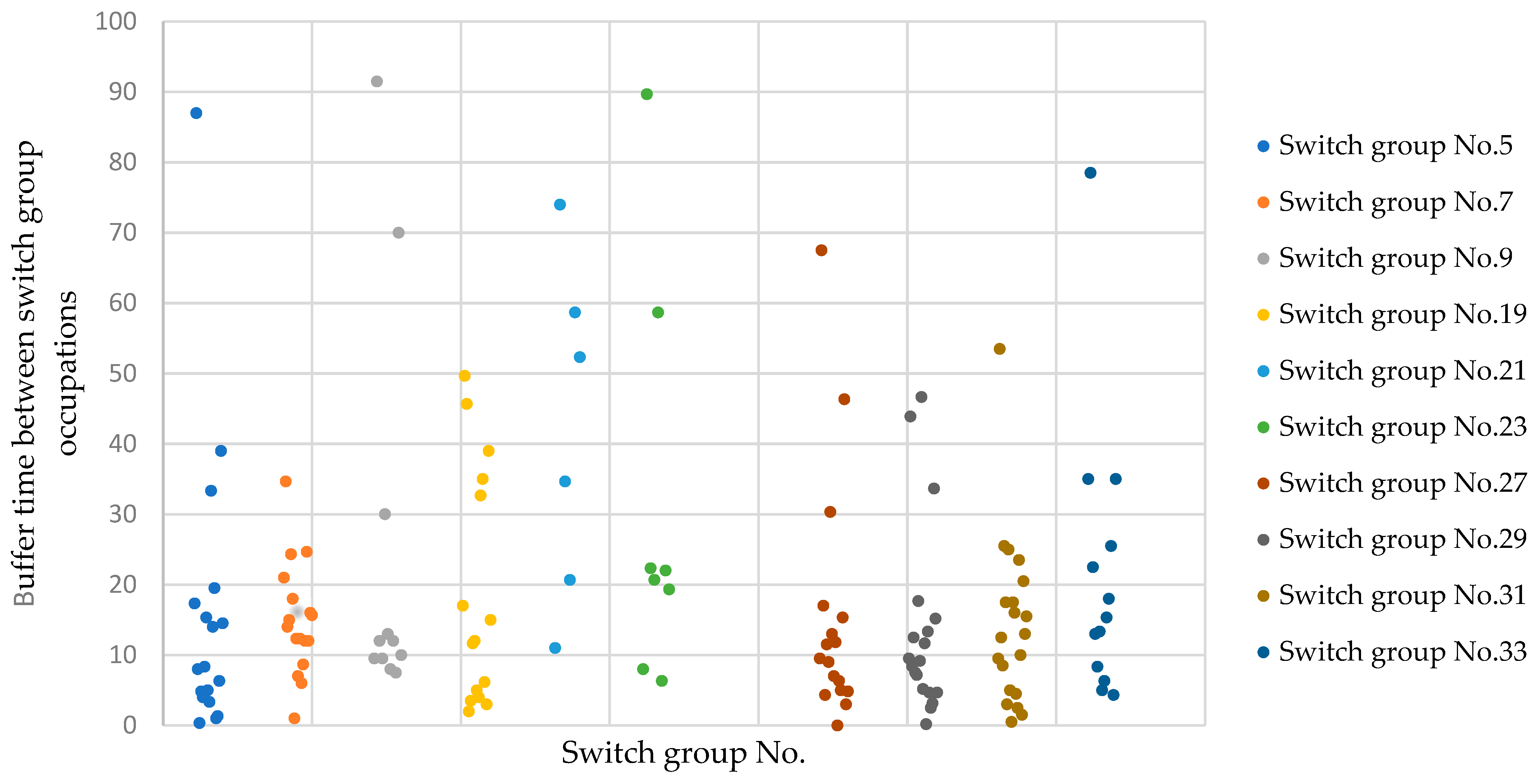
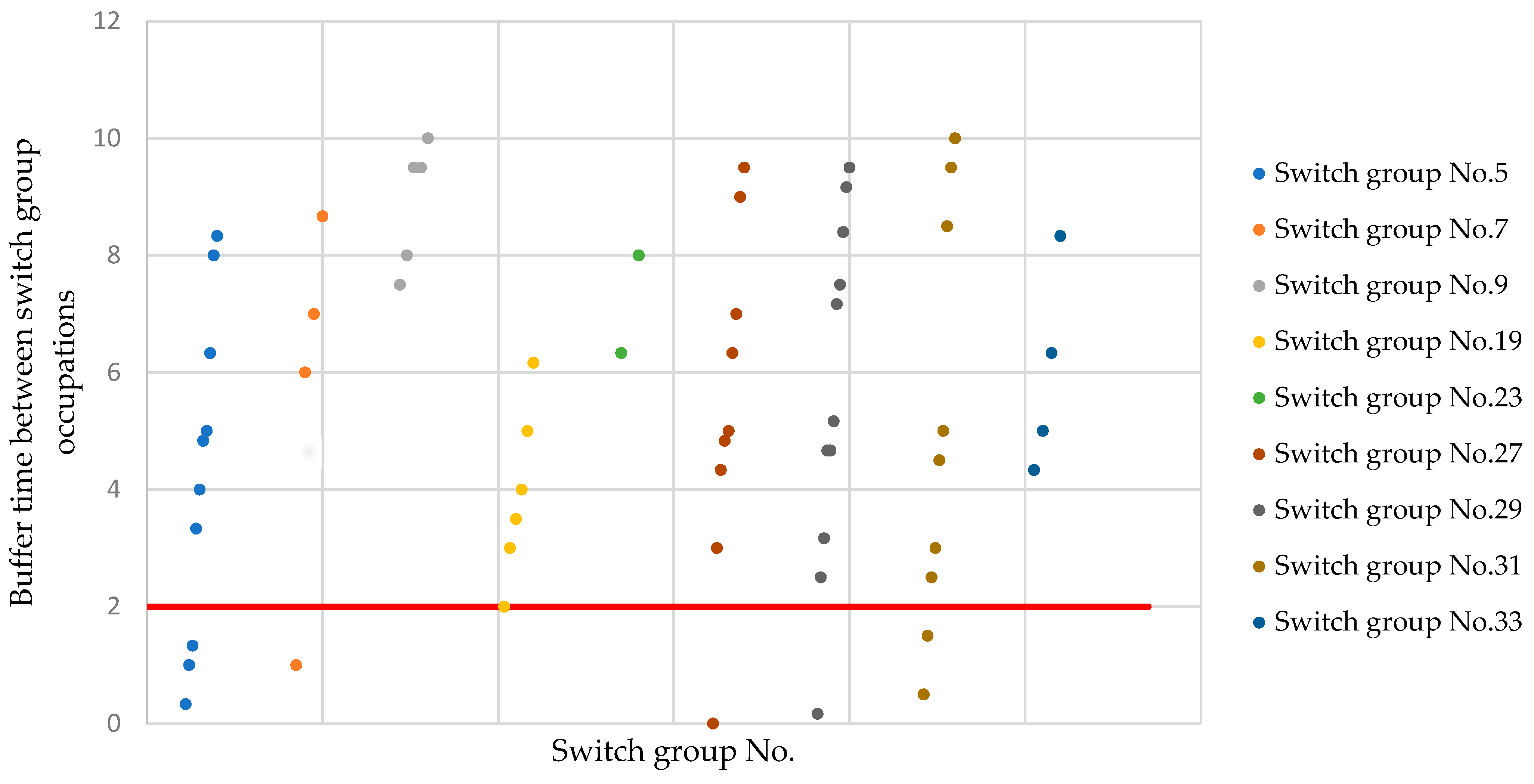
| Switch Group No. | Total Occupation Frequency | Shunting Operation Occupation Frequency | Arrival-Departure Operation Occupation Frequency |
|---|---|---|---|
| 5 | 20 | 0 | 20 |
| 7 | 18 | 0 | 18 |
| 9 | 12 | 0 | 12 |
| 19 | 16 | 1 | 15 |
| 21 | 7 | 1 | 6 |
| 23 | 9 | 0 | 9 |
| 25 | 3 | 0 | 3 |
| 27 | 18 | 8 | 10 |
| 29 | 20 | 15 | 5 |
| 31 | 21 | 7 | 14 |
| 33 | 14 | 8 | 6 |
| 35 | 2 | 0 | 2 |
| 37 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Hu, R.; Zeng, Q.; Wang, Y.; Liu, Y.; Huang, S. Optimal Train Platforming with Shunting Operations for Multidirectional Passenger Stations: A Case Study of Guangzhou Station. Mathematics 2023, 11, 3136. https://doi.org/10.3390/math11143136
Zhang Y, Hu R, Zeng Q, Wang Y, Liu Y, Huang S. Optimal Train Platforming with Shunting Operations for Multidirectional Passenger Stations: A Case Study of Guangzhou Station. Mathematics. 2023; 11(14):3136. https://doi.org/10.3390/math11143136
Chicago/Turabian StyleZhang, Yinggui, Ruihua Hu, Qiongfang Zeng, Yuhang Wang, Ya Liu, and Shan Huang. 2023. "Optimal Train Platforming with Shunting Operations for Multidirectional Passenger Stations: A Case Study of Guangzhou Station" Mathematics 11, no. 14: 3136. https://doi.org/10.3390/math11143136
APA StyleZhang, Y., Hu, R., Zeng, Q., Wang, Y., Liu, Y., & Huang, S. (2023). Optimal Train Platforming with Shunting Operations for Multidirectional Passenger Stations: A Case Study of Guangzhou Station. Mathematics, 11(14), 3136. https://doi.org/10.3390/math11143136





