A Decentralized Federated Learning Based on Node Selection and Knowledge Distillation

Abstract

Federated learning has become increasingly important for modern machine learning, especially for data privacy sensitive scenarios. Existing federated learning mainly adopts a central server-based network topology, however, the training process of which is susceptible to the central node. To address this problem, this article proposed a decentralized federated learning method based on node selection and knowledge distillation. Specifically, the central node in this method is variable, and it is selected by the indicator interaction between nodes. Meanwhile, the knowledge distillation mechanism is added to make the student model as close as possible to the teacher’s network and ensure the model’s accuracy. The experiments were conducted on the public MNIST, CIFAR-10, and FEMNIST datasets for both the Independent Identically Distribution (IID) setting and the non-IID setting. Numerical results show that the proposed method can achieve an improved accuracy as compared to the centralized federated learning method, and the computing time is reduced greatly with less accuracy loss as compared to the blockchain decentralized federated learning. Therefore, the proposed method guarantees the model effect while meeting the individual model requirements of each node and reducing the running time.

1. Introduction

In recent years, machine learning has been widely used in many fields, such as social networks and e-commerce [1]. In practical applications, the data is mostly isolated, which makes it difficult to fully explore the value of data [2]. In the face of data and security issues, federated learning has emerged as a new distributed machine learning method. In federated learning, nodes can cooperate to build models together with improved effectiveness. It is noted that the exchange between the central node and normal node is model parameters, rather than data itself, which can effectively avoid the problems arising from data transmission [3].

Federated learning mostly uses a centralized structure, which means that all local nodes need to interact with the central node for parameter exchange. In Federated learning, the final model is usually generated by aggregating the distributed models of different nodes. A typical Federated learning algorithm is Federated Averaging [4], where local models are collected by the central node, and the central node aggregates these models by averaging. Therefore, the quality of the aggregated model in Federated learning will be affected by each local model. Since the computational capabilities are different among local nodes, and their data may also be different, the generated local models may be distinct [5]. In [6], Li et al. proposed FedProx, which adds a proximal term to the FedAvg algorithm. It is used to control the magnitude of the variation of the local model parameters, which can alleviate the impact of data heterogeneity to some extent. However, the performance of the centralized topology depends on the central node and suffers from a heavy communication and computation burden [7]. If the central server is maliciously compromised, the entire training process will be controlled by the attacker [8]. In [9], Chen et al. proposed a game theory-based detection and incentive for Byzantine and inactive users. It is used to solve the problem of inactive users’ participation in federated learning with some effectiveness. Therefore, how to ensure training in a safe and stable environment with guaranteed model accuracy are a key problem in federated learning.

To further protect data privacy and avoid the communication bottleneck, the decentralized architecture has been recently proposed, where the centralized node has been removed. Decentralized federated learning is a typical parallel strategy that guarantees the privacy security of nodes and the high performance of the model [10]. It is especially preferred when the network condition is poor, or the number of nodes is very large [11]. Blockchain is an important implementation of the decentralized method to increase the throughput [12]. In [13], Caldarola et al. proposed a novel approach, the neural fairness protocol, which is a blockchain-based distributed ledger secured using neural networks and machine learning algorithms, enabling permissionless participation in the process of transition validation while concurrently providing strong assurance about the correct functioning of the entire network. In [14], Qiao et al. proposed a consensus mechanism based on proof-of-contribution (POC). Meanwhile, Zhou et al. proposed decentralized federated learning based on blockchain [15]. This method uses homomorphic cryptography in the blockchain to protect the privacy of parameters between nodes and has achieved some success. In decentralized federated learning, there are still many problems to be solved. The model training of decentralized federated learning may become unstable due to factors such as noise and data bias, which can lead to weak generalization ability or overfitting of the model.

Meanwhile, there is a lack of efficient methods to obtain the optimal nodes in a complex and dynamic network environment. Node selection is a viable solution that can effectively reduce the communication burden [16]. The literature [17] uses greedy algorithms to select nodes with shorter time consumption and discard nodes with poor communication conditions to improve overall efficiency. On the other hand, the algorithm convergence stability can be improved by correlating the label distribution of node combinations with the model convergence [18]. At the same time, selection fairness should be considered while focusing on reducing the average communication time [19], so that nodes are selected with a more even probability.

Meanwhile, to tackle the problem of high user communication costs, a knowledge distillation mechanism is used in this article. Knowledge distillation, as a practically widely used and easily trained model compression method in machine learning, is gradually becoming an important optimization tool in federated learning [20]. In [21], Zhu et al. proposed a method for knowledge distillation without agent datasets by learning a lightweight data generator that augments the dataset to weaken the effect of heterogeneity in terms of offsets. Sattler et al. [22] proposed quantization, lossless coding, and double distillation to further conserve the bandwidth occupied by transmitting soft targets.

The contribution of this article is summarized as follows:

• We proposed a decentralized federated learning method, which is using a common peer-to-peer model to select neighboring nodes through a node selection mechanism. In this article, local model performance and local dataset size for the current round are considered for important metrics to reflect data quality differences and resource heterogeneity across devices.
• We added a knowledge distillation mechanism to the method. The stability and running time of the method are guaranteed with less loss of precision.

2. Materials and Methods

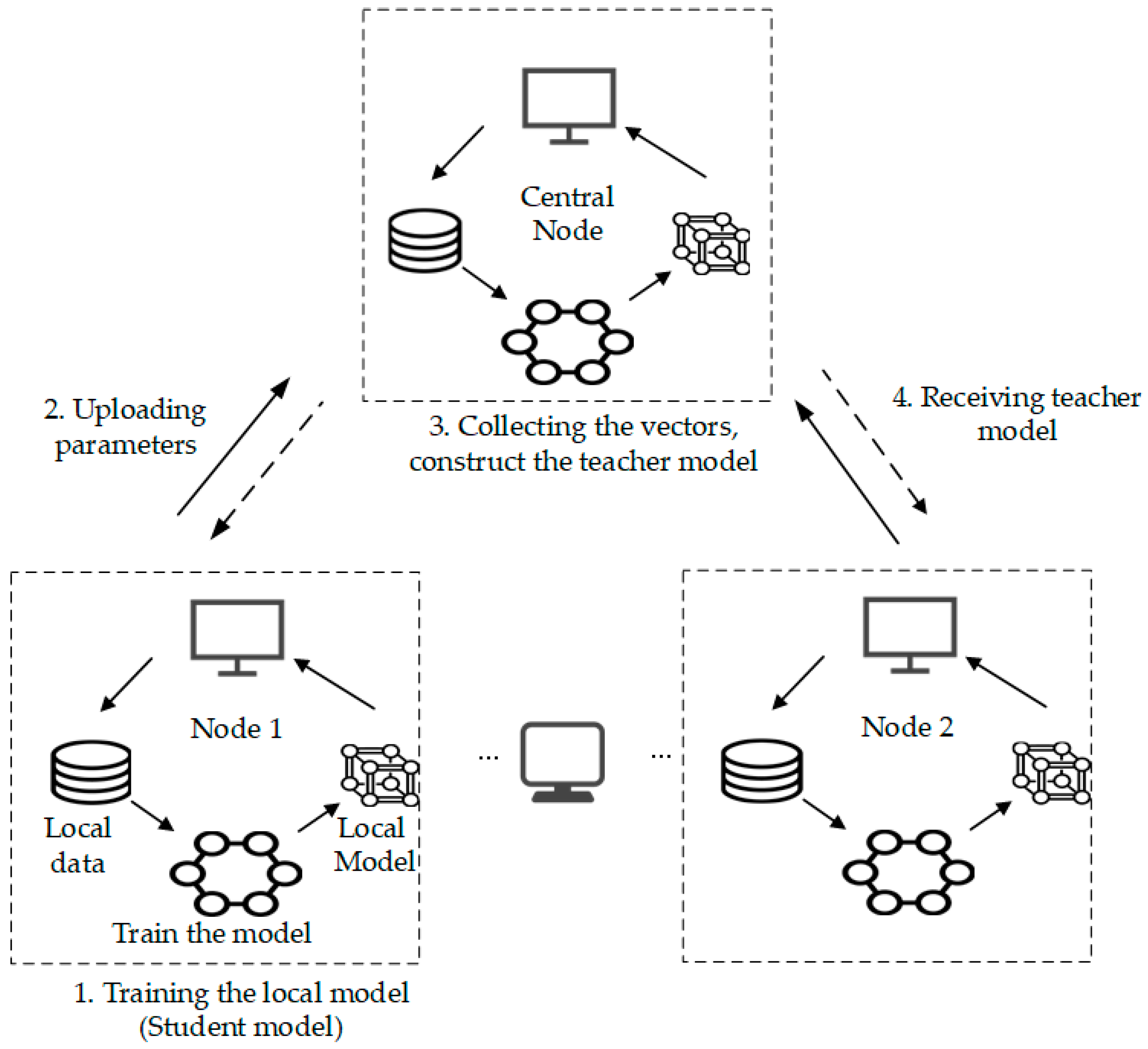
2.1. System Model

The proposed system structure is shown in Figure 1. Federated learning mainly includes local training of models, parameter uploading, building teacher models, and teacher model distribution. Each node initializes a model and uses its local data for model training (Step 1). The device obtains the model parameters and uploads them to the central node (Step 2). In knowledge distillation, the uploaded parameters are the Logits vectors computed by the final Softmax layer of the local model. The federated center integrates the Logits vectors to construct the teacher model (Step 3), and then each neighboring node receives the teacher model to guide the training of their student networks. The central nodes in Figure 1 represent only the central nodes that were selected in this round. The central idea is to use the local model performance and local dataset size of the current round to represent the data quality differences and resource heterogeneity of the nodes. The central node is then selected by means of evaluation of each node. Through the evaluation of the central nodes, the set of nodes with high quality is selected to complete the training.

2.2. The Decentralized Federated Learning

Consider a network with $N$ nodes, the topology can be represented by the directed graph $G=(node:[n],edge:E)$, and its corresponding adjacency matrix. If condition $(u,v)\in E\&(v,u)\in E$ holds for nodes $u$ and $v$, it means that there exists a connection between $u$ and $v$ for bidirectional communication. The main symbols used in the proposed method are defined in

Table 1. Commonly used symbols.

Symbol	Description	Symbol	Description
$N$	the total number of nodes	$S_t^{}$	the set of labeled Logits output of tags t
$\eta$	learning rate	$L_{total}$	the total loss of knowledge distillation
$\nabla$	gradient operator	$L_{KD}$	the loss between the student model and the teacher model
$b$	batch size	$D_k$	the local dataset of node k
$W_k$	the model parameters of node k	$y$	vector of hard labels
$\ell$	loss function	$p$	the class probability
$K$	set of nodes	$g$	logical units of the teacher model output

.

The network topology (Take $N$ = 5) is shown in Figure 2, and the weights in the adjacency matrix are the sizes of the bidirectional indicators between the nodes. If the initial weight in the matrix is 1, it means that the nodes are connected to each other, and their weights are variable. If the initial weight in the matrix is 0, it means that the nodes are not connected to each other, and their weights are not variable. Each node can be an edge node or other type of computing node, and the nodes have locally dedicated data and local machine learning models.

When a node acts as a central node, the neighbors are determined according to the network topology, after which federated training is turned on. The $N$ nodes are denoted by $\{1,2,3,\mathrm{\dots },N\}$ and the data are denoted as $\{D_1,D_2,D_3,\mathrm{\dots },D_N\}$. The main steps of decentralized federated learning are as follows:

Step 1: Determine the central node. The system selects a node to be the central node in order.

Step 2: Train the local model. The model for node $k$ is trained using the local dataset $D_k$. The local model parameters are updated at the nodes using the gradient descent method with the following update formula:

$$W_k^{t-1}-\eta \nabla \ell (W_k^{t-1},b)\to W_k^t$$

(1)

where $W_k^{t-1}$ and $W_k^t$ are the model parameters at moment $t-1$ and $t$ of node $k$; $\ell (W_k^{t-1},b)$ is the loss of node $k$ at moment $t-1$ after $b$ batches of training.

Step 3: Upload. The node acquires the model parameters and uploads them to the central node of this round.

Step 4: Aggregate the global model. The central node integrates the received model parameters to obtain the global model. The federated center executes Algorithm 1.

Step 5: Repeat steps 1 to 4 until convergence or training requirements are met.

Algorithm 1 Center Aggregation Algorithm

Input: node set $K$, label set $T$, maximum number of global model iterations $MaxEpoch$. for $epoch\leftarrow 1$ to $MaxEpoch$ do for $k$ in $K$ do Average Logits of the node k for $t$ in $T$ do $S_t^k\leftarrow S_t^k+S_t^{/k}$ // Accumulate Logits of other nodes end end for $k$ in $K$do for $t$ in $T$ do $S_t^{/k}\leftarrow \frac{S_t^k-S_t^{/k}}{\left|K\right|}$ end Sending Model Logits end end

In algorithm 1, Logits is the vector computed by the final Softmax layer of the model, $S_t^k$ and $S_t^{/k}$ denote the set of labeled Logits output by the student network in node $k$ and the set of summed labeled Logits of all other nodes with node $k$ removed, respectively, and $\left|K\right|$ is the number of participating training nodes.

In decentralized federated learning, the increase of nodes number places higher demands on the training speed of machine learning models. At the same time, with higher complexity of the model, more weight coefficients need to be exchanged for federated learning, which brings a high communication burden.

2.3. Knowledge Distillation Mechanism

In federated learning, training information needs to be exchanged frequently among nodes, which will lead to a dramatic increase in communication burden. Knowledge distillation [23] is a Teacher-Student training structure, in which usually a trained teacher model provides knowledge, and a student model is trained by distillation to acquire the teacher’s knowledge, migrating knowledge from a complex teacher network model to a simple student model at the cost of a slight performance loss. In the process of federated learning, each node considers itself as a student and uses the aggregated node model outputs from the central node as the teacher to perform model distillation for updating the local models. In this method of exchanging model outputs, the communication cost is no longer determined by the model size but rather depends on the dimensionality of the model outputs. This dimensionality is typically smaller than the volume of model parameters. The knowledge distillation structure is shown in Figure 3.

As shown in Figure 3, knowledge distillation involves averaging the weights of two different objective functions: the first function is the distillation loss, which is the cross-entropy loss of the teacher model and the student model. The second function is student loss, which is the cross-entropy loss of the student and the hard target. In federated distillation, each node can initialize a student model for training and upload the Logits vector obtained from the local model’s Softmax layer to the central node of the current round following the convergence of the local model training. The central node integrates the global Logits vector to construct the teacher model for the current round and distributes it to each federated node to guide its student model training. Therefore, the total loss of knowledge distillation can be expressed as:

$$L_{total}=\lambda \cdot L_{KD}(p(g,R),p(z,R))+(1-\lambda )\cdot L_S(y,p(z,1))$$

(2)

where $R$ is the temperature coefficient, which is used to control the degree of softening of the output probabilities, $g$ and $z$ are the logical units of the teacher and student model outputs, $y$ is the vector of hard labels, and $p$ is the class probability, $\lambda$ is the hyperparameter, $L_{KD}(p(g,R),p(z,R))$ is the distillation loss between the student model and the teacher model when the logical units are matched, and $L_s(y,p(z,R))$ is the student loss. It can be specifically expressed as:

$$L_s(y,p(z,1))={\displaystyle \sum _{i=0}^q{y}_i}\log (p_i(z_i,1))$$

(3)

Typically, knowledge distillation is usually done by making $R=1$ for testing and using a larger $R$ value for training. When the knowledge distillation is set to $R=1$ in the testing phase, the difference between logical unit values of the soft target varies greatly, so that the test is able can better distinguish the correct classes from the incorrect classes during testing. In contrast, during training the difference between the soft targets for larger $R$ values are smaller than that for $R=1$, and the model is trained for smaller logical unit values. The model training gives more attention to the smaller logical units, thus so that the student model learns the relationship between these negative and positive samples. The student model learns information about the relationship between these negative and positive samples.

2.4. Node Selection

In distributed federated learning, there is no fixed central node, and each node takes turns as the central node. Consequently, the system requires various resources from its nodes, including computation and communication resources. Therefore, this subsection will focus on studying the node selection method. To enable the efficient application of federated learning, a node selection mechanism is proposed in this article, which is illustrated in Figure 4.

In this article, node selection is divided into two parts: central node selection and neighboring node selection. In each global iteration, all nodes are trained as central nodes and communicate with other eligible neighboring nodes. After the training is completed, each node reports its metrics, which serve as evaluations of the other nodes. Subsequently, the node with the highest score is selected as the central node for the next round of training based on the evaluations from all nodes. Then, in the evaluation by the central node of other nodes, the node with a high score is chosen as the neighboring node for the next round of training. The specific workflow is as follows:

Step 1: Reports key indicators. In each round of global iteration, high-quality nodes are selected to participate in federated learning, and metrics are used to quantify each node. The key indicators depend on the local model performance and local dataset size of the current round, which reflect the data quality differences and resource heterogeneity of different nodes [24]. The specific expression is as follows:

$${\mu }^{t+1}=\frac{{\log }_2(1+d_k)}{{\mu }_k^t}$$

(4)

where ${\mu }_k^t$ is the local model accuracy of node $k$ in round $t$ and $d_k$ is the local dataset size of node $k$. If the local model accuracy is low, it indicates that the node’s data may not be fully utilized, and therefore the accuracy of its final trained model may be larger.

Step 2: Update the adjacency matrix. After each node completes the interaction of important indicators, the adjacency matrix of each node is updated and a logistic function is used to map the degree of contribution of the neighboring nodes to this node, where $\zeta$ is the important indicator result. The calculation is as follows:

$${\varphi }_n(\zeta )=\frac{1}{1+e^{-\zeta }}$$

(5)

Step 3: Node selection. After updating the adjacency matrix, the node with the highest score from the adjacency matrix of each node is selected as the central node for this training round. From the adjacency matrix of the central node, some of the nodes with high scores are selected as the neighboring nodes. There is a parameter $\epsilon$, which is set in the node selection to indicate the proportion of the selected neighboring nodes.

The main differences between this method and the traditional federated learning mechanism are: (1) adding the importance indicator reporting process, (2) dynamically selecting the number of nodes and node locations through bidirectional selection between nodes, thus retaining the respective advantages of both decentralization and knowledge distillation optimization, significantly reducing the convergence time of the loss function, and ensuring the accuracy of the model.

2.5. Complexity Analysis

In traditional federated learning, the model is complex and has many weight parameters, which are assigned to each device, and the model parameters are transmitted back to the federated center, which will occupy a large number of resources. In federated learning, the time for communication far exceeds the time for computation. Assuming that the parameter gradients are independent in the past moments. At each round of global iteration, the central node needs to communicate with each node, and the specific time complexity of the centralized federation learning method is expressed as:

$$O(N^2)$$

(6)

In conducting each round of global communication, the temporary central node needs to communicate to all the remaining nodes, so the decentralized specific time complexity is expressed as:

$$O(2N^2-2N)$$

(7)

In node selection federated learning, each node can act as both a central node and a neighboring node, and the neighbors are selected through the interaction of important indicators to complete the global model aggregation, so the specific time complexity of node selected federated learning is expressed as:

$$O((\epsilon N^2)+2(\epsilon N))$$

(8)

3. Results and Discussion

3.1. Experimental Environment and Evaluation Index

The Tensorflow deep learning framework is used for model built, and model training and testing are performed under Ubuntu 18.04 system. The CPU is Intel(R) Core (TM) i5-10400F with 2.9 GHz benchmark frequency, 16 GB RAM, and the GPU is NVIDIA GeForce GTX 1650 with 4 GB of video memory.

In this article, three public datasets, MNIST [25], CIFAR-10 [26] and FEMNIST [27], are chosen for the experiments. The MNIST dataset contains 70,000 handwritten digital body images of 0~9, each of which is a grayscale image of 28 $\times$ 28 pixels, with 60,000 samples for the training set and 10,000 samples for the test set. The CIFAR-10 dataset contains 10 classes of 32 $\times$ 32 pixel RGB images, which contain 50,000 samples for the training set and 10,000 samples for the test set. The FEMNIST dataset is a collection of 62 different categories of handwritten digits and characters (digits 0~9, 26 lowercase letters, 26 uppercase letters) containing handwritten digits and letters from 3500 users with a total data volume of 805,263. 10% of the dataset was selected for the experiment.

In the experiment, we consider a network with 10 nodes, and the connection relations among nodes can be given as node 1 has communication with all other nodes, node 2 has communication with nodes 1, 3, 4, 5, 7, and 10. Node 3 has communication with nodes 1, 2, 4, 7, 8, and 9, and node 4 has communication with nodes 1, 2, 3, 5, 6, and 10. Node 5 has communication with nodes 1, 2, 4, 7, and 10. Node 6 has communication with nodes 1, 4, 8, and 10. Node 7 has communication with nodes 1, 2, 3, 5, 8, 9, and 10. Node 8 has communication with nodes 1, 3, 6, and 7. Node 9 has communication with nodes 1, 3, and 7. Node 10 has communication with nodes 1, 2, 4, 5, 6, and 7. Due to data diversity, the models among nodes are different, which can avoid model overfitting, and improve the robustness and generalization of the model. Convolutional neural network (CNN) was used to generate five 2-layer and five 3-layer network structures, and the specific model parameters of the CNN network used in different nodes are shown in

Table 2. Specific model parameters.

Nodes	Model Type	1st Conv Layer Filters	2nd Conv Layer Filters	3rd Conv Layer Filters	Dropout Rate
node1	2-layer	128	256	None	0.2
node2	2-layer	128	384	None	0.2
node3	2-layer	128	512	None	0.2
node4	2-layer	256	256	None	0.3
node5	2-layer	256	512	None	0.4
node6	3-layer	64	128	256	0.2
node7	3-layer	64	128	192	0.2
node8	3-layer	64	192	256	0.2
node9	3-layer	128	128	128	0.3
node10	3-layer	128	128	192	0.5

. The experiments consider 2 cases in which the training data of different nodes are IID and Non-IID. In the case of the IID training set, the data is shuffled and randomly distributed to each node. In the case of the Non-IID training set, nodes are restricted to having access to only two locally labeled data categories, and within each category, 500 pieces of data are divided into one group. The nodes randomly select three groups from each category as their local data. This data partitioning enables us to explore the robustness of the proposed method for data with heterogeneous distribution.

3.2. Experimental Results

This subsection verifies the effectiveness of the proposed method by comparing its performance with Centralized Federated Learning (CFL) [3], the Blockchain Decentralized (BD) [15], Federated Distillation (FD) [28], and Fedprox (FP) [6] on different datasets. For decentralized federated learning, blockchain federated learning was selected as a benchmark for comparison. Blockchain, due to its immutable and decentralized nature, makes it possible to provide a reliable and trustworthy learning solution for federated learning. Meanwhile, FedProx is selected for comparison as a benchmark for personalized federated learning. FedProx takes into account the hardware differences between different nodes and adds an approximation term to the federated learning framework to aggregate partial information from incomplete computations.

Experiment 1: Accuracy experiments of different algorithms under IID data distribution.

When data distribution is IID, the average accuracy of each method under different rounds is shown in

Table 3. IID control experiment.

Dataset	Method	10 Rounds Accuracy	30 Rounds Accuracy	50 Rounds Accuracy
MNIST-IID	CFL	53.26%	76.26%	78.34%
	FD	57.32%	78.22%	79.23%
	BD	68.21%	86.41%	88.46%
	FP	54.13%	76.33%	78.56%
	The proposed method	64.47%	83.75%	87.59%
CIFAR-10-IID	CFL	58.36%	73.05%	85.03%
	FD	61.33%	79.36%	86.72%
	BD	74.66%	89.72%	93.71%
	FP	60.12%	77.83%	85.42%
	The proposed method	71.37%	87.32%	91.36%
FEMNIST-IID	CFL	52.42%	77.26%	81.12%
	FD	58.74%	81.65%	83.36%
	BD	62.13%	85.43%	90.42%
	FP	54.26%	79.41%	83.26%
	The proposed method	61.33%	83.97%	89.15%

, where the average accuracy can be obtained by averaging the results of the personalized local model for all nodes. It can be seen that the average accuracy of each method improves with an increasing number of rounds on different datasets. Compared with centralized federated learning, the blockchain decentralized method improves the accuracy by 14.95%, 10.15%, and 10.12% for rounds 10, 30, and 50, respectively, on the MNIST dataset, and by 16.3%, 16.67%, and 8.68%, respectively, on the CIFAR-10 dataset, and by 9.71%,8.17%, and 9.3%, respectively, on the FEMNIST dataset. Accordingly, the average accuracy of the proposed method reaches 87.59%, 91.36%, and 89.15% on MNIST, CIFAR-10, and FEMNIST at rounds of 50, respectively, which slightly decreases compared to the blockchain decentralized method with an accuracy loss of 0.87% and 2.35%, respectively. This is because, in each training round, there is no guarantee that all nodes will participate in this training. For blockchain federated learning, existing frameworks often require a large amount of network bandwidth to reach consensus results for individual nodes to improve the robustness of the global model. However, considering the inefficiency of decentralized methods, the proposed method can significantly reduce the complexity with less accuracy loss via node selection and knowledge distillation.

To visually represent the model accuracy of each node, the accuracy curves are plotted for each round for each node of the proposed method in Figure 5. From the results, the optimal number of training rounds is in the range of 30 to 40. When the number of nodes is certain, the recognition accuracy of each node increases rapidly as the number of training rounds increases.

Experiment 2: Accuracy experiments under different algorithms with Non-IID data distribution.

To test the generalizability of the improved method, the data distribution is set to Non-IID, and the overall model accuracy comparison is shown in

Table 4. Non-IID control experiment.

Dataset	Method	10 Rounds Accuracy	30 Rounds Accuracy	50 Rounds Accuracy
MNIST-Non-IID	CFL	47.25%	67.16%	70.23%
	FD	48.17%	68.73%	70.84%
	BD	49.96%	78.05%	84.12%
	FP	47.63%	67.92%	70.51%
	The proposed method	49.93%	76.84%	81.18%
CIFAR-10-Non-IID	CFL	58.33%	73.35%	76.53%
	FD	57.92%	75.84%	80.72%
	BD	63.47%	82.16%	85.23%
	FP	59.71%	74.29%	78.85%
	The proposed method	61.39%	78.95%	82.65%
FEMNIST-Non-IID	CFL	54.95%	68.73%	82.43%
	FD	65.43%	73.58%	85.30%
	BD	72.45%	79.67%	89.08%
	FP	61.22%	71.55%	84.18%
	The proposed method	69.21%	77.93%	85.39%

.

On the MNIST dataset, the blockchain decentralized method improves the model performance by 2.71%, 10.89% and 13.89% under 10, 30 and 50 rounds of training, respectively, compared to the centralized federated learning. The proposed method achieves 81.18% model accuracy after 50 rounds of training. On the CIFAR-10 dataset, the blockchain decentralized method improves by 5.14%, 8.81%, and 8.7%, respectively, compared to the centralized federated learning method. The accuracy of the model in this article reaches 82.65% after 50 rounds of training, which is only a 2.58% decrease compared to the blockchain approach. On the FEMNIST dataset, the FedProx method achieves 84.18%, which is 1.75% higher than the centralized method, while the model accuracy of this article reaches 85.39% after 50 rounds of training. FedProx adds to the centralized federated learning approach. A proximal term, which is used to control the variation of local model parameters, can mitigate the impact of data heterogeneity to a certain extent. The single knowledge distillation method has faster convergence compared to the centralized machine learning method, but only a small improvement in accuracy.

The model accuracy of each node is shown in Figure 6. It can be seen that when the data distribution is a Non-IID setting, the data is more complex and distributed differently between nodes, and the model accuracy is slightly decreased compared to the IID setting. Under the central federated learning method, the central node adopts the average weighting method, which brings a negative impact to the global model. The decentralized node selection federated learning method proposed by the method in this article, the global model can learn the local model more effectively and further improve the model accuracy. In the experiments, some of the node results oscillate because of the different network connection structures of the nodes and the imbalance of the data. The accuracy of recognition is reduced when there are fewer objects connected to the network, like node 9.

The loss results under different datasets are shown in Figure 7. With the increase in the number of iteration rounds, the method in this article can converge when the number of iteration rounds is less than 40 rounds, and the convergence speed is slightly better than the other three methods. At the same time, this method achieves lower losses on both datasets: on the MNIST dataset, the loss of this method is about 0.08; on the CIFAR-10 dataset, the loss of this method can reach 0.03, and on the FEMNIST dataset, the loss of this method can reach 0.04, which are lower than the other three methods.

Experiment 3: Selection scale verification.

To verify the effectiveness of the improved federated learning method for node selection, the running time of the algorithm is used as the evaluation criterion, while the selection factor $\epsilon$ is set to 30% and 50%, respectively. The experiments compared the running time of the centralized federated learning method with the blockchain decentralized method, the federated distillation method, and the node selection decentralized federated learning method for the same iteration time with a different number of nodes. The experimental results are shown in Figure 8.

As shown in Figure 8, the proposed method can ensure low running times when dealing with multiple numbers of nodes. This is because the method can effectively select high-quality nodes for model aggregation. Take 50 nodes as an example, the proposed method has a running time of 19,093 s, 20,163 s, and 21,078 s on three datasets with a selection scale of 30%. Compared to the blockchain-based decentralized training, the running times are reduced by 20%, 21%, and 21% respectively. In the case of a smaller ratio, the node selection mechanism plays a stronger role and the more obvious the comparison results, which demonstrates that the method can complete training faster while maintaining small model accuracy loss.

4. Conclusions

Complete synchronization of centralized federated learning is not easy to achieve. When there are large differences in data distribution among nodes, the central server directly calculates the average parameters, which will lead to a low accuracy problem of the model. To solve this problem, a decentralized node selection federated learning method is proposed in this article. To offset the communication burden from the decentralized mechanism, a node selection method is proposed to select the appropriate neighbors to speed up the overall running time of the algorithm. Meanwhile, the knowledge distillation mechanism is introduced to enable each node to build personalized models, which solves the problem of low performance of local node models when the data distribution is a Non-IID setting. The effectiveness of this approach has been demonstrated through simulation experiments conducted on MNIST datasets, CIFAR-10 datasets, and FEMNIST datasets. Specifically, the method achieves a shorter training time by approximately 20%, 21%, and 21% while only sacrificing about 5% of the model accuracy. This shows that the method has excellent convergence efficiency and recognition accuracy, which makes it a promising solution for practical applications.