Chaotic Vibration and Perforation Effects on the Sound Absorption of a Nonlinear Curved Panel Absorber
Abstract
:1. Introduction
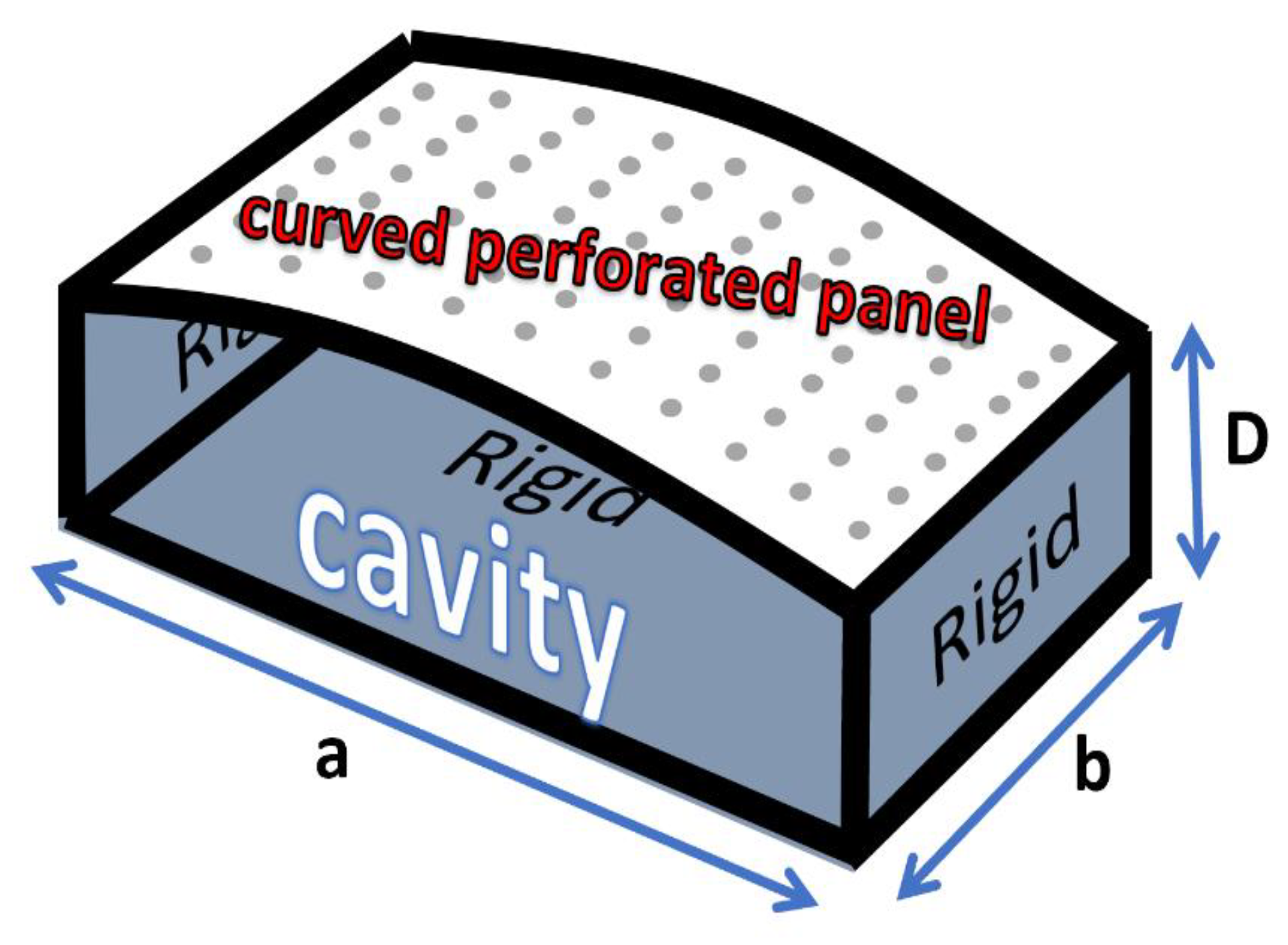
2. Theory
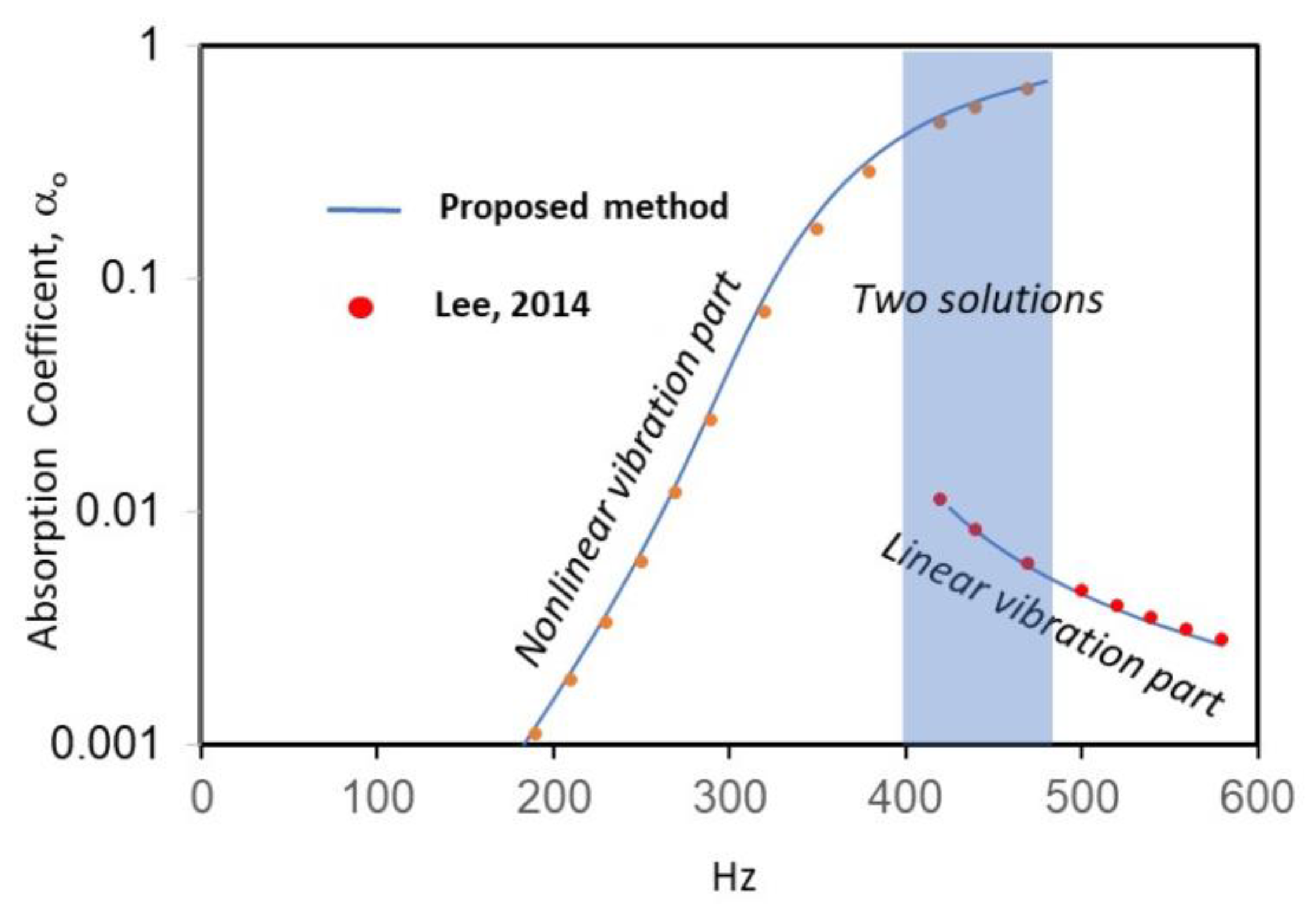
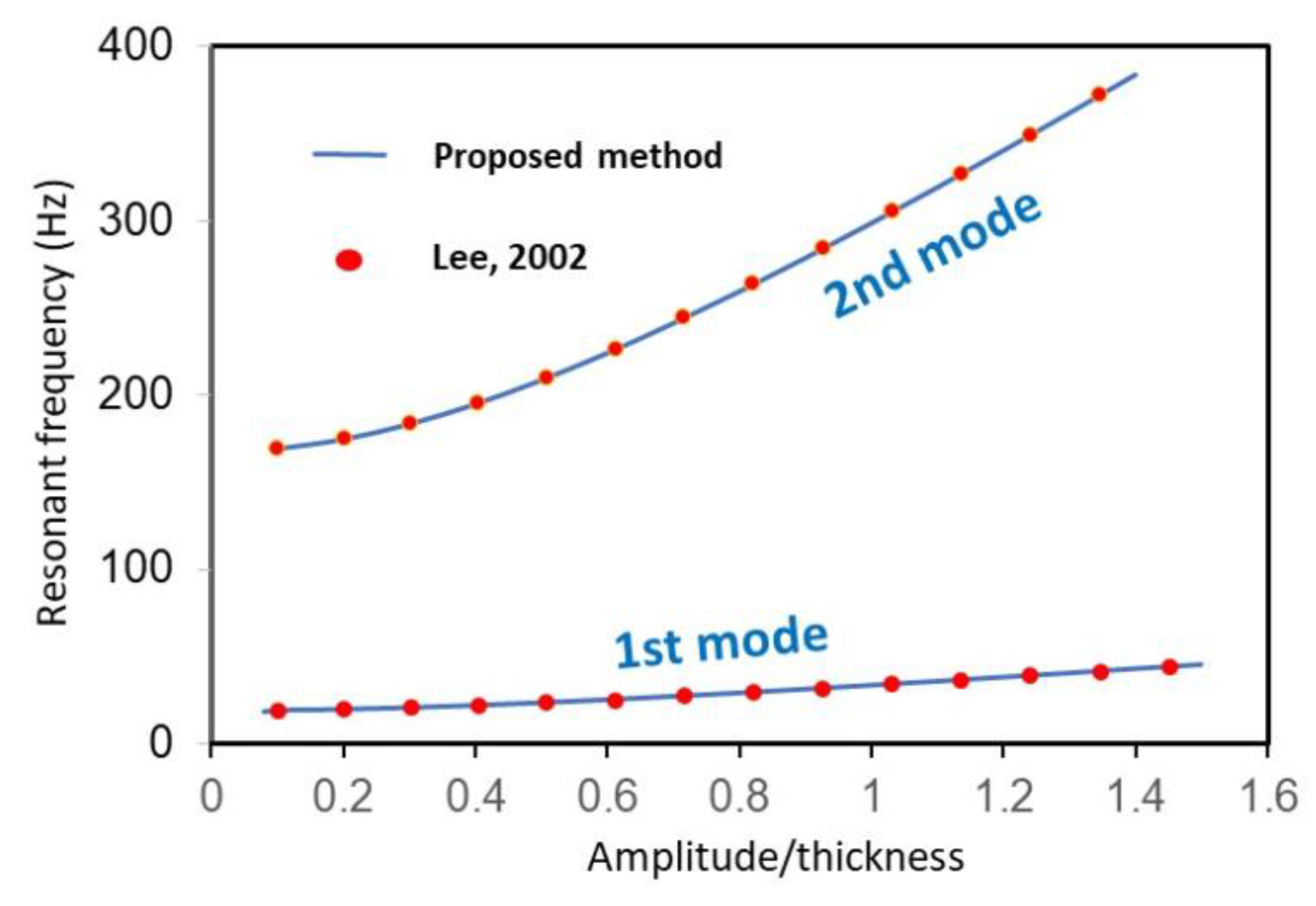
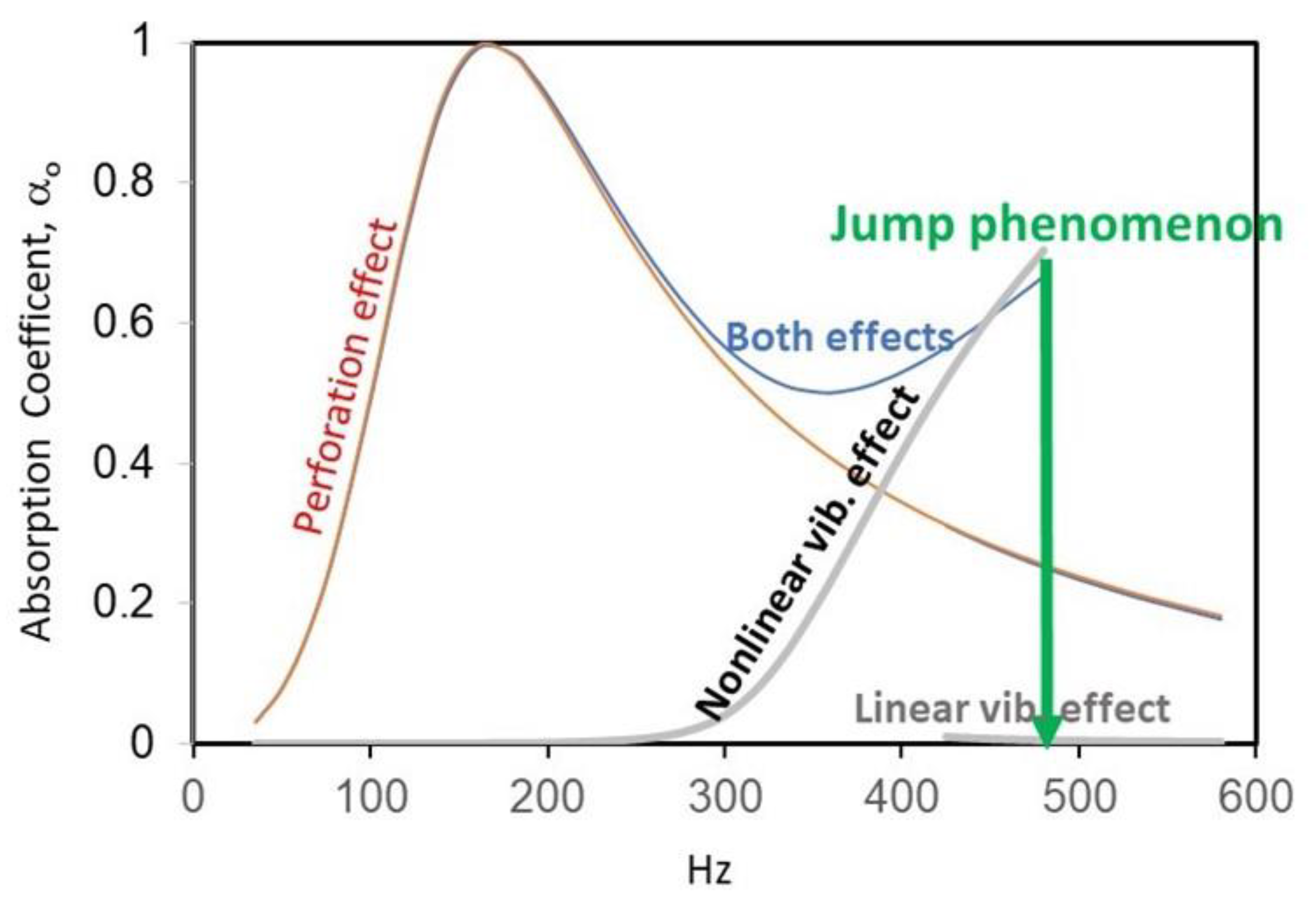
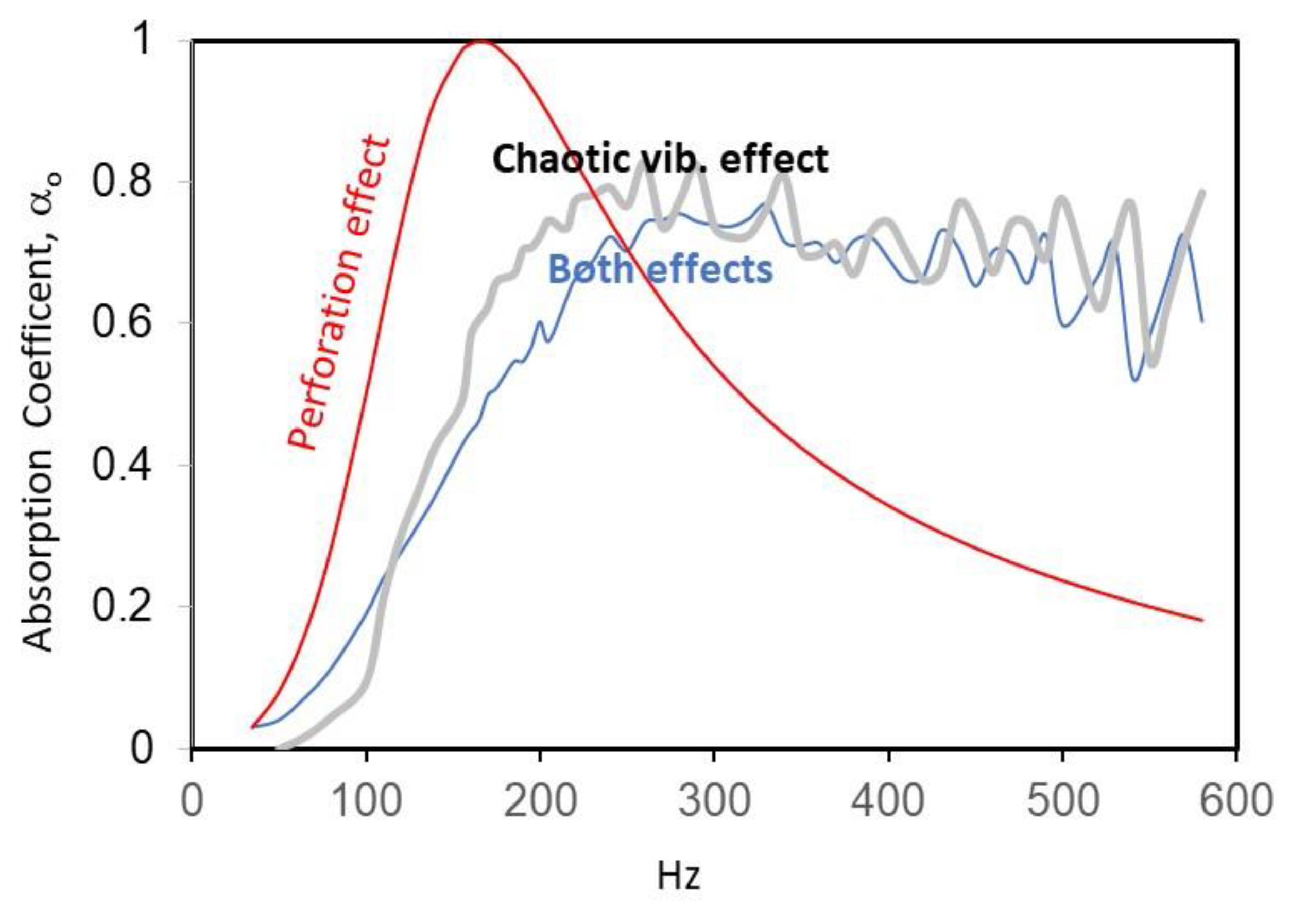
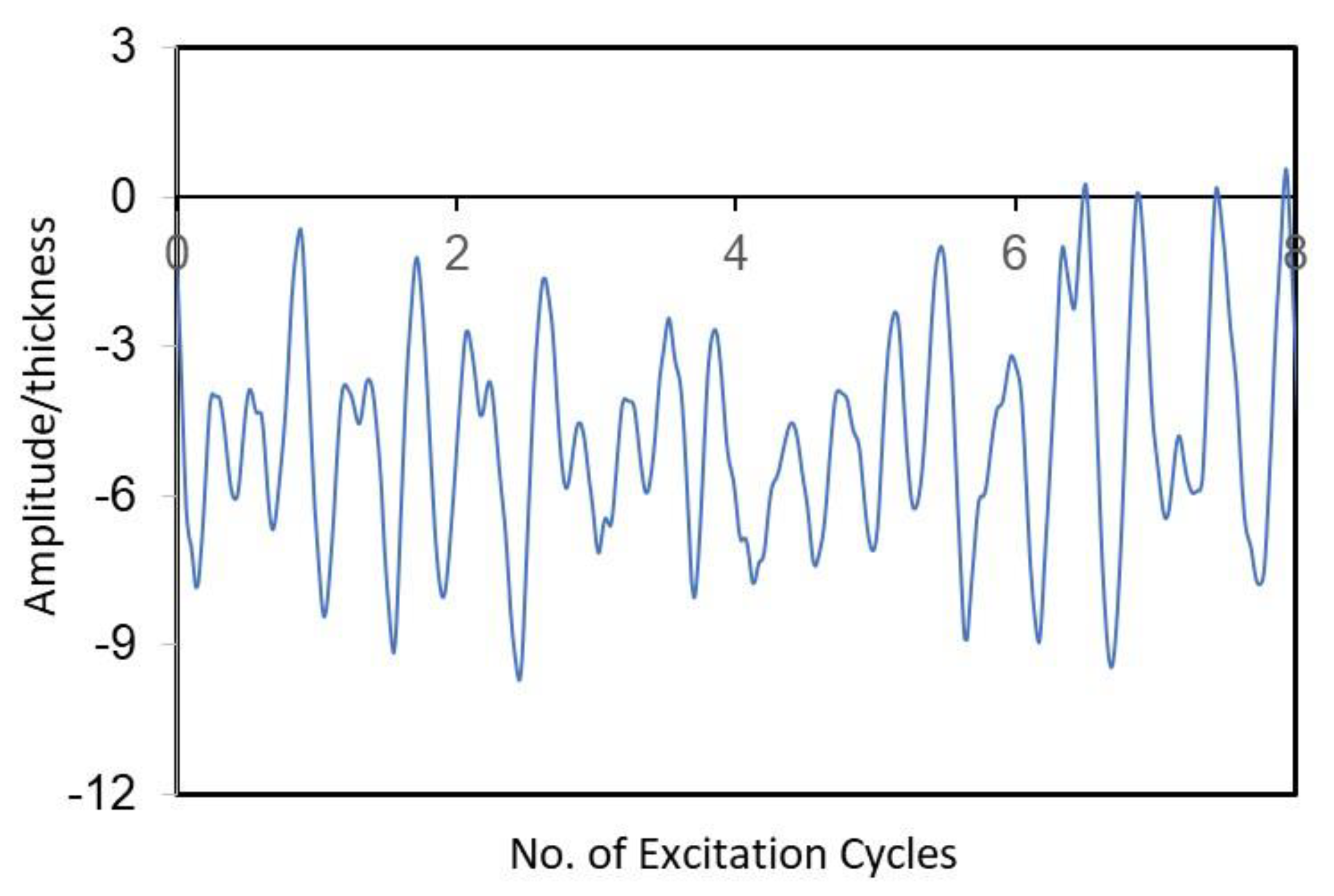
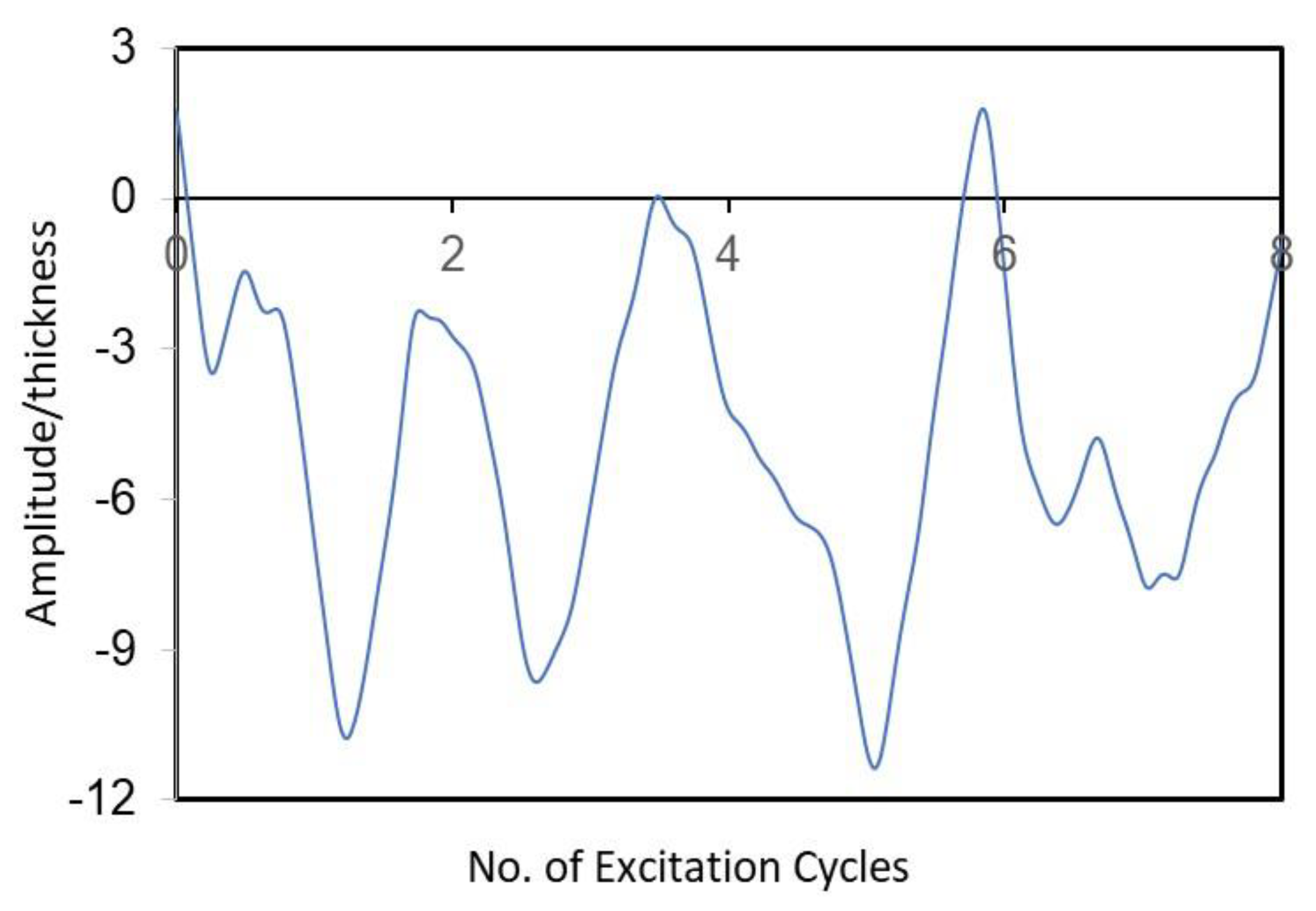
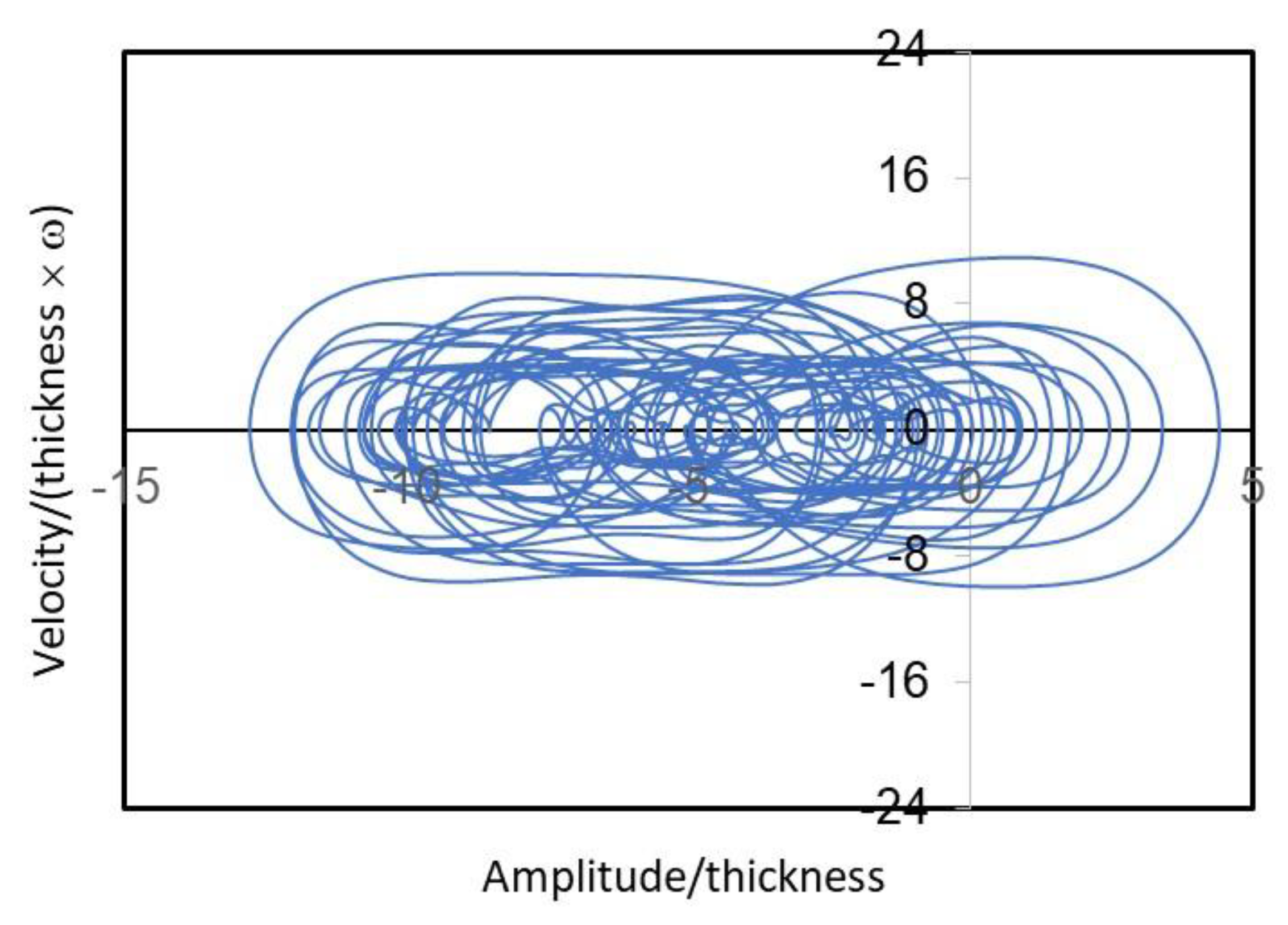
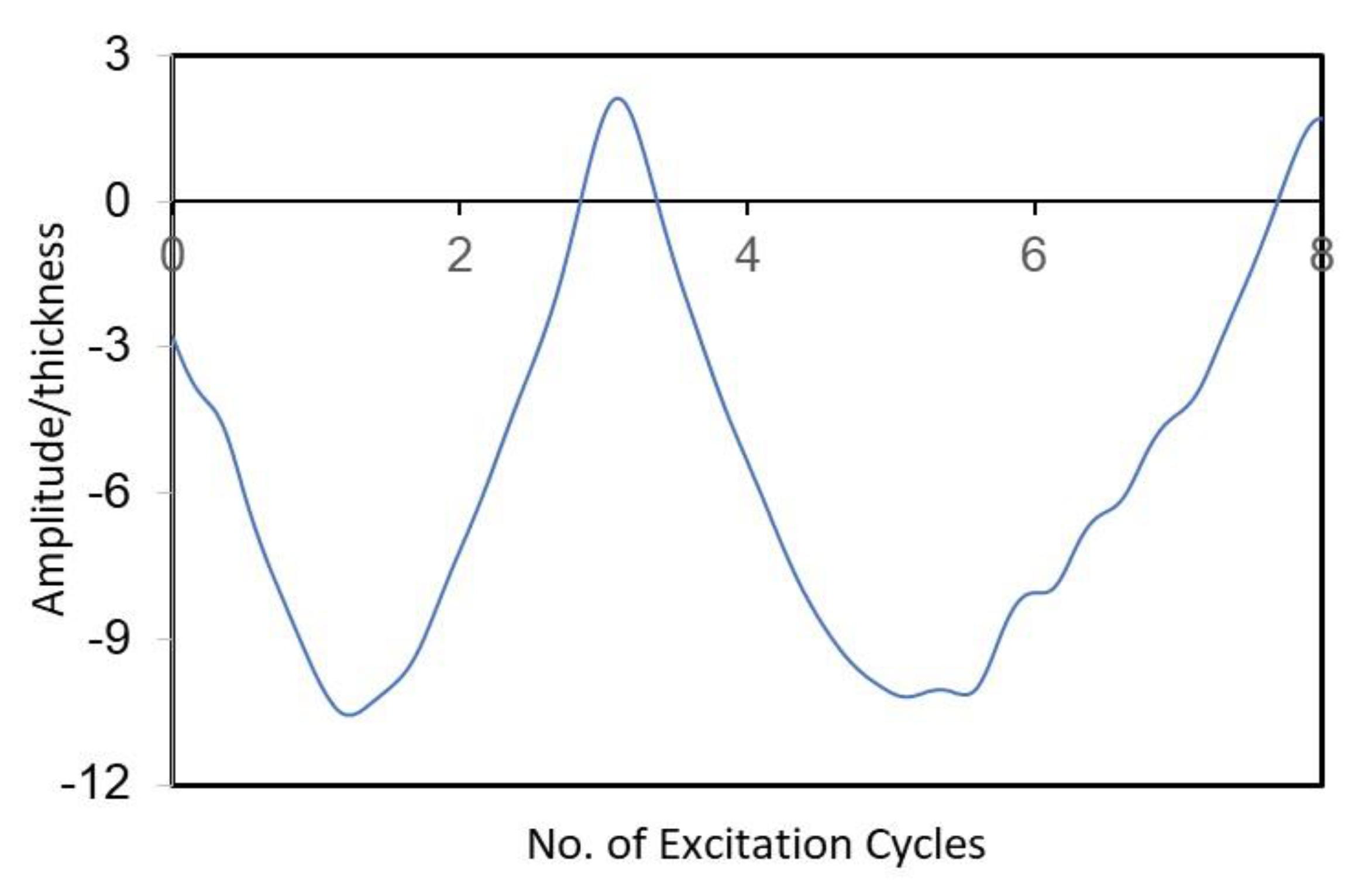
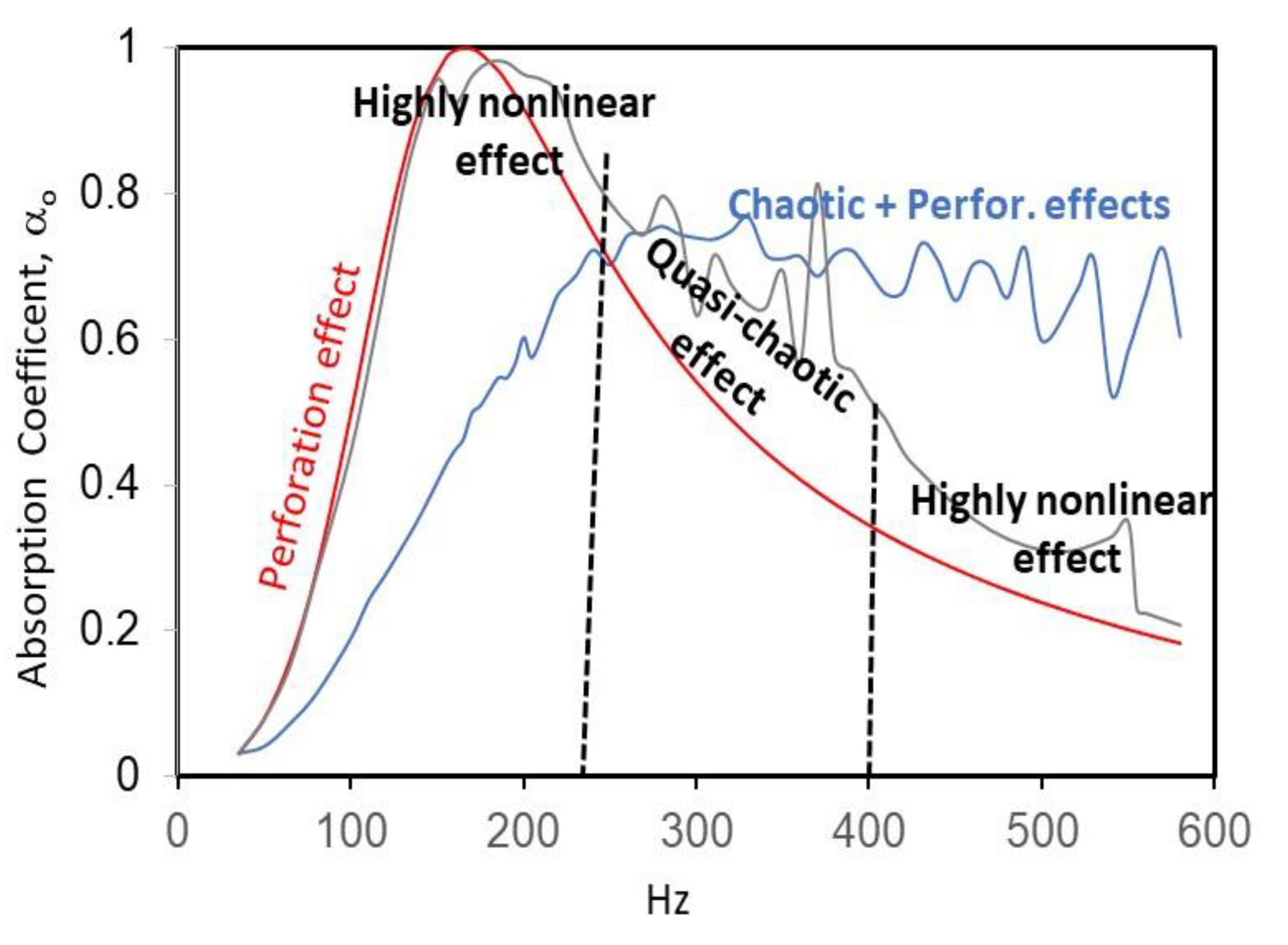
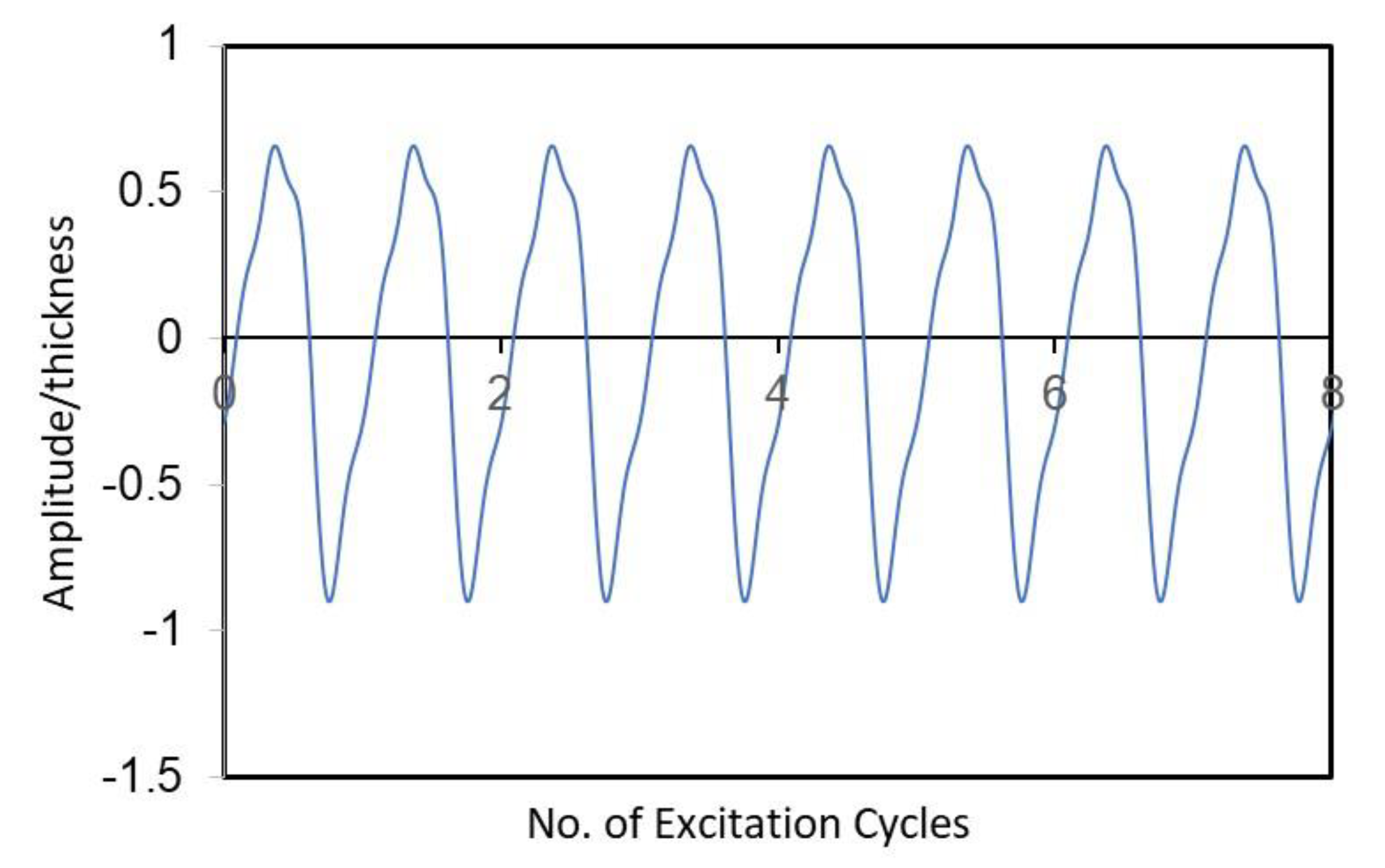
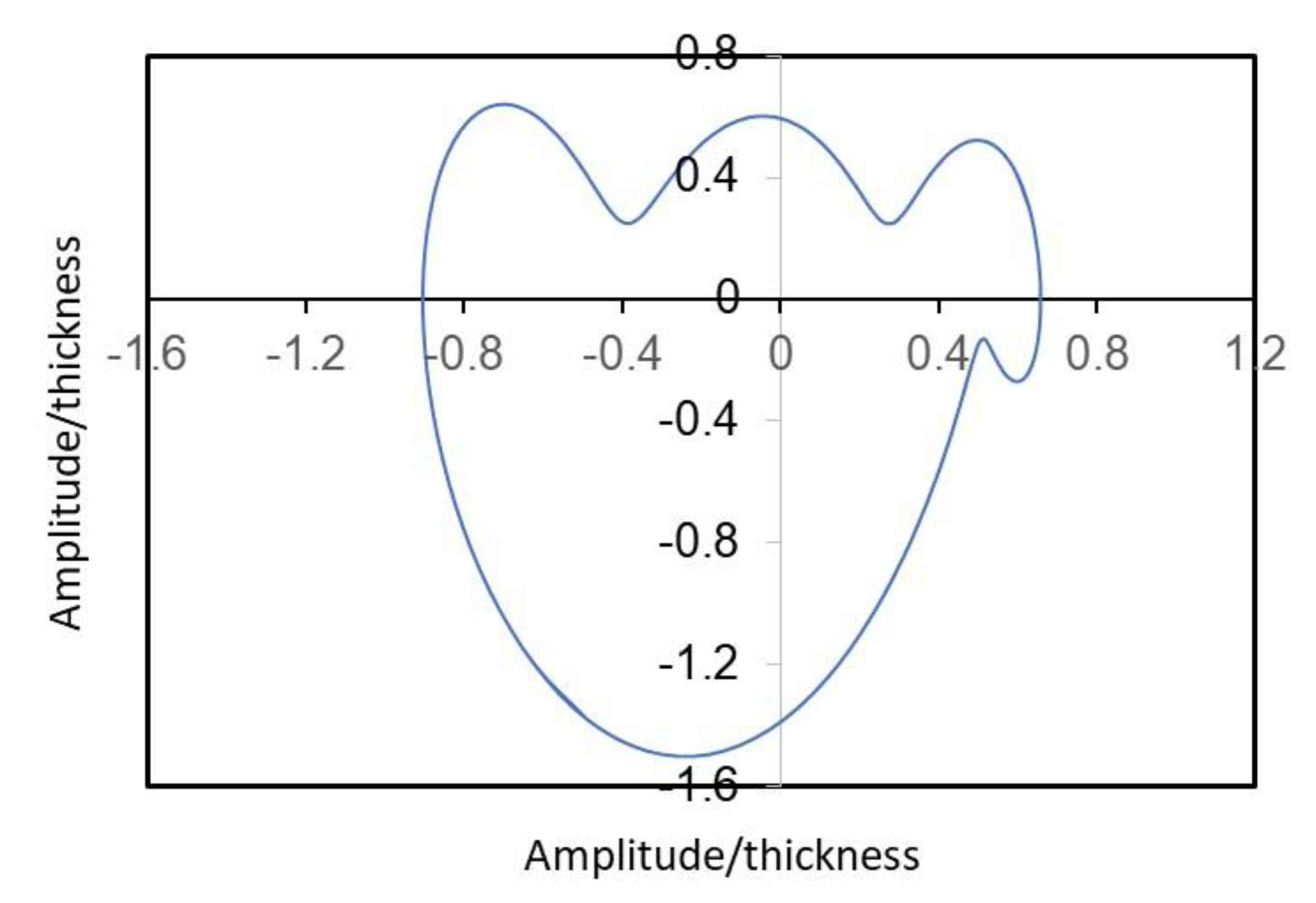
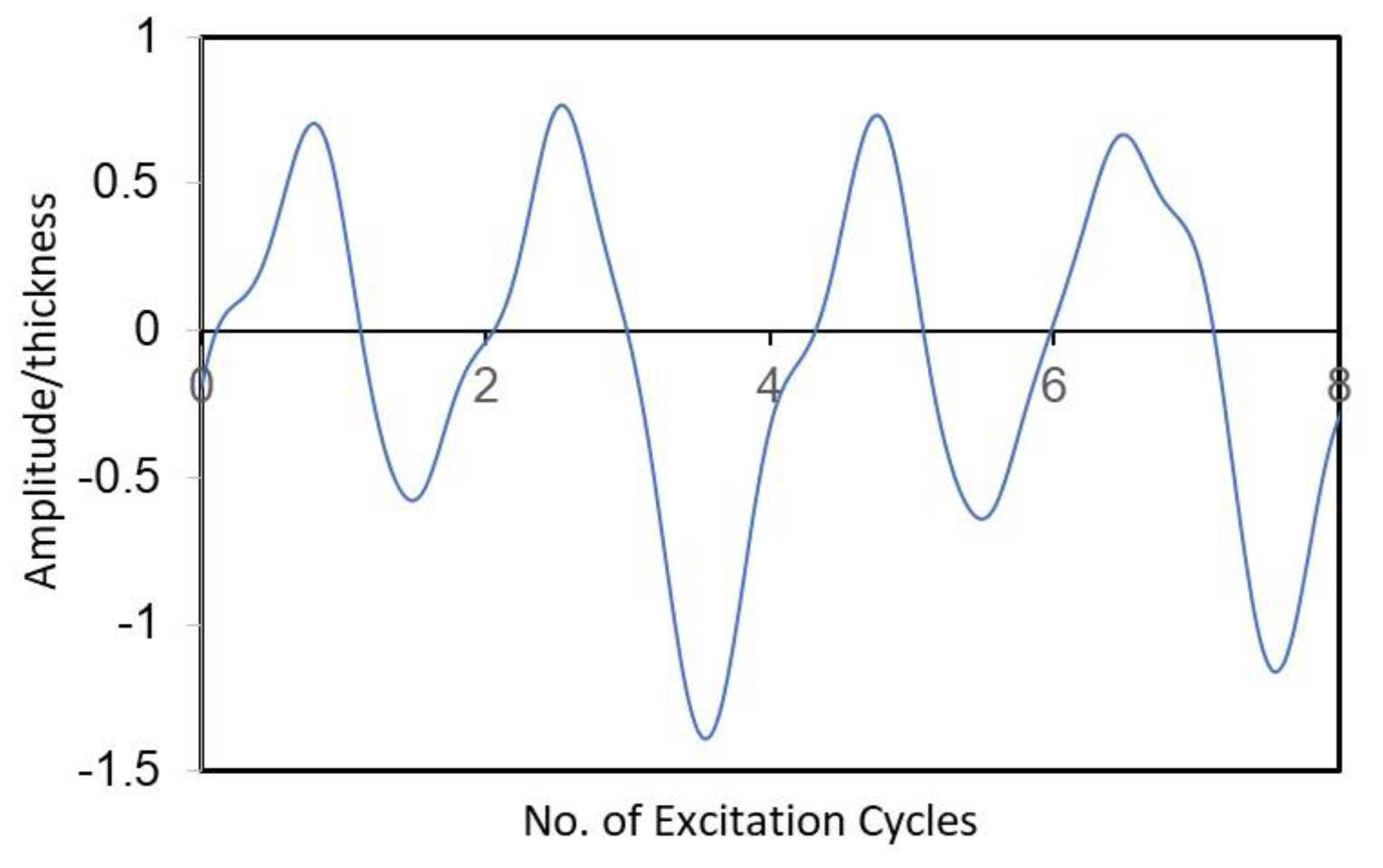
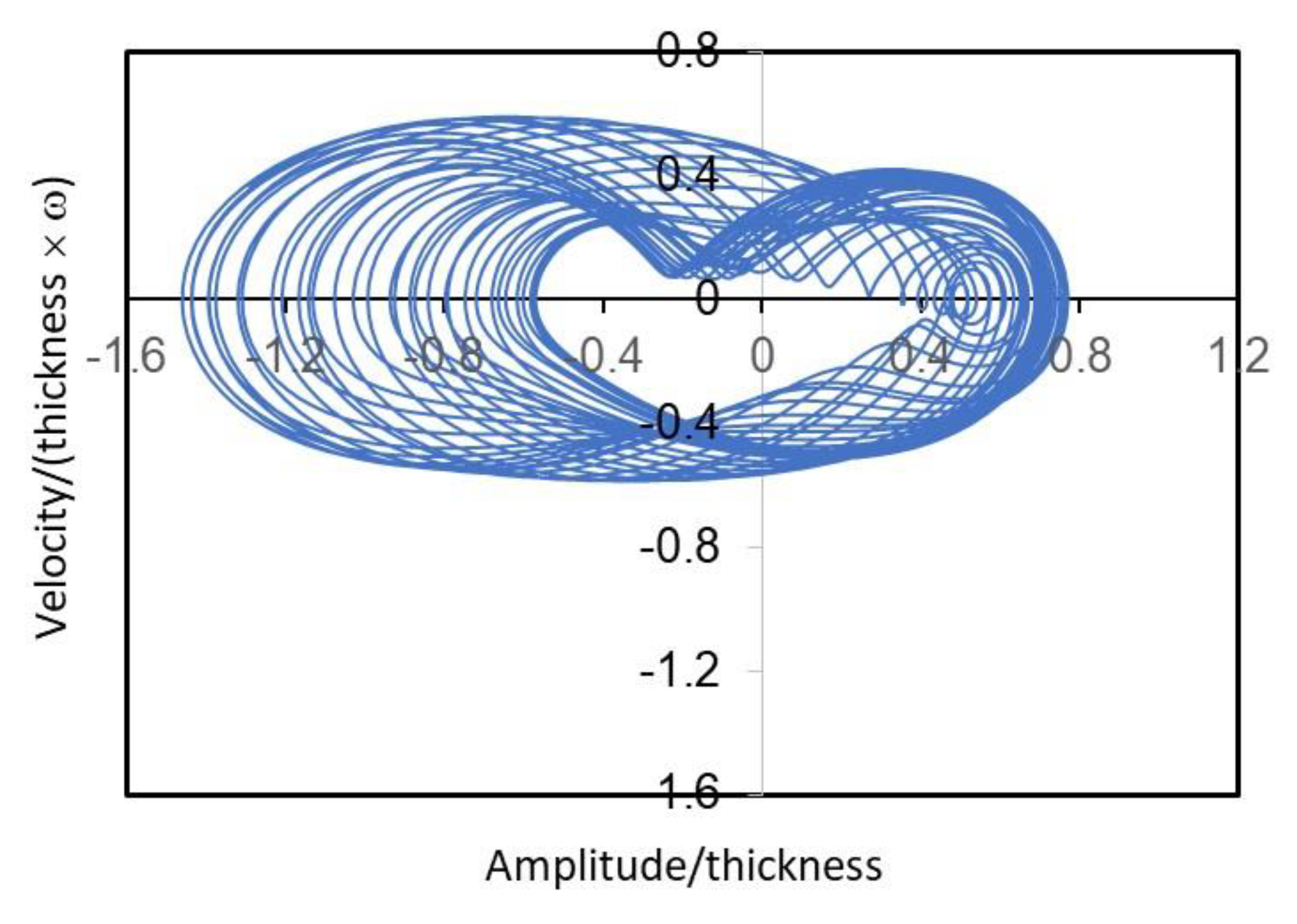
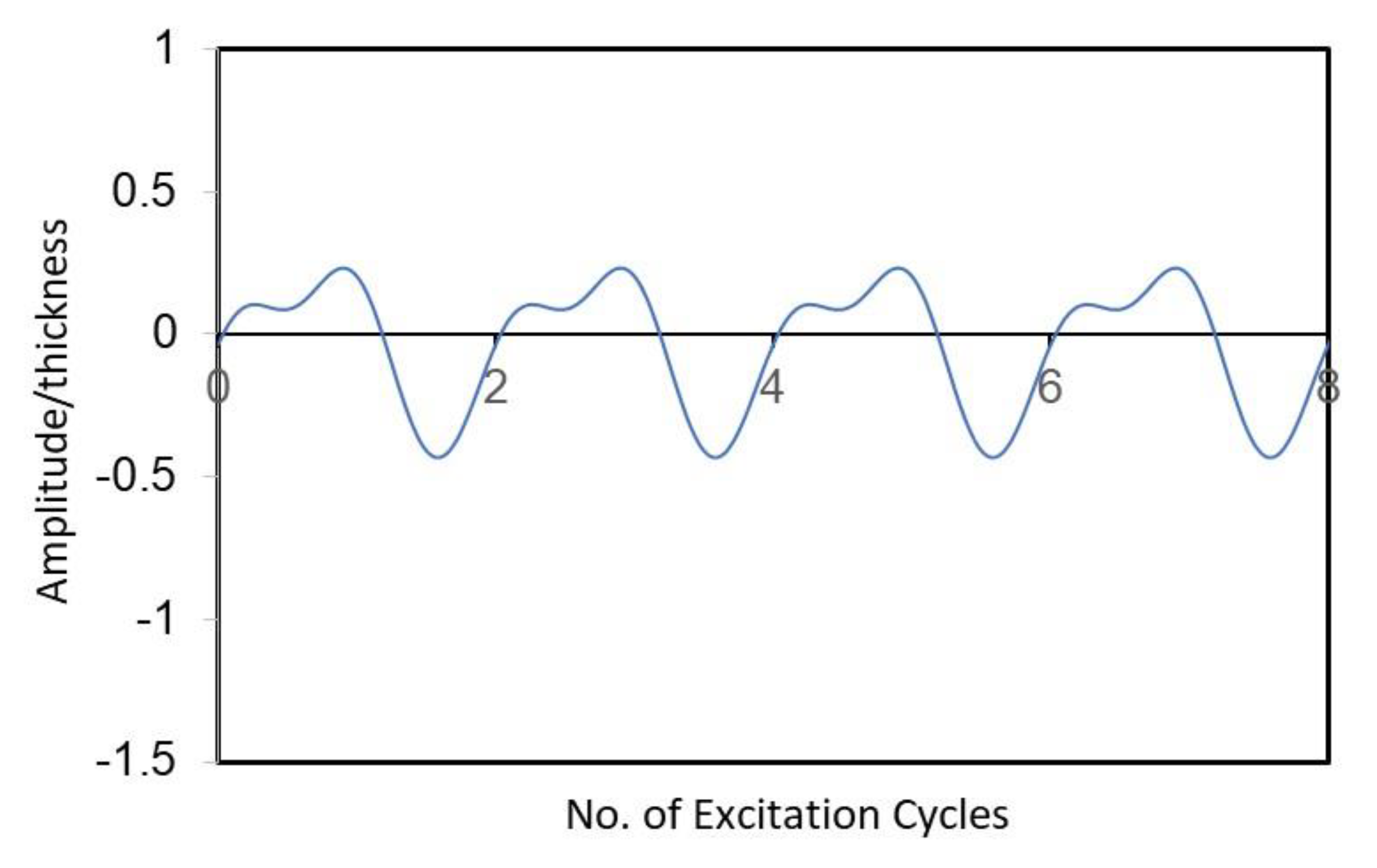
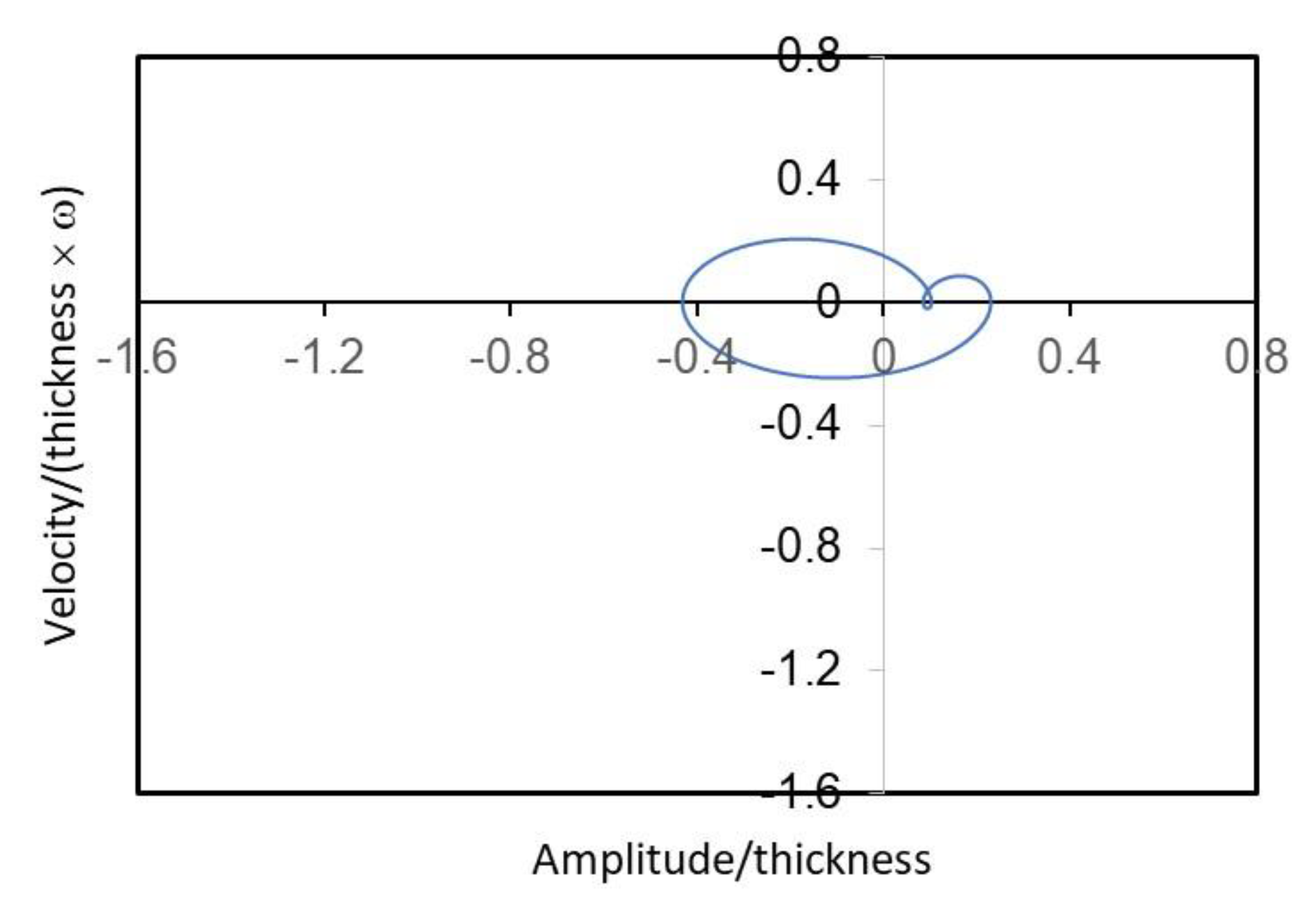
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Gorain, J.; Padmanabhana, C. Broadband low-frequency noise reduction using Helmholtz resonator-based metamaterial. Noise Control Eng. J. 2020, 69, 351–363. [Google Scholar] [CrossRef]
- Rahman, M.S.; Hasan, A.S.M.Z. Modified harmonic balance method for the solution of nonlinear jerk equations. Results Phys. 2018, 8, 893–897. [Google Scholar] [CrossRef]
- Ding, H.; Yan, Q.Y.; Chen, L.Q. Chaotic dynamics in the forced nonlinear vibration of an axially accelerating viscoelastic beam. ACTA Phys. Sin. 2013, 62, 200502. [Google Scholar] [CrossRef]
- Hirwani, C.K.; Mahapatra, T.R.; Panda, S.K.; Sahoo, S.S.; Singh, V.K.; Patle, B.K. Nonlinear free vibration analysis of laminated carbon/epoxy curved panels. Def. Sci. J. 2017, 67, 207–218. [Google Scholar] [CrossRef]
- Razzak, M.A.; Alam, M.Z.; Sharif, M.N. Modified multiple time scale method for solving strongly nonlinear damped forced vibration systems. Results Phys. 2018, 8, 231–238. [Google Scholar] [CrossRef]
- Ghafouri, M.; Ghassabi, M.; Zarastvand, M.R.; Talebitooti, R. Sound propagation of three-dimensional sandwich panels: Influence of three-dimensional re-entrant auxetic core. AIAA J. 2022, 60, 6374–6384. [Google Scholar] [CrossRef]
- Ghassabi, M.; Zarastvand, M.R.; Talebitooti, R. Investigation of state vector computational solution on modeling of wave propagation through functionally graded nanocomposite doubly curved thick structures. Eng. Comput. 2020, 36, 1417–1433. [Google Scholar] [CrossRef]
- Ghafouri, M.; Ghassabi, M.; Talebitooti, R. Acoustic sound propagation of a doubly curved shell with 3D re-entrant auxetic cellular metamaterials. Waves Random Complex Media 2020. [Google Scholar] [CrossRef]
- Zarastvand, M.R.; Ghassabi, M.; Talebitooti, R. A review approach for sound propagation prediction of plate constructions. Arch. Comput. Methods Eng. 2021, 28, 2817–2843. [Google Scholar] [CrossRef]
- Allam, S.; Abom, M. A new type of muffler based on microperforated tubes. J. Vib. Acoust. Trans. ASME 2011, 133, 031005. [Google Scholar] [CrossRef]
- Auriemma, F. Study of a new highly absorptive acoustic element. Acoust. Aust. 2017, 45, 411–419. [Google Scholar] [CrossRef]
- Pan, L.L.; Martellotta, F. A Parametric study of the acoustic performance of resonant absorbers made of micro-perforated membranes and perforated Panels. Appl. Sci. 2020, 10, 1581. [Google Scholar] [CrossRef] [Green Version]
- Beltran-Carbajal, F.; Abundis-Fong, H.F.; Trujillo-Franco, L.G.; Yanez-Badillo, H.; Favela-Contreras, A.; Campos-Mercado, E. Online frequency estimation on a building-like structure using a nonlinear flexible dynamic vibration absorber. Mathematics 2022, 10, 708. [Google Scholar] [CrossRef]
- Ozkaya, E.; Sarigul, M.; Boyaci, H. Nonlinear transverse vibrations of a slightly curved beam carrying a concentrated mass. ACTA Mech. Sin. 2009, 25, 871–882. [Google Scholar] [CrossRef]
- Chiang, Y.K.; Choy, Y.S. Acoustic behaviors of the microperforated panel absorber array in nonlinear regime under moderate acoustic pressure excitation. J. Acoust. Soc. Am. 2018, 143, 538–549. [Google Scholar] [CrossRef]
- Motaharifar, F.; Ghassabi, M.; Talebitooti, R. A variational iteration method (VIM) for nonlinear dynamic response of a cracked plate interacting with a fluid media. Eng. Comput. 2021, 37, 3299–3318. [Google Scholar] [CrossRef]
- Lee, Y.Y.; Huang, J.L.; Hui, C.K.; Ng, C.F. Sound absorption of a quadratic and cubic nonlinearly vibrating curved panel absorber. Appl. Math. Model. 2012, 36, 5574–5588. [Google Scholar] [CrossRef]
- Lee, Y.Y. The effect of leakage on the sound absorption of a nonlinear perforated panel backed by a cavity. Int. J. Mech. Sci. 2016, 107, 242–252. [Google Scholar] [CrossRef]
- Rudenko, O.V.; Khirnykh, K.L. Helmholtz resonator model for the absorption of high-intensity sound. Sov. Phys. Acoust. USSR 1990, 36, 527–534. [Google Scholar]
- Mariani, R.; Bellizzi, S.; Cochelin, B.; Herzog, P.; Mattei, P.O. Toward an adjustable nonlinear low frequency acoustic absorber. J. Sound Vib. 2011, 330, 5245–5258. [Google Scholar] [CrossRef] [Green Version]
- Freydin, M.; Dowell, E.H.; Spottswood, S.M.; Perez, R.A. Nonlinear dynamics and flutter of plate and cavity in response to supersonic wind tunnel start. Nonlinear Dyn. 2021, 103, 3019–3036. [Google Scholar] [CrossRef]
- Sadri, M.; Younesian, D. Nonlinear harmonic vibration analysis of a plate-cavity system. Nonlinear Dyn. 2013, 74, 1267–1279. [Google Scholar] [CrossRef]
- Sadri, M.; Younesian, D. Nonlinear free vibration analysis of a plate-cavity system. Thin-Walled Struct. 2014, 74, 191–200. [Google Scholar] [CrossRef]
- Anvariyeh, F.S.; Jalili, M.M.; Fotuhi, A.R. Nonlinear vibration analysis of a circular plate-cavity system. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 66. [Google Scholar] [CrossRef]
- Ganji, H.F.; Dowell, E.H. Sound transmission and radiation from a plate-cavity system in supersonic flow. J. Aircr. 2017, 54, 1877–1900. [Google Scholar] [CrossRef]
- Lee, Y.Y. Chaotic phenomena and nonlinear responses in a vibroacoustic system. Complexity 2018, 7076150. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.Y.; Poon, W.Y.; Ng, C.F. Anti-symmetric mode vibration of a curved beam subject to autoparametric excitation. J. Sound Vib. 2006, 290, 48–64. [Google Scholar] [CrossRef]
- Lee, Y.Y. Free vibration analysis of a nonlinear panel coupled with extended cavity using the multi-level residue harmonic balance method. Thin-Walled Struct. 2016, 98, 332–336. [Google Scholar] [CrossRef]
- Lee, Y.Y.; Ng, C.F. Sound insertion loss of stiffened enclosure plates using the finite element method and the classical approach. J. Sound Vib. 1998, 217, 239–260. [Google Scholar] [CrossRef]
- Maa, D. Microperforated panel wideband absorber. Noise Control. Eng. J. 1987, 29, 77–84. [Google Scholar] [CrossRef]
- Ford, R.D.; McCormick, M.A. Panel sound absorbers. J. Sound Vib. 1969, 10, 411–423. [Google Scholar] [CrossRef]
- Kang, K.; Fuchs, H.V. Predicting the absorption of open weave textiles and micro-perforated membranes backed by an air space. J. Sound Vib. 1999, 220, 905–920. [Google Scholar] [CrossRef]
- Lee, Y.Y. Analytic formulation for the sound absorption of a panel absorber under the effects of microperforation, air pumping, linear vibration and nonlinear vibration. Abstr. Appl. Anal. 2014, 906506. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.Y. Structural-acoustic coupling effect on the nonlinear natural frequency of a rectangular box with one flexible plate. Appl. Acoust. 2002, 63, 1157–1175. [Google Scholar] [CrossRef]
- Euler’s Method. Available online: https://lpsa.swarthmore.edu/NumInt/NumIntFirst.html (accessed on 1 May 2023).


| ω = 100 Hz, k = 1, x = 0.01 | ω = 300 Hz, k = 100, x = 0.04 | ω = 300 Hz, k = 50, x = 0.01 | ω = 300 Hz, k = 50, x = 0.04 | |
|---|---|---|---|---|
| 1 mode | 99.22% | 94.47% | 94.14% | 99.33% |
| 2 modes | 99.22% | 99.86% | 97.90% | 102.48% |
| 3 modes | 100.00% | 100.00% | 99.25% | 100.00% |
| 4 modes | 100.00% | 100.00% | 100.00% | 100.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.-Y. Chaotic Vibration and Perforation Effects on the Sound Absorption of a Nonlinear Curved Panel Absorber. Mathematics 2023, 11, 3178. https://doi.org/10.3390/math11143178
Lee Y-Y. Chaotic Vibration and Perforation Effects on the Sound Absorption of a Nonlinear Curved Panel Absorber. Mathematics. 2023; 11(14):3178. https://doi.org/10.3390/math11143178
Chicago/Turabian StyleLee, Yiu-Yin. 2023. "Chaotic Vibration and Perforation Effects on the Sound Absorption of a Nonlinear Curved Panel Absorber" Mathematics 11, no. 14: 3178. https://doi.org/10.3390/math11143178
APA StyleLee, Y.-Y. (2023). Chaotic Vibration and Perforation Effects on the Sound Absorption of a Nonlinear Curved Panel Absorber. Mathematics, 11(14), 3178. https://doi.org/10.3390/math11143178





