A Novel Hybrid Algorithm Based on Jellyfish Search and Particle Swarm Optimization

Abstract

Metaheuristic optimization is considered one of the most efficient and powerful techniques of recent decades as it can deal effectively with complex optimization problems. The performance of the optimization technique relies on two main components: exploration and exploitation. Unfortunately, the performance is limited by a weakness in one of the components. This study aims to tackle the issue with the exploration of the existing jellyfish search optimizer (JSO) by introducing a hybrid jellyfish search and particle swarm optimization (HJSPSO). HJSPSO is mainly based on a JSO structure, but the following ocean current movement operator is replaced with PSO to benefit from its exploration capability. The search process alternates between PSO and JSO operators through a time control mechanism. Furthermore, nonlinear and time-varying inertia weight, cognitive, and social coefficients are added to the PSO and JSO operators to balance between exploration and exploitation. Sixty benchmark test functions, including 10 CEC-C06 2019 large-scale benchmark test functions with various dimensions, are used to showcase the optimization performance. Then, the traveling salesman problem (TSP) is used to validate the performance of HJSPSO for a nonconvex optimization problem. Results demonstrate that compared to existing JSO and PSO techniques, HJSPSO contributes in terms of exploration and exploitation improvements, where it outperforms other well-known metaheuristic optimization techniques that include a hybrid algorithm. In this case, HJSPSO secures the first rank in classical and large-scale benchmark test functions by achieving the highest hit rates of 64% and 30%, respectively. Moreover, HJSPSO demonstrates good applicability in solving an exemplar TSP after attaining the shortest distance with the lowest mean and best fitness at 37.87 and 36.12, respectively. Overall, HJSPSO shows superior performance in solving most benchmark test functions compared to other optimization techniques, including JSO and PSO. As a conclusion, HJSPSO is a robust technique that can be applied to solve most optimization problems with a promising solution.

1. Introduction

Most problems in critical applications such as engineering, sciences, and economics require a decision-making mechanism or optimization technique. The optimization technique is used to choose between various possible solutions to reach the best decision based on a designated objective function [1]. Various types of optimization techniques are used to successfully solve problems in many applications. In the last two decades, metaheuristic optimization techniques have received more attention compared to classical optimization techniques [2]. The main reason behind this discrepancy is because classical optimizations are commonly trapped in a local optimum [3]. On the contrary, metaheuristic techniques can escape from the local optimum and search for a better solution, which leads to the global optimum. Furthermore, the classical optimization technique is highly dependent on the starting point to give a good solution. By contrast, the performance of metaheuristic optimization techniques is not significantly affected by the starting point [3].

The two major components in metaheuristic techniques are known as exploration and exploitation. Exploration is a search for possible solutions in promising areas within a search space, while exploitation is a search for a better solution within the surrounding area of the optimum solution so far. A good balance between exploration and exploitation should be arranged to achieve effective performance in solving an optimization problem [4]. However, many recent studies revealed that exploration and exploitation in most existing metaheuristic techniques are still not treated well [5]. For instance, particle swarm optimization (PSO), grey wolf optimizer (GWO), and heap-based optimizer (HBO) have poor exploitation but better exploration [6]. By contrast, artificial bee colony [7], firefly algorithm (FA) [8,9], and cuckoo search [10] have poor exploration but better exploitation. Consequently, several new hybrid techniques have been suggested to improve the balance between exploitation and exploration. The hybrid techniques consist of two or more metaheuristic algorithms to complement one another and take advantage of their good features to produce a more accurate technique [11,12].

In general, metaheuristic optimization techniques can be classified into four main categories: evolutionary-based, physical-based, human-based, and swarm-intelligence-based techniques [13]. Evolutionary-based techniques imitate the processes of biological evolution, which are selection, reproduction, mutation, and recombination. There are several popular evolutionary-based techniques, including genetic algorithm (GA) [14], differential evolution (DE) [15], and biography-based optimizer (BBO) [16]. Physical-based techniques are inspired by physical laws and phenomena such as gravitational force, inertia force, and lightning phenomena. Popular physical-based techniques include gravitational search algorithm [17], simulated annealing [18], and lightning search algorithm (LSA) [19]. Human-based techniques, such as teaching–learning-based optimization (TLBO) [20], HBO [13], and coronavirus herd immunity optimizer (CHIO) [21], mimic human social behavior. Swarm-intelligence-based techniques are inspired by the collective food-foraging behavior of social creatures in nature, such as flocks of birds, schools of fishes, and colonies of insects. The popular optimization techniques from this category are PSO [22], jellyfish search optimizer (JSO) [23], and rat swarm optimizer (RSO) [24].

JSO is one of the most recent swarm-intelligence-based techniques. This algorithm is inspired by the foraging behavior of jellyfish in the ocean [23]. Its competitive features make it popular, and it is used to solve various optimization problems and different engineering problems [25]. However, JSO has shown poor exploration capability [26]. Therefore, hybridizing the JSO with a good exploration technique will balance exploration and exploitation to improve the search process. In the last two decades, PSO has been presented as a robust metaheuristic optimization technique with many features, such as simplicity, fast convergence, and excellent exploration capability [27]. Therefore, the present paper proposes a novel hybrid optimization algorithm based on JSO and PSO, which is called hybrid jellyfish search and particle swarm optimization (HJSPSO). The main contributions of this paper are as follows:

• A significant improvement in HJSPSO in terms of accuracy at fast convergence rates compared to the original PSO and JSO techniques.
• The superiority of HJSPSO is verified by comparing it with nine well-known optimization techniques, including the existing hybrid algorithm.
• The robustness of HJSPSO is validated through unimodal, multimodal, and large-scale benchmark test functions.

The remaining sections of this paper are structured as follows: Section 2 reviews the recent literature on PSO and JSO, including their existing hybridization. Section 3 explains the original formulations of PSO and JSO, and Section 4 presents and discusses the proposed HJSPSO. Section 5 evaluates the performance of HJSPSO by using benchmark test functions and an exemplar TSP to showcase its effectiveness compared to other optimization techniques. Finally, Section 6 draws a conclusion.

2. Review of PSO and JSO Applications

Numerous studies have been published recently in the field of metaheuristic techniques, and this trend is expected to continue as more new techniques are introduced. Metaheuristic optimization techniques are popular and widely used in engineering applications because of their good performance in providing a promising solution [28]. Introduced by Kennedy and Eberhart [22] in 1995, PSO is now considered one of the most popular optimization techniques. In the last two decades, many studies have been conducted to improve the performance of PSO, whether by modifying the original form of PSO or hybridizing it with other metaheuristic techniques. Cui et al. [29] introduced a disturbance factor in PSO to improve its performance. In that case, a few particles are selected when no improvement is observed for a period longer than the disturbance factor, and then their velocities are modified to escape from the local optimum. Ibrahim et al. [30] adopted an artificial immune system in PSO to tackle the issue with constraint violations. Gupta and Devi [31] presented a modified PSO where the inertia weight and acceleration coefficients are varied nonlinearly along with iterations to balance global exploration and local exploitation. Yan et al. [32] modified PSO with an exponential decay weight where a constraint factor is inserted into the velocity-updating procedure. Al-Bahrani and Patra [33] presented an orthogonal PSO where the swarm particles are divided into two groups to enhance the diversity in the population. The first group comprises the active best personal experience, while the remaining particles form the second group, representing passive personal experiences. In each iteration, the positions of the active group are orthogonally diagonalized to enhance the exploration capability. Numerous researchers have also sought balance between exploration and exploitation in PSO by hybridizing it with other metaheuristic techniques. For instance, PSO is hybridized with the spotted hyena optimizer (HPSSHO), differential evolution (HPSO-DE), fireworks algorithm (PS-FW), and gravitational search algorithm (HGSPSO) [4,34,35,36].

JSO is one of the more recent swarm-based optimization techniques. It was introduced by Chou and Truong [23] in 2020 and, therefore, only several studies have been carried out to enhance its performance. Most previous studies focused on modifying the formulation of JSO to enhance its performance. Abdel-Basset et al. [37] proposed a premature convergence strategy in the JSO algorithm to improve its capability to search for the optimal solution. This strategy is based on a control mechanism to accelerate the convergence toward the best solution and decrease the probability of being stuck in the local optimum. It consists of two steps: (i) it randomly selects two particles from the population to relocate their positions and (ii) seeks better solutions between the current best and the random positions in the population. Manita and Zermani [26] proposed an orthogonal JSO that uses an orthogonal learning strategy to improve the exploration capability. This strategy helps to search for the best solution by forecasting the best combination between two solution vectors based on limited trials. In another work, Juhaniya et al. [38] improved the exploration capability of JSO by using an opposition-based learning strategy to solve an optimal stator and stator slot designs. Rajpurohit and Sharma [39] introduced seven chaotic maps into JSO by inserting these into the active movement step to improve its accuracy and efficiency. Only one study has been found to hybridize the JSO with another metaheuristic technique. Introduced by Ginidi et al. [40], the hybrid technique, called hybrid heap-based and jellyfish search algorithm (HBJSA), combined HBO and JSO to solve the combined heat and power economic dispatch problem. On the other hand, Chou et al. [41] presented a hybrid model that integrates JSO with a machine learning algorithm called convolutional neural network (CNN) to improve the predictive accuracy of energy consumption in 20 cities in Taiwan. The best CNN model was selected by evaluating available models with different training datasets before it was integrated with JSO. In this case, the role of JSO was limited to determining the best internal parameters of the CNN model, where the effectiveness of JSO in finding the best solution was very minimal. Therefore, similar work to that in [40] should be carried out to improve the performance of JSO and benefit from its advantages.

The prior literature clearly shows that numerous attempts have been made to achieve a balance between exploration and exploitation in JSO and PSO by either modifying their operators or hybridizing them with other metaheuristic optimization techniques. However, no hybrid technique that combines JSO and PSO has been found in the literature. It is important to utilize the advantages of PSO’s exploration capability and JSO’s exploitation capability by hybridizing them to achieve a balance between exploration and exploitation. The existing formulation of PSO and JSO is explained in the next section to provide a better understanding before they can be hybridized.

3. The Existing Optimization Formulation

3.1. PSO Formulation

PSO is a famous optimization technique based on swarm intelligence, which is inspired by the social behavior of animals during food collection, like bird flocks and fish schooling [22]. It is an iterative algorithm consisting of a swarm of particles where the position of each particle, X, is a potential solution for the optimization problem. A group of particles (population) is initialized by randomly locating the positions of each particle in the search space. In each iteration, the velocity of the i-th particle, $V_i$, is updated according to the individual best performance, known as the personal best ($Pbest$), and the best particle performance of the entire swarm, known as the global best ($Gbest$) using the following expression [22]:

$$V_i^{t+1}=w{V}_i^t+c_1{r}_1\left(Pbes{t}_i^t-X_i^t\right)+c_2{r}_2\left(Gbes{t}^t-X_i^t\right)$$

(1)

where w is the inertia weight that provides the balance between exploration and exploitation by decreasing the velocity while solutions reach the global minimum, $c_1$ and $c_2$ are the cognitive and social coefficients, and $r_1$ and $r_2$ are real random vectors in the range of [0, 1]. The position of each particle is updated as follows [22]:

$$X_i^{t+1}=X_i^t+V_i^{t+1}1\le i\le N$$

(2)

$Pbest$ is updated when individual particles find an improvement in their performance so far, and $Gbest$ is updated when the swarm finds a better solution. This process is repeated until the termination criterion is satisfied.

3.2. JSO Formulation

JSO, which is also derived from the swarm intelligence technique, simulates the foraging behavior of jellyfish in the ocean as they search for food [23]. JSO consists of two main movements: (i) following the ocean current and (ii) moving inside the swarm of jellyfish. A time control mechanism is used to switch between the movements. At the beginning, the swarm of jellyfish (population) is initialized randomly using one of the chaotic maps known as a logistic map. The logistic map provides better initialization by distributing jellyfish in the search space to ensure they are not trapped in the local optimum and improve the convergence accuracy. The initialization of JSO can be expressed as follows:

$$X_i=LB+\left(UB-LB\right)L_{i}1\le i\le N$$

(3)

where $X_i$ represents the position of the i-th jellyfish, and $UB$ and $LB$ are the upper and lower bounds of the search space, respectively. $L_i$ refers to the logistic value of the i-th jellyfish, which can be expressed as

$$L_i^{t+1}=\eta L_i^t\left(1-L_i^t\right)0\le L_i^0\le 1$$

(4)

where $L_i^0$ is the initial value of the jellyfish, $L_i^0\notin \{0,0.25,0.5,0.75,1\}$, and $\eta$ is set to 4.

The position of the jellyfish in each iteration is updated either by following the ocean current or moving inside the swarm of jellyfish with respect to the time control mechanism. A new location of the i-th jellyfish can be updated in the following ocean current as follows [23]:

$$X_i^{t+1}=X_i^t+r_1(X^{*}-3r_2{X}_i^t)1\le i\le N$$

(5)

where $X_i^{t+1}$ and $X_i^t$ are the updated and current positions of the i-th jellyfish, respectively. $r_1$ and $r_2$ are the random vectors generated between 0 and 1. $X^{*}$ refers to the current best location in the swarm so far.

On the other hand, movements inside the swarm are divided into two types: passive and active motions. In passive motion (type A), jellyfish move around their own positions to find better positions using the following expression [23]:

$$X_i^{t+1}=X_i^t+r_1\gamma (UB-LB)1\le i\le N$$

(6)

where $\gamma$ is the motion coefficient associated with the length of motion around the locations of jellyfish and is usually at 0.1 [23].

In active motion (type B), a random position of the j-th jellyfish is selected to compare with the current position of the i-th jellyfish to determine the direction of movement based on the food quality. If the food quality at the j-th jellyfish is better, then the i-th jellyfish moves toward the direction of the j-th jellyfish; otherwise, the i-th jellyfish moves away from the j-th jellyfish. The position-updating mechanism can be expressed as follows [23]:

$$X_i^{t+1}=X_i^t+r_1\overrightarrow{Step}1\le i\le N$$

(7)

$$\overrightarrow{Step}=\left\{\begin{array}{cc}{X}_i^t-X_j^t,\hfill & \mathrm{if} f\left(X_i^t\right)<f\left(X_j^t\right)\hfill \\ X_j^t-X_i^t,\hfill & \mathrm{if} f\left(X_j^t\right)<f\left(X_i^t\right)\hfill \end{array}\right.$$

(8)

As mentioned in Section 3.2, a time control mechanism is used to switch between following the ocean current and moving inside the swarm. This mechanism consists of a function of time control $c\left(t\right)$ and a constant $c_o$. $c\left(t\right)$ gives a random value that fluctuates between 0 and 1, while $c_o$ is a mean value between 0 and 1, in which $c_o=0.5$ [23]. The time control function $c\left(t\right)$ is computed using the following expression [23]:

$$c\left(t\right)=\left|\left(1-\frac{t}{T}\right)\times (2r-1)\right|$$

(9)

where T is the total number of iterations and r is a random number that distributes uniformly in a range of [0, 1].

The decided movement is to follow the ocean current when $c\left(t\right)$ is higher than $c_o$; otherwise, it is to move inside the swarm. At the same time, the time control function is used to switch between the active and passive motions inside the swarm. A function of $1-c\left(t\right)$ is compared with a random variable in the range of [0, 1], and then the passive motion (type A) is executed if $1-c\left(t\right)$ is higher than the random variable, or the active motion (type B) is executed otherwise. The value of $1-c\left(t\right)$ increases gradually from 0 to 1. In other words, the probability of the passive motion (type A) is higher than the active motion (type B) at the beginning, but the active motion (type B) has more probability to be selected as time goes on [23]. In JSO, following the ocean current represents the exploration (global search) while moving inside a swarm of jellyfish represents the exploitation (local search).

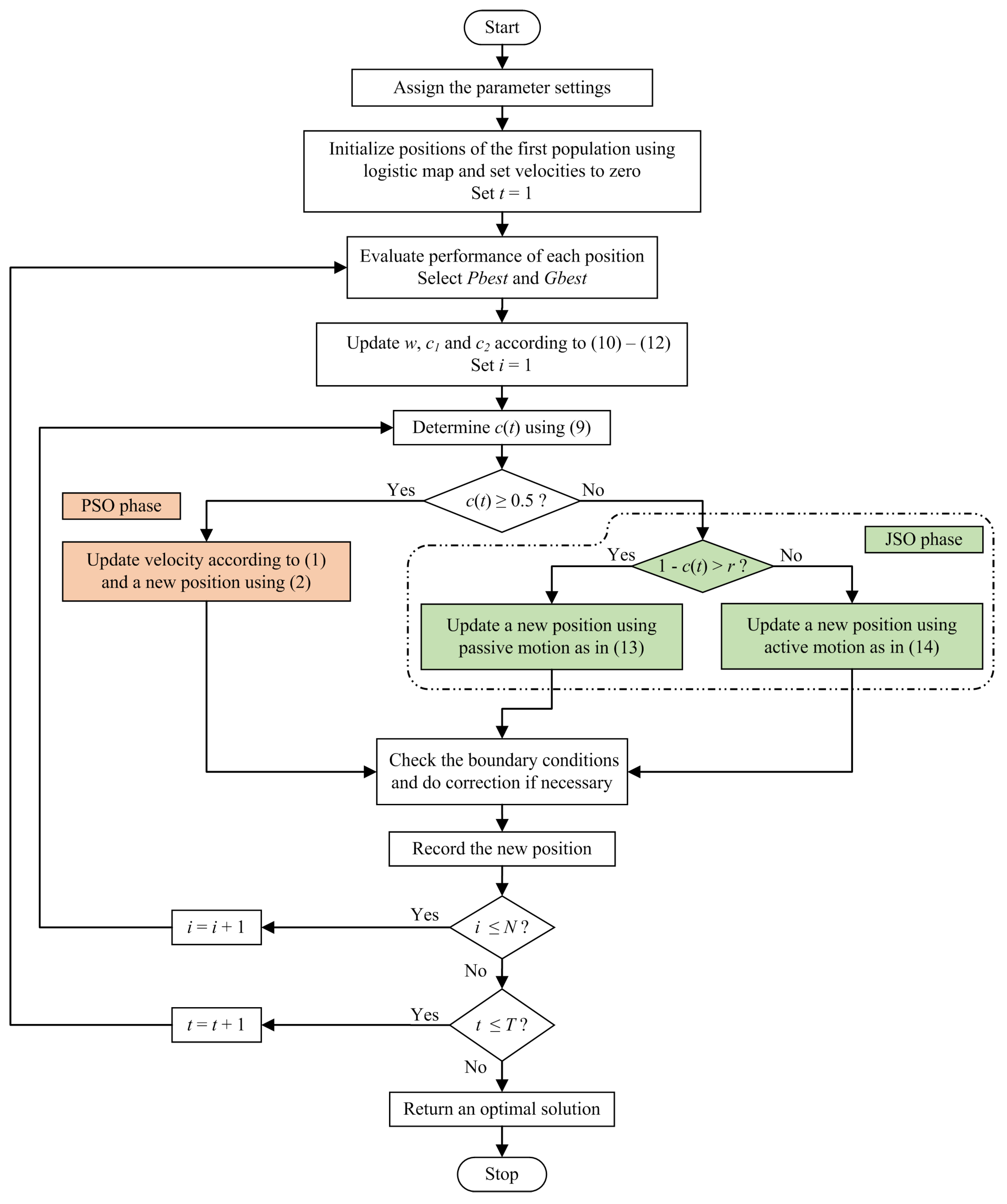
4. Proposed Optimization Formulation

The main goal of this study is to tackle the poor exploration capability of the existing JSO to achieve a proper balance between the exploration and exploitation through a combination with PSO, resulting in a hybrid algorithm called HJSPSO. In addition, the fusion between JSO and PSO enables HJSPSO to escape from the local optimum and avoid premature convergence. The basic structure of the HJSPSO algorithm is based on JSO but with some modifications to adopt PSO operators as follows:

• The movement of following the ocean current in JSO is replaced with the velocity and position-updating mechanism of PSO to take advantage of its exploration capability (referred as PSO phase).
• The passive motion in JSO is modified by introducing a new formulation with respect to the global solution to improve the exploration capability (referredto as JSO phase).
• Nonlinear time-varying inertia weight and cognitive and social coefficients are added to enable the technique to escape from the local optimum.
• The time control mechanism of JSO is used to switch between PSO and JSO phases.

An inertia weight is usually used in optimization techniques to adjust the treatment between exploration and exploitation. A low inertia weight gives high exploitation and low exploration. On the other hand, a high inertia weight gives low exploitation and high exploration. A linear transition from exploration to exploitation in the original PSO [22] is fixed and unable to be adjusted. As an alternative, a nonlinear decreasing inertia weight enables adjustment to give emphasis to either exploration or exploitation. Since JSO is lacking in terms of exploration, the introduced nonlinear decreasing inertia weight helps to improve the exploration and balance with the existing strong exploitation. Apart from that, cognitive and social coefficients are used in PSO to control the influence of exploration and exploitation, respectively. Similar to inertia weight, time-varying cognitive and social coefficients help to ensure high diversity for global exploration at the early stage and exploit around the global solution at the later stage. Then, sine and cosine functions are used in [42] to make them nonlinear and complementary to each other. The parameters w, $c_1$, and $c_2$ in (1) are modified as follows:

$$\begin{array}{c}w=w_{min}+(w_{max}-w_{min}){\left(1-\frac{t}{T}\right)}^{\beta }\end{array}$$

(10)

$$\begin{array}{c}{c}_1=c_{min}+(c_{max}-c_{min})\sin \left(\frac{\pi }{2}\left[1-\frac{t}{T}\right]\right)\end{array}$$

(11)

$$\begin{array}{c}{c}_2=c_{min}+(c_{max}-c_{min})\cos \left(\frac{\pi }{2}\left[1-\frac{t}{T}\right]\right)\end{array}$$

(12)

where $w_{min}=0.4$, $w_{max}=0.9$, $\beta =0.1$, $c_{min}=0.5$, and $c_{max}=2.5$. As more emphasis should be given to exploration at the early state, the cognitive coefficient is thus set at the maximum while the social coefficient is at the minimum. At a later stage, toward the end of the searching process, more emphasis is given to exploitation. In this case, $c_1$ varies from 2.5 to 0.5 and $c_2$ from 0.5 to 2.5 [42]. The inertia weight w nonlinearly decreases from 0.9 to 0.4 along with iteration.

Figure 1 presents the flowchart of HJSPSO. At the beginning, the position of each member in the population is initialized randomly by using a chaotic logistic map to avoid premature convergence as in (3), while the velocity of each member is set to 0. Next, the position is updated either by the PSO or JSO phase depending on the time control mechanism as in (9). If the PSO phase is selected, then the position is updated using (1) and (2), while inertia weight, cognitive coefficient, and social coefficient are based on expressions in (10)–(12). Otherwise, the JSO phase is selected, and the position is updated using the movement inside the swarm. The JSO phase retains the movement inside the swarm, which consists of passive motion (type A) and active motion (type B). However, the passive motion is replaced with the following ocean current movement as in (5), and the nonlinear time-varying inertia weight w is added to the equation to standardize between the phases. A new expression of passive motion in HJSPSO is obtained as follows:

$$X_i^{t+1}=X_i^t+w{r}_1\times (X^{*}-3r_2{X}_i^t)1\le i\le N$$

(13)

The nonlinear time-varying inertia weight w is also introduced in the active motion. As a result, the step in the active motion reduces gradually over time to avoid moving far away from the optimal solution at the later period. At the same time, the JSO phase has a higher probability to be selected according to the time control mechanism during this period. Therefore, the process of local exploitation to find the optimal solution can be improved. A new active motion in HJSPSO can be expressed as follows:

$$X_i^{t+1}=X_i^t+w{r}_1\overrightarrow{Step}1\le i\le N$$

(14)

The search process of HJSPSO swings between the PSO and JSO phases with respect to the time control function $c\left(t\right)$. If $c\left(t\right)$ is higher than or equal to $c_o$, then the PSO phase is selected; otherwise, the JSO phase is executed. According to the time control function, only the JSO phase is involved when the search reaches half of the total iteration. As a result, HJSPSO can benefit from the advantage of PSO at the early stage to explore the search space and the advantage of JSO at the later stage to exploit the global optimum solution.

5. Results and Discussion

This section showcases the performance of HJSPSO in solving 60 benchmark test functions and a TSP. The performance is compared with nine well-known metaheuristic optimization techniques, including PSO and JSO. The 60 benchmark test functions to evaluate performance are described in the next subsection.

5.1. Benchmark Test Functions

The performance of a new technique is typically evaluated using benchmark test functions with different characteristics and compared with various optimization techniques to showcase its effectiveness. A set of 50 classical benchmark test functions (

Table 1. Description of 50 classical benchmark test functions.

No.	Function’s Name	Types	Optimal Value	Dimension	Range
1	Setpint	US	0	5	[−5.12, 5.12]
2	Step	US	0	30	[−100, 100]
3	Sphere	US	0	30	[−100, 100]
4	SumSquares	US	0	30	[−10, 10]
5	Quartic	US	0	30	[−1.28, 1.28]
6	Beale	UN	0	2	[−4.5, 4.5]
7	Easom	UN	−1	2	[−100, 100]
8	Matyas	UN	0	2	[−10, 10]
9	Colville	UN	0	4	[−10, 10]
10	Trid 6	UN	−50	6	[−D2, D2]
11	Trid 10	UN	−210	10	[−D2, D2]
12	Zakharov	UN	0	10	[−5, 10]
13	Powell	UN	0	24	[−4, 5]
14	Schwefel 2.22	UN	0	30	[−10, 10]
15	Schwefel 1.2	UN	0	30	[−100, 100]
16	Rosenbrock	UN	0	30	[−30, 30]
17	Dixon-Price	UN	0	30	[−10, 10]
18	Foxholes	MS	0.998	2	[−65.536, 65.536]
19	Branin	MS	0.398	2	[−5, 10], [0, 15]
20	Bohachevsky1	MS	0	2	[−100, 100]
21	Booth	MS	0	2	[−10, 10]
22	Rastrigin	MS	0	30	[−5.12, 5.12]
23	Schwefel	MS	−12,569.5	30	[−500, 500]
24	Michalewicz 2	MS	−1.8013	2	[0, $\pi$]
25	Michalewicz 5	MS	−4.6877	5	[0, $\pi$]
26	Michalewicz 10	MS	−9.6602	10	[0, $\pi$]
27	Schaffer	MS	0	2	[−100, 100]
28	Six Hump Camel Back	MS	−1.03163	2	[−5, 5]
29	Bohachevsky 2	MS	0	2	[−100, 100]
30	Bohachevsky 3	MS	0	2	[−100, 100]
31	Shubert	MS	−186.73	2	[−10, 10]
32	Goldstein-Price	MS	3	2	[−2, 2]
33	Kowalik	MS	0.00031	4	[−5, 5]
34	Shekel 5	MS	−10.15	4	[0, 10]
35	Shekel 7	MS	−10.4	4	[0, 10]
36	Shekel 10	MS	−10.53	4	[0, 10]
37	Perm	MS	0	4	[−D, D]
38	Powersum	MS	0	4	[0, 1]
39	Hartman 3	MS	−3.86	3	[0, D]
40	Hartman 6	MS	−3.32	6	[0, 1]
41	Griewank	MS	0	30	[−600, 600]
42	Ackley	MS	0	30	[−32, 32]
43	Penalized	MS	0	30	[−50, 50]
44	Penalized 2	MS	0	30	[−50, 50]
45	Langermann 2	MS	−1.08	2	[0, 10]
46	Langermann 5	MS	−1.5	5	[0, 10]
47	Langermann 10	MS	NA	10	[0, 10]
48	Fletcher Powell 2	MS	0	2	[$-\pi ,\pi$]
49	Fletcher Powell 5	MS	0	5	[$-\pi ,\pi$]
50	Fletcher Powell 10	MS	0	10	[$-\pi ,\pi$]

US: unimodal and separable function; UN: unimodal and nonseparable function; MS: multimodal and separable function; and MN: multimodal and nonseparable function.

) and 10 CEC-C06 2019 test benchmark functions (

Table 2. Description of CEC-C06 2019 benchmark test functions.

No.	Function	Function’s Name	Optimal Value	Dimension	Range
1	CEC01	Storn’s Chebyshev polynomial fitting problem	1	9	[−5.12, 5.12]
2	CEC02	Inverse Hilbert matrix problem	1	16	[−100, 100]
3	CEC03	Lennard–Jones minimum energy cluster	1	18	[−100, 100]
4	CEC04	Rastrigin’s function	1	10	[−10, 10]
5	CEC05	Grienwank’s function	1	10	[−1.28, 1.28]
6	CEC06	Weierstrass function	1	10	[−4.5, 4.5]
7	CEC07	Modified Schwefel’s function	1	10	[−100, 100]
8	CEC08	Expanded Schaffer’s F6 function	1	10	[−10, 10]
9	CEC09	Happy CAT function	1	10	[−10, 10]
10	CEC10	Ackley Function	1	10	[−D2, D2]

) are used to evaluate the performance of HJSPSO. The classical test functions consist of unimodal, multimodal, regular, irregular, separable, and nonseparable functions with various dimensions in the range of 2–30 variables [43]. The first 17 functions (F1–F17) are unimodal and commonly used to evaluate the exploitation capability. The rest of the functions (F18–F50) are multimodal and have many local optima to test the exploration capability. On the other hand, the CEC-C06 2019 test benchmark functions (CEC01–CEC10) are multimodal large-scale optimization problems where the dimensions of the first three functions (CEC01–CEC03) are fixed, whereas the other seven functions (CEC04–CEC10) are shafted and rotated within their dimensions [44].

5.2. Metaheuristic Techniques for Comparison

The seven well-known techniques besides the original techniques (i.e., PSO and JSO) that are used for comparison are as follows:

• Grey Wolf Optimizer [45]: GWO was introduced in 2014. It is one of the swarm-intelligence-based techniques inspired by the hunting strategy of grey wolves, which includes searching, surrounding, and attacking the prey.
• Lightning Search Algorithm [19]: LSA was proposed in 2015. It is one of the physical-based techniques that simulates the lightning phenomena and the mechanism of spreading the step leader by using the conception of fast particles known as projectiles.
• Hybrid Heap-Based and Jellyfish Search Algorithm [40]: HBJSA was proposed in 2021. It is a hybrid optimization technique based on HBO and JSO that benefits from the exploration feature of HBO and the exploitation feature of JSO.
• Rat Swarm Optimizer [24]: RSO was introduced in 2020. It is one of the swarm-intelligence-based algorithms that imitates rats’ behavior in chasing and attacking prey.
• Ant Colony Optimization [46]: Ant colony optimization (ACO) was introduced in 1999. It is one of the intelligence-based swarm algorithms that simulates the foraging behavior of ants in finding food and depositing pheromones on the ground to guide other ants to the food.
• Biogeography-based Optimizer [16]: BBO was introduced in 2008. It is an evolutionary-based technique closely related to GA and DE. BBO is inspired by the migration behavior of species between habitats.
• Coronavirus Herd Immunity Optimizer [21]: CHIO was proposed in 2020. It is one of the human-based techniques that mimics the concept of herd immunity to face the coronavirus.

The parameter settings of the selected optimization techniques, including PSO, JSO, and HJSPSO, are tabulated in

Table 3. Parameter settings of the optimization techniques.

Technique	Parameter Settings
HJSPSO	$N=50$; $T=3000$; $c_{min}=0.5$; $c_{max}=2.5$; $w_{min}=0.4$; $w_{max}=0.9$; $\beta =0.1$; $\gamma =0.1$; $c_o=0.5$
PSO [22]	$N=50$; $T=3000$; $c_1=0.5$; $c_2=2.5$; $w_{min}=0.4$; $w_{max}=0.9$
JSO [23]	$N=50$; $T=3000$; $\gamma =0.1$, $c_o=0.5$
GWO [45]	$N=50$; $T=3000$; control parameter a linearly decreases from 2 to 0
LSA [19]	$N=50$; $T=3000$; channel time is set to 10
HBJSA [40]	$N=50$; $T=3000$; adaptive coefficient $\phi$ increases gradually until reaching 0.5
RSO [24]	$N=50$; $T=3000$; ranges of R and C are set to [1, 5] and [0, 2], respectively
ACO [46]	$N=50$; $T=3000$; pheromone evaporation rate, $\rho$ = 0.5; pheromone exponential weight; $\alpha$ = 1; heuristic exponential weight, $\beta$ = 2
BBO [16]	$N=50$; $T=3000$; habitat modification probability = 1; immigration probability bound per iteration = [0, 1]; step size for numerical integration of probability at 1; mutation probability, $M_{max}=0.005$; maximal immigration rate, $I=1$; maximal emigration rate, $E=1$; elitism parameter = 2
CHIO [21]	$N=50$; $T=3000$; number of initial infected cases = 1; basic reproduction rate, $BPr$, and maximum infected cases age, $MaxAge$, are positive integers

.

5.3. Comparison of Optimization Performance

The proposed HJSPSO and other optimization techniques were carried out within MATLAB environment using a PC with 2.7 GHz Core i7 processor and 20 GB memory. All optimization techniques were executed for 30 runs at each benchmark function to evaluate their effectiveness and robustness. The statistical results consist of the mean, standard deviation, and best and worst fitness values for each benchmark function tabulated in

Table A1. A performance comparison of classical test functions.

Function	Indicator	JSO	PSO	GWO	LSA	HBJSA	RSO	ACO	BBO	CHIO	HJSPSO
F1	Mean	0	0	0	0	0	0	0	0	0	0
	Std.	0	0	0	0	0	0	2.1909	0	0	0
	Best	0	0	0	0	0	0	0	0	0	0
	Worst	0	0	0	0	0	0	5	0	0	0
F2	Mean	0	0.066667	0	1	0	0	0.23333	0	0.033333	0
	Std.	0	0.25371	0	1.0828	0	0	0.50401	0	0.18257	0
	Best	0	0	0	0	0	0	0	0	0	0
	Worst	0	1	0	4	0	0	2	0	1	0
F3	Mean	$4.5\times {10}^{-134}$	$1.6\times {10}^{-258}$	$6.7\times {10}^{-262}$	$1.5\times {10}^{-151}$	0	0	$3.5\times {10}^{-170}$	0.024273	0.17284	0
	Std.	$1.4\times {10}^{-133}$	0	0	$4.1\times {10}^{-151}$	0	0	0	0.008728	0.22456	0
	Best	$4.2\times {10}^{-136}$	$9.3\times {10}^{-274}$	$7.7\times {10}^{-268}$	$1.0\times {10}^{-161}$	0	0	$2.5\times {10}^{-174}$	0.011924	$1.2\times {10}^{-11}$	0
	Worst	$7.2\times {10}^{-133}$	$4.7\times {10}^{-257}$	$1.4\times {10}^{-260}$	$1.5\times {10}^{-150}$	0	0	$4.2\times {10}^{-169}$	0.04123	1.1317	0
F4	Mean	$3.8\times {10}^{-135}$	$6.6\times {10}^{-259}$	$5.5\times {10}^{-264}$	$1.2\times {10}^{-150}$	0	0	$5.0\times {10}^{-171}$	0.003411	0.020798	0
	Std.	$7.5\times {10}^{-135}$	0	0	$6.1\times {10}^{-150}$	0	0	0	0.001301	0.02349	0
	Best	$9.4\times {10}^{-138}$	$7.1\times {10}^{-269}$	$1.1\times {10}^{-269}$	$1.2\times {10}^{-160}$	0	0	$1.0\times {10}^{-174}$	0.001423	$1.6\times {10}^{-8}$	0
	Worst	$3.0\times {10}^{-134}$	$2.0\times {10}^{-257}$	$6.8\times {10}^{-263}$	$3.3\times {10}^{-149}$	0	0	$5.2\times {10}^{-170}$	0.005714	0.088923	0
F5	Mean	0.000177	0.001899	0.000065	0.011081	0.000011	0.000023	0.002001	0.000768	0.08211	0.000113
	Std.	0.000062	0.000635	0.000041	0.002462	$7.0\times {10}^{-6}$	0.000023	0.000994	0.000203	0.019275	0.000052
	Best	0.000093	0.000813	0.000012	0.006049	$1.2\times {10}^{-6}$	$1.2\times {10}^{-6}$	0.000744	0.000373	0.041471	0.000045
	Worst	0.000338	0.003381	0.000169	0.015718	0.000027	0.000084	0.005450	0.001188	0.11218	0.000255
F6	Mean	0	0	$1.5\times {10}^{-9}$	0	0	0.000176	0	$1.7\times {10}^{-10}$	0.000097	0
	Std.	0	0	$1.5\times {10}^{-9}$	0	0	0.000186	0	$2.7\times {10}^{-10}$	0.000113	0
	Best	0	0	$3.7\times {10}^{-11}$	0	0	$2.2\times {10}^{-6}$	0	$2.3\times {10}^{-14}$	$5.5\times {10}^{-6}$	0
	Worst	0	0	$5.3\times {10}^{-9}$	0	0	0.000611	0.76207	$1.2\times {10}^{-9}$	0.000427	0
F7	Mean	−1	−1	−1	−1	−1	−0.9987	−1	−1	−0.9916	−1
	Std.	0	0	$3.8\times {10}^{-9}$	0	0	0.001276	0	0	0.031089	0
	Best	−1	−1	−1	−1	−1	−0.99995	−1	−1	−1	−1
	Worst	−1	−1	−1	−1	−1	−0.9938	−1	−1	−0.83808	−1
F8	Mean	0	0	0	0	0	0	0	$5.8\times {10}^{-13}$	0.000025	0
	Std.	0	0	0	0	0	0	0	$1.5\times {10}^{-12}$	0.000030	0
	Best	0	0	0	0	0	0	0	$3.3\times {10}^{-20}$	$9.2\times {10}^{-8}$	0
	Worst	0	0	0	0	0	0	0	$6.9\times {10}^{-12}$	0.000132	0
F9	Mean	$7.8\times {10}^{-17}$	$5.5\times {10}^{-12}$	0.13307	$5.5\times {10}^{-12}$	$2.8\times {10}^{-7}$	1.5407	0.001242	0.007284	0.4057	$4.8\times {10}^{-18}$
	Std.	$3.7\times {10}^{-16}$	$9.0\times {10}^{-12}$	0.406	$6.6\times {10}^{-12}$	$3.7\times {10}^{-7}$	0.2954	0.004956	0.006838	0.30376	$1.3\times {10}^{-17}$
	Best	$1.5\times {10}^{-21}$	$6.3\times {10}^{-14}$	$3.6\times {10}^{-7}$	$2.1\times {10}^{-16}$	$1.6\times {10}^{-10}$	0.29806	$2.5\times {10}^{-7}$	0.000147	0.065115	$1.9\times {10}^{-23}$
	Worst	$2.0\times {10}^{-15}$	$4.8\times {10}^{-11}$	1.3345	$2.5\times {10}^{-11}$	$1.5\times {10}^{-6}$	2.3817	0.025051	0.028474	1.0787	$6.4\times {10}^{-17}$
F10	Mean	−50	−50	−50	−50	−50	−19.3568	−50	−50	−49.952	−50
	Std.	$3.0\times {10}^{-14}$	$4.6\times {10}^{-14}$	$2.5\times {10}^{-6}$	$7.8\times {10}^{-14}$	$1.7\times {10}^{-6}$	10.2918	$1.0\times {10}^{-13}$	$3.0\times {10}^{-11}$	0.055344	$2.8\times {10}^{-14}$
	Best	−50	−50	−50	−50	−50	−38.6815	−50	−50	−49.9988	−50
	Worst	−50	−50	−50	−50	−50	0.48768	−50	−50	−49.7493	−50
F11	Mean	−210	−210	−204.5386	−210	−206.7294	−6.0603	−210	−209.9979	−206.3257	−210
	Std.	$4.8\times {10}^{-11}$	$6.3\times {10}^{-12}$	16.6674	$2.2\times {10}^{-9}$	0.9209	6.1459	$6.3\times {10}^{-12}$	0.00057	3.8949	$4.5\times {10}^{-9}$
	Best	−210	−210	−209.9999	−210	−209.0753	−22.3292	−210	−209.9992	−209.7321	−210
	Worst	−210	−210	−154.3612	−210	−204.6705	4.6506	−210	−209.9964	−192.7169	−210
F12	Mean	$2.7\times {10}^{-112}$	$1.1\times {10}^{-278}$	$4.9\times {10}^{-324}$	$6.8\times {10}^{-242}$	0	0	$4.0\times {10}^{-209}$	$2.3\times {10}^{-7}$	3.2438	$2.3\times {10}^{-216}$
	Std.	$9.1\times {10}^{-112}$	0	0	0	0	0	0	$1.8\times {10}^{-7}$	1.7601	0
	Best	$4.0\times {10}^{-118}$	$1.9\times {10}^{-292}$	0	$6.8\times {10}^{-254}$	0	0	$1.3\times {10}^{-217}$	$2.6\times {10}^{-8}$	0.43572	$3.7\times {10}^{-227}$
	Worst	$4.3\times {10}^{-111}$	$2.77\times {10}^{-277}$	$1.5\times {10}^{-323}$	$2.0\times {10}^{-240}$	0	0	$1.1\times {10}^{-207}$	$7.9\times {10}^{-7}$	7.1901	$6.8\times {10}^{-215}$
F13	Mean	$2.57\times {10}^{-6}$	0.000212	$2.1\times {10}^{-6}$	0.000038	0	0	0.000107	0.015393	0.44318	$2.4\times {10}^{-7}$
	Std.	$7.3\times {10}^{-6}$	0.000277	$2.6\times {10}^{-6}$	0.000074	0	0	$2.2\times {10}^{-5}$	0.004426	0.24949	$5.7\times {10}^{-7}$
	Best	$2.2\times {10}^{-8}$	0.000031	$1.6\times {10}^{-8}$	$4.8\times {10}^{-6}$	0	0	$5.3\times {10}^{-5}$	0.007004	0.085003	$3.2\times {10}^{-105}$
	Worst	0.000040	0.001514	$9.6\times {10}^{-6}$	0.000381	0	0	0.000134	0.022289	1.0397	$3.0\times {10}^{-6}$
F14	Mean	$4.2\times {10}^{-70}$	0.000021	$1.7\times {10}^{-150}$	$1.1\times {10}^{-6}$	0	0	$2.9\times {10}^{-102}$	0.044577	0.19129	$5.6\times {10}^{-177}$
	Std.	$1.9\times {10}^{-69}$	0.000077	$2.2\times {10}^{-150}$	$4.0\times {10}^{-6}$	0	0	$6.1\times {10}^{-102}$	0.008846	0.079441	0
	Best	$2.9\times {10}^{-74}$	$1.6\times {10}^{-13}$	$1.6\times {10}^{-152}$	$1.1\times {10}^{-26}$	0	0	$9.1\times {10}^{-104}$	0.029445	0.000365	$9.1\times {10}^{-180}$
	Worst	$1.1\times {10}^{-68}$	0.000347	$9.1\times {10}^{-150}$	0.000021	0	0	$3.3\times {10}^{-101}$	0.063703	0.34191	$5.9\times {10}^{-176}$
F15	Mean	$3.7\times {10}^{-133}$	$2.1\times {10}^{-260}$	$2.1\times {10}^{-263}$	$6.6\times {10}^{-149}$	0	0	$2.3\times {10}^{-168}$	0.34451	2.314	0
	Std.	$1.0\times {10}^{-132}$	0	0	$3.5\times {10}^{-148}$	0	0	0	0.11744	4.7075	0
	Best	$6.3\times {10}^{-135}$	$1.3\times {10}^{-272}$	$8.9\times {10}^{-268}$	$2.8\times {10}^{-160}$	0	0	$1.1\times {10}^{-172}$	0.17032	$1.5\times {10}^{-6}$	0
	Worst	$5.6\times {10}^{-132}$	$3.7\times {10}^{-259}$	$3.0\times {10}^{-262}$	$1.9\times {10}^{-147}$	0	0	$4.5\times {10}^{-167}$	0.63924	25.4599	0
F16	Mean	0.05827	29.6144	26.0825	3.7089	15.546	28.3194	21.6441	59.0824	134.028	20.3876
	Std.	0.19107	24.266	0.73251	3.8172	11.2623	0.37112	28.0842	37.7391	65.8768	0.32964
	Best	0.000018	0.93178	24.9843	0.000141	0.000035	27.7826	0.000653	25.015	7.0648	19.7712
	Worst	1.0276	76.6784	27.9087	15.1608	28.1724	28.9608	111.2683	142.212	265.6228	21.3463
F17	Mean	0.01068	0.66667	0.66667	0.66667	0.54369	0.66667	0.66667	0.9842	2.4386	0.66667
	Std.	0.05605	$3.2\times {10}^{-16}$	$2.3\times {10}^{-8}$	$6.0\times {10}^{-16}$	0.18008	$4.3\times {10}^{-8}$	$2.1\times {10}^{-17}$	0.83249	1.6745	$8.4\times {10}^{-16}$
	Best	$1.4\times {10}^{-9}$	0.66667	0.66667	0.66667	0.070622	0.66667	0.66667	0.66887	0.087339	0.66667
	Worst	0.30717	0.66667	0.66667	0.66667	0.68381	0.66667	0.66667	4.8128	5.5449	0.66667
F18	Mean	0.998	1.3291	2.4375	0.998	0.998	1.9239	2.0781	2.3097	0.998	0.998
	Std.	$1.1\times {10}^{-16}$	0.60211	2.9447	$1.4\times {10}^{-16}$	$1.1\times {10}^{-16}$	1.0068	2.5852	2.5508	$2.7\times {10}^{-12}$	$1.1\times {10}^{-16}$
	Best	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998
	Worst	0.998	2.9821	10.7632	0.998	0.998	2.9821	10.7632	10.7632	0.998	0.998
F19	Mean	0.39789	0.39789	0.39789	0.39789	0.39789	0.57724	0.39789	0.39789	0.39789	0.39789
	Std.	0	0	$4.8\times {10}^{-8}$	0	0	0.15066	$2.9\times {10}^{-14}$	$1.9\times {10}^{-15}$	$3.3\times {10}^{-8}$	0
	Best	0.39789	0.39789	0.39789	0.39789	0.39789	0.39805	0.39789	0.39789	0.39789	0.39789
	Worst	0.39789	0.39789	0.39789	0.39789	0.39789	0.93725	0.39789	0.39789	0.39789	0.39789
F20	Mean	0	0	0	0	0	0	0	0	$9.6\times {10}^{-6}$	0
	Std.	0	0	0	0	0	0	0	0	0.000047	0
	Best	0	0	0	0	0	0	0	0	0	0
	Worst	0	0	0	0	0	0	0	0	0.000259	0
F21	Mean	0	0	$5.0\times {10}^{-9}$	0	0	0.000138	0	$3.8\times {10}^{-11}$	$3.7\times {10}^{-6}$	0
	Std.	0	0	$5.5\times {10}^{-9}$	0	0	0.000185	0	$9.8\times {10}^{-11}$	0.000013	0
	Best	0	0	$1.4\times {10}^{-10}$	0	0	$3.2\times {10}^{-6}$	0	0	$1.3\times {10}^{-10}$	0
	Worst	0	0	$2.1\times {10}^{-8}$	0	0	0.000761	0	$3.9\times {10}^{-10}$	0.000068	0
F22	Mean	4.5872	42.9158	0	57.9397	0	0	16.6821	21.8759	3.2392	0
	Std.	4.752	12.9218	0	13.4727	0	0	4.1204	6.1509	1.7512	0
	Best	0	25.8689	0	37.8084	0	0	9.9496	12.9555	0.041411	0
	Worst	13.9294	70.642	0	80.5915	0	0	25.8689	44.78	6.2076	0
F23	Mean	−8097.69	−6548.23	−5987.234	−8279.335	−10486.3	−5822.831	−8765.300	−9168.879	−11631.16	−8249.76
	Std.	596.0855	862.8825	627.9572	622.6347	1663.726	701.2344	635.8039	504.1961	190.2833	460.9557
	Best	−9209.117	−8339.086	−7508.985	−9544.808	−12150.5	−6951.771	−9915.361	−9959.251	−12029.93	−9248.716
	Worst	−6651.382	−5101.433	−4716.264	−7156.004	−7486.446	−3579.892	−7572.415	−8123.383	−11300.07	−7432.332
F24	Mean	−1.8013	−1.8013	−1.8013	−1.8013	−1.8013	−1.4896	−1.8013	−1.8013	−1.8013	−1.8013
	Std.	$9.0\times {10}^{-16}$	$9.0\times {10}^{-16}$	$4.6\times {10}^{-8}$	$9.0\times {10}^{-16}$	$9.0\times {10}^{-16}$	0.27273	$9.0\times {10}^{-16}$	$9.5\times {10}^{-16}$	$7.8\times {10}^{-14}$	$9.0\times {10}^{-16}$
	Best	−1.8013	−1.8013	−1.8013	−1.8013	−1.8013	−1.7815	−1.8013	−1.8013	−1.8013	−1.8013
	Worst	−1.8013	−1.8013	−1.8013	−1.8013	−1.8013	−0.94607	−1.8013	−1.8013	−1.8013	−1.801
F25	Mean	−4.6793	−4.538	−4.5439	−4.6003	−4.6877	−2.3764	−4.5908	−4.6491	−4.6877	−4.6701
	Std.	0.016991	0.18897	0.2033	0.089854	$1.8\times {10}^{-15}$	0.31557	0.0897	0.054374	$6.9\times {10}^{-8}$	0.047281
	Best	−4.6877	−4.6877	−4.6876	−4.6877	−4.6877	−2.8405	−4.6877	−4.6877	−4.6877	−4.6877
	Worst	−4.6459	−3.8658	−3.8446	−4.3331	−4.6877	−1.7803	−4.3331	−4.4831	−4.6877	−4.5377
F26	Mean	−9.5319	−8.8762	−7.9497	−8.9966	−9.6602	−3.7965	−9.3772	−9.2552	−9.6589	−9.5186
	Std.	0.094523	0.57564	1.0323	0.30029	$4.4\times {10}^{-6}$	0.58715	0.16955	0.26029	0.002079	0.093213
	Best	−9.6602	−9.5527	−9.3656	−9.4641	−9.6602	−5.0334	−9.6602	−9.6176	−9.6602	−9.6184
	Worst	−9.3281	−6.9144	−5.7263	−8.3181	−9.6591	−2.8528	−9.0305	−8.5856	−9.6526	−9.3356
F27	Mean	0	0	0	0.002911	0	0	0.0044	0	0.002658	0
	Std.	0	0	0	0.01108	0	0	0.0133	0	0.008571	0
	Best	0	0	0	0	0	0	0	0	$1.5\times {10}^{-10}$	0
	Worst	0	0	0	0.043671	0	0	0.043671	0	0.043671	0
F28	Mean	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316
	Std.	$6.8\times {10}^{-16}$	$6.8\times {10}^{-16}$	$2.4\times {10}^{-10}$	$6.8\times {10}^{-16}$	$6.8\times {10}^{-16}$	$7.8\times {10}^{-6}$	$6.8\times {10}^{-16}$	$6.1\times {10}^{-16}$	$8.7\times {10}^{-10}$	$6.8\times {10}^{-16}$
	Best	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316
	Worst	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316
F29	Mean	0	0	0	0	0	0	0	0	$1.5\times {10}^{-6}$	0
	Std.	0	0	0	0	0	0	0	0	$3.9\times {10}^{-6}$	0
	Best	0	0	0	0	0	0	0	0	0	0
	Worst	0	0	0	0	0	0	0	0	0.000017	0
F30	Mean	0	0	0	0	0	0	0	$7.1\times {10}^{-9}$	0.001155	0
	Std.	0	0	0	0	0	0	0	$1.3\times {10}^{-8}$	0.001576	0
	Best	0	0	0	0	0	0	0	$4.9\times {10}^{-15}$	$9.2\times {10}^{-8}$	0
	Worst	0	0	0	0	0	0	0	$6.8\times {10}^{-8}$	0.007948	0
F31	Mean	−186.7309	−186.7309	−186.7284	−186.7309	−186.7309	−186.7286	−186.7309	−186.7309	−186.7308	−186.7309
	Std.	$1.8\times {10}^{-14}$	$4.0\times {10}^{-14}$	0.009404	$3.4\times {10}^{-14}$	$2.0\times {10}^{-14}$	0.007582	$3.9\times {10}^{-14}$	$3.9\times {10}^{-14}$	0.000254	$2.8\times {10}^{-14}$
	Best	−186.7309	−186.7309	−186.7309	−186.7309	−186.7309	−186.7309	−186.7309	−186.7309	−186.7309	−186.7309
	Worst	−186.7309	−186.7309	−186.6817	−186.7309	−186.7309	−186.6946	−186.7309	−186.7309	−186.7297	−186.7309
F32	Mean	3	3	3	3	3	3	3	3	3	3
	Std.	$2.0\times {10}^{-15}$	$2.0\times {10}^{-15}$	$1.0\times {10}^{-7}$	$1.3\times {10}^{-15}$	$1.7\times {10}^{-15}$	$3.6\times {10}^{-8}$	$1.3\times {10}^{-15}$	$3.4\times {10}^{-15}$	0.000013	$1.3\times {10}^{-15}$
	Best	3	3	3	3	3	3	3	3	3	3
	Worst	3	3	3	3	3	3	3	3	3.0001	3
F33	Mean	0.000307	0.000368	0.002435	0.000338	0.000307	0.000675	0.001675	0.000354	0.000677	0.000307
	Std.	$1.9\times {10}^{-19}$	0.000244	0.006086	0.000167	$5.6\times {10}^{-9}$	0.000267	0.005083	0.00006	0.000123	$1.2\times {10}^{-19}$
	Best	0.000307	0.000307	0.000307	0.000307	0.000307	0.000354	0.000307	0.000307	0.000317	0.000307
	Worst	0.000307	0.001594	0.020363	0.001223	0.000308	0.0013	0.020363	0.000514	0.00087	0.000307
F34	Mean	−10.1532	−5.9744	−9.6449	−8.3806	−10.1532	−1.3749	−6.2478	−7.228	−10.1528	−10.1532
	Std.	$7.2\times {10}^{-15}$	3.37	1.5509	2.5859	$7.2\times {10}^{-15}$	0.77448	3.7292	3.2898	0.000973	$7.2\times {10}^{-15}$
	Best	−10.1532	−10.1532	−10.1532	−10.1532	−10.1532	−3.1593	−10.1532	−10.1532	−10.1532	−10.1532
	Worst	−10.1532	−2.6305	−5.0552	−2.6305	−10.1532	−0.4962	−2.6305	−2.6305	−10.1489	−10.1532
F35	Mean	−10.4029	−7.6896	−10.2257	−8.1426	−10.4029	−1.5068	−7.9193	−7.7295	−10.4024	−10.4029
	Std.	$1.8\times {10}^{-15}$	3.4513	0.97043	3.2909	$1.6\times {10}^{-15}$	1.3311	3.5796	3.5849	0.00173	$1.8\times {10}^{-15}$
	Best	−10.4029	−10.4029	−10.4029	−10.4029	−10.4029	−7.7302	−10.4029	−10.4029	−10.4029	−10.4029
	Worst	−10.4029	−2.7519	−5.0877	−2.7659	−10.4029	−0.58241	−2.7519	−2.7519	−10.3939	−10.4029
F36	Mean	−10.5364	−7.9068	−10.5364	−9.4643	−10.5364	−1.6671	−7.0608	−7.9283	−10.5349	−10.5364
	Std.	$1.8\times {10}^{-15}$	3.7907	0.000015	2.4485	$1.8\times {10}^{-15}$	0.88478	3.8008	3.5144	0.003992	$1.7\times {10}^{-15}$
	Best	−10.5364	−10.5364	−10.5364	−10.5364	−10.5364	−4.4413	−10.5364	−10.5364	−10.5364	−10.5364
	Worst	−10.5364	−2.4217	−10.5363	−3.8354	−10.5364	−0.67852	−2.4273	−1.6766	−10.515	−10.5364
F37	Mean	0.00485	0.095574	0.33591	0.014761	0.016679	4.0769	0.1465	0.11938	0.11862	0.004616
	Std.	0.001181	0.15826	0.5384	0.036154	0.019922	5.7771	0.18854	0.13962	0.09118	0.001398
	Best	0.002045	$2.9\times {10}^{-6}$	$6.4\times {10}^{-6}$	$7.1\times {10}^{-6}$	0.001936	0.06555	$5.6\times {10}^{-6}$	0.00062	0.00169	0.000088
	Worst	0.006389	0.47231	1.5377	0.13066	0.090347	28.3114	0.47231	0.47231	0.37234	0.006388
F38	Mean	0.000114	0.000221	0.030126	0.000192	0.005479	17.2902	0.000938	0.001726	0.010195	0.000083
	Std.	0.000173	0.000177	0.16084	0.000173	0.003202	24.8812	0.003020	0.002537	0.007209	0.000093
	Best	$5.5\times {10}^{-7}$	$1.0\times {10}^{-9}$	0.000026	$6.4\times {10}^{-9}$	0.001122	0.38614	$3.1\times {10}^{-14}$	$6.9\times {10}^{-7}$	0.000441	$7.3\times {10}^{-7}$
	Worst	0.000831	0.000428	0.88168	0.000419	0.011985	124.7192	0.015394	0.008246	0.030697	0.000325
F39	Mean	−3.8628	−3.8628	−3.8628	−3.8628	−3.8628	−2.7081	−3.8628	−3.8628	−3.8628	−3.8628
	Std.	$2.7\times {10}^{-15}$	$2.7\times {10}^{-15}$	0.002405	$2.7\times {10}^{-15}$	$2.7\times {10}^{-15}$	0.924	$2.7\times {10}^{-15}$	$2.5\times {10}^{-15}$	$5.2\times {10}^{-10}$	$2.7\times {10}^{-15}$
	Best	−3.8628	−3.8628	−3.8628	−3.8628	−3.8628	−3.8537	−3.8628	−3.8628	−3.8628	−3.8628
	Worst	−3.8628	−3.8628	−3.8549	−3.8628	−3.8628	−0.57993	−3.8628	−3.8628	−3.8628	−3.8628
F40	Mean	−3.3224	−3.2588	−3.2579	−3.2469	−3.3224	−2.1921	−3.2826	−3.3065	−3.3224	−3.3224
	Std.	$5.9\times {10}^{-16}$	0.060487	0.067123	0.058427	$6.4\times {10}^{-16}$	0.44001	0.057155	0.041215	$3.0\times {10}^{-8}$	$5.7\times {10}^{-16}$
	Best	−3.3224	−3.3224	−3.3224	−3.3224	−3.3224	−2.9142	−3.3224	−3.3224	−3.3224	−3.3224
	Worst	−3.3224	−3.2032	−3.1376	−3.2032	−3.3224	−1.3712	−3.2032	−3.2032	−3.3224	−3.3224
F41	Mean	0	0.010826	0	0.008372	0	0	0.000986	0.062207	0.14432	0
	Std.	0	0.012326	0	0.011661	0	0	0.003077	0.022368	0.14044	0
	Best	0	0	0	0	0	0	0	0.027649	$1.2\times {10}^{-7}$	0
	Worst	0	0.051369	0	0.044263	0	0	0.012321	0.12754	0.46368	0
F42	Mean	$4.9\times {10}^{-15}$	0.15683	$8.0\times {10}^{-15}$	1.8126	$8.9\times {10}^{-16}$	$2.6\times {10}^{-15}$	$5.9\times {10}^{-15}$	0.040649	0.11434	$3.3\times {10}^{-15}$
	Std.	$1.2\times {10}^{-15}$	0.41725	0	1.1327	0	$1.8\times {10}^{-15}$	$1.8\times {10}^{-15}$	0.007439	0.097559	$1.5\times {10}^{-15}$
	Best	$4.4\times {10}^{-15}$	$8.0\times {10}^{-15}$	$8.0\times {10}^{-15}$	$8.0\times {10}^{-15}$	$8.9\times {10}^{-16}$	$8.9\times {10}^{-16}$	$4.4\times {10}^{-16}$	0.025084	$4.7\times {10}^{-6}$	$4.4\times {10}^{-16}$
	Worst	$8.0\times {10}^{-15}$	1.5017	$8.0\times {10}^{-15}$	3.9346	$8.9\times {10}^{-16}$	$4.4\times {10}^{-15}$	$8.0\times {10}^{-15}$	0.055848	0.31791	$4.0\times {10}^{-15}$
F43	Mean	$3.3\times {10}^{-27}$	0.003456	0.009783	0.27412	$3.6\times {10}^{-9}$	0.31638	0.027645	0.000057	0.002775	$1.3\times {10}^{-27}$
	Std.	$1.7\times {10}^{-26}$	0.018927	0.008449	0.6863	$2.7\times {10}^{-9}$	0.12895	0.081371	0.000023	0.002182	$2.9\times {10}^{-27}$
	Best	$2.1\times {10}^{-30}$	$1.6\times {10}^{-32}$	$3.9\times {10}^{-8}$	$2.1\times {10}^{-32}$	$9.0\times {10}^{-10}$	0.091686	$1.6\times {10}^{-32}$	0.000019	$2.2\times {10}^{-9}$	$1.7\times {10}^{-30}$
	Worst	$9.2\times {10}^{-26}$	0.10367	0.039231	3.4496	$1.2\times {10}^{-8}$	0.78704	0.41467	0.000119	0.008432	$1.6\times {10}^{-26}$
F44	Mean	0.006036	0.003383	0.1448	0.006264	$2.7\times {10}^{-8}$	2.7347	$4.1\times {10}^{-32}$	0.000697	0.036811	0.029482
	Std.	0.022972	0.018532	0.10267	0.023854	$1.6\times {10}^{-8}$	0.055416	$1.1\times {10}^{-31}$	0.000236	0.034919	0.051025
	Best	$2.2\times {10}^{-29}$	$1.5\times {10}^{-33}$	$2.7\times {10}^{-7}$	$2.5\times {10}^{-32}$	$5.3\times {10}^{-9}$	2.6245	$1.5\times {10}^{-33}$	0.000278	$5.3\times {10}^{-12}$	$2.0\times {10}^{-22}$
	Worst	0.090543	0.1015	0.38505	0.097371	$7.2\times {10}^{-8}$	2.8429	$6.1\times {10}^{-31}$	0.001363	0.10215	0.14521
F45	Mean	−1.0809	−1.0809	−1.0809	−1.0809	−1.0809	−0.73561	−1.0809	−1.0494	−1.0809	−1.0809
	Std.	$4.5\times {10}^{-16}$	$4.5\times {10}^{-16}$	$3.8\times {10}^{-9}$	$4.5\times {10}^{-16}$	$4.5\times {10}^{-16}$	0.23848	$4.5\times {10}^{-16}$	0.058208	0.000013	$4.5\times {10}^{-16}$
	Best	−1.0809	−1.0809	−1.0809	−1.0809	−1.0809	−1.0661	−1.0809	−1.0809	−1.0809	−1.0809
	Worst	−1.0809	−1.0809	−1.0809	−1.0809	−1.0809	−0.098209	−1.0809	−0.94563	−1.0809	−1.0809
F46	Mean	−1.5	−1.1997	−1.2323	−1.2909	−1.5	−0.21821	−1.3641	−1.0043	−1.4064	−1.5
	Std.	$6.8\times {10}^{-16}$	0.28879	0.29904	0.28109	$6.8\times {10}^{-16}$	0.22497	0.25189	0.36935	0.21175	$6.8\times {10}^{-16}$
	Best	−1.5	−1.5	−1.5	−1.5	−1.5	−0.90126	−1.5	−1.5	−1.5	−1.5
	Worst	−1.5	−0.73607	−0.57409	−0.79773	−1.5	−0.011193	−0.79782	−0.51319	−0.90597	−1.5
F47	Mean	−0.97768	−0.71091	−0.62771	−0.58377	−0.89084	−0.000724	−0.89442	−0.56605	−0.77381	−0.72769
	Std.	0.35818	0.36188	0.36267	0.27362	0.2944	0.001587	0.24859	0.24859	0.093677	0.22809
	Best	−1.5	−1.5	−1.5	−1.5	−1.4993	−0.006644	−1.5	−0.79769	−0.96436	−1.5
	Worst	−0.46585	−0.27494	−0.13427	−0.27494	−0.41215	$-8.0\times {10}^{-7}$	−0.35577	−0.14546	−0.51318	−0.27494
F48	Mean	0	0	0.000029	0	$1.9\times {10}^{-14}$	0.018916	$5.5\times {10}^{-18}$	$9.8\times {10}^{-6}$	0.007613	0
	Std.	0	0	0.000054	0	$9.4\times {10}^{-14}$	0.030807	$3.0\times {10}^{-17}$	0.000026	0.009496	0
	Best	0	0	$7.0\times {10}^{-8}$	0	0	0.000327	0	$3.3\times {10}^{-10}$	0.00021	0
	Worst	0	0	0.000194	0	$5.1\times {10}^{-13}$	0.1483	$1.7\times {10}^{-16}$	0.000121	0.03329	0
F49	Mean	$6.6\times {10}^{-28}$	463.6839	75.4101	158.0587	152.2686	1842.241	91.0691	231.8756	7.5535	$6.5\times {10}^{-6}$
	Std.	$4.1\times {10}^{-28}$	1188.208	167.4468	291.4037	273.25	1737.654	200.0792	324.0105	6.1844	0.000035
	Best	0	0	0.004088	0	0.000025	92.7308	$1.1\times {10}^{-25}$	$5.0\times {10}^{-14}$	0.16645	0
	Worst	$1.0\times {10}^{-27}$	5066.931	692.4573	677.3945	692.4565	6188.255	677.3945	692.4565	29.5654	0.000194
F50	Mean	$7.1\times {10}^{-28}$	528.6916	81.3611	67.7395	426.0675	1824.006	63.7245	209.8042	6.1735	$5.3\times {10}^{-28}$
	Std.	$6.6\times {10}^{-28}$	1084.965	165.7652	206.6924	302.0439	2047.863	170.1124	317.1288	5.3754	$5.2\times {10}^{-28}$
	Best	0	0	10.5397	0	3.1356	72.1616	$2.8\times {10}^{-26}$	$2.2\times {10}^{-14}$	0.23867	0
	Worst	$3.4\times {10}^{-27}$	4348.837	692.4587	677.3945	692.4565	6139.581	692.4565	692.4565	23.6686	$1.6\times {10}^{-27}$
Number of best hits		23	14	9	13	29	15	13	8	3	32
Hit rate (%)		46	28	18	26	58	30	26	16	6	64

and

Table A2. A performance comparison of CEC-C06 2019 test functions.

Function	Indicator	JSO	PSO	GWO	LSA	HBJSA	RSO	ACO	BBO	CHIO	HJSPSO
CEC01	Mean	1897.46	9347.033	471.4735	7110.052	1	1	30345.25	75567.76	2159895	47.7927
	Std.	2867.538	10741.98	1809.455	10272.97	$4.2\times {10}^{-10}$	0	30030.01	79953.37	1323728	103.9644
	Best	7.8959	8.663	1	2.6238	1	1	397.1488	278.5102	329903.2	1
	Worst	12599.68	35716.12	9008.052	41270.07	1	1	94955.56	338853.2	5778371	465.4388
CEC02	Mean	158.8989	211.8816	182.3192	276.0412	4.9543	4.3106	334.29	274.2638	1456.037	22.8269
	Std.	71.7895	98.4277	157.8209	88.4675	0.16205	0.18938	130.13	92.8797	336.3427	18.0358
	Best	28.4168	41.025	5.359	129.4601	4.246	4.2195	4.2181	140.061	809.6388	4.2165
	Worst	347.462	413.0268	607.7932	468.4655	5	5	689.29	562.2011	2146.505	66.2613
CEC03	Mean	1.7018	1.6056	1.7967	1.6192	4.316	4.7439	4.6179	2.2463	1.8273	1.3745
	Std.	0.38958	1.1557	1.1508	1.1505	0.4813	1.0933	0.5127	2.1707	0.28045	0.1407
	Best	1.4092	1	1	1.4091	3.506	1.5614	3.3381	1.4091	1.4713	1
	Worst	2.8196	7.7119	6.6594	7.7109	5.33	7.4524	5.3898	7.7104	2.5396	1.6115
CEC04	Mean	5.227	16.6208	11.489	24.5473	15.161	58.7958	8.0011	9.3577	9.4372	8.7707
	Std.	2.2936	9.0368	5.9399	10.6468	3.1066	10.0195	6.9928	3.7647	2.5852	3.1094
	Best	2.0785	5.9748	2.9972	6.9698	9.8662	41.6655	1	2.9899	5.4216	3.9849
	Worst	11.9445	39.8033	24.7274	46.768	22.4859	79.5955	72.0561	18.9092	15.5778	15.9244
CEC05	Mean	1.0372	1.118	1.3418	1.1254	1.0715	37.0238	1.0400	1.0865	1.0832	1.0343
	Std.	0.02394	0.076811	0.21881	0.073322	0.037814	9.068	0.0954	0.04696	0.046503	0.023769
	Best	1.0074	1.0296	1.0807	1.0172	1.0085	22.8897	1	1.0197	1.0114	1
	Worst	1.0935	1.3568	1.7945	1.3761	1.1425	66.7916	1.5356	1.2143	1.1841	1.0935
CEC06	Mean	1.1217	1.6565	1.6752	2.991	1.0389	7.3074	1.3068	1.3217	2.5675	1.1953
	Std.	0.21817	0.87821	0.65429	1.3046	0.033307	0.99091	0.4634	0.6039	0.48689	0.39333
	Best	1	1	1.079	1.0813	1.0042	5.6741	1	1.0083	1.6862	1
	Worst	1.965	4.1344	3.4022	5.5246	1.1199	9.6955	2.5143	3.4939	3.6444	2.5774
CEC07	Mean	176.394	780.0061	506.8545	770.3265	640.8752	1231.502	103.99	676.6212	310.6974	309.9096
	Std.	157.7418	226.8214	243.8092	325.8487	119.8646	199.7113	108.2556	299.1341	98.4024	145.5422
	Best	1.1249	416.0599	1.4188	126.5957	388.7151	837.7197	7.8924	4.6023	38.2768	1.2498
	Worst	544.3641	1284.386	1073.91	1705.947	855.2098	1662.029	506.7367	1138.152	508.1458	593.3495
CEC08	Mean	2.2995	3.4544	3.0741	3.4037	3.7788	4.5351	2.2804	3.3504	3.3275	2.2913
	Std.	0.43068	0.57327	0.60597	0.50727	0.1974	0.2013	0.43776	0.53345	0.26203	0.41965
	Best	1.2409	2.4356	2.201	2.0071	3.1342	4.1857	1.6891	2.0506	2.834	1.6462
	Worst	3.1437	4.475	4.524	4.4785	4.0983	5.0861	3.2139	4.4073	3.6896	3.1452
CEC09	Mean	1.0775	1.1329	1.0951	1.2409	1.2019	1.5009	1.0804	1.0943	1.1646	1.1155
	Std.	0.025239	0.052233	0.044148	0.12048	0.035946	0.41023	0.017094	0.038149	0.03367	0.029268
	Best	1.0369	1.0522	1.0509	1.0451	1.1324	1.3755	1.0346	1.0273	1.1144	1.0635
	Worst	1.1524	1.2664	1.2025	1.6425	1.257	3.6701	1.1132	1.177	1.2318	1.1796
CEC10	Mean	5.8004	20.327	19.9744	19.1228	15.8228	21.1176	20.5397	20.9998	19.6332	4.2985
	Std.	7.9161	3.6503	4.9802	5.7526	8.9673	0.51525	3.7005	0.000733	4.3111	6.833
	Best	1	1	1.0836	2.1551	1.0044	18.764	1	20.9961	5.8547	1
	Worst	21.3698	21	21.3918	21.1417	21.209	21.4353	21.4105	21	21.0587	21.3619
Number of best hits		2	0	0	0	1	2	2	0	0	3
Hit rate (%)		20	0	0	0	10	20	20	0	0	30

in the Appendix A. The mean and standard deviation of fitness are considered the key indicators to determine the best performance. The lowest mean value is considered as the best performance, but the lowest standard deviation is selected if their mean values are equal (the best performance techniques are highlighted in bold). A hit rate is used to determine the overall best performance to count how many times the individual optimization technique achieves the best performance score from the total number of test functions [23]. A fitness value below ${10}^{-12}$ is normally assumed to be 0 in [43,47] for simplification purposes. However, this criterion misleads the selection of best performance and causes confusion in the comparison, especially for those very competitive optimization techniques. Therefore, the actual mean values used are those presented in the tables.

Table 4. Performance comparison of classical test functions.

Function	JSO	PSO	GWO	LSA	HBJSA	RSO	ACO	BBO	CHIO	HJSPSO
F1	1	1	1	1	1	1	1	1	1	1
F2	1	8	1	10	1	9	1	1	7	1
F3	9	6	5	8	1	1	7	9	10	1
F4	8	6	4	7	1	1	5	9	10	1
F5	5	7	3	9	1	2	8	6	10	4
F6	1	1	8	1	1	10	1	7	9	1
F7	1	1	8	1	1	9	1	1	10	1
F8	1	1	1	1	1	1	1	9	10	1
F9	2	4	8	3	5	10	6	7	9	1
F10	2	3	8	4	7	10	5	6	9	1
F11	3	1	9	4	8	10	1	6	7	5
F12	7	4	3	5	1	1	8	9	10	6
F13	5	8	3	6	1	1	7	9	10	4
F14	6	8	4	7	1	1	5	9	10	3
F15	8	5	4	7	1	1	6	9	10	1
F16	1	8	6	2	3	7	5	9	10	4
F17	1	3	6	4	8	7	2	9	10	5
F18	1	6	10	4	1	7	8	9	5	1
F19	1	1	9	1	1	10	7	6	8	1
F20	1	1	1	1	1	1	1	1	10	1
F21	1	1	8	1	1	10	1	7	9	1
F22	6	9	1	10	1	1	7	8	5	1
F23	7	8	9	5	2	10	4	3	1	6
F24	1	1	9	1	1	10	1	7	8	1
F25	3	9	8	6	1	10	7	5	2	4
F26	3	8	9	7	1	10	5	6	2	4
F27	1	1	1	9	1	1	10	1	8	1
F28	2	2	8	2	2	10	2	1	9	2
F29	1	1	1	1	1	1	1	1	10	1
F30	1	1	1	1	1	1	1	9	10	1
F31	1	7	10	4	2	9	5	5	8	3
F32	5	5	9	1	4	8	1	7	10	1
F33	2	6	10	4	3	7	9	5	8	1
F34	1	9	5	6	1	10	8	7	4	1
F35	2	9	5	6	1	10	7	8	4	2
F36	2	8	4	6	2	10	9	7	5	1
F37	2	5	9	3	4	10	8	7	6	1
F38	2	4	9	3	7	10	5	6	8	1
F39	2	2	9	2	2	10	2	1	8	2
F40	2	7	8	9	3	10	6	5	4	1
F41	1	8	1	7	1	1	6	9	10	1
F42	4	9	6	10	1	2	5	7	8	3
F43	2	6	7	9	3	10	8	4	5	1
F44	5	4	9	6	2	10	1	3	8	7
F45	1	1	7	1	1	10	1	9	8	1
F46	1	8	7	6	1	10	5	9	4	1
F47	1	6	7	8	3	10	2	9	4	5
F48	1	1	8	1	6	10	5	7	9	1
F49	1	9	4	7	6	10	5	8	3	2
F50	2	9	6	5	8	10	4	7	3	1
No. best hits	23	14	9	13	29	15	13	8	2	32
Hit rate (%)	46	28	18	26	58	30	26	16	4	64

and

Table 5. Performance comparison of CEC-C06 2019 test functions.

Function	JSO	PSO	GWO	LSA	HBJSA	RSO	ACO	BBO	CHIO	HJSPSO
CEC01	5	7	4	6	2	1	8	9	10	3
CEC02	4	6	5	8	2	1	9	7	10	3
CEC03	4	2	5	3	8	10	9	7	6	1
CEC04	1	8	6	9	7	10	2	4	5	3
CEC05	2	7	9	8	4	10	3	6	5	1
CEC06	2	6	7	9	1	10	4	5	8	3
CEC07	2	9	5	8	6	10	1	7	4	3
CEC08	3	8	4	7	9	10	1	6	5	2
CEC09	1	6	4	9	8	10	2	3	7	5
CEC10	2	7	6	4	3	10	8	9	5	1
No. best hits	2	0	0	0	1	2	2	0	0	3
Hit rate (%)	20	0	0	0	10	20	20	0	0	30

are used to simplify the presentation by ranking the techniques based on their performance, where the same rank is given if they share the same mean and standard deviation values. In the tables, the optimization techniques that provide the best solution (i.e., first rank) are highlighted in bold.

Table 4 clearly shows that the exploration capability of HJSPSO is superior to its competitors in solving 22 out of 33 multimodal classical test functions (F18–F50) with the best solution, while the rest solved as follows: HBJSA (17/33), JSO (16/33), PSO (9/33), LSA (9/33), ACO (8/33), GWO (6/33), RSO (6/33), BBO (5/33), and CHIO (1/33). At the same time, HJSPSO demonstrates better exploitation capability compared to the other eight optimization techniques in solving 10 functions out of 17 unimodal test functions (F1–F17) with the best solution, while the rest solved as follows: RSO (9/17), JSO (7/17), ACO (5/17), PSO (5/17), LSA (4/17), GWO (3/17), BBO (3/17), and CHIO (1/17). In this case, HBJSA shows better exploitation when performed in 12 of the 17 unimodal test functions compared to HJSPSO, which had an advantage in only two functions. Note that HBJSA and HJSPSO provide similar solutions in eight of the test functions. In other words, HJSPSO has better exploitation than HBJSA in two other functions (F9 and F10), where it is solely the best performer in solving the functions, whereas HBJSA shares the same best performance with RSO in three different test functions (F12–F14). HBJSA secures the first rank only in one function (F5). Therefore, HJSPSO has a good and unique exploitation capability. Apart from the above results, HJSPSO has shown superiority in solving large-scale, shifted, and rotated benchmark test functions (CEC-C06 2019) compared to other optimization techniques after providing the best solution in three functions out of 10, while the rest solved as follows (Table 5): JSO (2/10), RSO (2/10), ACO (2/10), HBJSA (1/10), PSO (0/10), GWO (0/10), LSA (0/10), BBO (0/10), and CHIO (0/10). Although HBJSA is a good competitor, as it secured the first and second places for the classical test functions, it is far behind HJSPSO in terms of solving the large-scale test functions.

Overall, HJSPSO outperforms the other optimization techniques by securing the first rank in the classical and large-scale benchmark test functions. This outcome clearly indicates the ability of HJSPSO to efficiently solve unimodal, multimodal, separate, nonseparable, rotated, and shifted composite functions. HJSPSO attains 64% of the hit rate, higher than all the competing techniques in the classical benchmark test functions: HBJSA (58%), JSO (46%), RSO (30%), PSO (28%), LSA (26%), ACO (26%), GWO (18%), BBO (16%), and CHIO (4%). On the other hand, the HJSPSO attains 30% of the hit rate in the large-scale benchmark test functions, higher than JSO (20%), RSO (20%), ACO (20%), HBJSA (10%), PSO (0%), GWO (0%), LSA (0%), BBO (0%), and CHIO (0%). Therefore, HJSPSO can be considered a robust metaheuristic optimization technique based on its ability to explore the search space and exploit unvisited areas in the search space to avoid the local optimum and find a better solution efficiently [23].

5.4. Convergence Performance Analysis

Six functions are selected from the benchmark test functions where two functions are randomly taken to represent the main three categories: unimodal (F7 and F9), multimodal (F33 and F50), and large-scale (CEC03 and CEC10). The convergence curves of HJSPSO and other optimization techniques in solving the selected benchmark functions are shown in Figure 2. The figure shows that HJSPSO has faster convergence in most cases compared to other optimization techniques. A notable ability of HJSPSO to exploit the promising areas can be observed in its solving of the unimodal benchmark functions (F7 and F9). Likewise, HJSPSO demonstrates the ability to escape quickly from the local optimum when solving the multimodal functions (F33, F50, CEC03, CEC10). It is important to note that PSO has good performance at the beginning because it converges fast, but there is no improvement in the later period. This behavior can be considered as premature convergence, which PSO is unable to exploit for a better solution. On the other hand, JSO has shown good exploitation in the unimodal test functions where the optimal solution is improved slowly until it reaches maximum iteration. Therefore, a combination of JSO and PSO in the form of HJSPSO, supported by some modifications, improved the performance significantly.

A computational time analysis of the obtained results in Figure 2 is carried out to explain the time complexity of HJSPSO compared to other optimization techniques.

Table 6. Time complexity analysis of the selected test functions.

Technique	Time Taken per Iteration (ms)						Convergence Point (Iteration)
	F7	F9	F33	F50	CEC03	CEC10	F7	F9	F33	F50	CEC03	CEC10
JSO	0.228	0.255	0.216	0.475	0.957	0.883	183	2989	2978	1750	2998	2115
PSO	1.329	2.218	1.531	1.519	2.980	3.049	114	3000	2969	2034	324	714
GWO	0.359	0.344	0.362	0.595	0.756	0.646	2997	2999	2999	3000	3000	1999
LSA	1.367	3.490	3.792	6.153	16.40	7.193	37	2998	1059	225	397	522
HBJSA	0.344	0.316	0.438	0.482	1.076	1.043	435	2198	2231	2238	403	2163
RSO	0.147	0.123	0.126	0.233	0.507	0.524	1933	2321	2359	2597	2913	1369
ACO	1.162	2.674	2.676	3.249	10.47	9.009	38	3000	3000	2315	2447	169
BBO	0.719	1.437	1.548	2.239	5.988	4.252	724	2999	3000	2605	2960	2939
CHIO	1.064	1.049	1.127	1.109	2.666	2.522	2800	2322	2903	2922	2869	2997
HJSPSO	0.268	0.255	0.233	0.467	0.870	1.001	229	2971	1616	1755	2994	2367

shows a computational time and convergence point for each optimization technique in solving the selected six benchmark test functions. The results generally show that HJSPSO has a slightly higher computational time than JSO due to a combination with PSO. On a positive note, the computational time of HJSPSO is significantly less than PSO. This computational performance of HJSPSO can be achieved because it alternates between the operators of JSO and PSO instead of cascading them. A convergence point is also important to give the actual time taken to obtain the optimal solution. Although LSA shows high computational burden, it is usually converged at the lowest iteration, which leads to a significantly low time taken if it stops at the convergence point. In this perspective, HJSPSO is almost similar to most of the selected optimization techniques with less computational time. Accordingly, HJSPSO gives better results for the time taken compared to the optimization techniques.

5.5. Nonparametric Statistical Test

The performance of metaheuristic techniques is normally evaluated using basic statistics such as mean value, standard deviation, best fitness, and worst fitness, as presented earlier. However, this evaluation method requires a more accurate statistical test [48]. The best-performing technique should give a mean value that is as small (i.e., minimization problems) as possible and a standard deviation of 0. It is difficult to decide which one has better performance when one of the techniques has a slightly small mean value but higher standard deviation. As an alternative, a nonparametric statistical test is used to evaluate the performance of metaheuristic techniques. The statistical test is considered more suitable for metaheuristic techniques owing to their stochastic behavior [49]. The nonparametric statistical test can be divided into two types: (i) pairwise comparison and (ii) multiple comparisons. Pairwise comparison is used to compare two techniques, whereas multiple comparisons are used for more than two techniques [49]. Two well-known nonparametric tests are used, namely, Wilcoxon signed-rank test (pairwise comparison) and Friedman test (multiple comparisons). Only the large-scale (CEC-C06 2019) benchmark test functions are used to highlight the effectiveness of HJSPSO in this section.

The Wilcoxon signed-rank test is based on the significance level $\alpha$ at 5%. If the p value is higher than $\alpha$, a null hypothesis $H_0$ is confirmed where there is no difference between HJSPSO and the compared optimization technique. Otherwise, when the p value is less than or equal to $\alpha$, an alternative hypothesis $H_1$ is confirmed where a significant difference is found between the two optimization techniques.

Table 7. Statistical results of Wilcoxon signed–ranked test.

Function	JSO	PSO	GWO	LSA	HBJSA	RSO	ACO	BBO	CHIO
CEC01	$9\times {10}^{-6}$	$2\times {10}^{-6}$	0.943	$2\times {10}^{-6}$	$2\times {10}^{-6}$	$2\times {10}^{-6}$	$2\times {10}^{-6}$	$2\times {10}^{-6}$	$2\times {10}^{-6}$
CEC02	$3\times {10}^{-6}$	$2\times {10}^{-6}$	$7\times {10}^{-6}$	$2\times {10}^{-6}$	$4\times {10}^{-5}$	$6\times {10}^{-6}$	$2\times {10}^{-6}$	$2\times {10}^{-6}$	$2\times {10}^{-6}$
CEC03	$2\times {10}^{-6}$	0.053	0.002	0.059	$2\times {10}^{-6}$	$2\times {10}^{-6}$	$2\times {10}^{-6}$	$5\times {10}^{-5}$	$2\times {10}^{-6}$
CEC04	$8\times {10}^{-5}$	$6\times {10}^{-5}$	0.079	$2\times {10}^{-6}$	$2\times {10}^{-6}$	$2\times {10}^{-6}$	0.015	0.393	0.658
CEC05	0.704	$2\times {10}^{-6}$	$2\times {10}^{-6}$	$3\times {10}^{-6}$	0.001	$2\times {10}^{-6}$	0.043	$4\times {10}^{-6}$	$8\times {10}^{-5}$
CEC06	0.544	0.045	$5\times {10}^{-4}$	$4\times {10}^{-6}$	0.171	$2\times {10}^{-6}$	0.688	0.382	$2\times {10}^{-6}$
CEC07	0.003	$2\times {10}^{-6}$	0.002	$2\times {10}^{-6}$	$3\times {10}^{-6}$	$2\times {10}^{-6}$	$1\times {10}^{-5}$	$5\times {10}^{-5}$	0.910
CEC08	0.910	$2\times {10}^{-6}$	$3\times {10}^{-5}$	$5\times {10}^{-6}$	$2\times {10}^{-6}$	$2\times {10}^{-6}$	0.471	$2\times {10}^{-6}$	$2\times {10}^{-6}$
CEC09	$2\times {10}^{-4}$	0.229	0.052	$5\times {10}^{-6}$	$3\times {10}^{-6}$	$2\times {10}^{-6}$	0.072	0.03	$2\times {10}^{-5}$
CEC10	0.295	$7\times {10}^{-6}$	$2\times {10}^{-5}$	$9\times {10}^{-6}$	$2\times {10}^{-4}$	$2\times {10}^{-6}$	$3\times {10}^{-6}$	$5\times {10}^{-6}$	$6\times {10}^{-6}$

presents the p values of HJSPSO compared to the nine other optimization techniques in solving the CEC-C06 2019 benchmark test functions. HJSPSO scores p values higher than $\alpha$ or the alternative hypothesis $H_1$ in most cases and only a few cases are null hypotheses $H_0$ (bold). This finding indicates that the reported performance of HJSPSO in Section 5.3 is significantly different from the existing optimization techniques, especially with RSO when all test functions are less than 5%. Furthermore, HJSPSO is improved significantly compared to the original JSO and PSO when the majority of test functions are $H_1$.

The Friedman test is likewise used to compare the performance of HJSPSO with all the selected optimization techniques. The lowest value in the Friedman test indicates the best performance among the selected techniques.

Table 8. Statistical results of the Friedman test.

Function	JSO	PSO	GWO	LSA	HBJSA	RSO	ACO	BBO	CHIO	HJSPSO
CEC01	5.60	7.00	3.63	6.13	2.03	1.12	7.47	8.47	10	3.55
CEC02	5.20	6.03	5.57	6.93	2.17	1.17	7.93	7.20	10	2.80
CEC03	5.83	2.43	4.90	2.42	8.43	8.93	8.40	4.87	6.40	2.35
CEC04	2.28	6.60	5.30	7.95	7.00	9.97	0.48	4.58	4.53	4.30
CEC05	2.62	6.17	8.53	6.43	4.67	10	3.45	5.60	5.20	2.33
CEC06	3.38	4.73	6.20	7.77	3.30	10	3.38	4.77	7.93	3.53
CEC07	2.33	7.50	5.33	7.60	6.77	9.73	1.57	6.77	3.83	3.57
CEC08	2.57	6.43	5.13	6.37	8.10	9.93	1.80	6.23	6.10	2.33
CEC09	2.67	5.07	3.23	7.77	7.97	9.40	3.70	3.40	6.77	4.50
CEC10	3.08	3.52	8.30	4.32	5.73	8.17	9.17	4.67	5.63	2.42

shows scores using the Friedman test, where the first ranks are in bold. It clearly shows that HJSPSO secured the highest number of first ranks (3/10), which is like the hit rate in the previous subsection. This confirms the previous performance evaluation and accepts that HJSPSO outperforms other selected optimization techniques.

5.6. Case Study: Traveling Salesman

A simple traveling salesman problem (TSP) is used to find the shortest route for visiting all cities u, as given in

Table 9. Coordinates of cities in a sample TSP [19].

Cities	Coordinates		Cities	Coordinates		Cities	Coordinates		Cities	Coordinates
	$\mathit{x}$	$\mathit{y}$		$\mathit{x}$	$\mathit{y}$		$\mathit{x}$	$\mathit{y}$		$\mathit{x}$	$\mathit{y}$
1	4.38	7.51	6	4.89	9.59	11	2.76	8.4	16	4.98	3.49
2	3.81	2.55	7	4.45	5.47	12	6.79	2.54	17	9.59	1.96
3	7.65	5.05	8	6.46	1.38	13	6.55	8.14	18	3.4	2.51
4	7.9	6.99	9	7.09	1.49	14	1.62	2.43	19	5.85	6.16
5	1.86	8.9	10	7.54	2.57	15	1.19	9.29	20	2.23	4.73

[19]. The control variable in this problem is to decide whether to travel between the i-th city ($u_i$) and the j-th city ($u_j$) or not as given by the following expression:

$$c_{ij}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{there}\mathrm{is}\mathrm{a}\mathrm{path}\mathrm{between}{u}_i\mathrm{and}{u}_j\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(15)

The objective is to minimize the total traveling distance, subject to the condition of visiting each city only once and then returning to the initial city where the trip began [19] as follows:

$$\begin{array}{c}{f}_{tsp}=\min \left(\sum _{i=1}^{nc}\sum _{i\ne j,j=1}^{nc}{d}_{ij}{c}_{ij}\right)\end{array}$$

(16)

$$\begin{array}{c}{d}_{ij}=\sqrt{[{(u_i\left(x\right)-u_j\left(x\right)]}^2+{[u_i\left(y\right)-u_j\left(y\right)]}^2}\end{array}$$

(17)

subject to

$$\begin{array}{c}\sum _{i=1,i\ne j}^{nc}{c}_{ij}=1,\forall j\end{array}$$

(18)

$$\begin{array}{c}\sum _{j=1,j\ne i}^{nc}{c}_{ij}=1,\forall i\end{array}$$

(19)

$$\begin{array}{c}\sum _{i\in Q}\sum _{j\ne i,j\in Q}{c}_{ij}\le \left|Q\right|-1,\forall Q⊊\{1,\dots ,nc\},\left|Q\right|\ge 2\end{array}$$

(20)

The optimization techniques were executed for 30 runs like in the previous analysis, but the total number of iterations T and population size N were set to 500 and 50, respectively. The results show that HJSPSO outperforms other optimization techniques and gives the lowest best, worst, and mean fitness values (bold) as tabulated in

Table 10. Optimization performance in solving TSP.

Indicator	JSO	PSO	GWO	LSA	HBJSA	RSO	ACO	BBO	CHIO	HJSPSO
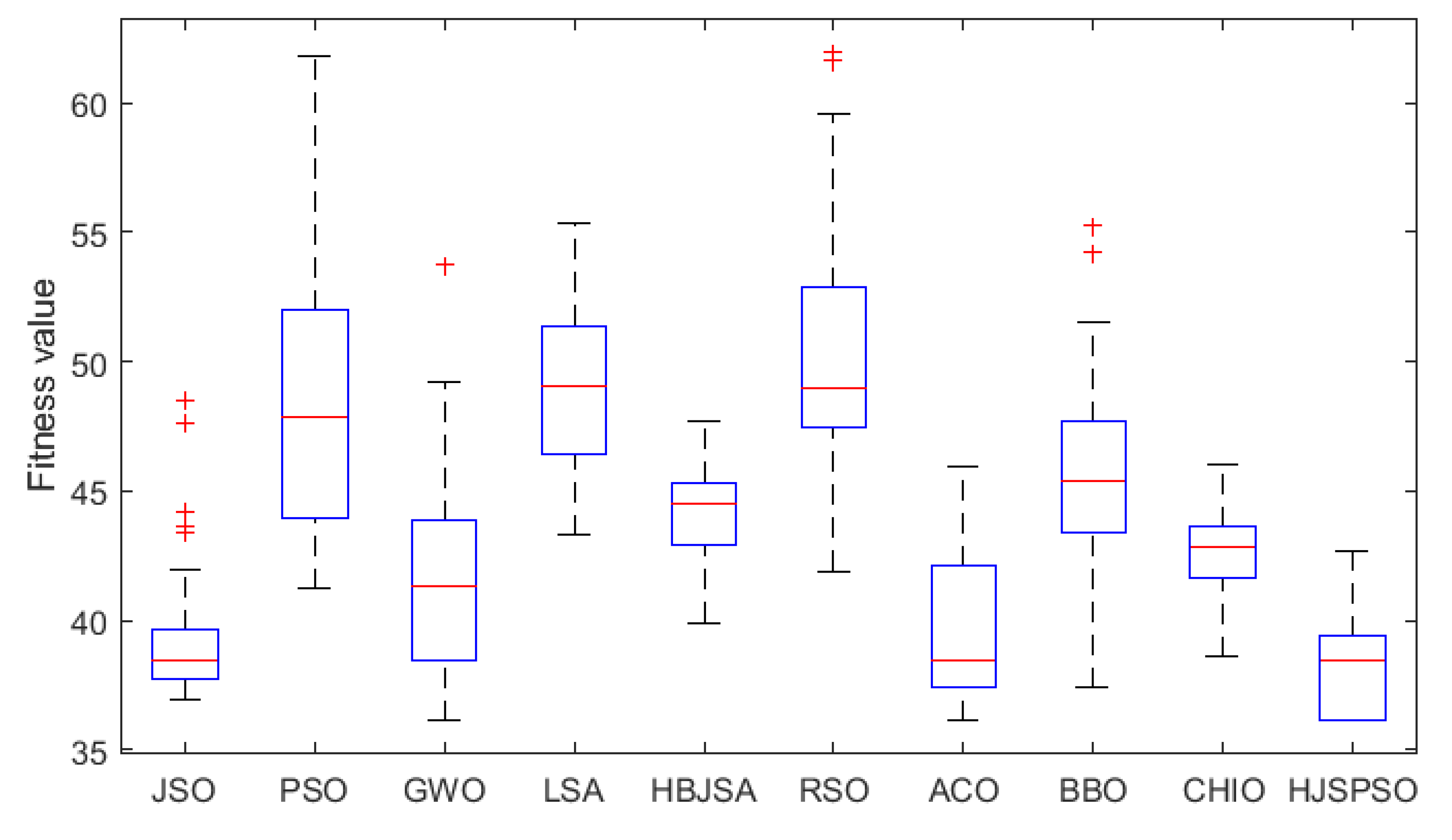
Mean	39.67	48.84	41.83	48.94	44.08	50.42	39.51	45.71	42.61	37.87
Std.	2.98	5.08	4.00	3.35	1.80	5.51	2.58	4.16	1.53	1.87
Best	36.97	41.22	36.12	43.32	39.90	41.91	36.12	37.42	38.60	36.12
Worst	48.47	61.80	53.77	55.33	47.70	61.98	45.93	55.26	46.05	45.36

. However, HJSPSO is behind CHIO and HBJSA in terms of standard deviation. The performance comparison can also be presented in a statistical box plot as in Figure 3, where the red + represents outliers. In this case, HJSPSO has shown the best fitness within the box without any outliers. Therefore, HJSPSO can be considered as having the best performance among the optimization techniques. Figure 4 shows the shortest path obtained by the optimization techniques where HJSPSO provides the best shortest distance at 36.12. The solution is the same for GWO and ACO, but their starting points are different (HJSPSO at 3, ACO at 7, and GWO at 13). Nevertheless, the solutions provided by HJSPSO are more accurate and precise than GWO and ACO because HJSPSO gives significantly lower mean and standard deviation values.

6. Conclusions

This paper presents a novel HJSPSO that is based on JSO to benefit from the advantage of its exploitation (local search) capability and adopted a PSO operator to tackle exploration (global search). The movement of following the ocean current in JSO is replaced with a PSO operator and the movement of swimming inside the swarm uses a operator with some modifications. A time control mechanism is used to switch between the two operators to gain a good balance between exploration and exploitation. The effectiveness of HJSPSO was tested using a set of 50 classical and 10 large-scale (CEC-C06 2019) benchmark test functions and compared with 9 well-known metaheuristic optimization techniques, including PSO and JSO. In addition, a case study of TSP is used to demonstrate the effectiveness of HJSPSO in solving a nonconvex optimization problem. The results show that HJSPSO contributes in terms of exploration and exploitation improvements compared to the existing JSO and PSO techniques, where it ultimately secures the first rank in 64% and 30% of the classical and large-scale benchmark test functions, respectively. The Wilcoxon signed-ranked and Friedman rank tests also confirm that HJSPSO is significantly improved in obtaining the optimal solution for the complex optimization problems (large-scale benchmark test functions). In the TSP case study, HJSPSO outperforms the other selected optimization techniques at the first rank in finding the shortest distance between 20 cities after providing the lowest mean and best fitness at 38.82 and 36.12, respectively. The results clearly show that HJSPSO is a robust technique that can be applied to most optimization problems. Nevertheless, this work can be extended by conducting a sensitivity analysis on the parameter settings to provide the highest performance. Afterwards, HJSPSO can be applied in a real-world setting, especially in solving nonlinear and nonconvex power system problems, such as optimal power flow, transmission line planning, electric vehicle scheduling, and economic load dispatch.