Fuzzy Analytic Network Process with Principal Component Analysis to Establish a Bank Performance Model under the Assumption of Country Risk
Abstract
:1. Introduction
2. Literature Review
2.1. Country Risk Assessment
2.2. Bank Performance and Country Risk
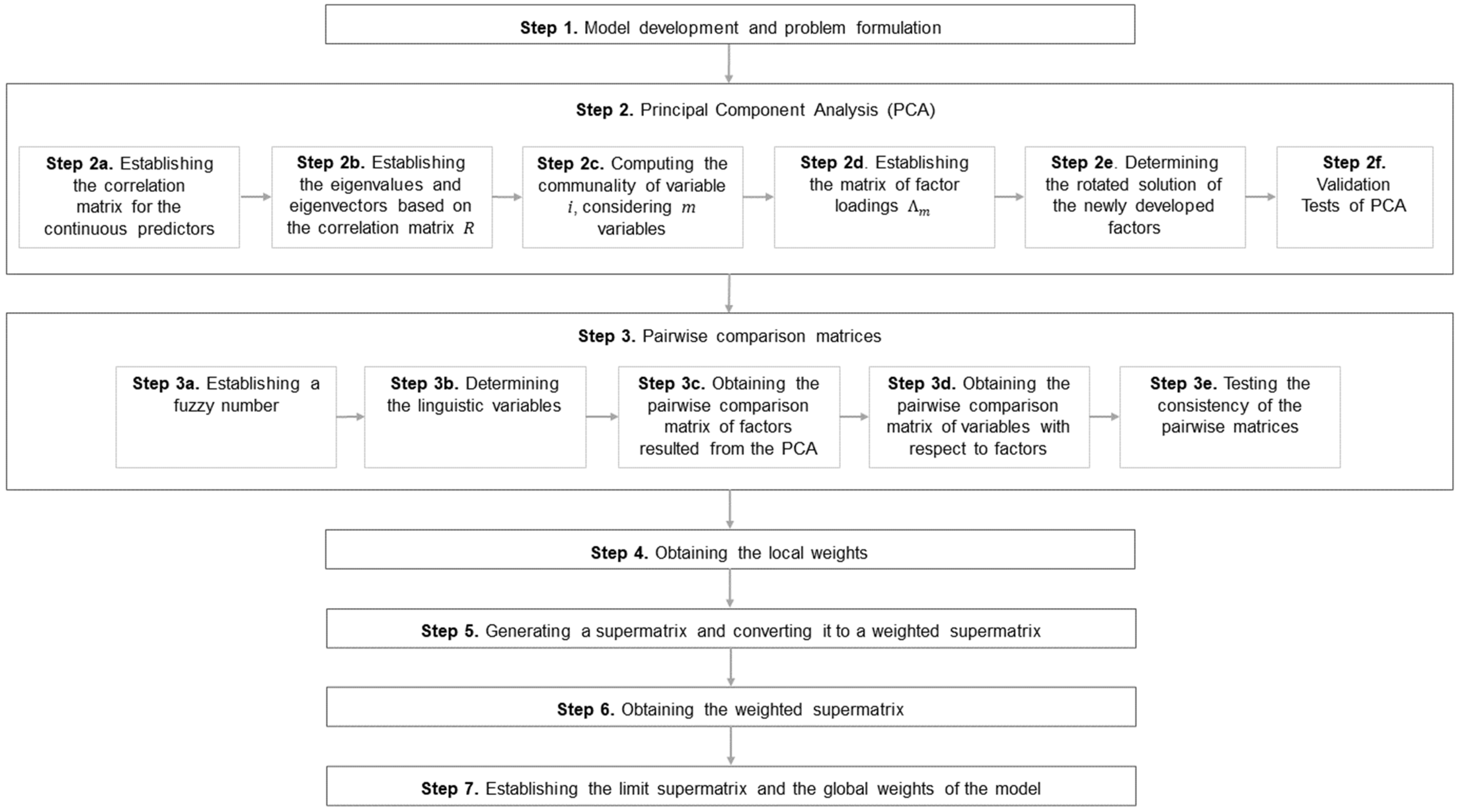
3. Method
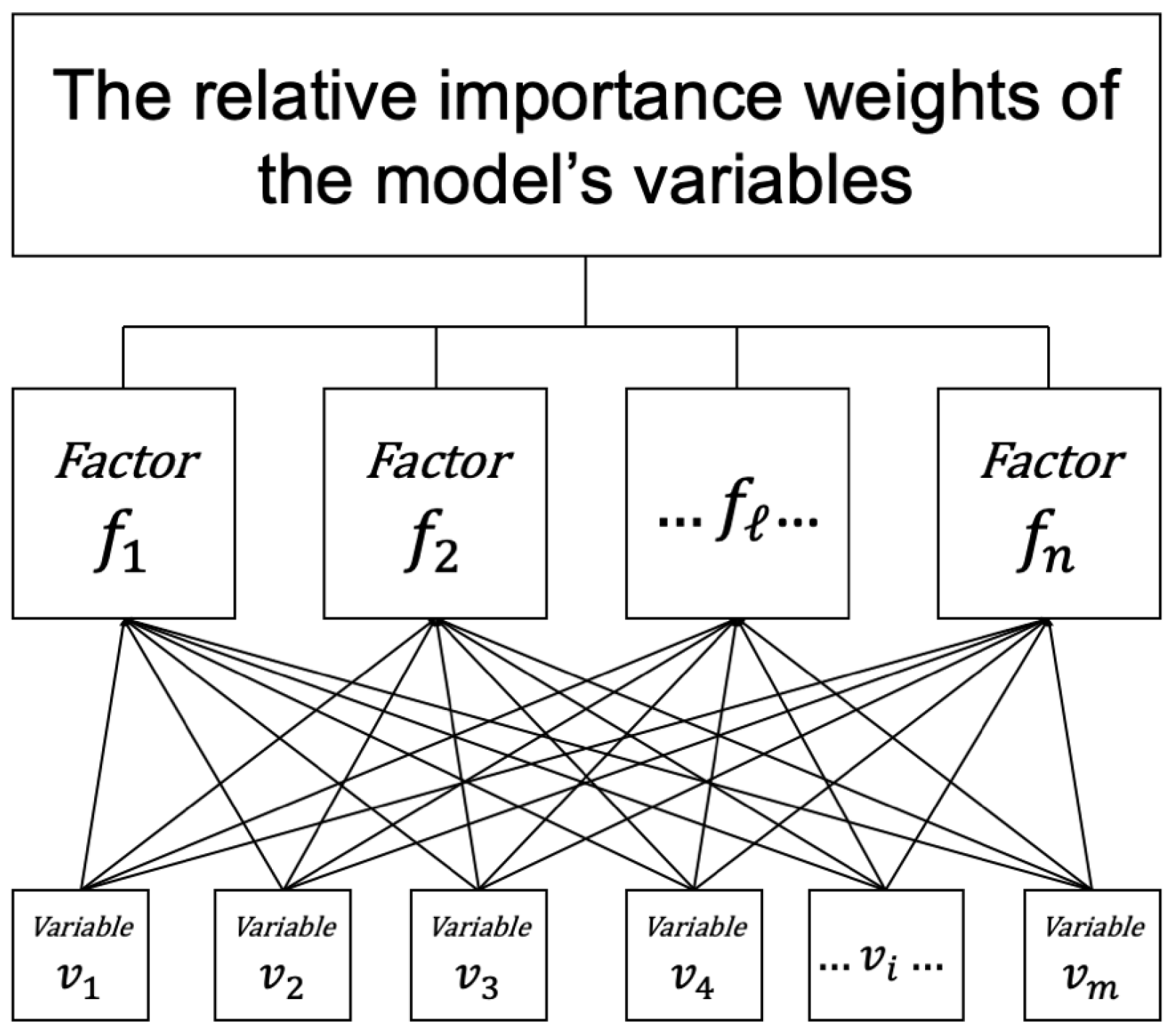
3.1. Proposed Method of Fuzzy-ANP with PCA
- Step 1. Model development and problem formulation
- Step 2. Principal Component Analysis (PCA)
- Step 2a. Establishing the correlation matrix for the continuous predictors
- Step 2b. Establishing the eigenvalues and eigenvectors based on the correlation matrix R
- Step 2c. Computing the communality of variable i, considering m variables
- Step 2e. Determining the rotated solution of the newly developed factors
- Step 2f. Validation Tests of PCA
- Step 3. Pairwise comparison matrices
- Step 3a. Establishing a fuzzy number
- Step 3b. Determining the linguistic variables
- Step 3c. Obtaining the pairwise comparison matrix of factors resulted from the PCA
- Step 3e. Testing the consistency of the pairwise matrices
- Step 4. Obtaining the local weights
- Step 5. Generating a supermatrix and converting it to a weighted supermatrix
- Step 6. Obtaining the weighted supermatrix
- Step 7. Establishing the limit supermatrix and the global weights of the model
3.2. Method for Country Risk Assessment
3.2.1. Extracting Country Risk Factors with PCA
3.2.2. Constructing Pairwise Comparison Matrices for Factors and Variables: Obtaining the Local Weights for the Country Risk Model
3.2.3. Determining the Unweighted Supermatrix and Converting It to a Weighted Supermatrix
3.2.4. Establishing the Limit Supermatrix and the Global Weights for the Country Risk Model
3.3. Method for Bank Performance Model under the Assumption of Country Risk
| Description | Mean | SD | |||||
|---|---|---|---|---|---|---|---|
| 7.83 b | −0.12 b | ROA | Ratio of net profit to total assets (%, 4-year average) | 1.12 | 0.62 | ||
| 14 a | 0.25 a | AQ | Ratio of impaired loans to gross loans (%, 4-year average) | 2.17 | 3.34 | ||
| 5 a | −0.25 a | E&P | Ratio of operating profit to risk-weighted assets (%, 4-year average) | 4.14 | 36.78 | ||
| 22 a | 6 a | C&L | Core capital ratio (%) | 15.09 | 4.54 | ||
| 250 a | 45 a | F&L | Ratio of loans to customer deposits (%, 4-year average) | 109.20 | 63.12 | ||
| 29.14 b | 18.94 b | SIZE | Natural logarithm of total assets (%, 4-year average) | 23.19 | 1.98 | ||
| 46.65 b | 2.46 b | EQUITY | Ratio of equity to total assets (%, 4-year average) | 10.71 | 3.39 | ||
| 13.55 b | −15.70 b | GDP | GDP growth rate of the country (%) | 2.07 | 3.89 | ||
| 64.27 b | 2 | INF | Inflation rate of the country (%) | 4.66 | 5.96 |
3.3.1. Extracting Bank Performance Factors with PCA
3.3.2. Constructing the Pairwise Comparison Matrices for Factors and Variables: Obtaining Local Weights for the Bank Performance Model under the Assumption of Country Risk
3.3.3. Determining the Unweighted Supermatrix and Converting It to a Weighted Supermatrix
3.3.4. Establishing the Limit Supermatrix and the Global Weights of the Bank Performance Model under Assumption of Country Risk
4. Empirical Analysis and Results
4.1. Country Risk Model
4.1.1. Extracting the Country Risk Factors with PCA
4.1.2. Constructing Pairwise Comparison Matrices, and Obtaining Local Weights for the Country Risk Model
4.1.3. Determining the Supermatrices for the Country Risk Model
4.1.4. Establishing the Limit Supermatrix and the Global Weights of the Country Risk Model
4.2. Bank Performance Model under the Assumption of Country Risk
4.2.1. Extracting Bank Performance Factors with PCA
4.2.2. Constructing the Pairwise Comparison Matrices and Obtaining Local Weights for the Bank Performance Model
4.2.3. Determining Supermatrices for the Bank Performance Model
4.2.4. Establishing the Limit Supermatrix and the Global Weights of the Bank Performance Model under Country Risk Assumption
4.3. Exemplification of Bank Performance Model under the Assumption of Country Risk
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 1 | 2 | 2 | 1/2 | 1/4 | 1/3 | 2 | 2 | 1/2 | 1/4 | 1/3 | 1/3 | 1/4 | 1/3 | 1/4 | 3 | 1/2 | |
| 1/2 | 1 | 2 | 1/2 | 1/5 | 1/4 | 1/2 | 2 | 1/2 | 1/5 | 1/4 | 1/4 | 1/5 | 1/4 | 1/4 | 3 | 1/2 | |
| 1/2 | 1/2 | 1 | 1/3 | 1/6 | 1/6 | 1/2 | 1/2 | 1/2 | 1/6 | 1/6 | 1/5 | 1/6 | 1/5 | 1/6 | 2 | 1/3 | |
| 2 | 2 | 3 | 1 | 1/3 | 1/2 | 2 | 3 | 2 | 1/3 | 1/2 | 1/2 | 1/3 | 1/2 | 1/3 | 4 | 2 | |
| 4 | 5 | 6 | 3 | 1 | 2 | 4 | 5 | 4 | 2 | 2 | 2 | 1/2 | 2 | 2 | 9 | 3 | |
| 3 | 4 | 6 | 2 | 1/2 | 1 | 4 | 4 | 3 | 1/2 | 1/2 | 2 | 1/2 | 2 | 1/2 | 8 | 3 | |
| 1/2 | 2 | 2 | 1/2 | 1/4 | 1/4 | 1 | 2 | 1/2 | 1/4 | 1/4 | 1/3 | 1/4 | 1/3 | 1/4 | 3 | 1/2 | |
| 1/2 | 1/2 | 2 | 1/3 | 1/5 | 1/4 | 1/2 | 1 | 1/2 | 1/5 | 1/5 | 1/4 | 1/5 | 1/4 | 1/5 | 2 | 1/2 | |
| 2 | 2 | 2 | 1/2 | 1/4 | 1/3 | 2 | 2 | 1 | 1/4 | 1/3 | 1/3 | 1/4 | 1/3 | 1/3 | 3 | 1/2 | |
| 4 | 5 | 6 | 3 | 1/2 | 2 | 4 | 5 | 4 | 1 | 2 | 2 | 1/2 | 2 | 2 | 9 | 3 | |
| 3 | 4 | 6 | 2 | 1/2 | 2 | 4 | 5 | 3 | 1/2 | 1 | 2 | 1/2 | 2 | 1/2 | 8 | 3 | |
| 3 | 4 | 5 | 2 | 1/2 | 1/2 | 3 | 4 | 3 | 1/2 | 1/2 | 1 | 1/2 | 1/2 | 1/2 | 7 | 3 | |
| 4 | 5 | 6 | 3 | 2 | 2 | 4 | 5 | 4 | 2 | 2 | 2 | 1 | 2 | 2 | 9 | 3 | |
| 3 | 4 | 5 | 2 | 1/2 | 1/2 | 3 | 4 | 3 | 1/2 | 1/2 | 2 | 1/2 | 1 | 1/2 | 7 | 3 | |
| 4 | 4 | 6 | 3 | 1/2 | 2 | 4 | 5 | 3 | 1/2 | 2 | 2 | 1/2 | 2 | 1 | 9 | 3 | |
| 1/3 | 1/3 | 1/2 | 1/4 | 1/9 | 1/8 | 1/3 | 1/2 | 1/3 | 1/9 | 1/8 | 1/7 | 1/9 | 1/7 | 1/9 | 1 | 1/4 | |
| 2 | 2 | 3 | 1/2 | 1/3 | 1/3 | 2 | 2 | 2 | 1/3 | 1/3 | 1/3 | 1/3 | 1/3 | 1/3 | 4 | 1 |
| (1, 1, 1) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | |
| (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1/6, 1/5, 1/4) | (1/5, 1/4, 1/3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 1, 1) | (1/4, 1/3, 1/2) | (1/7, 1/6, 1/5) | (1/7, 1/6, 1/5) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | |
| (1, 2, 3) | (1, 2, 3) | (2, 3, 4) | (1, 1, 1) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1, 2, 3) | (2, 3, 4) | (1, 2, 3) | |
| (3, 4, 5) | (4, 5, 6) | (5, 6, 7) | (2, 3, 4) | (1, 1, 1) | (1, 2, 3) | (3, 4, 5) | (4, 5, 6) | (3, 4, 5) | |
| (2, 3, 4) | (3, 4, 5) | (5, 6, 7) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 1, 1) | (3, 4, 5) | (3, 4, 5) | (2, 3, 4) | |
| (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (1, 1, 1) | (1, 2, 3) | (1/3, 1/2, 1) | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/4, 1/3, 1/2) | (1/6, 1/5, 1/4) | (1/5, 1/4, 1/3) | (1/3, 1/2, 1) | (1, 1, 1) | (1/3, 1/2, 1) | |
| (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1, 2, 3) | (1, 2, 3) | (1, 1, 1) | |
| (3, 4, 5) | (4, 5, 6) | (5, 6, 7) | (2, 3, 4) | (1/3, 1/2, 1) | (1, 2, 3) | (3, 4, 5) | (4, 5, 6) | (3, 4, 5) | |
| (2, 3, 4) | (3, 4, 5) | (5, 6, 7) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (3, 4, 5) | (4, 5, 6) | (2, 3, 4) | |
| (2, 3, 4) | (3, 4, 5) | (4, 5, 6) | (1, 2, 3) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (2, 3, 4) | (3, 4, 5) | (2, 3, 4) | |
| (3, 4, 5) | (4, 5, 6) | (5, 6, 7) | (2, 3, 4) | (1, 2, 3) | (1, 2, 3) | (3, 4, 5) | (4, 5, 6) | (3, 4, 5) | |
| (2, 3, 4) | (3, 4, 5) | (4, 5, 6) | (1, 2, 3) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (2, 3, 4) | (3, 4, 5) | (2, 3, 4) | |
| (3, 4, 5) | (3, 4, 5) | (5, 6, 7) | (2, 3, 4) | (1/3, 1/2, 1) | (1, 2, 3) | (3, 4, 5) | (4, 5, 6) | (2, 3, 4) | |
| (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1/5, 1/4, 1/3) | (1/9, 1/9, 1/9) | (1/9, 1/8, 1/7) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1/4, 1/3, 1/2) | |
| (1, 2, 3) | (1, 2, 3) | (2, 3, 4) | (1/3, 1/2, 1) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) |
| (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/5, 1/4, 1/3) | (2, 3, 4) | (1/3, 1/2, 1) | (9.8, 15.8333, 23.3333) | 0.0002 | |
| (1/6, 1/5, 1/4) | (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (1/6, 1/5, 1/4) | (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (2, 3, 4) | (1/3, 1/2, 1) | (8.1667, 12.35, 18.4167) | 0.0000 | |
| (1/7, 1/6, 1/5) | (1/7, 1/6, 1/5) | (1/6, 1/5, 1/4) | (1/7, 1/6, 1/5) | (1/6, 1/5, 1/4) | (1/7, 1/6, 1/5) | (1, 2, 3) | (1/4, 1/3, 1/2) | (5.3571, 7.5667, 11.7) | 0.0000 | |
| (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1/4, 1/3, 1/2) | (3, 4, 5) | (1, 2, 3) | (15.3333, 24.3333, 35) | 0.0441 | |
| (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (9, 9, 9) | (2, 3, 4) | (42.3333, 56.5, 71) | 0.1321 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (7, 8, 9) | (2, 3, 4) | (32.6667, 44.5, 58) | 0.1056 | |
| (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/5, 1/4, 1/3) | (2, 3, 4) | (1/3, 1/2, 1) | (9.0333, 14.1667, 21) | 0.0000 | |
| (1/6, 1/5, 1/4) | (1/6, 1/5, 1/4) | (1/5, 1/4, 1/3) | (1/6, 1/5, 1/4) | (1/5, 1/4, 1/3) | (1/6, 1/5, 1/4) | (1, 2, 3) | (1/3, 1/2, 1) | (6.35, 9.5833, 14.75) | 0.0000 | |
| (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (2, 3, 4) | (1/3, 1/2, 1) | (10.5167, 17.4167, 25.5) | 0.0096 | |
| (1, 1, 1) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (9, 9, 9) | (2, 3, 4) | (41.6667, 55, 69) | 0.1290 | |
| (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (7, 8, 9) | (2, 3, 4) | (34.3333, 47, 61) | 0.1117 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 1, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (6, 7, 8) | (2, 3, 4) | (28.3333, 38.5, 51) | 0.0897 | |
| (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 1, 1) | (1, 2, 3) | (1, 2, 3) | (9, 9, 9) | (2, 3, 4) | (43, 58, 73) | 0.1351 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 1, 1) | (1/3, 1/2, 1) | (6, 7, 8) | (2, 3, 4) | (29, 40, 53) | 0.0941 | |
| (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1, 1, 1) | (9, 9, 9) | (2, 3, 4) | (39, 51.5, 65) | 0.1215 | |
| (1/9, 1/9, 1/9) | (1/9, 1/8, 1/7) | (1/8, 1/7, 1/6) | (1/9, 1/9, 1/9) | (1/8, 1/7, 1/6) | (1/9, 1/9, 1/9) | (1, 1, 1) | (1/5, 1/4, 1/3) | (3.9833, 4.8135, 6.7302) | 0.0000 | |
| (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (3, 4, 5) | (1, 1, 1) | (13.3333, 21.1667, 30) | 0.0274 | |
| (371.2071, 518.2302, 687.4302) | ||||||||||
| 1 | 1/2 | 1/2 | 4 | 3 | 3 | 5 | 2 | 1/2 | 7 | 5 | 6 | 7 | 3 | 5 | 8 | 4 | |
| 2 | 1 | 1/2 | 4 | 4 | 4 | 6 | 2 | 2 | 8 | 5 | 7 | 8 | 3 | 6 | 9 | 4 | |
| 2 | 2 | 1 | 4 | 4 | 4 | 6 | 2 | 2 | 9 | 5 | 7 | 8 | 3 | 6 | 9 | 4 | |
| 1/4 | 1/4 | 1/4 | 1 | 1/2 | 1/2 | 2 | 1/3 | 1/4 | 3 | 2 | 2 | 2 | 1/2 | 2 | 3 | 1/2 | |
| 1/3 | 1/4 | 1/4 | 2 | 1 | 1/2 | 2 | 1/3 | 1/4 | 3 | 2 | 2 | 3 | 1/2 | 2 | 3 | 2 | |
| 1/3 | 1/4 | 1/4 | 2 | 2 | 1 | 2 | 1/3 | 1/4 | 3 | 2 | 3 | 3 | 1/2 | 2 | 3 | 2 | |
| 1/5 | 1/6 | 1/6 | 1/2 | 1/2 | 1/2 | 1 | 1/4 | 1/6 | 2 | 1/2 | 2 | 2 | 1/3 | 1/2 | 2 | 1/2 | |
| 1/2 | 1/2 | 1/2 | 3 | 3 | 3 | 4 | 1 | 1/2 | 6 | 4 | 5 | 6 | 2 | 4 | 7 | 3 | |
| 2 | 1/2 | 1/2 | 4 | 4 | 4 | 6 | 2 | 1 | 8 | 5 | 7 | 7 | 3 | 5 | 9 | 4 | |
| 1/7 | 1/8 | 1/9 | 1/3 | 1/3 | 1/3 | 1/2 | 1/6 | 1/8 | 1 | 1/2 | 1/2 | 1/2 | 1/4 | 1/2 | 2 | 1/3 | |
| 1/5 | 1/5 | 1/5 | 1/2 | 1/2 | 1/2 | 2 | 1/4 | 1/5 | 2 | 1 | 2 | 2 | 1/2 | 2 | 2 | 1/2 | |
| 1/6 | 1/7 | 1/7 | 1/2 | 1/2 | 1/3 | 1/2 | 1/5 | 1/7 | 2 | 1/2 | 1 | 2 | 1/3 | 1/2 | 2 | 1/2 | |
| 1/7 | 1/8 | 1/8 | 1/2 | 1/3 | 1/3 | 1/2 | 1/6 | 1/7 | 2 | 1/2 | 1/2 | 1 | 1/3 | 1/2 | 2 | 1/2 | |
| 1/3 | 1/3 | 1/3 | 2 | 2 | 2 | 3 | 1/2 | 1/3 | 4 | 2 | 3 | 3 | 1 | 2 | 4 | 2 | |
| 1/5 | 1/6 | 1/6 | 1/2 | 1/2 | 1/2 | 2 | 1/4 | 1/5 | 2 | 1/2 | 2 | 2 | 1/2 | 1 | 2 | 1/2 | |
| 1/8 | 1/9 | 1/9 | 1/3 | 1/3 | 1/3 | 1/2 | 1/7 | 1/9 | 1/2 | 1/2 | 1/2 | 1/2 | 1/4 | 1/2 | 1 | 1/3 | |
| 1/4 | 1/4 | 1/4 | 2 | 1/2 | 1/2 | 2 | 1/3 | 1/4 | 3 | 2 | 2 | 2 | 1/2 | 2 | 3 | 1 |
| (1, 1, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (3, 4, 5) | (2, 3, 4) | (2, 3, 4) | (4, 5, 6) | (1, 2, 3) | (1/3, 1/2, 1) | |
| (1, 2, 3) | (1, 1, 1) | (1/3, 1/2, 1) | (3, 4, 5) | (3, 4, 5) | (3, 4, 5) | (5, 6, 7) | (1, 2, 3) | (1, 2, 3) | |
| (1, 2, 3) | (1, 2, 3) | (1, 1, 1) | (3, 4, 5) | (3, 4, 5) | (3, 4, 5) | (5, 6, 7) | (1, 2, 3) | (1, 2, 3) | |
| (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (1, 1, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/4, 1/3, 1/2) | (1/5, 1/4, 1/3) | |
| (1/4, 1/3, 1/2) | (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (1, 2, 3) | (1, 1, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/4, 1/3, 1/2) | (1/5, 1/4, 1/3) | |
| (1/4, 1/3, 1/2) | (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (1, 2, 3) | (1, 2, 3) | (1, 1, 1) | (1, 2, 3) | (1/4, 1/3, 1/2) | (1/5, 1/4, 1/3) | |
| (1/6, 1/5, 1/4) | (1/7, 1/6, 1/5) | (1/7, 1/6, 1/5) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 1, 1) | (1/5, 1/4, 1/3) | (1/7, 1/6, 1/5) | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (2, 3, 4) | (2, 3, 4) | (2, 3, 4) | (3, 4, 5) | (1, 1, 1) | (1/3, 1/2, 1) | |
| (1, 2, 3) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (3, 4, 5) | (3, 4, 5) | (3, 4, 5) | (5, 6, 7) | (1, 2, 3) | (1, 1, 1) | |
| (1/8, 1/7, 1/6) | (1/9, 1/8, 1/7) | (1/9, 1/9, 1/9) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1/7, 1/6, 1/5) | (1/9, 1/8, 1/7) | |
| (1/6, 1/5, 1/4) | (1/6, 1/5, 1/4) | (1/6, 1/5, 1/4) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/5, 1/4, 1/3) | (1/6, 1/5, 1/4) | |
| (1/7, 1/6, 1/5) | (1/8, 1/7, 1/6) | (1/8, 1/7, 1/6) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1/6, 1/5, 1/4) | (1/8, 1/7, 1/6) | |
| (1/8, 1/7, 1/6) | (1/9, 1/8, 1/7) | (1/9, 1/8, 1/7) | (1/3, 1/2, 1) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1/7, 1/6, 1/5) | (1/8, 1/7, 1/6) | |
| (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (2, 3, 4) | (1/3, 1/2, 1) | (1/4, 1/3, 1/2) | |
| (1/6, 1/5, 1/4) | (1/7, 1/6, 1/5) | (1/7, 1/6, 1/5) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/5, 1/4, 1/3) | (1/6, 1/5, 1/4) | |
| (1/9, 1/8, 1/7) | (1/9, 1/9, 1/9) | (1/9, 1/9, 1/9) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1/8, 1/7, 1/6) | (1/9, 1/9, 1/9) | |
| (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/4, 1/3, 1/2) | (1/5, 1/4, 1/3) |
| (6, 7, 8) | (4, 5, 6) | (5, 6, 7) | (6, 7, 8) | (2, 3, 4) | (4, 5, 6) | (7, 8, 9) | (3, 4, 5) | (51, 64.5, 79) | 0.1778 | |
| (7, 8, 9) | (4, 5, 6) | (6, 7, 8) | (7, 8, 9) | (2, 3, 4) | (5, 6, 7) | (9, 9, 9) | (3, 4, 5) | (61.3333, 75.5, 90) | 0.2115 | |
| (9, 9, 9) | (4, 5, 6) | (6, 7, 8) | (7, 8, 9) | (2, 3, 4) | (5, 6, 7) | (9, 9, 9) | (3, 4, 5) | (64, 78, 92) | 0.2187 | |
| (2, 3, 4) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (2, 3, 4) | (1/3, 1/2, 1) | (12.3833, 20.3333, 29.8333) | 0.0000 | |
| (2, 3, 4) | (1, 2, 3) | (1, 2, 3) | (2, 3, 4) | (1/3, 1/2, 1) | (1, 2, 3) | (2, 3, 4) | (1, 2, 3) | (14.7667, 24.4167, 35) | 0.0000 | |
| (2, 3, 4) | (1, 2, 3) | (2, 3, 4) | (2, 3, 4) | (1/3, 1/2, 1) | (1, 2, 3) | (2, 3, 4) | (1, 2, 3) | (16.4333, 26.9167, 38) | 0.0115 | |
| (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (8.0452, 13.2833, 20.6833) | 0.0000 | |
| (5, 6, 7) | (3, 4, 5) | (4, 5, 6) | (5, 6, 7) | (1, 2, 3) | (3, 4, 5) | (6, 7, 8) | (2, 3, 4) | (40.3333, 53, 67) | 0.1375 | |
| (7, 8, 9) | (4, 5, 6) | (6, 7, 8) | (6, 7, 8) | (2, 3, 4) | (4, 5, 6) | (9, 9, 9) | (3, 4, 5) | (58.6667, 72, 86) | 0.2010 | |
| (1, 1, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/5, 1/4, 1/3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/4, 1/3, 1/2) | (5.4679, 7.754, 12.0968) | 0.0000 | |
| (1, 2, 3) | (1, 1, 1) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (9.5333, 16.55, 25.3333) | 0.0000 | |
| (1, 2, 3) | (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (7.1845, 11.4619, 17.95) | 0.0000 | |
| (1, 2, 3) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 1, 1) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (6.3651, 9.7024, 15.319) | 0.0000 | |
| (3, 4, 5) | (1, 2, 3) | (2, 3, 4) | (2, 3, 4) | (1, 1, 1) | (1, 2, 3) | (3, 4, 5) | (1, 2, 3) | (20.3333, 31.8333, 44) | 0.0421 | |
| (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (8.819, 14.9833, 23.2333) | 0.0000 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/5, 1/4, 1/3) | (1/3, 1/2, 1) | (1, 1, 1) | (1/4, 1/3, 1/2) | (4.7694, 6.1845, 9.9762) | 0.0000 | |
| (2, 3, 4) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (2, 3, 4) | (1, 1, 1) | (13.05, 21.8333, 31.8333) | 0.0000 | |
| (402.4845, 548.2528, 717.2587) |
| 1 | 1/2 | 1/2 | 1/4 | 2 | 1/2 | 1/6 | 1/3 | 1/2 | 1/2 | 1/2 | 1/2 | 2 | 1/2 | 2 | 1/7 | 1/4 | |
| 2 | 1 | 2 | 1/4 | 2 | 1/2 | 1/5 | 1/2 | 2 | 2 | 2 | 2 | 2 | 1/2 | 2 | 1/6 | 1/4 | |
| 2 | 1/2 | 1 | 1/4 | 2 | 1/2 | 1/5 | 1/2 | 2 | 1/2 | 1/2 | 2 | 2 | 1/2 | 2 | 1/7 | 1/4 | |
| 4 | 4 | 4 | 1 | 5 | 3 | 1/2 | 2 | 4 | 4 | 4 | 4 | 5 | 4 | 6 | 1/2 | 2 | |
| 1/2 | 1/2 | 1/2 | 1/5 | 1 | 1/2 | 1/6 | 1/3 | 1/2 | 1/2 | 1/2 | 1/2 | 2 | 1/2 | 2 | 1/8 | 1/4 | |
| 2 | 2 | 2 | 1/3 | 2 | 1 | 1/4 | 1/2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1/6 | 1/3 | |
| 6 | 5 | 5 | 2 | 6 | 4 | 1 | 3 | 6 | 5 | 5 | 5 | 6 | 5 | 7 | 1/2 | 2 | |
| 3 | 2 | 2 | 1/2 | 3 | 2 | 1/3 | 1 | 3 | 2 | 2 | 3 | 3 | 2 | 3 | 1/4 | 1/2 | |
| 2 | 1/2 | 1/2 | 1/4 | 2 | 1/2 | 1/6 | 1/3 | 1 | 1/2 | 1/2 | 1/2 | 2 | 1/2 | 2 | 1/7 | 1/4 | |
| 2 | 1/2 | 2 | 1/4 | 2 | 1/2 | 1/5 | 1/2 | 2 | 1 | 1/2 | 2 | 2 | 1/2 | 2 | 1/7 | 1/4 | |
| 2 | 1/2 | 2 | 1/4 | 2 | 1/2 | 1/5 | 1/2 | 2 | 2 | 1 | 2 | 2 | 1/2 | 2 | 1/6 | 1/4 | |
| 2 | 1/2 | 1/2 | 1/4 | 2 | 1/2 | 1/5 | 1/3 | 2 | 1/2 | 1/2 | 1 | 2 | 1/2 | 2 | 1/7 | 1/4 | |
| 1/2 | 1/2 | 1/2 | 1/5 | 1/2 | 1/2 | 1/6 | 1/3 | 1/2 | 1/2 | 1/2 | 1/2 | 1 | 1/2 | 2 | 1/8 | 1/5 | |
| 2 | 2 | 2 | 1/4 | 2 | 1/2 | 1/5 | 1/2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 1/6 | 1/4 | |
| 1/2 | 1/2 | 1/2 | 1/6 | 1/2 | 1/2 | 1/7 | 1/3 | 1/2 | 1/2 | 1/2 | 1/2 | 1/2 | 1/2 | 1 | 1/9 | 1/5 | |
| 7 | 6 | 7 | 2 | 8 | 6 | 2 | 4 | 7 | 7 | 6 | 7 | 8 | 6 | 9 | 1 | 2 | |
| 4 | 4 | 4 | 1/2 | 4 | 3 | 1/2 | 2 | 4 | 4 | 4 | 4 | 5 | 4 | 5 | 1/2 | 1 |
| (1, 1, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/5, 1/4, 1/3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/7, 1/6, 1/5) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | |
| (1, 2, 3) | (1, 1, 1) | (1, 2, 3) | (1/5, 1/4, 1/3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/6, 1/5, 1/4) | (1/3, 1/2, 1) | (1, 2, 3) | |
| (1, 2, 3) | (1/3, 1/2, 1) | (1, 1, 1) | (1/5, 1/4, 1/3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/6, 1/5, 1/4) | (1/3, 1/2, 1) | (1, 2, 3) | |
| (3, 4, 5) | (3, 4, 5) | (3, 4, 5) | (1, 1, 1) | (4, 5, 6) | (2, 3, 4) | (1/3, 1/2, 1) | (1, 2, 3) | (3, 4, 5) | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/6, 1/5, 1/4) | (1, 1, 1) | (1/3, 1/2, 1) | (1/7, 1/6, 1/5) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | |
| (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/4, 1/3, 1/2) | (1, 2, 3) | (1, 1, 1) | (1/5, 1/4, 1/3) | (1/3, 1/2, 1) | (1, 2, 3) | |
| (5, 6, 7) | (4, 5, 6) | (4, 5, 6) | (1, 2, 3) | (5, 6, 7) | (3, 4, 5) | (1, 1, 1) | (2, 3, 4) | (5, 6, 7) | |
| (2, 3, 4) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (2, 3, 4) | (1, 2, 3) | (1/4, 1/3, 1/2) | (1, 1, 1) | (2, 3, 4) | |
| (1, 2, 3) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/5, 1/4, 1/3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/7, 1/6, 1/5) | (1/4, 1/3, 1/2) | (1, 1, 1) | |
| (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/5, 1/4, 1/3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/6, 1/5, 1/4) | (1/3, 1/2, 1) | (1, 2, 3) | |
| (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/5, 1/4, 1/3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/6, 1/5, 1/4) | (1/3, 1/2, 1) | (1, 2, 3) | |
| (1, 2, 3) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/5, 1/4, 1/3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/6, 1/5, 1/4) | (1/4, 1/3, 1/2) | (1, 2, 3) | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/6, 1/5, 1/4) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/7, 1/6, 1/5) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | |
| (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/5, 1/4, 1/3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/6, 1/5, 1/4) | (1/3, 1/2, 1) | (1, 2, 3) | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/7, 1/6, 1/5) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/8, 1/7, 1/6) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | |
| (6, 7, 8) | (5, 6, 7) | (6, 7, 8) | (1, 2, 3) | (7, 8, 9) | (5, 6, 7) | (1, 2, 3) | (3, 4, 5) | (6, 7, 8) | |
| (3, 4, 5) | (3, 4, 5) | (3, 4, 5) | (1/3, 1/2, 1) | (3, 4, 5) | (2, 3, 4) | (1/3, 1/2, 1) | (1, 2, 3) | (3, 4, 5) |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/8, 1/7, 1/6) | (1/5, 1/4, 1/3) | (7.5845, 12.1429, 19.5333) | 0.0000 | |
| (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/7, 1/6, 1/5) | (1/5, 1/4, 1/3) | (11.7095, 21.3667, 32.1167) | 0.0000 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/8, 1/7, 1/6) | (1/5, 1/4, 1/3) | (9.6917, 16.8429, 26.0833) | 0.0000 | |
| (3, 4, 5) | (3, 4, 5) | (3, 4, 5) | (4, 5, 6) | (3, 4, 5) | (5, 6, 7) | (1/3, 1/2, 1) | (1, 2, 3) | (42.6667, 57, 72) | 0.1867 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/9, 1/8, 1/7) | (1/5, 1/4, 1/3) | (6.8706, 10.575, 17.4262) | 0.0000 | |
| (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/7, 1/6, 1/5) | (1/4, 1/3, 1/2) | (13.1762, 24.5833, 36.5333) | 0.0000 | |
| (4, 5, 6) | (4, 5, 6) | (4, 5, 6) | (5, 6, 7) | (4, 5, 6) | (6, 7, 8) | (1/3, 1/2, 1) | (1, 2, 3) | (58.3333, 73.5, 89) | 0.2651 | |
| (1, 2, 3) | (1, 2, 3) | (2, 3, 4) | (2, 3, 4) | (1, 2, 3) | (2, 3, 4) | (1/5, 1/4, 1/3) | (1/3, 1/2, 1) | (20.1167, 32.5833, 45.8333) | 0.0325 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/8, 1/7, 1/6) | (1/5, 1/4, 1/3) | (8.2512, 13.6429, 21.5333) | 0.0000 | |
| (1, 1, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/8, 1/7, 1/6) | (1/5, 1/4, 1/3) | (10.3583, 18.3429, 28.0833) | 0.0000 | |
| (1, 2, 3) | (1, 1, 1) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/7, 1/6, 1/5) | (1/5, 1/4, 1/3) | (11.0429, 19.8667, 30.1167) | 0.0000 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/8, 1/7, 1/6) | (1/5, 1/4, 1/3) | (8.9417, 15.1762, 23.5833) | 0.0000 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 1, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/9, 1/8, 1/7) | (1/6, 1/5, 1/4) | (6.1706, 9.025, 15.3429) | 0.0000 | |
| (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 1, 1) | (1, 2, 3) | (1/7, 1/6, 1/5) | (1/5, 1/4, 1/3) | (12.3762, 22.8667, 34.1167) | 0.0000 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 1, 1) | (1/9, 1/9, 1/9) | (1/6, 1/5, 1/4) | (5.4623, 7.454, 13.2278) | 0.0000 | |
| (6, 7, 8) | (5, 6, 7) | (6, 7, 8) | (7, 8, 9) | (5, 6, 7) | (9, 9, 9) | (1, 1, 1) | (1, 2, 3) | (80, 95, 110) | 0.3489 | |
| (3, 4, 5) | (3, 4, 5) | (3, 4, 5) | (4, 5, 6) | (3, 4, 5) | (4, 5, 6) | (1/3, 1/2, 1) | (1, 1, 1) | (40, 53.5, 68) | 0.1669 | |
| (352.7524, 503.4683, 682.5302) | ||||||||||
| Economy Type | N | Countries |
|---|---|---|
| Advanced Economies | 331 | Australia, Austria, Belgium, Canada, Croatia, Cyprus, Czech Republic, Denmark, Estonia, Finland, France, Germany, Greece, Hong Kong, Iceland, Ireland, Israel, Italy, Japan, Latvia, Lithuania, Luxembourg, Malta, Netherlands, New Zealand, Norway, Portugal, Singapore, Slovakia, Slovenia, South Korea, Spain, Sweden, Switzerland, Taiwan, United Kingdom, and United States |
| Emerging and Developing Asia | 55 | Bangladesh, Bhutan, Brunei, Cambodia, China (Mainland), East Timor/Timor-Leste, Fiji, India, Indonesia, Kiribati, Laos, Malaysia, Maldives, Mongolia, Myanmar, Nepal, Papua New Guinea, Philippines, Samoa, Solomon Islands, Sri Lanka, Thailand, Tonga, Vanuatu, and Vietnam |
| Emerging and Developing Europe | 20 | Albania, Belarus, Bosnia and Herzegovina, Bulgaria, Hungary, Moldova, Montenegro, Poland, Romania, Russia, Serbia, Turkey, and Ukraine |
| Latin America and the Caribbean | 8 | Antigua and Barbuda, Bahamas, Barbados, Belize, Bolivia, Brazil, Chile, Colombia, Costa Rica, Dominica, Dominican Republic, Ecuador, El Salvador, Grenada, Guatemala, Guyana, Haiti, Honduras, Jamaica, Mexico, Nicaragua, Panama, Paraguay, Peru, Saint Kitts and Nevis, Saint Lucia, Saint Vincent and the Grenadines, Suriname, Trinidad and Tobago, and Uruguay |
| Middle East and Central Asia | 60 | Algeria, Armenia, Azerbaijan, Bahrain, Djibouti, Egypt, Georgia, Iran, Iraq, Jordan, Kazakhstan, Kuwait, Kyrgyzstan, Libya, Mauritania, Morocco, Oman, Pakistan, Qatar, Saudi Arabia, Tajikistan, Tunisia, Turkmenistan, Uzbekistan, and Yemen |
| Sub-Saharan Africa | 22 | Angola, Benin, Botswana, Burkina Faso, Burundi, Cameroon, Cape Verde, Central African Republic, Chad, Comoros, and Congo (DRC), Congo (RC), Equatorial Guinea, Eswatini, Ethiopia, Gabon, Gambia, Ghana, Guinea, Guinea-Bissau, Ivory Coast, Kenya, Lesotho, Liberia, Madagascar, Malawi, Mali, Mauritius, Mozambique, Namibia, Niger, Nigeria, Rwanda, Sao Tome and Principe, Senegal, Seychelles, Sierra Leone, South Africa, Tanzania, Togo, Uganda, and Zambia |
| Economy Type | Countries | No. of Banks | Countries | No. of Banks | Countries | No. of Banks |
|---|---|---|---|---|---|---|
| Advanced Economies | Austria | 5 | Greece | 1 | Portugal | 1 |
| Belgium | 1 | Hong Kong | 5 | Singapore | 3 | |
| Canada | 1 | Israel | 5 | Slovakia | 1 | |
| Cyprus | 1 | Italy | 9 | Spain | 5 | |
| Czech Republic | 2 | South Korea | 3 | Sweden | 5 | |
| Denmark | 7 | Lithuania | 1 | Switzerland | 7 | |
| Finland | 3 | Netherlands | 2 | United Kingdom | 8 | |
| France | 14 | Norway | 18 | United States | 222 | |
| Germany | 1 | |||||
| Emerging and Developing Asia | China (Mainland) | 33 | Malaysia | 7 | Sri Lanka | 1 |
| Indonesia | 12 | Philippines | 1 | Thailand | 1 | |
| Emerging and Developing Europe | Bulgaria | 2 | Poland | 4 | Russia | 2 |
| Hungary | 1 | Romania | 2 | Turkey | 9 | |
| Latin America and the Caribbean | Brazil | 3 | Mexico | 1 | Peru | 3 |
| Colombia | 1 | |||||
| Middle East and Central Asia | Bahrain | 4 | Jordan | 13 | Pakistan | 2 |
| Egypt | 8 | Kazakhstan | 2 | Qatar | 7 | |
| Georgia | 1 | Kuwait | 7 | Saudi Arabia | 9 | |
| Iraq | 1 | Oman | 6 | Pakistan | 2 | |
| Sub-Saharan Africa | Botswana | 3 | Mauritius | 1 | South Africa | 4 |
| Kenya | 6 | Nigeria | 7 | Uganda | 1 |
References
- Lee, C.C.; Lin, C.W.; Lee, C.C. Globalization, government regulation, and country risk: International evidence. J. Int. Trade Econ. Dev. 2023, 32, 132–162. [Google Scholar] [CrossRef]
- Sargen, N. Economic indicators and country risk appraisal. Econ. Rev. 1977, 19–35. [Google Scholar]
- Nagy, P. Quantifying country risk-system developed by economists at the bank of Montreal. Columbia J. World Bus. 1978, 13, 135–147. [Google Scholar]
- Sun, X.; Feng, Q.; Li, J. Understanding country risk assessment: A historical review. Appl. Econ. 2021, 53, 4329–4341. [Google Scholar] [CrossRef]
- Meier, S.; Strobl, E.; Elliott, R.J.; Kettridge, N. Cross-country risk quantification of extreme wildfires in Mediterranean Europe. Risk Anal. 2022. online ahead of print. [Google Scholar] [CrossRef]
- Lee, C.-C.; Chen, M.-P. Ecological footprint, tourism development, and country risk: International evidence. J. Clean. Prod. 2020, 279, 123671. [Google Scholar] [CrossRef]
- Chaudhry, S.M.; Ahmed, R.; Shafiullah, M.; Huynh, T.L.D. The impact of carbon emissions on country risk: Evidence from the G7 economies. J. Environ. Manag. 2020, 265, 110533. [Google Scholar] [CrossRef]
- Peiró-Signes, Á.; Cervelló-Royo, R.; Segarra-Oña, M. Can a country’s environmental sustainability exert influence on its economic and financial situation? The relationship between environmental performance indicators and country risk. J. Clean. Prod. 2022, 375, 134121. [Google Scholar] [CrossRef]
- Đukan, M.; Kitzing, L. A bigger bang for the buck: The impact of risk reduction on renewable energy support payments in Europe. Energy Policy 2023, 173, 113395. [Google Scholar] [CrossRef]
- Li, Y.; Huang, J.; Zhang, H. The impact of country risks on cobalt trade patterns from the perspective of the industrial chain. Resour. Policy 2022, 77, 102641. [Google Scholar] [CrossRef]
- Qazi, A.; Simsekler, M.C.E.; Formaneck, S. Impact assessment of country risk on logistics performance using a Bayesian Belief Network model. Kybernetes 2023, 52, 1620–1642. [Google Scholar] [CrossRef]
- Filipović, S.; Radovanović, M.; Golušin, V. Macroeconomic and political aspects of energy security–Exploratory data analysis. Renew. Sustain. Energy Rev. 2018, 97, 428–435. [Google Scholar] [CrossRef]
- Zhang, W.; Chiu, Y.B. Do country risks influence carbon dioxide emissions? A non-linear perspective. Energy 2020, 206, 118048. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Yang, C.; Guo, Y. The impact of country risk on energy trade patterns based on complex network and panel regression analyses. Energy 2021, 222, 119979. [Google Scholar] [CrossRef]
- Özkan, B.; Erdem, M.; Özceylan, E. Evaluation of Asian Countries using Data Center Security Index: A Spherical Fuzzy AHP-based EDAS Approach. Comput. Secur. 2022, 122, 102900. [Google Scholar] [CrossRef]
- Angosto-Fernández, P.L.; Ferrández-Serrano, V. Independence day: Political risk and cross-sectional determinants of firm exposure after the Catalan crisis. Int. J. Financ. Econ. 2022, 27, 4318–4335. [Google Scholar] [CrossRef]
- Lee, C.-C.; Lee, C.-C. Oil price shocks and Chinese banking performance: Do country risks matter? Energy Econ. 2019, 77, 46–53. [Google Scholar] [CrossRef]
- Mascarenhas, B.; Christian Sand, O. Country-Risk Assessment System in Banks: Patterns and Performance. J. Int. Bus. Stud. 1985, 16, 19–35. [Google Scholar] [CrossRef]
- Somerville, R.A.; Taffler, R.J. Banker judgement versus formal forecasting models: The case of country risk assessment. J. Bank. Financ. 1995, 19, 281–297. [Google Scholar] [CrossRef]
- Simpson, J. An Empirical Economic Development Based Model of International Banking Risk and Risk Scoring. Rev. Dev. Econ. 2002, 6, 91–102. [Google Scholar] [CrossRef]
- Cherubini, U.; Mulinacci, S. Contagion-based distortion risk measures. Appl. Math. Lett. 2014, 27, 85–89. [Google Scholar] [CrossRef]
- Babayeva, S.; Rzayeva, I.; Babayev, T. Weighted Estimate of Country Risk Using a Fuzzy Method of Maxmin Convolution. Adv. Intell. Syst. Comput. 2018, 896, 559–567. [Google Scholar] [CrossRef]
- Li, J.; Dong, X.; Jiang, Q.; Dong, K. Analytical Approach to Quantitative Country Risk Assessment for the Belt and Road Initiative. Sustainability 2021, 13, 423. [Google Scholar] [CrossRef]
- Yim, J.; Mitchell, H. Comparison of country risk models: Hybrid neural networks, logit models, discriminant analysis and cluster techniques. Expert Syst. Appl. 2005, 28, 137–148. [Google Scholar] [CrossRef]
- Coccia, M. A new taxonomy of country performance and risk based on economic and technological indicators. J. Appl. Econ. 2007, 10, 29–42. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Wang, W.; Guo, Y.; Yang, J. Study on the country risk rating with distributed crawling system. J. Supercomput. 2019, 75, 6159–6177. [Google Scholar] [CrossRef]
- Kouzez, M. Political environment and bank performance: Does bank size matter? Econ. Syst. 2023, 47, 101056. [Google Scholar] [CrossRef]
- Niemira, M.P.; Saaty, T.L. An Analytic Network Process Model for Financial-Crisis Forecasting. Int. J. Forecast. 2004, 20, 573–587. [Google Scholar] [CrossRef]
- Brown, C.L.; Cavusgil, S.T.; Lord, A.W. Country-risk measurement and analysis: A new conceptualization and managerial tool. Int. Bus. Rev. 2015, 24, 246–265. [Google Scholar] [CrossRef]
- Albaity, M.; Mallek, R.S.; Bakather, A.; Al-Tamimi, H. Heterogeneity of the MENA region’s bank stock returns: Does country risk matter? J. Open Innov. Technol. Mark. Complex. 2023, 9, 100057. [Google Scholar] [CrossRef]
- Bouchet, M.H.; Clark, E.; Groslambert, B. Country Risk Assessment: A Guide to Global Investment Strategy; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Refinitiv Thomson Reuters. Available online: https://www.refinitiv.com/content/dam/marketing/en_us/documents/brochures/country-risk-ranking-brochure.pdf (accessed on 1 March 2023).
- Gelemerova, L.; Harvey, J.; van Duyne, P.C. Banks assessing corruption risk: A risky undertaking. In Corruption in Commercial Enterprise; Routledge: London, UK, 2018; pp. 182–198. [Google Scholar]
- Roe, M.J.; Siegel, J.I. Political instability: Effects on financial development, roots in the severity of economic inequality. J. Comp. Econ. 2011, 39, 279–309. [Google Scholar] [CrossRef] [Green Version]
- Lehkonen, H.; Heimonen, K. Democracy, political risks and stock market performance. J. Int. Money Financ. 2015, 59, 77–99. [Google Scholar] [CrossRef] [Green Version]
- Hayakawa, K.; Kimura, F.; Lee, H.H. How does country risk matter for foreign direct investment? Dev. Econ. 2013, 51, 60–78. [Google Scholar] [CrossRef] [Green Version]
- Park, S.J.; Lee, K.M.; Yang, J.S. Calculating the country risk embedded in treaty-shopping networks. Technol. Forecast. Soc. Chang. 2023, 189, 122354. [Google Scholar] [CrossRef]
- Ghirelli, C.; Gil, M.; Pérez, J.J.; Urtasun, A. Measuring economic and economic policy uncertainty and their macroeconomic effects: The case of Spain. Empir. Econ. 2021, 60, 869–892. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.C.; Lin, H.C. Country Risk and Bank Stability. J. Econ. Forecast. 2021, 24, 72–96. [Google Scholar]
- Walter, I. Country risk, portfolio decisions and regulation in international bank lending. J. Bank. Financ. 1981, 5, 77–92. [Google Scholar] [CrossRef]
- Aragonés-Beltrán, P.; Chaparro-González, F.; Pastor-Ferrando, J.P.; Pla-Rubio, A. An AHP (Analytic Hierarchy Process)/ANP (Analytic Network Process)-based multi-criteria decision approach for the selection of solar-thermal power plant investment projects. Energy 2014, 66, 222–238. [Google Scholar] [CrossRef]
- Sun, C.C. A performance evaluation model by integrating fuzzy AHP and fuzzy TOPSIS methods. Expert Syst. Appl. 2010, 37, 7745–7754. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making—The analytic hierarchy and network processes (AHP/ANP). J. Syst. Sci. Syst. Eng. 2004, 13, 1–35. [Google Scholar] [CrossRef]
- Kumar, M.; Choubey, V.K.; Raut, R.D.; Jagtap, S. Enablers to achieve zero hunger through IoT and blockchain technology and transform the green food supply chain systems. J. Clean. Prod. 2023, 405, 136894. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Çifçi, G. A novel hybrid MCDM approach based on fuzzy DEMATEL, fuzzy ANP and fuzzy TOPSIS to evaluate green suppliers. Expert Syst. Appl. 2012, 39, 3000–3011. [Google Scholar] [CrossRef]
- Ergu, D.; Kou, G.; Shi, Y.; Shi, Y. Analytic network process in risk assessment and decision analysis. Comput. Oper. Res. 2014, 42, 58–74. [Google Scholar] [CrossRef]
- Uygun, Ö.; Kaçamak, H.; Kahraman, Ü.A. An integrated DEMATEL and Fuzzy ANP techniques for evaluation and selection of outsourcing provider for a telecommunication company. Comput. Ind. Eng. 2015, 86, 137–146. [Google Scholar] [CrossRef]
- Mistarihi, M.Z.; Okour, R.A.; Mumani, A.A. An integration of a QFD model with Fuzzy-ANP approach for determining the importance weights for engineering characteristics of the proposed wheelchair design. Appl. Soft Comput. 2020, 90, 106136. [Google Scholar] [CrossRef]
- Schulze-González, E.; Pastor-Ferrando, J.-P.; Aragonés-Beltrán, P. Testing a Recent DEMATEL-Based Proposal to Simplify the Use of ANP. Mathematics 2021, 9, 1605. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Chen, J.-M.; Tseng, S.-H.; Lin, L.-F. Key Factors for a Successful OBM Transformation with DEMATEL–ANP. Mathematics 2023, 11, 2439. [Google Scholar] [CrossRef]
- Dincer, H. HHI-based evaluation of the European banking sector using an integrated fuzzy approach. Kybernetes 2019, 48, 1195–1215. [Google Scholar] [CrossRef]
- Sánchez-Garrido, A.J.; Navarro, I.J.; García, J.; Yepes, V. An Adaptive ANP & ELECTRE IS-Based MCDM Model Using Quantitative Variables. Mathematics 2022, 10, 2009. [Google Scholar] [CrossRef]
- Khalilzadeh, M.; Katoueizadeh, L.; Zavadskas, E.K. Risk identification and prioritization in banking projects of payment service provider companies: An empirical study. Front. Bus. Res. China 2020, 14, 1–27. [Google Scholar] [CrossRef]
- Dincer, H.; Hacioglu, U.; Tatoglu, E.; Delen, D. Developing a hybrid analytics approach to measure the efficiency of deposit banks. J. Bus. Res. 2019, 104, 131–145. [Google Scholar] [CrossRef]
- Pearson, K.F.R.S. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Malhotra, N. Marketing Research: An Applied Orientation, 7th ed.; Pearson Education: Harlow, UK, 2020. [Google Scholar]
- Ďuriš, V.; Bartková, R.; Tirpáková, A. Principal Component Analysis and Factor Analysis for an Atanassov IF Data Set. Mathematics 2021, 9, 2067. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E.; Tatham, R.L. Multivariate Data Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 2017. [Google Scholar]
- Widaman, K.F. Common factor analysis versus principal component analysis: Differential bias in representing model parameters? Multivar. Behav. Res. 1993, 28, 263–311. [Google Scholar] [CrossRef] [PubMed]
- IBM Corp. IBM SPSS Statistics Algorithms; IBM Corp.: Armonk, NY, USA, 2017. [Google Scholar]
- Rummel, R.J. Applied Factor Analysis; Northwestern University Press: Evanston, IL, USA, 1988. [Google Scholar]
- Kaiser, H.F. A second generation little jiffy. Psychometrika 1970, 35, 401–415. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis for Special Types of Data; Springer: New York, NY, USA, 2002; pp. 338–372. [Google Scholar]
- Harman, H.H. Modern Factor Analysis; University of Chicago Press: Chicago, IL, USA, 1976. [Google Scholar]
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Kaiser, H.F. An index of factorial simplicity. Psychometrika 1974, 39, 31–36. [Google Scholar] [CrossRef]
- Cerny, B.A.; Kaiser, H.F. A Study of a Measure of Sampling Adequacy For Factor-Analytic Correlation Matrices. Multivar. Behav. Res. 1977, 12, 43–47. [Google Scholar] [CrossRef]
- Chang, D.Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- De Andrés-Sánchez, J. A systematic review of the interactions of fuzzy set theory and option pricing. Expert Syst. Appl. 2023, 223, 119868. [Google Scholar] [CrossRef]
- de Andrés-Sánchez, J.; Puchades, L.G.V. Using fuzzy random variables in life annuities pricing. Fuzzy Sets Syst. 2012, 188, 27–44. [Google Scholar] [CrossRef]
- Kheybari, S.; Rezaie, F.M.; Farazmand, H. Analytic network process: An overview of applications. Appl. Math. Comput. 2020, 367, 124780. [Google Scholar] [CrossRef]
- Herrera, F.; Alonso, S.; Chiclana, F.; Herrera-Viedma, E. Computing with words in decision making: Foundations, trends and prospects. Fuzzy Optim. Decis. Mak. 2009, 8, 337–364. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Tong, H. Data Mining: Concepts and Techniques; Morgan Kaufmann: Cambridge, MA, USA, 2022. [Google Scholar]
- Singh, D.; Singh, B. Investigating the impact of data normalization on classification performance. Appl. Soft Comput. 2020, 97, 105524. [Google Scholar] [CrossRef]
- Arias-Oliva, M.; de Andrés-Sánchez, J.; Pelegrín-Borondo, J. Fuzzy Set Qualitative Comparative Analysis of Factors Influencing the Use of Cryptocurrencies in Spanish Households. Mathematics 2021, 9, 324. [Google Scholar] [CrossRef]
- Míguez, J.L.; Rivo-López, E.; Porteiro, J.; Pérez-Orozco, R. Selection of non-financial sustainability indicators as key elements for multi-criteria analysis of hotel chains. Sustain. Prod. Consum. 2023, 35, 495–508. [Google Scholar] [CrossRef]
- Yüksel, İ.; Dağdeviren, M. Using the fuzzy analytic network process (ANP) for Balanced Scorecard (BSC): A case study for a manufacturing firm. Expert Syst. Appl. 2010, 37, 1270–1278. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Diagnosis with dependent symptoms: Bayes theorem and the analytic hierarchy process. Oper. Res. 1998, 46, 491–502. [Google Scholar] [CrossRef]
- Chen, H.K.; Liao, Y.C.; Lin, C.Y.; Yen, J.F. The effect of the political connections of government bank CEOs on bank performance during the financial crisis. J. Financ. Stab. 2018, 36, 130–143. [Google Scholar] [CrossRef]
- Elyasiani, E.; Jia, J. Relative performance and systemic risk contributions of small and large banks during the financial crisis (Jane). Q. Rev. Econ. Financ. 2019, 74, 220–241. [Google Scholar] [CrossRef]
- Fitch. Bank Rating Criteria. Available online: https://www.fitchratings.com/research/banks/bank-rating-criteria-07-09-2022 (accessed on 1 March 2023).
- Bitar, M.; Kabir Hassan, M.; Hippler, W.J. The determinants of Islamic bank capital decisions. Emerg. Mark. Rev. 2018, 35, 48–68. [Google Scholar] [CrossRef]
- Alraheb, T.H.; Nicolas, C.; Tarazi, A. Institutional environment and bank capital ratios. J. Financ. Stab. 2019, 43, 1–24. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Huang, J.-J. Integrating Dynamic Bayesian Networks and Analytic Hierarchy Process for Time-Dependent Multi-Criteria Decision-Making. Mathematics 2023, 11, 2362. [Google Scholar] [CrossRef]
- Wang, C.-N.; Pan, C.-F.; Nguyen, H.-P.; Fang, P.-C. Integrating Fuzzy AHP and TOPSIS Methods to Evaluate Operation Efficiency of Daycare Centers. Mathematics 2023, 11, 1793. [Google Scholar] [CrossRef]
- Peña, A.; Bonet, I.; Lochmuller, C.; Chiclana, F.; Góngora, M. Flexible inverse adaptive fuzzy inference model to identify the evolution of operational value at risk for improving operational risk management. Appl. Soft Comput. 2018, 65, 614–631. [Google Scholar] [CrossRef] [Green Version]
- Shukla, A.K.; Prakash, V.; Nath, R.; Muhuri, P.K. Type-2 intuitionistic fuzzy TODIM for intelligent decision-making under uncertainty and hesitancy. Soft Comput. 2022. online ahead of print. [Google Scholar] [CrossRef]
- Runkler, T.; Coupland, S.; John, R. Interval type-2 fuzzy decision making. Int. J. Approx. Reason. 2017, 80, 217–224. [Google Scholar] [CrossRef] [Green Version]


| Saaty’s Scale | Linguistic Terms | Fuzzy Triangular Scale |
|---|---|---|
| 9 | Extremely importance | (9, 9, 9) |
| 8 | Very, very strong | (7, 8, 9) |
| 7 | Very strong importance | (6, 7, 8) |
| 6 | Strong plus | (5, 6, 7) |
| 5 | Strong importance | (4, 5, 6) |
| 4 | Moderate plus | (3, 4, 5) |
| 3 | Moderate importance | (2, 3, 4) |
| 2 | Weak | (1, 2, 3) |
| 1 | Equal importance | (1, 1, 1) |
| Environment | Variable | Variable Description | Mean | SD | |
|---|---|---|---|---|---|
| Political environment | X1 | Type of governance | Progress and transformation process towards democracy and market economy | 2.7749 | 1.0648 |
| X2 | Civil liberties & political rights | Freedom of individuals in terms of individual rights and personal autonomy, and government functioning along with electoral and political participation | 2.8978 | 1.1917 | |
| X3 | Freedom of the press | Journalistic freedom and free flow of news | 2.9111 | 1.0568 | |
| X4 | Political stability | Likelihood of political destabilization and interferences in governmental jurisdiction | 2.9045 | 0.9760 | |
| X5 | Regulatory quality | Sound policies to support private sector activity | 2.9668 | 0.9583 | |
| X6 | Rule of law | Aggregated individual governance indicators of economies | 3.0291 | 0.9836 | |
| X7 | Armed conflict | Potential conflict based on clashing interests | 2.9203 | 0.9880 | |
| X8 | Human rights | State respect regarding human rights indicators | 2.9543 | 1.0333 | |
| X9 | Voice & accountability | Perceptions of citizens’ freedom of expression and association | 2.9668 | 1.0414 | |
| Economic environment | X10 | Average earnings | Economy classification based on Gross National Income per capita | 3.0739 | 1.1713 |
| X11 | Economic freedom | Benchmarks highlighting freedom of trade, business, investment, etc. | 2.9344 | 1.0168 | |
| X12 | Sovereign credit ratings | Risk level of debt that is guaranteed by the sovereign | 3.0033 | 0.9181 | |
| X13 | Competitiveness | Economic classification based on the Global Competitiveness Index | 3.0008 | 1.0351 | |
| Criminal environment | X14 | Corruption | Abuse level of power for personal gain | 2.9236 | 1.0495 |
| X15 | Natural resources industry controls | Assessment of industry controls in resource-rich countries | 2.8887 | 1.1694 | |
| X16 | Terrorism | Assessment of country terrorism fatalities and threats | 2.9618 | 0.8074 | |
| X17 | Absence of violence | Assessment of ‘peace’ level based on internal and external conflicts | 2.8912 | 0.9738 |
| Initial Eigenvalues | Extraction Sums of Squared Loading | Rotation Sums of Squared Loading | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Total | % of Variance | Cumulative % | Total | % of Variance | Cumulative % | % of Variance | Cumulative % | ||
| 1 | 10.5550 | 62.0885 | 62.0885 | 10.5550 | 62.0885 | 62.0885 | 6.0475 | 35.5738 | 35.5738 |
| 2 | 1.6996 | 9.9978 | 72.0863 | 1.6996 | 9.9978 | 72.0863 | 4.6261 | 27.2126 | 62.7864 |
| 3 | 1.2309 | 7.2404 | 79.3267 | 1.2309 | 7.2404 | 79.3267 | 2.8119 | 16.5403 | 79.3267 |
| Description | Variables | ||||
|---|---|---|---|---|---|
| Type of governance | X1 → | 0.8034 | 0.3881 | 0.7871 | 0.1824 |
| Civil liberties and political rights | X2 → | 0.8979 | 0.3195 | 0.8614 | 0.2319 |
| Freedom of the press | X3 → | 0.8739 | 0.2151 | 0.8821 | 0.2225 |
| Political stability | X4 → | 0.8039 | 0.5103 | 0.3823 | 0.6303 |
| Regulatory quality | X5 → | 0.8805 | 0.8325 | 0.4010 | 0.1633 |
| Rule of law | X6 → | 0.8500 | 0.7716 | 0.4262 | 0.2702 |
| Armed conflict | X7 → | 0.7570 | 0.3405 | 0.2769 | 0.7512 |
| Human rights | X8 → | 0.7735 | 0.2915 | 0.7078 | 0.4330 |
| Voice and accountability | X9 → | 0.9192 | 0.4076 | 0.8475 | 0.1865 |
| Average earnings | X10 → | 0.7621 | 0.8271 | 0.1665 | 0.2242 |
| Economic freedom | X11 → | 0.7516 | 0.7765 | 0.3111 | 0.2279 |
| Sovereign credit ratings | X12 → | 0.5925 | 0.7043 | 0.2246 | 0.2143 |
| Competitiveness | X13 → | 0.7506 | 0.8347 | 0.1936 | 0.1279 |
| Corruption | X14 → | 0.8077 | 0.7149 | 0.4880 | 0.2417 |
| Natural resources industry controls | X15 → | 0.7408 | 0.8082 | 0.2929 | 0.0436 |
| Terrorism | X16 → | 0.7957 | −0.0102 | 0.1327 | 0.8820 |
| Absence of violence | X17 → | 0.7252 | 0.4341 | 0.3846 | 0.6236 |
| Linguistic Pairwise Comparison | Corresponding TFNs | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 9 | (1, 1, 1) | (1, 2, 3) | (9, 9, 9) | (11, 12, 13) | 0.9489 | |
| 1/2 | 1 | 6 | (1/3, 1/2, 1) | (1, 1, 1) | (5, 6, 7) | (6.3333, 7.5, 9) | 0.0511 | |
| 1/9 | 1/6 | 1 | (1/9, 1/9, 1/9) | (1/7, 1/6, 1/5) | (1, 1, 1) | (1.254, 1.2778, 1.3111) | 0.0000 | |
| (18.5873, 20.7778, 23.3111) | ||||||||
| Goal | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Goal | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.9489 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0511 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.0002 | 0.1778 | 0.0000 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.0000 | 0.2115 | 0.0000 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.0000 | 0.2187 | 0.0000 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.0441 | 0.0000 | 0.1867 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.1321 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.1056 | 0.0115 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.0000 | 0.0000 | 0.2651 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.0000 | 0.1375 | 0.0325 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.0096 | 0.2010 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.1290 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.1117 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.0897 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.1351 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 0.0941 | 0.0421 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 0.1215 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 0.0000 | 0.0000 | 0.3489 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 0 | 0.0274 | 0.0000 | 0.1669 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Goal | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Goal | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0093 | 0.0002 | 0.1778 | 0.0000 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0108 | 0.0000 | 0.2115 | 0.0000 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0112 | 0.0000 | 0.2187 | 0.0000 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0418 | 0.0441 | 0.0000 | 0.1867 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.1253 | 0.1321 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.1008 | 0.1056 | 0.0115 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0000 | 0.0000 | 0.0000 | 0.2651 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0070 | 0.0000 | 0.1375 | 0.0325 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0193 | 0.0096 | 0.2010 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.1224 | 0.1290 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.1060 | 0.1117 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0851 | 0.0897 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 0.1282 | 0.1351 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 0.0915 | 0.0941 | 0.0421 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 0.1153 | 0.1215 | 0.0000 | 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 0.0000 | 0.0000 | 0.0000 | 0.3489 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 0.0260 | 0.0274 | 0.0000 | 0.1669 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Variables (Xi) | Corresponding to PCA | Description | |
|---|---|---|---|
| X1 | Type of governance | 0.0093 | |
| X2 | Civil liberties and political rights | 0.0108 | |
| X3 | Freedom of the press | 0.0112 | |
| X4 | Political stability | 0.0418 | |
| X5 | Regulatory quality | 0.1253 | |
| X6 | Rule of law | 0.1008 | |
| X7 | Armed conflict | 0.0000 | |
| X8 | Human rights | 0.0070 | |
| X9 | Voice and accountability | 0.0193 | |
| X10 | Average earnings | 0.1224 | |
| X11 | Economic freedom | 0.1060 | |
| X12 | Sovereign credit ratings | 0.0851 | |
| X13 | Competitiveness | 0.1282 | |
| X14 | Corruption | 0.0915 | |
| X15 | Natural resources industry controls | 0.1153 | |
| X16 | Terrorism | 0.0000 | |
| X17 | Absence of violence | 0.0260 |
| Economy Type a | N | Indicator | 2022 | 2021 | 2020 | 2019 | 2018 | 2017 | 2016 |
|---|---|---|---|---|---|---|---|---|---|
| Advanced Economies | 37 | Mean | 1.5982 | 1.6326 | 1.6310 | 1.6128 | 1.6454 | 1.6622 | 1.6781 |
| SD | 0.4045 | 0.4020 | 0.4096 | 0.4397 | 0.4754 | 0.4698 | 0.4910 | ||
| Emerging and Developing Asia | 25 | Mean | 3.2304 | 3.2412 | 3.2049 | 3.2071 | 3.2430 | 3.2212 | 3.2664 |
| SD | 0.4059 | 0.4194 | 0.4334 | 0.4194 | 0.4224 | 0.4101 | 0.4687 | ||
| Emerging and Developing Europe | 13 | Mean | 2.8559 | 2.8198 | 2.8632 | 2.8923 | 2.9240 | 2.9268 | 2.9316 |
| SD | 0.4022 | 0.3669 | 0.3649 | 0.4092 | 0.4050 | 0.4466 | 0.4463 | ||
| Latin America and The Caribbean | 30 | Mean | 3.0005 | 3.0148 | 3.0659 | 3.0672 | 3.0527 | 3.0651 | 3.0691 |
| SD | 0.4715 | 0.4572 | 0.4515 | 0.4390 | 0.4301 | 0.4192 | 0.4050 | ||
| Middle East and Central Asia | 25 | Mean | 3.4207 | 3.3810 | 3.4185 | 3.4241 | 3.4306 | 3.3652 | 3.3473 |
| SD | 0.6272 | 0.6566 | 0.6931 | 0.6358 | 0.6191 | 0.6216 | 0.6519 | ||
| Sub-Saharan Africa | 42 | Mean | 3.7170 | 3.7206 | 3.7119 | 3.7154 | 3.7024 | 3.6762 | 3.6689 |
| SD | 0.4844 | 0.4829 | 0.5013 | 0.4957 | 0.5052 | 0.4649 | 0.4449 | ||
| All countries | 172 | Mean | 2.9574 | 2.9612 | 2.9711 | 2.9716 | 2.9815 | 2.9684 | 2.9750 |
| SD | 0.8960 | 0.8848 | 0.8924 | 0.8950 | 0.8860 | 0.8639 | 0.8643 |
| Initial Eigenvalues | Extraction Sums of Squared Loading | Rotation Sums of Squared Loading | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Total | % of Variance | Cumulative % | Total | % of Variance | Cumulative % | % of Variance | Cumulative % | ||
| 1 | 6.520 | 72.439 | 72.439 | 6.520 | 72.439 | 72.439 | 3.921 | 43.572 | 43.572 |
| 2 | 0.859 | 9.545 | 81.984 | 0.859 | 9.545 | 81.984 | 3.457 | 38.412 | 81.984 |
| Variables | Corresponding in PCA | |||
|---|---|---|---|---|
| UROA | 0.8069 | 0.8714 | 0.2181 | |
| UAQ | 0.8609 | 0.6792 | 0.6321 | |
| UE&P | 0.8155 | 0.4894 | 0.7590 | |
| UC&L | 0.7491 | 0.4661 | 0.7293 | |
| UF&L | 0.6545 | 0.6783 | 0.4409 | |
| USIZE | 0.8541 | 0.1080 | 0.9179 | |
| UEQUITY | 0.8456 | 0.8918 | 0.2241 | |
| UGDP | 0.8518 | 0.6897 | 0.6133 | |
| UINF | 0.9401 | 0.7081 | 0.6624 |
| Linguistic Pairwise Comparison | Corresponding TFNs | |||||
|---|---|---|---|---|---|---|
| 1 | 9 | (1, 1, 1) | (9, 9, 9) | (10, 10, 10) | 1.0000 | |
| 1/9 | 1 | (1/9, 1/9, 1/9) | (1, 1, 1) | (1.1111, 1.1111, 1.1111) | 0.0000 | |
| (11.1111, 11.1111, 11.1111) | ||||||
| 1 | 2 | 2 | 2 | 2 | 2 | 1/2 | 2 | 2 | |
| 1/2 | 1 | 2 | 2 | 2 | 2 | 1/2 | 1/2 | 1/2 | |
| 1/2 | 1/2 | 1 | 2 | 1/2 | 2 | 1/2 | 1/2 | 1/2 | |
| 1/2 | 1/2 | 1/2 | 1 | 1/2 | 2 | 1/2 | 1/2 | 1/2 | |
| 1/2 | 1/2 | 2 | 2 | 1 | 2 | 1/2 | 1/2 | 1/2 | |
| 1/2 | 1/2 | 1/2 | 1/2 | 1/2 | 1 | 1/3 | 1/2 | 1/2 | |
| 2 | 2 | 2 | 2 | 2 | 3 | 1 | 2 | 2 | |
| 1/2 | 2 | 2 | 2 | 2 | 2 | 1/2 | 1 | 1/2 | |
| 1/2 | 2 | 2 | 2 | 2 | 2 | 1/2 | 2 | 1 |
| (1, 1, 1) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (8.3333, 15.5, 23) | 0.1406 | |
| (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (6.3333, 11, 17) | 0.1157 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (5, 8, 13) | 0.0928 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 1, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (4.3333, 6.5, 11) | 0.0786 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (1, 1, 1) | (1, 2, 3) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (5.6667, 9.5, 15) | 0.1051 | |
| (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (1, 1, 1) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1/3, 1/2, 1) | (3.5833, 4.8333, 8.5) | 0.0578 | |
| (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (2, 3, 4) | (1, 1, 1) | (1, 2, 3) | (1, 2, 3) | (10, 18, 26) | 0.1512 | |
| (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 1, 1) | (1/3, 1/2, 1) | (7, 12.5, 19) | 0.1250 | |
| (1/3, 1/2, 1) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1, 2, 3) | (1/3, 1/2, 1) | (1, 2, 3) | (1, 1, 1) | (7.6667, 14, 21) | 0.1332 | |
| (57.9167, 99.8333, 153.5) |
| - | 1 | 1 | 1 | 1 | 1 | 0.9299 | 1 | 1 | |
| 0.8415 | - | 1 | 1 | 1 | 1 | 0.7651 | 0.9429 | 0.8902 | |
| 0.6937 | 0.8591 | - | 1 | 0.9258 | 1 | 0.6140 | 0.7987 | 0.7438 | |
| 0.6007 | 0.7673 | 0.9128 | - | 0.8358 | 1 | 0.5200 | 0.7060 | 0.6508 | |
| 0.7730 | 0.9354 | 1 | 1 | - | 1 | 0.6948 | 0.8766 | 0.8226 | |
| 0.4639 | 0.6307 | 0.7826 | 0.8765 | 0.7015 | - | 0.3823 | 0.5685 | 0.5132 | |
| 1 | 1 | 1 | 1 | 1 | 1 | - | 1 | 1 | |
| 0.9011 | 1 | 1 | 1 | 1 | 1 | 0.8268 | - | 0.9487 | |
| 0.9535 | 1 | 1 | 1 | 1 | 1 | 0.8813 | 1 | - |
| Goal | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Goal | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.1406 | 0.0651 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.1157 | 0.1154 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.0928 | 0.1386 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.0786 | 0.1318 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.1051 | 0.0941 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 0.0578 | 0.1447 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 0.1512 | 0.0808 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 0.1250 | 0.1055 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 0 | 0.1332 | 0.1241 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Goal | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Goal | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.1406 | 0.1406 | 0.0651 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.1157 | 0.1157 | 0.1154 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0928 | 0.0928 | 0.1386 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0786 | 0.0786 | 0.1318 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 0.1051 | 0.1051 | 0.0941 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 0.0578 | 0.0578 | 0.1447 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 0.1512 | 0.1512 | 0.0808 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 0.1250 | 0.1250 | 0.1055 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 0.1332 | 0.1332 | 0.1241 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Bank Groups by Economy Type | N | 2022 | 2021 | 2020 | 2019 | |
|---|---|---|---|---|---|---|
| Advanced Economies | 331 | Mean | 0.1243 | 0.1183 | 0.1122 | 0.1320 |
| SD | 0.0297 | 0.0312 | 0.0300 | 0.0299 | ||
| Min | 0.0409 | 0.0393 | 0.0266 | 0.0241 | ||
| Max | 0.2292 | 0.2324 | 0.2172 | 0.2301 | ||
| Emerging and Developing Asia | 55 | Mean | 0.0307 | 0.0345 | 0.0345 | 0.0356 |
| SD | 0.0111 | 0.0104 | 0.0108 | 0.0124 | ||
| Min | 0.0091 | 0.0161 | 0.0176 | 0.0188 | ||
| Max | 0.0599 | 0.0628 | 0.0639 | 0.0691 | ||
| Emerging and Developing Europe | 20 | Mean | 0.0365 | 0.0395 | 0.0352 | 0.0393 |
| SD | 0.0179 | 0.0172 | 0.0185 | 0.0208 | ||
| Min | 0.0200 | 0.0227 | 0.0190 | 0.0221 | ||
| Max | 0.0712 | 0.0727 | 0.0729 | 0.0815 | ||
| Latin America and the Caribbean | 8 | Mean | 0.0290 | 0.0309 | 0.0259 | 0.0286 |
| SD | 0.0056 | 0.0072 | 0.0064 | 0.0064 | ||
| Min | 0.0211 | 0.0214 | 0.0178 | 0.0198 | ||
| Max | 0.0369 | 0.0402 | 0.0334 | 0.0372 | ||
| Middle East and Central Asia | 60 | Mean | 0.0329 | 0.0345 | 0.0337 | 0.0336 |
| SD | 0.0143 | 0.0154 | 0.0151 | 0.0161 | ||
| Min | 0.0095 | 0.0095 | 0.0074 | 0.0086 | ||
| Max | 0.0689 | 0.0753 | 0.0735 | 0.0756 | ||
| Sub-Saharan Africa | 22 | Mean | 0.0224 | 0.0217 | 0.0214 | 0.0224 |
| SD | 0.0119 | 0.0106 | 0.0100 | 0.0131 | ||
| Min | 0.0100 | 0.0107 | 0.0104 | 0.0089 | ||
| Max | 0.0427 | 0.0439 | 0.0435 | 0.0495 | ||
| All sample | 496 | Mean | 0.0933 | 0.0900 | 0.0856 | 0.0992 |
| SD | 0.0509 | 0.0482 | 0.0457 | 0.0534 | ||
| Min | 0.0091 | 0.0095 | 0.0074 | 0.0086 | ||
| Max | 0.2292 | 0.2324 | 0.2172 | 0.2301 |
| Description | Variables | France | Czech Republic | Romania | |
|---|---|---|---|---|---|
| Type of governance | X1 | 0.0093 | 2 | 1 | 2 |
| Civil liberties and political rights | X2 | 0.0108 | 2 | 1 | 2 |
| Freedom of the press | X3 | 0.0112 | 2 | 2 | 2 |
| Political stability | X4 | 0.0418 | 2 | 2 | 2 |
| Regulatory quality | X5 | 0.1253 | 2 | 2 | 3 |
| Rule of law | X6 | 0.1008 | 2 | 2 | 3 |
| Armed conflict | X7 | 0.0000 | 3 | 2 | 1 |
| Human rights | X8 | 0.0070 | 1 | 1 | 2 |
| Voice & accountability | X9 | 0.0193 | 2 | 2 | 2 |
| Average earnings | X10 | 0.1224 | 2 | 2 | 2 |
| Economic freedom | X11 | 0.1060 | 2 | 2 | 2 |
| Sovereign credit ratings | X12 | 0.0851 | 2 | 2 | 3 |
| Competitiveness | X13 | 0.1282 | 1 | 2 | 3 |
| Corruption | X14 | 0.0915 | 1 | 2 | 3 |
| Natural resources industry controls | X15 | 0.1153 | 1 | 1 | 2 |
| Terrorism | X16 | 0.0000 | 4 | 3 | 3 |
| Absence of violence | X17 | 0.0260 | 3 | 1 | 2 |
| ) | - | - | 1.6840 | 1.8316 | 2.5309 |
| Variables | Weights | Societe Generale SA (France) | Komercni Banka as (Czech Republic) | BRD Groupe Societe Generale SA (Romania) |
|---|---|---|---|---|
| - | 1.6840 | 1.8316 | 2.5309 | |
| 0.0108 | 0.2364 | 1.1579 | 2.0223 | |
| 0.0112 | 2.5514 | 2.4286 | 3.3305 | |
| 0.0418 | 4.2502 | 9.2841 | 5.1919 | |
| 0.1253 | 16.2900 | 18.9000 | 20.6400 | |
| 0.1008 | 90.6945 | 77.9352 | 69.0012 | |
| 0.0000 | 27.9937 | 24.5852 | 23.3242 | |
| 0.0070 | 4.4672 | 9.6728 | 13.2372 | |
| 0.0193 | 2.6060 | 2.4420 | 4.7910 | |
| 0.1224 | 6.9580 | 15.7590 | 16.3710 | |
| Bank Performance Scores | - | 0.1064 | 0.0965 | 0.0507 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Opreana, A.; Vinerean, S.; Mihaiu, D.M.; Barbu, L.; Șerban, R.-A. Fuzzy Analytic Network Process with Principal Component Analysis to Establish a Bank Performance Model under the Assumption of Country Risk. Mathematics 2023, 11, 3257. https://doi.org/10.3390/math11143257
Opreana A, Vinerean S, Mihaiu DM, Barbu L, Șerban R-A. Fuzzy Analytic Network Process with Principal Component Analysis to Establish a Bank Performance Model under the Assumption of Country Risk. Mathematics. 2023; 11(14):3257. https://doi.org/10.3390/math11143257
Chicago/Turabian StyleOpreana, Alin, Simona Vinerean, Diana Marieta Mihaiu, Liliana Barbu, and Radu-Alexandru Șerban. 2023. "Fuzzy Analytic Network Process with Principal Component Analysis to Establish a Bank Performance Model under the Assumption of Country Risk" Mathematics 11, no. 14: 3257. https://doi.org/10.3390/math11143257








