Retrieval-Augmented Knowledge Graph Reasoning for Commonsense Question Answering
Abstract
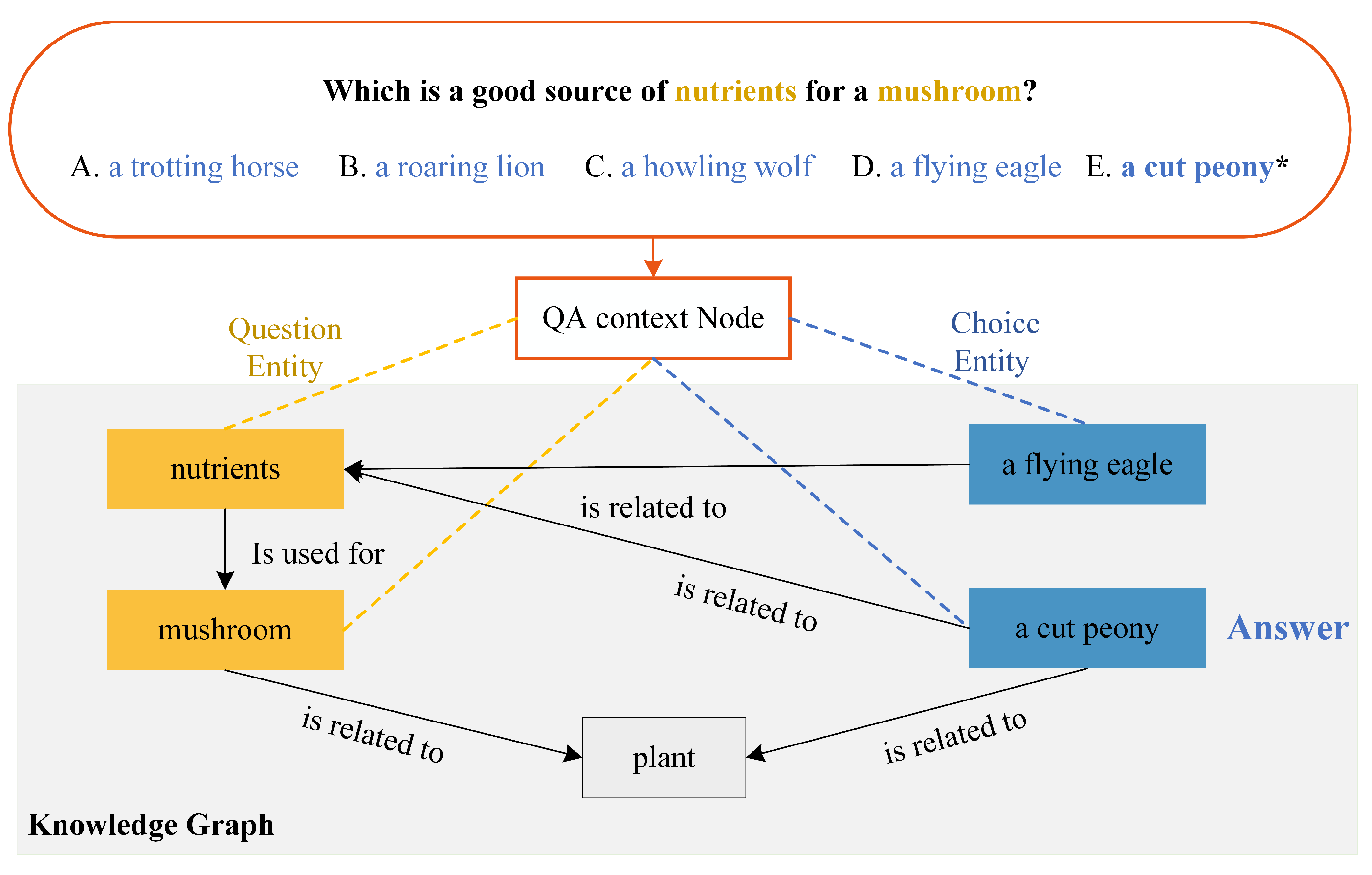
:1. Introduction
- (1)
- We propose a novel RAKG model with a retrieval-augmented KG subgraph for question answering. The augmented subgraph is extracted using the density matrix, which removes any irrelevant nodes at each layer of the RAKG.
- (2)
- Our model utilizes a bidirectional attention strategy to effectively integrate the representations of both language models and knowledge graphs. Moreover, we use R-dropout to prevent overfitting and improve model generalization.
- (3)
- The experimental results show that the proposed RAKG achieves better performance than several baselines on the CommonsenseQA and OpenbookQA benchmarks.
2. Related Work
2.1. Knowledge-Graph-Based Question Answering
2.2. Graph Convolutional Network
3. Methodology
3.1. Task Formulation
3.2. Language Context Encoder
3.3. KG Subgraph Extraction
3.4. Retrieval-Augmented Knowledge Graph Module
3.5. Answer Prediction
4. Experimental Setup
4.1. Datasets
4.2. Implementation Details
4.3. Baselines
5. Results and Analysis
5.1. Main Results
5.2. Ablation Studies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| KG | Knowledge graph. |
| QA | Question answering. |
| GCN | Graph convolutional network. |
| KG-QA | Knowledge graph-based question answering. |
References
- Li, J.; Niu, L.; Zhang, L. From Representation to Reasoning: Towards both Evidence and Commonsense Reasoning for Video Question-Answering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 21273–21282. [Google Scholar]
- Liu, J.; Hallinan, S.; Lu, X.; He, P.; Welleck, S.; Hajishirzi, H.; Choi, Y. Rainier: Reinforced knowledge introspector for commonsense question answering. arXiv 2022, arXiv:2210.03078. [Google Scholar]
- Peters, M.E.; Neumann, M.; Iyyer, M.; Gardner, M.; Clark, C.; Lee, K.; Zettlemoyer, L. Deep Contextualized Word Representations. arXiv 2018, arXiv:1802.05365v2. [Google Scholar]
- Zhan, X.; Huang, Y.; Dong, X.; Cao, Q.; Liang, X. PathReasoner: Explainable reasoning paths for commonsense question answering. Knowl.-Based Syst. 2022, 235, 107612. [Google Scholar] [CrossRef]
- Seo, J.; Oh, D.; Eo, S.; Park, C.; Yang, K.; Moon, H.; Park, K.; Lim, H. PU-GEN: Enhancing generative commonsense reasoning for language models with human-centered knowledge. Knowl.-Based Syst. 2022, 256, 109861. [Google Scholar] [CrossRef]
- Speer, R.; Chin, J.; Havasi, C. Conceptnet 5.5: An open multilingual graph of general knowledge. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31, pp. 1–8. [Google Scholar]
- Bollacker, K.; Evans, C.; Paritosh, P.; Sturge, T.; Taylor, J. Freebase: A collaboratively created graph database for structuring human knowledge. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 9–12 June 2008; pp. 1247–1250. [Google Scholar]
- Bhargava, P.; Ng, V. Commonsense knowledge reasoning and generation with pre-trained language models: A survey. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 22 February–1 March 2022; Volune 36, pp. 12317–12325. [Google Scholar]
- Qiao, Z.; Ye, W.; Zhang, T.; Mo, T.; Li, W.; Zhang, S. Exploiting Hybrid Semantics of Relation Paths for Multi-hop Question Answering over Knowledge Graphs. arXiv 2022, arXiv:2209.00870. [Google Scholar]
- Zhang, Q.; Chen, S.; Fang, M.; Chen, X. Joint reasoning with knowledge subgraphs for Multiple Choice Question Answering. Inf. Process. Manag. 2023, 60, 103297. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Yu, J.; Tang, J.; Tang, J.; Li, C.; Chen, H. Subgraph Retrieval Enhanced Model for Multi-hop Knowledge Base Question Answering. Assoc. Comput. Linguist. 2022, 5773–5784. [Google Scholar]
- Cui, L.; Zhu, W.; Tao, S.; Case, J.T.; Bodenreider, O.; Zhang, G.Q. Mining non-lattice subgraphs for detecting missing hierarchical relations and concepts in SNOMED CT. J. Am. Med. Inform. Assoc. 2017, 24, 788–798. [Google Scholar] [CrossRef] [Green Version]
- Yasunaga, M.; Ren, H.; Bosselut, A.; Liang, P.; Leskovec, J. QA-GNN: Reasoning with Language Models and Knowledge Graphs for Question Answering. arXiv 2021, arXiv:2104.06378. [Google Scholar]
- Feng, Y.; Chen, X.; Lin, B.Y.; Wang, P.; Yan, J.; Ren, X. Scalable multi-hop relational reasoning for knowledge-aware question answering. arXiv 2020, arXiv:2005.00646. [Google Scholar]
- Zhang, Y.; Jin, L.; Li, X.; Wang, H. Edge-Aware Graph Neural Network for Multi-Hop Path Reasoning over Knowledge Base. Comput. Intell. Neurosci. 2022, 2022, 4734179. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Dai, H.; Dai, B.; Chen, X.; Zhou, D.; Leskovec, J.; Schuurmans, D. Smore: Knowledge graph completion and multi-hop reasoning in massive knowledge graphs. In Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 1472–1482. [Google Scholar]
- Zheng, C.; Kordjamshidi, P. Dynamic Relevance Graph Network for Knowledge-Aware Question Answering. arXiv 2022, arXiv:2209.09947. [Google Scholar]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Van Den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In The Semantic Web: 15th International Conference, ESWC 2018, Heraklion, Crete, Greece, 3–7 June 2018, Proceedings 15; Springer International Publishing: Cham, Switzerland, 2018; pp. 593–607. [Google Scholar]
- Wang, X.; Kapanipathi, P.; Musa, R.; Yu, M.; Talamadupula, K.; Abdelaziz, I.; Chang, M.; Fokoue, A.; Makni, B.; Mattei, N.; et al. Improving natural language inference using external knowledge in the science questions domain. In Proceedings of the Association for the Advancement of Artificial Intelligence Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volune 33, pp. 7208–7215. [Google Scholar]
- Zhang, Q.; Chen, S.; Xu, D.; Cao, Q.; Chen, X.; Cohn, T.; Fang, M. A survey for efficient open domain question answering. arXiv 2022, arXiv:2211.07886. [Google Scholar]
- Zhang, Y.; Dai, H.; Kozareva, Z.; Smola, A.; Song, L. Variational reasoning for question answering with knowledge graph. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orlean, LA, USA, 2–7 February 2018; Volune 32. [Google Scholar]
- Abacha, A.B.; Zweigenbaum, P. MEANS: A medical question-answering system combining NLP techniques and semantic Web technologies. Inf. Process. Manag. 2015, 51, 570–594. [Google Scholar] [CrossRef]
- Li, Z.; Zhong, Q.; Yang, J.; Duan, Y.; Wang, W.; Wu, C.; He, K. DeepKG: An end-to-end deep learning-based workflow for biomedical knowledge graph extraction, optimization and applications. Bioinformatics 2022, 38, 1477–1479. [Google Scholar] [CrossRef] [PubMed]
- Tiddi, I.; Schlobach, S. Knowledge graphs as tools for explainable machine learning: A survey. Artif. Intell. 2022, 302, 103627. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, W.; Zhu, Y.; Zhou, H.; Yuan, Z.; Xu, C.; Chen, H. Meta-knowledge transfer for inductive knowledge graph embedding. In Proceedings of the ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, 11–15 July 2022; pp. 927–937. [Google Scholar]
- Howard, P.; Ma, A.; Lal, V.; Simoes, A.P.; Korat, D.; Pereg, O.; Wasserblat, M.; Singer, G. Cross-Domain Aspect Extraction using Transformers Augmented with Knowledge Graphs. In Proceedings of the ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 780–790. [Google Scholar]
- Lin, B.Y.; Chen, X.; Chen, J.; Ren, X. Kagnet: Knowledge-aware graph networks for commonsense reasoning. arXiv 2019, arXiv:1909.02151. [Google Scholar]
- Gao, H.; Wang, Z.; Ji, S. Large-Scale Learnable Graph Convolutional Networks. arXiv 2018, arXiv:1808.03965. [Google Scholar]
- Parisot, S.; Ktena, S.I.; Ferrante, E.; Lee, M.; Moreno, R.G.; Glocker, B.; Rueckert, D. Spectral graph convolutions for population-based disease prediction. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2017: 20th International Conference, Quebec City, QC, Canada, 11–13 September 2017, Proceedings, Part III; Springer International Publishing: Cham, Switzerland, 2017; pp. 177–185. [Google Scholar]
- Therasa, M.; Mathivanan, G. ARNN-QA: Adaptive Recurrent Neural Network with feature optimization for incremental learning-based Question Answering system. Appl. Soft Comput. 2022, 124, 109029. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, P.; Luo, D.; Zhu, X.; Zhou, M.; Liang, Q.; Wang, B. Syntax-based graph matching for knowledge base question answering. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Singapore, 23–27 May 2022; pp. 8227–8231. [Google Scholar]
- Shan, Y.; Che, C.; Wei, X.; Wang, X.; Zhu, Y.; Jin, B. Bi-graph attention network for aspect category sentiment classification. Knowl.-Based Syst. 2022, 258, 109972. [Google Scholar] [CrossRef]
- Li, J.; Peng, J.; Chen, L.; Zheng, Z.; Liang, T.; Ling, Q. Spectral Adversarial Training for Robust Graph Neural Network. IEEE Trans. Knowl. Data Eng. 2022, 1, 1–14. [Google Scholar] [CrossRef]
- Wu, L.; Li, J.; Wang, Y.; Meng, Q.; Qin, T.; Chen, W.; Zhang, M.; Liu, T.Y. R-drop: Regularized dropout for neural networks. Adv. Neural Inf. Process. Syst. 2021, 34, 10890–10905. [Google Scholar]
- Talmor, A.; Herzig, J.; Lourie, N.; Berant, J. CommonsenseQA: A question answering challenge targeting commonsense knowledge. arXiv 2018, arXiv:1811.00937. [Google Scholar]
- Mihaylov, T.; Clark, P.; Khot, T.; Sabharwal, A. Can a suit of armor conduct electricity? a new dataset for open book question answering. arXiv 2018, arXiv:1809.02789. [Google Scholar]
- Liu, L.; Jiang, H.; He, P.; Chen, W.; Liu, X.; Gao, J.; Han, J. On the variance of the adaptive learning rate and beyond. arXiv 2019, arXiv:1908.03265. [Google Scholar]
- Liu, Y.; Ott, M.; Goyal, N.; Du, J.; Joshi, M.; Chen, D.; Levy, O.; Lewis, M.; Zettlemoyer, L.; Stoyanov, V. Roberta: A robustly optimized bert pretraining approach. arXiv 2019, arXiv:1907.11692. [Google Scholar]
- Santoro, A.; Raposo, D.; Barrett, D.G.; Malinowski, M.; Pascanu, R.; Battaglia, P.; Lillicrap, T. A simple neural network module for relational reasoning. arXiv 2017, arXiv:1706.01427. [Google Scholar]



| Dataset | Train | Dev | Test | Choices |
|---|---|---|---|---|
| CSQA | 9741 | 1221 | 1140 | 5 |
| OBQA | 4957 | 500 | 500 | 4 |
| Methods | IHdev-Acc. (%) | IHtest-Acc. (%) |
|---|---|---|
| RoBERTa-large [38] | 73.07 | 68.69 |
| +R-GCN [18] | 72.69 | 68.41 |
| +GconAttn [19] | 72.61 | 68.59 |
| +KagNet [27] | 73.47 | 69.01 |
| +RN [39] | 74.57 | 69.08 |
| +MHGRN [14] | 74.45 | 71.11 |
| +QA-GNN [13] | 76.50 | 73.40 |
| +RAKG (Ours) | 76.74 | 73.51 |
| Methods | IHdev-Acc. (%) | IHtest-Acc. (%) |
|---|---|---|
| RoBERTa-large [38] | 66.7 | 64.8 |
| +R-GCN [18] | 65.0 | 62.4 |
| +GconAttn [19] | 64.5 | 61.9 |
| +RN [39] | 66.8 | 65.2 |
| +MHGRN [14] | 68.1 | 66.8 |
| +QA-GNN [13] | 68.9 | 67.8 |
| +DRGN [17] | 70.1 | 69.6 |
| +RAKG (Ours) | 73.0 | 77.0 |
| Methods | IHdev-Acc. (%) |
|---|---|
| RAKG (N = 5) w/o KG subgraph | 69.6 |
| +KG subgraph | 72.6 |
| +density matrix | 75.4 |
| +bidirectional attention | 76.2 |
| +R-Dropout | 76.7 |
| RAKG + R-Dropout (%) | |
|---|---|
| = 0.5 | 74.5 |
| = 0.7 | 76.7 |
| = 0.9 | 76.3 |
| = 1.0 | 75.6 |
| = 5.0 | 75.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, Y.; Feng, Y.; He, M.; Liu, S.; Ji, Y. Retrieval-Augmented Knowledge Graph Reasoning for Commonsense Question Answering. Mathematics 2023, 11, 3269. https://doi.org/10.3390/math11153269
Sha Y, Feng Y, He M, Liu S, Ji Y. Retrieval-Augmented Knowledge Graph Reasoning for Commonsense Question Answering. Mathematics. 2023; 11(15):3269. https://doi.org/10.3390/math11153269
Chicago/Turabian StyleSha, Yuchen, Yujian Feng, Miao He, Shangdong Liu, and Yimu Ji. 2023. "Retrieval-Augmented Knowledge Graph Reasoning for Commonsense Question Answering" Mathematics 11, no. 15: 3269. https://doi.org/10.3390/math11153269
APA StyleSha, Y., Feng, Y., He, M., Liu, S., & Ji, Y. (2023). Retrieval-Augmented Knowledge Graph Reasoning for Commonsense Question Answering. Mathematics, 11(15), 3269. https://doi.org/10.3390/math11153269









