An Enhanced Dwarf Mongoose Optimization Algorithm for Solving Engineering Problems
Abstract
:1. Introduction
2. EDMOA Version with Alpha-Directed LS
2.1. Standard DMOA
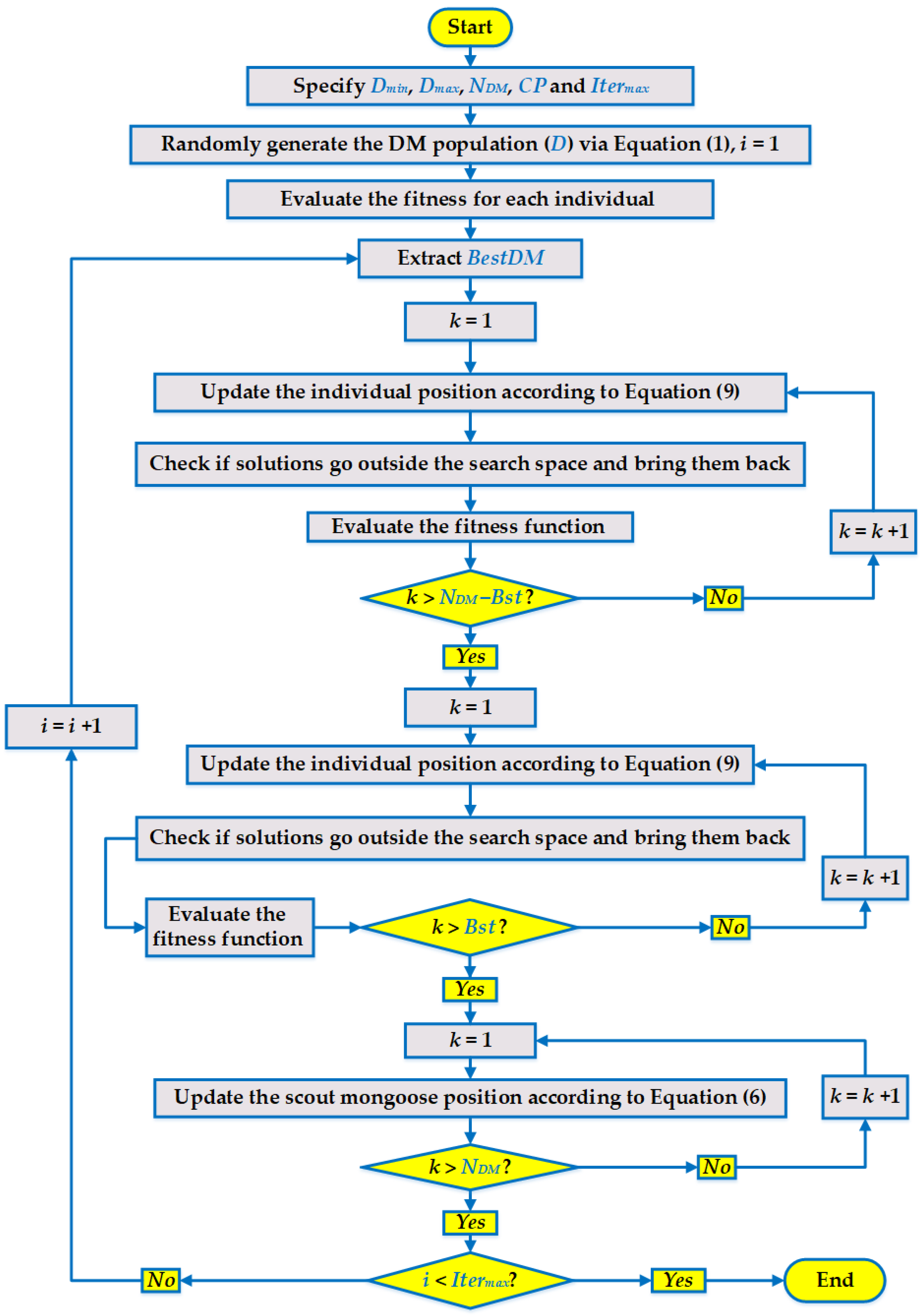
2.2. Proposed EDMOA
3. Application Assessment for Benchmarking Models
4. Application Assessment for Benchmarking Models
5. Application for Engineering Optimization Problem: Optimal Dispatch of Combined Power and Heat
6. Conclusions
- For the first 13 benchmarks, the proposed EDMOA outperforms the regular DMOA in terms of obtaining the lowest mean, STd, and median in more than 80% of benchmark functions. Furthermore, the provided EDMOA achieves the greatest performance by ranking first among DE, MVO, SSA, DMOA, SCA, and PSO.
- For the CEC 2017 benchmarks, the suggested EDMOA has a higher strength compared to the standard DMOA in terms of obtaining the lowest mean, STd, and median in more than 85% of benchmark functions. Also, the provided EDMOA achieves the best performance by recording the top rank compared to SMA, DMOA, GWO, Circle, and PSO.
- For the DCPH engineering problem, the proposed EDMOA outperforms the basic DMOA by obtaining lower costs in all completed runs with savings ranging from 3.3% to 5.78%. Furthermore, the suggested DMOA surpasses not only the standard DMOA but also a number of other recent methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hajipour, V.; Mehdizadeh, E.; Tavakkoli-Moghaddam, R. A novel Pareto-based multi-objective vibration damping optimization algorithm to solve multi-objective optimization problems. Sci. Iran. 2014, 21, 2368–2378. [Google Scholar]
- Hajipour, V.; Kheirkhah, A.S.; Tavana, M.; Absi, N. Novel Pareto-based meta-heuristics for solving multi-objective multi-item capacitated lot-sizing problems. Int. J. Adv. Manuf. Technol. 2015, 80, 31–45. [Google Scholar] [CrossRef]
- Wu, G. Across neighborhood search for numerical optimization. Inf. Sci. 2016, 329, 597–618. [Google Scholar] [CrossRef] [Green Version]
- Sergeyev, Y.D.; Kvasov, D.E.; Mukhametzhanov, M.S. On the efficiency of nature-inspired metaheuristics in expensive global optimization with limited budget. Sci. Rep. 2018, 8, 453. [Google Scholar] [CrossRef] [Green Version]
- Alshamrani, A.M.; Alrasheedi, A.F.; Alnowibet, K.A.; Mahdi, S.; Mohamed, A.W. A Hybrid Stochastic Deterministic Algorithm for Solving Unconstrained Optimization Problems. Mathematics 2022, 10, 3032. [Google Scholar] [CrossRef]
- Koc, I.; Atay, Y.; Babaoglu, I. Discrete tree seed algorithm for urban land readjustment. Eng. Appl. Artif. Intell. 2022, 112, 104783. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovská, E.; Trojovský, P. A new human-based metaheuristic algorithm for solving optimization problems on the base of simulation of driving training process. Sci. Rep. 2022, 12, 9924. [Google Scholar] [CrossRef]
- Agrawal, P.; Alnowibet, K.; Mohamed, A.W. Gaining-sharing knowledge based algorithm for solving stochastic programming problems. Comput. Mater. Contin. 2022, 71, 2847–2868. [Google Scholar] [CrossRef]
- Bertsimas, D.; Mundru, N. Optimization-Based Scenario Reduction for Data-Driven Two-Stage Stochastic Optimization. Oper. Res. 2022. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, M.; Wang, F.; Xiao, W. A dynamic stochastic search algorithm for high-dimensional optimization problems and its application to feature selection. Knowl.-Based Syst. 2022, 244, 108517. [Google Scholar] [CrossRef]
- de Armas, J.; Lalla-Ruiz, E.; Tilahun, S.L.; Voß, S. Similarity in metaheuristics: A gentle step towards a comparison methodology. Nat. Comput. 2022, 21, 265–287. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Futur. Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubalovsky, S.; Trojovsky, P. Tasmanian Devil Optimization: A New Bio-Inspired Optimization Algorithm for Solving Optimization Algorithm. IEEE Access 2022, 10, 19599–19620. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning, 1989th ed.; Addison-Wesley Publishing Company, Inc.: Redwood City, CA, USA, 1989. [Google Scholar]
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Das, D.; Patvardhan, C. A new hybrid evolutionary strategy for reactive power dispatch. Electr. Power Syst. Res. 2003, 65, 83–90. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Chou, J.S.; Truong, D.N. A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean. Appl. Math. Comput. 2021, 389, 125535. [Google Scholar] [CrossRef]
- Askari, Q.; Saeed, M.; Younas, I. Heap-based optimizer inspired by corporate rank hierarchy for global optimization. Expert Syst. Appl. 2020, 161, 113702. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine predators algorithm: A nature-inspired Metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Dehghani, M.; Mardaneh, M.; Malik, O.P.; Guerrero, J.M.; Sotelo, C.; Sotelo, D.; Nazari-Heris, M.; Al-Haddad, K.; Ramirez-Mendoza, R.A. Genetic algorithm for energy commitment in a power system supplied by multiple energy carriers. Sustainability 2020, 12, 10053. [Google Scholar] [CrossRef]
- Montazeri, Z.; Niknam, T. Optimal utilization of electrical energy from power plants based on final energy consumption using gravitational search algorithm. Electr. Eng. Electromech. 2018, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Li, K.; Xu, B.; Yang, Z. Biogeography-based learning particle swarm optimization for combined heat and power economic dispatch problem. Knowl.-Based Syst. 2020, 208, 106463. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Geem, Z.W. A comprehensive survey of the harmony search algorithm in clustering applications. Appl. Sci. 2020, 10, 3827. [Google Scholar] [CrossRef]
- Khan, A.T.; Cao, X.; Liao, B.; Francis, A. Bio-inspired Machine Learning for Distributed Confidential Multi-Portfolio Selection Problem. Biomimetics 2022, 7, 124. [Google Scholar] [CrossRef]
- Chen, Z.; Francis, A.; Li, S.; Liao, B.; Xiao, D.; Ha, T.T.; Li, J.; Ding, L.; Cao, X. Egret Swarm Optimization Algorithm: An Evolutionary Computation Approach for Model Free Optimization. Biomimetics 2022, 7, 144. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Li, S.; Cao, X. Time-varying minimum-cost portfolio insurance under transaction costs problem via Beetle Antennae Search Algorithm (BAS). Appl. Math. Comput. 2020, 385, 125453. [Google Scholar] [CrossRef]
- Rohman, M.N.; Hidayat, M.I.P.; Purniawan, A. Prediction of composite fatigue life under variable amplitude loading using artificial neural network trained by genetic algorithm. AIP Conf. Proc. 2018, 1945, 020019. [Google Scholar]
- Moustafa, G.; Elshahed, M.; Ginidi, A.R.; Shaheen, A.M.; Mansour, H.S.E. A Gradient-Based Optimizer with a Crossover Operator for Distribution Static VAR Compensator (D-SVC) Sizing and Placement in Electrical Systems. Mathematics 2023, 11, 1077. [Google Scholar] [CrossRef]
- Hidayat, M.I.P. System Identification Technique and Neural Networks for Material Lifetime Assessment Application. Stud. Fuzziness Soft Comput. 2015, 319, 773–806. [Google Scholar]
- Hidayat, M.I.P.; Yusoff, P.S.M.M. Optimizing neural network prediction of composite fatigue life under variable amplitude loading using bayesian regularization. In Composite Materials Technology: Neural Network Applications; CRC Press: Boca Raton, FL, USA, 2009; pp. 221–250. [Google Scholar] [CrossRef]
- Khan, A.H.; Cao, X.; Xu, B.; Li, S. Beetle Antennae Search: Using Biomimetic Foraging Behaviour of Beetles to Fool a Well-Trained Neuro-Intelligent System. Biomimetics 2022, 7, 84. [Google Scholar] [CrossRef]
- Aribia, H.B.; El-Rifaie, A.M.; Tolba, M.A.; Shaheen, A.; Moustafa, G.; Elsayed, F.; Elshahed, M. Growth Optimizer for Parameter Identification of Solar Photovoltaic Cells and Modules. Sustainability 2023, 15, 7896. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Abualigah, L. Dwarf Mongoose Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2022, 391, 114570. [Google Scholar] [CrossRef]
- Akinola, O.A.; Ezugwu, A.E.; Oyelade, O.N.; Agushaka, J.O. A hybrid binary dwarf mongoose optimization algorithm with simulated annealing for feature selection on high dimensional multi-class datasets. Sci. Rep. 2022, 12, 14945. [Google Scholar] [CrossRef]
- Singh, B.; Bishnoi, S.K.; Sharma, M. Frequency Regulation Scheme for PV integrated Power System using Energy Storage Device. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power, ICICCSP 2022, Chengdu, China, 19–22 August 2022. [Google Scholar] [CrossRef]
- Sadoun, A.M.; Najjar, I.R.; Alsoruji, G.S.; Wagih, A.; Elaziz, M.A. Utilizing a Long Short-Term Memory Algorithm Modified by Dwarf Mongoose Optimization to Predict Thermal Expansion of Cu-Al2O3 Nanocomposites. Mathematics 2022, 10, 1050. [Google Scholar] [CrossRef]
- Abirami, A.; Kavitha, R. An efficient early detection of diabetic retinopathy using dwarf mongoose optimization based deep belief network. Concurr. Comput. Pract. Exp. 2022, 34, e7364. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Ewees, A.A.; Al-qaness, M.A.A.; Alshathri, S.; Ibrahim, R.A. Feature Selection for High Dimensional Datasets Based on Quantum-Based Dwarf Mongoose Optimization. Mathematics 2022, 10, 4565. [Google Scholar] [CrossRef]
- Balasubramaniam, S.; Satheesh Kumar, K.; Kavitha, V.; Prasanth, A.; Sivakumar, T.A. Feature Selection and Dwarf Mongoose Optimization Enabled Deep Learning for Heart Disease Detection. Comput. Intell. Neurosci. 2022, 2022, 2819378. [Google Scholar] [CrossRef]
- Mehmood, K.; Chaudhary, N.I.; Khan, Z.A.; Cheema, K.M.; Raja, M.A.Z.; Milyani, A.H.; Azhari, A.A. Dwarf Mongoose Optimization Metaheuristics for Autoregressive Exogenous Model Identification. Mathematics 2022, 10, 3821. [Google Scholar] [CrossRef]
- Dora, B.K.; Bhat, S.; Halder, S.; Srivastava, I. A Solution to the Techno-Economic Generation Expansion Planning Using Enhanced Dwarf Mongoose Optimization Algorithm. In Proceedings of the IBSSC 2022—IEEE Bombay Section Signature Conference, Mumbai, India, 8–10 December 2022. [Google Scholar] [CrossRef]
- Aldosari, F.; Abualigah, L.; Almotairi, K.H. A Normal Distributed Dwarf Mongoose Optimization Algorithm for Global Optimization and Data Clustering Applications. Symmetry 2022, 14, 1021. [Google Scholar] [CrossRef]
- Sarhan, S.; Shaheen, A.M.; El-Sehiemy, R.A.; Gafar, M. An Enhanced Slime Mould Optimizer That Uses Chaotic Behavior and an Elitist Group for Solving Engineering Problems. Mathematics 2022, 10, 1991. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Shen, Y.; Liang, Z.; Kang, H.; Sun, X.; Chen, Q. A modified jso algorithm for solving constrained engineering problems. Symmetry 2021, 13, 63. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Turky, R.A.; Alghuwainem, S.; Tostado-Véliz, M.; Jurado, F. Circle Search Algorithm: A Geometry-Based Metaheuristic Optimization Algorithm. Mathematics 2022, 10, 1626. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Mahdy, A.; Shaheen, A.; El-Sehiemy, R.; Ginidi, A.; Al-Gahtani, S.F. Single- and Multi-Objective Optimization Frameworks of Shape Design of Tubular Linear Synchronous Motor. Energies 2023, 16, 2409. [Google Scholar] [CrossRef]
- Abid, S.; El-Rifaie, A.M.; Elshahed, M.; Ginidi, A.R.; Shaheen, A.M.; Moustafa, G.; Tolba, M.A. Development of Slime Mold Optimizer with Application for Tuning Cascaded PD-PI Controller to Enhance Frequency Stability in Power Systems. Mathematics 2023, 11, 1796. [Google Scholar] [CrossRef]
- Khan, A.T.; Senior, S.L.; Stanimirovic, P.S. Model-Free Optimization Using Eagle Perching Optimizer. Available online: https://www.mathworks.com/matlabcentral/fileexchange/67978-model-free-optimization-using-eagle-perching-optimizer (accessed on 20 June 2023).
- Sarhan, S.; El-Sehiemy, R.A.; Shaheen, A.M.; Gafar, M. TLBO merged with studying effect for Economic Environmental Energy Management in High Voltage AC Networks Hybridized with Multi-Terminal DC Lines. Appl. Soft Comput. 2023, 143, 110426. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Elsayed, A.M.; Elattar, E.E.; El-Sehiemy, R.A.; Ginidi, A.R. An Intelligent Heap-Based Technique With Enhanced Discriminatory Attribute for Large-Scale Combined Heat and Power Economic Dispatch. IEEE Access 2022, 10, 64325–64338. [Google Scholar] [CrossRef]
- Kaur, P.; Chaturvedi, K.T.; Kolhe, M.L. Techno-Economic Power Dispatching of Combined Heat and Power Plant Considering Prohibited Operating Zones and Valve Point Loading. Processes 2022, 10, 817. [Google Scholar] [CrossRef]
- El-Sehiemy, R.; Shaheen, A.; Ginidi, A.; Elhosseini, M. A Honey Badger Optimization for Minimizing the Pollutant Environmental Emissions-Based Economic Dispatch Model Integrating Combined Heat and Power Units. Energies 2022, 15, 7603. [Google Scholar] [CrossRef]
- Sarhan, S.; Shaheen, A.; El-Sehiemy, R.; Gafar, M. A Multi-Objective Teaching-Learning Studying-Based Algorithm for Large-Scale Dispatching of Combined Electrical Power and Heat Energies. Mathematics 2022, 10, 2278. [Google Scholar] [CrossRef]
- Ginidi, A.R.; Elsayed, A.M.; Shaheen, A.M.; Elattar, E.E.; El-Sehiemy, R.A. A Novel Heap based Optimizer for Scheduling of Large-scale Combined Heat and Power Economic Dispatch. IEEE Access 2021, 9, 83695–83708. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Elattar, E.; Ginidi, A.R. An Amalgamated Heap and Jellyfish Optimizer for economic dispatch in Combined heat and power systems including N-1 Unit outages. Energy 2022, 246, 123351. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mehdinejad, M.; Mohammadi-Ivatloo, B.; Babamalek-Gharehpetian, G. Combined heat and power economic dispatch problem solution by implementation of whale optimization method. Neural Comput. Appl. 2019, 31, 421–436. [Google Scholar] [CrossRef]
- Mahdy, A.; El-Sehiemy, R.; Shaheen, A.; Ginidi, A.; Elbarbary, Z.M.S. An Improved Artificial Ecosystem Algorithm for Economic Dispatch with Combined Heat and Power Units. Appl. Sci. 2022, 12, 11773. [Google Scholar] [CrossRef]
- Ginidi, A.; Elsayed, A.; Shaheen, A.; Elattar, E.; El-Sehiemy, R. An Innovative Hybrid Heap-Based and Jellyfish Search Algorithm for Combined Heat and Power Economic Dispatch in Electrical Grids. Mathematics 2021, 9, 2053. [Google Scholar] [CrossRef]
- Beigvand, S.D.; Abdi, H.; La Scala, M. Combined heat and power economic dispatch problem using gravitational search algorithm. Electr. Power Syst. Res. 2016, 133, 160–172. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Ginidi, A.R.; El-Sehiemy, R.A.; Ghoneim, S.S.M. Economic Power and Heat Dispatch in Cogeneration Energy Systems Using Manta Ray Foraging Optimizer. IEEE Access 2020, 8, 208281–208295. [Google Scholar] [CrossRef]
- Mohammadi-Ivatloo, B.; Moradi-Dalvand, M.; Rabiee, A. Combined heat and power economic dispatch problem solution using particle swarm optimization with time varying acceleration coefficients. Electr. Power Syst. Res. 2013, 95, 9–18. [Google Scholar] [CrossRef]











| Function | Minimum | Dim | Bounds |
|---|---|---|---|
| 0 | 30 | [−100, 100] | |
| 0 | 30 | [−10, 10] | |
| 0 | 30 | [−100, 100] | |
| 0 | 30 | [−100, 100] | |
| 0 | 30 | [−30, 30] | |
| 0 | 30 | [−100, 100] | |
| 0 | 30 | [−128, 128] |
| Function | Min. | Dim | Bounds |
|---|---|---|---|
| −418.9829 × Dim | 30 | [−500, 500] | |
| 0 | 30 | [−5.12, 5.12] | |
| 0 | 30 | [−32, 32] | |
| 0 | 30 | [−600, 600] | |
| 0 | 30 | [−50, 50] | |
| 0 | 30 | [−50, 50] |
| Task | Standard DMOA | Proposed EDMOA | Average | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Best | Average | Worst | Std | Best | Average | Worst | Std | Improvement | |
| Fn1 | 1.79 × 10−5 | 8.76 × 10−5 | 0.000296 | 5.90 × 10−5 | 6.61 × 10−27 | 1.17 × 10−24 | 9.46 × 10−24 | 2.28 × 10−24 | 100% |
| Fn2 | 1.03 × 10−5 | 2.00 × 10−5 | 3.54 × 10−5 | 6.11 × 10−6 | 7.96 × 10−17 | 1.06 × 10−14 | 1.06 × 10−13 | 2.03 × 10−14 | 100% |
| Fn3 | 5743.5 | 8781.6 | 12,966 | 1668.8 | 2.8971 | 27.368 | 83.87 | 21.48 | 99.40% |
| Fn4 | 14.815 | 20.841 | 27.163 | 3.221 | 0.33587 | 1.5053 | 3.4605 | 0.77068 | 88.50% |
| Fn5 | 77.956 | 237.03 | 393.41 | 83.866 | 0.78762 | 32.275 | 88.215 | 28.605 | 82.20% |
| Fn6 | 1.65 × 10−5 | 7.08 × 10−5 | 0.000165 | 3.21 × 10−5 | 9.37 × 10−27 | 1.09 × 10−24 | 1.13 × 10−23 | 2.30 × 10−24 | 100% |
| Fn7 | 0.11238 | 0.5481 | 1.0747 | 0.27023 | 0.084286 | 0.52282 | 0.93326 | 0.28925 | 8.90% |
| Fn8 | −7211.4 | −5642.5 | −4571.6 | 681.27 | −11,207 | −9752.5 | −7496.1 | 846.28 | −34.1% |
| Fn9 | 104.94 | 153.31 | 197.11 | 26.503 | 27.902 | 40.152 | 66.662 | 9.0548 | 69.80% |
| Fn10 | 0.001129 | 0.002626 | 0.004452 | 0.000796 | 3.29 × 10−14 | 0.044681 | 1.3404 | 0.24473 | −48.4% |
| Fn11 | 0.000112 | 0.032583 | 0.40399 | 0.079176 | 0 | 0.009682 | 0.032006 | 0.010785 | 87.20% |
| Fn12 | 2.719 | 7.6682 | 12.87 | 2.4431 | 3.43 × 10−25 | 0.096802 | 0.82919 | 0.19629 | 96.10% |
| Fn13 | 1.2364 | 9.3512 | 24.069 | 5.0609 | 2.30 × 10−25 | 0.078774 | 1.2225 | 0.25351 | 97.30% |
| Algorithm | Specified Metaparameters | Size of Population | Number of Iterations | Number of Fitness Calculations |
|---|---|---|---|---|
| SCA | Parameter constant (a) = 2 | 30 | 1000 | 30,000 |
| SSA | Parameters c1 = c2 are random numbers [0, 1] | 30 | 1000 | 30,000 |
| MVO | Travelling distance rate is random number [0.6, 1] Existence probability is random number [0.2, 1] | 30 | 1000 | 30,000 |
| PSO | Parameters c1 = c2 = 2 Maximum Velocity (vMax) = 6 | 30 | 1000 | 30,000 |
| DE | Crossover probability = 0.5 Scaling factor = 0.5 | 30 | 1000 | 30,000 |
| DMOA | Number of babysitters = 3 Alpha female vocalization (peep = 2) | 30 | 1000 | 30,000 |
| EDMOA | Number of babysitters = 3 Alpha female vocalization (peep = 2) | 30 | 1000 | 30,000 |
| Task | Index | SCA | SSA | MVO | PSO | DE | DMOA | EDMOA |
|---|---|---|---|---|---|---|---|---|
| Fn1 | Mean | 1.52 × 10−2 | 1.23 × 10−8 | 3.19 × 10−1 | 1.29 × 102 | 3.03 × 10−12 | 1.79 × 10−5 | 6.61 × 10−27 |
| STd | 3.00 × 10−2 | 3.54 × 10−9 | 1.12 × 10−1 | 1.54 × 101 | 3.45 × 10−12 | 5.90 × 10−5 | 2.28 × 10−24 | |
| Fn2 | Mean | 1.15 × 10−5 | 8.48 × 10−1 | 3.89 × 10−1 | 8.61 × 101 | 3.72 × 10−8 | 1.03 × 10−5 | 7.96 × 10−17 |
| STd | 2.74 × 10−5 | 9.42 × 10−1 | 1.38 × 10−1 | 6.53 × 101 | 1.20 × 10−8 | 6.11 × 10−6 | 2.03 × 10−14 | |
| Fn3 | Mean | 3.26 × 103 | 2.37 × 102 | 4.81 × 101 | 4.07 × 102 | 2.42 × 104 | 5.74 × 103 | 2.9 |
| STd | 2.94 × 103 | 1.56 × 102 | 2.18 × 101 | 7.13 × 101 | 4.17 × 103 | 1.67 × 103 | 2.15 × 101 | |
| Fn4 | Mean | 2.05 × 101 | 8.25 | 1.08 | 4.5 | 1.97 | 1.48 × 101 | 3.36 × 10−1 |
| STd | 1.10 × 101 | 3.29 | 3.11 × 10−1 | 3.29 × 10−1 | 4.31 × 10−1 | 3.22 | 7.71 × 10−1 | |
| Fn5 | Mean | 5.33 × 102 | 1.36 × 102 | 4.08 × 102 | 1.55 × 105 | 4.61 × 101 | 7.80 × 101 | 7.88 × 10−1 |
| STd | 1.91 × 103 | 1.74 × 102 | 6.15 × 102 | 3.60 × 104 | 2.73 × 101 | 8.39 × 101 | 2.66 × 101 | |
| Fn6 | Mean | 4.55 | 0 | 3.24 × 10−1 | 1.33 × 102 | 3.10 × 10−12 | 1.65 × 10−5 | 9.37 × 10−27 |
| STd | 3.57 × 10−1 | 0 | 9.74 × 10−2 | 1.52 × 101 | 1.46 × 10−12 | 3.21 × 10−5 | 2.30 × 10−24 | |
| Fn7 | Mean | 2.44 × 10−2 | 9.55 × 10−2 | 2.09 × 10−2 | 1.11 × 102 | 2.69 × 10−2 | 1.12 × 10−1 | 8.43 × 10−2 |
| STd | 2.07 × 10−2 | 5.05 × 10−2 | 9.58 × 10−3 | 2.15 × 101 | 6.32 × 10−3 | 2.70 × 10−1 | 2.89 × 10−1 | |
| Fn8 | Mean | −3.89 × 103 | −7.82 × 103 | −7.74 × 103 | −6.73 × 103 | −1.24 × 104 | −7.21 × 103 | −1.12 × 104 |
| STd | 2.26 × 102 | 8.42 × 102 | 6.93 × 102 | 6.50 × 102 | 1.49 × 102 | 6.81 × 102 | 8.46 × 102 | |
| Fn9 | Mean | 1.84 × 101 | 5.66 × 101 | 1.13 × 102 | 3.69 × 102 | 5.93 × 101 | 1.05 × 102 | 2.79 × 101 |
| STd | 2.14 × 101 | 1.29 × 101 | 2.46 × 101 | 1.87 × 101 | 6.08 | 2.65 × 101 | 9.05 | |
| Fn10 | Mean | 1.13 × 101 | 2.26 | 1.15 | 8.42 | 4.64 × 10−7 | 1.13 × 10−3 | 3.29 × 10−14 |
| STd | 9.66 | 7.21 × 10−1 | 7.03 × 10−1 | 4.11 × 10−1 | 1.38 × 10−7 | 7.96 × 10−4 | 2.45 × 10−1 | |
| Fn11 | Mean | 2.35 × 10−1 | 1.01 × 10−2 | 5.75 × 10−1 | 1.03 | 9.76 × 10−11 | 1.12 × 10−4 | 0 |
| STd | 2.25 × 10−1 | 1.07 × 10−2 | 8.75 × 10−2 | 4.89 × 10−3 | 2.13 × 10−10 | 7.92 × 10−2 | 1.08 × 10−2 | |
| Fn12 | Mean | 2.29 | 5.54 | 1.29 | 4.8 | 3.63 × 10−13 | 2.72 | 3.43 × 10−25 |
| STd | 2.96 | 3.12 | 1.1 | 8.67 × 10−1 | 3.40 × 10−13 | 2.44 | 1.96 × 10−1 | |
| Fn13 | Mean | 5.19 × 102 | 1.01 | 8.13 × 10−2 | 2.32 × 101 | 1.69 × 10−12 | 1.24 | 2.30 × 10−25 |
| STd | 2.78 × 103 | 4.7 | 4.32 × 10−2 | 4.2 | 1.16 × 10−12 | 5.06 | 2.54 × 10−1 |
| Task | Index | SCA | SSA | MVO | PSO | DE | DMOA | EDMOA |
|---|---|---|---|---|---|---|---|---|
| Fn1 | Mean | 5 | 3 | 6 | 7 | 2 | 4 | 1 |
| STd | 5 | 3 | 6 | 7 | 2 | 4 | 1 | |
| Fn2 | Mean | 4 | 6 | 5 | 7 | 2 | 3 | 1 |
| STd | 4 | 6 | 5 | 7 | 2 | 3 | 1 | |
| Fn3 | Mean | 7 | 3 | 2 | 4 | 5 | 6 | 1 |
| STd | 6 | 4 | 2 | 3 | 7 | 5 | 1 | |
| Fn4 | Mean | 7 | 5 | 2 | 4 | 3 | 6 | 1 |
| STd | 7 | 6 | 1 | 2 | 3 | 5 | 4 | |
| Fn5 | Mean | 6 | 4 | 5 | 7 | 2 | 3 | 1 |
| STd | 6 | 4 | 5 | 7 | 2 | 3 | 1 | |
| Fn6 | Mean | 6 | 1 | 5 | 7 | 3 | 4 | 2 |
| STd | 6 | 1 | 5 | 7 | 3 | 4 | 2 | |
| Fn7 | Mean | 2 | 6 | 1 | 7 | 3 | 5 | 4 |
| STd | 3 | 4 | 2 | 7 | 1 | 5 | 6 | |
| Fn8 | Mean | 7 | 3 | 4 | 6 | 1 | 5 | 2 |
| STd | 2 | 5 | 4 | 3 | 1 | 7 | 6 | |
| Fn9 | Mean | 1 | 3 | 6 | 7 | 4 | 5 | 2 |
| STd | 5 | 3 | 6 | 4 | 1 | 7 | 2 | |
| Fn10 | Mean | 7 | 5 | 4 | 6 | 2 | 3 | 1 |
| STd | 7 | 6 | 5 | 4 | 1 | 2 | 3 | |
| Fn11 | Mean | 5 | 4 | 6 | 7 | 2 | 3 | 1 |
| STd | 7 | 3 | 6 | 2 | 1 | 5 | 4 | |
| Fn12 | Mean | 4 | 7 | 3 | 6 | 2 | 5 | 1 |
| STd | 6 | 7 | 4 | 3 | 1 | 5 | 2 | |
| Fn13 | Mean | 7 | 4 | 3 | 6 | 2 | 5 | 1 |
| STd | 7 | 5 | 2 | 4 | 1 | 6 | 3 | |
| Summation | 139 | 111 | 105 | 141 | 59 | 118 | 55 | |
| Mean Rank | 5.35 | 4.27 | 4.04 | 5.42 | 2.27 | 4.54 | 2.12 | |
| Final Ranking | 6 | 4 | 3 | 7 | 2 | 5 | 1 | |
| Function No. | Function | Minimum | Dim | Bounds |
|---|---|---|---|---|
| Fn14 | Shifted and Rotated Bent Cigar Function | 100 | 30 | [−100, 100] |
| Fn15 | Shifted and Rotated Zakharov Function | 300 | 30 | [−100, 100] |
| Fn16 | Shifted and Rotated Rosenbrock’s Function | 400 | 30 | [−100, 100] |
| Fn17 | Shifted and Rotated Rastrigin’s Function | 500 | 30 | [−100, 100] |
| Fn18 | Shifted and Rotated Expanded Scaffer’s F6 Function | 600 | 30 | [−100, 100] |
| Fn19 | Shifted and Rotated Lunacek Bi-Rastrigin Function | 700 | 30 | [−100, 100] |
| Fn20 | Shifted and Rotated Noncontinuous Rastrigin’s Function | 800 | 30 | [−100, 100] |
| Fn21 | Shifted and Rotated Levy Function | 900 | 30 | [−100, 100] |
| Fn22 | Shifted and Rotated Schwefel’s Function | 1000 | 30 | [−100, 100] |
| Fn23 | Hybrid Function 1 (N = 3) | 1100 | 30 | [−100, 100] |
| Fn24 | Hybrid Function 2 (N = 3) | 1200 | 30 | [−100, 100] |
| Fn25 | Hybrid Function 3 (N = 3) | 1300 | 30 | [−100, 100] |
| Task | Best | Average | Worst | ||||||
|---|---|---|---|---|---|---|---|---|---|
| DMOA | EDMOA | Improve | DMOA | EDMOA | Improve | DMOA | EDMOA | Improve | |
| Fn14 | 103.10 | 100.79 | 2% | 4947.71 | 1833.43 | 63% | 63,834.88 | 10,627.66 | 83% |
| Fn15 | 426.95 | 300.00 | 30% | 1075.82 | 300.00 | 72% | 2487.44 | 300.07 | 88% |
| Fn16 | 400.56 | 400.01 | 0% | 405.29 | 403.16 | 1% | 406.86 | 405.07 | 0% |
| Fn17 | 518.01 | 502.98 | 3% | 530.04 | 510.00 | 4% | 539.60 | 521.85 | 3% |
| Fn18 | 600.00 | 600.00 | 0% | 600.00 | 600.00 | 0% | 600.00 | 600.00 | 0% |
| Fn19 | 728.61 | 701.99 | 4% | 743.07 | 724.95 | 2% | 753.99 | 750.16 | 1% |
| Fn20 | 811.29 | 804.97 | 1% | 829.65 | 811.34 | 2% | 841.71 | 826.86 | 2% |
| Fn21 | 900.00 | 900.00 | 0% | 900.00 | 900.02 | 0% | 900.00 | 900.45 | 0% |
| Fn22 | 1615.59 | 1003.66 | 38% | 2276.48 | 1528.55 | 33% | 3534.00 | 2498.38 | 29% |
| Fn23 | 1103.03 | 1100.35 | 0% | 1107.10 | 1104.63 | 0% | 1112.53 | 1113.66 | 0% |
| Fn24 | 7581.32 | 1215.06 | 84% | 1.48 × 105 | 1.76 × 104 | 88% | 8.49 × 105 | 5.58 × 105 | 93% |
| Fn25 | 1471.09 | 1309.99 | 11% | 4806.37 | 5704.65 | −19% | 14,058.03 | 2.06 × 105 | −47% |
| Algorithm | Parameters | Population Size | Number of Iterations | Number of Fitness Calculations |
|---|---|---|---|---|
| Circle | % Parameter (p) decreases linearly from 1 to 0.05 % Parameter c = 0.8 | 30 | 500 | 15,000 |
| GWO | % Parameter (a) decreases linearly from 2 to 0 | 30 | 500 | 15,000 |
| PSO | % Parameters c1 = c2 = 2 % Maximum Velocity (vMax) = 6 | 30 | 500 | 15,000 |
| SMA | % z parameter = 0.03 | 30 | 500 | 15,000 |
| DMOA | % Number of babysitters = 3 % Alpha female vocalization (peep = 2) | 30 | 500 | 15,000 |
| EDMOA | % Number of babysitters = 3 % Alpha female vocalization (peep = 2) | 30 | 500 | 15,000 |
| EPO | % The Area to Search: l_scale = 1000; % Resolution Range: res = 0.05; % Shrinking Coefficient: eta = (res/l_scale)^(1/MaxIt); | 30 | 500 | 15,000 |
| BAS | % antenna distance: d0 = 0.001; d1 = 3; d = d1; eta_d = 0.95; % random walk: l0 = 0.0; l1 = 0.0; l = l1; eta_l = 0.95; % steps: step = 0.8; % step length eta_step = 0.95; | 30 | 500 | 15,000 |
| Task | Circle | GWO | PSO | SMA | DMOA | EDMOA | EPO | BAS |
|---|---|---|---|---|---|---|---|---|
| Fn14 | 1.33 × 109 | 94,119,626 | 1.12 × 109 | 4047.105 | 4947.71 | 1833.43 | 8,814,768 | 2.3 × 1010 |
| Fn15 | 14,241.48 | 3268.186 | 1578.377 | 300.0529 | 1075.82 | 300 | 16,333,666 | 783,773.90 |
| Fn16 | 506.2511 | 420.6218 | 458.378 | 407.543 | 405.29 | 403.16 | 2353.768 | 3390.97 |
| Fn17 | 561.921 | 519.452 | 527.4131 | 514.8857 | 530.04 | 510 | 528.8325 | 658.1569 |
| Fn18 | 645.2603 | 601.8139 | 603.4523 | 600.1722 | 600 | 600 | 645.6735 | 686.2571 |
| Fn19 | 789.0027 | 735.5862 | 726.2797 | 725.503 | 743.07 | 724.95 | 737.4825 | 1131.222 |
| Fn20 | 846.8571 | 815.9346 | 819.8598 | 816.6209 | 829.65 | 811.34 | 823.9785 | 934.9389 |
| Fn21 | 1631.005 | 915.9064 | 906.119 | 900.2505 | 900 | 900.02 | 1738.447 | 3657.722 |
| Fn22 | 2610.173 | 1763.644 | 1725.071 | 1511.829 | 2276.48 | 1528.55 | 2691.075 | 3454.588 |
| Fn23 | 2005.97 | 1157.378 | 1205.218 | 1137.776 | 1107.1 | 1104.63 | 1,003,627 | 25,751.55 |
| Fn24 | 2.49 × 108 | 1.14 × 106 | 1.18 × 107 | 2.08 × 105 | 1.48 × 105 | 1.76 × 104 | 2.75 × 109 | 2.6 × 109 |
| Fn25 | 10,842,625 | 12,488.38 | 15,339.44 | 8132.892 | 4806.37 | 5704.65 | 4.64 × 108 | 3.02 × 108 |
| Task | Circle | GWO | PSO | SMA | DMOA | EDMOA | EPO | BAS |
|---|---|---|---|---|---|---|---|---|
| Fn14 | 7 | 4 | 6 | 3 | 2 | 1 | 5 | 8 |
| Fn15 | 4 | 6 | 5 | 2 | 3 | 1 | 7 | 8 |
| Fn16 | 6 | 4 | 5 | 3 | 2 | 1 | 7 | 8 |
| Fn17 | 8 | 3 | 4 | 2 | 5 | 1 | 6 | 7 |
| Fn18 | 6 | 4 | 5 | 3 | 1 | 1 | 7 | 8 |
| Fn19 | 8 | 4 | 3 | 2 | 5 | 1 | 6 | 8 |
| Fn20 | 7 | 2 | 4 | 3 | 5 | 1 | 6 | 8 |
| Fn21 | 6 | 5 | 4 | 3 | 1 | 2 | 7 | 8 |
| Fn22 | 6 | 4 | 3 | 1 | 5 | 2 | 7 | 8 |
| Fn23 | 6 | 4 | 5 | 3 | 2 | 1 | 8 | 7 |
| Fn24 | 6 | 4 | 5 | 3 | 2 | 1 | 8 | 7 |
| Fn25 | 6 | 4 | 5 | 3 | 1 | 2 | 8 | 7 |
| Summation | 70 | 47 | 53 | 31 | 34 | 15 | 82 | 92 |
| Mean Rank | 5.892857 | 4.142857 | 4.392857 | 2.464286 | 2.714286 | 1.357143 | 6.8333 | 7.6667 |
| Final Ranking | 6 | 4 | 5 | 2 | 3 | 1 | 7 | 8 |
| Task | Computational Complexity | Average Run Time (Seconds)/Iteration | Task | Computational Complexity | Average Run Time (Seconds)/Iteration | ||
|---|---|---|---|---|---|---|---|
| DMOA | EDMOA | DMOA | EDMOA | ||||
| Fn1 | O (30 × 30 × 1000) | 0.001763 | 0.001772 | Fn14 | O (30 × 30 × 500) | 0.0023906 | 0.002345 |
| Fn2 | O (30 × 30 × 1000) | 0.001851 | 0.001798 | Fn15 | O (30 × 30 × 500) | 0.0027801 | 0.002817 |
| Fn3 | O (30 × 30 × 1000) | 0.001592 | 0.001608 | Fn16 | O (30 × 30 × 500) | 0.0029567 | 0.002966 |
| Fn4 | O (30 × 30 × 1000) | 0.001723 | 0.001739 | Fn17 | O (30 × 30 × 500) | 0.0021253 | 0.002111 |
| Fn5 | O (30 × 30 × 1000) | 0.001577 | 0.001528 | Fn18 | O (30 × 30 × 500) | 0.0024131 | 0.002387 |
| Fn6 | O (30 × 30 × 1000) | 0.001414 | 0.001464 | Fn19 | O (30 × 30 × 500) | 0.0026615 | 0.0026914 |
| Fn7 | O (30 × 30 × 1000) | 0.001695 | 0.001691 | Fn20 | O (30 × 30 × 500) | 0.0027411 | 0.002802 |
| Fn8 | O (30 × 30 × 1000) | 0.001823 | 0.001854 | Fn21 | O (30 × 30 × 500) | 0.0030125 | 0.002929 |
| Fn9 | O (30 × 30 × 1000) | 0.002011 | 0.001902 | Fn22 | O (30 × 30 × 500) | 0.0022145 | 0.0022941 |
| Fn10 | O (30 × 30 × 1000) | 0.001886 | 0.001935 | Fn23 | O (30 × 30 × 500) | 0.0023897 | 0.0023014 |
| Fn11 | O (30 × 30 × 1000) | 0.001698 | 0.001725 | Fn24 | O (30 × 30 × 500) | 0.0023187 | 0.002408 |
| Fn12 | O (30 × 30 × 1000) | 0.001598 | 0.001554 | Fn25 | O (30 × 30 × 500) | 0.0024519 | 0.002415 |
| Fn13 | O (30 × 30 × 1000) | 0.001821 | 0.001875 | DCPH | O (60 × 100 × 3000) | 0.4152 | 0.4211 |
| Variable | DMOA | EDMOA | Variable | DMOA | EDMOA | Variable | DMOA | EDMOA |
|---|---|---|---|---|---|---|---|---|
| PG1 | 410.919 | 538.715 | PG22 | 91.269 | 159.899 | HT31 | 42.388 | 40.211 |
| PG2 | 236.598 | 225.129 | PG23 | 75.045 | 78.120 | HT32 | 17.572 | 22.192 |
| PG3 | 320.459 | 150.068 | PG24 | 108.805 | 77.390 | HT33 | 108.227 | 105.055 |
| PG4 | 70.230 | 159.774 | PG25 | 94.984 | 94.666 | HT34 | 88.715 | 79.077 |
| PG5 | 174.784 | 161.645 | PG26 | 115.530 | 92.638 | HT35 | 111.902 | 105.339 |
| PG6 | 159.518 | 109.808 | PG27 | 98.847 | 97.820 | HT36 | 82.122 | 89.306 |
| PG7 | 110.100 | 110.431 | PG28 | 61.626 | 40.246 | HT37 | 34.690 | 41.207 |
| PG8 | 130.571 | 112.748 | PG29 | 99.781 | 85.629 | HT38 | 21.411 | 25.351 |
| PG9 | 105.985 | 109.874 | PG30 | 54.100 | 53.532 | HT39 | 479.032 | 442.594 |
| PG10 | 88.365 | 77.377 | PG31 | 16.333 | 10.502 | HT40 | 54.581 | 59.883 |
| PG11 | 82.701 | 77.516 | PG32 | 42.676 | 39.931 | H41 | 56.888 | 59.970 |
| PG12 | 95.346 | 92.383 | PG33 | 92.902 | 81.538 | H42 | 103.343 | 119.627 |
| PG13 | 79.876 | 92.440 | PG34 | 56.262 | 44.747 | H43 | 117.539 | 119.798 |
| PG14 | 533.413 | 450.161 | PG35 | 105.643 | 82.097 | H44 | 459.364 | 447.482 |
| PG15 | 12.329 | 224.017 | PG36 | 49.405 | 56.616 | H45 | 54.980 | 59.976 |
| PG16 | 292.225 | 150.102 | PG37 | 15.492 | 12.834 | H46 | 57.474 | 59.996 |
| PG17 | 109.793 | 161.726 | PG38 | 43.820 | 46.780 | H47 | 110.577 | 119.681 |
| PG18 | 65.965 | 159.664 | HT27 | 112.829 | 114.220 | H48 | 108.102 | 119.984 |
| PG19 | 158.946 | 110.029 | HT28 | 89.529 | 75.174 | Sum (PG) | 2500.0000 | 2500.0000 |
| PG20 | 139.222 | 111.665 | HT29 | 108.118 | 107.347 | Sum (HT) | 4700.0000 | 4700.0000 |
| PG21 | 100.136 | 159.743 | HT30 | 80.615 | 86.532 | Fn ($) | 121,431.6763 | 116,406.3772 |
| Optimizer | Worst Fn ($/hr) | Average Fn ($/hr) | Best Fn ($/h) |
|---|---|---|---|
| Proposed EDMOA | 117,973.7 | 117,331.3 | 116,406.4 |
| Standard DMOA | 123,551.6 | 122,238.4 | 121,431.7 |
| Improved artificial ecosystem algorithm [67] | 119,424.033 | 118,004.349 | 116,897.888 |
| Artificial ecosystem algorithm [67] | 124,396.472 | 120,045.695 | 118,881.447 |
| Jellyfish search algorithm [68] | - | - | 117,365.09 |
| Gravitational search algorithm [69] | - | - | 119,775.9 |
| Manta Ray Foraging Optimizer [70] | 118,217.5 | 117,875.4 | 117,336.9 |
| CPSO [71] | - | - | 120,918.9 |
| TVAC-PSO [71] | - | - | 118,962.5 |
| MVO [70] | 119,249.3 | 118,724 | 117,657.9 |
| SSA [70] | 122,636.8 | 121,110.2 | 120,174.1 |
| Algorithm | Parameters | Population Size | No. of Iterations | No. of Fitness Calculations |
|---|---|---|---|---|
| DMOA | Number of babysitters = 3 Alpha female vocalization (peep = 2) | 100 | 3000 | 300,000 |
| EDMOA | Number of babysitters = 3 Alpha female vocalization (peep = 2) | 100 | 3000 | 300,000 |
| Improved artificial ecosystem algorithm [67] | Adaptive parameters a = (1 − iter/MaxIt) × r1; | 100 | 3000 | 300,000 |
| Artificial ecosystem algorithm [67] | Adaptive parameters a = (1 − iter/MaxIt) × r1; | 100 | 3000 | 300,000 |
| Jellyfish search algorithm [68] | Adaptive parameters Ar = (1 − iter × ((1)/MaxIt)) × (2 × rand − 1) | 100 | 3000 | 300,000 |
| Gravitational search algorithm [69] | Parameters: G0 = 400, δ = 0.01 | 100 | 500 | 50,000 |
| Manta Ray Foraging Optimizer [70] | Adaptive parameters Coef = iter/MaxIt | 100 | 3000 | 300,000 |
| CPSO [71] | Parameters: ωmax = 0.9, ωmin = 0.4; C1f = C2i = 0.5, C1i = C2f = 2.5; Rmin = 5, Rmax = 10 | 500 | 300 | 150,000 |
| TVAC-PSO [71] | Parameters: ωmax = 0.9, ωmin = 0.4; C1f = C2i = 0.5, C1i = C2f = 2.5; Rmin = 5, Rmax = 10 | 500 | 300 | 150,000 |
| MVO [70] | Travelling distance rate is random number [0.6, 1] Existence probability is random number [0.2, 1] | 100 | 3000 | 300,000 |
| SSA [70] | Parameters c1 = c2 are random numbers [0, 1] | 100 | 3000 | 300,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moustafa, G.; El-Rifaie, A.M.; Smaili, I.H.; Ginidi, A.; Shaheen, A.M.; Youssef, A.F.; Tolba, M.A. An Enhanced Dwarf Mongoose Optimization Algorithm for Solving Engineering Problems. Mathematics 2023, 11, 3297. https://doi.org/10.3390/math11153297
Moustafa G, El-Rifaie AM, Smaili IH, Ginidi A, Shaheen AM, Youssef AF, Tolba MA. An Enhanced Dwarf Mongoose Optimization Algorithm for Solving Engineering Problems. Mathematics. 2023; 11(15):3297. https://doi.org/10.3390/math11153297
Chicago/Turabian StyleMoustafa, Ghareeb, Ali M. El-Rifaie, Idris H. Smaili, Ahmed Ginidi, Abdullah M. Shaheen, Ahmed F. Youssef, and Mohamed A. Tolba. 2023. "An Enhanced Dwarf Mongoose Optimization Algorithm for Solving Engineering Problems" Mathematics 11, no. 15: 3297. https://doi.org/10.3390/math11153297









