Thermal Responses and the Energy Spectral of Diatomic Molecules Using Nikiforov–Uvarov Methodology
Abstract
:1. Introduction
2. Any -State Solutions through the Greene–Aldrich Approximation and Parametric Nikiforov–Uvarov Approach
3. The Thermal Behaviour of the Schrödinger Equation with MDH-IFM Potential
3.1. Partition Function
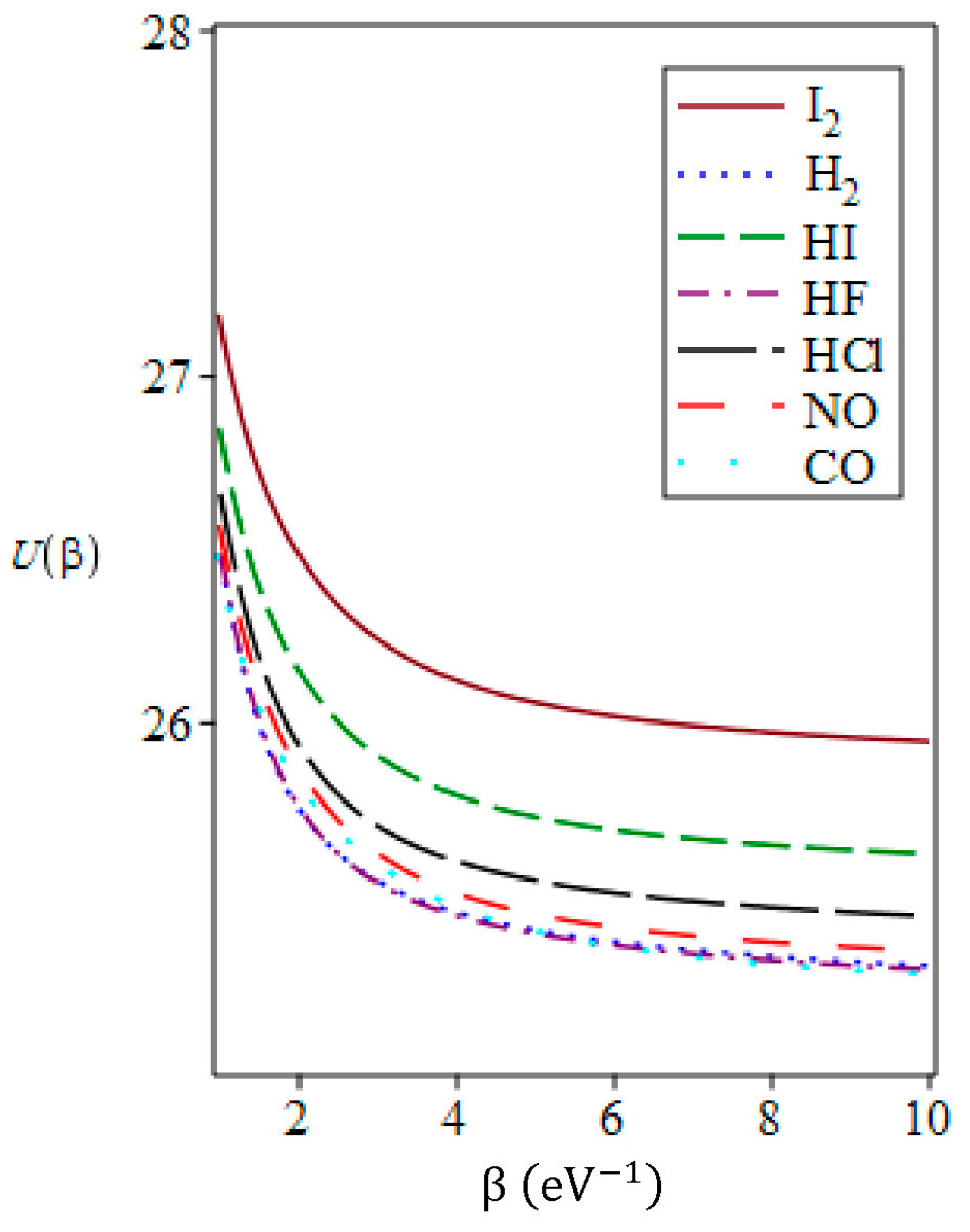
3.2. The Vibrational Mean Energy
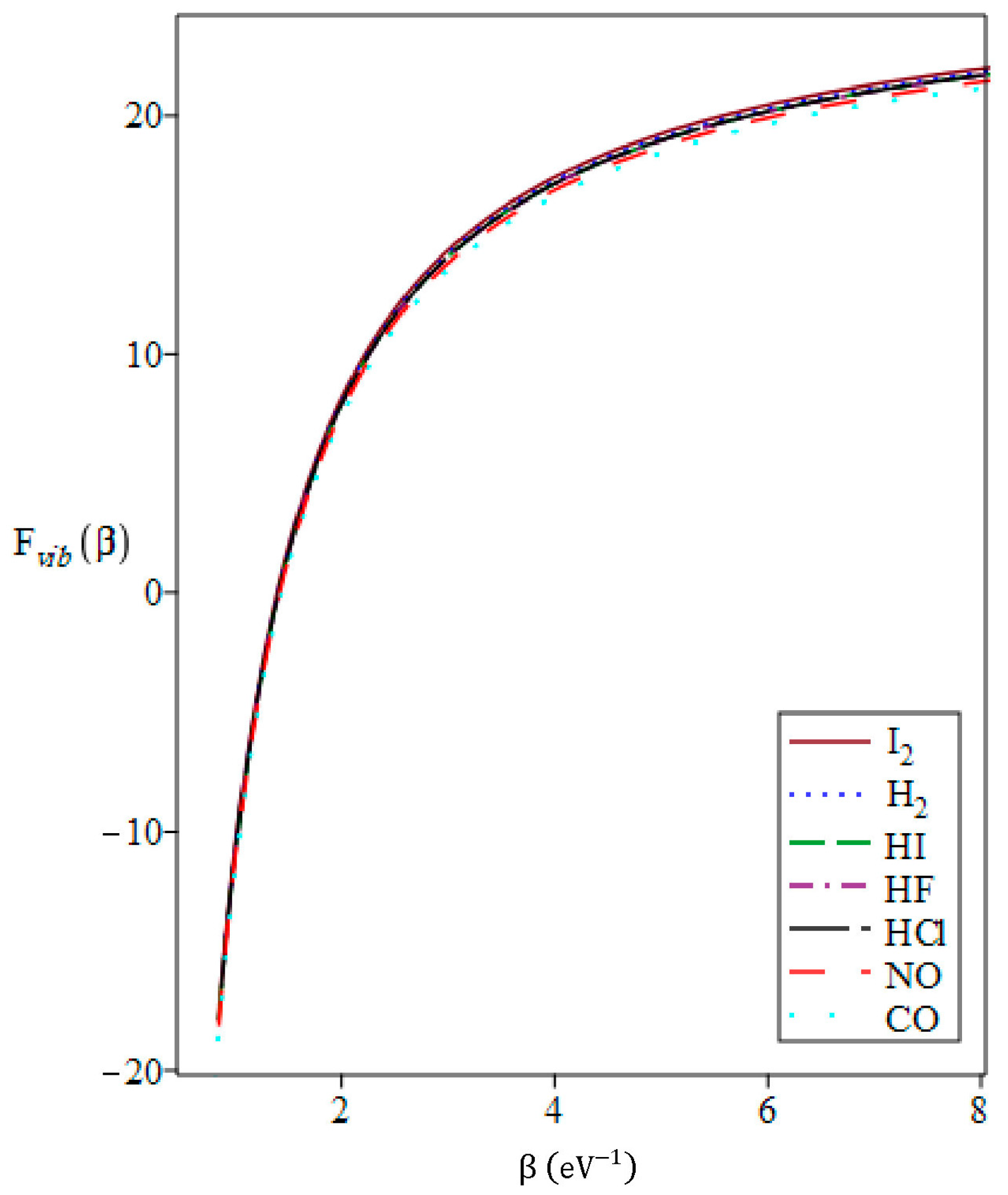
3.3. The Vibrational Mean Free Energy
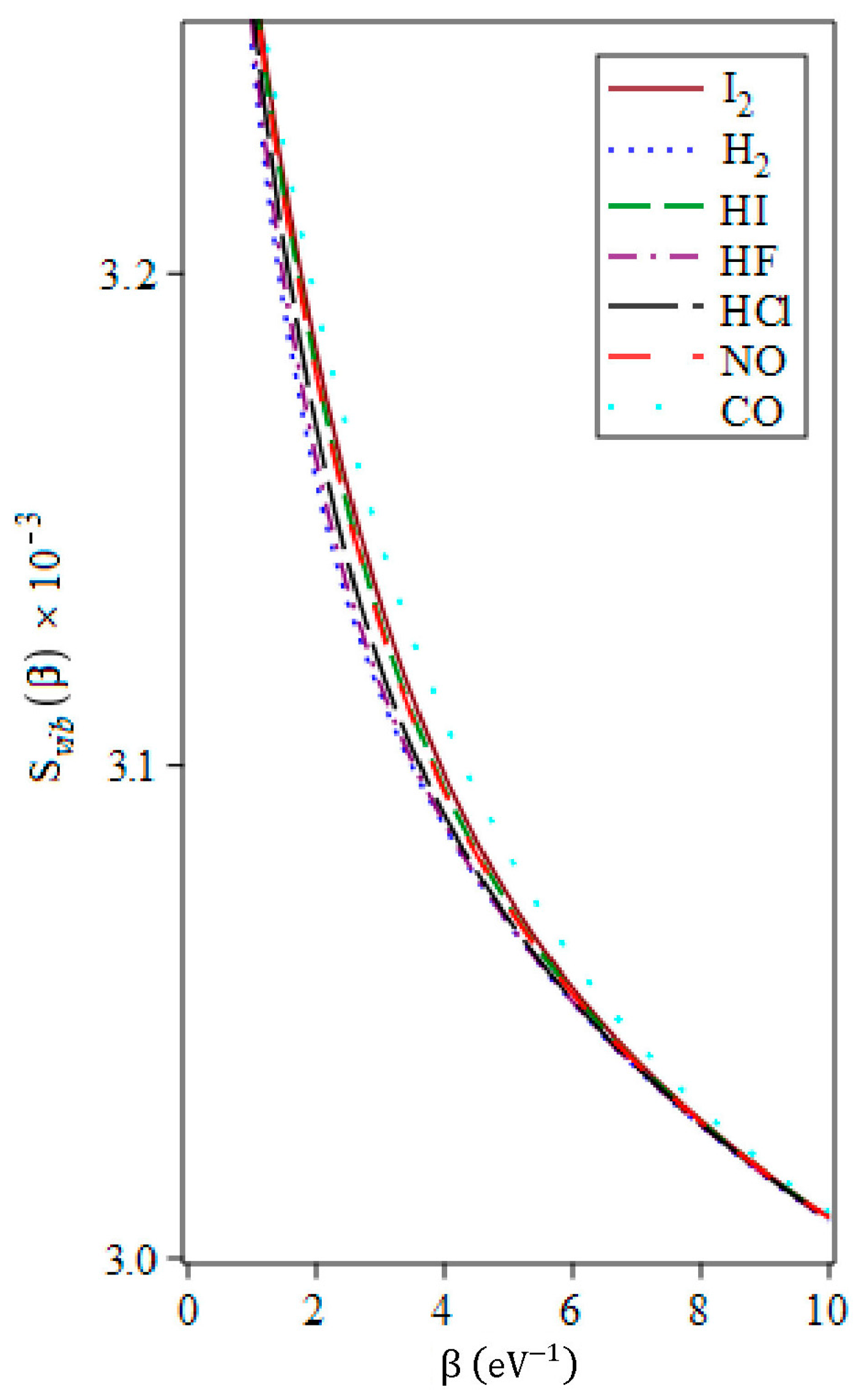
3.4. The Vibrational Entropy
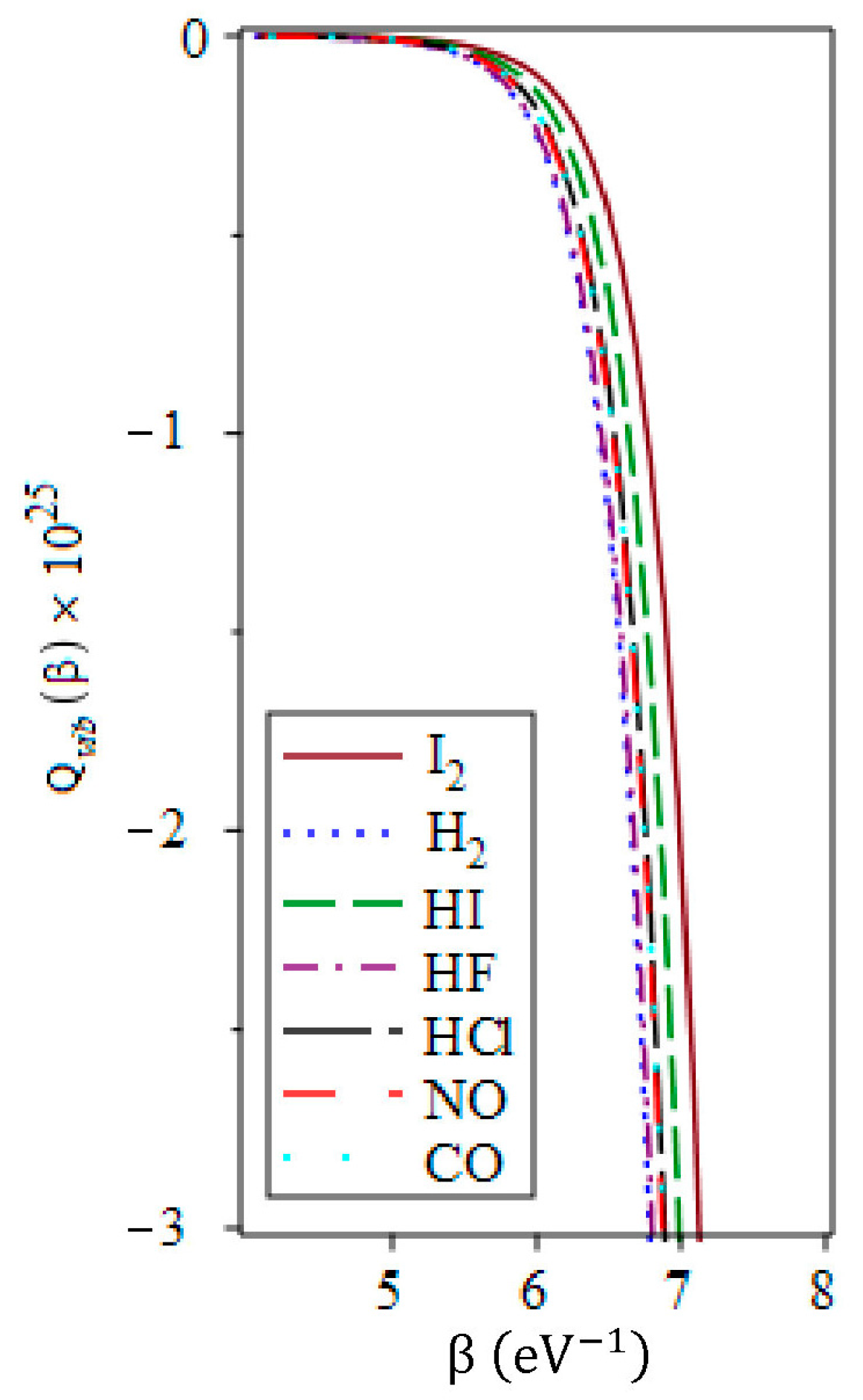
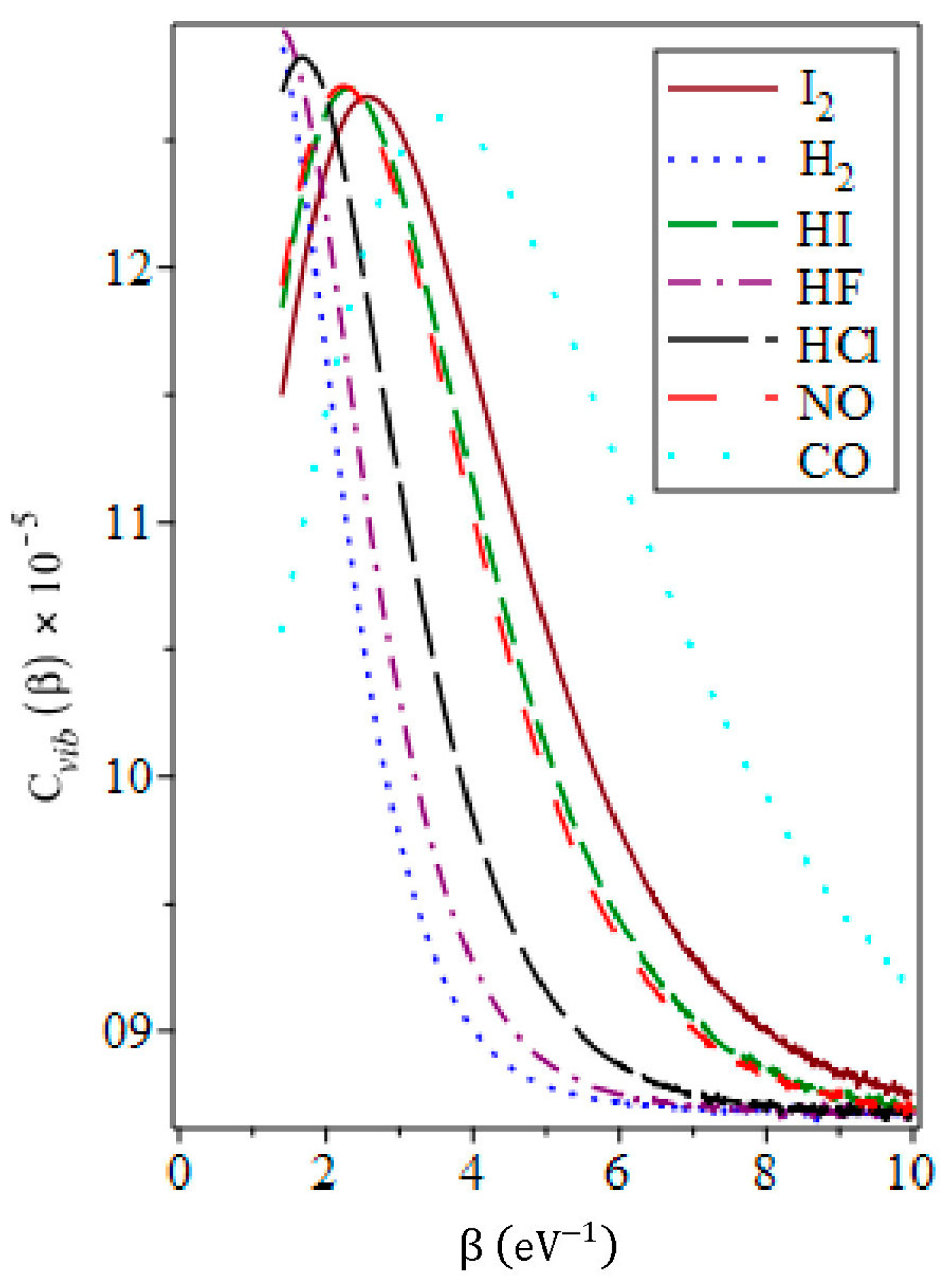
3.5. The Vibrational Specific Heat
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oluwadare, O.J.; Oyewumi, K.J. The scattering phase shifts of the Hulthén-type potential plus Yukawa potential. Eur. Phys. J. Plus 2016, 131, 295. [Google Scholar] [CrossRef] [Green Version]
- Onyeaju, M.C.; Ikot, A.N.; Chukwuocha, E.O.; Obong, H.P.; Zare, S.; Hassanabadi, H. Scattering and Bound States of Klein-Gordon Particle with Hylleraas Potential Within Effective Mass Formalism. Few Body Syst. 2016, 57, 823–831. [Google Scholar] [CrossRef]
- Onate, C.A.; Onyeaju, M.C.; Ikot, A.N. Analytical solutions of the Dirac equation under Hellmann–Frost-Musulin potential. Ann. Phys. 2016, 375, 239–250. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Sun, D.-S.; Lu, F.-L. Approximate analytical solutions of Klein-Gordon equation with Hulthén potentials for nonzero angular momentum. Phys. Lett. A 2007, 370, 219–221. [Google Scholar] [CrossRef]
- Bayrak, O.; Soylu, A.; Boztosun, I. The relativistic treatment of spin-0 particles under the rotating Morse oscillator. J. Math. Phys. 2010, 51, 112301. [Google Scholar] [CrossRef]
- Onate, C.A.; Onyeaju, M.C.; Ituen, E.E.; Ikot, A.N.; Ebomwonyi, O.; Okoro, J.O.; Dopamu, K.O. Eigensolutions, Shannon entropy and information energy for modified Tietz-Hua potential. Ind. J. Phys. 2018, 92, 487–493. [Google Scholar] [CrossRef]
- Abu-Shady, M.; Abdel-Karim, T.A.; Ezz-Alarab, S.Y. Masses and thermodynamic properties of heavy mesons in the non-relativistic quark model using the Nikiforov–Uvarov method. J. Egypt Math. Soc. 2019, 27, 14. [Google Scholar] [CrossRef] [Green Version]
- Khokha, E.M.; Abu-Shady, M.T.; Abdel-Karim, A. Quarkonium masses in the N-dimensional space using the analytical exact iteration method. Int. J. Theor. Appl. Math. 2016, 2, 86–92. [Google Scholar]
- Abu-Shady, M. Heavy Quarkonia and Mesons in the Cornell Potential with Harmonic Oscillator Potential in the N-dimensional Schrödinger Equation. Int. J. Appl. Math. Theor. Phys. 2016, 2, 16–20. [Google Scholar]
- Omugbe, E. Non-relativistic eigensolutions of molecular and heavy quarkonia interacting potentials via the Nikiforov Uvarov method. Can J. Phys. 2020, 98, 1125–1132. [Google Scholar] [CrossRef]
- Omugbe, E. Non-relativistic Energy Spectrum of the Deng-Fan Oscillator via the WKB Approximation Method. Asian J. Phys. Chem. Sci. 2020, 8, 26–36. [Google Scholar] [CrossRef]
- Roy, K.A. Ro-vibrational spectroscopy of molecules represented by a Tietz-Hua oscillator potential. J. Math. Chem. 2014, 52, 1405–1413. [Google Scholar] [CrossRef] [Green Version]
- Diaf, A. Arbitrary l-state solutions of the Feynman propagator with the Deng-Fan molecular potential. J. Phys. Conf. Ser. 2015, 574, 012022. [Google Scholar] [CrossRef]
- Wang, P.-Q.; Zhang, L.-H.; Jia, C.-H.; Liu, J.-Y. Equivalence of the three empirical potential energy models for diatomic molecules. J. Mol. Spec. 2012, 274, 5–8. [Google Scholar] [CrossRef]
- Messiah, A. Quantum Mechanics; Dover Publication: New York, NY, USA, 2014. [Google Scholar]
- Dong, S.-H. Factorization Method in Quantum Mechanics; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, Non-Relativistic Theory, 3rd ed.; Pergamon: New York, NY, USA, 1977. [Google Scholar]
- Ikot, A.N.; Awoga, O.A.; Hassanabadi, H.; Maghsoodi, E. Analytical approximate solution of Schrödinger equation in D-dimensions with quadratic exponential-type potential for arbitrary l-State. Commun. Theor. Phys. 2014, 61, 457–463. [Google Scholar] [CrossRef]
- Greene, R.L.; Aldrich, C. Variational wave functions for a screened coulomb potential. Phys. Rev. A 1976, 14, 2363–2366. [Google Scholar] [CrossRef]
- Falaye, B.J. Arbitrary l-State Solutions of the Hyperbolical Potential by the Asymptotic Iteration Method. Few Body Syst. 2012, 53, 557–562. [Google Scholar] [CrossRef]
- Rey, A.K. Studies on the Bound-State Spectrum of Hyperbolic Potential. Few-Body Syst. 2014, 55, 143–150. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.-Y.; Zhang, G.-D.; Jia, C.-S. Calculation of the interaction potential energy curve and vibrational levels for the a 3Σu + state of Li27 molecule. Phys. Lett. A 2013, 377, 1444–1447. [Google Scholar] [CrossRef]
- Jia, C.-S.; Chen, T.; He, S. Bound state solutions of the Klein–Gordon equation with the improved expression of the Manning-Rosen potential energy model. Phys. Lett. A 2013, 37, 682–686. [Google Scholar] [CrossRef]
- Roy, B.; Roychoudhury, R. The shifted 1/N expansion and the energy eigenvalues of the Hulthén potential for l ≠ 0. J. Phys. A Math. Gen. 1987, 20, 3051–3055. [Google Scholar] [CrossRef]
- Nikiforov, A.F.; Uvarov, V.B. Functions of Mathematical Physics; Birkhäuser: Basel, Switzerland, 1988. [Google Scholar] [CrossRef] [Green Version]
- Roshanzamir, M. The Information-Theoretic Treatment of Spinless Particles with the Assorted Diatomic Molecular Potential. Adv. High Energy Phys. 2022, 2022, 6621156. [Google Scholar] [CrossRef]
- Tezcan, C.; Sever, R. A General Approach for the Exact Solution of the Schrödinger Equation. Int. J. Theor. Phys. 2009, 48, 337–350. [Google Scholar] [CrossRef] [Green Version]
- Bayrak, O.; Boztosun, I.; Çiftci, H. Exact analytical solutions to the Kratzer potential by the asymptotic iteration method. Int. J. Quantum Chem. 2006, 107, 540–544. [Google Scholar] [CrossRef]
- Stahlhofen, A.; Bleuler, K. An algebraic form of the factorization method. Nuov. Cim. B 1989, 104, 447–465. [Google Scholar] [CrossRef]
- Edelstein, R.M.; Govinder, K.S.; Mahomed, F.M. Solution of ordinary differential equations via nonlocal transformations. J. Phys. A Math. Gen. 2001, 34, 1141–1152. [Google Scholar] [CrossRef]
- Falaye, B.J.; Ikhdair, S.M.; Hamzavi, M. Formula Method for Bound State Problems. Few Body Syst. 2015, 56, 63–78. [Google Scholar] [CrossRef] [Green Version]
- Ikot, A.N.; Hassanabadi, H.; Maghsoodi, E.; Zarrinkamar, S. D-Dimensional Dirac Equation for Energy-Dependent Pseudoharmonic and Mie-type Potentials via SUSYQM. Commun. Theor. Phys. 2014, 61, 436–446. [Google Scholar] [CrossRef]
- Fa-Lin, L.; Chang-Yuan, C.; Dong-Sheng, S. Bound states of Klein–Gordon equation for double ring-shaped oscillator scalar and vector potentials. Chin. Phys. 2005, 14, 463–467. [Google Scholar] [CrossRef]
- Dong, S.-H.; Ma, Z.-Q. Exact solutions to the Schrödinger equation for the potential V(r) = ar2 + br−4 + cr−6 in two dimensions. J. Phys. A Math. Gen. 1998, 31, 9855–9859. [Google Scholar] [CrossRef]
- Roshanzamir-Nikou, M.; Goudarzi, H. The Laplace transform approach for a Dirac isotonic oscillator with a tensor potential in D-dimensions. Phys. Scr. 2013, 89, 015001. [Google Scholar] [CrossRef]
- Roshanzamir-Nikou, M.; Goudarzi, H. Pauli isotonic oscillator with an anomalous magnetic moment in the presence of the Aharonov–Bohm effect: Laplace transform approach. Theor. Math. Phys. 2016, 186, 286–293. [Google Scholar] [CrossRef]
- Tang, H.-M.; Liang, G.-C.; Zhang, L.-H.; Zhao, F.; Jia, C.-S. Diatomic molecule energies of the modified Rosen−Morse potential energy model. Can. J. Chem. 2014, 92, 341–345. [Google Scholar] [CrossRef]
- Hu, X.-T.; Zhang, L.-H.; Jia, C.-S. D-dimensional energies for cesium and sodium dimers. Can. J. Chem. 2014, 92, 386–391. [Google Scholar] [CrossRef]
- Qiang, W.-C.; Dong, S.-H. Proper quantization rule. EPL (Europhys. Lett.) 2010, 89, 10003. [Google Scholar] [CrossRef]
- Oluwadare, O.J.; Oyewumi, K.J. Scattering state solutions of the Duffin-Kemmer-Petiau equation with the Varshni potential model. Eur. Phys. J. A 2017, 53, 29. [Google Scholar] [CrossRef]
- Jing, J.; Zhang, Y.-F.; Wang, K.; Long, Z.-W.; Dong, S.-H. On the time-dependent Aharonov-Bohm effect. Phys. Lett. B 2017, 774, 87–90. [Google Scholar] [CrossRef]
- Yeşiltaş, Ö.; Şimşek, M.; Sever, R.; Tezcan, C. Exponential Type Complex and Non-Hermitian Potentials in PT-Symmetric Quantum Mechanics. Phys. Scr. 2003, 67, 472–475. [Google Scholar] [CrossRef] [Green Version]
- Onyenegecha, C.P.; Onate, C.A.; Echendu, O.K.; Ibe, A.A.; Hassanabadi, H. Erratum to: Solutions of Schrodinger equation for the modified Mobius square plus Kratzer potential. Eur. Phys. J. Plus 2020, 135, 382. [Google Scholar] [CrossRef]
- Hatami, N.; Naji, J.; Pananch, M. Analytical solutions of the Klein-Gordon equation for the deformed generalized Deng-Fan potential plus deformed Eckart potential. Eur. Phys. J. Plus 2019, 134, 90. [Google Scholar] [CrossRef]
- Hassanabadi, H.; Maghsoodi, E.; Zarrinkamar, S.; Rahimov, H. An approximate solution of the Dirac equation for hyperbolic scalar and vector potentials and a Coulomb tensor interaction by SUSYQM. Mod. Phys. Lett. A 2011, 26, 2703–2718. [Google Scholar] [CrossRef]
- Dong, S.-H.; Cruz-Irisson, M. Energy spectrum for a modified Rosen-Morse potential solved by proper quantization rule and its thermodynamic properties. J. Math. Chem. 2012, 50, 881–892. [Google Scholar] [CrossRef]
- Ikot, A.N.; Akpan, I.O. Bound State Solutions of the Schrödinger Equation for a More General Woods-Saxon Potential with Arbitrary l-state. Chin. Phys. Lett. 2012, 29, 090302. [Google Scholar] [CrossRef] [Green Version]
- Peña, J.J.; García-Martínez, J.; García-Ravelo, J.; Morales, J. Bound state solutions of D-dimensional schrödinger equation with exponential-type potentials. Int. J. Quantum Chem. 2014, 115, 158–164. [Google Scholar] [CrossRef]
- Suparmi, A.; Cari, C.; Pratiwi, B.N. Thermodynamics properties study of diatomic molecules with q-deformed modified Poschl-Teller plus Manning Rosen non-central potential in D dimensions using SUSYQM approach. J. Phys. Conf. Ser. 2016, 710, 012026. [Google Scholar] [CrossRef]
- Ikhdair, S.M.; Sever, R. Polynomial solutions of the Mie-type potential in the D-dimensional Schrödinger equation. J. Mol. Struct. Theochem 2008, 855, 13–17. [Google Scholar] [CrossRef]
- Oyewumi, K.J. Analytical Solutions of the Kratzer-Fues Potential in an Arbitrary Number of Dimensions. Found. Phys. Lett. 2005, 18, 75–84. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 7th ed.; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2007; ISBN 978-0-12-373637-6/978-0-12-373637-4. [Google Scholar]
- Gensterblum, Y.; Busch, A.; Krooss, B.M. Molecular concept and experimental evidence of competitive adsorption of H2O, CO2 and CH4 on organic material. Fuel 2014, 115, 581–588. [Google Scholar] [CrossRef]
- Skouteris, D.; Calderini, D.; Barone, V. Methods for calculating partition functions of molecules involving large amplitude and/or anharmonic motions. J. Chem. Theory Comput. 2016, 12, 1011–1018. [Google Scholar] [CrossRef]
- Ikot, A.N.; Chukwuocha, E.O.; Onyeaju, M.C.; Onate, C.A.; Ita, B.I.; Udoh, M.E. Thermodynamic properties of diatomic molecules with general molecular potential. Pramana J. Phys. 2018, 90, 22. [Google Scholar] [CrossRef]
- Njegic, B.; Gordon, M.S. Exploring the effect of anharmonicity of molecular vibrations on thermodynamic properties. J. Chem. Phys. 2006, 125, 224102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, X.-Q.; Wang, C.-W.; Jia, C.-S. Thermodynamic properties for the sodium dimer. Chem. Phys. Lett. 2017, 673, 50–55. [Google Scholar] [CrossRef]
- Ebeling, W.; Sokolov, I.M. Statistical Thermodynamics and Stochastic Theory of Nonequilibrium Systems; World Scientific: Singapore, 2005. [Google Scholar] [CrossRef]
- Song, W.; Martsinovich, N.; Hecklabd, W.M.; Lackinger, M. Thermodynamics of halogen bonded monolayer self-assembly at the liquid–solid interface. Chem. Commun. 2014, 50, 13465–13468. [Google Scholar] [CrossRef]
- Yahiatène, I.; Hennig, S.; Huser, T. Optical fluctuation microscopy based on calculating local entropy values. Chem. Phys. Lett. 2013, 587, 1–6. [Google Scholar] [CrossRef]
- Ammendola, P.; Raganati, F.; Chirone, R. CO2 adsorption on a fine activated carbon in a sound assisted fluidized bed: Thermodynamics and kinetics. Chem. Eng. J. 2017, 322, 302–313. [Google Scholar] [CrossRef]
- Moses, S.A.; Covey, J.P.; Miecnikowski, M.T.; Yan, B.; Gadway, B.; Ye, J.; Jin, D.S. Creation of a low-entropy quantum gas of polar molecules in an optical lattice. Science 2015, 350, 659–662. [Google Scholar] [CrossRef] [Green Version]
- Tzeng, S.R.; Kalodimos, C.G. Protein activity regulation by conformational entropy. Nature 2012, 488, 236–240. [Google Scholar] [CrossRef]
- Varshni, Y.P. Comparative Study of Potential Energy Functions for Diatomic Molecules. Rev. Mod. Phys. 1957, 29, 664–682. [Google Scholar] [CrossRef] [Green Version]
- Ejere, A.I.I.; Ebomwonyi, O. Hylleraas potential quantum well in Cu2ZnSnS4 quaternary semiconductor alloy in the presence of magnetic field. Mater. Res. Express 2019, 6, 096411. [Google Scholar] [CrossRef]
- Pöschl, G.; Teller, E. Bemerkungen zur Quantenmechanik des anharmonischen Oszillators. Z. Physik 1933, 83, 143–151. [Google Scholar] [CrossRef]
- Akcay, H.; Sever, R. Analytical solutions of Schrödinger equation for the diatomic molecular potentials with any angular momentum. J. Math. Chem. 2012, 50, 1973–1987. [Google Scholar] [CrossRef]
- Aydoğdu, O.; Arda, A.; Sever, R. Scattering of a spinless particle by an asymmetric Hulthén potential within the effective mass formalism. J. Math. Phys. 2012, 53, 102111. [Google Scholar] [CrossRef] [Green Version]
- Onyeaju, M.C.; Idiodi, J.O.A.; Ikot, A.N.; Solaimani, M.; Hassanabadi, H. Linear and Nonlinear Optical Properties in Spherical Quantum Dots: Generalized Hulthén Potential. Few Body Syst. 2016, 57, 793–805. [Google Scholar] [CrossRef]
- Taskin, F.; Kocak, G. Approximate solutions of Schrödinger equation for Eckart potential with centrifugal term. Chin. Phys. B 2010, 19, 090314. [Google Scholar] [CrossRef]
- Liverts, E.Z.; Drukarev, E.G.; Krivec, R.; Mandelzweig, V.B. Analytic presentation of a solution of the Schrödinger equation. Few Body Syst. 2008, 44, 367–370. [Google Scholar] [CrossRef] [Green Version]
- Edet, C.O.; Okorie, U.S.; Ngiangia, A.T.; Ikot, A.N. Bound state solutions of the Schrodinger equation for the modified Kratzer potential plus screened Coulomb potential. Indian J. Phys. 2020, 94, 425–433. [Google Scholar] [CrossRef]
- Bayrak, O.; Boztosun, I. Bound state solutions of the Hulthén potential by using the asymptotic iteration method. Phys. Scr. 2007, 76, 92. [Google Scholar] [CrossRef]
- Eckart, C. The Penetration of a Potential Barrier by Electrons. Phys. Rev. 1930, 35, 1303–1309. [Google Scholar] [CrossRef]
- Cimas, A.; Aschi, M.; Barrientos, C.; Rayón, V.M.; Sordo, J.A.; Largo, A. Computational study on the kinetics of the reaction of N(4S) with CH2F. Chem. Phys. Lett. 2003, 374, 594–600. [Google Scholar] [CrossRef]
- Jia, C.-S.; Dai, J.-W.; Zhang, L.-H.; Liu, J.-Y.; Zhang, G.-D. Molecular spinless energies of the modified Rosen–Morse potential energy model in higher spatial dimensions. Chem. Phys. Lett. 2015, 619, 54–60. [Google Scholar] [CrossRef]
- Ikot, A.N.; Awoga, O.A.; Antia, A.D. Bound state solutions of D-dimensional Schrödinger equation with Eckart potential plus modified deformed Hylleraas potential. Chin. Phys. B 2013, 22, 020304. [Google Scholar] [CrossRef]
- Frost, A.A.; Musulin, B. Semiempirical Potential Energy Functions. I. The H2 and H2+ Diatomic Molecules. J. Chem. Phys. 1954, 22, 1017. [Google Scholar] [CrossRef]
- Jia, C.-S.; Diao, Y.-F.; Liu, X.-J.; Wang, P.-Q.; Liu, J.-Y.; Zhang, G.-D. Equivalence of the Wei potential model and Tietz potential model for diatomic molecules. J. Chem. Phys. 2012, 137, 014101. [Google Scholar] [CrossRef] [PubMed]
- Adepoju, A.G.; Eweh, E.J. Approximate and analytical bound state solutions of the Frost–Musulin potential. Can. J. Phys. 2014, 92, 18–21. [Google Scholar] [CrossRef]
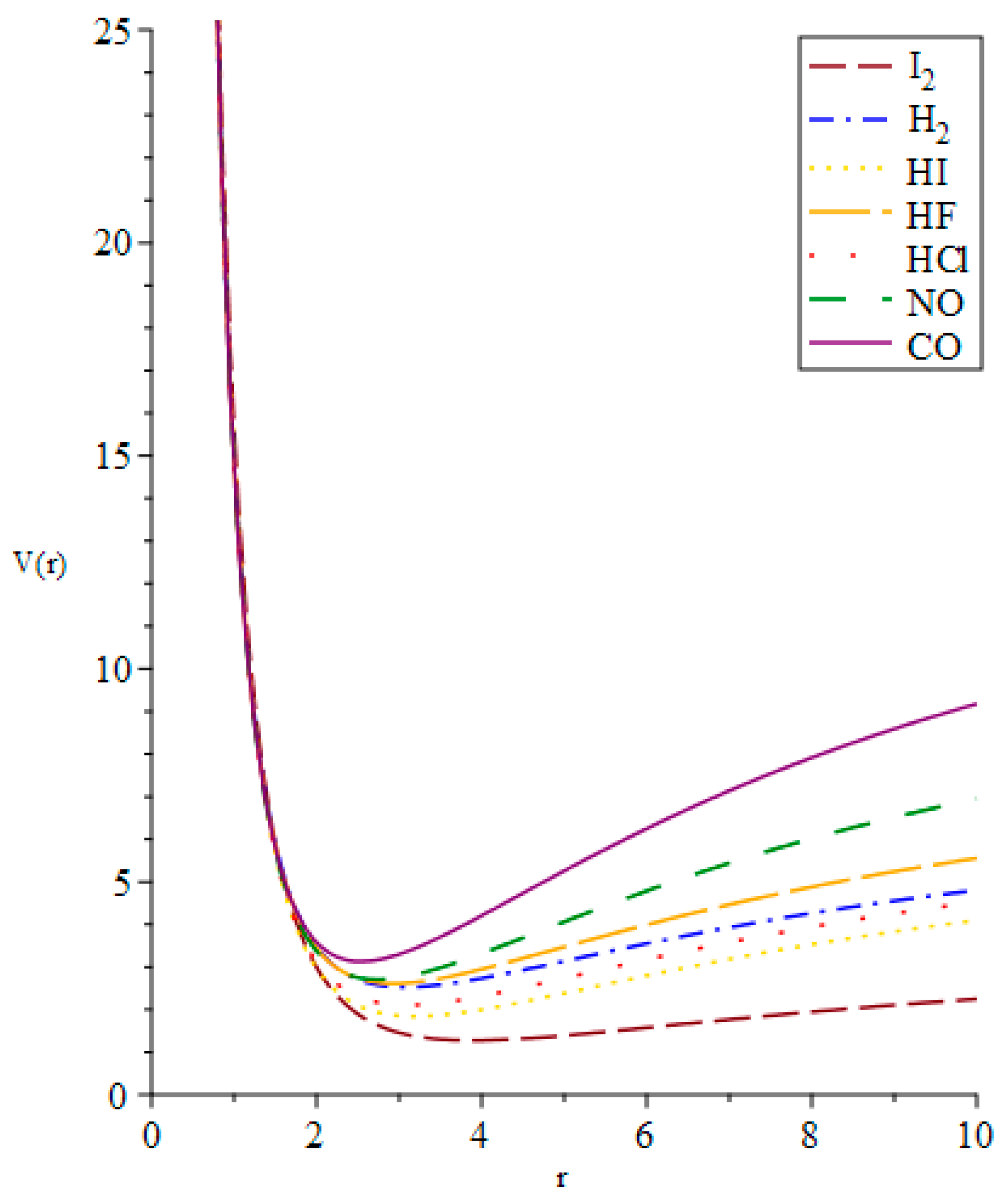
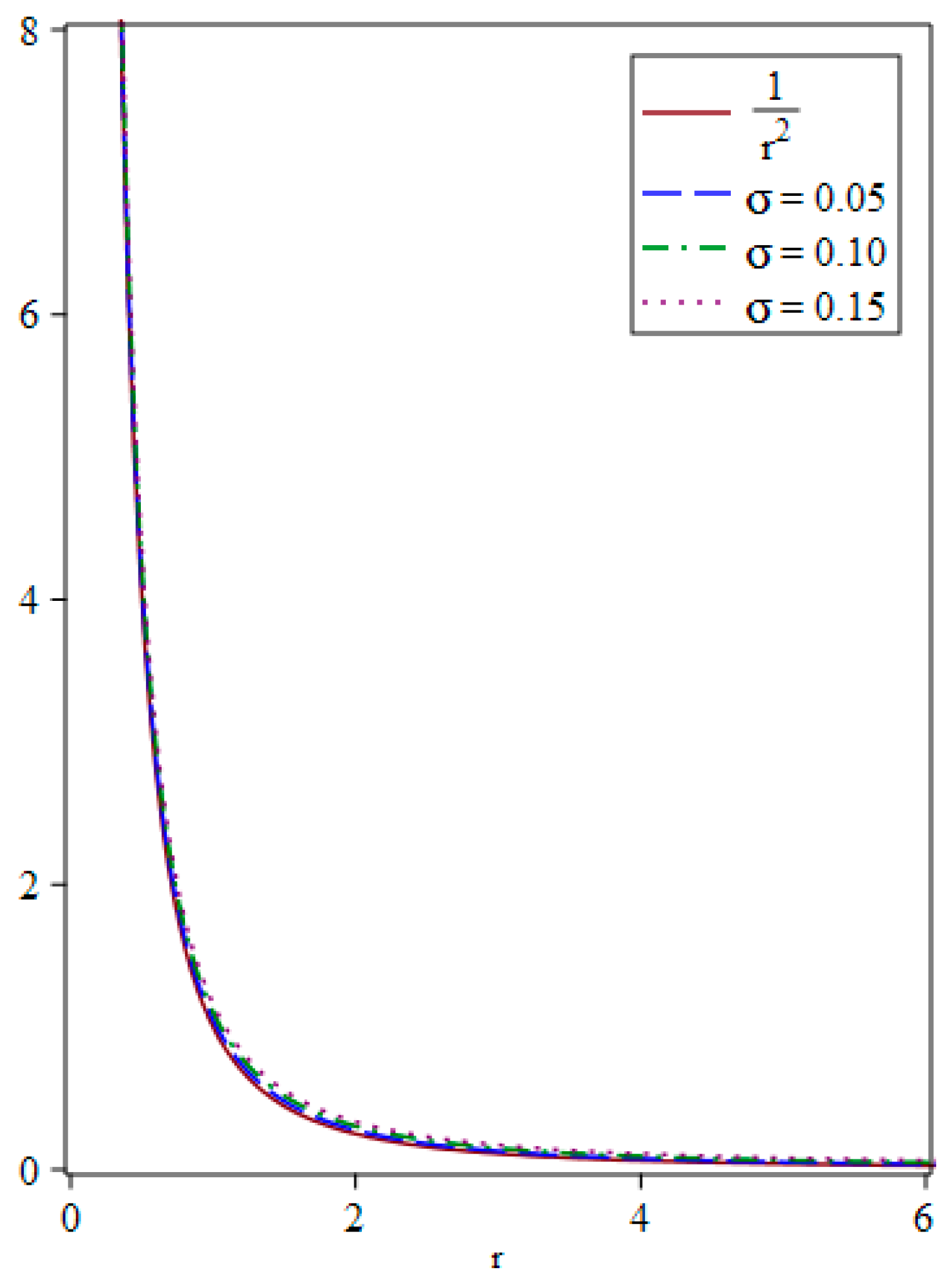
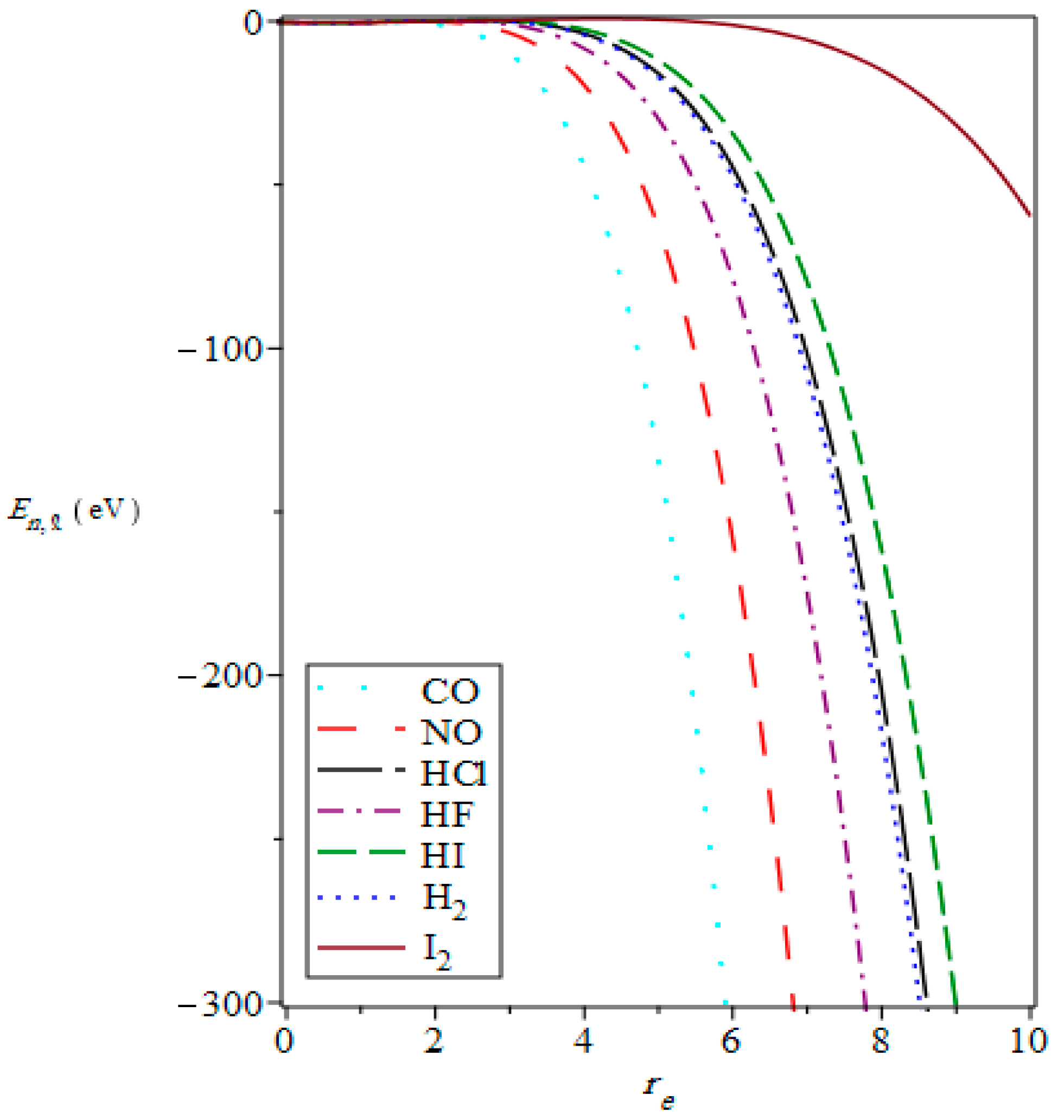
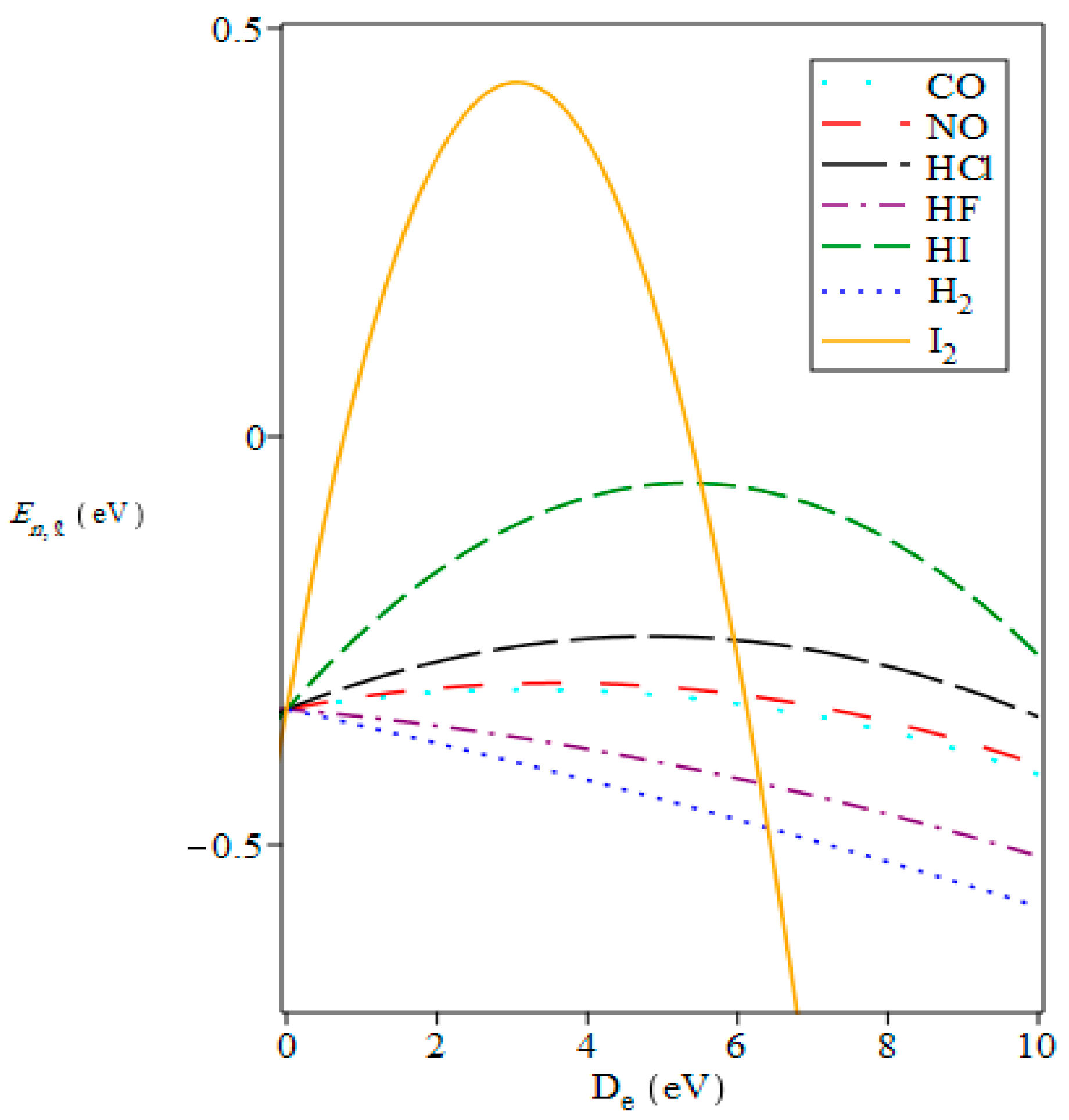

| Molecules | |||
|---|---|---|---|
| 2.662 | 1.5556 | 63.45223 | |
| 1.6040 | 4.1493 | 1.00018 | |
| 0.9171 | 5.8856 | 0.95736 | |
| 1.2746 | 4.6190 | 0.98010 | |
| 1.1508 | 8.0437 | 7.46844 | |
| 1.1283 | 11.2256 | 6.86067 | |
| 0.7416 | 4.7446 | 0.50391 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roshanzamir, M. Thermal Responses and the Energy Spectral of Diatomic Molecules Using Nikiforov–Uvarov Methodology. Mathematics 2023, 11, 3338. https://doi.org/10.3390/math11153338
Roshanzamir M. Thermal Responses and the Energy Spectral of Diatomic Molecules Using Nikiforov–Uvarov Methodology. Mathematics. 2023; 11(15):3338. https://doi.org/10.3390/math11153338
Chicago/Turabian StyleRoshanzamir, Muhammad. 2023. "Thermal Responses and the Energy Spectral of Diatomic Molecules Using Nikiforov–Uvarov Methodology" Mathematics 11, no. 15: 3338. https://doi.org/10.3390/math11153338






