A Methodology for Planning City Logistics Concepts Based on City-Dry Port Micro-Consolidation Centres
Abstract
:1. Introduction
2. Literature Review
| Literature | Distinct Feature | Case Study | Objective Functions/ Criteria | Solution Approach | Method |
|---|---|---|---|---|---|
| [29] | Utilizes map layers for decision criteria using ArcGIS | Melbourne | existing infrastructure, demographics, urban plans, access restrictions, implementation costs, effects on residents | GIS-MCDM | GIS, AHP, TOPSIS |
| [30] | Location selection for one MCC | Pardubice | distance from logistics centers, expansion capacities, resource availability, traveled distance, development costs | Hybrid MCDM | BWM, CRITIC, WASPAS |
| [31] | Location selection for one MCC by considering the goals of multiple stakeholders | Vienna | environmental, social, and spatial aspect | Hybrid | AHP, DEA |
| [51] | Commercial density considered | Sevilla | operational costs | Metaheuristic | Genetic Algorithm |
| [52] | Mobile micro hubs | Hypothetical example | economic efficiency, time efficiency, environmental performances | Simulation- Analytical approach | Simulation- Analytical approach |
| [53] | Mathematical formulation and efficient heuristic for locating multiple MCCs | New York | operational costs, environmental costs, | Heuristic | Greedy heuristic |
| [54] | GIS-based data processing | Stuttgart | demand volume, urban planning, available infrastructure | Hybrid MCDM | AHP, PROMETHEE |
| [55] | Strategic last-mile network design problem through a three-echelon capacitated location-routing problem | Sao Paolo | development costs, operational costs | Hybrid | MILP, Continuous Approximation |
| [56] | Different settings and configurations of a location model | Barcelona | development costs, operational costs | Exact | MILP |
3. City Logistics Concepts Based on City-DP MCCs
4. Methodology for Selecting the Most Sustainable City-DP MCC Concept Variant
4.1. Location Model
4.2. ADAM MCDM Method
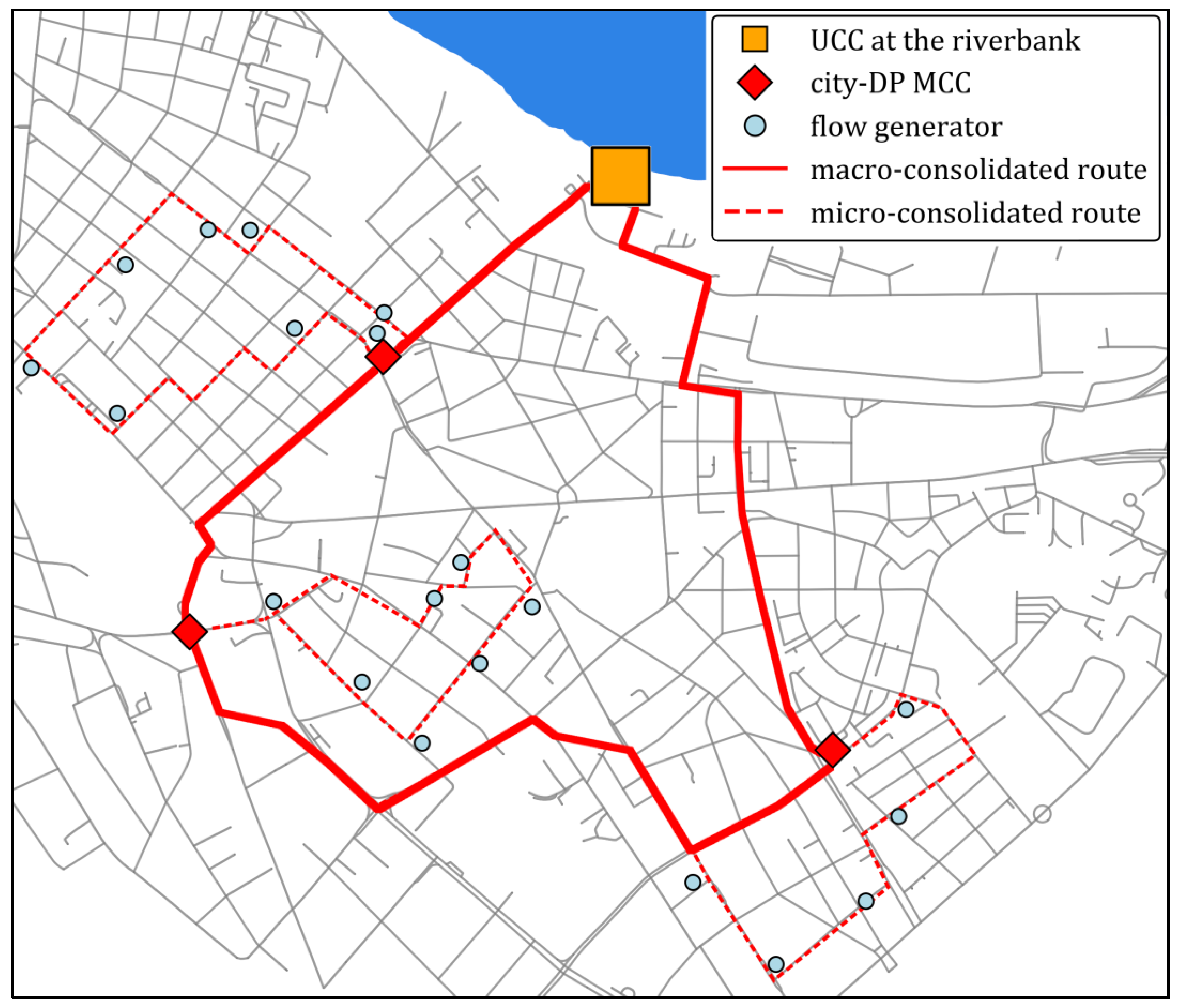
5. Case Study and the Application of the Developed Methodology
- C1—the number of city-DP MCCs required for development;
- C2—the number of delivery vehicle trips;
- C3—traveled distance by delivery vehicles;
- C4—expansion capacities and land ownership;
- C5—delivery reliability and flexibility;
- C6—availability of traffic infrastructure.
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Macharis, C.; Kin, B. The 4 A’s of sustainable city distribution: Innovative solutions and challenges ahead. Int. J. Sust. Transp. 2017, 11, 59–71. [Google Scholar] [CrossRef]
- Bosona, T. Urban freight last mile logistics—Challenges and opportunities to improve sustainability: A literature review. Sustainability 2020, 12, 8769. [Google Scholar] [CrossRef]
- Tadić, S.; Zečević, S. Modelling city logistics concepts; University of Belgrade, Faculty of Transport and Traffic Engineering: Belgrade, Serbia, 2016. [Google Scholar]
- Neghabadi, P.D.; Samuel, K.E.; Espinouse, M.L. Systematic literature review on city logistics: Overview, classification and analysis. Int. J. Prod. Res. 2018, 57, 865–887. [Google Scholar] [CrossRef]
- Tadić, S. City logistics—Sustainable urban development strategy. In Proceedings of the international symposium “Traffic strategic development in South East Europe”, Budva, Montengero, 30–31 May 2018; pp. 187–193. [Google Scholar]
- Tadić, S.; Zečević, S.; Krstić, M. A novel hybrid MCDM model based on fuzzy DEMATEL, fuzzy ANP and fuzzy VIKOR for city logistics concept selection. Expert Syst. Appl. 2014, 41, 8112–8128. [Google Scholar] [CrossRef]
- Rzesny-Cieplinska, J.; Szmelter-Jarosz, A. Environmental sustainability in city logistics measures. Energies 2020, 13, 1303. [Google Scholar] [CrossRef] [Green Version]
- Katsela, K.; Browne, M. Importance of the stakeholders’ interaction: Comparative, longitudinal study of two city logistics initiatives. Sustainability 2019, 11, 5844. [Google Scholar] [CrossRef] [Green Version]
- Rzesny-Cieplinska, J.; Szmelter-Jarosz, A.; Moslem, S. Priority-based stakeholders analysis in the view of sustainable city logistics: Evidence for Tricity, Poland. Sust. Cities Soc. 2021, 67, 102751. [Google Scholar] [CrossRef]
- De Marco, A.; Mangano, G.; Zenezini, G. Classification and benchmark of city logistics measures: An empirical analysis. Int. J. Logist. Res. Appl. 2018, 21, 1–19. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Comi, A.; Ibeas, A.; Moura, J.L. Urban freight transport and city logistics policies: Indications from Rome, Barcelona, and Santander. Int. J. Sust. Transp. 2016, 10, 552–566. [Google Scholar] [CrossRef]
- Tadić, S.; Krstić, M.; Kovač, M. Assessment of city logistics initiative categories sustainability: Case of Belgrade. Env. Dev. Sust. 2022, 25, 1383–1419. [Google Scholar] [CrossRef]
- Raicu, S.; Costescu, D.; Burciu, S. Distribution system with flow consolidation at the boundary of urban congested areas. Sustainability 2020, 12, 990. [Google Scholar] [CrossRef] [Green Version]
- Janjević, M.; Ndiaye, A.B. Development and application of a transferability framework for micro-consolidation schemes in urban freight transport. Procedia–Soc. Behav. Sci. 2014, 125, 284–296. [Google Scholar] [CrossRef] [Green Version]
- He, Z.; Haasis, H.D. Integration of urban freight innovations: Sustainable inner-urban intermodal transportation in the retail/postal industry. Sustainability 2019, 11, 1749. [Google Scholar] [CrossRef] [Green Version]
- Maes, J.; Vanelslander, T. City logistics by water: Good practices and scope for expansion. Oper. Res./Comput. Sci. Interfaces Series. 2015, 58, 413–437. [Google Scholar] [CrossRef]
- Wojewodzka-Krol, K.; Rolbiecki, R. The role of inland waterway transport in city logistics. Transp. Econom. Logist. 2019, 84, 103–114. [Google Scholar] [CrossRef]
- Janjević, M.; Ndiaye, A.B. Inland waterways transport for city logistics: A review of experiences and the role of local public authorities. WIT Trans. Built Environ. 2014, 138, 279–290. [Google Scholar] [CrossRef] [Green Version]
- Wojewodzka-Krol, K.; Rolbiecki, R. Innovative solutions for inland waterway transport. Transp. Econom. Logist. 2018, 80, 245–255. [Google Scholar] [CrossRef]
- Khaslavskaya, A.; Roso, V. Dry ports: Research outcomes, trends, and future implications. Maritime Econom. Logist. 2020, 22, 265–292. [Google Scholar] [CrossRef] [Green Version]
- Kovač, M.; Tadić, S.; Krstić, M.; Roso, V. Modelling dry port systems in the framework of inland waterway container terminals. Comput. Model. Eng. Sci. 2023, 137, 1019–1046. [Google Scholar] [CrossRef]
- Krstić, M.; Agnusdei, G.P.; Tadić, S.; Kovač, M.; Miglietta, P.P. A novel Axial-Distance-Based Aggregated Measurement (ADAM) method for the evaluation of agri-food circular-economy-based business models. Mathematics 2023, 11, 1334. [Google Scholar] [CrossRef]
- Montreuil, B. Toward a Physical Internet: Meeting the global logistics sustainability grand challenge. Logist. Res. 2011, 3, 71–87. [Google Scholar] [CrossRef]
- Montreuil, B.; Ballot, E.; Fontane, F. An open logistics interconnection model for the Physical Internet. IFAC Proc. Vol. 2012, 45, 327–332. [Google Scholar] [CrossRef]
- Sluijk, N.; Florio, A.M.; Kinable, J.; Dellaert, N.; Van Woensel, T. Two-echelon vehicle routing problems: A literature review. Eur. J. Oper. Res. 2023, 304, 865–886. [Google Scholar] [CrossRef]
- Tadić, S.; Kovač, M.; Čokorilo, O. The application of drones in city logistics concepts. Promet–Traffic Transp. 2021, 33, 451–462. [Google Scholar] [CrossRef]
- Abbassi, A.; Kharraja, S.; Alaoui, A.E.A.; Boukachour, J.; Paras, D. Multi-objective two-echelon location-distribution of non-medical products. Int. J. Prod. Res. 2021, 59, 5284–5300. [Google Scholar] [CrossRef]
- Darvish, M.; Archetti, S.; Coelho, L.C.; Speranza, M.G. Flexible two-echelon location routing problem. Eur. J. Oper. Res. 2019, 277, 1124–1136. [Google Scholar] [CrossRef]
- Aljohani, K.; Thompson, R.G. A multi-criteria spatial evaluation framework to optimise the siting of freight consolidation facilities in inner-city areas. Transp. Res. Part A. 2020, 138, 51–69. [Google Scholar] [CrossRef]
- Novotna, M.; Švadlenka, L.; Jovčić, S.; Simić, V. Micro-hub location selection for sustainable last-mile delivery. PLoS ONE 2022, 17, e0270926. [Google Scholar] [CrossRef]
- Bajec, P.; Tuljak-Suban, D.; Slapnik, V. Micro-depots site selection for last-mile delivery, considering the needs of post-pandemic parcel recipients. Trans. Res. Procedia. 2023, 69, 496–503. [Google Scholar] [CrossRef]
- Mirhedayatian, S.M.; Crainic, T.G.; Guajardo, M.; Wallace, S.W. A two-echelon location-routing problem with synchronization. J. Oper. Res. Soc. 2019, 72, 145–160. [Google Scholar] [CrossRef]
- Arias-Osorio, J.; Camacho-Pinto, J. New hybrid metaheuristic for the 2eLIRP. Rev. UIS Ingenierias. 2021, 20, 151–162. [Google Scholar] [CrossRef]
- Liu, D.; Deng, Z.; Zhang, W.; Wang, Y.; Kaisar, E.I. Design of sustainable urban electronic grocery distribution network. Alexandria Eng. J. 2021, 60, 145–157. [Google Scholar] [CrossRef]
- Govindan, K.; Jafarian, A.; Khodaverdi, R.; Devika, K. Two-echelon multiple-vehicle location–routing problem with time windows for optimization of sustainable supply chain network of perishable food. Int. J. Prod. Econ. 2014, 152, 9–28. [Google Scholar] [CrossRef]
- Heidari, A.; Imani, D.M.; Khalilzadeh, M.; Sarbazvatan, M. Green two-echelon closed and open location-routing problem: Application of NSGA-II and MOGWO metaheuristic approaches. Environ. Dev. Sustain. 2022. [Google Scholar] [CrossRef] [PubMed]
- Vidović, M.; Ratković, B.; Bjelić, N.; Popović, D. A two-echelon location-routing model for designing recycling logistics networks with profit: MILP and heuristic approach. Expert Syst. Appl. 2016, 51, 34–48. [Google Scholar] [CrossRef]
- Hu, W.; Dong, J.; Hwang, B.; Ren, R.; Chen, Z. Hybrid optimization procedures applying for two-echelon urban underground logistics network planning: A case study of Beijing. Comp. Ind. Eng. 2020, 144, 106452. [Google Scholar] [CrossRef]
- Tofighi, S.; Torabi, S.A.; Mansouri, S.A. Humanitarian logistics network design under mixed uncertainty. Eur. J. Oper. Res. 2016, 250, 239–250. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Wang, X.; Wu, X.; Zhou, F.; Zhou, L. Multi-objective optimization for two-echelon joint delivery location routing problem considering carbon emission under online shopping. Transp. Lett. 2022. [Google Scholar] [CrossRef]
- Fallahtafti, A.; Ardjmand, E.; Young II, W.A.; Weckman, G.R. A multi-objective two-echelon location-routing problem for cash logistics: A metaheuristic approach. Appl. Soft Comput. 2021, 111, 107685. [Google Scholar] [CrossRef]
- Cheng, C.; Zhu, R.; Costa, A.M.; Thompson, R.G.; Huang, X. Multi-period two-echelon location routing problem for disaster waste clean-up. Transp. A Transp. Sci. 2022, 18, 1053–1083. [Google Scholar] [CrossRef]
- Cao, J.X.; Wang, X.; Gao, J. A two-echelon location-routing problem for biomass logistics systems. Biosyst. Eng. 2021, 202, 106–118. [Google Scholar] [CrossRef]
- Li, H.; Yuan, J.; Lv, T.; Chang, X. The two-echelon time-constrained vehicle routing problem in linehaul-delivery systems considering carbon dioxide emissions. Transp. Res. Part D. 2016, 49, 231–245. [Google Scholar] [CrossRef]
- Li, J.; Ensafian, H.; Bell, M.G.H.; Geers, D.G. Deploying autonomous mobile lockers in a two-echelon parcel operation. Transp. Res. Part C. 2021, 128, 103155. [Google Scholar] [CrossRef]
- Rahmani, Y.; Cherif-Khettaf, W.R.; Oulamara, A. The two-echelon multi-products location-routing problem with pickup and delivery: Formulation and heuristic approaches. Int. J. Prod. Res. 2016, 54, 999–1019. [Google Scholar] [CrossRef]
- Azad, N.; Davoudpour, H. A two echelon location-routing model with considering Value-at-Risk measure. Int. J. Manag. Sci. Eng. Manag. 2010, 5, 235–240. [Google Scholar] [CrossRef]
- Kechmane, L.; Nsiri, B.; Baalal, A. Optimization of a two-echelon location lot-sizing routing problem with deterministic demand. Math. Probl. Eng. 2018, 2018, 2745437. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, S.; Zhou, X.; Mahmoudi, M.; Zhen, L. Green logistics location-routing problem with eco-packages. Transp. Res. Part E. 2020, 143, 102118. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Prins, C.; Prodhon, C. Solving the two-echelon location routing problem by a GRASP reinforced by a learning process and path relinking. Eur. J. Oper. Res. 2012, 216, 113–126. [Google Scholar] [CrossRef]
- Munuzuri, J.; Cortes, P.; Grosso, R.; Guadix, J. Selecting the location of minihubs for freight delivery in congested downtown areas. J. Comput. Sci. 2012, 3, 228–237. [Google Scholar] [CrossRef]
- Faugere, L.; White, C.; Montreuil, B. Mobile access hub deployment for urban parcel logistics. Sustainability 2020, 12, 7213. [Google Scholar] [CrossRef]
- Arrieta-Prieto, M.; Ismael, A.; Rivera-Gonzalez, C.; Mitchell, J.E. Location of urban micro-consolidation centers to reduce the social cost of last-mile deliveries of cargo: A heuristic approach. Networks 2021, 79, 292–313. [Google Scholar] [CrossRef]
- Rudolph, C.; Nsamzinshuti, A.; Bonsu, S.; Ndiaye, A.B.; Rigo, N. Localization of relevant urban micro-consolidation centres for last-mile cargo bike delivery based on real demand data and city characteristics. Transp. Res. Rec. 2022, 2676, 365–375. [Google Scholar] [CrossRef]
- Janjević, M.; Merchan, D.; Wilkenbach, M. Designing multi-tier, multi-service-level, and multi-modal last-mile distribution networks for omni-channel operations. Eur. J. Oper. Res. 2021, 294, 1059–1077. [Google Scholar] [CrossRef]
- Savall-Manyo, M.; Ribas, I. Location of micro-urban consolidation centres for the superblocs in Barcelona. IFAC PapersOnLine 2022, 55, 145–150. [Google Scholar] [CrossRef]
- Crainic, T.G.; Montreuil, B. Physical Internet enabled hyperconnected city logistics. Transp. Res. Proc. 2016, 12, 383–398. [Google Scholar] [CrossRef] [Green Version]
- Fontaine, P.; Minner, S.; Schiffer, M. Smart and sustainable city logistics: Design, consolidation, and regulation. Eur. J. Oper. Res. 2023, 307, 1071–1084. [Google Scholar] [CrossRef]
- Kovač, M.; Tadić, S.; Krstić, M. Sustainable city logistics concepts—Elements and conceptualization. Tehnika 2023, 70, 197–206. [Google Scholar] [CrossRef]
- Ambra, T.; Caris, A.; Macharis, C. Towards freight transport system unification: Reviewing and combining the advancements in the Physical Internet and synchromodal transport research. Int. J. Prod. Res. 2019, 57, 1606–1623. [Google Scholar] [CrossRef]
- Ben Mohamed, I.; Klibi, W. Modelling and solution approaches for the interconnected city logistics. Int. J. Prod. Res. 2017, 55, 2664–2684. [Google Scholar] [CrossRef]
- Rosenkrantz, D.; Stearns, R.; Lewis II, P. An analysis of several heuristics for the traveling salesman problem. SIAM J. Comput. 1977, 6, 563–581. [Google Scholar] [CrossRef]
- Agnusdei, L.; Krstić, M.; Palmi, P.; Miglietta, P.P. Digitalization as driver to achieve circularity in the agroindustry: A SWOT-ANP-ADAM approach. Sci. Total Env. 2023, 882, 163441. [Google Scholar] [CrossRef] [PubMed]
- Krstić, M.; Tadić, S.; Kovač, M.; Roso, V.; Zečević, S. A novel hybrid MCDM model for the evaluation of sustainable last mile solutions. Math. Probl. Eng. 2021, 2021, 5969788. [Google Scholar] [CrossRef]
- Tadić, S.; Krstić, M.; Zečević, S. Evaluation of the logistics system development scenarios—Case study of the trading company. Tehnika 2020, 67, 343–354. [Google Scholar] [CrossRef]
- Boeing, G. OSMnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef] [Green Version]
- Gurobi Optimization Software. Available online: https://www.gurobi.com/solutions/gurobi-optimizer (accessed on 28 June 2023).
- Krstić, M.; Kovač, M. Axial-Distance-Based Aggregated Measurement (ADAM) MCDM Software. Available online: http://adam-mcdm.com (accessed on 10 July 2023).
- Keshavarz-Ghorabaee, M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-criteria inventory classification using a new method of Evaluation based on Distance from Average Solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of Alternatives and Ranking according to Compromise Solution (MARCOS). Comptut. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Pamučar, D.; Ćirović, G. The selection of transport and handling resources in logistics centers using Multi-Attributive Border Approximation area Comparison (MABAC). Expert Syst. Appl. 2015, 42, 3016–3028. [Google Scholar] [CrossRef]
- Lai, Y.J.; Liu, T.Y.; Hwang, C.L. TOPSIS for MODM. Eur. J. Oper. Res. 1994, 76, 486–500. [Google Scholar] [CrossRef]
- Kovač, M.; Tadić, S.; Krstić, M. Novel spherical fuzzy MARCOS method for assessment of drone-based city logistics concepts. Complexity. 2021, 2021, 2374955. [Google Scholar] [CrossRef]
- Treiblmaier, H.; Mirkovski, K.; Lowry, P.B.; Zacharia, Z.G. The physical internet as a new supply chain paradigm: A systematic literature review and a comprehensive framework. Int. J. Logist. Manag. 2020, 31, 239–287. [Google Scholar] [CrossRef]
- Maslarić, M.; Nikoličić, S.; Mirčetić, D. Logistics response to the Industry 4.0: The Physical Internet. Open Eng. 2016, 6, 511–517. [Google Scholar] [CrossRef]
- Nathanail, E.; Mitropoulos, L.; Adamos, G.; Gogas, M.; Karakikes, I.; Iwan, S.; Kiba-Janiak, M.; Kotowska, I.; Kijewska, K.; Jedlinski, M.; et al. Evaluation Tool; NOVELOG-D.3.2.-v3; NOVELOG Project: Brussels, Belgium, 2016. [Google Scholar]
- Xenou, E.; Madas, M.; Ayfandopoulou, G. Developing a smart city logistics assessment framework (SCLAF): A conceptual tool for identifying the level of smartness of a city logistics system. Sustainability 2022, 14, 6039. [Google Scholar] [CrossRef]
- Zanezini, G.; De Marco, A. City logistics policy evaluation with system dynamics. Transp. Res. Proc. 2020, 46, 253–260. [Google Scholar] [CrossRef]
- Anand, N.; Van Duin, J.H.R.; Tavasszy, L. Framework for modelling multi-stakeholder city logistics domain using the agent based modelling approach. Transp. Res. Proc. 2016, 16, 4–15. [Google Scholar] [CrossRef] [Green Version]
- Golini, R.; Guerlain, C.; Lagorio, A.; Pinto, R. An assessment framework to support collective decision making on urban freight transport. Transport 2018, 33, 890–901. [Google Scholar] [CrossRef] [Green Version]



| Literature | Distinct Feature | Objective Functions 1 | Solution Approach | Method |
|---|---|---|---|---|
| [27] | Time makespan of distribution | min: Cost, min: DistrTime | Metaheuristic | Particle Swarm Optimization, Genetic Algorithm, Variable Neighborhood Search |
| [28] | Flexibility in network design and due dates of customer service | min: Cost | Heuristic | Variable Mixed-Integer Programming Neighborhood Descent, Enhanced Parallel Exact Method |
| [32] | Synchronization between echelons | min: Cost | Heuristic | Decomposition-based heuristic |
| [33] | Inventory routing | min: Cost | Metaheuristic | Tabu search, Genetic Algorithm |
| [34] | Heterogeneous fleet and satellites | min: Cost, min: ExtCost | Metaheuristic | Immune algorithm |
| [35] | Time windows and perishable products | min: Cost, min: ExtCost | Metaheuristic | Particle Swarm Optimization, Variable Neighborhood Search |
| [36] | Incorporation of company-owned and rented vehicles | min: Cost, min: ExtCost | Metaheuristic | Genetic Algorithm, Gray Wolf Optimizer |
| [37] | Profit and distance-dependent collection rate | max: Profit | Heuristic | Greedy heuristic approach |
| [38] | Underground logistics system planning as a 2E-LRP | min: Cost, max: UtilRate | Metaheuristic | Genetic Algorithm, Particle Swarm Optimization |
| [39] | Humanitarian logistics network design as a 2E-LRP | min: Cost, min: DistrTime, max: DemCov | Metaheuristic | Differential Evolution algorithm |
| [40] | Horizontal cooperation among service providers | min: Cost, min: ExtCost, max: CustSat | Metaheuristic | Immune algorithm, Genetic algorithm |
| [41] | Adaptation for cash logistics | min: Cost, min: Risk | Metaheuristic | Genetic Algorithm, Pareto Evolutionary Algorithm, Simulated Annealing |
| [42] | Multi-period variant of the 2E-LRP | min: Cost | Metaheuristic | Genetic Algorithm |
| [43] | Adaptation for a biomass logistics system | min: Cost | Metaheuristic | Tabu search, Variable Neighborhood Search |
| [44] | Linehaul transportation between distribution centers | min: ExtCost | Heuristic | Clarke-Wright algorithm, Local search |
| [45] | Autonomous mobile lockers as facilities | min: Cost | Heuristic | Clarke-Wright algorithm |
| [46] | Multi-product with pickup and delivery | min: Cost | Heuristic | Nearest Neighbor, Clustering approach |
| [47] | Stochastic demand and value-at-risk incorporation in the decision-making | min: Cost | Metaheuristic | Tabu search |
| [48] | Multi-period location lot-sizing | min: Cost | Metaheuristic | Genetic Algorithm, Local search |
| [49] | Lifecycle of green eco-packages considered | min: Cost | Metaheuristic | Gaussian mixture clustering, Clarke-Wright algorithm, Genetic Algorithm |
| [50] | GRASP complemented by a learning process and path relinking | min: Cost | Metaheuristic | Greedy Randomized Adaptive Search Procedure, Variable Neighborhood Descent |
| City Logistics Concept | Number of UCCs | Transportation UCC—City-DP MCCs | Transportation—Last Phase | Service Provider |
|---|---|---|---|---|
| CL-city-DP-01 | 1 | road (electric vehicles) | electric vehicles/autonomous vehicles/ bicycles/on foot/etc. | logistics service provider |
| CL-city-DP-02 | 1 | road (electric vehicles) | passenger vehicles/bicycles/scooters/ on foot/etc. | crowdsourcing agents |
| CL-city-DP-03 | 1 | road (electric vehicles) | electric vehicles/autonomous vehicles/ bicycles/on foot/etc. | combined logistics service provider and crowdsourcing agents |
| CL-city-DP-04 | 1 | rail | electric vehicles/autonomous vehicles/ bicycles/on foot/etc. | logistics service provider |
| CL-city-DP-05 | 1 | rail | passenger vehicles/bicycles/scooters/ on foot/etc. | crowdsourcing agents |
| CL-city-DP-06 | 1 | rail | electric vehicles/autonomous vehicles/ bicycles/on foot/etc. | combined logistics service provider & crowdsourcing agents |
| CL-city-DP-07 | multiple | road (electric vehicles) | electric vehicles/autonomous vehicles/ bicycles/on foot/etc. | logistics service provider |
| CL-city-DP-08 | multiple | road (electric vehicles) | passenger vehicles/bicycles/ scooters/on foot/etc. | crowdsourcing agents |
| CL-city-DP-09 | multiple | road (electric vehicles) | electric vehicles/autonomous vehicles/ bicycles/on foot/etc. | combined logistics service provider and crowdsourcing agents |
| CL-city-DP-10 | multiple | rail | electric vehicles/autonomous vehicles/ bicycles/on foot/etc. | logistics service provider |
| CL-city-DP-11 | multiple | rail | passenger vehicles/bicycles/scooters/on foot/etc. | crowdsourcing agents |
| CL-city-DP-12 | multiple | rail | electric vehicles/autonomous vehicles/ bicycles/on foot/etc. | combined logistics service provider and crowdsourcing agents |
| Generator Type | Delivery Size (kg) |
|---|---|
| Type 1 | U~[0.5, 1.0] |
| Type 2 | U~[1.0, 5.0] |
| Type 3 | U~[5.0, 10.0] |
| Type 4 | U~[10.0, 20.0] |
| Type 5 | U~[20.0, 50.0] |
| Generator Type | Distribution of Generators | ||||
|---|---|---|---|---|---|
| Type 1 | Type 2 | Type 3 | Type 4 | Type 5 | |
| Zone 1 | 0% | 0% | 15% | 40% | 45% |
| Zone 2 | 5% | 10% | 20% | 45% | 20% |
| Zone 3 | 25% | 35% | 20% | 10% | 10% |
| Zone 4 | 35% | 25% | 25% | 7.5% | 7.5% |
| Concept Variant | UCC Location | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|---|
| city-DP-V1 | UCC 1 | 12 | 32 | 792 | 6 | 2 | 9 |
| city-DP-V2 | UCC 2 | 11 | 33 | 617 | 2 | 7 | 4 |
| city-DP-V3 | UCC 3 | 10 | 31 | 584 | 4 | 8 | 7 |
| city-DP-V4 | UCC 4 | 11 | 31 | 622 | 5 | 6 | 5 |
| city-DP-V5 | UCC 5 | 11 | 32 | 588 | 1 | 8 | 2 |
| city-DP-V6 | UCC 6 | 12 | 32 | 632 | 7 | 4 | 5 |
| city-DP-V7 | UCC 7 | 12 | 32 | 693 | 8 | 3 | 6 |
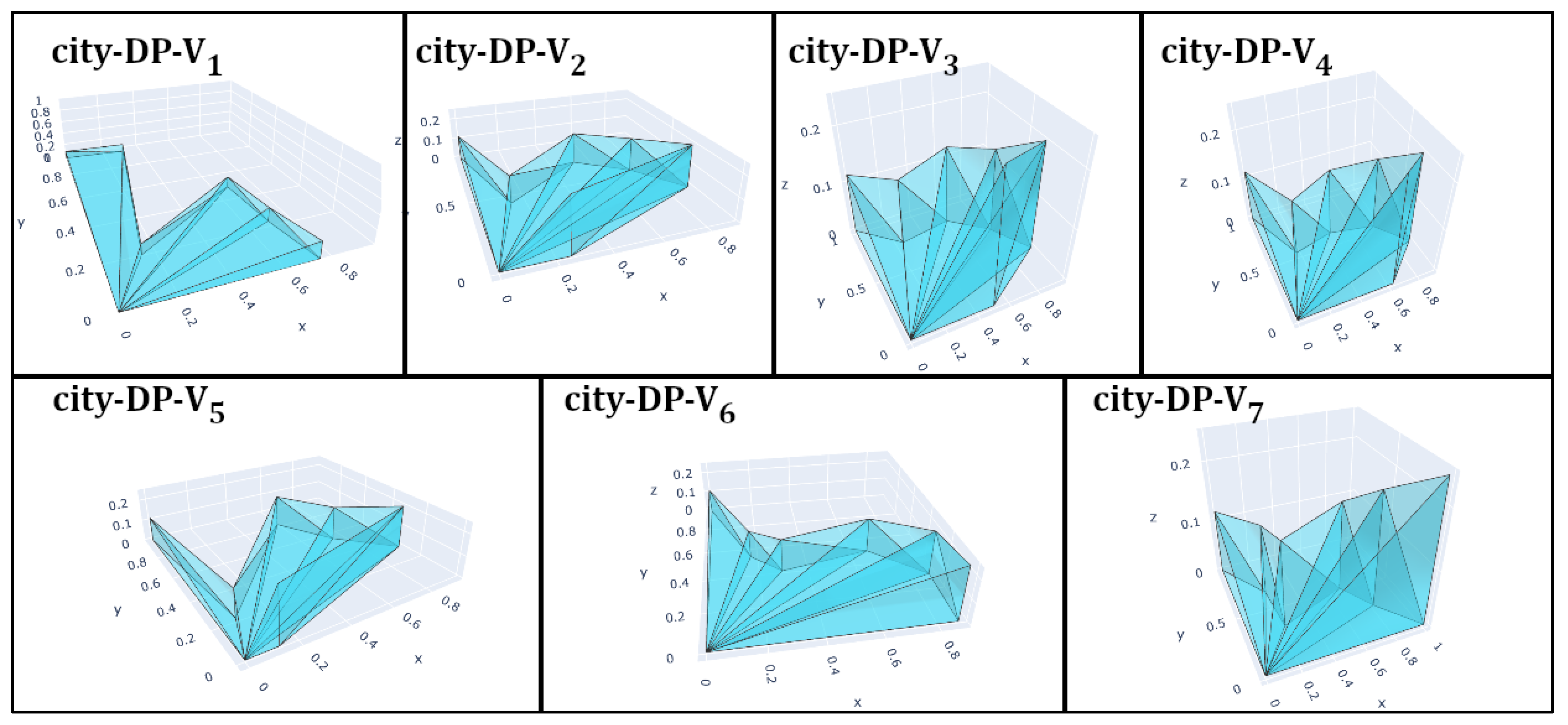
| Concept Variant | UCC Location | Vi | Rank |
|---|---|---|---|
| city-DP-V1 | UCC 1 | 0.043 | 6 |
| city-DP-V2 | UCC 2 | 0.045 | 5 |
| city-DP-V3 | UCC 3 | 0.067 | 1 |
| city-DP-V4 | UCC 4 | 0.053 | 2 |
| city-DP-V5 | UCC 5 | 0.040 | 7 |
| city-DP-V6 | UCC 6 | 0.050 | 3 |
| city-DP-V7 | UCC 7 | 0.049 | 4 |
| Concept Variant | Sc. 0 | Sc. 1 | Sc. 2 | Sc. 3 | Sc. 4 | Sc. 5 | Sc. 6 | Sc. 7 | Sc. 8 | Sc. 9 | Sc. 10 | Sc. 11 | Sc. 12 | Sc. 13 | Average Rank | Final Rank |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| city-DP-V1 | 6 | 2 | 5 | 2 | 5 | 2 | 3 | 3 | 5 | 3 | 5 | 2 | 5 | 2 | 3.57 | 4 |
| city-DP-V2 | 5 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 5.93 | 6 |
| city-DP-V3 | 1 | 1 | 1 | 3 | 1 | 1 | 1 | 2 | 1 | 5 | 1 | 4 | 1 | 4 | 1.93 | 1 |
| city-DP-V4 | 2 | 4 | 2 | 5 | 2 | 3 | 5 | 5 | 4 | 4 | 4 | 5 | 4 | 5 | 3.86 | 5 |
| city-DP-V5 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7.00 | 7 |
| city-DP-V6 | 3 | 5 | 3 | 4 | 4 | 5 | 4 | 4 | 3 | 2 | 3 | 3 | 3 | 3 | 3.50 | 3 |
| city-DP-V7 | 4 | 3 | 4 | 1 | 3 | 4 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2.21 | 2 |
| Concept Variant | UCC Location | ADAM Rank | EDAS Rank | MARCOS Rank | MABAC Rank | TOPSIS Rank |
|---|---|---|---|---|---|---|
| city-DP-V1 | UCC 1 | 6 | 4 | 5 | 7 | 3 |
| city-DP-V2 | UCC 2 | 5 | 6 | 6 | 6 | 6 |
| city-DP-V3 | UCC 3 | 1 | 1 | 1 | 1 | 1 |
| city-DP-V4 | UCC 4 | 2 | 5 | 4 | 2 | 5 |
| city-DP-V5 | UCC 5 | 7 | 7 | 7 | 5 | 7 |
| city-DP-V6 | UCC 6 | 3 | 3 | 3 | 3 | 4 |
| city-DP-V7 | UCC 7 | 4 | 2 | 2 | 4 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovač, M.; Tadić, S.; Krstić, M.; Veljović, M. A Methodology for Planning City Logistics Concepts Based on City-Dry Port Micro-Consolidation Centres. Mathematics 2023, 11, 3347. https://doi.org/10.3390/math11153347
Kovač M, Tadić S, Krstić M, Veljović M. A Methodology for Planning City Logistics Concepts Based on City-Dry Port Micro-Consolidation Centres. Mathematics. 2023; 11(15):3347. https://doi.org/10.3390/math11153347
Chicago/Turabian StyleKovač, Milovan, Snežana Tadić, Mladen Krstić, and Miloš Veljović. 2023. "A Methodology for Planning City Logistics Concepts Based on City-Dry Port Micro-Consolidation Centres" Mathematics 11, no. 15: 3347. https://doi.org/10.3390/math11153347
APA StyleKovač, M., Tadić, S., Krstić, M., & Veljović, M. (2023). A Methodology for Planning City Logistics Concepts Based on City-Dry Port Micro-Consolidation Centres. Mathematics, 11(15), 3347. https://doi.org/10.3390/math11153347








