An Inhomogeneous Model for Laser Welding of Industrial Interest
Abstract
:1. Introduction to the Problem
2. Melting–Resolidification Process
3. Governing Equation
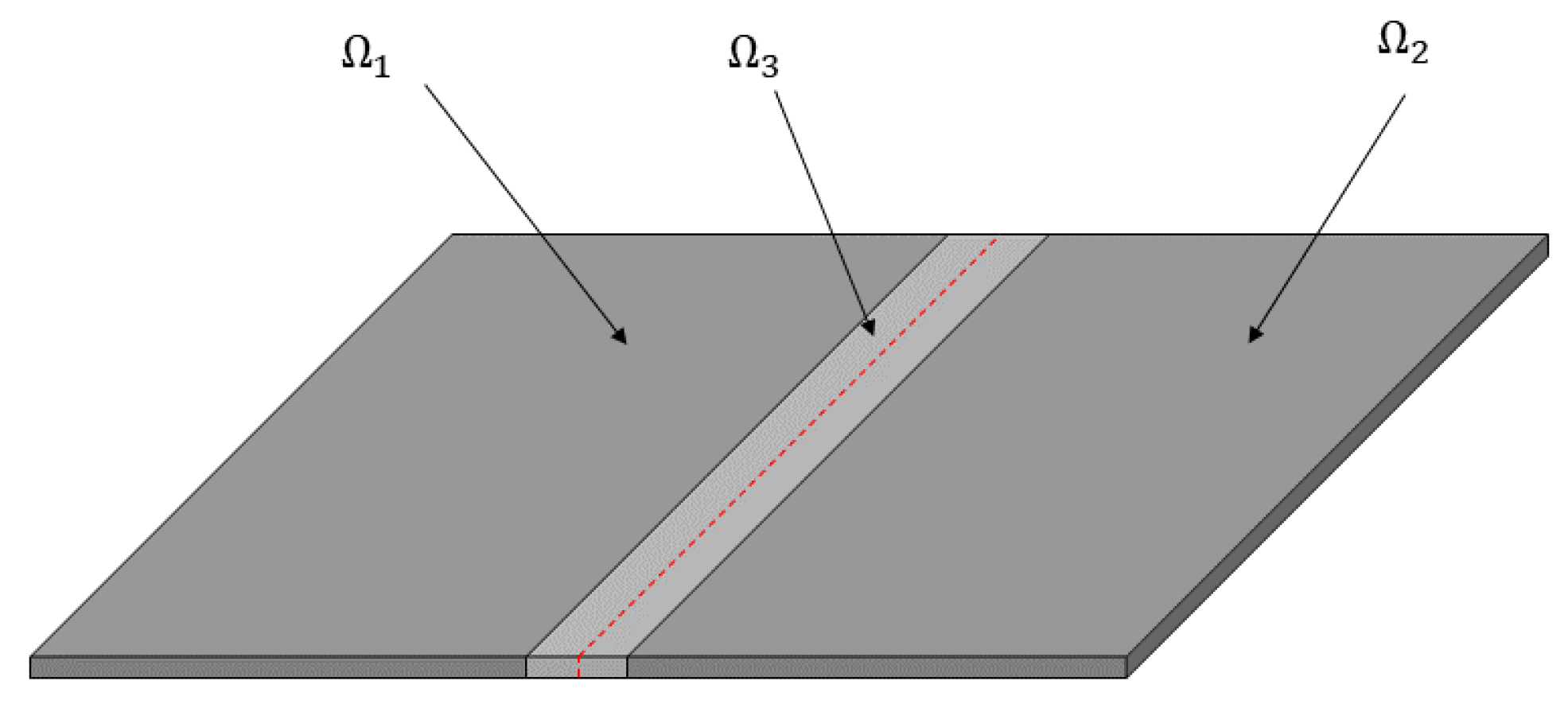
3.1. Material and Geometries
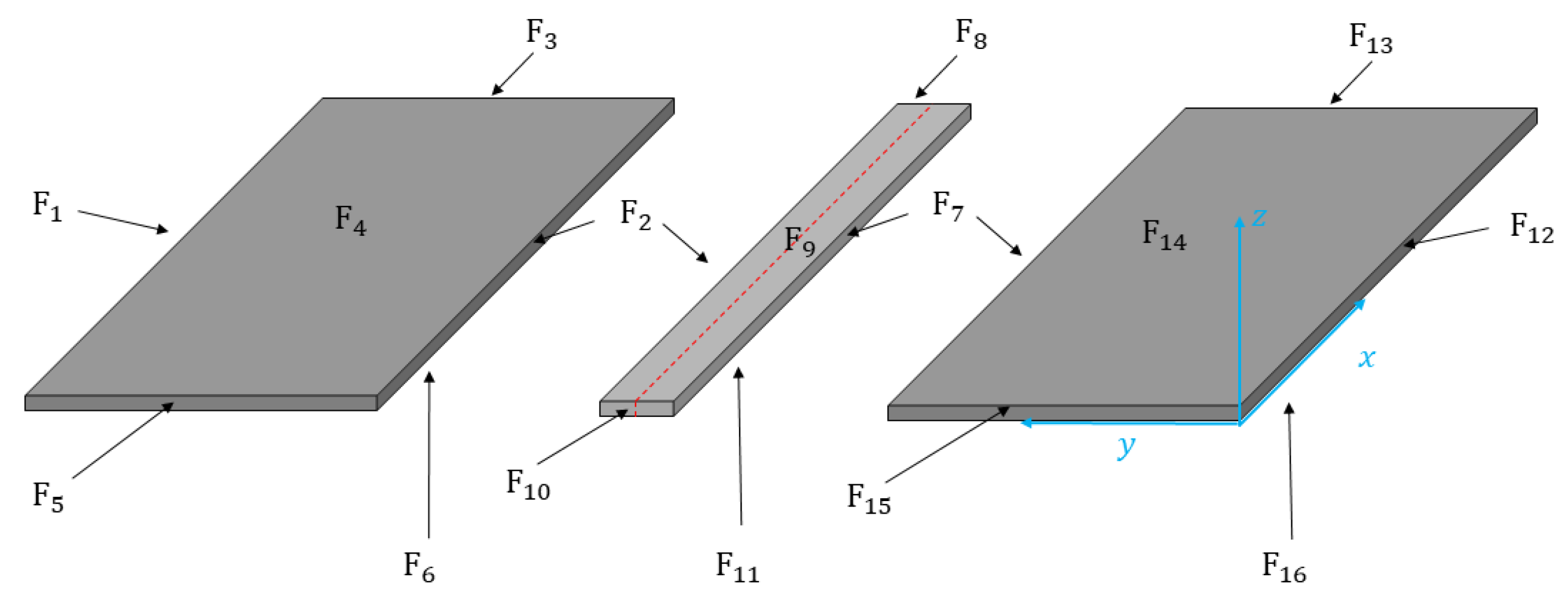
3.2. Domains Not Belonging to the Laser Welding Domain: Model, Initial and Boundary Conditions
3.3. Laser Welding Domain: The Model
3.4. Full Model in the Domain
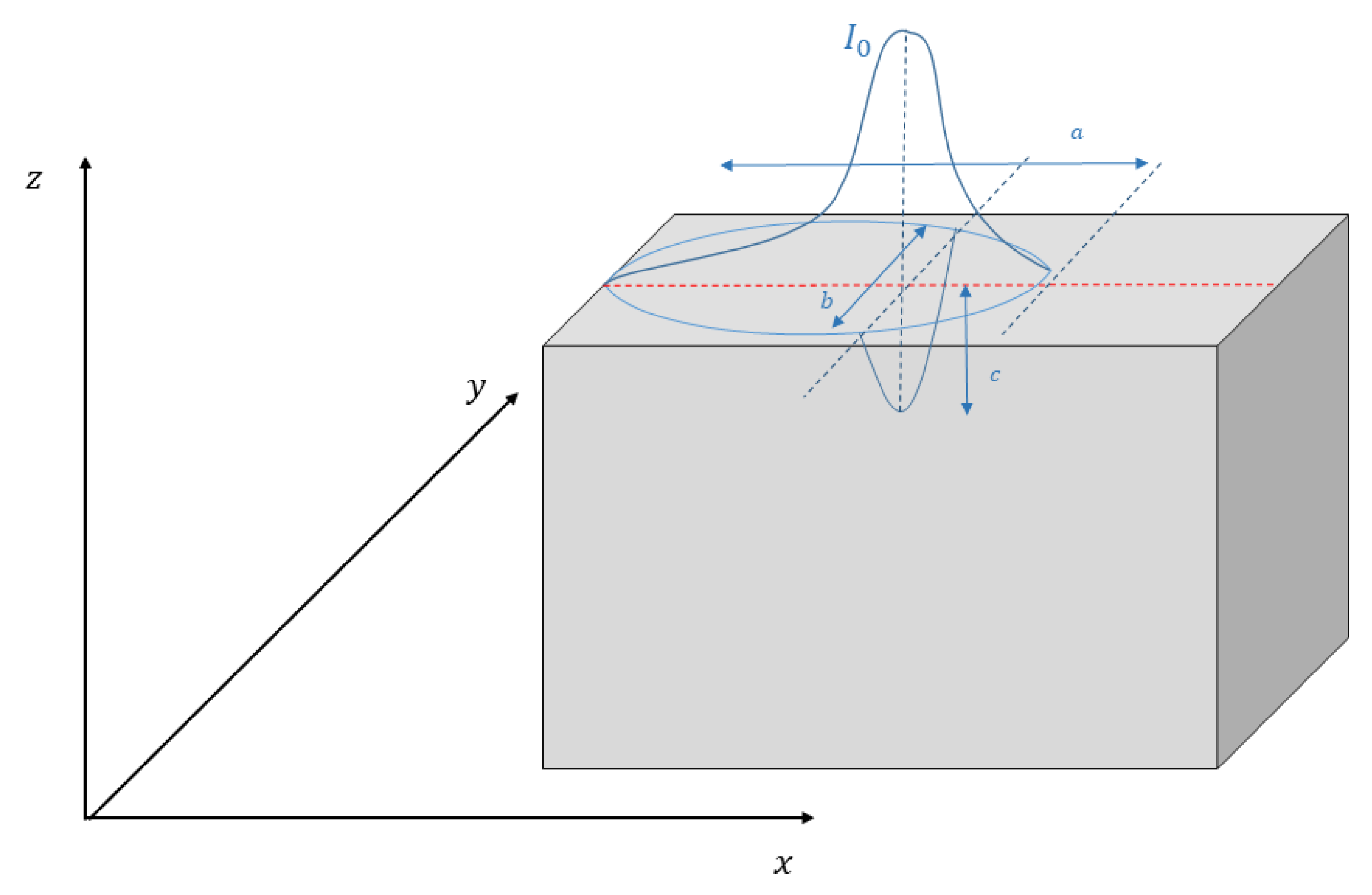
3.5. Realistic Formulations for Both Volumetric and Superficial Laser Heat Sources
3.5.1. Classical Gaussian Laser Heat Source
3.5.2. Conical Laser Heat Source
3.5.3. Ellipsoid Laser Heat Source
4. The Galerkin-FEM Approach
4.1. Some Remarks on Existence, Uniqueness and Regularity of the Solution
- (1)
- , , , and are non-negative constants;
- (2)
- is a positive and bounded real function of class with a bounded derivative;
- (3)
- assumed to satisfy the following inequality:where , are constants;
- (4)
- is a positive bounded real function;
- (5)
- with ;
- (6)
- ;
- (7)
- , verifying
4.2. Galerkin-FEM Basics
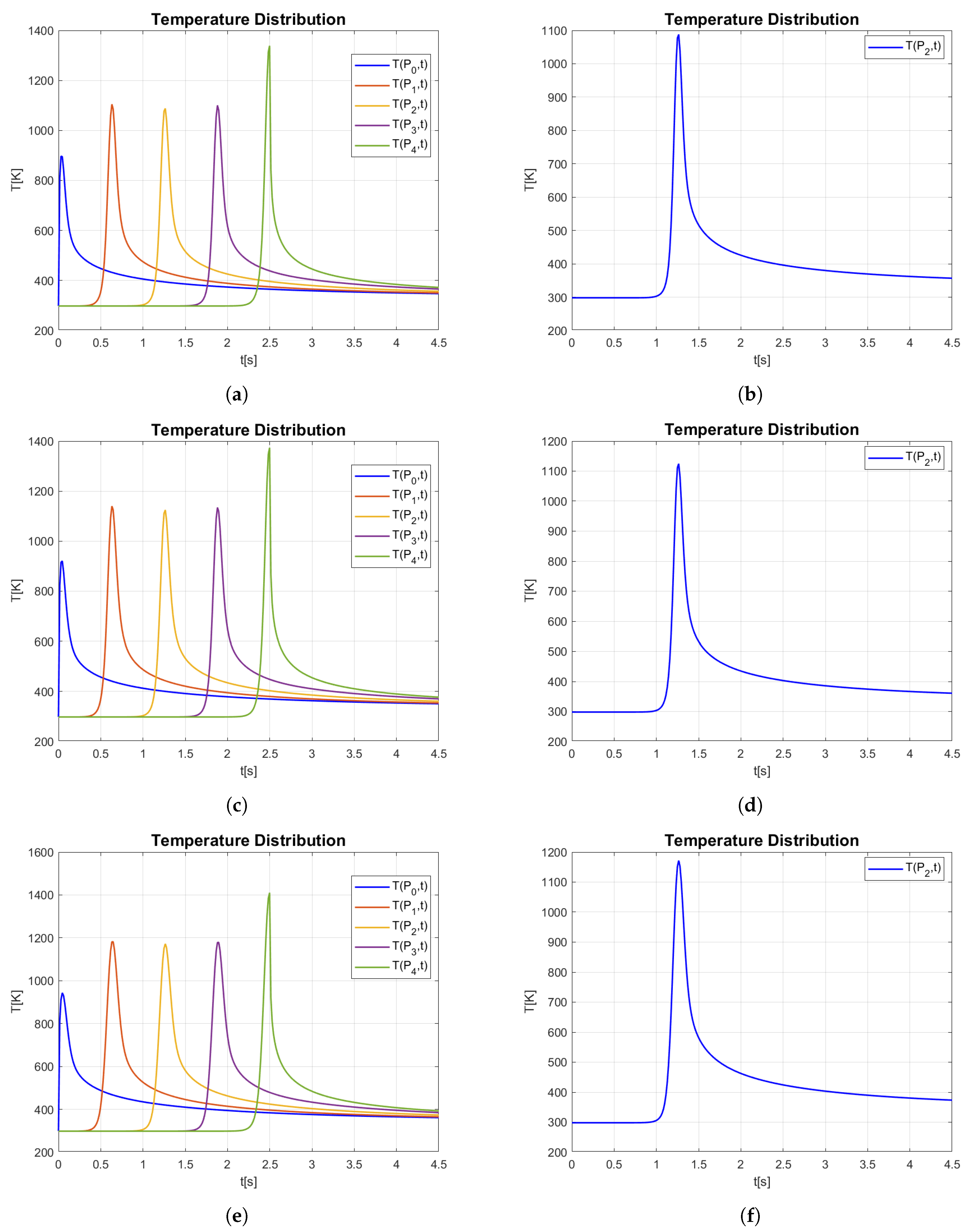
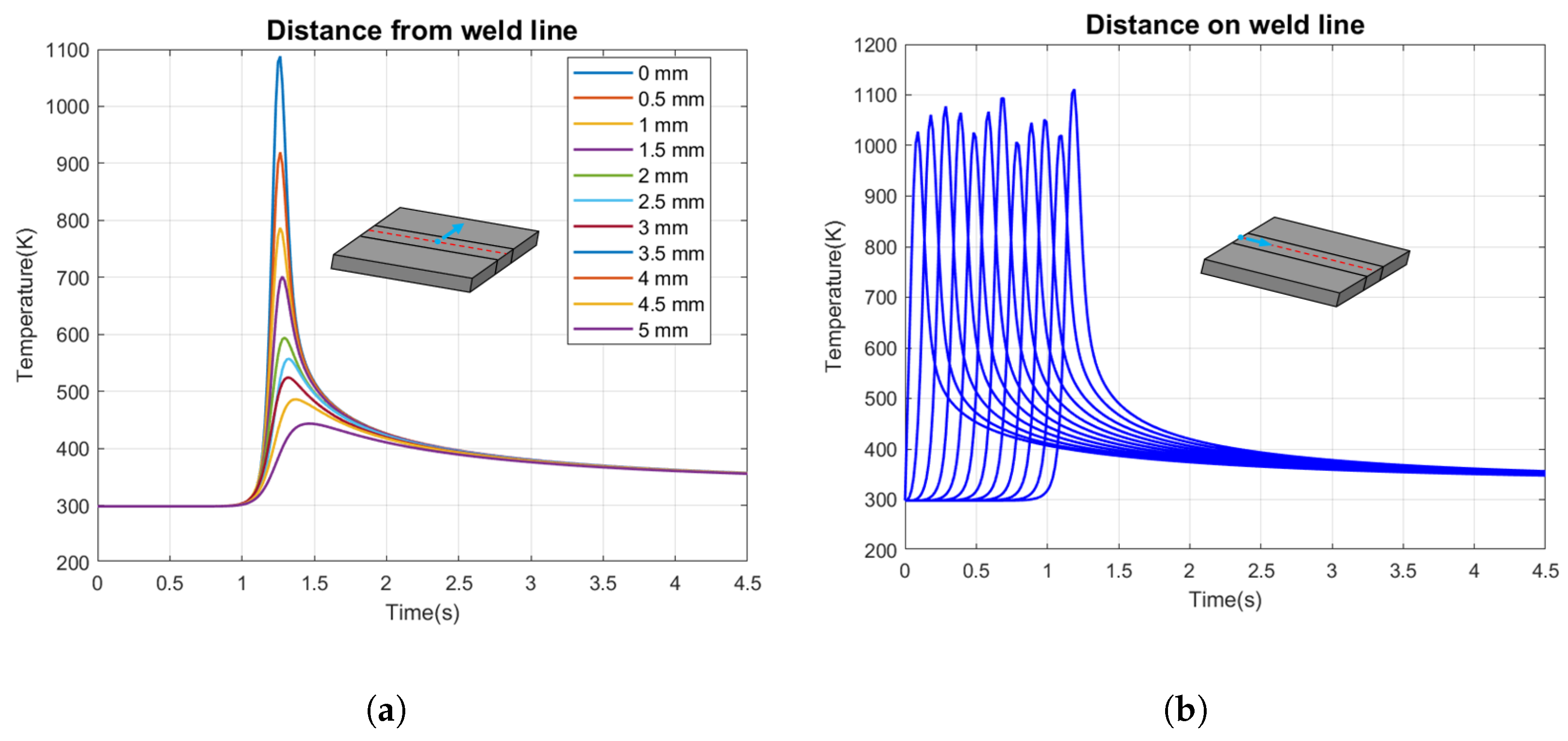
5. Results of Computations
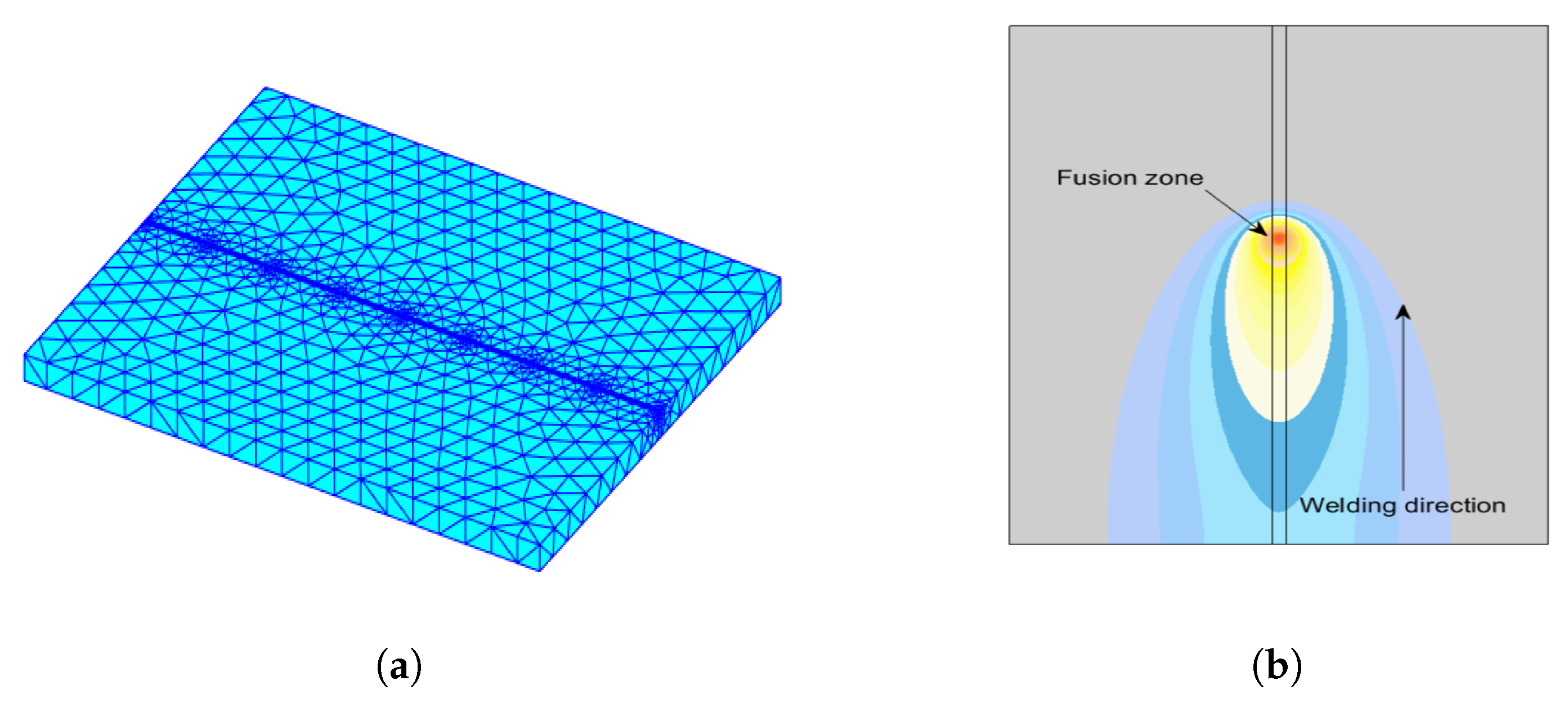
5.1. Mesh Creation
5.2. Exploiting Classical Gaussian Laser Heat Source
5.3. Exploiting Conical 3D Laser Heat Source
5.4. Exploiting Ellipsoid Laser Heat Source
6. Conclusions and Perspectives
- -
- The proposed model is quite realistic since it simulates the welding process of Al-Si 5% alloy plates, used on an industrial level with appreciable results, placed side by side, which takes the form of the creation of a fusion/resolidification bead, in compliance with regulatory standards, without the addition of additional material which, usually, causes unwanted thickening.
- -
- The process implemented, based on a temperature melting range of the alloy, fits well with the needs of modern metallurgy.
- -
- The further boundary condition, taking into account the fact that the plates are placed on a workbench, lays the first foundations for more accurate modeling, which begins to take into account any thermal losses.
- -
- As further highlighted in Figure 12, the laser beam modeled by the classic 3D Gaussian formulation fits well with the proposed analytical approach, leaving the operator the right choice of laser beam power (strictly linked to the laser electrical current) to avoid damage to the material structure.
- -
- The proposed polynomial-shaped substitute thermal capacity makes it possible to obtain maps, highlighting gradual variations in temperature, which agree well with the fact that the analytical solution is unique and regular (also providing the volumetric solid-state fraction, which, as is known, defines the mechanical properties of the weld). Obviously, the topic is far from being fully studied, and several more studies need to be conducted to optimize the proposed process and then evaluate with standardized characterization tests. Particularly, the ongoing research foresees the following future developments:
- Considering non-linearity in thermal conductivity, where the thermal conductivity depends on temperature, would enhance the model’s accuracy. This improvement would better reflect real-world conditions and contribute to more precise predictions;
- Upgrading the model to account for the effects of significant thermal expansion in the alloy would be beneficial. Considering the resulting solidification shrinkage and the associated risk of cracks will further improve the model’s predictive capabilities.
- To better simulate real laser welding behavior, future research should consider phenomena such as the production of vapor bubbles (keyholes) and surface tension imbalances caused by temperature gradients (Marangoni effect). Incorporating these factors will contribute to a more comprehensive understanding of the welding process.
- The model should be extended to account for the non-instantaneous temperature distribution during welding. Additionally, considering the microstructural disturbances caused by the laser beam’s interaction with restricted areas of material will enhance the model’s accuracy.
- Exploring the versatility of laser sources, particularly in terms of power and power density management, would allow for localized heating to facilitate specific metallurgical processes. Integrating this capability into the model would increase its practicality and applicability.
- Future research should investigate the impact of the laser beam’s power density, interaction time with the material, and total energy on the localized treatment phase. Understanding these factors will enable optimization of the welding process.
- Although the power of the laser is high, it must be taken into account that it takes some time for the electrical power, converted into the thermal equivalent, to penetrate the material, causing it to melt. Then it would be appropriate to consider the response time of the material before the heat input from the laser penetrates deeply, and introduce one/two relaxation times, considering a Maxwell–Cattaneo–Vernotte/dual-phase lag-type model.
- The dynamic problem studied, if framed in the context of non-homogeneous materials in contact with each other, requires highly non-uniform meshes (to be appropriately refined and re-refined) with preconditions that are difficult to formulate. Then, we find it interesting to reformulate the problem in this framework to obtain optimized numerical solutions using two-level approaches.
- Finally, it would be desirable for the proposed model to explain the presence of the electric current generating the laser beam so as to clearly highlight the cause–effect link on which to implement specific control actions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Katayamas, S. Fundamentals and Details of Laser Welding; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Min, K.E.; Jang, J.W.; Kim, C. New Frontiers of Laser Welding Technology. Appl. Sci. 2023, 13, 1840. [Google Scholar] [CrossRef]
- Dal Fabbro, M. An overview of the state of the art in laser welding simulation. Opt. Laser Technol. 2016, 78, 2–14. [Google Scholar]
- Hong, K.M.; Shin, Y.C. Prospects of laser welding technology in the automotive industry: A review. J. Mater. Process. Technol. 2017, 245, 46–49. [Google Scholar] [CrossRef]
- Mohr, M.A.; Bushey, D.; Aggarwal, A.; Marvin, J.S.; Kim, J.J.; Jimenez Marquez, E.; Liang, Y.; Patel, R.; Macklin, J.J.; Lee, C.Y.; et al. jYCaMP: An optimized calcium indicator for two-photon imaging at fiber laser wavelengths. Nat. Methods 2020, 17, 694–697. [Google Scholar] [CrossRef] [PubMed]
- Rimalc, V.; Shishodia, S.; Srivastava, P.K. Novel synthesis of high-thermal stability carbon dots and nanocomposites from oleic acid as an organic substrate. Appl. Nanosci. 2020, 10, 455–464. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, R.; Pan, L.; Ma, J.; Zhu, Y.; Diao, T.; Zhang, L. A lightweight deep learning algorithm for inspection of laser welding defects on safety vent of power battery. Comput. Ind. 2020, 123, 103306. [Google Scholar] [CrossRef]
- Xiadong, N.A. Laser Welding; BoD-Books on Demand: Singapore, 2010. [Google Scholar]
- Dos Santos Paes, L.E.; Pereira, M.; Xavier, F.A.; Lindolfo, W.; Vlarinho, L.O. Lack of fusion mitigation in directed energy deposition with laser (DED-L) additive manufacturing through laser remelting. J. Manuf. Process. 2022, 73, 67–77. [Google Scholar] [CrossRef]
- Ren, Z.; Fang, F.; Yan, N.; Wu, Y. State of the art in defect detection based on machine vision. Int. J. Precis. Eng. Manuf.-Green Technol. 2022, 9, 661–691. [Google Scholar] [CrossRef]
- Ghosh, A.; Chattopadhyay, H. Mathematical modeling of moving heat source shape for submerged arc welding process. Int. J. Adv. Manuf. Technol. 2013, 69, 2691–2701. [Google Scholar] [CrossRef]
- Morosanu, C.; Satco, B. Qualitative and quantitative analysis for a nonlocal and nonlinear reaction-diffusion problem with in-homogeneous Neumann boundary conditions. Am. Inst. Math. Sci. 2023, 16, 1–15. [Google Scholar] [CrossRef]
- Kaplan, A.F.H. Influence of the beam profile formulation when modeling fiber-guided laser welding. J. Laser Appl. 2011, 23, 42005. [Google Scholar] [CrossRef]
- Ragavendra, N.M.; Vasudevan, M. Effect of laser and hybrid laser welding processes on the residual stresses and distortion in AISI type 316 LN stainless steel weld joints. Metall. Mater. Trans. B 2021, 52, 2582–2603. [Google Scholar] [CrossRef]
- Unni, A.K.; Vasudevan, M. Determination of heat source Model for simulating full penetration laser welding of 316 LN stainless steel by computational fluid dynamics. Mater. Today Proc. 2021, 45, 4465–4471. [Google Scholar] [CrossRef]
- Fakir, R.; Barka, N.; Brousseau, J. Case study of laser hardening process applied to 4340 steel cylindrical specimens using simulation and experimental validation. Case Stud. Therm. Eng. 2018, 11, 15–25. [Google Scholar] [CrossRef]
- Oussaid, K.; Ouafi, A.E.I. A three-dimensional numerical model for predicting the Weld bead geometry characteristics in laser overlap welding of low carbon galvanized steel. J. Appl. Math. Phys. 2019, 7, 2169–2186. [Google Scholar] [CrossRef] [Green Version]
- Sarila, V.K.; Moiniddin, S.Q.; Cheepu, M.; Rajendran, H.; Kantumuchu, V.C. Characterization of microstructural anisotropy in 17–4 PH stainless steel fabricated by DMLS additive manufacturing and laser shot peening. Trans. Indian Inst. Met. 2023, 76, 403–410. [Google Scholar] [CrossRef]
- Belyaev, V.V.; Kovalev, O.B. Simulation of ome method of laser welding of metal plates involving an SHS-reacting powder ixture. Int. J. Heat Mass Transf. 2009, 52, 173–180. [Google Scholar] [CrossRef]
- Wang, H.F.; Zho, D.W.; Huand, M.M.; Miao, H. Study on mathematical model off temperature field in the laser welding process. J. Artifacturing Process. 2021, 63, 121–129. [Google Scholar]
- Giglio, N.C.; Fried, N.M. Computational simulations for infrared laser sealing and cutting of blood vessel. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 7200608. [Google Scholar] [CrossRef]
- Majachrzak, E.; Mochnaki, B.; Suchy, J.S. Kinetics of casting solidification—An inverse approach. Sci. Res. Inst. Math. Comput. Sci. 2007, 6, 169–178. [Google Scholar]
- Miranville, A.; Morosanu, C. A Qualitative analysis of a nonlinear second-order anisotropic diffusion problem with non-homogeneous Cauchy–Stefan–Boltzmann boundary conditions. Appl. Math. Optim. 2021, 84, 227–244. [Google Scholar] [CrossRef]
- Mohan, A.; Ceglarek, D.; Auinger, M. Numerical modelling of thermal quantities for improving remote laser welding process capability space with consideration to beam oscillation. Int. J. Adv. Manuf. Technol. 2022, 123, 761–782. [Google Scholar] [CrossRef]
- Ciesielski, M.; Mochnacki, B. Comparison of approaches to the numerical modelling of pure metals solidification using the control volume method. Int. J. Cast Met. Res. 2019, 32, 213–220. [Google Scholar] [CrossRef]
- DebRoy, T.; Mukherjee, T.; Wei, H.L.; Elmer, J.W.; Milewsi, J.O. Metallurgy, mechanistic models and machine learning in metal printing. Nat. Rev. Mater. 2021, 6, 48–68. [Google Scholar] [CrossRef]
- Nudez del Prado, E.; Challamel, N.; Picandet, V. Discrete and nonlocal solutions for the lattice Cattaneo–Vernotte heat diffusion equation. Math. Mech. Complex Syst. 2021, 9, 367–396. [Google Scholar] [CrossRef]
- Pyo, C.; Jeong, S.M.; Kim, J.; Park, M.; Shin, J.; Kim, Y.; Son, J.; Kim, J.H.; Kim, M.H. A study on the enhanced process of elaborate heat source model parameters for flux core arc welding of 9% for cryogenic storage tank. J. Mar. Sci. Eng. 2022, 10, 1810. [Google Scholar] [CrossRef]
- Chen, J.; Yang, Y.; Sang, C.; Wang, D.; Wu, S.; Zhang, M. Influence mechanism of process parameters on the interfacial characterization of selective laser melting 316L/CuSn10. Mater. Sci. Eng. 2020, 792, 139316. [Google Scholar] [CrossRef]
- Goldak, J.A.; Akhlaghi, M. Computational Welding Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Quarteroni, A. Numerical Models for Differential Problems; Springer: Milano, Italy, 2015. [Google Scholar]
- Balbaa, M.; Hussein, R.; Hackel, L.; Elbestawi, M. A novel post-processing approach towards improving hole accuracy and surface integrity in laser powder bed fusion of IN625. Int. J. Adv. Manuf. Technol. 2022, 119, 6225–6234. [Google Scholar] [CrossRef]
- D’Ostuni, S.; Leo, P.; Casalino, G. FEM simulation of dissimilar aluminum titanium fiber laser welding using 2D and 3D gaussian heat sources. Metals 2017, 7, 307. [Google Scholar] [CrossRef] [Green Version]
- Escribano-García, R.; Alvarez, P.; Marquez-Monje, D. Calibration of finite element model of titanium laser welding by fractional factorial design. J. Manuf. Mater. Process. 2022, 6, 130. [Google Scholar] [CrossRef]
- Ma, D.; Jang, P.; Shu, L.; Gang, Z.; Wang, Y.; Geng, S. Online porosity prediction in laser welding of aluminum alloys based on a multi-fidelity deep learning framework. J. Intell. Manuf. 2022. [Google Scholar] [CrossRef]
- Mascenik, J.; Pavlenko, S.; Sci, J. Determination of stress and deformation during laser welding of aluminum alloys with the PC support. MM Sci. J. 2020, 4, 4104–4107. [Google Scholar] [CrossRef]
- Park, Y.W.; Rhee, S. Process modeling and parameter optimization using neural network and genetic algorithms for aluminum laser welding automation. Int. J. Adv. Manuf. Technol. 2008, 37, 1014–1021. [Google Scholar] [CrossRef]
- Ramiarison, H.; Barka, N.; Mirakhorli, F.; Nadeau, F.; Pilcher, C. Parameter optimization for laser welding of Diissimilar aluminum alloy: 5052-H32 and 6061-T6 considering wobbling technique. Int. J. Adv. Manuf. Technol. 2021, 118, 4195–4211. [Google Scholar] [CrossRef]
- Salsa, S. Partial Differential Equations in Action: From Modelling to Theory; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Tsirkas, S.A.; Papanikos, P.; Kermanidis, T. Numerical simulation of the laser welding process in butt-joint specimens. J. Mater. Process. Technol. 2010, 134, 59–69. [Google Scholar] [CrossRef]
- Xu, T.; Zhou, S.; Ma, X.; Wu, H.; Zhang, L.; Li, M. Significant reinforcement of mechanical properties in laser welding aluminum alloy with carbon manotubes added. Carbon 2022, 191, 36–37. [Google Scholar] [CrossRef]






| Length (mm) | Width (mm) | Thickness (mm) | |
|---|---|---|---|
| 39 | 100 | 4 | |
| 39 | 100 | 4 | |
| 2 | 100 | 4 |
| Length (mm) | Length (mm) | ||
|---|---|---|---|
| Label | Dimensions | Label | Dimensions |
|---|---|---|---|
| Parameter | Value | Unit |
|---|---|---|
| J/(m3 K) | ||
| J/(m3 K) | ||
| 290 | W/(m K) | |
| J/(m3) | ||
| K | ||
| K | ||
| Parameter | Significance | Value | Unit |
|---|---|---|---|
| v | velocity | 40 | mm/s |
| P | power | 2400 | W |
| radius | mm | ||
| reflexivity | |||
| intensity | 340 | W/mm2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munafò, C.F.; Palumbo, A.; Versaci, M. An Inhomogeneous Model for Laser Welding of Industrial Interest. Mathematics 2023, 11, 3357. https://doi.org/10.3390/math11153357
Munafò CF, Palumbo A, Versaci M. An Inhomogeneous Model for Laser Welding of Industrial Interest. Mathematics. 2023; 11(15):3357. https://doi.org/10.3390/math11153357
Chicago/Turabian StyleMunafò, Carmelo Filippo, Annunziata Palumbo, and Mario Versaci. 2023. "An Inhomogeneous Model for Laser Welding of Industrial Interest" Mathematics 11, no. 15: 3357. https://doi.org/10.3390/math11153357
APA StyleMunafò, C. F., Palumbo, A., & Versaci, M. (2023). An Inhomogeneous Model for Laser Welding of Industrial Interest. Mathematics, 11(15), 3357. https://doi.org/10.3390/math11153357








