Analytical Model for Information Flow Management in Intelligent Transport Systems
Abstract
1. Introduction
2. Materials and Methods
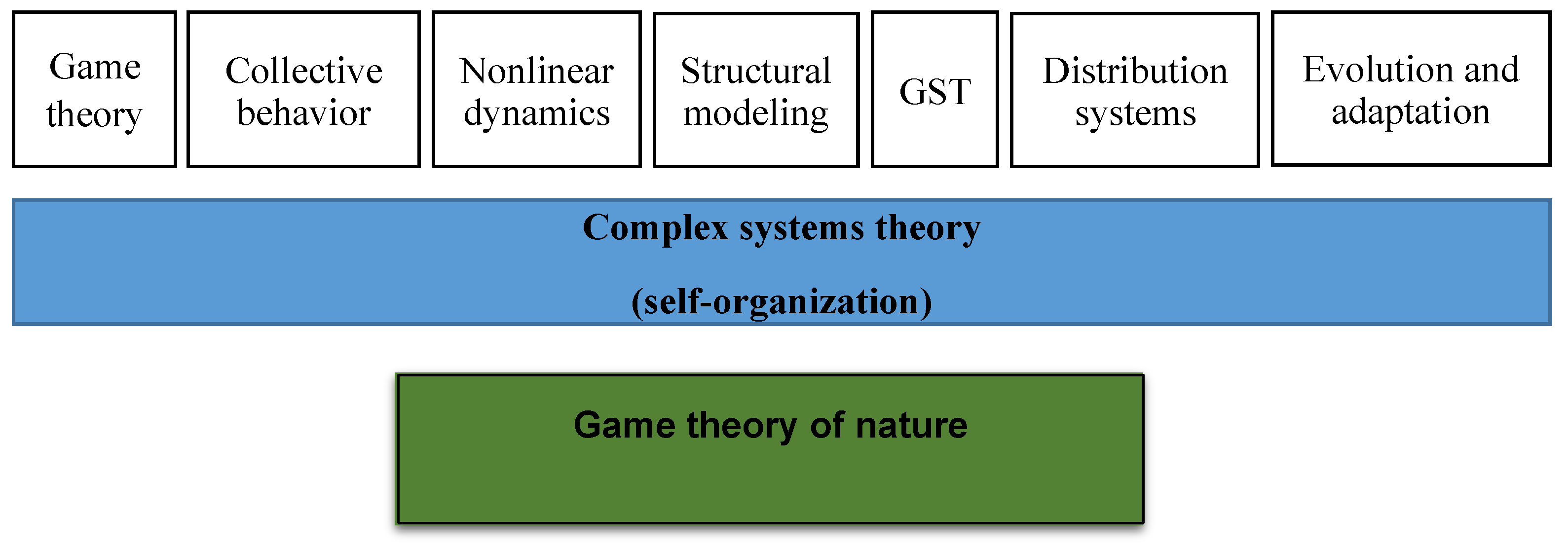
- Ensure that the ITS is presented simply, with all its dominant features, i.e., there should be a balance between the description of complexity and the simplicity of modeling.
- Give theoretical form to the complexity of ITS, using as a basis the system’s information states, which, in turn, depend on possible internal and external disturbances.
- Identify divisibility criteria with due account of the heterogeneity of elements within the ITS [31].
- Design the tools for managing and optimizing ITS performance using the existing decision-making methodologies. This is particularly important from the perspective of the system management processes, as their level of complexity is growing steadily, requiring new, CST-based models.
3. Theoretical Studies
- Since zoning represents an inverse parametric problem of linear programming, it is expedient that zoning is performed based on the principle of maintaining a preset hierarchical relationship between all possible environmental states, not according to the dominant effect principle.
- When dealing with “game with nature”-related problems, it is expedient to use vector optimization techniques, and many multicriterion problems can generally be solved using the tools of game theory of nature. When passing from a multicriterion problem to a “game with nature”, the probabilities of nature states are coincident with relative significance coefficients for criteria , i.e., .
- The procedure for zoning that uses hierarchical relationships between the probabilities of possible environment states is determined by manifestations of the ESs under analysis.
- —number of possible action scenarios;
- —number of possible environmental states or criteria that correspond to them;
- —effectiveness of i-th action for j-th criterion, = , = .
- With the distribution of the field of relative significance coefficients degenerates into a right triangle with ordinary sides (Figure 3). The number of subsets, each having its own relative significance ratio, equals ;
- With (Figure 4), the number of subsets, each having its own relative significance ratio, equals .
4. Results
- The relative significance of indicators , or their corresponding criteria, will be arranged as a sequence (14);
- For each comparable variant i, there is a linear programming problem:
- The values of the relative significance coefficients will be determined analytically:
- The study has no clearly defined quantitative or qualitative characteristics of its target;
- The object of the study has not received thorough analysis at the stage of investigating the phenomena accompanying the system’s performance; or
- The external environment causes no counteraction to system parameters or the process under analysis.
5. Discussion
- On the one hand, when the task is to provide the state forecast, any object or process should be considered as an organized, dialectically developing system.
- On the other hand, when the task is to analyze this system for structural arrangement, properties, and internal and external interactions with the environment, a multidimensional study is required – the one that will provide an in-depth knowledge and description of the system’s current state as a prerequisite of problem solving.
6. Conclusions
- Formalizing a transport system with due account of its information states, which, in turn, are determined by exposure to internal and external disturbances;
- Identifying a transport system’s criteria that take into account the heterogeneity of its elements;
- Achieving the tools for managing and optimizing transport systems’ performance, that build on the existing decision-making methods and allow the disadvantages of the heuristic methods used in determining the weighted coefficients of factors to be avoided.
- Big data in transportation systems to be processed;
- AI-based analysis of transport systems’ operating environments that involves an unlimited number of criteria or performance attributes.
- The a priori ranking of factors (methods based on expert assessments);
- The a priori distribution of probabilities;
- Ensuring guaranteed decision levels.
- The absence of a formalized relationship between the weighted coefficients obtained for individual criteria and action options in transport systems;
- The resultant decision being the maximum possible under the initial values of performance indicators for the criteria under consideration;
- The resultant decision allowing not only the desired Pareto-optimal decisions to be obtained, but also the number of required computations to be substantially reduced.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gou, C.; Wang, K.; Yao, Y.; Li, Z. Vehicle License Plate Recognition Based on Extremal Regions and Restricted Boltzmann Machines. IEEE Trans. Intell. Transp. Syst. 2015, 17, 1096–1107. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.; Hua, Q.; Shang, W.-L.; Luo, Q.; Yu, K. AI-Empowered Speed Extraction via Port-Like Videos for Vehicular Trajectory Analysis. IEEE Trans. Intell. Transp. Syst. 2022, 24, 4541–4552. [Google Scholar] [CrossRef]
- Ryabchikov, D.; Marusina, I.; Shemyakin, A.; Alexeevsky, M.; Malchikov, V. The relevance of the Use of Electric Buses at Motor Transport Enterprises for Intracity Passenger Routes. In Proceedings of the 2022 International Conference on Engineering Management of Communication and Technology (EMCTECH), Vienna, Austria, 20–22 October 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Terentyev, V.; Zabara, K.; Shemyakin, A.; Andreev, K. Advanced solution for improving safety of agricultural machinery during storage. In Robotics, Machinery and Engineering Technology for Precision Agriculture; Shamtsyan, M., Pasetti, M., Beskopylny, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; pp. 403–412. [Google Scholar] [CrossRef]
- Shepelev, V.; Zhankaziev, S.; Aliukov, S.; Varkentin, V.; Marusin, A.; Marusin, A.; Gritsenko, A. Forecasting the Passage Time of the Queue of Highly Automated Vehicles Based on Neural Networks in the Services of Cooperative Intelligent Transport Systems. Mathematics 2022, 10, 282. [Google Scholar] [CrossRef]
- Ostroukh, A.; Berner, L.; Karelina, M.; Kravchenko, P.; Evtiukov, S. Intelligent control system for distributed gas transport facilities. Transp. Res. Procedia 2021, 57, 376–384. [Google Scholar] [CrossRef]
- Makarova, I.; Mavrin, V.; Sadreev, D.; Buyvol, P.; Boyko, A.; Belyaev, E. Rational Organization of Urban Parking Using Microsimulation. Infrastructures 2022, 7, 140. [Google Scholar] [CrossRef]
- Shepelev, V.; Glushkov, A.; Bedych, T.; Gluchshenko, T.; Almetova, Z. Predicting the Traffic Capacity of an Intersection Using Fuzzy Logic and Computer Vision. Mathematics 2021, 9, 2631. [Google Scholar] [CrossRef]
- Glushkov, A.; Shepelev, V. Development of Reliable Models of Signal-Controlled Intersections. Transp. Telecommun. J. 2021, 22, 417–424. [Google Scholar] [CrossRef]
- Malygin, I.; Komashinskiy, V.; Korolev, O. Cognitive technologies for providing road traffic safety in intelligent transport systems. Transp. Res. Procedia 2018, 36, 487–492. [Google Scholar] [CrossRef]
- Marusin, A.; Tian, H.; Safiullin, R.; Safiullin, R.; Marusina, I. Integral Evaluation of the Effectiveness of the Implementation of Automated Technical Means of Controlling the Movement of Vehicles on the Road. In Proceedings of the 2022 International Conference on Engineering Management of Communication and Technology (EMCTECH), Vienna, Austria, 20–22 October 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Malchikov, V.N.; Shemyakin, A.V.; Ryabchikov, D.S.; Marusin, A.V.; Polyarush, A.A. Implementation of Unmanned Vehicles to Improve the Quality of Passenger Transposration. In Proceedings of the 2022 International Conference on Engineering Management of Communication and Technology (EMCTECH), Vienna, Austria, 20–22 October 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Novikov, A.; Pribyl, P.; Vasileva, V.; Katunin, A. ITS Control of Highways Capacity. Transp. Res. Procedia 2017, 20, 468–473. [Google Scholar] [CrossRef]
- Seliverstov, Y.A.; Seliverstov, S.A.; Lukomskaya, O.Y.; Nikitin, K.V.; Grigoriev, V.A.; Vydrina, E.O. The method of selecting a preferred route based on subjective criteria. In Proceedings of the 2017 IEEE II International Conference on Control in Technical Systems (CTS 2017), St. Petersburg, Russia, 25–27 October 2017; pp. 126–130. [Google Scholar] [CrossRef]
- Korchagin, V.A.; Novikov, A.N.; Lyapin, S.A.; Rizaeva, J.N.; Novikov, I.A. Complex self-developing transport systems. Int. J. Pharm. Technol. 2016, 8, 15253–15261. [Google Scholar]
- Zagorodnikh, N.; Novikov, A.; Yastrebkov, A. Algorithm and software for identifying accident-prone road sections. Transp. Res. Procedia 2018, 36, 817–825. [Google Scholar] [CrossRef]
- Novikov, A.; Shevtsova, A.; Evtyukov, S.; Marusin, A. Establishment of Causal Relationships of the Occurrence of Road Accidents. In Proceedings of the 2022 International Conference on Engineering Management of Communication and Technology (EMCTECH), Vienna, Austria, 20–22 October 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Yakupova, G.; Buyvol, P.; Shepelev, V. Identification of factors affecting the road traffic injury rate. Transp. Res. Procedia 2020, 50, 735–742. [Google Scholar] [CrossRef]
- Gabsalikhova, L.; Makarova, I.; Shepelev, V.; Fatikhova, L.; Belyaev, E. Connected vehicles fleet expanding problems. In Proceedings of the 6th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2020), Online, 2–4 May 2020; pp. 642–650. [Google Scholar]
- Sayama, H. Introduction to the Modeling and Analysis of Complex Systems; Open SUNY Textbooks; Milne Library: Geneseo, NY, USA, 2015. [Google Scholar]
- Terentyev, A.; Karelina, M.; Karelina, E. Analytical models of decision-making theory in digital transport logistics. J. Phys. Conf. Ser. 2021, 2061, 012129. [Google Scholar] [CrossRef]
- Tsvetkov, V.Y. Emergentism. Int. J. Appl. Fundam. Res. 2017, 2, 137–138. [Google Scholar]
- Ashby, U.R. Self-Organization Principles; Mir Publishers: Moscow, Russia, 1966; 332p. [Google Scholar]
- Diner, I.Y. Zoning of the Set of Vectors of the State of Nature and the Challenge of Choosing a Solution. In Operations Research; Nauka: Moscow, Russia, 1972; pp. 43–62. [Google Scholar]
- Tsvetkov, V.Y. Cognitive Aspects of Building Virtual Educational Models. Prospect. Sci. Educ. 2013, 3, 38–46. [Google Scholar]
- Simon, H.A. The Architecture of Complexity. Proc. Am. Philos. Soc. 1962, 106, 467–482. [Google Scholar]
- Matrusova, T.N. Organization as a Socio-Technical System and Personnel Management in a Japanese Firm; Research Institute of Labor: Moscow, Russia, 1999; Volume 4, pp. 77–93. [Google Scholar]
- Kornakov, A.N. Model of a Complex Organizational and Technical System. Prospect. Sci. Educ. 2015, 44–50. [Google Scholar]
- Parsons, T. International Encyclopedia of the Social Sciences; Sills, D.L., Ed.; The Macmillan, Co.: New York, NY, USA, 1968; Volume 15, pp. 458–473. [Google Scholar]
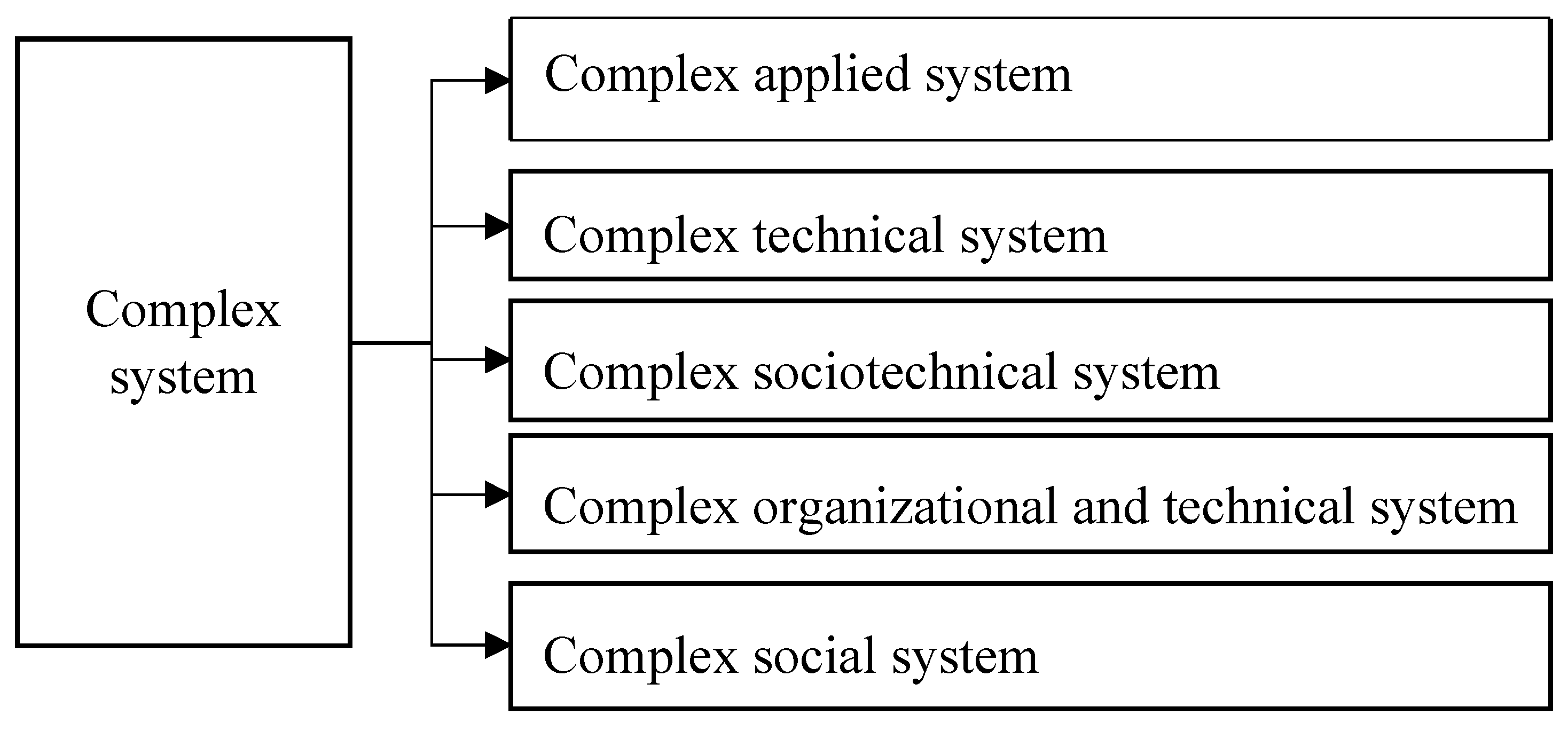
- Tsvetkov, V.Y. Systematics of Complex Systems. Mod. Manag. Technol. 2017, 7, 7903. [Google Scholar]
- Tsvetkov, V.Y.; Lobanov, A.A. Big Data as Information Barrier. Eur. Res. Ser. A 2014, 78, 1237–1242. [Google Scholar]
- Tsyganov, V.V. Intellectual Enterprise: Mechanisms of Mastering Capital and Power. In Theory and Practice of Managing the Evolution of an Organization; Tsyganov, V.V., Borodin, V.A., Shishkin, G.B., Eds.; Moscow University Press: Moscow, Russia, 2004; 768p. [Google Scholar]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References, and DEA-Solver Software; Kluwer Academic Publishers: Boston, MA, USA, 2000; 318p. [Google Scholar]
- Charnes, A.; Cooper, W.W.; Lewin, A.Y.; Seiford, L.M. Data Envelopment Analysis: Theory, Methodology, and Application; Kluwer Academic Publishers: Boston, MA, USA, 1994; 513p. [Google Scholar]
- Bowlin, W.F.; Charnes, A.; Cooper, W.W.; Sherman, H.D. Data Envelopment Analysis and Regression Approaches to Efficiency Estimation and Evaluation. Ann. Oper. Res. 1985, 2, 113–138. [Google Scholar]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the Efficiency of Decision Making Units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar]
- Farrell, M.J. The Measurement of Productive Efficiency. J. R. Stat. Soc. Ser. A 1957, 120, 253–281. [Google Scholar]
- Grossi, G.; Scappini, A. National Tourism Policy: Analytical Framework for the Evaluation of Efficiency and Effictiveness: The Case of Itali University della SvizzeraItaliana. Master’s Thesis, USI Università della Svizzera Italiana, Lugano, Switzerland, 2010. [Google Scholar]
- Krivonozhko, E.; Propoy, A.I.; Senkov, R.V.; Rodchenkov, I.V.; Anokhin, P.M. Analysis of the Efficiency of Complex Systems Functioning. Des. Autom. 1999, 2–7. [Google Scholar]
- Taha, A.H. Introduction to Operations Research; Williams Publishing House: London, UK, 2005; 912p. [Google Scholar]
- Terentyev, A.V.; Prudovsky, B.D. Methods for determining the Pareto set in some linear programming problems. Proc. Min. Inst. 2015, 211, 86–90. [Google Scholar]
- Jarratano, D.; Riley, G. Expert Systems: Principles of Development and Programming, 4th ed.; Williams Publishing House LLC: London, UK, 2007; 1152p. [Google Scholar]
- Terentyev, A.V.; Efimenko, D.B.; Karelina, M.Y. Methods of Zoning as Methods of Optimizing Motor Transport Processes. Bull. Civ. Eng.—SPb SPbGASU 2017, 6, 291–294. [Google Scholar]
- Terentyev, A.V.; Evtyukov, S.S.; Karelina, E.A.; Kurakina, E.V. Analytical Methods for Removing Uncertainty Are the Basis for Digitalization of Road Transport Production; Petropolis Publishing House: St. Petersburg, Russia, 2018; 210p. [Google Scholar]
- Safiullin, R.; Kerimov, M.; Afanasyev, A.; Marusin, A. A model for justification of the number of traffic enforcement facilities in the region. Transp. Res. Procedia 2018, 36, 493–499. [Google Scholar]
- Lomakin, D.; Novikov, A.; Eremin, S. Design concept of hierarchical system for assessing traffic safety in regions. Transp. Res. Procedia 2020, 50, 373–380. [Google Scholar] [CrossRef]
- Lomakin, D.; Fabrichnyi, E.; Novikov, A. Improving the system of traffic management at crossings. Transp. Res. Procedia 2018, 36, 446–452. [Google Scholar] [CrossRef]
- Kushchenko, L.; Kushchenko, S.; Novikov, A. Analysis of congestion occurrence cycles. Transp. Res. Procedia 2020, 50, 346–354. [Google Scholar] [CrossRef]
- Gavrilyuk, M.; Vorob’yova, T.; Shalagina, E. Effects of road blocking on traffic flows in Moscow. Transp. Res. Procedia 2020, 50, 1–11. [Google Scholar] [CrossRef]
- Averyanov, Y.; Golenyaev, N.; Giniyatullin, I. Method for the organization of non-stop passage of public transport through a controlled intersection. Transp. Res. Procedia 2020, 50, 28–36. [Google Scholar] [CrossRef]
- Drapalyuk, M.; Dorokhin, S.; Artemov, A. Estimation of efficiency of different traffic management methods in isolated area. Transp. Res. Procedia 2020, 50, 106–112. [Google Scholar] [CrossRef]
- Dygalo, V.; Keller, A.; Shcherbin, A. Principles of application of virtual and physical simulation technology in production of digital twin of active vehicle safety systems. Transp. Res. Procedia 2020, 50, 121–129. [Google Scholar] [CrossRef]
- Ganichev, A.; Batishcheva, O. Evaluating the conflicts between vehicles and pedestrians. Transp. Res. Procedia 2020, 50, 145–151. [Google Scholar] [CrossRef]
- Gorelik, S.; Grudinin, V.; Lecshinskiy, V.; Khaskelberg, E. Method for assessing the influence of psychophysical state of drivers on control safety based on monitoring of vehicle movement parameters. Transp. Res. Procedia 2020, 50, 152–159. [Google Scholar] [CrossRef]
- Zakharov, D.; Fadyushin, A. The Efficiency of some Activities for the Development of Urban Infrastructure for Public Transport, Cyclists and Pedestrians. Int. J. Transp. Dev. Integr. 2021, 5, 136–149. [Google Scholar] [CrossRef]
- Gorodokin, V.; Mavrin, V.; Almetova, Z.; Shepeleva, E. Method to ensure crossing capacity when limiting the cycle time and roadway width. Transp. Res. Procedia 2020, 50, 167–173. [Google Scholar] [CrossRef]
- Shepelev, V.; Glushkov, A.; Almetova, Z.; Mavrin, V. A Study of the Travel Time of Intersections by Vehicles using Computer Vision. In Proceedings of the 6th International Conference on Vehicle Technology and Intelligent Transport Systems, Online, 2–4 May 2020; pp. 653–658. [Google Scholar]
- Kapitanov, V.; Monina, O.; Silyanov, V.; Chubukov, A. Probabilistic assessment of main factors determining the road traffic accident rate in regions of Russia. Transp. Res. Procedia 2020, 50, 218–225. [Google Scholar] [CrossRef]
- Kataev, G.; Varkentin, V.; Nikolskaia, K. Method to estimate pedestrian traffic using convolutional neural network. Transp. Res. Procedia 2020, 50, 234–241. [Google Scholar] [CrossRef]
- Kolesov, V.; Petrov, A. Entropy and risks in regional road traffic safety systems. Transp. Res. Procedia 2020, 50, 262–272. [Google Scholar] [CrossRef]
- Makarova, I.; Shubenkova, K.; Pashkevich, A. Efficiency Assessment of Measures to Increase Sustainability of the Transport System. Transport 2021, 36, 123–133. [Google Scholar] [CrossRef]
- Kravchenko, P.; Zhankaziev, S.; Oleshchenko, E. Multi-faceted approach to solving issue of ensuring “zero mortality” on Russian roads. Transp. Res. Procedia 2020, 50, 310–320. [Google Scholar] [CrossRef]
- Krylatov, A.; Puzach, V.; Shatalova, N.; Asaul, M. Optimization of traffic lights operation using network load data. Transp. Res. Procedia 2020, 50, 321–329. [Google Scholar] [CrossRef]
- Makarova, I.; Mavrin, V.; Buyvol, P.; Boyko, A. Digitalization and New Opportunities of Urban Mobility. In Proceedings of the 20th International Conference on Reliability and Statistics in Transportation and Communication, Riga, Latvia, 14–17 October 2020; Volume 195, pp. 559–569. [Google Scholar]
- Kuraksin, A.; Shemyakin, A.; Parshkov, A. Integrated assessment of traffic management efficiency in real time based on DTA model. Transp. Res. Procedia 2020, 50, 337–345. [Google Scholar] [CrossRef]
- Qi, Z.; Li, M.; Liu, C.; Zhao, M.; Long, M. A measurement method for vehicle queue length of intersection based on image processing. In Proceedings of the Eighth International Conference on Image Processing Theory, Tools and Applications, Xi’an, China, 7–10 November 2018; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Tan, C.; Yao, J.; Tang, K.; Sun, J. Cycle-Based Queue Length Estimation for Signalized Intersections Using Sparse Vehicle Trajectory Data. IEEE Trans. Intell. Transp. Syst. 2019, 22, 91–106. [Google Scholar] [CrossRef]
- Makarova, I.; Boyko, A.; Almetova, Z. Decision-making on development of cycling infrastructure through safety assessment at design and operation stages. Transp. Res. Procedia 2020, 50, 397–404. [Google Scholar] [CrossRef]
- Matveev, A.; Maximov, A.; Bogdanova, E. Intelligent decision support system for transportation emergency response. Transp. Res. Procedia 2020, 50, 444–450. [Google Scholar] [CrossRef]
- Mikhailov, A.; Shesterov, E. Estimation of traffic flow parameters of U-turns. Transp. Res. Procedia 2020, 50, 458–465. [Google Scholar] [CrossRef]
- Shepelev, V.; Aliukov, S.; Nikolskaya, K.; Shabiev, S. The Capacity of the Road Network: Data Collection and Statistical Analysis of Traffic Characteristics. Energies 2020, 13, 1765. [Google Scholar] [CrossRef]
- Novikov, A.; Eremin, S. Patterns of passenger traffic formation in urban public transport. Transp. Res. Procedia 2020, 50, 483–490. [Google Scholar] [CrossRef]
- Gorodokin, V.; Almetova, Z.; Shepelev, V. Algorithm of signalized crossroads passage within the range of permissive-to-restrictive signals exchange. Transp. Res. Procedia 2017, 20, 225–230. [Google Scholar]
- Plotnikov, A.; Asaul, M. New methods for traffic safety rating at at-grade intersections. Transp. Res. Procedia 2020, 50, 528–532. [Google Scholar] [CrossRef]
- Plotnikov, A.; Gurin, D. Approach to ensure set traffic safety level at signalized intersections. Transp. Res. Procedia 2020, 50, 533–537. [Google Scholar] [CrossRef]
- Podoprigora, N.; Stepina, P.; Dobromirov, V.; Kotikov, J. Determination of driver’s reaction time in expert studies of road traffic accidents using software and hardware complex. Transp. Res. Procedia 2020, 50, 538–544. [Google Scholar] [CrossRef]
- Popova, I.; Danilov, I.; Abdulina, E. Intelligent driver assistance systems as factor of transportation safety assurance. Transp. Res. Procedia 2020, 50, 552–558. [Google Scholar] [CrossRef]
- Saveliev, A.; Izhboldina, V.; Letenkov, M.; Aksamentov, E.; Vatamaniuk, I. Method for automated generation of road accident scene sketch based on data from mobile device camera. Transp. Res. Procedia 2020, 50, 608–613. [Google Scholar] [CrossRef]
- Seliverstov, S.; Gavkalyk, B.; Fahmi, S. Development of transport infrastructure organization model for modern cities with growing effectiveness. Transp. Res. Procedia 2020, 50, 614–625. [Google Scholar] [CrossRef]
- Seliverstov, Y.; Malygin, I.; Korolev, O. Traffic safety evaluation in Northwestern Federal District using sentiment analysis of Internet users’ reviews. Transp. Res. Procedia 2020, 50, 626–635. [Google Scholar] [CrossRef]
- Sharov, M. Reliability as index of formation of sustainable urban passenger transport system, exemplified by cities in Russian Federation. Transp. Res. Procedia 2020, 50, 647–653. [Google Scholar] [CrossRef]
- Simdyankin, A.; Uspensky, I.; Belyu, L. Mechanism of improving safety of freight transportation by road with route optimization by organizing areas with increased freight tariffs. Transp. Res. Procedia 2020, 50, 662–673. [Google Scholar] [CrossRef]
- Tokunova, G.; Rajczyk, M. Smart technologies in development of urban agglomerations (case study of St. Petersburg transport infrastructure). Transp. Res. Procedia 2020, 50, 681–688. [Google Scholar] [CrossRef]
- Trofimenko, Y.; Komkov, V.; Trofimenko, K. Forecast of energy consumption and greenhouse gas emissions by road transport in Russia up to 2050. Transp. Res. Procedia 2020, 50, 698–707. [Google Scholar] [CrossRef]
- Vladyko, A.; Elagin, V.; Rogozinsky, G. Method of early pedestrian warning in developing intelligent transportation system infrastructure. Transp. Res. Procedia 2020, 50, 708–715. [Google Scholar] [CrossRef]
- Yakimov, M. Methods for assessing road traffic accident risks with changes in transport demand structure in cities. Transp. Res. Procedia 2020, 50, 727–734. [Google Scholar] [CrossRef]
- Zedgenizov, A.; Seliangin, K.; Efremenko, I. Methodology for assessing required area for allocating centers of mass attraction in layout of urbanized territories and their impact on quality of traffic management in adjacent street and road network. Transp. Res. Procedia 2020, 50, 743–748. [Google Scholar] [CrossRef]
- Zhankaziev, S.; Vorob’yov, A.; Morozov, D. Principles of creating range for testing technologies and technical solutions related to intelligent transportation systems and unmanned driving. Transp. Res. Procedia 2020, 50, 757–765. [Google Scholar] [CrossRef]
- Zhankaziev, S.; Vorob’yov, A.; Zabudsky, A. Designing human-machine interface for unmanned vehicle with account for time for control transfer. Transp. Res. Procedia 2020, 50, 749–756. [Google Scholar] [CrossRef]

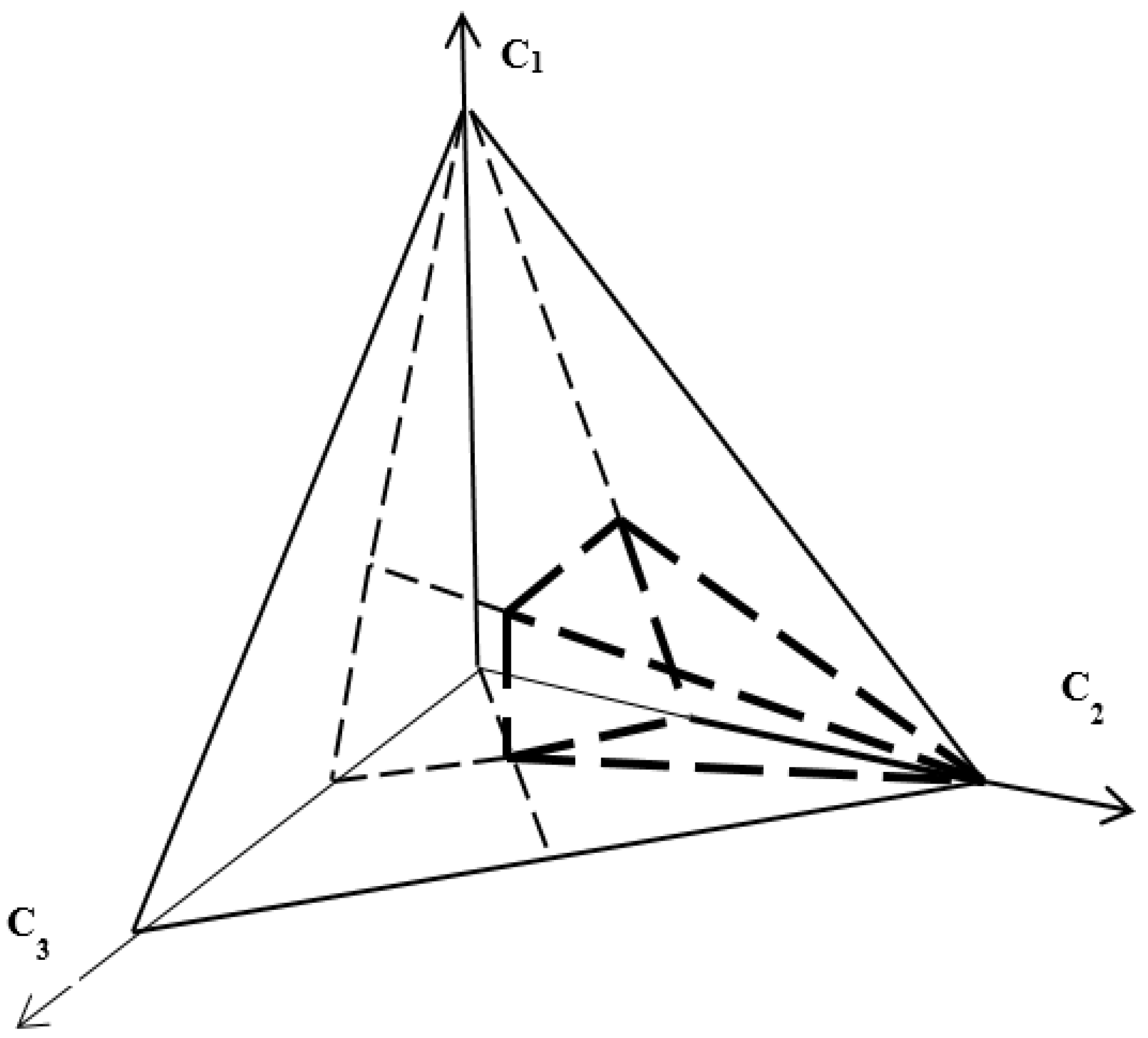
| Triangle Segments | Segment Equations |
|---|---|
| AB side | |
| AC side | |
| BC side | |
| AE median | |
| BF median | |
| CD median |
| Subset | Triangle | Coefficients Ratio |
|---|---|---|
| I | AOD | |
| II | DOB | |
| III | BOE | |
| IV | EOC | |
| V | COF | |
| VI | FOA |
| Decision-Making Method | Solution Variant | Quantified Effectiveness |
|---|---|---|
| Wald criterion | 1 | 0.200 |
| Savage criterion | 2 | 0.660 |
| Hurwitz criterion | 3 (4) | 0.366 (0.676) |
| Laplace criterion | 4 | 0.4975 |
| Fishburne sequences | 4 | 0.5034 |
| Proposed method | 4 | 0.8400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terentyev, A.; Marusin, A.; Evtyukov, S.; Marusin, A.; Shevtsova, A.; Zelenov, V. Analytical Model for Information Flow Management in Intelligent Transport Systems. Mathematics 2023, 11, 3371. https://doi.org/10.3390/math11153371
Terentyev A, Marusin A, Evtyukov S, Marusin A, Shevtsova A, Zelenov V. Analytical Model for Information Flow Management in Intelligent Transport Systems. Mathematics. 2023; 11(15):3371. https://doi.org/10.3390/math11153371
Chicago/Turabian StyleTerentyev, Alexey, Alexey Marusin, Sergey Evtyukov, Aleksandr Marusin, Anastasia Shevtsova, and Vladimir Zelenov. 2023. "Analytical Model for Information Flow Management in Intelligent Transport Systems" Mathematics 11, no. 15: 3371. https://doi.org/10.3390/math11153371
APA StyleTerentyev, A., Marusin, A., Evtyukov, S., Marusin, A., Shevtsova, A., & Zelenov, V. (2023). Analytical Model for Information Flow Management in Intelligent Transport Systems. Mathematics, 11(15), 3371. https://doi.org/10.3390/math11153371







