New Physical–Mathematical Analysis of Cardiac Dynamics and Temperature for the Diagnosis of Infectious Disease
Abstract
:1. Introduction
2. Materials and Methods
Procedure: Analysis of the Cardiac Dynamics
3. Results
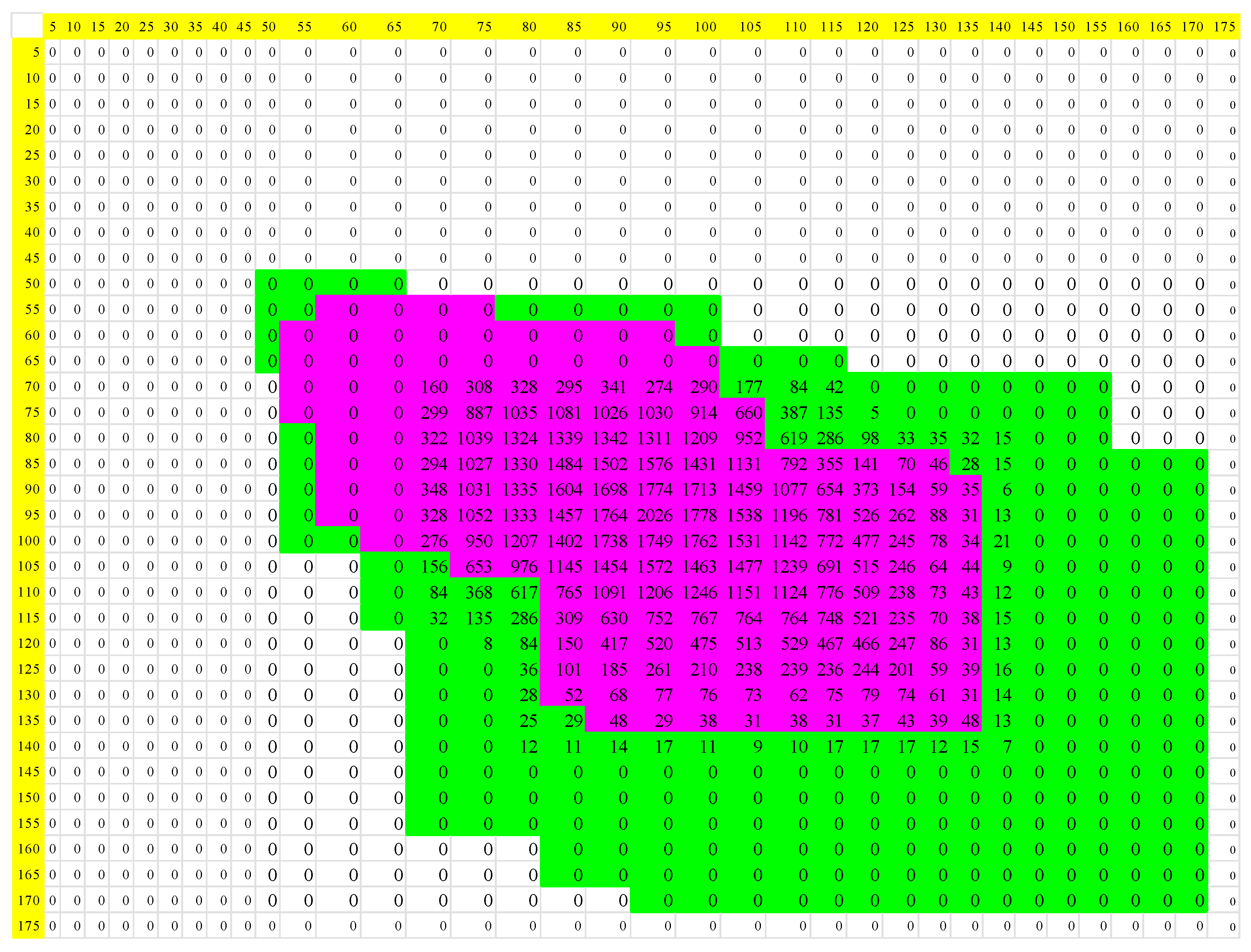
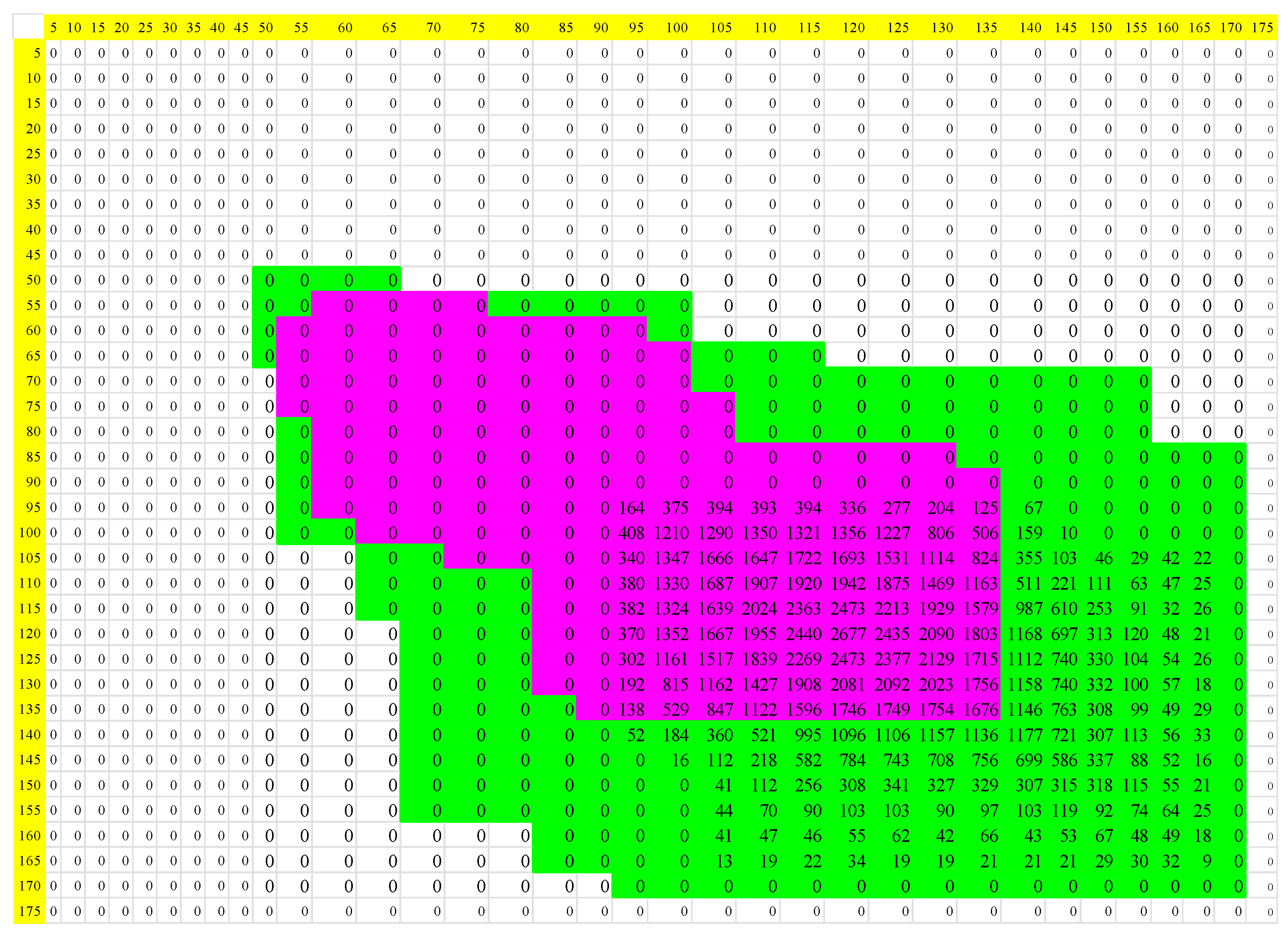
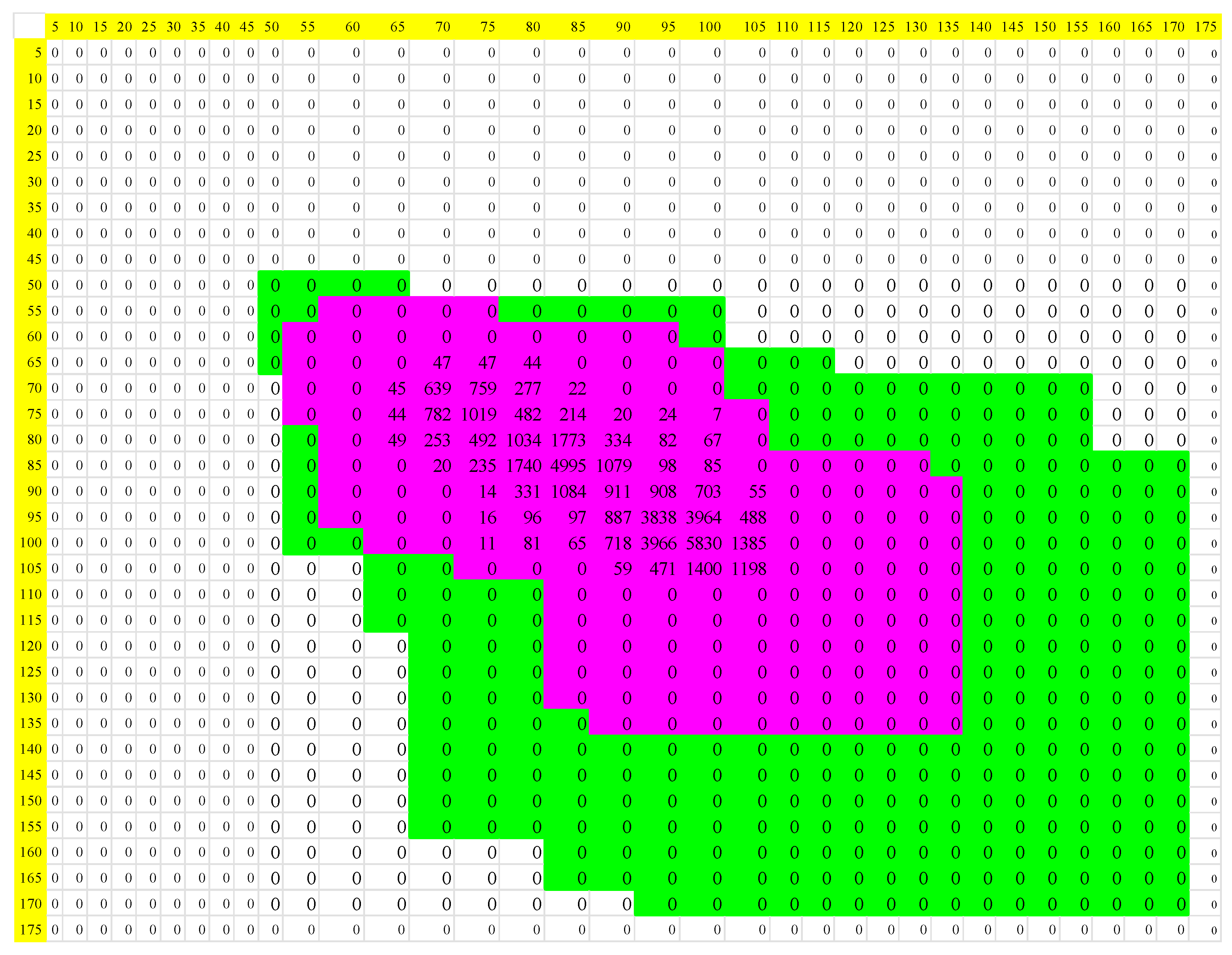
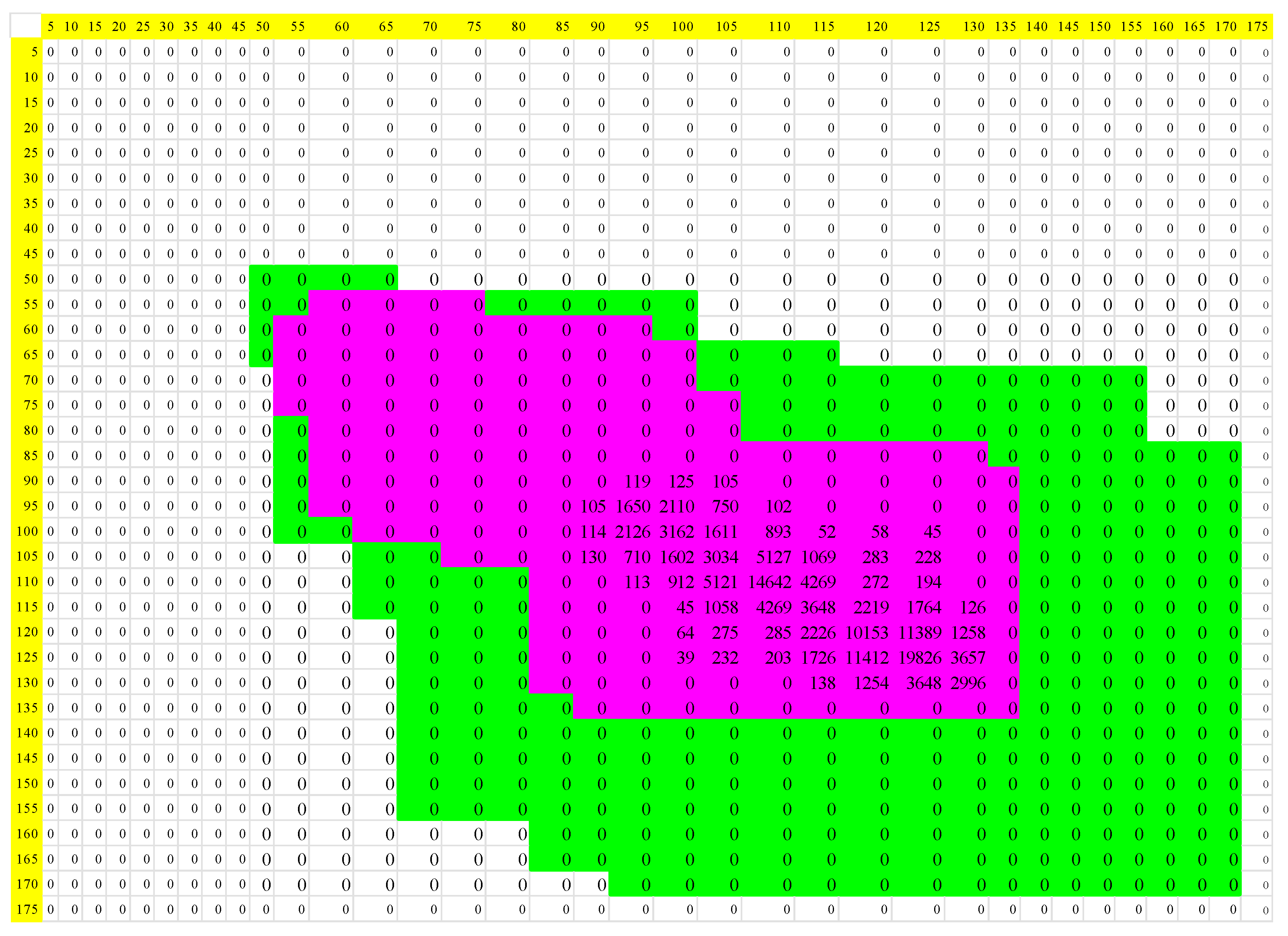
Simulations of Cardiac Dynamics
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pascarella, G.; Strumia, A.; Piliego, C.; Bruno, F.; Del Buono, R.; Costa, F.; Scarlata, S.; Agrò, F.E. COVID-19 diagnosis and management: A comprehensive review. J. Intern. Med. 2020, 288, 192–206. [Google Scholar] [CrossRef]
- World Health Organization. In Proceedings of the Virtual Press Conference on COVID-19, Virtual, 20 April 2020. Available online: https://www.who.int/docs/default-source/coronaviruse/transcripts/who-audio-emergencies-coronavirus-press-conference-20apr2020.pdf (accessed on 26 April 2020).
- Johns Hopkins Coronavirus Resource Center (CRC). COVID-19 Data in Motion. Available online: https://coronavirus.jhu.edu/ (accessed on 2 June 2020).
- Adhikari, S.P.; Meng, S.; Wu, Y.-J.; Mao, Y.-P.; Ye, R.-X.; Wang, Q.-Z.; Sun, C.; Sylvia, S.; Rozelle, S.; Raat, H.; et al. Epidemiology, causes, clinical manifestation and diagnosis, prevention and control of coronavirus disease (COVID-19) during the early outbreak period: A scoping review. Infect. Dis. Poverty 2020, 9, 29. [Google Scholar] [CrossRef] [Green Version]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Ann. Intern. Med. 2020, 172, 577. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Yao, L.; Wei, T.; Tian, F.; Jih, D.Y.; Chen, L. Presumed asymptomatic carrier transmission of COVID-19. J. Am. Med. Assoc. 2020, 323, 1406–1407. [Google Scholar] [CrossRef] [Green Version]
- Rothe, C.; Schunk, M.; Sothmann, P.; Bretzel, G.; Froeschl, G.; Wallrauch, C.; Zimmer, T.; Thiel, V.; Janke, C.; Guggemos, W.; et al. Transmission of 2019-nCoV Infection from an Asymptomatic Contact in Germany. N. Engl. J. Med. 2020, 382, 970–971. [Google Scholar] [CrossRef] [Green Version]
- The Novel Coronavirus Pneumonia Emergency Response Epidemiology Team. The epidemiological characteristics of an outbreak of 2019 novel coronavirus disease (COVID-19)—China. China CDC Wkly. 2020, 41, 145–151. [Google Scholar]
- Chang, D.; Xu, H.; Rebaza, A.; Sharma, L.; Dela Cruz, C.S. Protecting health-care workers from subclinical coronavirus infection. Lancet Respir Med. 2020, 8, e13. [Google Scholar] [CrossRef] [Green Version]
- Yu, P.; Zhu, J.; Zhang, Z.; Han, Y. A Familial cluster of infection associated with the 2019 novel coronavirus indicating possible person-to-person transmission during the incubation period. J. Infect. Dis. 2020, 221, 1457–1761. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Yang, R. COVID-19 transmission through asymptomatic carriers is a challenge to containment. Influenza Other Respir. Viruses 2020, 14, 474–475. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.-Y.; Huang, H.-J.; Zhuang, D.-L.; Nasser, M.I.; Yang, M.-H.; Zhu, P.; Zhao, M.-Y. Biological, clinical and epidemiological features of COVID-19, SARS and MERS and AutoDock simulation of ACE2. Infect. Dis. Poverty 2020, 9, 99. [Google Scholar] [CrossRef]
- Testo SE & Co. KGaA. Instruments. Set FeverDetection testo. Available online: https://www.testo.com/es-CO/set-feverdetection-testo-890/p/0563-0890-X7 (accessed on 21 August 2020).
- EL TIEMPO Casa Editorial. New. COVID-19: Uno de cada ocho pacientes sufre síntomas prolongados. Available online: https://www.eltiempo.com/salud/covid-19-uno-de-cada-ocho-pacientes-sufre-sintomas-prolongados-692666 (accessed on 5 August 2022).
- Jensen, M.M.; Kellett, J.G.; Hallas, P.; Brabrand, M. Fever increases heart rate and respiratory rate; a prospective observational study of acutely admitted medical patients. Acute Med. 2019, 18, 141–143. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.M.; Brabrand, M. The relationship between body temperature, heart rate, and respiratory rate in acute patients on admission to a medical care unit. Scand. J. Trauma Resusc. Emerg. Med. 2015, 23 (Suppl. 1), A12. [Google Scholar] [CrossRef] [Green Version]
- Broman, M.E.; Vincent, J.L.; Ronco, C.; Hansson, F.; Bell, M. The Relationship between Heart Rate and Body Temperature in Critically Ill Patients. Crit. Care Med. 2021, 49, e327–e331. [Google Scholar] [CrossRef]
- Angelidis, G.; Bratsas, C.; Makris, G.; Ioannidis, E.; Varsakelis, N.C.; Antoniou, I.E. Global Value Chains of COVID-19 Materials: A Weighted Directed Network Analysis. Mathematics 2021, 9, 3202. [Google Scholar] [CrossRef]
- Kalayjian, B.C.; Conner, K.; Butler, R.; Myers, L.; Telleria, C.; Panchang, D. Race, Heart Rate, and Temperature Are Strongly Associated with COVID-19 at Community-based Clinic in New Orleans. Mayo Clin. Proc. Innov. Qual. Outcomes 2020, 4, 683–686. [Google Scholar] [CrossRef]
- Tharakan, S.; Nomoto, K.; Miyashita, S.; Ishikawa, K. Body temperature correlates with mortality in COVID-19 patients. Crit. Care 2020, 24, 298. [Google Scholar] [CrossRef]
- Bajić, D.; Đajić, V.; Milovanović, B. Entropy Analysis of COVID-19 Cardiovascular Signals. Entropy 2021, 23, 87. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Portesi, M.; Vampa, V.; Losada, M.; Holik, F. Entropy-Based Informational Study of the COVID-19 Series of Data. Mathematics 2022, 10, 4590. [Google Scholar] [CrossRef]
- Martínez-Fernández, P.; Fernández-Muñiz, Z.; Cernea, A.; Fernández-Martínez, J.L.; Kloczkowski, A. Three Mathematical Models for COVID-19 Prediction. Mathematics 2023, 11, 506. [Google Scholar] [CrossRef]
- Alghamdi, A.S.; Abd El-Raouf, M.M. Exploring the Dynamics of COVID-19 with a Novel Family of Models. Mathematics 2023, 11, 1641. [Google Scholar] [CrossRef]
- Feynman, R.P.; Leighton, R.B.; Sands, M. Probability. In Physics Vol 1: Mechanics, Radiation, and Heat; Addison Wesley Iberoamericana: Wilmington, NC, USA, 1964; pp. 1–11. [Google Scholar]
- Suarez, J.F. Introduction to Probability Theory; Department of Mathematics and Statistics, National University of Colombia: Manizales, Colombia, 2002. [Google Scholar]
- Mood, A.M.; Graybill, F.A.; Boes, D.C. Introduction to the Theory of Statistics, 3rd ed.; McGraw-Hill: Singapore, 1974. [Google Scholar]
- Hirsch, M.W.; Devaney, R.L.; Smale, S. Nonlinear Systems. In Differential Equations, Dynamical Systems, and an Introduction to Chaos, 3rd ed.; Academic Press: Waltham, MA, USA, 2013; pp. 139–157. ISBN 978-0-12-382010-5. [Google Scholar]
- Grebogi, C.; Ott, E.; Yorke, J.A. Chaos, strange attractors, and fractal basin boundaries in nonlinear dynamics. Science 1987, 238, 632–638. Available online: http://www.jstor.org/stable/1700479?origin=JSTOR-pdf (accessed on 26 April 2020). [CrossRef] [Green Version]
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling chaos. Phys. Rev. Lett. APS 1990, 64, 1196. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westview Press: Boulder, CO, USA, 2014; ISBN 13:978-0-8133-4910-7. [Google Scholar]
- The Entropy Law as Law of Disorder (Boltzmann’s Interpretation: The Statistical View) [Internet]. Foundations of Physics, Life and Cognition: Basic Texts, Reviews, Research Material. Available online: http://www.entropylaw.com/entropydisorder.html (accessed on 4 July 2017).
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. Available online: https://people.math.harvard.edu/~ctm/home/text/others/shannon/entropy/entropy.pdf (accessed on 26 April 2020). [CrossRef] [Green Version]
- Machta, J. Entropy, information, and computation. Am. J. Phys. AAPT 1999, 67, 1074–1077. [Google Scholar] [CrossRef]
- Rodríguez Velásquez, J.; Prieto Bohórquez, S.; Ramírez López, L.J. Armonía del Caos: Fractales, Sistemas Dinámicos y Dinámica Cardiaca; Editorial Neogranadina: Cajicá, Colombia, 2021. [Google Scholar] [CrossRef]
- Tolman, R. Principles of Statistical Mechanics, 1st ed.; Dover Publications: New York, NY, USA, 1979; 662p. [Google Scholar]
- Matveev, A.N. Molecular Physics; MIR: Moscow, Russia, 1987. [Google Scholar]
- Bekenstein, J.D. Information in the holographic Universe. I investigated Cienc. Sci. Am. 2003, 289, 58–65. [Google Scholar] [CrossRef]
- Costa, M.D.; Goldberger, A.L. Generalized multiscale entropy analysis: Application to quantifying the complex volatility of human heartbeat time series. Entropy 2015, 17, 1197–1203. [Google Scholar] [CrossRef]
- Huo, Z.; Zhang, Y.; Shu, L. A short survey on fault diagnosis of rotating machinery using entropy techniques. In Proceedings of the 3rd EAI International Conference on Industrial Networks and Intelligent Systems, Ho Chi Minh City, Vietnam, 4 September 2017; Available online: https://eudl.eu/pdf/10.1007/978-3-319-74176-5_24 (accessed on 10 September 2022).
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Baumert, M.; Baier, V.; Voss, A.; Brechtel, L.; Haueisen, J. Estimating the complexity of heart rate fluctuations—An approach based on compression entropy. Fluct. Noise Lett. World Sci. 2005, 5, L557–L563. [Google Scholar] [CrossRef]
- Baumert, M.; Baier, V.; Haueisen, J.; Wessel, N.; Meyerfeldt, U.; Schirdewan, A.; Voss, A. Forecasting of life threatening arrhythmias using the compression entropy of heart rate. Methods Inf. Med. Inf. Med. 2004, 43, 202. [Google Scholar] [CrossRef] [Green Version]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Phys. Circ. Phys. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [Green Version]
- Hrbacek, K.; Jech, T. Introduction to Set Theory, 3rd ed.; Marcel Dekker, Inc.: New York, NY, USA, 1999. [Google Scholar]
- Rodríguez, J.; Prieto, S.; Ramirez, L.J. A novel heart rate attractor for the prediction of cardiovascular disease. Inf. Med. Unlocked 2019, 15, 100174. [Google Scholar] [CrossRef]
- Rodríguez, J.; Prieto, S.; Melo, M.; Domínguez, D.; Correa, C.; Soracipa, Y.; Mejía, M.; Valero, L.; Salamanca, A. Prediction of the number of CD4 T lymphocytes in peripheral blood from set theory and probability in patients with HIV/AIDS. Immunology 2014, 33, 113–120. [Google Scholar]
- Mayo Clinic. COVID-19: Who’s at Higher Risk of Serious Symptoms? Available online: https://www.mayoclinic.org/coronavirus-who-is-at-risk/art-20483301 (accessed on 22 December 2020).
- Upshur, R.E.G. A short note on probability in clinical medicine. J. Eval. Clin. Prac. 2013, 19, 463–466. [Google Scholar] [CrossRef] [PubMed]
- Fatovich, D.M.; Phillips, M. The probability of probability and research truths. Emerg. Med. Australas. 2017, 29, 242–244. [Google Scholar] [CrossRef] [PubMed]
- Perkiomaki, J.S.; Zareba, W.; Badilini, F.; Moss, A.J. Influence of atropine on fractal and complexity measures of heart rate variability. Ann. Noninvasive Electr. 2002, 7, 326–331. [Google Scholar] [CrossRef]
- Norris, P.R.; Anderson, S.M.; Jenkins, J.M.; Williams, A.E.; Morris Jr, J.A. Heart rate multiscale entropy at three hours predicts hospital mortality in 3154 trauma patients. Shock LWW 2008, 30, 17–22. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 1985, 57, 617. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, T.; Xi, B.; Fan, Y.; Wang, K.; Bi, J.; Wang, Y. Automatic recognition of cardiac arrhythmias based on the geometric patterns of Poincare plots. Physiol. Meas. 2015, 36, 283–301. [Google Scholar] [CrossRef]
- Kamen, P.W.; Tonkin, A.M. Application of the Poincare plot to heart rate variability: A new measure of functional status in heart failure. Aust. N. Z. J. Med. 1995, 25, 18–26. [Google Scholar] [CrossRef]
- Kamen, P.W.; Krum, H.; Tonkin, A.M. Poincare plot of heart rate variability allows quantitative display of parasympathetic nervous activity in humans. Clin. Sci. 1996, 91, 201–208. [Google Scholar] [CrossRef] [Green Version]
- Goshvarpour, A.; Goshvarpour, A. Poincare indices for analyzing meditative heart rate signals. Biomed. J. 2015, 38, 229–234. [Google Scholar] [CrossRef] [PubMed]
- Fishman, M.; Jacono, F.J.; Park, S.; Jamasebi, R.; Thungtong, A.; Loparo, K.A.; Dick, T.E. A method for analyzing temporal patterns of variability of a time series from Poincare plots. J. Appl. Physiol. 2012, 113, 297–306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodríguez, J. Binding to Class II HLA Theory: Probability, Combinatory and Entropy Applied to Peptide Sequences. Immunology 2008, 27, 151–166. [Google Scholar] [CrossRef]
- Rodriguez, J.; Prieto, S.; Correa, C.; Melo, M.; Dominguez, D.; Olarte, N.; Suárez, D.; Aragón, L.; Torres, F.; Santacruz, F. Prediction of CD4+ Cells Counts in HIV/AIDS Patients based on Sets and Probability Theories. Curr. HIV Res. 2018, 6, 416–424. [Google Scholar] [CrossRef]
- Rodríguez, J. Dynamical systems applied to dynamic variables of patients from the intensive care unit (ICU): Physical and mathematical mortality predictions on ICU. J. Med. Med. Sci. 2015, 6, 209–220. [Google Scholar]
- Prieto Bohórquez, S.E.; Velásquez, J.O.R.; Correa Herrera, S.C.; Soracipa Muñoz, M.Y. Diagnosis of cervical cells based on fractal and Euclidian geometrical measurements: Intrinsic Geometric Cellular Organization. BMC Med. Phys. 2014, 14, 2. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Liu, Z.; Pang, Y.; Akgül, A. Stochastic analysis of a COVID-19 model with effects of vaccination and different transition rates: Real data approach. Chaos Solitons Fractals 2023, 170, 113395. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Pang, Y.; Akgül, A.; Baleanu, D. Dynamics of HIV-TB coinfection model using classical and Caputo piecewise operator: A dynamic approach with real data from South-East Asia, European and American regions. Chaos Solitons Fractals 2022, 165, 112879. [Google Scholar] [CrossRef]
- Li, P.; Gao, R.; Xu, C.; Li, Y.; Akgül, A.; Baleanu, D. Dynamics exploration for a fractional-order delayed zooplankton–phytoplankton system. Chaos Solitons Fractals 2023, 166, 112975. [Google Scholar] [CrossRef]
| Normal | Acute Myocardial Infarction | |||||
|---|---|---|---|---|---|---|
| Hypothermia | Normal | Fever | Hypothermia | Normal | Fever | |
| Minimum | 6.19 × 10−23 | 6.15 × 10−23 | 6.17 × 10−23 | 2.82 × 10−23 | 2.83 × 10−23 | 2.82 × 10−23 |
| Maximum | 6.58 × 10−23 | 6.56 × 10−23 | 6.57 × 10−23 | 5.95 × 10−23 | 6.02 × 10−23 | 6.05 × 10−23 |
| Normal | Acute Myocardial Infarction | ||||||
|---|---|---|---|---|---|---|---|
| Hypothermia | Normal | Fever | Hypothermia | Normal | Fever | ||
| U/T | Minimum | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Maximum | 0.0030 | 0.0074 | 0.0010 | 0.1260 | 0.0894 | 0.0445 | |
| D/T | Minimum | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Maximum | 0.0540 | 0.0717 | 0.0656 | 0.1561 | 0.2043 | 0.0851 | |
| C/T | Minimum | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Maximum | 0.7919 | 0.5121 | 0.3422 | 0.5933 | 0.5594 | 0.3558 | |
| M/T | Minimum | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Maximum | 0.3948 | 0.6170 | 0.7506 | 0.8689 | 0.9074 | 0.9257 | |
| C/M | Minimum | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0802 |
| Maximum | 13.6037 | 1.4749 | 3.1693 | 30.1757 | 6.0689 | 3.9159 | |
| D/C | Minimum | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Maximum | 0.5850 | 3.0694 | 2.4003 | 3.5322 | 8.0288 | 9.4918 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramirez Lopez, L.J.; Correa Herrera, S.C.; Lagos Sandoval, J.A. New Physical–Mathematical Analysis of Cardiac Dynamics and Temperature for the Diagnosis of Infectious Disease. Mathematics 2023, 11, 3374. https://doi.org/10.3390/math11153374
Ramirez Lopez LJ, Correa Herrera SC, Lagos Sandoval JA. New Physical–Mathematical Analysis of Cardiac Dynamics and Temperature for the Diagnosis of Infectious Disease. Mathematics. 2023; 11(15):3374. https://doi.org/10.3390/math11153374
Chicago/Turabian StyleRamirez Lopez, Leonardo Juan, Sandra Catalina Correa Herrera, and José Arturo Lagos Sandoval. 2023. "New Physical–Mathematical Analysis of Cardiac Dynamics and Temperature for the Diagnosis of Infectious Disease" Mathematics 11, no. 15: 3374. https://doi.org/10.3390/math11153374
APA StyleRamirez Lopez, L. J., Correa Herrera, S. C., & Lagos Sandoval, J. A. (2023). New Physical–Mathematical Analysis of Cardiac Dynamics and Temperature for the Diagnosis of Infectious Disease. Mathematics, 11(15), 3374. https://doi.org/10.3390/math11153374







