Dynamics of Benjamin–Ono Solitons in a Two-Layer Ocean with a Shear Flow
Abstract
:1. Introduction
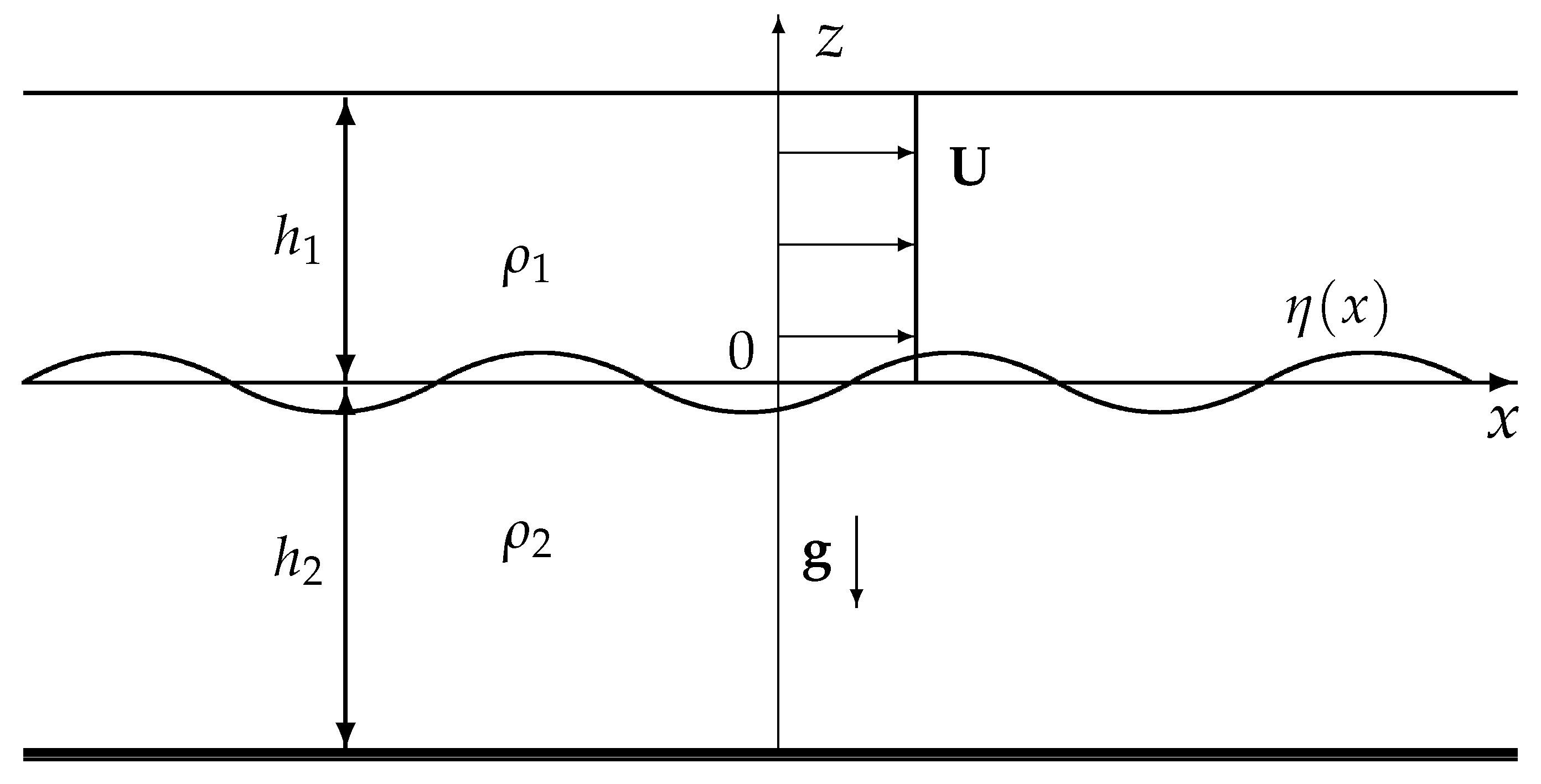
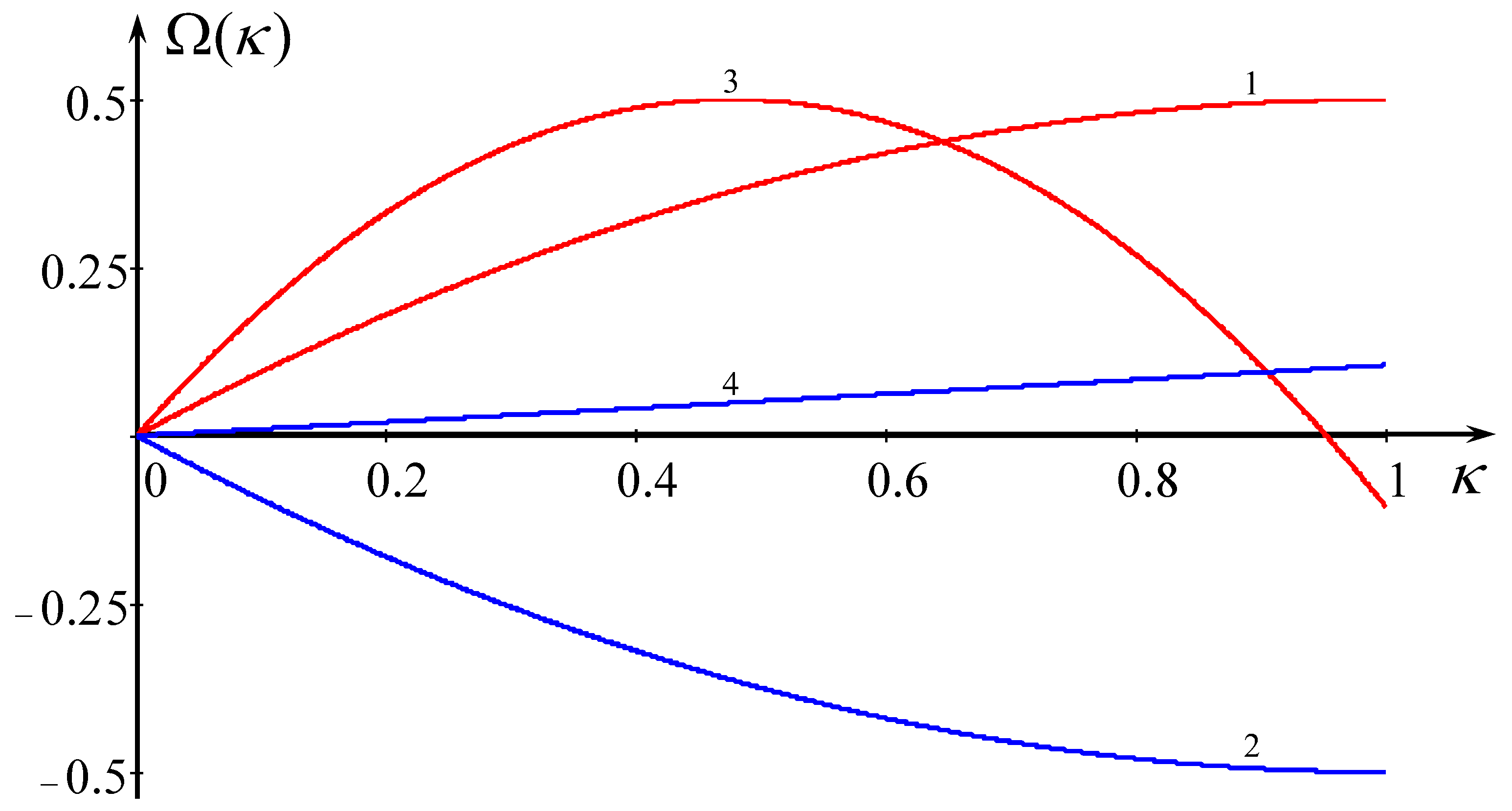
2. Dispersion Relations for a Two-Layer Fluid with a Shear Flow
Analysis of the Dispersion Relation
3. Generalized Benjamin–Ono Equations with Dissipative Terms
3.1. Linear Evolution Equations
3.2. Derivation of the Nonlinear Term in the BO Equation
4. Dynamics of a Solitary Wave Under the Influence of Dissipation
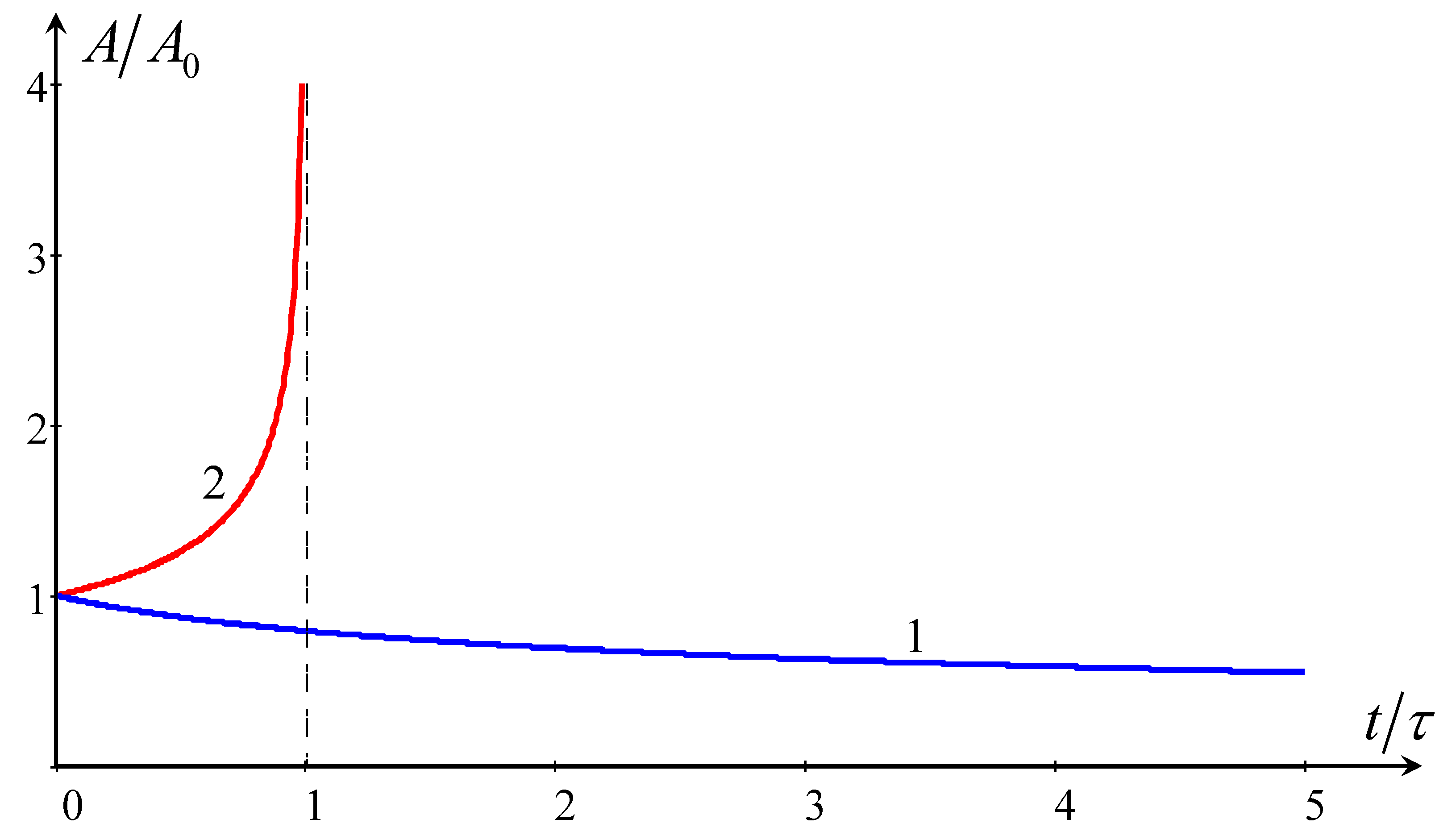
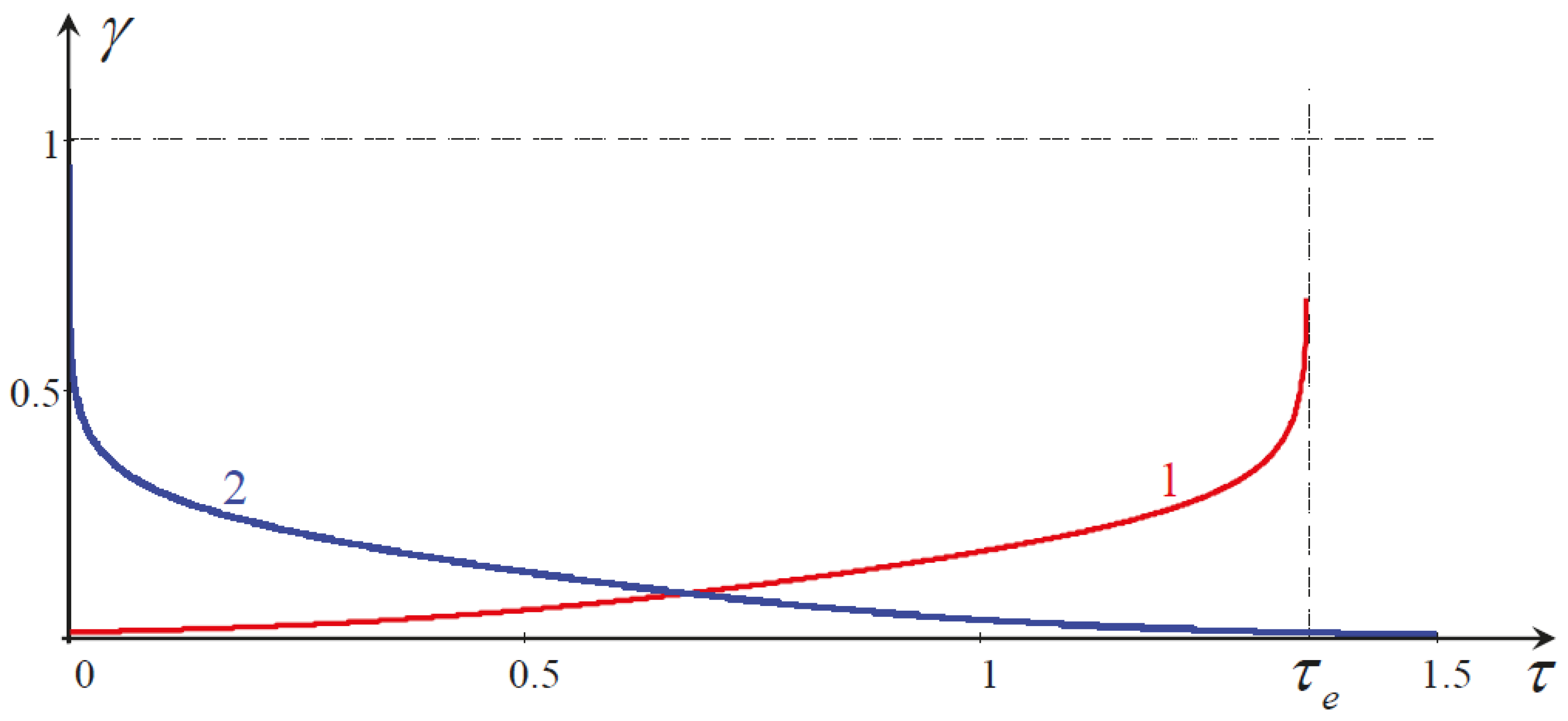
4.1. Soliton Decay Due to Reynolds-Type Dissipation
4.2. Soliton Dynamics under the Influence of Viscosity in a Moving Upper Layer
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
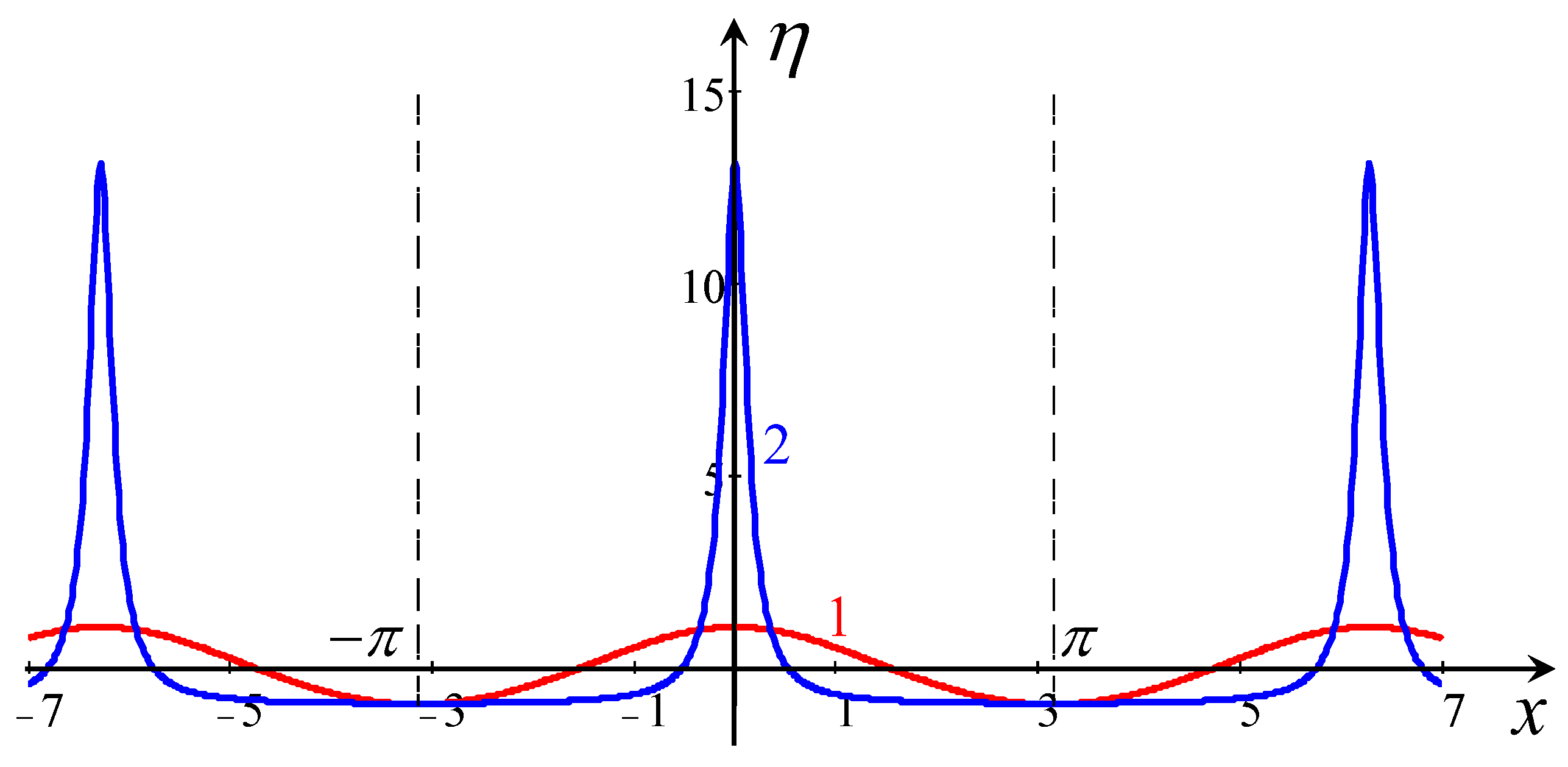
Appendix A. Dynamics of Periodic Waves within the genBO Equation with Dissipative Terms
References
- Benjamin, T. Internal waves of permanent form in fluids of great depth. J. Fluid Mech. 1967, 29, 559–592. [Google Scholar] [CrossRef]
- Ono, H. Algebraic solitary waves in stratified fluids. J. Phys. Soc. Jpn. 1975, 39, 1082–1091. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Ostrovsky, L.A.; Stepanyants, Y.A. Internal solitons in laboratory experiments: Comparison with theoretical models. Chaos 2005, 15, 37111. [Google Scholar] [CrossRef] [PubMed]
- Grimshaw, R.; Smyth, N.; Stepanyants, Y. Decay of Benjamin–Ono solitons under the influence of dissipation. Wave Motion 2018, 78, 98–115. [Google Scholar] [CrossRef] [Green Version]
- Korpel, A.; Banerjee, P. A heuristic guide to nonlinear dispersive wave equations and soliton-type solutions. In Proceedings of the IEEE, Bangalore, India, 9–12 December 1984; Volume 72, pp. 1109–1130. [Google Scholar]
- Benjamin, T.B. A new kind of solitary wave. J. Fluid Mech. 1992, 245, 401–411. [Google Scholar] [CrossRef]
- Nezlin, M.V. Negative-energy waves and the anomalous Doppler effect. Sov. Phys. Uspekhi 1976, 19, 946. [Google Scholar] [CrossRef]
- Ostrovski, L.A.; Rybak, S.A.; Tsimring, L.S. Negative energy waves in hydrodynamics. Sov. Phys. Uspekhi 1986, 29, 1040. [Google Scholar] [CrossRef]
- Fabrikant, A.L.; Stepanyants, Y.A. Propagation of Waves in Shear Flows; World Scientific Publishing Company: Singapore, 1998. [Google Scholar]
- Maïssa, P.; Rousseaux, G.; Stepanyants, Y. Negative energy waves in shear flow with a linear profile. Eur. J. Mech. B/Fluids 2016, 56, 1082–1091. [Google Scholar] [CrossRef]
- Alias, A.; Grimshaw, R.; Khusnutdinova, K. Coupled Ostrovsky equations for internal waves in a shear flow. Phys. Fluids 2014, 26, 126603. [Google Scholar] [CrossRef]
- Alias, A.; Grimshaw, R.; Khusnutdinova, K. Coupled Ostrovsky equations for internal waves, with a background shear flow. Proc. IUTAM 2014, 11, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Lifshits, E.M. Fluid Mechanics; Butterworth-Heinemann: Burlington, MA, USA, 1987. [Google Scholar]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ostrovsky, L.A.; Stepanyants, Y.A. Nonlinear stage of the shearing instability in a stratified liquid of finite depth. Izv. Acad. Sci. Ussr. Fluid Dyn. 1983, 17, 540–546. [Google Scholar] [CrossRef]
- Jochum, M.; Danabasoglu, G.; Holland, M.; Kwon, Y.O.; Large, W.G. Ocean viscosity and climate. J. Geophys. Res. 2008, 113, 84. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Ostrovsky, L.A. Asymptotic Perturbation Theory of Waves; Imperial College Press: London, UK, 2015. [Google Scholar]
- Ostrovsky, L.A.; Stepanyants, Y.A.; Tsimring, L.S. Radiation instability in a stratified shear flow. Iny. J. Nonlin. Mech. 1984, 19, 151–161. [Google Scholar]
- Matsuno, Y. Oblique interaction of interfacial solitary waves in a two-layer deep fluid. Proc. R. Soc. Lond. A 1998, 454, 835–856. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Long internal waves in fluids of great depth. Stud. Appl. Math. 1980, 62, 249–262. [Google Scholar] [CrossRef]
- Grimshaw, R.; Zhu, Y. Oblique interaction between internal solitary waves. Stud. Appl. Math. 1994, 92, 249–270. [Google Scholar] [CrossRef]
- Satsuma, J.; Ishimori, Y. Periodic wave and rational soliton solutions of the Benjamin–One equation. J. Phys. Soc. Jpn. 1979, 46, 681–687. [Google Scholar] [CrossRef]
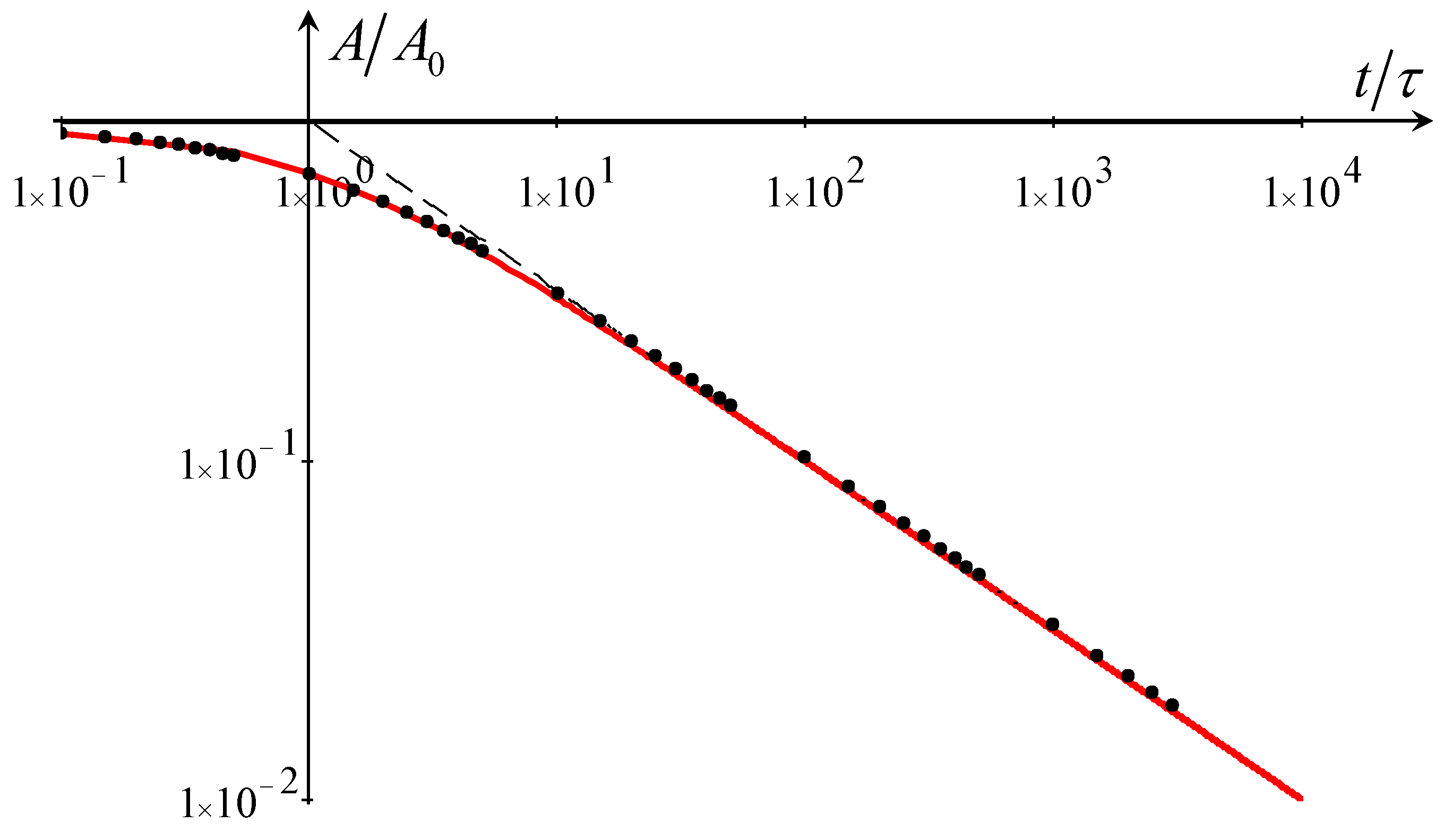

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Negi, P.; Sahoo, T.; Singh, N.; Stepanyants, Y. Dynamics of Benjamin–Ono Solitons in a Two-Layer Ocean with a Shear Flow. Mathematics 2023, 11, 3399. https://doi.org/10.3390/math11153399
Negi P, Sahoo T, Singh N, Stepanyants Y. Dynamics of Benjamin–Ono Solitons in a Two-Layer Ocean with a Shear Flow. Mathematics. 2023; 11(15):3399. https://doi.org/10.3390/math11153399
Chicago/Turabian StyleNegi, Pawan, Trilochan Sahoo, Niharika Singh, and Yury Stepanyants. 2023. "Dynamics of Benjamin–Ono Solitons in a Two-Layer Ocean with a Shear Flow" Mathematics 11, no. 15: 3399. https://doi.org/10.3390/math11153399
APA StyleNegi, P., Sahoo, T., Singh, N., & Stepanyants, Y. (2023). Dynamics of Benjamin–Ono Solitons in a Two-Layer Ocean with a Shear Flow. Mathematics, 11(15), 3399. https://doi.org/10.3390/math11153399