Controlled Invariant Sets of Discrete-Time Linear Systems with Bounded Disturbances
Abstract
:1. Introduction
2. Preliminaries
3. Robustly Controlled Invariant Sets Based on Difference Inequality
- (i)
- ;
- (ii)
- ;
- (iii)
- .
4. Robustly Controlled Invariant Sets Based on Logarithmic Norm
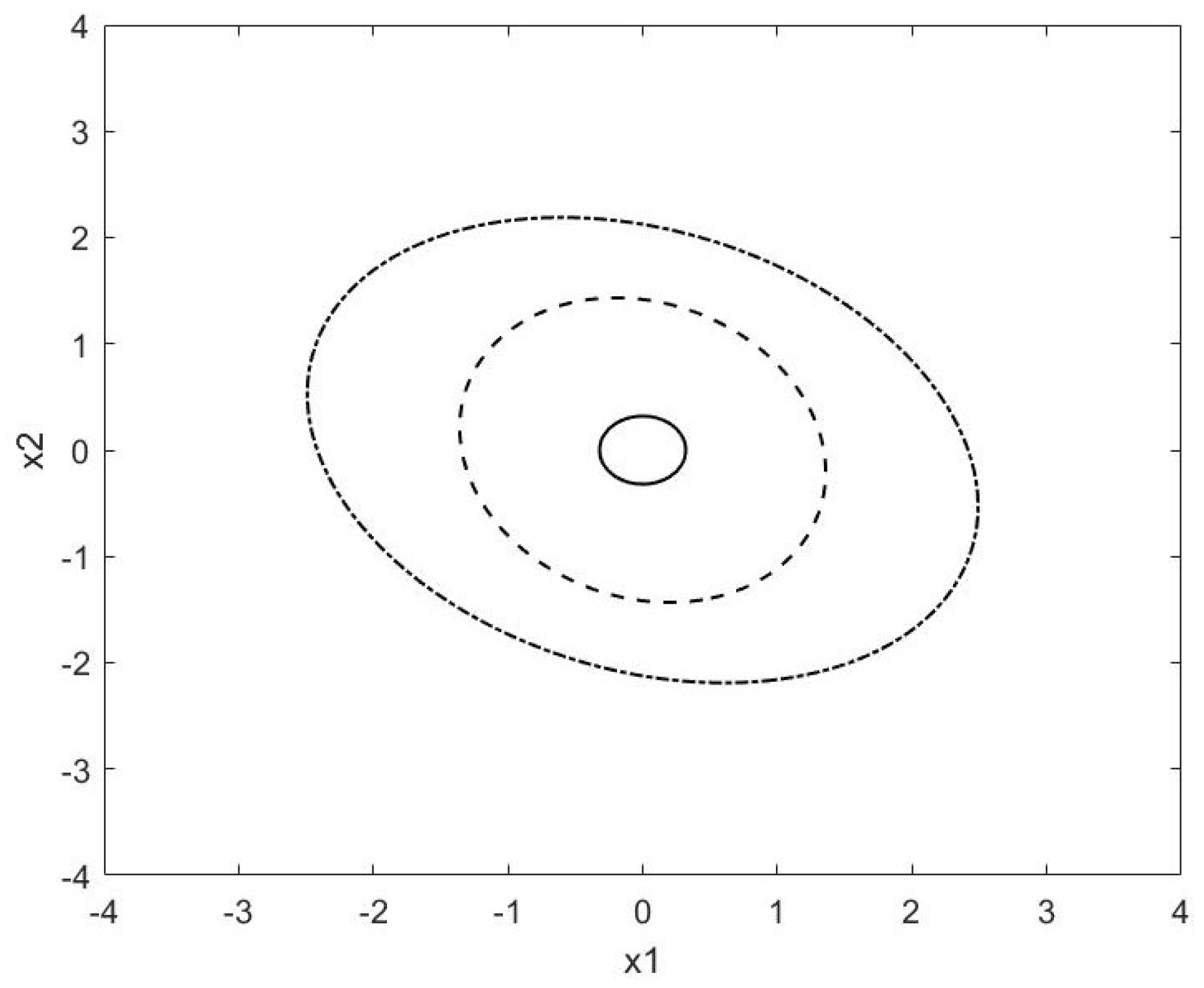
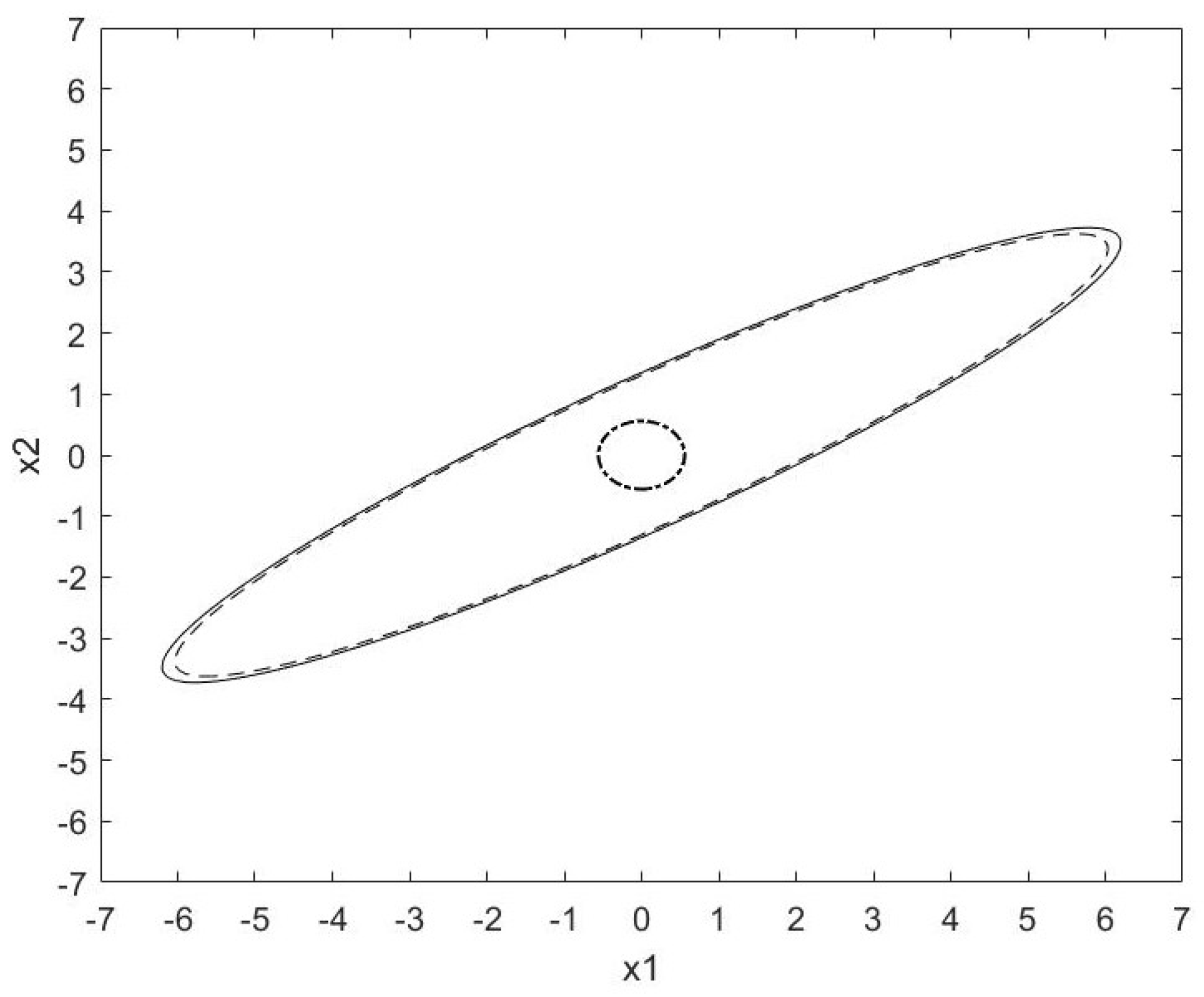
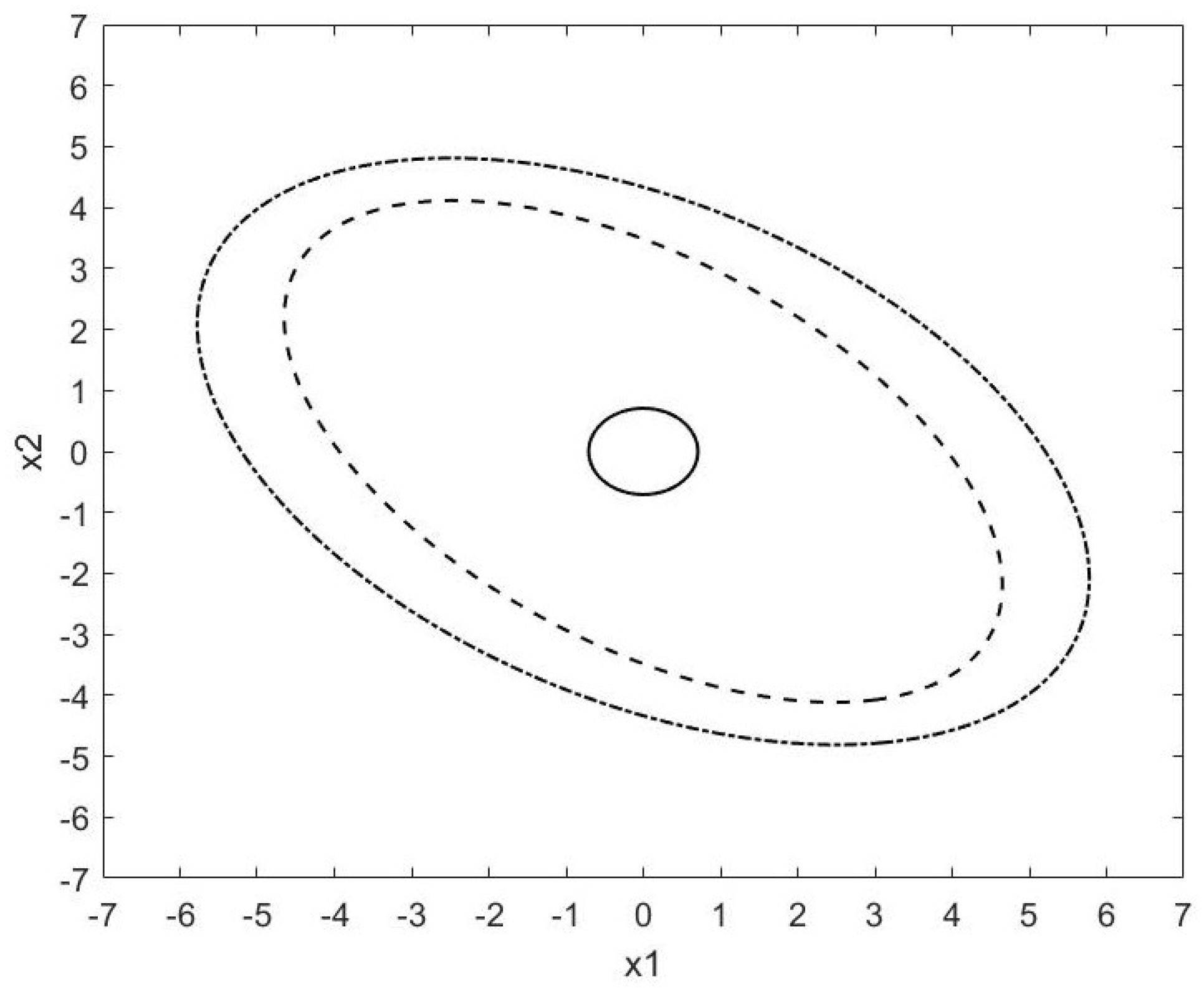
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rakovic, S.V.; Baric, M. Parameterized robust control invariant sets for linear systems: Theoretical advances and computational remarks. IEEE Trans. Autom. Control 2010, 55, 1599–1614. [Google Scholar] [CrossRef]
- Tahir, F.; Jaimoukha, I.M. Robust Positively Invariant Sets for Linear Systems Subject to Model-Uncertainty and Disturbances. Ifac Proc. Vol. 2012, 45, 213–217. [Google Scholar] [CrossRef]
- Raković, S.V.; Kerrigan, E.C.; Mayne, D.Q.; Kouramas, K.I. Optimized robust control invariance for linear discrete-time systems: Theoretical foundations. Automatica 2007, 43, 831–841. [Google Scholar] [CrossRef]
- Tarraf, D.C.; Bauso, D. Finite alphabet control of logistic networks with discrete uncertainty. Syst. Control. Lett. 2014, 64, 20–26. [Google Scholar] [CrossRef]
- Blanchini, F. Set invariance in control. Automatica 1999, 35, 1747–1767. [Google Scholar] [CrossRef]
- Fiacchini, M.; Alamo, T.; Camacho, E.F. On the computation of convex robust control invariant sets for nonlinear systems. Automatica 2010, 46, 1334–1338. [Google Scholar] [CrossRef]
- Blanchini, F.; Miani, S. Set-Theoretic Methods in Control; Birkhäuser: Boston, MA, USA, 2008; Volume 78. [Google Scholar]
- Li, H.; Xie, L.; Wang, Y. On robust control invariance of Boolean control networks. Automatica 2016, 68, 392–396. [Google Scholar] [CrossRef]
- Parise, F.; Valcher, M.E.; Lygeros, J. On the reachable set of the controlled gene expression system. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 4597–4604. [Google Scholar]
- Rungger, M.; Tabuada, P. Computing Robust Controlled Invariant Sets of Linear Systems. IEEE Trans. Autom. Control 2017, 62, 3665–3670. [Google Scholar] [CrossRef]
- Dorea, C.E.T.; Hennet, J.C. On Robust Positive Invariance of Unbounded Polyhedra. Ifac Proc. Vol. 1995, 28, 231–236. [Google Scholar] [CrossRef]
- Rakovic, S.V.; Kerrigan, E.C.; Kouramas, K.I.; Mayne, D.Q. Invariant approximations of the minimal robust positively invariant set. IEEE Trans. Autom. Control 2005, 50, 406–410. [Google Scholar] [CrossRef] [Green Version]
- Tahir, F.; Jaimoukha, I.M. Low-Complexity Polytopic Invariant Sets for Linear Systems Subject to Norm-Bounded Uncertainty. IEEE Trans. Autom. Control 2014, 60, 1416–1421. [Google Scholar] [CrossRef] [Green Version]
- Lei, Y.; Yang, H. Dual optimization approach to set invariance conditions for discrete-time dynamic systems. Optim. Eng. 2023, 1–18. [Google Scholar] [CrossRef]
- Si, X.; Yang, H. Constrained regulation problem for continuous-time stochastic systems under state and control constraints. J. Vib. Control 2022, 28, 3218–3230. [Google Scholar] [CrossRef]
- Yu, S.; Zhou, Y.; Qu, T.; Xu, F.; Ma, Y. Control invariant sets of linear systems with bounded disturbances. Int. J. Control. Autom. Syst. 2018, 16, 622–629. [Google Scholar] [CrossRef]
- Hewing, L.; Carron, A.; Wabersich, K.P.; Zeilinger, M.N. On a correspondence between probabilistic and robust invariant sets for linear systems. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018. [Google Scholar]
- Gao, D.; Li, Q.; Wang, M.; Luo, J.; Li, J. Ellipsoidal approximations of the minimal robust positively invariant set. ISA Trans. 2023; in press. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, H.; Grizzle, J.; Ozay, N. Data-driven computation of minimal robust control invariant set. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakishnan, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- That, N.D.; Nam, P.T.; Ha, Q.P. Reachable Set Bounding for Linear Discrete-Time Systems with Delays and Bounded Disturbances. J. Optim. Theory Appl. 2013, 157, 96–107. [Google Scholar] [CrossRef]
- Shingin, H.; Ohta, Y. Optimal Invariant Sets for Discrete-Time Systems Approximation of the Reachable Sets for Bounded Inputs. Trans. Soc. Instrum. Control. Eng. 2004, 40, 842–848. [Google Scholar] [CrossRef] [Green Version]
- Yu, L. Robust Control: Linear Matrix Inequality Approach; Tsinghua University: Beijing, China, 2002. [Google Scholar]
- Harville, D.A. Matrix Algebra from a Statistician’S Perspective; Taylor & Francis: Abingdon, UK, 1998. [Google Scholar]
- Hu, G.D.; Liu, M. The weighted logarithmic matrix norm and bounds of the matrix exponentia. Linear Algebra Its Appl. 2004, 390, 145–154. [Google Scholar] [CrossRef] [Green Version]
- Ström, T. On logarithmic norms. Siam J. Numer. Ann. 1975, 12, 741–753. [Google Scholar] [CrossRef]
- Martin, R.H., Jr. Logarithmic norms and projections applied to linear differential systems. J. Math. Anal. Appl. 1974, 45, 432–454. [Google Scholar] [CrossRef] [Green Version]
- Ding, W.; Hou, Z.; Wei, Y. Tensor logarithmic norm and its applications. Numer. Linear Algebra Appl. 2016, 23, 989–1006. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, G.; Sun, L. Finite-time robust simultaneous stabilization of a set of nonlinear time-delay systems. Int. J. Robust Nonlinear Control 2020, 30, 1733–1753. [Google Scholar] [CrossRef]
- Liu, X.; Liu, W.; Li, Y.; Zhuang, J. Finite-time H∞ control of stochastic time-delay Markovian jump systems. J. Shandong Univ. Sci. Technol. 2022, 41, 75–84. [Google Scholar]
- Drazin, P.G. Nonlinear Systems; Cambridge University Press: Cambridge, UK, 1992; Volume 10. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Yang, H.; Ivanov, I.G. Controlled Invariant Sets of Discrete-Time Linear Systems with Bounded Disturbances. Mathematics 2023, 11, 3421. https://doi.org/10.3390/math11153421
Wang C, Yang H, Ivanov IG. Controlled Invariant Sets of Discrete-Time Linear Systems with Bounded Disturbances. Mathematics. 2023; 11(15):3421. https://doi.org/10.3390/math11153421
Chicago/Turabian StyleWang, Chengdan, Hongli Yang, and Ivan Ganchev Ivanov. 2023. "Controlled Invariant Sets of Discrete-Time Linear Systems with Bounded Disturbances" Mathematics 11, no. 15: 3421. https://doi.org/10.3390/math11153421







