Variational Approach to Modeling of Curvilinear Thin Inclusions with Rough Boundaries in Elastic Bodies: Case of a Rod-Type Inclusion
Abstract
1. Introduction
2. Statement of the Initial Problem
- on ;
- on ;
- on ;
- The graph of the function is located strictly inside the domain .
3. Transformations of Coordinates
4. Decomposition and Transformation of the Problem
5. Justification of the Asymptotic Analysis
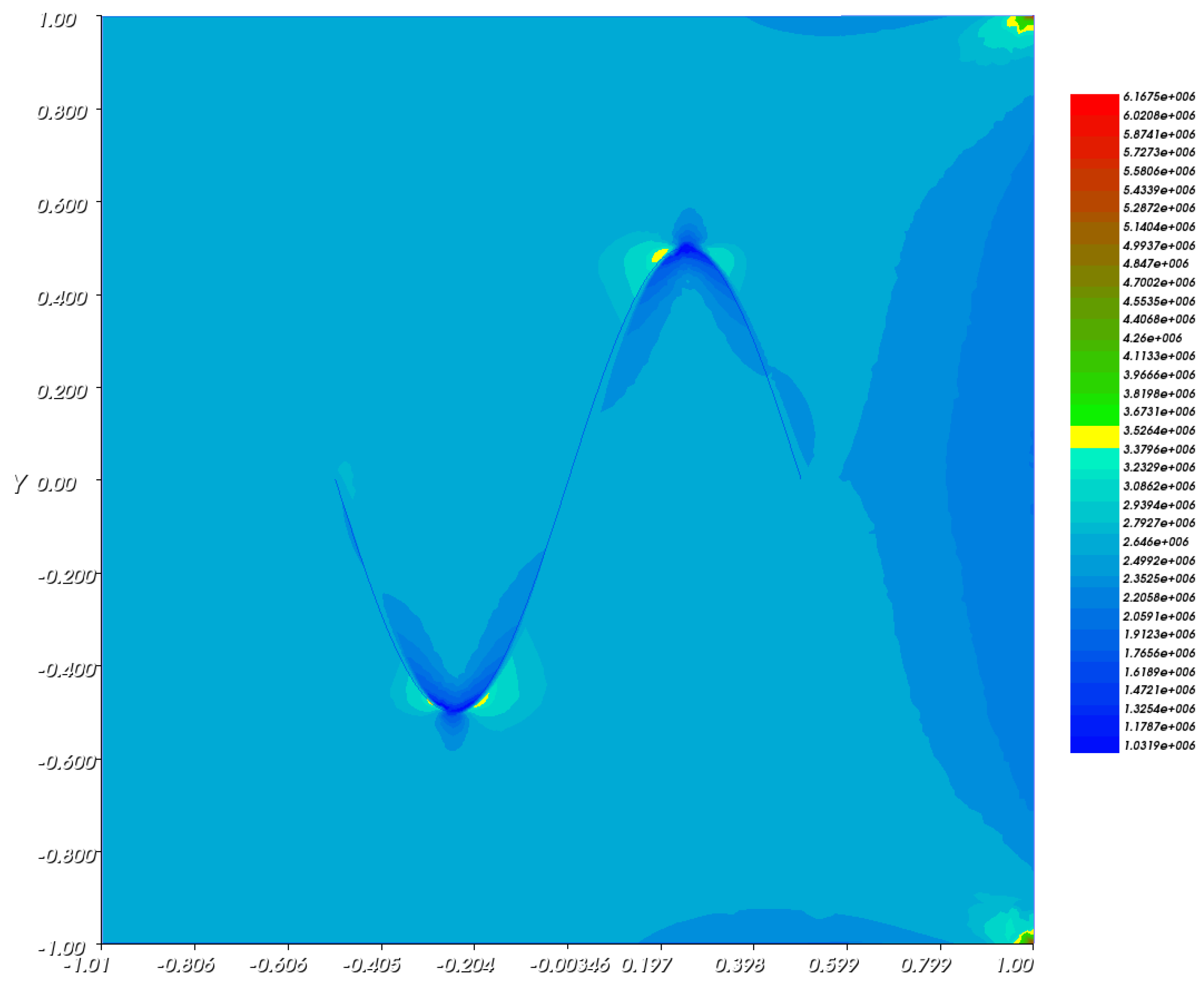
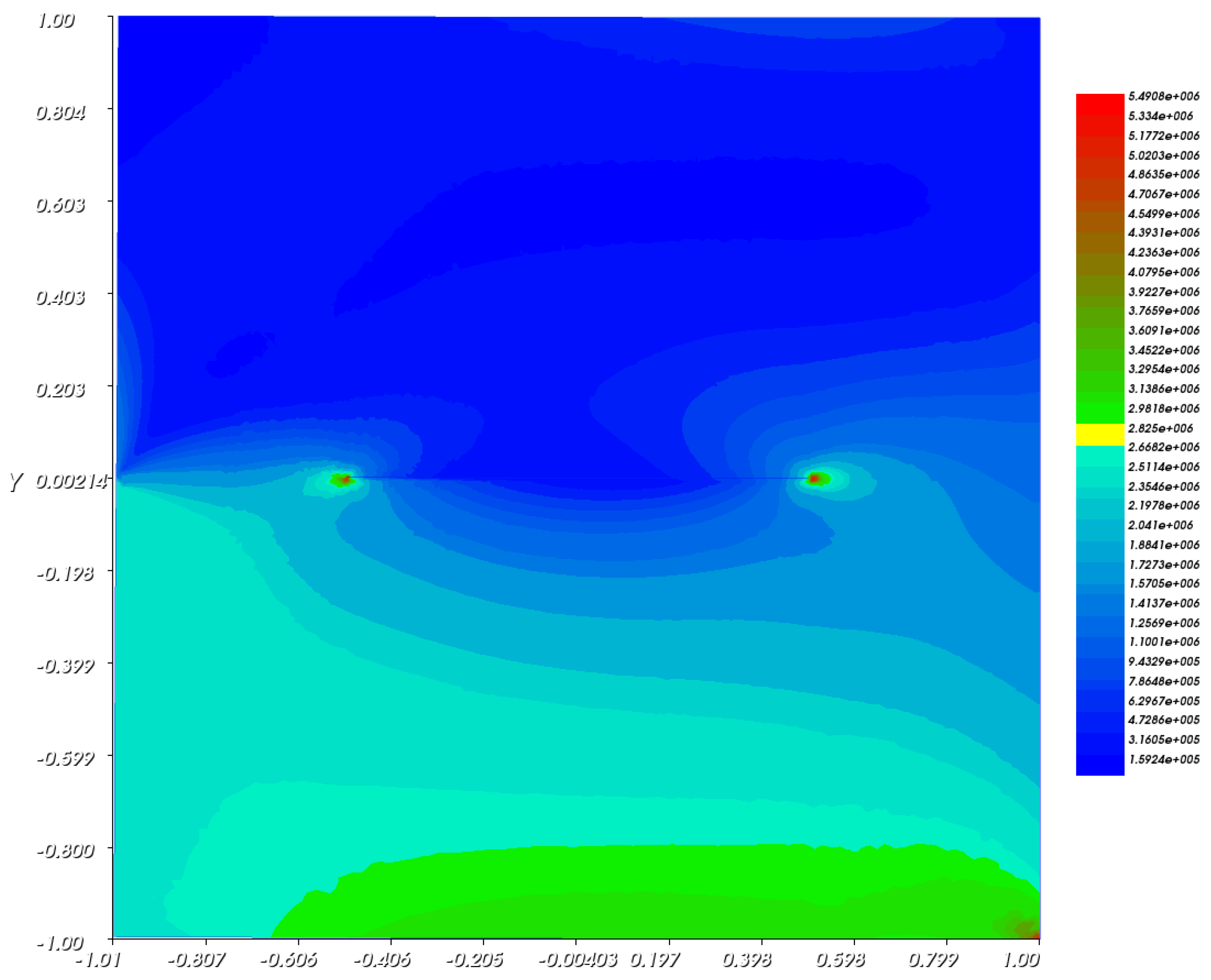
6. Numerical Examples
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fankina, I.V.; Furtsev, A.I.; Rudoy, E.M.; Sazhenkov, S.A. Asymptotic modeling of curvilinear narrow inclusions with rough boundaries in elastic bodies: Case of a soft inclusion. Sib. Electron. Math. Rep. 2022, 19, 935–948. [Google Scholar]
- Furtsev, A.; Rudoy, E. Variational approach to modeling soft and stiff interfaces in the Kirchhoff-Love theory of plates. Int. J. Solids Struct. 2020, 202, 562–574. [Google Scholar] [CrossRef]
- Rudoy, E.M. Asymptotic justification of models of plates containing inside hard thin inclusions. Technologies 2017, 8, 59. [Google Scholar] [CrossRef]
- Itou, H.; Khludnev, A.M. On delaminated thin Timoshenko inclusions inside elastic bodies. ZAMM Z. Angew. Math. Mech. 2016, 24, 4980–4993. [Google Scholar] [CrossRef]
- Khludnev, A.; Negri, M. Crack on the boundary of a thin elastic inclusion inside an elastic body. ZAMM Z. Angew. Math. Mech. 2012, 95, 341–354. [Google Scholar] [CrossRef]
- Khludnev, A. On thin inclusions in elastic bodies with defects. Z. Angew. Math. Phys. 2019, 70, 45. [Google Scholar] [CrossRef]
- Khludnev, A. T-shape inclusion in elastic body with a damage parameter. J. Comput. Appl. Math. 2021, 393, 113540. [Google Scholar] [CrossRef]
- Khludnev, A. Non-coercive problems for Kirchhoff–Love plates with thin rigid inclusion. Z. Angew. Math. Phys. 2022, 73, 54. [Google Scholar] [CrossRef]
- Lazarev, N.P. Equilibrium problem for a thermoelastic Kirchhoff-Love plate with a delaminated flat rigid inclusion. Philos. Trans. R. Soc. A 2022, 380, 20210363. [Google Scholar] [CrossRef] [PubMed]
- Lazarev, N.P.; Kovtunenko, V.A. Signorini-type problems over non-convex sets for composite bodies contacting by sharp edges of rigid inclusions. Mathematics 2022, 10, 250. [Google Scholar] [CrossRef]
- Khludnev, A. Junction problem for thin elastic and volume rigid inclusions in elastic bod. Philos. Trans. R. Soc. A 2022, 380, 20210360. [Google Scholar] [CrossRef]
- Khludnev, A. On the Crossing Bridge between Two Kirchhoff–Love Plates. Axioms 2023, 12, 120. [Google Scholar] [CrossRef]
- Khludnev, A. Asymptotic analysis of thin elastic junction between two elastic bodies. Appl. Anal. 2023, 102, 800–814. [Google Scholar] [CrossRef]
- Baranova, S.; Mogilevskaya, S.G.; Nguyen, T.H.; Schilling, D. Higher-order imperfect interface modeling via complex variables based asymptotic analysis. Int. J. Eng. Sci. 2021, 57, 103399. [Google Scholar]
- Fankina, I.V.; Furtsev, A.I.; Rudoy, E.M.; Sazhenkov, S.A. Multiscale analysis of stationary thermoelastic vibrations of a composite material. Philos. Trans. R. Soc. A 2022, 380, 20210354. [Google Scholar]
- Mokhtari, H.; Rahmani, L. Asymptotic modeling of the behavior of a reinforced plate governed by a full von Karman thermo-elastic system with nonlinear thermal coupling. Ann. Univ. Ferrara Sez. VII Sci. Mat. 2021, 67, 387–414. [Google Scholar] [CrossRef]
- Serpilli, M.; Dumont, S.; Rizzoni, R.; Lebon, F. Interface Models in Coupled Thermoelasticity. Technologies 2021, 9, 17. [Google Scholar] [CrossRef]
- Benveniste, Y.; Miloh, T. Imperfect soft and stiff interfaces in two-dimensional elasticity. Mech. Mater. 2001, 33, 309–323. [Google Scholar] [CrossRef]
- Bessoud, A.-L.; Krasucki, F.; Serpilli, M. Plate-like and shell-like inclusions with high rigidity. Comptes Rendus Math. 2009, 346, 697–702. [Google Scholar]
- Ljulj, M.; Tambaca, J. 3D structure—2D plate interaction model. Math. Mech. Solids 2019, 24, 3354–3377. [Google Scholar] [CrossRef]
- Serpilli, M.; Rizzoni, R.; Rodríguez-Ramos, R.; Lebon, F.; Dumont, S. A novel form of imperfect contact laws in flexoelectricity. Compos. Struct. 2022, 300, 116059. [Google Scholar] [CrossRef]
- Bessoud, A.-L.; Krasucki, F.; Michaille, G. Multi-materials with strong interface: Variational modelings. Asymptot. Anal. 2012, 61, 1–19. [Google Scholar] [CrossRef]
- Dumont, S.; Lebon, F.; Raffa, M.L.; Rizzoni, R. Towards nonlinear imperfect interface models including micro-cracks and smooth roughness. Ann. Solid Struct. Mech. 2017, 9, 13–27. [Google Scholar] [CrossRef][Green Version]
- Fouchal, F.; Lebon, F.; Raffa, M.L.; Vairo, G. An interface model including cracks and roughness applied to masonry. Open Civ. Eng. J. 2014, 8, 263–271. [Google Scholar] [CrossRef]
- Kunets, Y.I.; Matus, V.V. Asymptotic approach in the dynamic problems of the theory of elasticity for bodies with thin elastic inclusions. J. Math. Sci. 2023, 270, 87–106. [Google Scholar] [CrossRef]
- Mokhtari, H.; Rahmani, L. Asymptotic modeling of a reinforced plate with a thin layer of variable thickness. Meccanica 2022, 57, 2155–2172. [Google Scholar] [CrossRef]
- Dong, H.; Zheng, X.; Cui, J.; Nie, Y.; Yang, Z.; Ma, Q. Multi-scale computational method for dynamic thermo-mechanical performance of heterogeneous shell structures with orthogonal periodic configurations. Comput. Methods Appl. Mech. Eng. 2019, 354, 143–180. [Google Scholar] [CrossRef]
- Ma, Q.; Li, Z.; Cui, J. Multi-scale asymptotic analysis and computation of the elliptic eigenvalue problems in curvilinear coordinates. Comput. Methods Appl. Mech. Eng. 2018, 340, 340–365. [Google Scholar] [CrossRef]
- Ma, Q.; Cui, J.; Li, Z.; Wang, Z. Second-order asymptotic algorithm for heat conduction problems of periodic composite materials in curvilinear coordinates. J. Comput. Appl. Math. 2016, 306, 87–115. [Google Scholar] [CrossRef]
- Khludnev, A.M.; Kovtunenko, V.A. Analysis of Cracks in Solids; WIT-Press: Southampton, UK, 2000. [Google Scholar]
- Nečas, J. Direct Methods in the Theory of Elliptic Equations; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Rudoy, E.M.; Itou, H.; Lazarev, N.P. Asymptotic Justification of the Models of Thin Inclusions in an Elastic Body in the Antiplane Shear Problem. J. Appl. Ind. Math. 2021, 15, 129–140. [Google Scholar] [CrossRef]
- Rudoy, E. First-order and second-order sensitivity analyses for a body with a thin rigid inclusion. Math. Methods Appl. Sci. 2016, 39, 4994–5006. [Google Scholar] [CrossRef]
- Rudoy, E.; Shcherbakov, V. First-Order Shape Derivative of the Energy for Elastic Plates with Rigid Inclusions and Interfacial Cracks. Appl. Math. Optim. 2021, 84, 2775–2802. [Google Scholar] [CrossRef]
- Freddi, L.; Morassi, A.; Paroni, R. Thin-Walled Beams: The Case of the Rectangular Cross-Section. J. Elast. 2004, 76, 45–66. [Google Scholar] [CrossRef]
- Gaudiello, A.; Sili, A. Limit models for thin heterogeneous structures with high contrast. J. Differ. Equ. 2021, 302, 37–63. [Google Scholar] [CrossRef]
- Nazarov, S.A. Weighted anisotropic Korn’s inequality for a junction of a plate and a rod. Sb. Math. 2004, 195, 553–583. [Google Scholar] [CrossRef]
- Baranova, S.; Mogilevskaya, S.G. On the Bovik–Benveniste methodology and related approaches for modelling thin layers. Philos. Trans. R. Soc. A 2022, 380, 20210420. [Google Scholar] [CrossRef] [PubMed]
- Fankina, I.V.; Furtsev, A.I.; Rudoy, E.M.; Sazhenkov, S.A. The homogenized quasi-static model of a thermoelastic composite stitched with reinforcing threads. J. Comput. Appl. Math. 2023, 434, 115346. [Google Scholar] [CrossRef]
- Kushch, V.I.; Mogilevskaya, S.G. Higher order imperfect interface models of conductive spherical interphase. Math. Mech. Solids 2022. [Google Scholar] [CrossRef]
- Ventcel, A.D. On boundary conditions for multi-dimensional diffusion processes. Theory Probab. Appl. 1959, 42, 164–177. [Google Scholar]
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–265. [Google Scholar] [CrossRef]
- Itou, H.; Khludnev, A.M.; Rudoy, E.M.; Tani, A. Asymptotic behaviour at a tip of a rigid line inclusion in linearized elasticity. ZAMM Z. Angew. Math. Mech. 2012, 92, 716–730. [Google Scholar] [CrossRef]
- Rudoy, E.M. On numerical solving a rigid inclusions problem in 2D elasticity. ZAMP Z. Angew. Math. Phys. 2017, 68, 19. [Google Scholar] [CrossRef]

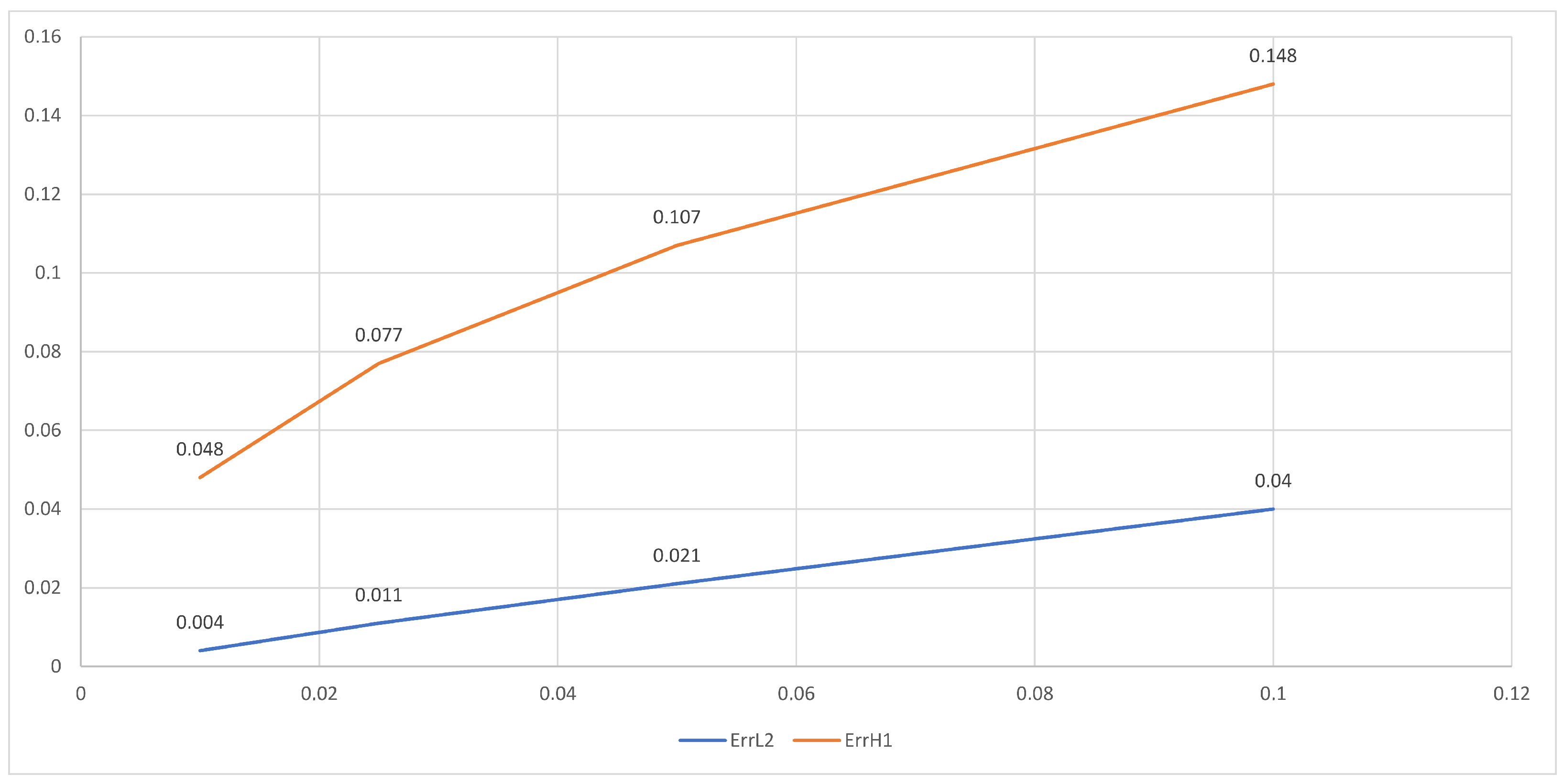
| ErrL2 | 0.04 | 0.021 | 0.011 | 0.004 |
| ErrH1 | 0.148 | 0.107 | 0.077 | 0.048 |
| ErrL2 | 0.001 | 0.004 | 0.005 | 0.008 | 0.019 |
| ErrH1 | 0.013 | 0.043 | 0.048 | 0.056 | 0.086 |
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
|---|---|---|---|---|---|---|
| ErrL2 | 0.002 | 0.004 | 0.005 | 0.005 | 0.004 | 0.005 |
| ErrH1 | 0.054 | 0.051 | 0.052 | 0.05 | 0.048 | 0.048 |
| ErrL2 | ErrH1 | ||
|---|---|---|---|
| 0.08 | 0.28 | 0.013 | 0.074 |
| 0.03 | 0.14 | 0.005 | 0.057 |
| 0.013 | 0.076 | 0.005 | 0.051 |
| 0.009 | 0.048 | 0.005 | 0.049 |
| 0.005 | 0.042 | 0.004 | 0.048 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudoy, E.; Sazhenkov, S. Variational Approach to Modeling of Curvilinear Thin Inclusions with Rough Boundaries in Elastic Bodies: Case of a Rod-Type Inclusion. Mathematics 2023, 11, 3447. https://doi.org/10.3390/math11163447
Rudoy E, Sazhenkov S. Variational Approach to Modeling of Curvilinear Thin Inclusions with Rough Boundaries in Elastic Bodies: Case of a Rod-Type Inclusion. Mathematics. 2023; 11(16):3447. https://doi.org/10.3390/math11163447
Chicago/Turabian StyleRudoy, Evgeny, and Sergey Sazhenkov. 2023. "Variational Approach to Modeling of Curvilinear Thin Inclusions with Rough Boundaries in Elastic Bodies: Case of a Rod-Type Inclusion" Mathematics 11, no. 16: 3447. https://doi.org/10.3390/math11163447
APA StyleRudoy, E., & Sazhenkov, S. (2023). Variational Approach to Modeling of Curvilinear Thin Inclusions with Rough Boundaries in Elastic Bodies: Case of a Rod-Type Inclusion. Mathematics, 11(16), 3447. https://doi.org/10.3390/math11163447







