Outer Synchronization of Two Muti-Layer Dynamical Complex Networks with Intermittent Pinning Control
Abstract
:1. Introduction
2. Model Description and Preliminaries
- (1)
- ;
- (2)
- .
3. Main Results
3.1. Synchronization with State-Feedback Intermittent Pinning Controller
3.2. Synchronization with Adaptive Intermittent Pinning Controller
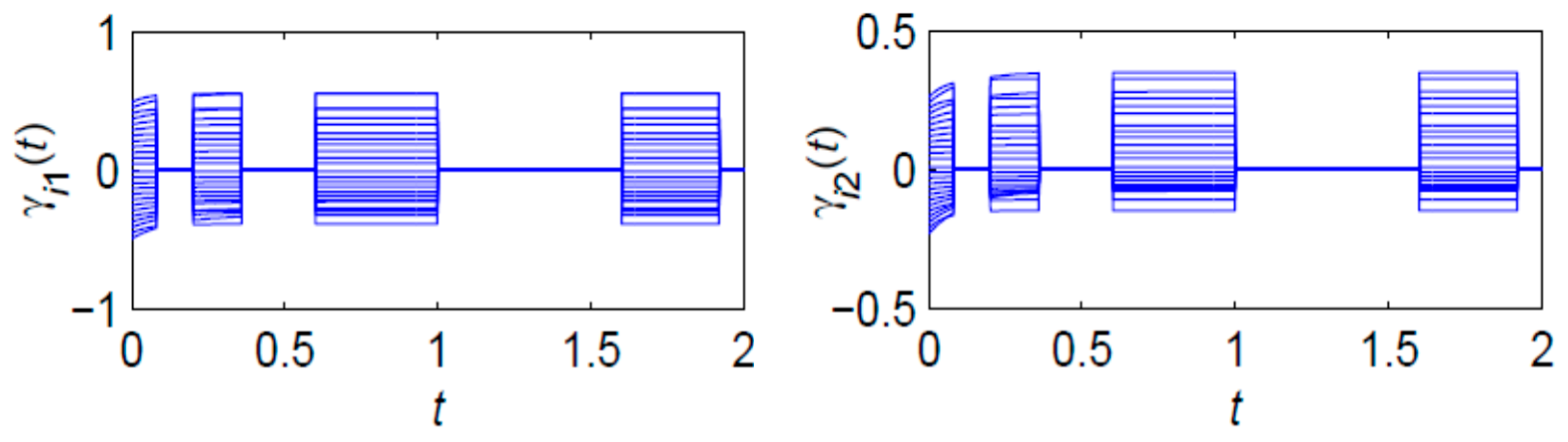
4. Simulation Examples
4.1. Simulation Example with State-Feedback Intermittent Pinning Controller
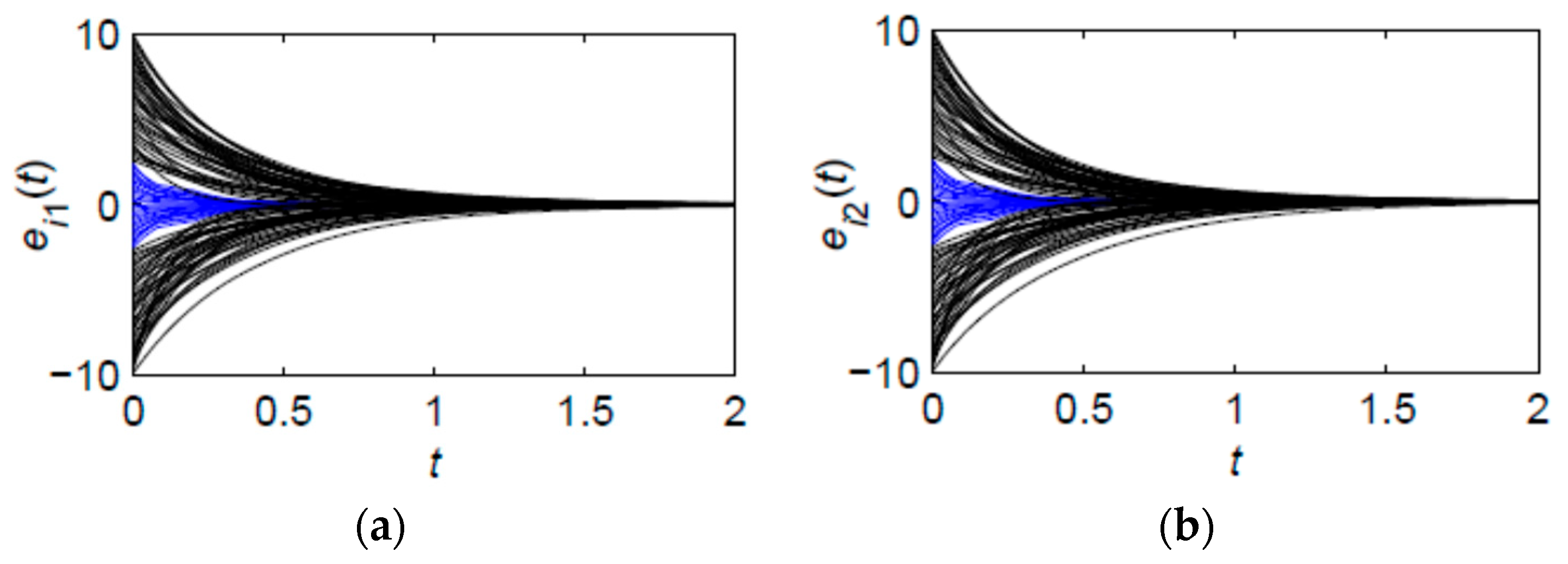
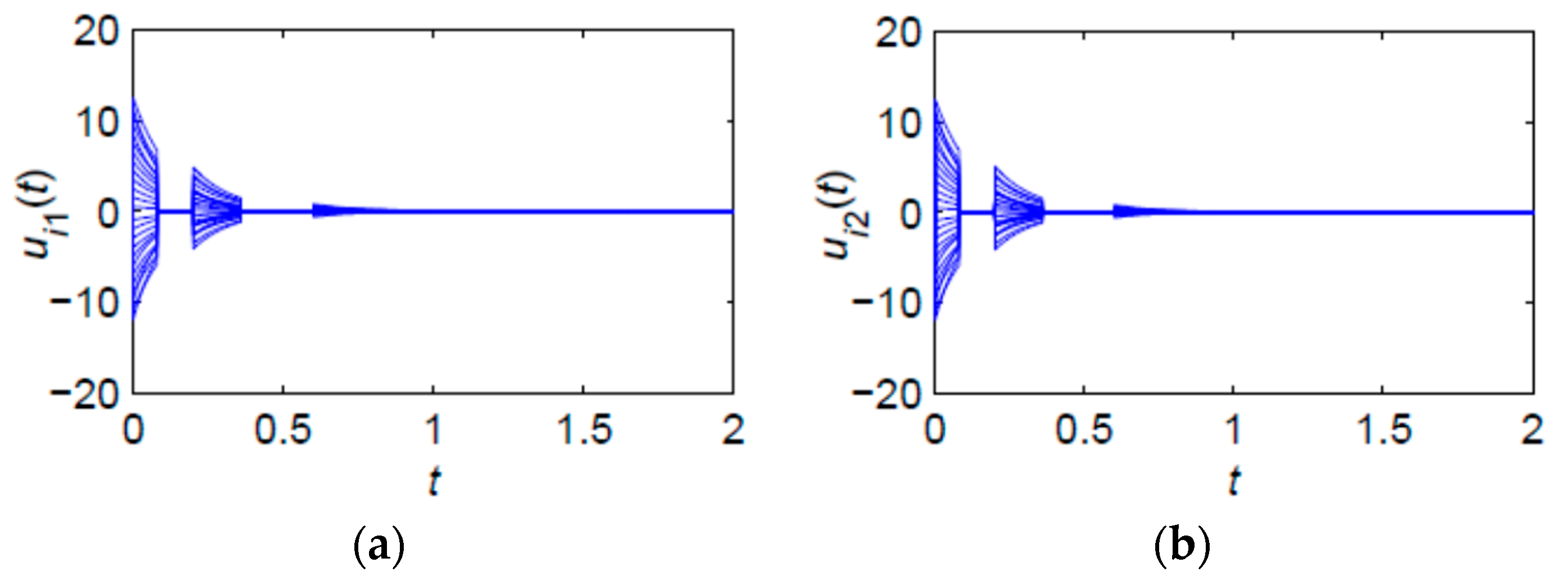
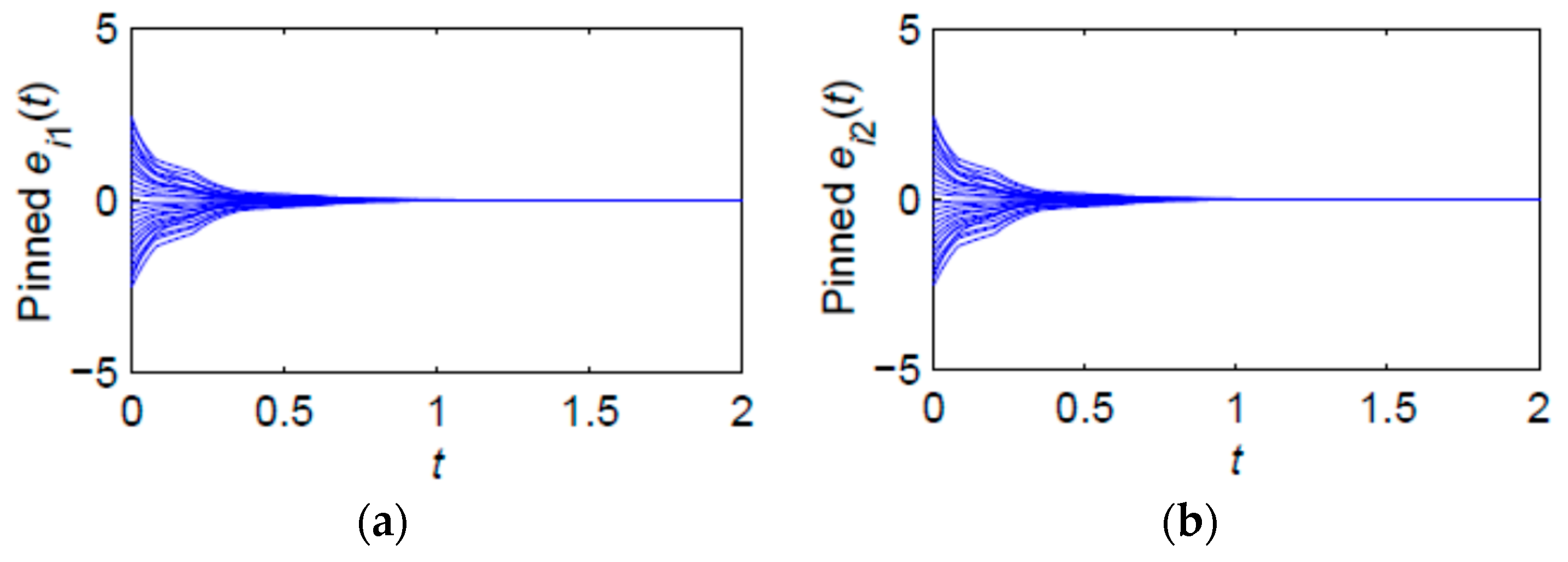
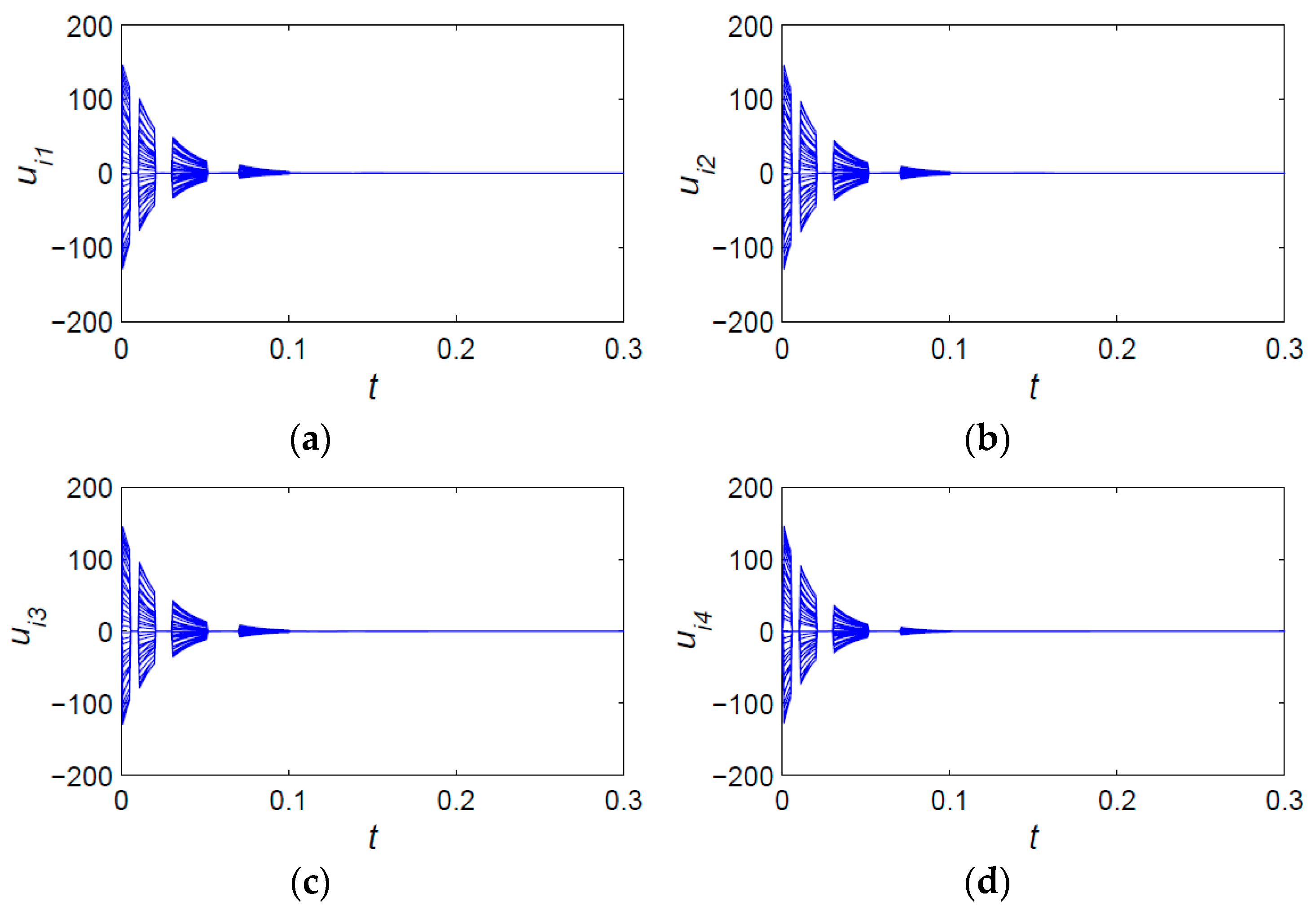
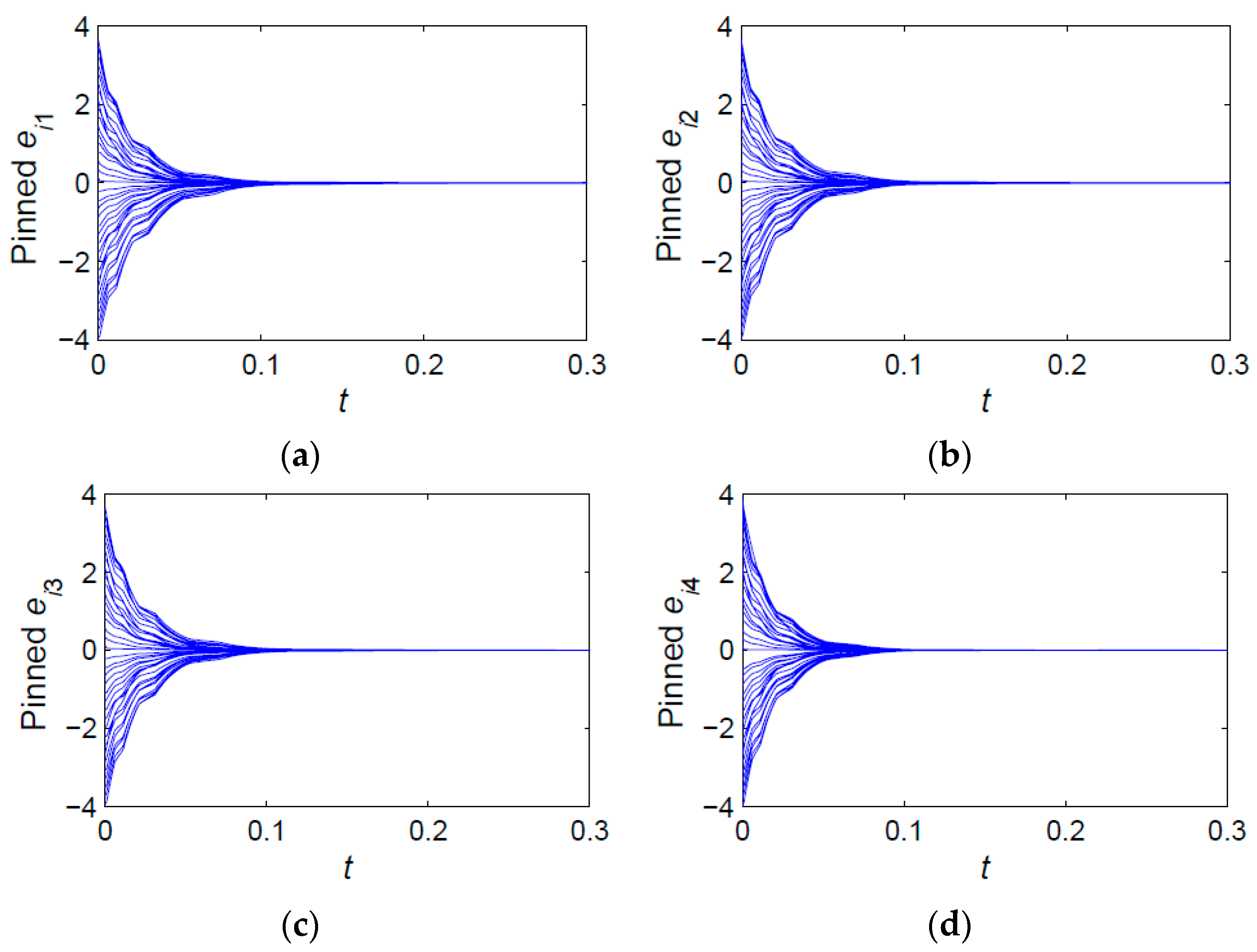
4.1.1. Simulation Example 1
4.1.2. Simulation Example 2
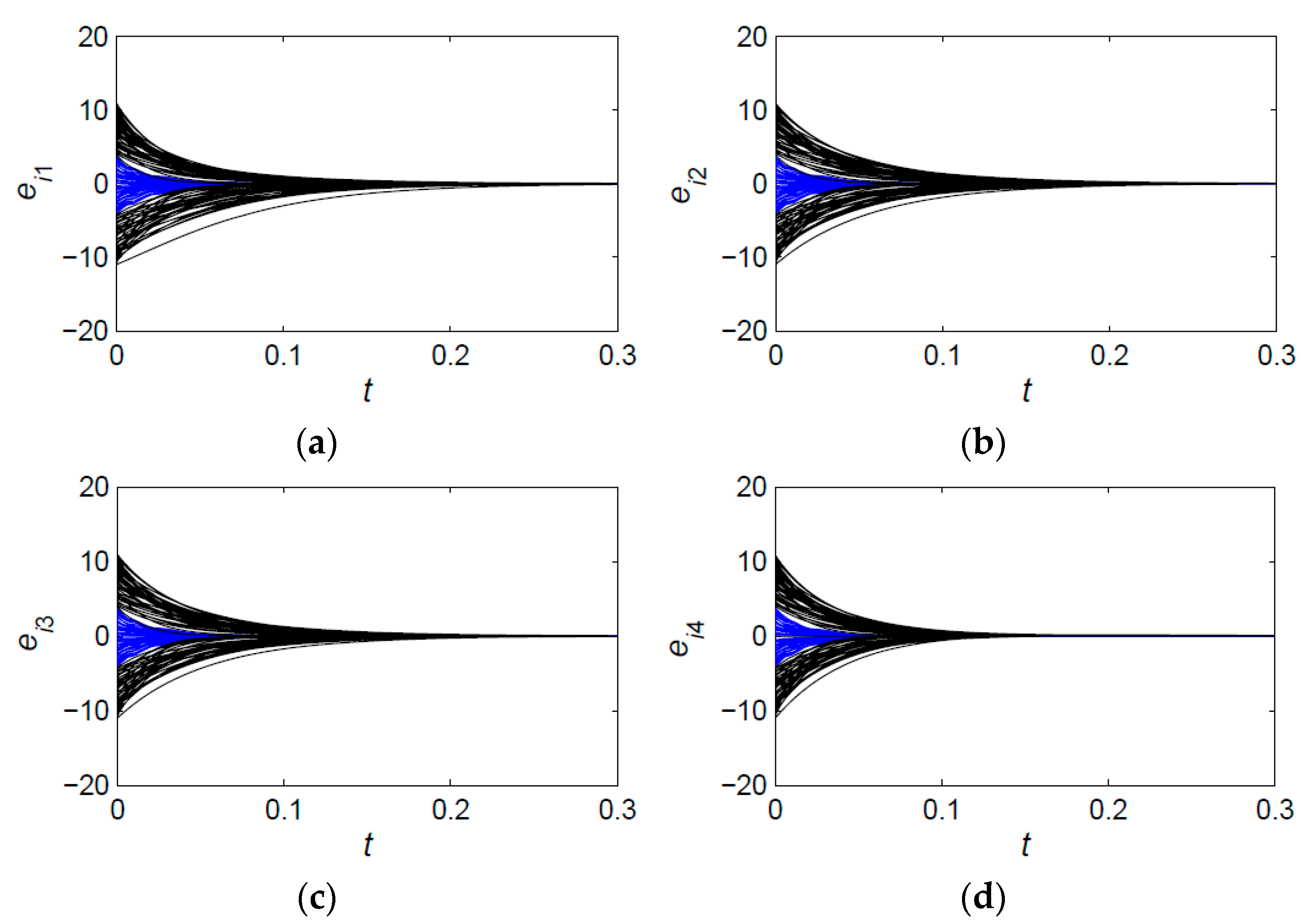
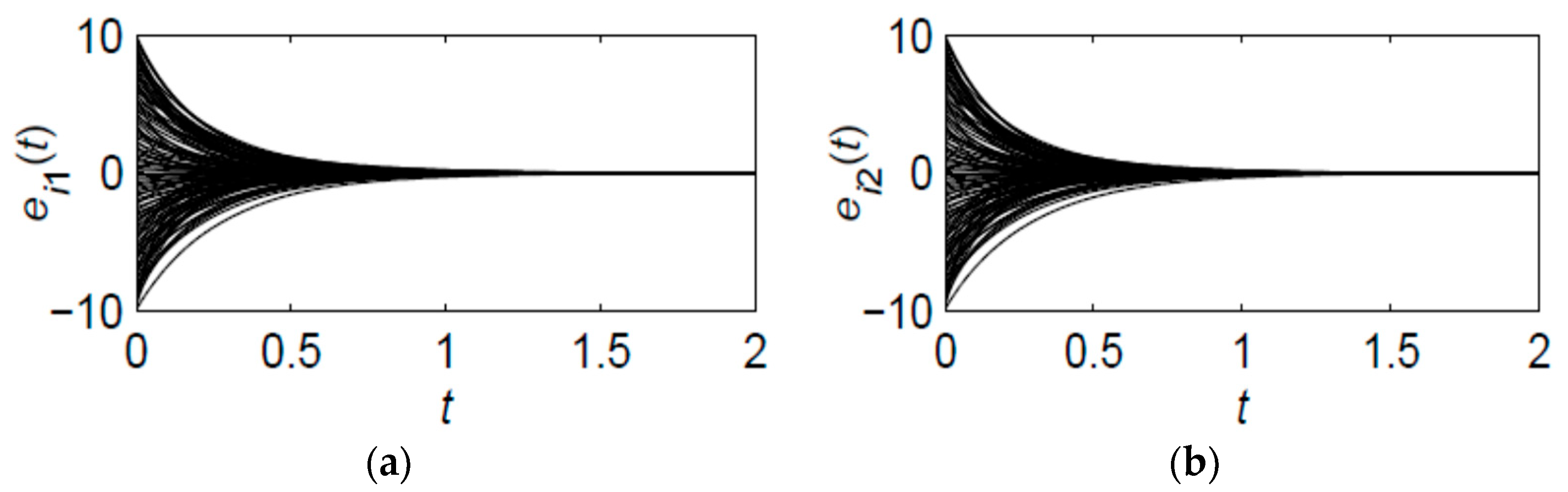
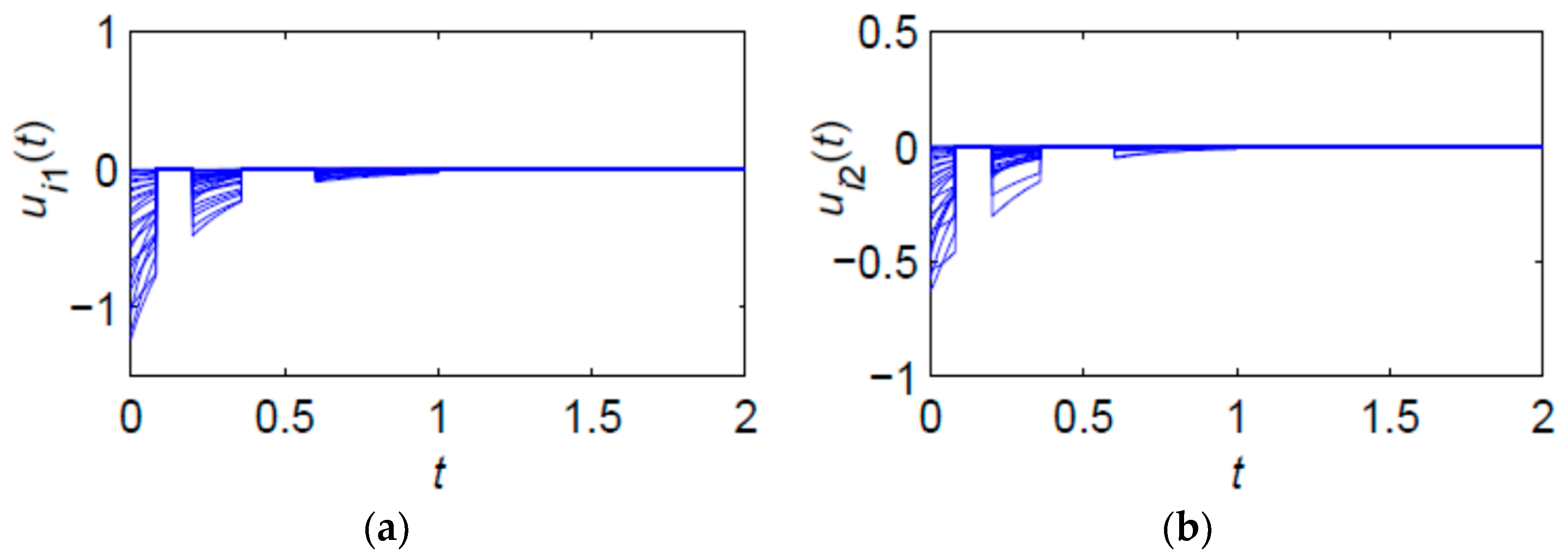
4.2. Simulation Example with Adaptive Intermittent Pinning Controller
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhoug, C. Synchronization in complex networks. Phys. Rep. 2008, 469, 93–153. [Google Scholar] [CrossRef]
- Zhu, J.; Lu, J.; Yu, X. Flocking of Multi-Agent Non-Holonomic Systems with Proximity Graphs. IEEE Trans. Circuits Syst. I 2013, 60, 199–210. [Google Scholar] [CrossRef]
- Xie, Q.; Chen, G.; Bollt, E. Hybrid chaos synchronization and its application in information processing. Math. Comput. Model. 2002, 35, 145–163. [Google Scholar] [CrossRef]
- Wang, P.; Lü, J.; Ogorzalek, M.J. Global relative parameter sensitivities of the feed-forward loops in genetic networks. Neurocomputing 2012, 78, 155–165. [Google Scholar] [CrossRef]
- Tang, Y.; Qian, F.; Gao, H.; Kurths, J. Synchronization in complex networks and its application—A survey of recent advances and challenges. Annu. Rev. Control 2014, 38, 184–198. [Google Scholar] [CrossRef]
- Zhao, L.-H.; Wen, S.; Li, C.; Shi, K.; Huang, T. A Recent Survey on Control for Synchronization and Passivity of Complex Networks. IEEE Trans. Netw. Sci. Eng. 2022, 9, 4235–4254. [Google Scholar] [CrossRef]
- Boccaletti, S.; Bianconi, G.; Criado, R.; del Genio, C.; Gómez-Gardeñes, J.; Romance, M.; Sendiña-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef]
- Tang, L.; Wu, X.; Lü, J.; Lu, J.; Raissa, M.D. Master stability functions for complete, intralayer and interlayer synchronization in multiplex networks of coupled Rossler oscillators. Phys. Rev. E 2019, 99, 012304. [Google Scholar] [CrossRef]
- Tang, L.; Lu, J.; Lü, J. A threshold effect of coupling delays on intra-layer synchronization in duplex networks. Sci. China-Technol. Sci. 2018, 61, 1907–1914. [Google Scholar] [CrossRef]
- Bera, B.K.; Rakshit, S.; Ghosh, D. Intralayer synchronization in neuronal multiplex network. Eur. Phys. J. Spec. Top. 2019, 228, 2441–2454. [Google Scholar] [CrossRef]
- Kivela, M.; Arenas, A.; Barthelemy, M. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
- Wang, G.; Cao, J.; Lu, J. Outer synchronization between two nonidentical networks with circumstance noise. Phys. A Stat. Mech. Appl. 2010, 389, 1480–1488. [Google Scholar] [CrossRef]
- Hymavathi, M.; Ibrahim, T.F.; Syed Ali, M.; Stamov, G.; Stamova, I.; Younis, B.A.; Osman, K.I. Synchronization of fractional-order neural networks with time delays and reaction-diffusion terms via pinning control. Mathematics 2022, 10, 3916. [Google Scholar] [CrossRef]
- Zhuang, J.; Zhou, Y.; Xia, Y. Synchronization analysis of drive-response multi-layer dynamical networks with additive couplings and stochastic perturbations. Discret. Contin. Dyn. Syst. S 2021, 14, 1607–1629. [Google Scholar] [CrossRef]
- Żochowski, M. Intermittent dynamical control. Phys. D Nonlinear Phenom. 2000, 145, 181–190. [Google Scholar] [CrossRef]
- Xia, W.; Cao, J. Pinning synchronization of delayed dynamical networks via periodically intermittent control. Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 013120. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.; Hao, J.; He, Q.; Liu, Z. Exponential synchronization of complex delayed dynamical networks via pinning periodically intermittent control. Phys. Lett. A 2011, 375, 1965–1971. [Google Scholar] [CrossRef]
- Hu, C.; Yu, J.; Jiang, H.; Teng, Z. Exponential Synchronization of Complex Networks with Finite Distributed Delays Coupling. IEEE Trans. Neural Netw. 2011, 22, 1999–2010. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Wang, X. Synchronization in complex networks with non-delay and delay couplings via intermittent control with two switched periods. Phys. A Stat. Mech. Its Appl. 2013, 395, 434–444. [Google Scholar] [CrossRef]
- Liang, Y.; Qi, X.; Wei, Q. Synchronization of delayed complex networks via intermittent control with non-period. Phys. A Stat. Mech. Its Appl. 2018, 492, 1327–1339. [Google Scholar] [CrossRef]
- Li, W.; Zhou, J.; Li, J.; Xie, T.; Lu, J.-A. Cluster Synchronization of Two-Layer Networks via Aperiodically Intermittent Pinning Control. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1338–1342. [Google Scholar] [CrossRef]
- Jing, T.; Zhang, D.; Zhang, X. New Criteria for Synchronization of Multilayer Neural Networks via Aperiodically Intermittent Control. Comput. Intell. Neurosci. 2022, 2022, 8157794. [Google Scholar] [CrossRef]
- Yang, H.; Wang, X.; Zhong, S.; Shu, L. Synchronization of nonlinear complex dynamical systems via delayed impulsive distributed control. Appl. Math. Comput. 2018, 320, 75–85. [Google Scholar] [CrossRef]
- Zhuang, J.; Zhou, Y.; Xia, Y. Intra-layer synchronization in duplex networks with time-varying delays and stochastic perturba-tions under impulsive control. Neural Process. Lett. 2021, 52, 785–804. [Google Scholar] [CrossRef]
- Liu, X.; Fu, H.; Liu, L. Leader-Following Mean Square Consensus of Stochastic Multi-agent Systems via Periodically Intermittent Event-Triggered Control. Neural Process. Lett. 2020, 53, 275–298. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, C.; Meng, F.W.; Liang, Y. Event-Triggered Control for In-tra/Inter-Layer Synchronization and Quasi-Synchronization in Two-Layer Coupled Networks. Mathematics 2023, 11, 1458. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, C.; Zhang, X.; Wang, F.; Liang, Y. Dynamic event-triggered control for intra/inter-layer synchronization in multi-layer networks. Commun. Nonlinear Sci. Numer. Simul. 2023, 119, 107124. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, G. Pinning control of scale-free dynamical networks. Phys. A Stat. Mech. Appl. 2002, 310, 521–531. [Google Scholar] [CrossRef]
- Porfiri, M.; Bernardo, M.D. Criteria for global pinning-controllability of complex networks. Automatica 2008, 44, 3100–3106. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Lü, J.; Kurths, J.; Yu, G.C.W.; Jin, S.; Wang, D.; Zou, X.; Yan, F.; Gu, G.; et al. Synchronization via Pinning Control on General Complex Networks. SIAM J. Control Optim. 2013, 51, 1395–1416. [Google Scholar] [CrossRef]
- Zhao, X.; Zhou, J.; Lu, J.-A. Pinning Synchronization of Multiplex Delayed Networks with Stochastic Perturbations. IEEE Trans. Cybern. 2019, 49, 4262–4270. [Google Scholar] [CrossRef] [PubMed]
- Hai, X.; Ren, G.; Yu, Y.; Xu, C. Adaptive Pinning Synchronization of Fractional Complex Networks with Impulses and Reaction–Diffusion Terms. Mathematics 2019, 7, 405. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Z.; Yang, H.; Song, Q.; Xiao, M. Synchronization of multiplex networks with stochastic perturbations via pinning adaptive control. J. Frankl. Inst. 2021, 358, 3994–4012. [Google Scholar] [CrossRef]
- He, W.; Chen, G.; Han, Q.-L.; Du, W.; Cao, J.; Qian, F. Multiagent Systems on Multilayer Networks: Synchronization Analysis and Network Design. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1655–1667. [Google Scholar] [CrossRef]
- Zhuang, J.; Cao, J.; Tang, L.; Xia, Y.; Perc, M. Synchronization Analysis for Stochastic Delayed Multilayer Network with Additive Couplings. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4807–4816. [Google Scholar] [CrossRef]
- Zhang, F. Matrix Theory; Springer: New York, NY, USA, 1999. [Google Scholar]
- Lütkepohl, H. Handbook of Matrices; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Liang, Y.; Wang, X. A method of quickly calculating the number of pinning nodes on pinning synchronization in complex networks. Appl. Math. Comput. 2014, 246, 743–751. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Matsumoto, T. A chaotic attractor from Chua’s circuit. IEEE Trans. Circuits Syst. 1984, 31, 1055–1058. [Google Scholar] [CrossRef]
- Lü, J.; Chen, G. A new chaotic attractor coined. Int. J. Bifurc. Chaos 2002, 12, 659–661. [Google Scholar] [CrossRef]
- Al-Hayali, M.A.; Al-Azzawi, F.S. A 4D hyperchaotic Sprott S system with multistability and hidden attractors. J. Phys. Conf. Ser. 2021, 1879, 032031. [Google Scholar] [CrossRef]
- Nadia, M.M.; Zeena, N.A. A new secure encryption algorithm based on RC4 cipher and 4D hyperchaotic Sprott-S system. In Proceedings of the 5th College of science International Conference on Recent Trends in Information Technology, Baghdad, Iraq, 15–16 November 2022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Deng, Y.; Zhang, C. Outer Synchronization of Two Muti-Layer Dynamical Complex Networks with Intermittent Pinning Control. Mathematics 2023, 11, 3543. https://doi.org/10.3390/math11163543
Liang Y, Deng Y, Zhang C. Outer Synchronization of Two Muti-Layer Dynamical Complex Networks with Intermittent Pinning Control. Mathematics. 2023; 11(16):3543. https://doi.org/10.3390/math11163543
Chicago/Turabian StyleLiang, Yi, Yunyun Deng, and Chuan Zhang. 2023. "Outer Synchronization of Two Muti-Layer Dynamical Complex Networks with Intermittent Pinning Control" Mathematics 11, no. 16: 3543. https://doi.org/10.3390/math11163543
APA StyleLiang, Y., Deng, Y., & Zhang, C. (2023). Outer Synchronization of Two Muti-Layer Dynamical Complex Networks with Intermittent Pinning Control. Mathematics, 11(16), 3543. https://doi.org/10.3390/math11163543





