Numerical Investigation of Key Structural Parameters for Middle-Buried Rubber Waterstops
Abstract
:1. Introduction
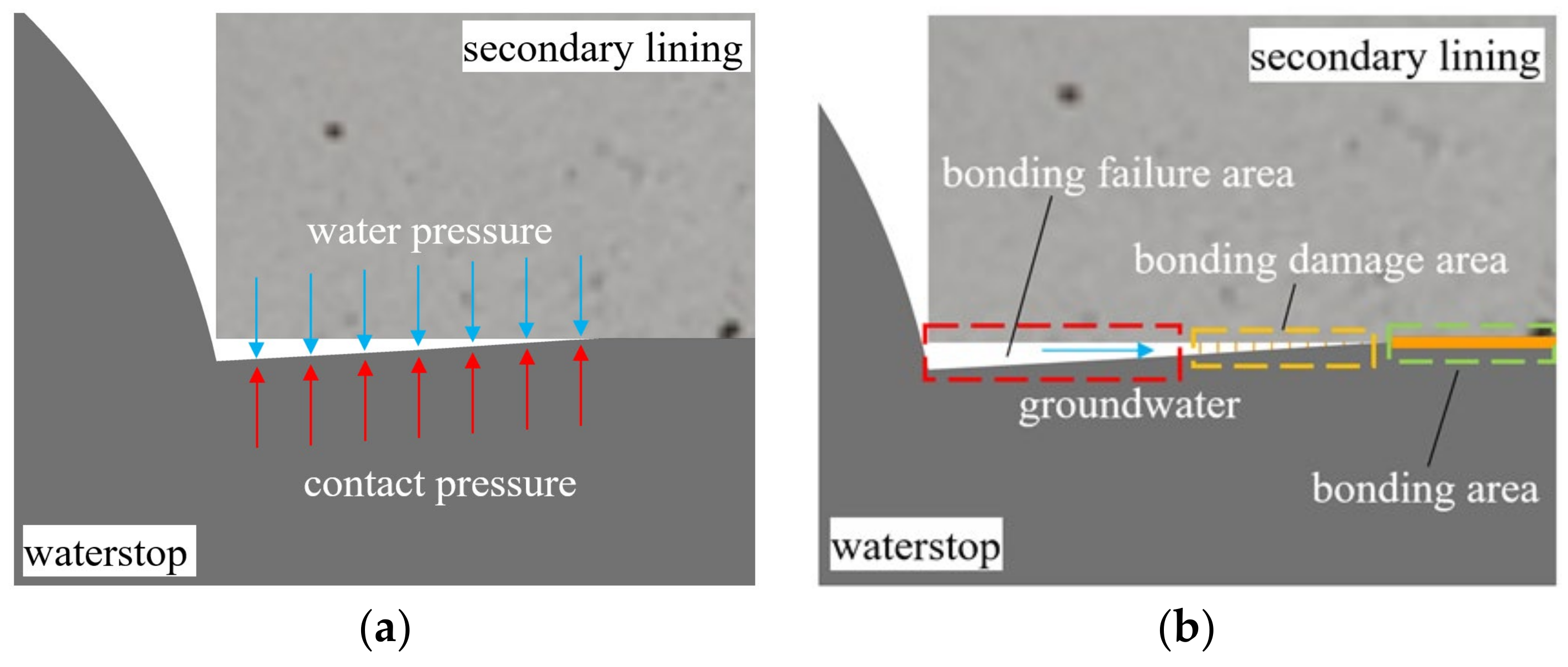
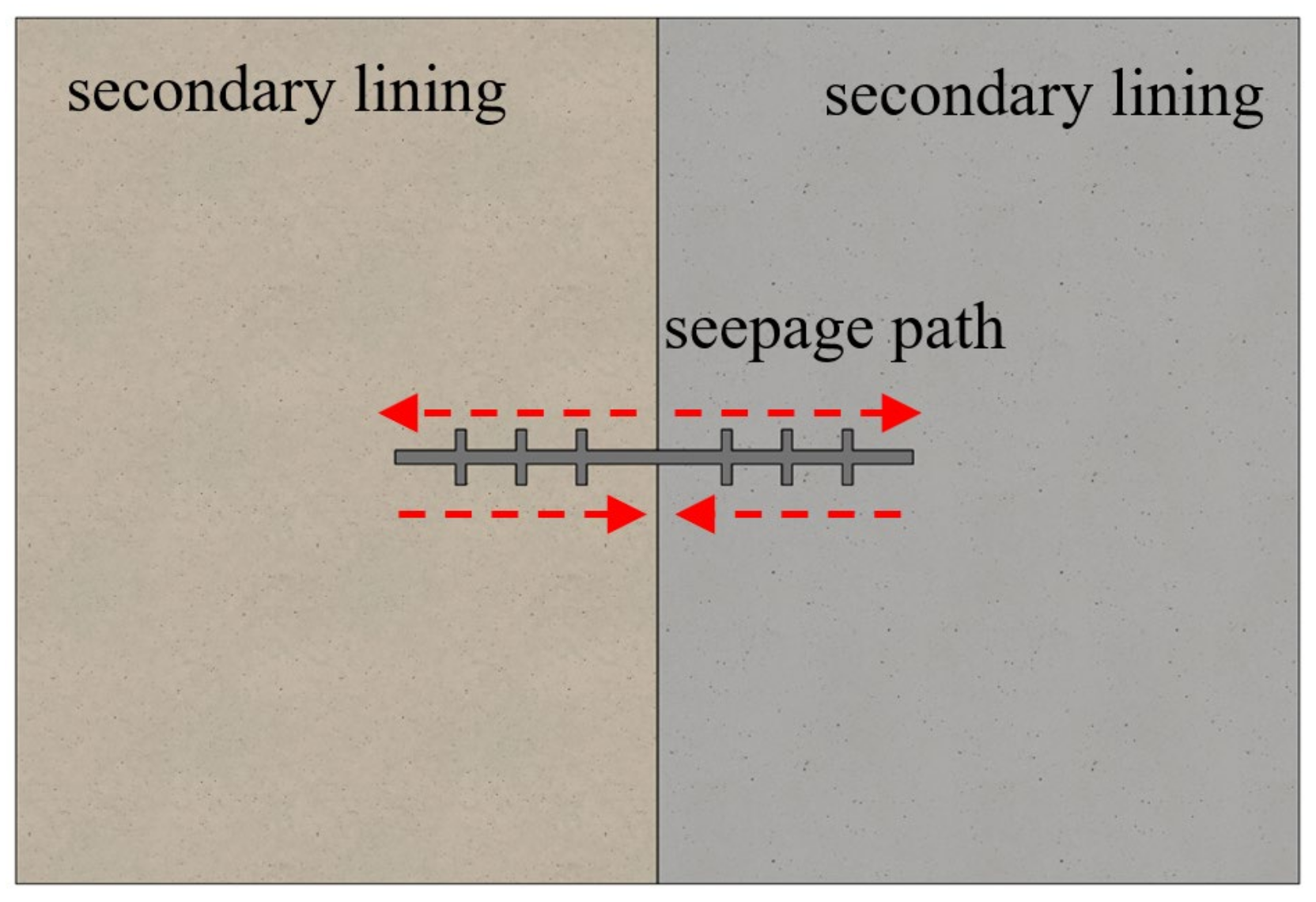
2. Waterproofing Mechanism of Middle-Buried Rubber Waterstops
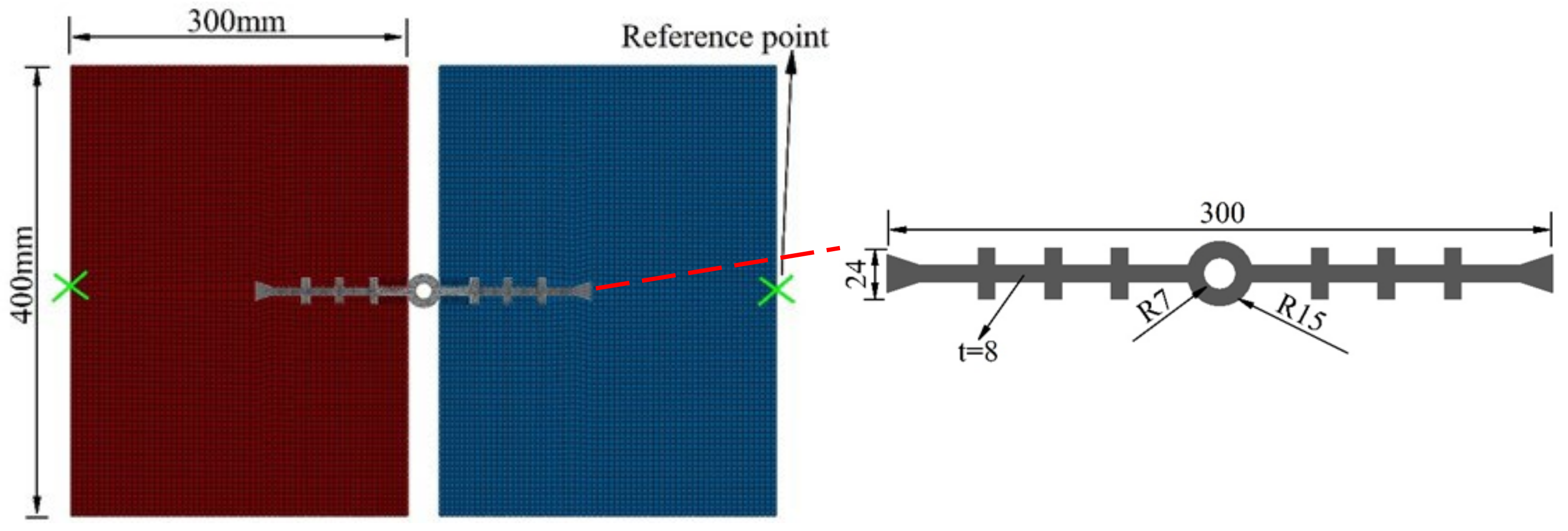
3. Numerical Model Setups
3.1. Constitutive Models of Materials
3.1.1. Constitutive Model of Concrete
3.1.2. Constitutive Model of Rubber Waterstop
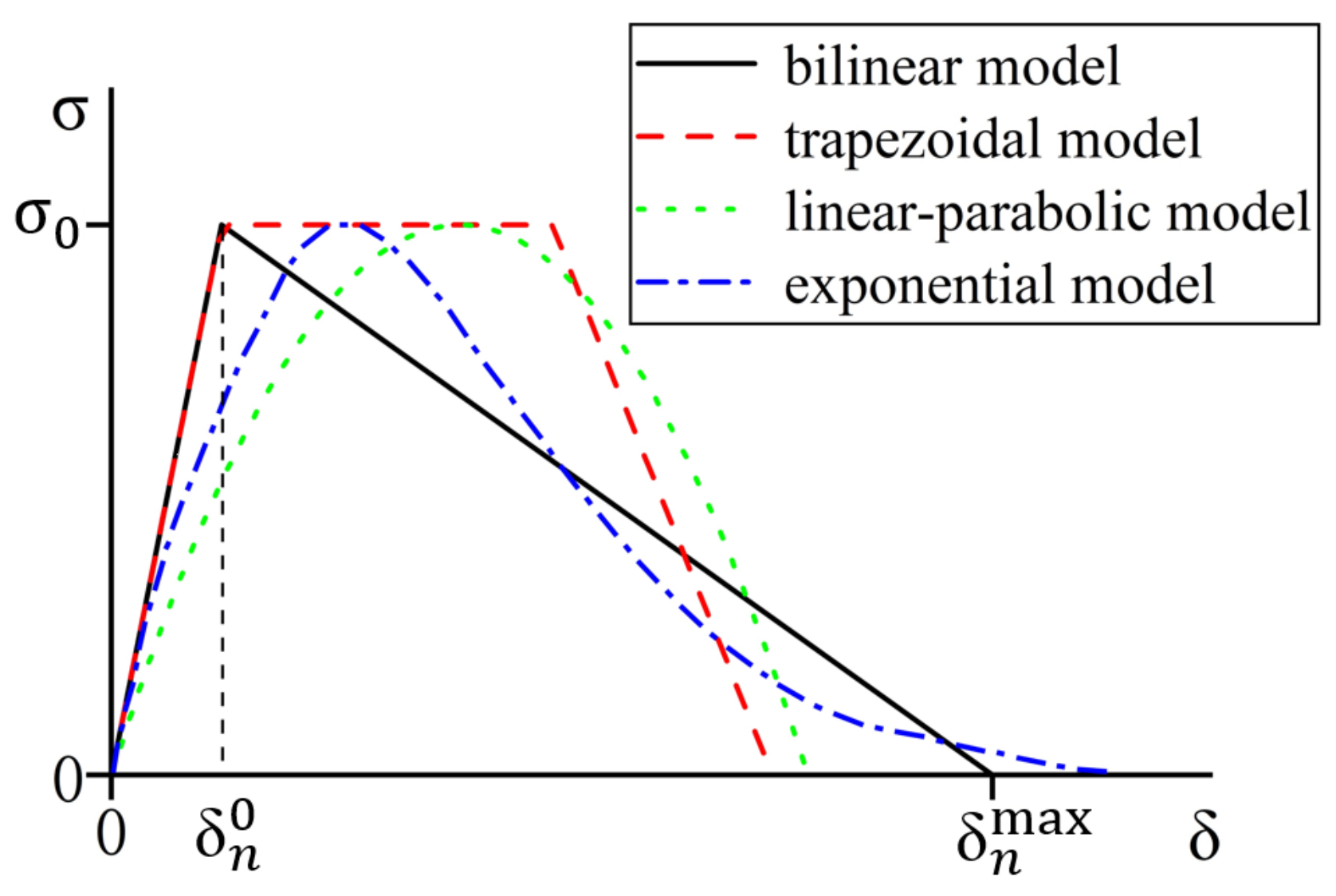
3.2. Contact Model
- (1)
- Maximum nominal stress criterion:
- (2)
- Maximum nominal strain criterion:
- (3)
- Secondary nominal stress criterion:
- (4)
- Secondary nominal strain criterion:
3.3. Element Types and Boundary Conditions
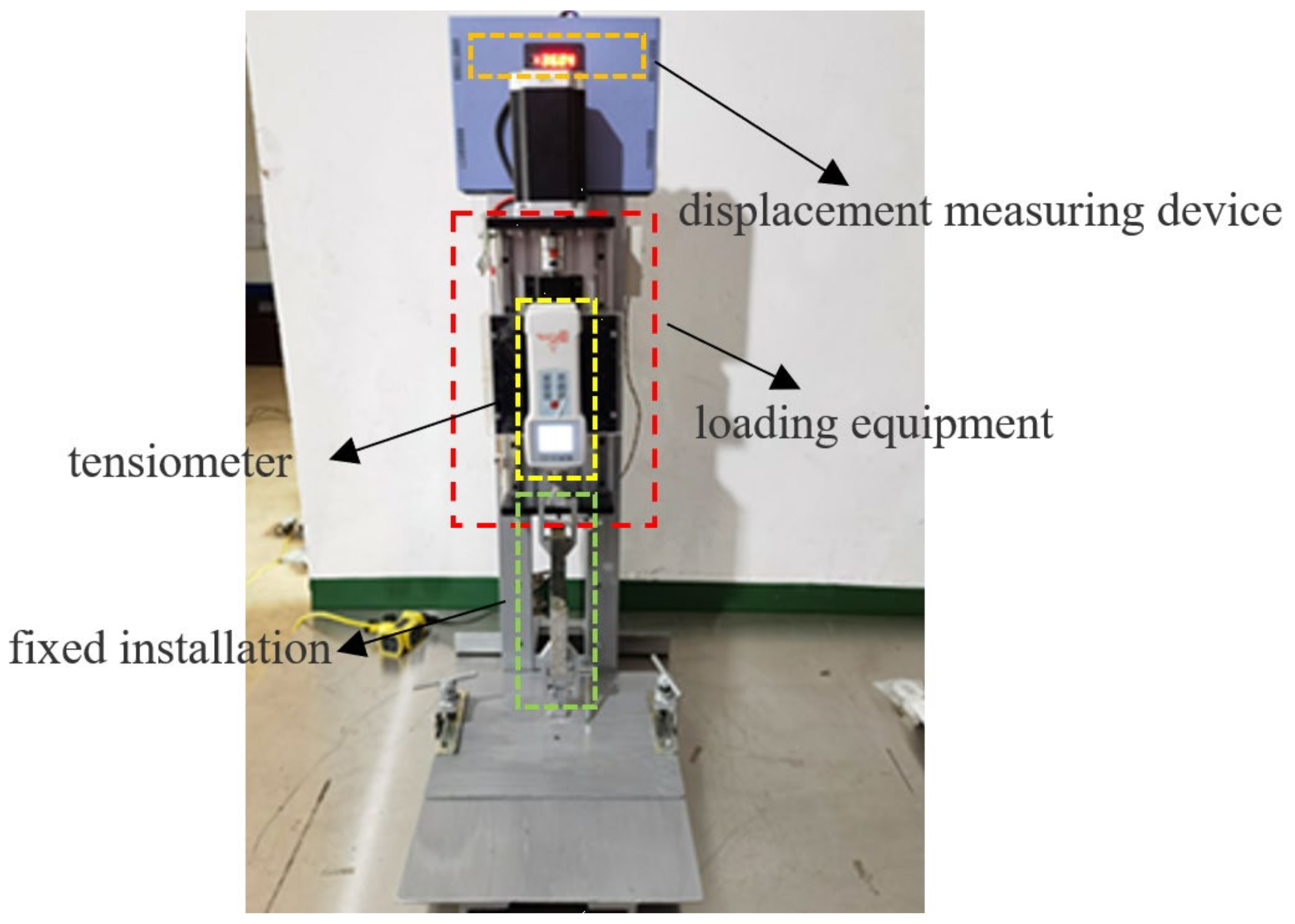
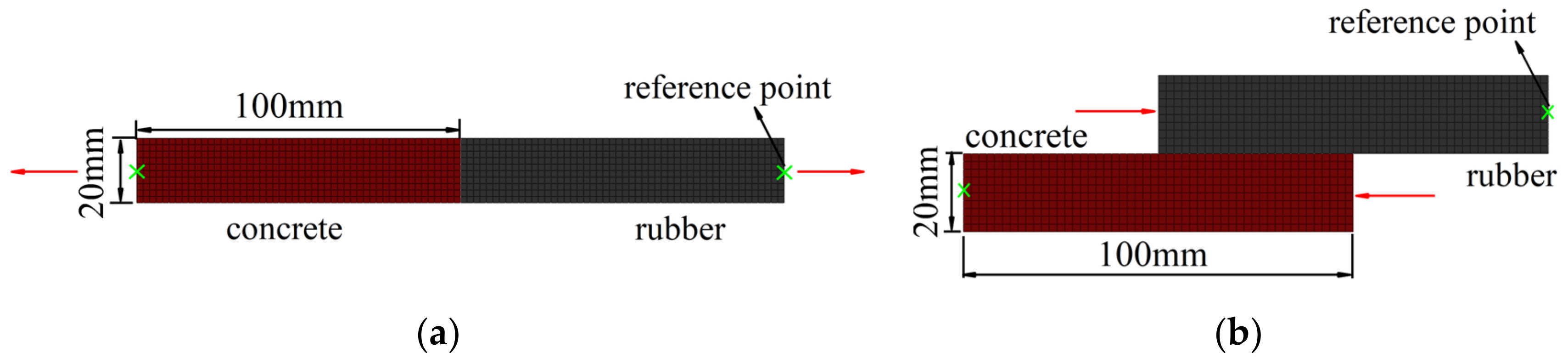
4. Adhesive Force Test and Numerical Model Verification
4.1. Adhesive Force Test
4.2. Numerical Model Validation
5. Numerical Analysis of Key Structural Parameters
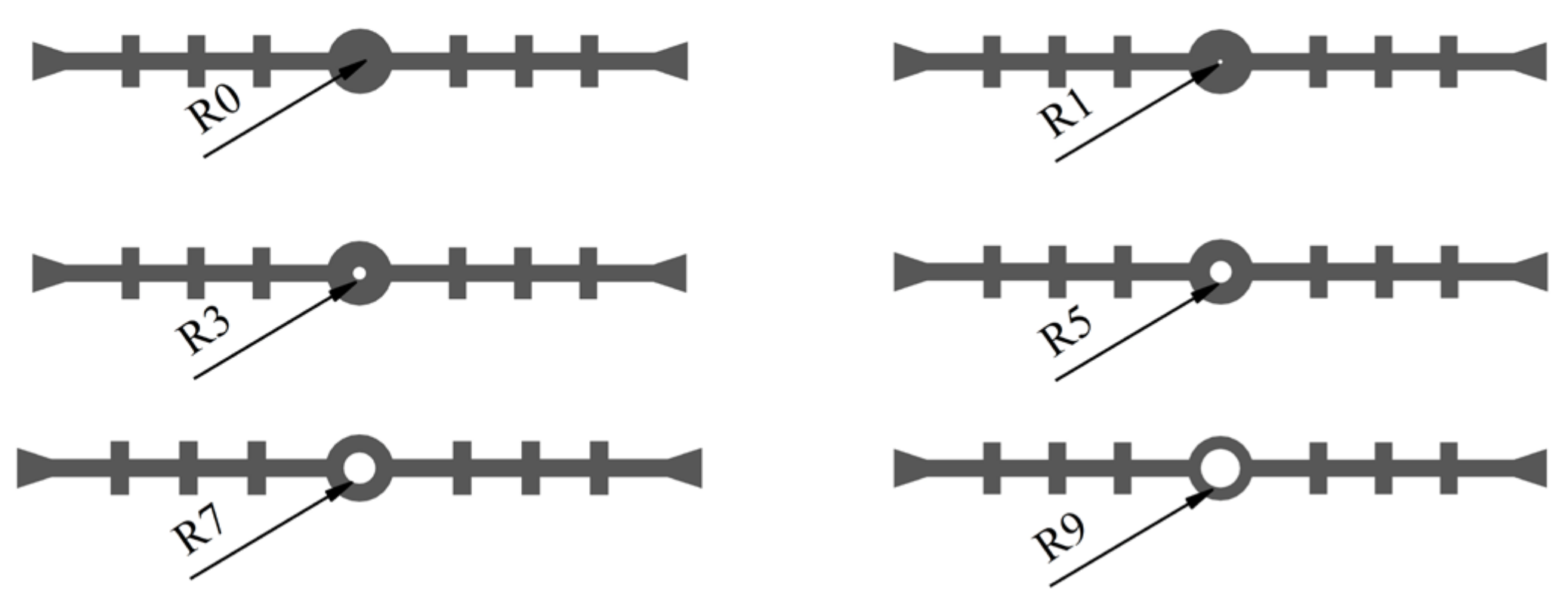
5.1. Different Parameters of Waterstop Center Hole
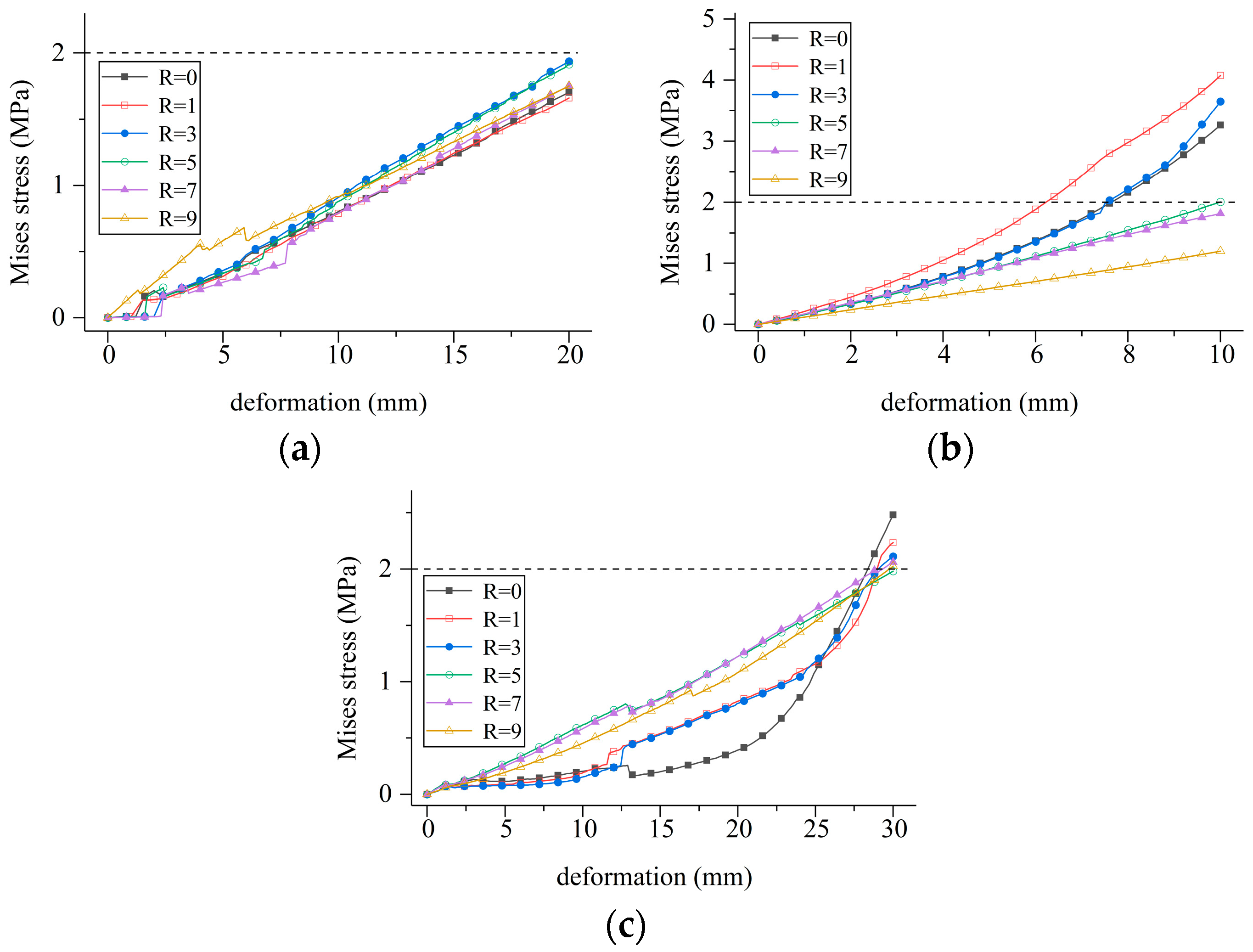
5.1.1. Fixed Outer Diameter of the Center Hole
- (1)
- Under tensile deformation, the deformation stress initially increases and then decreases with an increase in the aperture size. The maximum stress occurs when the aperture size is R = 3 mm, possibly due to the aperture size being too small, thus resulting in stress concentration during deformation. The deformation stress in all scenarios remains below the critical stress value.
- (2)
- During compressive deformation, the overall deformation stress decreases with an increase in the aperture size (though stress concentration may occur when 0 < R ≤ 3). However, when the aperture size is less than 5 mm, the deformation stress of the waterstop exceeds the critical stress value.
- (3)
- During settlement deformation, the deformation stress initially decreases and then increases with an increase in the aperture size. The minimum stress occurs when the aperture size is R = 5 mm, and only in this case is the deformation stress below the critical stress.
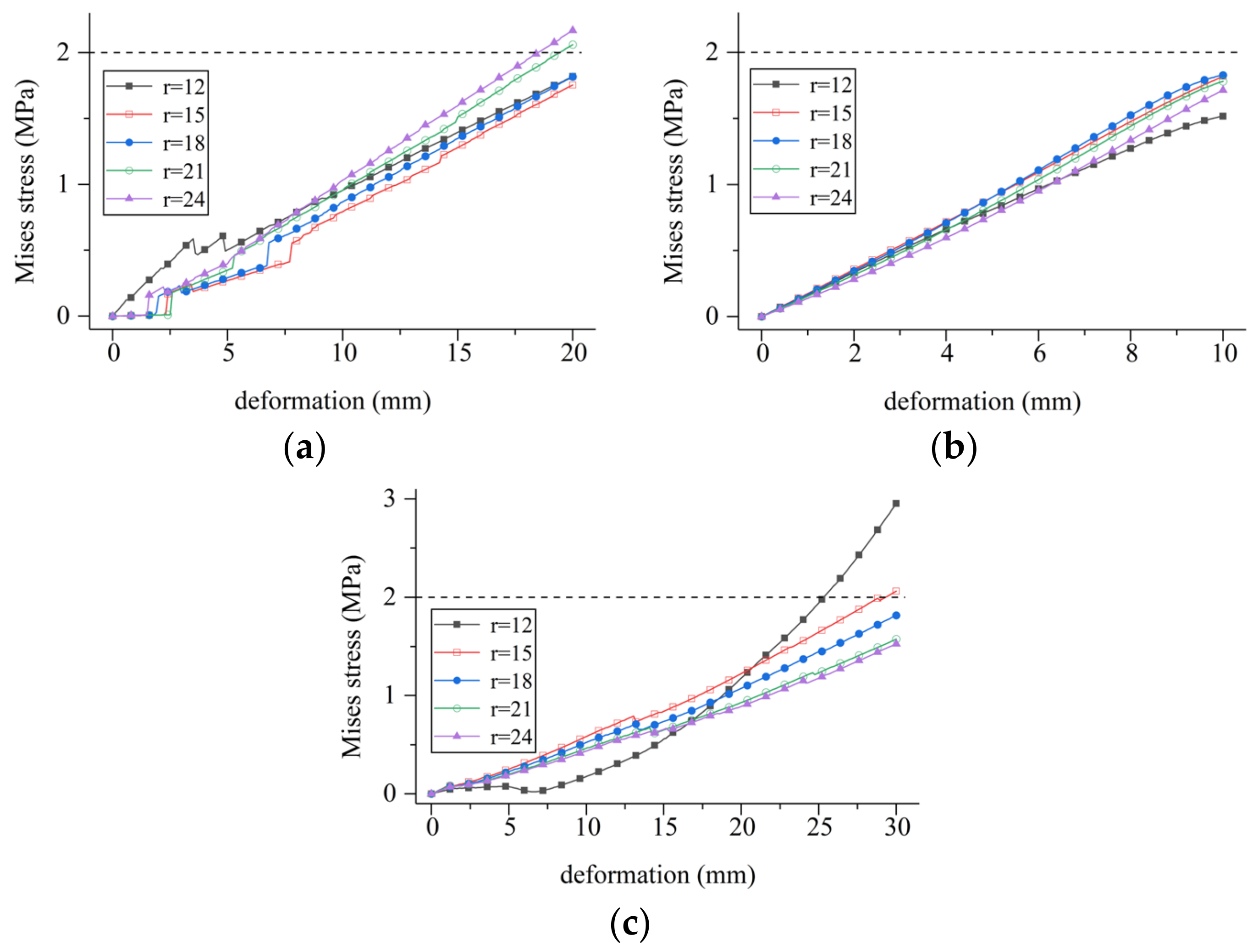
5.1.2. Fixed Inner Hole Diameter
- (1)
- During tensile deformation, the deformation stress generally increases with an increase in the outer diameter. When the outer diameter of the aperture r > 21 mm, the deformation stress exceeds the critical stress threshold.
- (2)
- During compressive deformation, the deformation stress initially increases and then decreases with an increase in the outer diameter of the aperture. The deformation stress in all scenarios remains below the critical stress level.
- (3)
- During settlement deformation, the deformation stress shows a notable change with variations in the outer diameter of the aperture. It decreases as the outer diameter of the waterstop aperture increases. When the outer diameter r > 15 mm, the deformation stress is below the critical stress threshold.
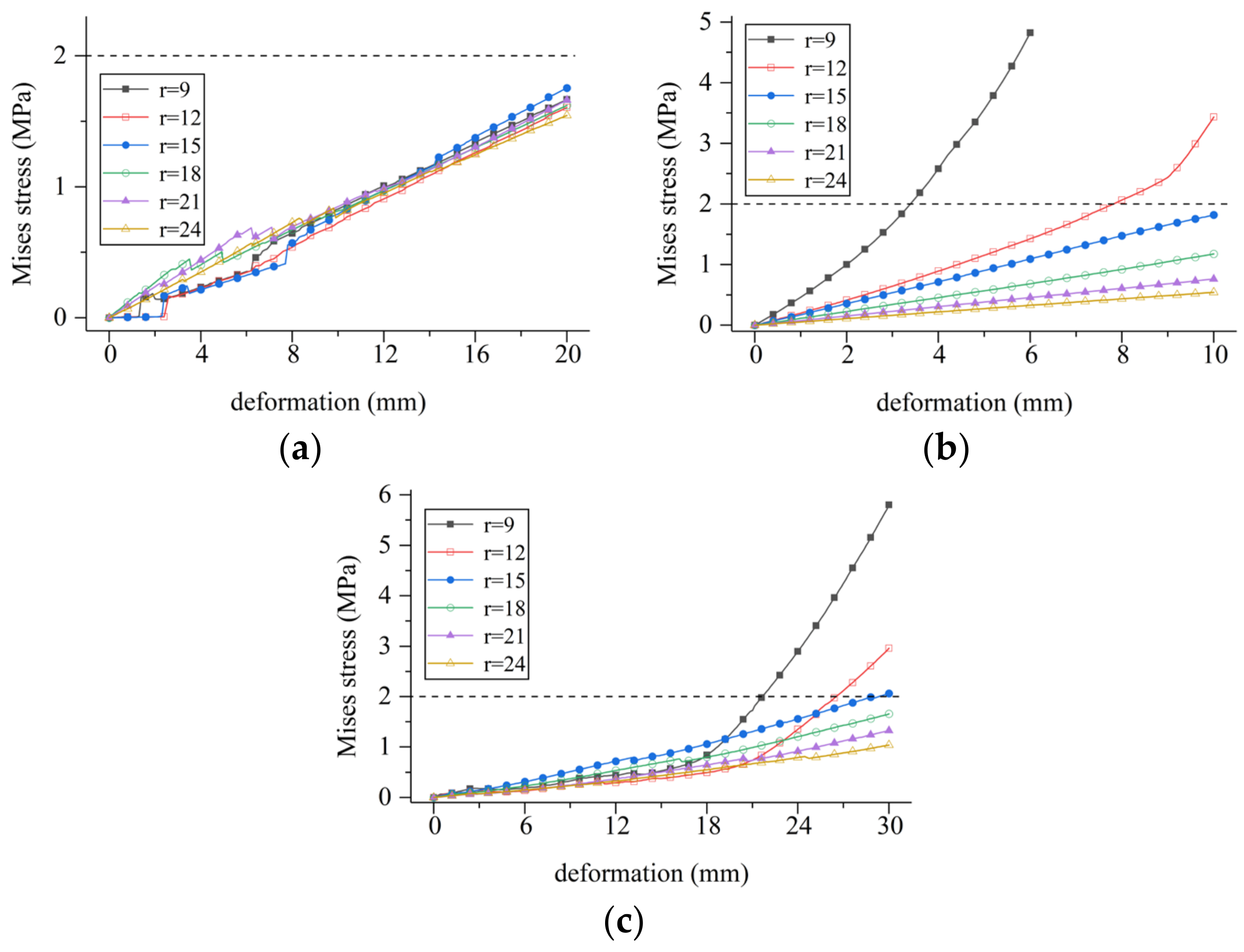
5.1.3. Fixed Thickness of the Center Hole
- (1)
- During tensile deformation, the deformation stresses in all scenarios are below the critical stress value.
- (2)
- During compression deformation, the deformation stress decreases with an increase in the aperture size. When the aperture outer diameter r ≥ 15 mm, the deformation stress is below the critical stress value (at r = 9 mm, the deformation stress is excessively high, and the complete curve is not shown in the graph).
- (3)
- During settlement deformation, the deformation stress decreases with an increase in the aperture size. When the aperture outer diameter r > 15 mm, the deformation stress is below the critical stress value.
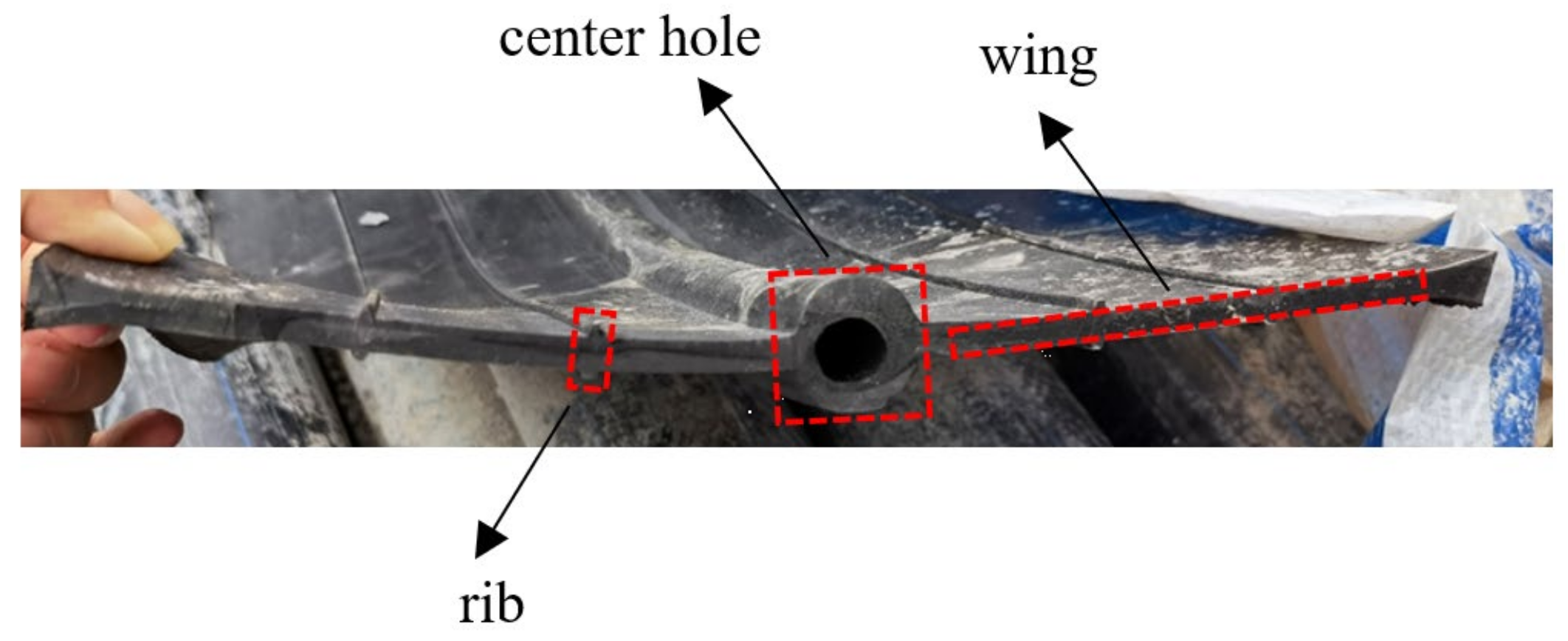
5.2. Different Parameters of Waterstop Ribs
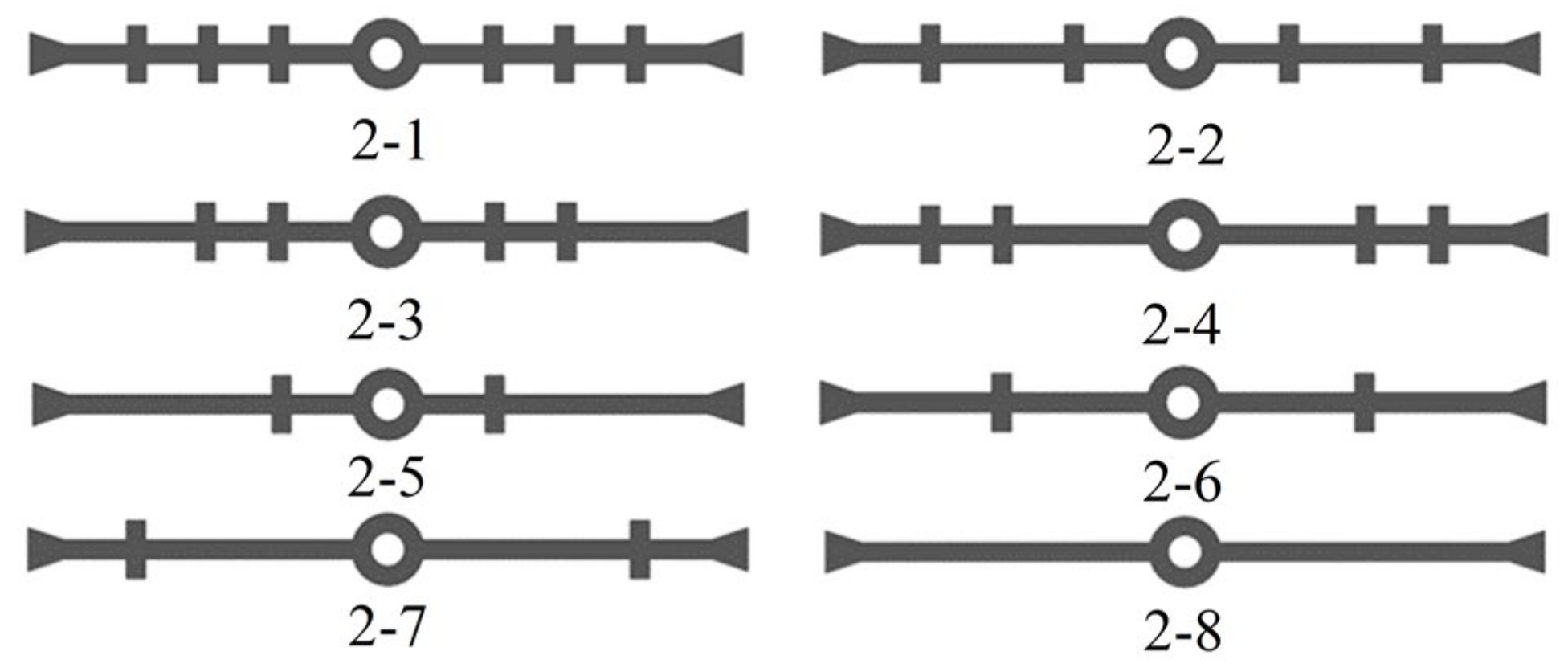
5.2.1. Number and Placement of Waterstop Ribs
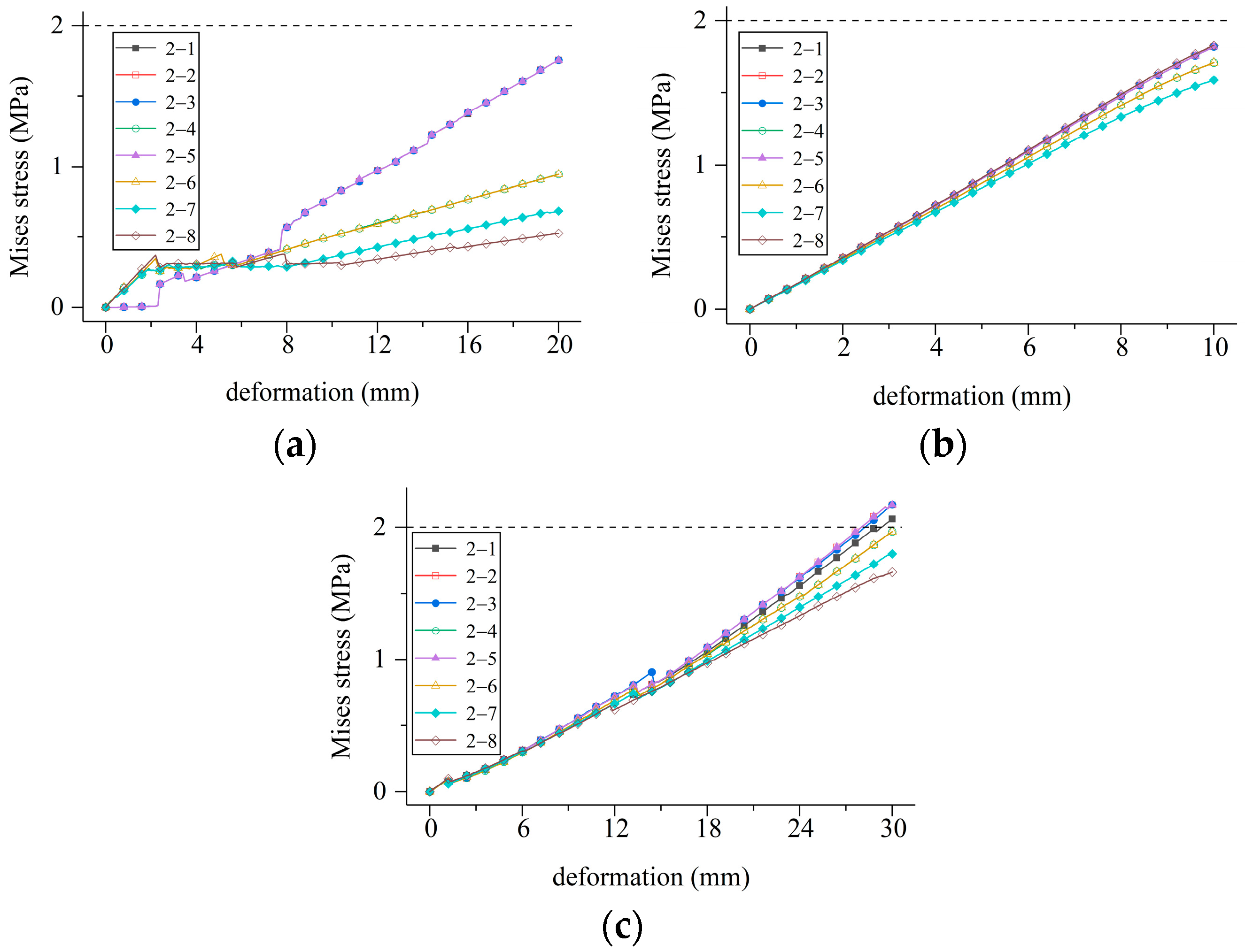
- (1)
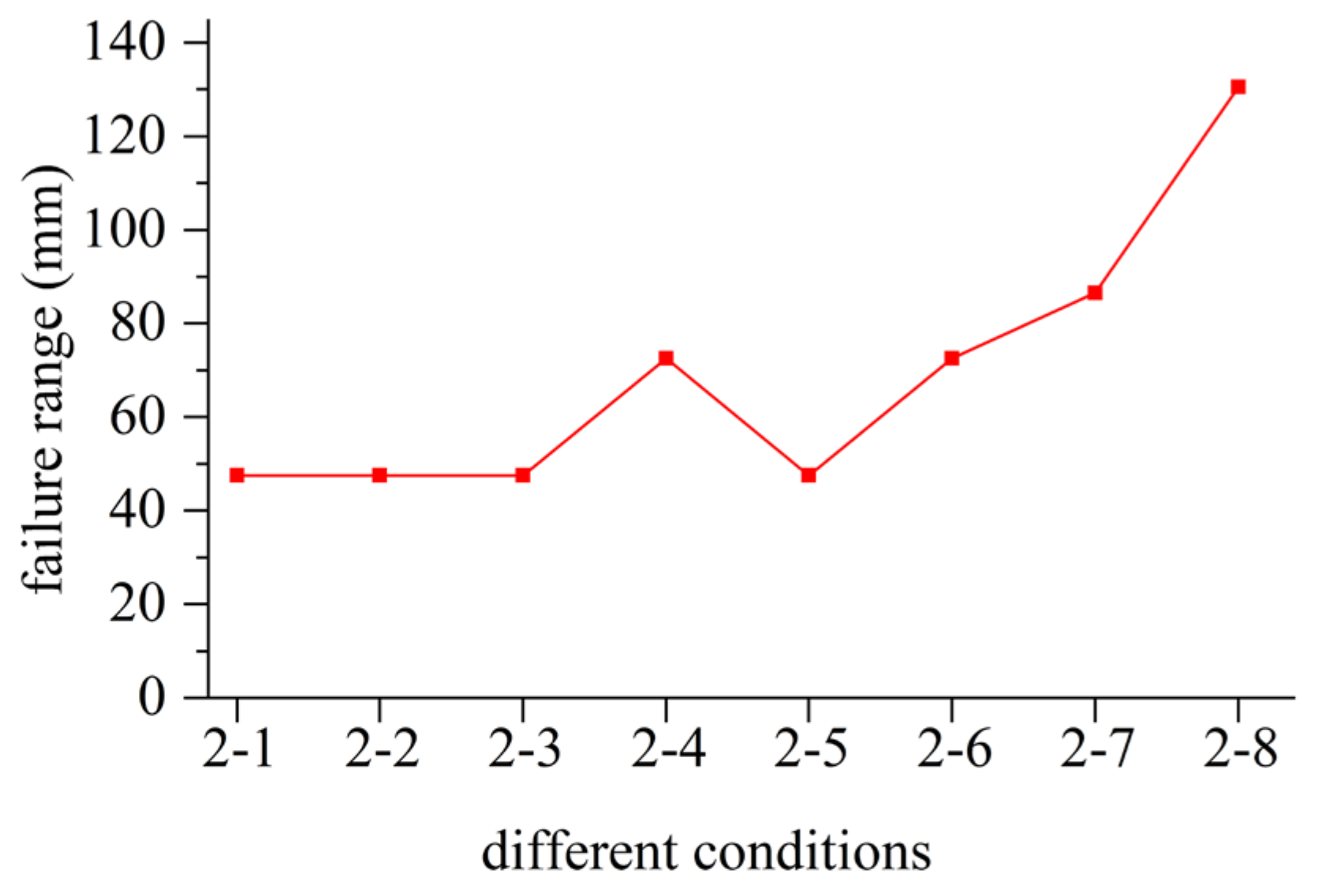
- Under tensile deformation, the stress values in all conditions are below the critical stress. Conditions 2-1, 2-2, 2-3, and 2-5 exhibit nearly identical deformation stresses, while conditions 2-4 and 2-6 also exhibit similar deformation stresses. The common factor among these pairs of waterstops with similar deformation stresses is that the position of the first waterstop rib on both sides is the same, with the difference being the number of ribs or the positions of the remaining ribs. Furthermore, conditions 2-5, 2-6, 2-7, and 2-8 demonstrate that as the distance between the first rib on both sides and the waterstop orifice increases, the tensile deformation stress of the waterstop decreases continuously. The difference between the maximum and minimum tensile deformation stresses can reach 233.5%.
- (2)
- Under compressive deformation, the deformation stresses in all conditions are below the critical stress. Similarly to tensile deformation, the deformation stress of the waterstop is also primarily influenced by the distance between the first rib on both sides and the waterstop orifice.
- (3)
- Under settlement deformation, when the distance between the first rib on both sides and the waterstop orifice exceeds 60 mm, the deformation stress is below the critical stress. The deformation stress of the waterstop under settlement deformation follows a similar pattern as described above.
5.2.2. Spacing between Waterstop Ribs
5.3. Different Parameters of Waterstop Wing
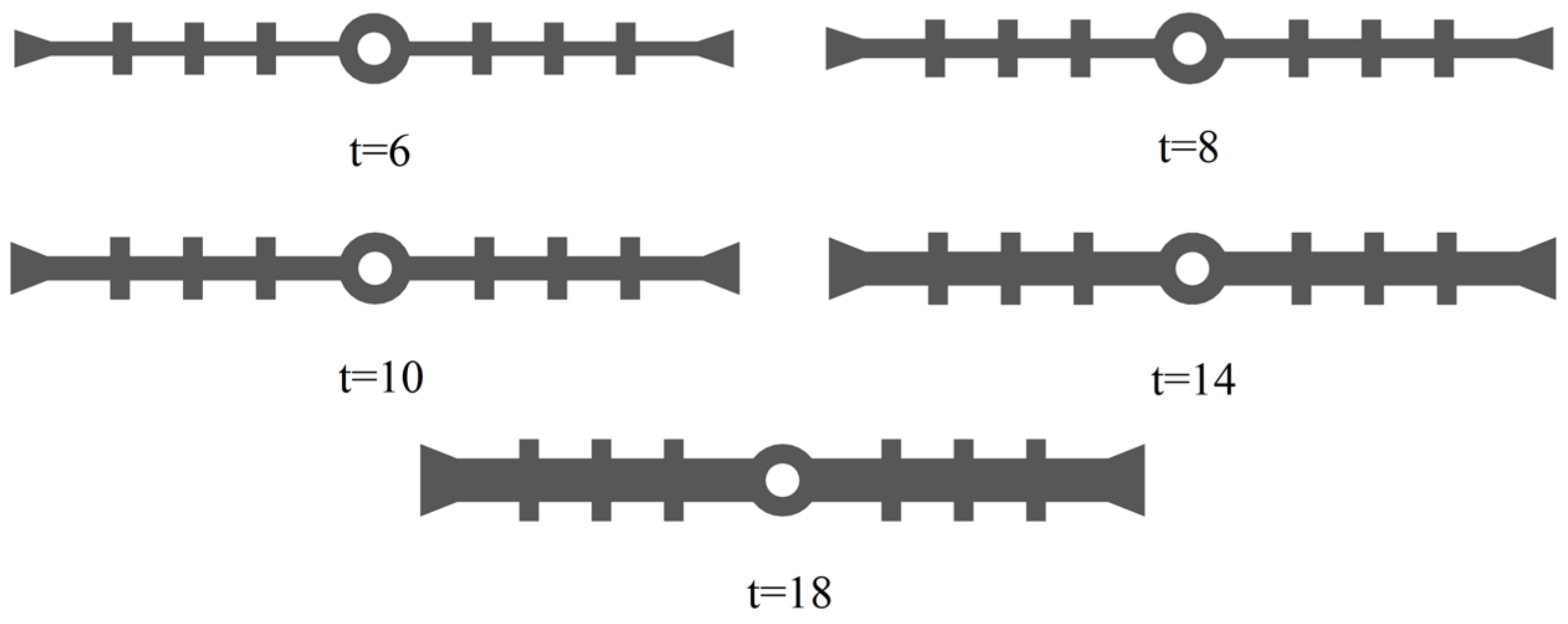
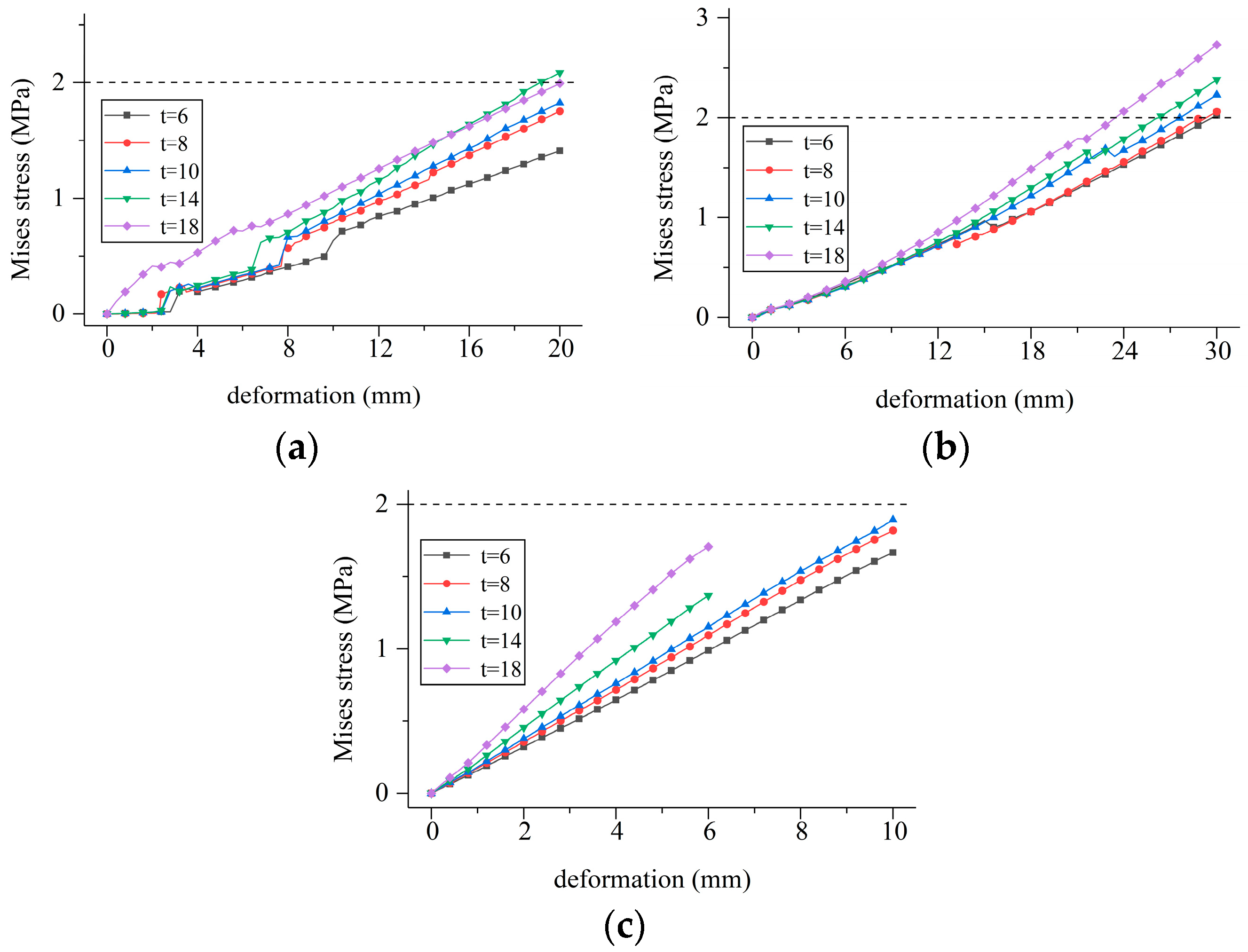
5.3.1. Wing Thickness
- (1)
- During tensile deformation, when the thickness of the wing plate is greater than or equal to 14 mm, the tensile deformation stress is greater than the critical stress level.
- (2)
- During compression deformation, when the flange thickness is greater than or equal to 14 mm, the compression deformation leads to tensile damage in the concrete lining (only partial curves are shown for the cases of t = 14 mm and t = 18 mm). The damage is due to the fact that when the other parameters of the waterstop belt remain unchanged and the thickness of the wing plate increases, the outer contour of the hole in the waterstop belt decreases, the concrete lining joint narrows, and the compression deformation of the hole in the waterstop belt becomes increasingly intense with an increase in the thickness of the wing plate.
- (3)
- During settlement deformation, the deformation stress for all cases exceeds the critical stress value.
5.3.2. Wing Length
6. Conclusions
- (1)
- The bond strength between rubber and concrete was tested, and the feasibility of using the Mooney–Rivlin model and bilinear cohesive force model to simulate the bonding between rubber and rubber–concrete interface was verified.
- (2)
- The center hole of the waterstop primarily serves to accommodate the deformation of the joint and reduce the deformation stress. In the design of the center hole, increasing the outer diameter and reducing the wall thickness of the center hole can help mitigate excessive deformation stress.
- (3)
- The waterstop ribs primarily enhance the anchorage between the waterstop and the concrete. As the deformation stress is mainly borne by the first ribs on both sides of the waterstop, the deformation stress of the waterstop is independent of the number of ribs but depends on the distance between the first ribs and the center hole. A greater distance between the first ribs and the center hole results in lower deformation stress. To reduce the deformation stress of the waterstop, it is recommended to increase the distance between the ribs and the center hole, for example, increasing the spacing from 30 mm to over 35 mm. Additionally, to ensure the quality of the concrete between the ribs, it is suggested to have a rib spacing greater than 25 mm.
- (4)
- The wing of the waterstop serves as a part that is embedded in the concrete to provide fixation. The thicker the wing, the greater the deformation stress. To avoid excessive deformation stress and reduce the risk of tearing or puncturing the waterstop, it is recommended to have a wing thickness of 4–10 mm. Moreover, the wing contributes to the leakage pathway, and a longer length of the wing enhances the waterproofing reliability of the waterstop. However, the wing cuts into the concrete, and the longer the flanges, the more severe the cutting effect on the concrete. The existing waterstop structure has difficulty reconciling the contradiction between the leakage pathway and the cutting effect, thus requiring the proposal of new waterstop structures to address this issue.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gong, C.; Wang, Y.; Peng, Y.; Ding, W.; Lei, M.; Da, Z.; Shi, C. Three-Dimensional Coupled Hydromechanical Analysis of Localized Joint Leakage in Segmental Tunnel Linings. Tunn. Undergr. Space Technol. 2022, 130, 104726. [Google Scholar] [CrossRef]
- Muhammad, N.Z.; Keyvanfar, A.; Majid, M.Z.A.; Shafaghat, A.; Mirza, J. Waterproof Performance of Concrete: A Critical Review on Implemented Approaches. Constr. Build. Mater. 2015, 101, 80–90. [Google Scholar] [CrossRef]
- Zhou, Z.Q.; Li, S.C.; Li, L.P.; Shi, S.S.; Xu, Z.H. An Optimal Classification Method for Risk Assessment of Water Inrush in Karst Tunnels Based on Grey System Theory. Geomech. Eng. 2015, 8, 631–647. [Google Scholar] [CrossRef]
- Sañudo, R.; Miranda, M.; García, C.; García-Sanchez, D. Drainage in Railways. Constr. Build. Mater. 2019, 210, 391–412. [Google Scholar] [CrossRef]
- Yuan, Y.; Jiang, X.; Lee, C.F. Tunnel Waterproofing Practices in China. Tunn. Undergr. Space Technol. 2000, 15, 227–233. [Google Scholar] [CrossRef]
- Peng, L.J. Existing Operational Railway Tunnel Water Leakage Causes and Remediation Technologies. In Advanced Materials Research; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2014; Volume 1004, pp. 1444–1449. [Google Scholar]
- Li, S.; Zhou, Z.; Li, L.; Xu, Z.; Zhang, Q.; Shi, S. Risk Assessment of Water Inrush in Karst Tunnels Based on Attribute Synthetic Evaluation System. Tunn. Undergr. Space Technol. 2013, 38, 50–58. [Google Scholar] [CrossRef]
- GB 18173.2-2014; Polymeric Waterproofing Materials Part 2: Waterstops. Standards Press of China: Beijing, China, 2014.
- DL/T 5215-2005; Technical Specification for Waterstops in Hydraulic Structures. China Electric Power Press: Beijing, China, 2005.
- TB/T 3360.2-2014; Waterproofing Materials for Railway Tunnels Part 2: Waterstops. China Railway Publishing House: Beijing, China, 2015.
- Luo, Y.; Feng, Z.; Liu, J.; He, B.; Guo, H. Research on Structure and Performance of Internal Rubber Waterstop. Railw. Eng. 2013, 93–96. [Google Scholar]
- Wang, W.; Luo, Y.; Kong, L.; Zhang, Y.; Chen, Y. Numerical Simulation and Experimental Study on Mechanical Properties of GINA Waterstop. Mod. Tunn. Technol. 2021, 58, 237–243. [Google Scholar] [CrossRef]
- Chen, E.; Chen, K.; Ma, C.; Xin, Y. Finite Element Analysis of Rubber Waterstop Belt under Stress State. World Rubber Ind. 2010, 37, 15–19. [Google Scholar]
- Lin, P.; Zhao, Z.; Fan, B.; Han, S.; Liu, G. Analysis of the Deformation Capacity and Size Optimization of Rubber Waterstop in the Deformation Joint of Utility Tunnel. Bull. Sci. Technol. 2020, 36, 57–63. [Google Scholar] [CrossRef]
- Meng, C.; Li, R.; Liu, J.; Xu, Y.; Li, J.; Hao, J. Research on Internally-Side Attached Rubber Waterstop Belt: Part I Pull-out Tests of Rubber Strip and Its Numerical Simulation. Water Power 2021, 47, 69–72+95. [Google Scholar]
- Li, R.; Meng, C.; Zhou, J.; Xu, Y.; Li, J.; Hao, J. Research on Interally-Side Attached Rubber Waterstop Belt: Part II Numerical Simulation on Waterstop Belt and Its Model Test. Water Power 2021, 47, 42–45. [Google Scholar]
- Zhang, H.; Yang, X.; Tang, Q.; Xu, D. A Robust Error Analysis of the OSC Method for a Multi-Term Fourth-Order Sub-Diffusion Equation. Comput. Math. Appl. 2022, 109, 180–190. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Tang, J. The OSC Solver for the Fourth-Order Sub-Diffusion Equation with Weakly Singular Solutions. Comput. Math. Appl. 2021, 82, 1–12. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Wang, W.; Zhang, H. A Predictor-Corrector Compact Difference Scheme for a Nonlinear Fractional Differential Equation. Fractal Fract. 2023, 7, 521. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, H.; Chu, D.; Feng, S.; Zhang, J.; Wu, H. Failure Mechanism Analysis and Optimization Analysis of Tunnel Joint Waterstop Considering Bonding and Extrusion. Appl. Sci. 2022, 12, 5737. [Google Scholar] [CrossRef]
- Ma, J.; Pei, H.; Zhu, H.; Shi, B.; Yin, J. A Review of Previous Studies on the Applications of Fiber Optic Sensing Technologies in Geotechnical Monitoring. Rock Mech. Bull. 2023, 2, 100021. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Gong, C. Hybrid Semantic Segmentation for Tunnel Lining Cracks Based on Swin Transformer and Convolutional Neural Network. Comput.-Aided Civ. Infrastruct. Eng. 2023. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, F.; Wei, X.; Yang, H.-Q.; Fu, S.; Huang, J.; Gao, L. Polynomial Chaos Surrogate and Bayesian Learning for Coupled Hydro-Mechanical Behavior of Soil Slope. Rock Mech. Bull. 2023, 2, 100023. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, D.; Wang, R.; Li, J.; Huang, Z. SBD-K-Medoids-Based Long-Term Settlement Analysis of Shield Tunnel. Transp. Geotech. 2023, 42, 101053. [Google Scholar] [CrossRef]
- Gu, G. Mechanical Analysis of Rubber Waterstop Belt and Plastic Waterstop Belt; Chinese Society of Hydroelectric Engineering: Beijing, China, 2004; pp. 399–406. [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. China Building Industry press: Beijing, China, 2015.
- Ponnamma, D.; Thomas, S. Origin of Nonlinear Viscoelasticity in Filled Rubbers: Theory and Practice. In Non-Linear Viscoelasticity of Rubber Composites and Nanocomposites: Influence of Filler Geometry and Size in Different Length Scales; Ponnamma, D., Thomas, S., Eds.; Springer-Verlag Berlin: Berlin, Germany, 2014; Volume 264, pp. 1–13. ISBN 978-3-319-08702-3. [Google Scholar]
- Yang, X.; Wu, L.; Zhang, H. A Space-Time Spectral Order Sinc-Collocation Method for the Fourth-Order Nonlocal Heat Model Arising in Viscoelasticity. Appl. Math. Comput. 2023, 457, 128192. [Google Scholar] [CrossRef]
- Tian, Q.; Yang, X.; Zhang, H.; Xu, D. An Implicit Robust Numerical Scheme with Graded Meshes for the Modified Burgers Model with Nonlocal Dynamic Properties. Comput. Appl. Math. 2023, 42, 246. [Google Scholar] [CrossRef]
- Peng, X.; Han, L.; Li, L. A Consistently Compressible Mooney-Rivlin Model for the Vulcanized Rubber Based on the Penn’s Experimental Data. Polym. Eng. Sci. 2021, 61, 2287–2294. [Google Scholar] [CrossRef]
- Destrade, M.; Dorfmann, L.; Saccomandi, G. The Ogden Model of Rubber Mechanics: 50 Years of Impact on Nonlinear Elasticity. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2022, 380, 20210332. [Google Scholar] [CrossRef]
- Gajewski, M.D.; Miecznikowski, M. Assessment of the Suitability of Elastomeric Bearings Modeling Using the Hyperelasticity and the Finite Element Method. Materials 2021, 14, 7665. [Google Scholar] [CrossRef] [PubMed]
- Hossain, M.; Steinmann, P. Modelling and Simulation of the Curing Process of Polymers by a Modified Formulation of the Arruda-Boyce Model. Arch. Mech. 2011, 63, 621–633. [Google Scholar]
- Yang, L.; Yang, L. Note on Gent’s Hyperelastic Model. Rubber Chem. Technol. 2018, 91, 296–301. [Google Scholar] [CrossRef]
- Kossa, A.; Valentine, M.T.T.; McMeeking, R.M.M. Analysis of the Compressible, Isotropic, Neo-Hookean Hyperelastic Model. Meccanica 2023, 58, 217–232. [Google Scholar] [CrossRef]
- Nguyen, H.-D.; Huang, S.-C. The Uniaxial Stress-Strain Relationship of Hyperelastic Material Models of Rubber Cracks in the Platens of Papermaking Machines Based on Nonlinear Strain and Stress Measurements with the Finite Element Method. Materials 2021, 14, 7534. [Google Scholar] [CrossRef] [PubMed]
- Rubin, M.B.; Ehret, A.E. An Invariant-Based Ogden-Type Model for Incompressible Isotropic Hyperelastic Materials. J. Elast. 2016, 125, 63–71. [Google Scholar] [CrossRef]
- Melly, S.K.; Liu, L.; Liu, Y.; Leng, J. Modified Yeoh Model with Improved Equibiaxial Loading Predictions. Acta Mech. 2022, 233, 437–453. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, S.; Li, L.; Fu, Y. An Evaluation of the Gent and Gent-Gent Material Models Using Inflation of a Plane Membrane. Int. J. Mech. Sci. 2018, 146, 39–48. [Google Scholar] [CrossRef]
- Gent, A.N. (Ed.) Engineering with Rubber: How to Design Rubber Components, 3rd ed.; Hanser Publishers: Munich, Germany; Cincinnati, OH, USA, 2012; ISBN 978-3-446-42764-8. [Google Scholar]
- XiaoXiang, Y.; MingWang, F.; XiuRong, W.; XiaoYing, L. Nonlinear Finite Element Analysis of Crack Growth at the Interface of Rubber-like Bimaterials. Sci. China Phys. Mech. Astron. 2011, 54, 1866–1874. [Google Scholar] [CrossRef]
- Gong, C.; Ding, W.; Soga, K.; Mosalam, K.M.; Tuo, Y. Sealant Behavior of Gasketed Segmental Joints in Shield Tunnels: An Experimental and Numerical Study. Tunn. Undergr. Space Technol. 2018, 77, 127–141. [Google Scholar] [CrossRef]
- Ouyang, W. Mechanical Test and Numerical Analysis of Elastic Gaskets of Shield Tunnels. Tunn. Constr. 2013, 33, 933–936. [Google Scholar]
- Lu, Z. A Simple Review for Cohesive Zone Models of Composite Interface and Their Applications. Chin. J. Solid Mech. 2015, 36, 85–94. [Google Scholar] [CrossRef]
- Zhuo, X.R.; Ma, A. Molecular Dynamics-Based Cohesive Zone Model for Mg/Mg17Al12Interface. Metals 2020, 10, 836. [Google Scholar] [CrossRef]
- Barthel, E. Adhesive Contact: A Few Comments on Cohesive Zone Models and Self-Consistency. J. Adhes. 2012, 88, 55–69. [Google Scholar] [CrossRef]
- Alfano, G. On the Influence of the Shape of the Interface Law on the Application of Cohesive-Zone Models. Compos. Sci. Technol. 2006, 66, 723–730. [Google Scholar] [CrossRef]
- Gong, C.; Kang, L.; Zhou, W.; Liu, L.; Lei, M. Tensile Performance Test Research of Hybrid Steel Fiber—Reinforced Self-Compacting Concrete. Materials 2023, 16, 1114. [Google Scholar] [CrossRef]
- Gong, C.; Kang, L.; Liu, L.; Lei, M.; Ding, W.; Yang, Z. A Novel Prediction Model of Packing Density for Single and Hybrid Steel Fiber-Aggregate Mixtures. Powder Technol. 2023, 418, 118295. [Google Scholar] [CrossRef]









| σc | σt | ||
|---|---|---|---|
| 14.070 | 0 | 2.030 | 0 |
| 20.100 | 0.000802 | 2.010 | 0.000028 |
| 14.637 | 0.002456 | 1.232 | 0.000149 |
| 10.073 | 0.004080 | 0.849 | 0.000257 |
| 7.501 | 0.005638 | 0.661 | 0.000359 |
| 5.931 | 0.007162 | 0.548 | 0.000458 |
| 4.890 | 0.008668 | 0.473 | 0.000556 |
| 4.153 | 0.010165 | 0.419 | 0.000653 |
| 3.607 | 0.011655 | 0.378 | 0.000749 |
| 3.186 | 0.013141 | 0.346 | 0.000846 |
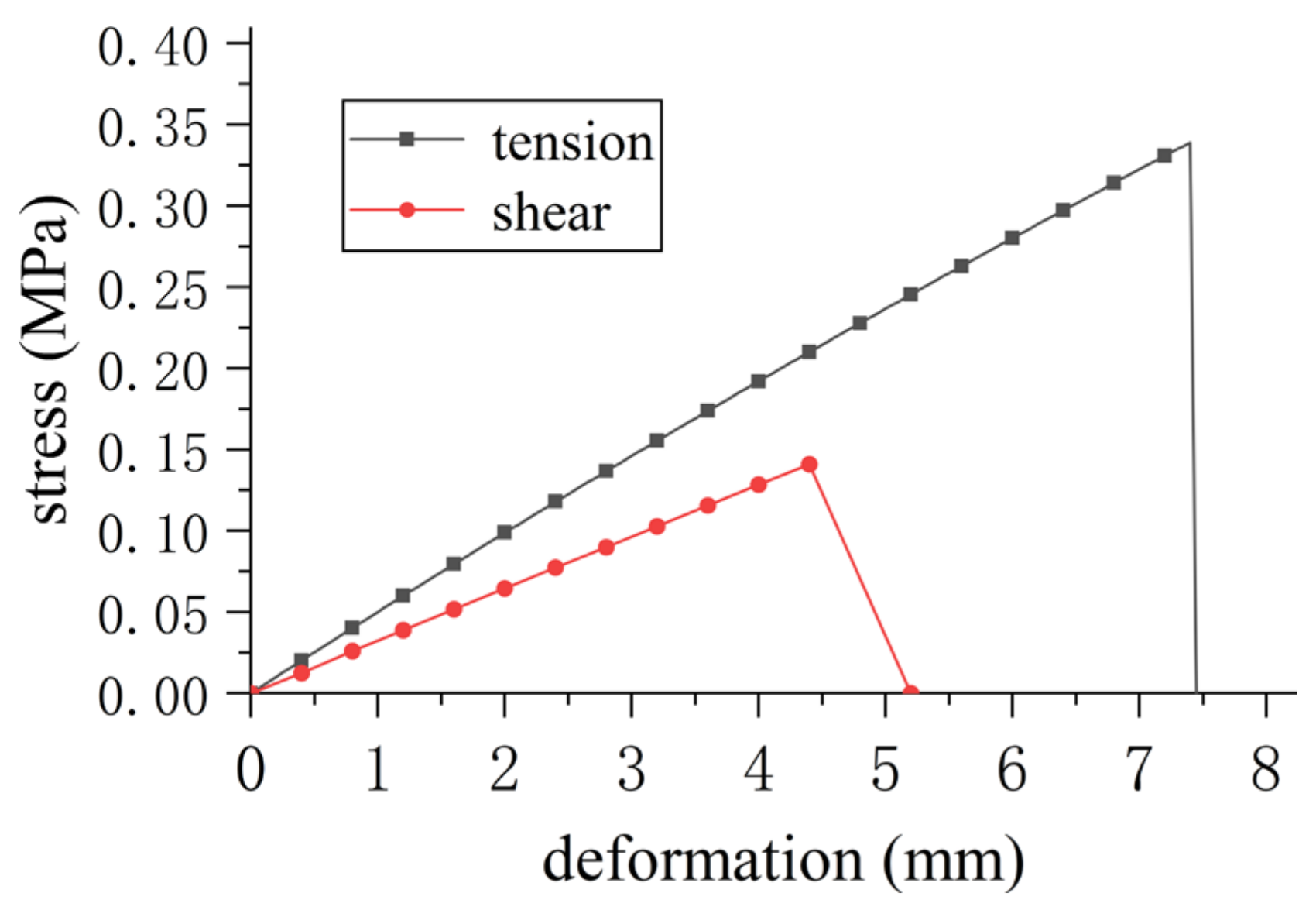
| Conditions | 1/MPa | 2/MPa | 3/MPa | Bonding Strength/MPa |
|---|---|---|---|---|
| Tensile specimen | 0.414 | 0.387 | 0.356 | 0.386 |
| Shear specimen | 0.162 | 0.141 | 0.149 | 0.151 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Wu, H.; Gong, C.; Huang, L. Numerical Investigation of Key Structural Parameters for Middle-Buried Rubber Waterstops. Mathematics 2023, 11, 3546. https://doi.org/10.3390/math11163546
Wu Y, Wu H, Gong C, Huang L. Numerical Investigation of Key Structural Parameters for Middle-Buried Rubber Waterstops. Mathematics. 2023; 11(16):3546. https://doi.org/10.3390/math11163546
Chicago/Turabian StyleWu, Yimin, Haiping Wu, Chenjie Gong, and Le Huang. 2023. "Numerical Investigation of Key Structural Parameters for Middle-Buried Rubber Waterstops" Mathematics 11, no. 16: 3546. https://doi.org/10.3390/math11163546
APA StyleWu, Y., Wu, H., Gong, C., & Huang, L. (2023). Numerical Investigation of Key Structural Parameters for Middle-Buried Rubber Waterstops. Mathematics, 11(16), 3546. https://doi.org/10.3390/math11163546






