Controlled Arrivals on the Retrial Queueing–Inventory System with an Essential Interruption and Emergency Vacationing Server
Abstract
:1. Introduction
1.1. Motivation
1.2. Research Gap
1.3. Contribution of the Model
- This model investigates the controlled arrival, essential interruption, and emergency vacation of a retrial queueing-inventory system.
- This model uses the matrix geometric method to determine the proposed system’s steady-state probability vector.
- The numerical illustration analyzed the system performance measures using parameter variation.
- The optimal cost of the model is obtained under parameter variation.
1.4. Layout of the Article
2. Model Description
2.1. Arrival Process
2.2. Controlled Arrival Process (F-Policy)
2.3. Retrial Process and Customer Impatience
2.4. Service Process
2.5. Replenishment
2.6. Essential Interruption
2.7. Emergency Vacation
3. Transition Analysis
3.1. Elucidation of Transitions
- Transitions due to the arrival of customers to the orbit.The arriving customers may choose to enter the orbit with probability p whenever the waiting space is prohibited upon their arrival.
- (a)
- Transitions due to the customers’ arrival to the waiting space.Customers can arrive at the waiting space in two ways: one is customers directly enter the waiting space when the waiting space is in an allowed state; another one is customers from orbit enter via retrials.
- (a)
- (b)
- (c)
- Transitions due to the successful retrials:
- (a)
- (b)
- (c)
- Transitions due to the service completion.Customers from the waiting space complete their service by attaining one unit of an item, which makes the transitions take the following forms:
- (a)
- (b)
- Transitions due to replenishment of inventory.
- (a)
- (b)
- Transitions due to the occurrence of essential interruptions.An essential interruption may occur at any time in between customer service.
- (a)
- (b)
- Transitions due to the essential interruption.The occurrence of essential interruption takes the server to an emergency vacation during the service.
- (a)
- (b)
- Transitions due to the setup time of the server.The server needs some setup time to allow the customers to enter the waiting space whenever the system reaches F after the service of the customers.
- (a)
- (b)
3.2. Construction of Block Matrix
4. Matrix Geometric Approximation
4.1. Stability Criterion
4.2. Steady-State Probability Vector
4.3. Choice of N
5. Performance Measures of the System
- Mean Inventory Level:Let be the mean inventory level of the retrial queueing–inventory system in the steady state, which is determined using the vector and the positive inventory level.
- Mean Reorder Rate:Suppose the system has items in its current inventory level. The inventory level is depleted by one as a consequence of the completion of the service; then, the inventory level becomes s, which triggers the system to place an order for Q according to the policy. Let denote the mean reorder level of the retrial queueing–inventory system in a steady state, defined using the vector .
- Mean Number of Customers in the Orbit:At least one customer should wait to enter the orbit. Let denote the mean number of customers in the orbit of the retrial queueing–inventory system in a steady state, defined using the vector .
- Mean Number of Customers in the Waiting Space:At least one customer should wait in the queue before receiving service. Let be the mean number of customers in the waiting space of the retrial queueing–inventory system in a steady state, defined using the vector .
- Average Waiting Time of Customers in the Waiting SpaceLet define the mean waiting time of the customers in the waiting space, which is attained using Little’s formulawhere is the effective arrival rate (Ross [34]).
- Mean Number of Customers Becoming Impatient:The unsuccessful retrial makes customers in the orbit impatient. Let define the mean number of customers who become impatient in the retrial queueing–inventory system in a steady state. It is defined using the vector .
- Overall Retrial Rate:The potential of an orbital customer to enter the queue is also known as the overall retrial rate . The vector defines the of the retrial queueing–inventory system in a steady state.
- Successful Retrial Rate:The likelihood of an orbital demand successfully entering the queue is the successful retrial rate . The vector defines the of the retrial queueing–inventory system in a steady state.
- Probability of the Occurrence of an Essential Interruption:The probability of the occurrence of an essential interruption during the service of the customer is defined using the vector .
- Probability of Time being Spent in an Emergency Vacation by the Server:The probability of time being spent by the server in an emergency vacation , which is caused by the occurrence of an essential interruption, is defined using the vector .
6. Numerical Illustration
- Exponential
- Hyper Exponential (HEX)
- Erlang
- Negative Correlation (NC)
- Positive Correlation (PC)
Results and Discussion
- Figure 1 depicts the effect of on with respect to different . That is, for each retrial rate , the mean number of customers in the system increases as the arrival rate increases and vice versa. This means that when there is more arrivals to the system lead to an increase in the number of customers in orbit because of the incorporated arrival control policy.
- The repercussions of and on are shown in Figure 2. As the service rate increases, the corresponding mean reorder rate decreases, for each arrival rate . In turn, as the arrival rate increases, the mean reorder rate also increases for each service rate because the reordering depends on the service rate and arrival rate.
- In Figure 3, we discussed the repercussion on by the rates and . The figure shows that for each reorder rate , the mean number of customers in the waiting space has slightly increased as the service rate increases. And also for each service rate, the mean number of customers in the waiting space decreases very slightly as the reorder rate increases.
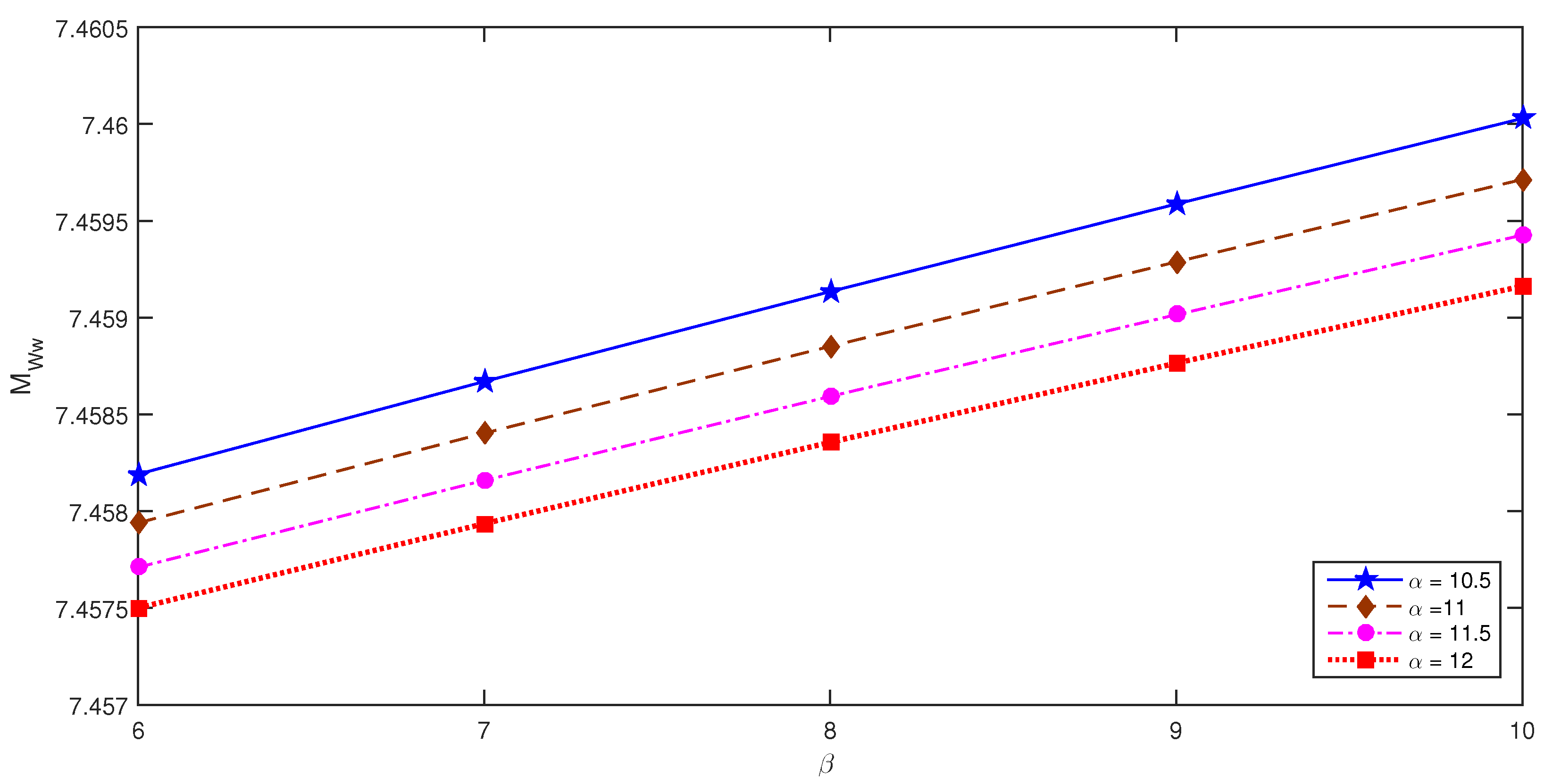
- We demonstrated the repercussion of and on graphically in Figure 4. The graph shows that as the parameter of the occurrence of an emergency situation increases, the probability of the server going on an emergency vacation increases for each value of the emergency vacation rate . Similarly, for each value of , the value of decreases as the value of increases.
- Figure 5 explains the repercussion on by the parameters and . When the retrial rate increases, the mean value of an impatient customer decreases for each service rate . That means the inter-retrial time becomes small when the rate increases, leading the customers to becoming less impatient while staying in orbit, and this can also depend on the number of customers in orbit. For each retrial rate, the mean impatient value very slightly decreases as the service rate increases.
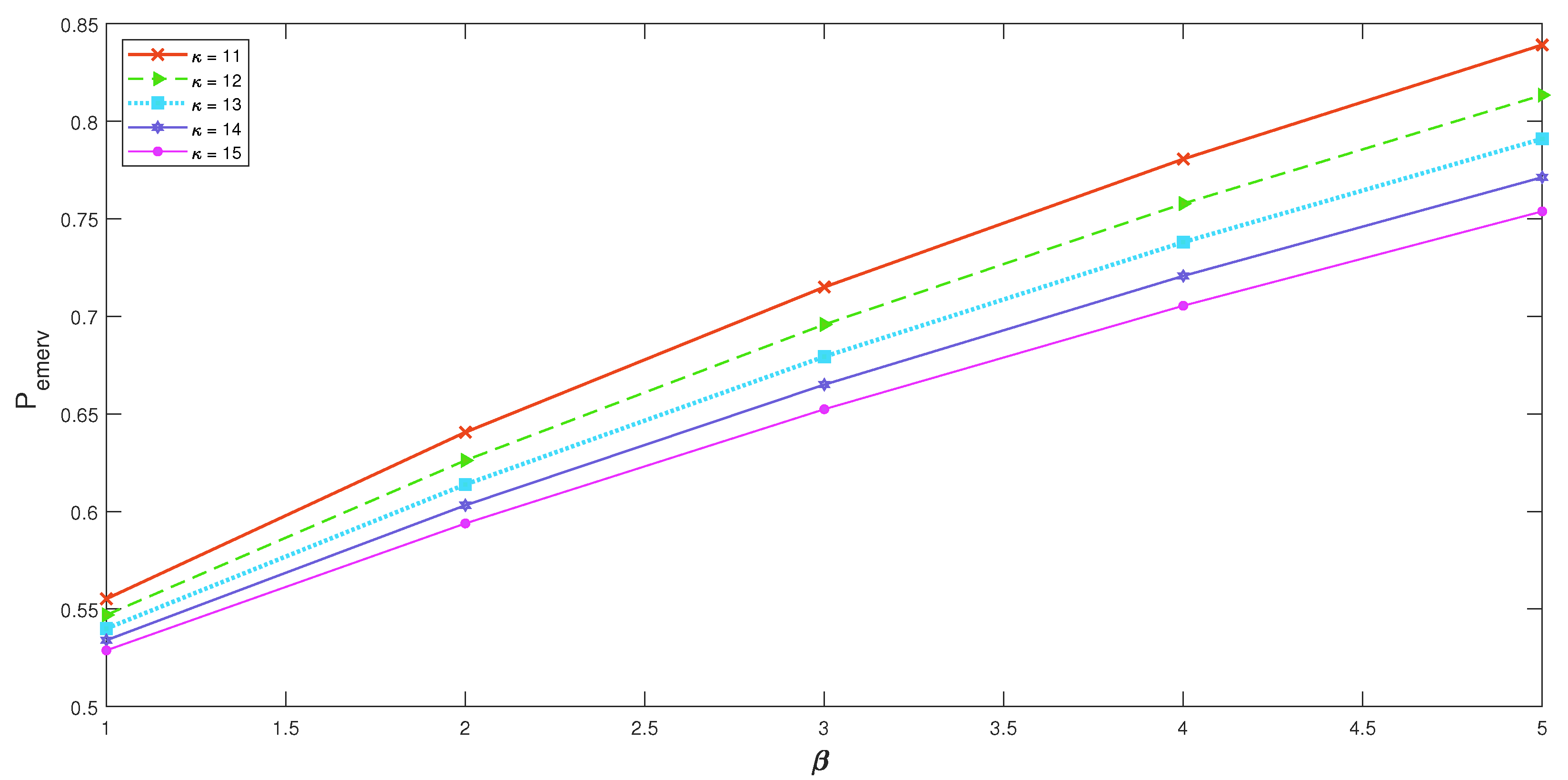
- Figure 6 explains the effect of on with respect to different values of . The graph shows that as the parameter of the arrival of essential interruptions increases, the average waiting time of the customers in the waiting space increases for each value of service rate . That means when the occurrence of an essential interruption increases, it increases the waiting time of the customers in the waiting space. Similarly, for each value of the occurrence of an essential interruption, the average waiting time of customers in the waiting space decreases slightly as the service rate increases.
7. Cost Analysis
- Ch: The holding cost per unit inventory per unit time;
- Cs: The ordering cost of an item per order;
- Cw: The waiting cost of customers in a waiting space per unit time;
- Co: The waiting cost of an orbiting customer per unit time;
- Cv: Cost per unit time spent by the server in emergency vacation;
- Cl: Cost of a lost customer from the orbit due to impatience.
8. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anbazhagan, N.; Joshi, G.P.; Suganya, R.; Amutha, S.; Vinitha, V.; Shrestha, B. Queueing-Inventory System for Two Commodities with Optional Demands of Customers and MAP Arrivals. Mathematics 2022, 10, 1801. [Google Scholar] [CrossRef]
- Jeganathan, K.; Selvakumar, S.; Saravanan, S.; Anbazhagan, N.; Amutha, S.; Cho, W.; Joshi, G.P.; Ryoo, J. Performance of Stochastic Inventory System with a Fresh Item, Returned Item, Refurbished Item, and Multi-Class Customers. Mathematics 2022, 10, 1137. [Google Scholar] [CrossRef]
- Samanta, S.K.; Isotupa, K.S.; Verma, A. Continuous review (s, Q) inventory system at a service facility with positive order lead times. Ann. Oper. Res. 2023. [Google Scholar] [CrossRef]
- Gupta, S.M. Interrelationship between controlling arrival and service in queueing systems. Comput. Oper. Res. 1995, 22, 1005–1014. [Google Scholar] [CrossRef]
- Wang, K.H.; Yang, D.Y. Controlling arrivals for a queueing system with an unreliable server: Newton-Quasi method. Appl. Math. Comput. 2009, 213, 92–101. [Google Scholar] [CrossRef]
- Yang, D.Y.; Wang, K.H.; Wu, C.H. Optimization and sensitivity analysis of controlling arrivals in the queueing system with single working vacation. J. Comput. Appl. Math. 2010, 234, 545–556. [Google Scholar] [CrossRef]
- Chang, C.J.; Chang, F.M.; Ke, J.C. Economic application in a Bernoulli F-policy queueing system with server breakdown. Int. J. Prod. Res. 2014, 52, 743–756. [Google Scholar] [CrossRef]
- Chang, C.J.; Ke, J.C.; Huang, H.I. The optimal management of a queueing system with controlling arrivals. J. Chin. Inst. Eng. 2011, 28, 226–236. [Google Scholar] [CrossRef]
- Jain, M.; Sanga, S.S. State dependent queueing models under admission control F-policy: A survey. J. Ambient Intell. Humaniz. Comput. 2020, 11, 3873–3891. [Google Scholar] [CrossRef]
- Ke, J.C.; Chang, C.J.; Chang, F.M. Controlling arrivals for a Markovian queueing system with a second optional service. Int. J. Ind. Eng. 2010, 17, 48–57. [Google Scholar]
- Jain, M.; Shekhar, C.; Shukla, S. Queueing analysis of machine repair problem with controlled rates and working vacation under F-policy. Proc. Natl. Acad. Sci. India Phys. Sci. 2016, 86, 21–31. [Google Scholar] [CrossRef]
- Nithya, N.; Anbazhagan, N.; Koushick, B.; Amutha, S.; Jeganathan, K. Working Vacation in Queueing-Stock System with Delusive Server. Glob. Stoch. Anal. 2021, 8, 61–80. [Google Scholar]
- Rani, S.; Jain, M.; Meena, R.K. Queueing modeling and optimization of a fault-tolerant system with reboot, recovery, and vacationing server operating under admission control policy. Math. Comput. Simul. 2023, 209, 408–425. [Google Scholar] [CrossRef]
- Zhang, Y.; Yue, D.; Yue, W. A queueing-inventory system with random order size policy and server vacations. Ann. Oper. Res. 2022, 310, 595–620. [Google Scholar] [CrossRef]
- Shekhar, C.; Varshney, S.; Kumar, A. Optimal control of a service system with emergency vacation using bat algorithm. J. Comput. Appl. Math. 2020, 364, 112332. [Google Scholar] [CrossRef]
- Ayyappan, G.; Thamizhselvi, P. Transient Analysis of M[X1],M[X2]/G1,G2/1 Retrial Queueing System with Priority Services, Working Vacations and Vacation Interruption, Emergency Vacation, Negative Arrival and Delayed Repair. Int. J. Comput. Math. 2018, 4, 1–35. [Google Scholar]
- Ayyappan, G.; Udayageetha, J. Retrial Queueing System with Priority Services, Working Breakdown, Non-Persistent Customers, Modified Bernoulli Vacation, Emergency Vacation and Repair. Int. J. Stat. Syst. 2018, 13, 23–39. [Google Scholar]
- Vaishnawi, M.; Upadhyaya, S.; Kulshrestha, R. Optimal Cost Analysis for Discrete-Time Recurrent Queue with Bernoulli Feedback and Emergency Vacation. Int. J. Comput. Math. 2022, 8, 1–31. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Nair, S.S.; Narayanan, V.C. An inventory model with server interruptions and retrials. Oper. Res. 2012, 12, 151–171. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Nair, S.S.; Narayanan, V.C. Production inventory with service time and interruptions. Int. J. Syst. Sci. 2015, 46, 1800–1816. [Google Scholar] [CrossRef]
- Fiems, D.; Maertens, T.; Bruneel, H. Queueing systems with different types of server interruptions. Eur. J. Oper. Res. 2008, 188, 838–845. [Google Scholar] [CrossRef]
- Ke, J.C. The optimal control of an M/G/1 queueing system with server vacations, startup and breakdowns. Comput. Ind. Eng. 2003, 44, 567–579. [Google Scholar] [CrossRef]
- Wu, J.; Lian, Z. A single-server retrial G-queue with priority and unreliable server under Bernoulli vacation schedule. Comput. Ind. Eng. 2013, 64, 84–93. [Google Scholar] [CrossRef]
- Xu, J.; Hou, I.-H.; Gautam, N. Age of information for single user system with vacation server. IEEE Trans. Netw. Sci. Eng. 2022, 9, 11981214. [Google Scholar] [CrossRef]
- Anbazhagan, N. Stochastic Inventory System with Compliment Item and Retrial Customers. In Stochastic Processes and Models Operations Research; IGI Global: Hershey, PA, USA, 2016; pp. 148–164. [Google Scholar]
- Anbazhagan, N.; Jeganathan, K. Two-commodity Markovian inventory system with compliment and retrial demand. Brit. J. Math. Comput. Sci. 2013, 3, 115–134. [Google Scholar] [CrossRef] [PubMed]
- Melikov, A.Z.; Shahmaliyev, M.O. Queueing System M/M/1/∞ with Perishable Inventory and Repeated Customers. Autom. Remote 2019, 80, 53–65. [Google Scholar] [CrossRef]
- Al Hamadi, H.M.; Sangeetha, N.; Sivakumar, B. Optimal control of service parameter for a perishable inventory system maintained at service facility with impatient customers. Ann. Oper. Res. 2015, 233, 3–23. [Google Scholar] [CrossRef]
- Chakravarthy, S.R. Markovian arrival processes. In Wiley Encyclopedia of Operations Research and Management Science; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Neuts, M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach; Dover Publication: New York, NY, USA, 1994. [Google Scholar]
- Neuts, M.F.; Rao, B.M. Numerical investigation of a multiserver retrial model. Queueing Syst. 1990, 7, 169–189. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Krishnamoorthy, A.; Joshua, V.C. Analysis of a multi-server retrial queue with search of customers from the orbit. Perform. Eval. 2006, 63, 776–798. [Google Scholar] [CrossRef]
- Latouche, G.; Ramaswami, V. A Logarithmic Reduction Algorithm for Quasi-Birth-Death Processes. J. Appl. Probab. 1993, 30, 650–674. [Google Scholar] [CrossRef]
- Ross, S.M. Introduction to Probability Models; Harcourt Asia PTE Ltd.: Singapore, 2000. [Google Scholar]

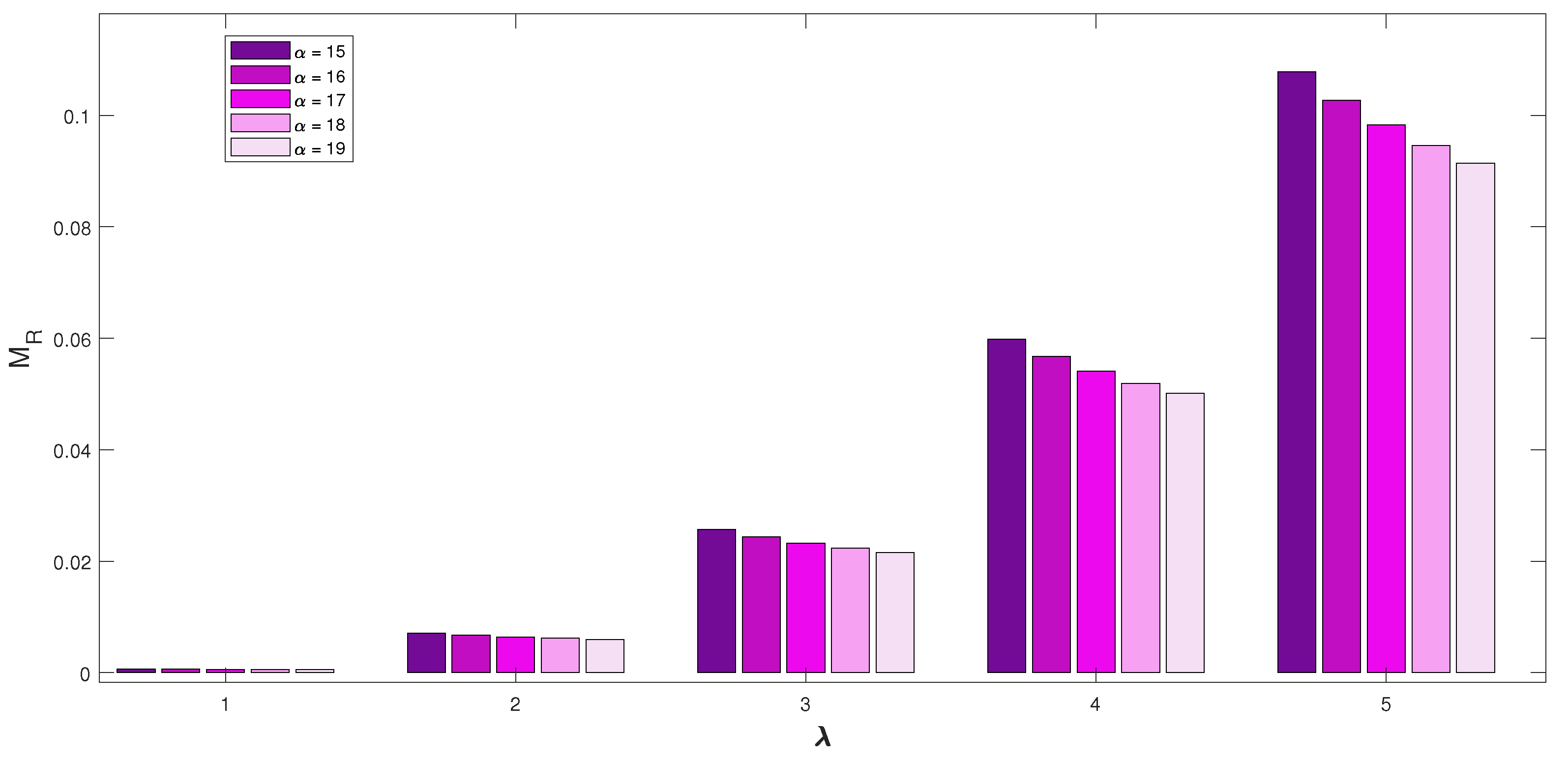
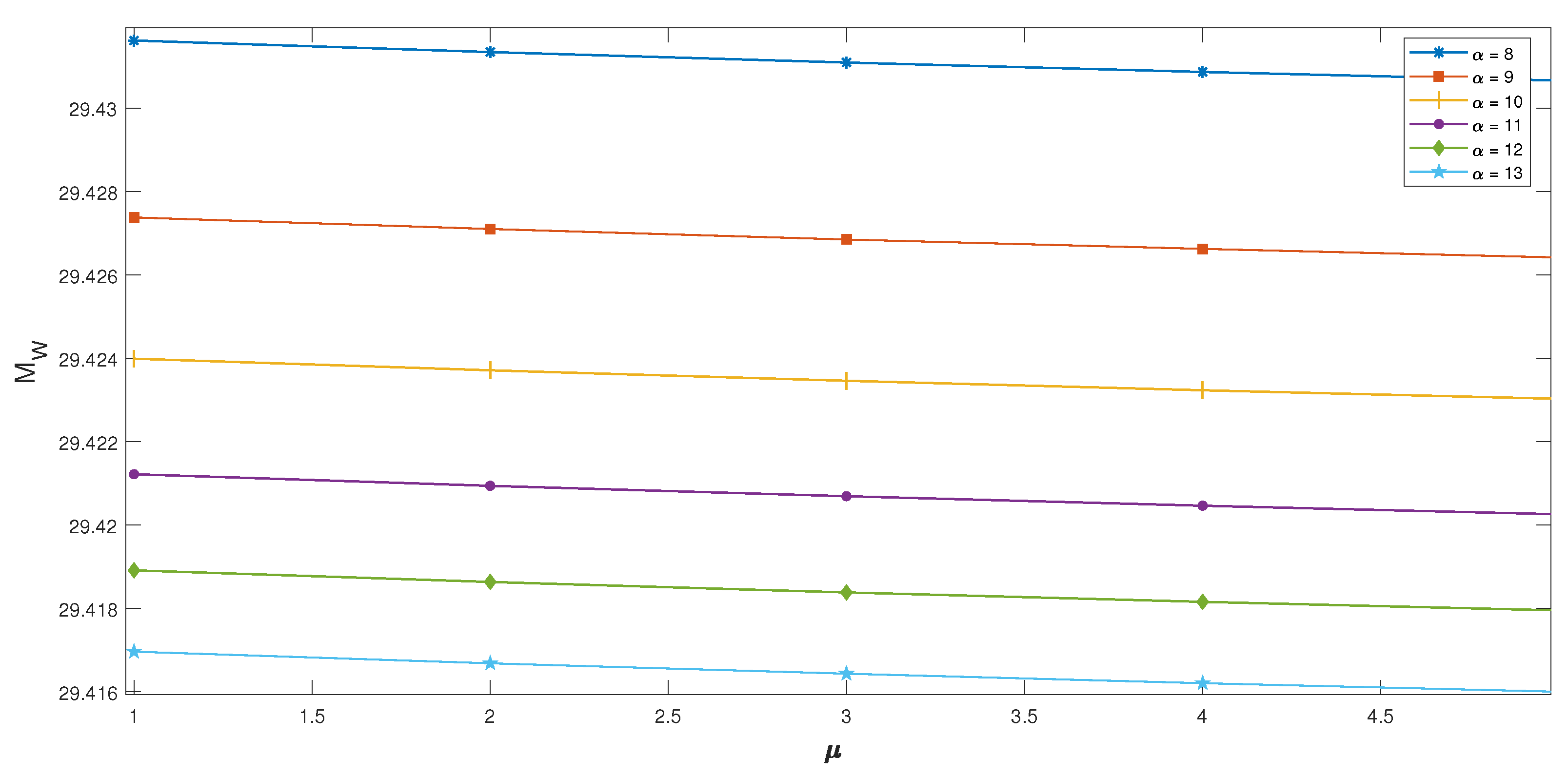

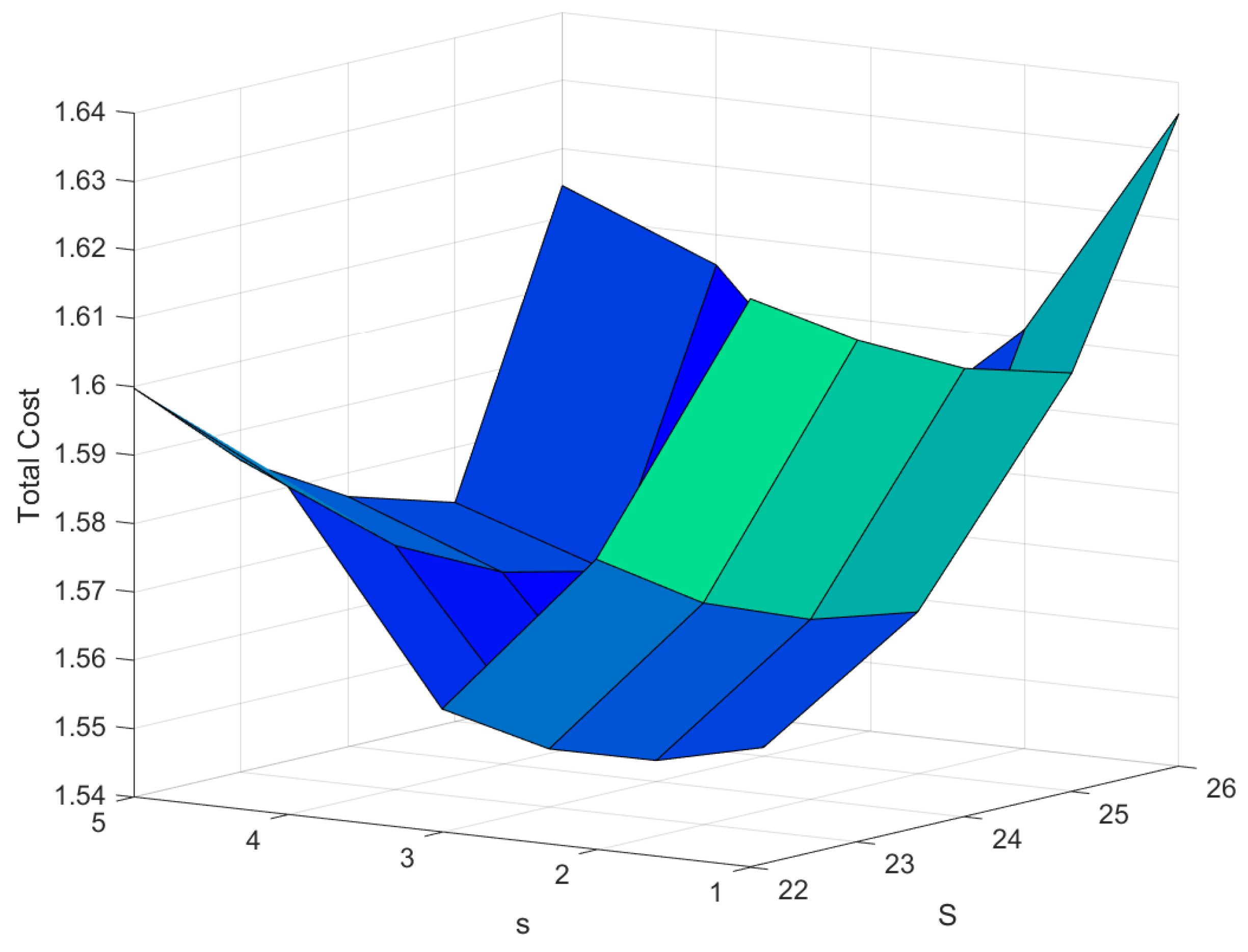
| S/s | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|
| 22 | 1.62314 | 1.58248 | 1.55802 | 1.58798 | 1.59981 |
| 23 | 1.61340 | 1.57238 | 1.54848 | 1.57566 | 1.58554 |
| 24 | 1.60556 | 1.56629 | 1.54310 | 1.56807 | 1.57655 |
| 25 | 1.60120 | 1.56368 | 1.54131 | 1.56452 | 1.57199 |
| 26 | 1.63544 | 1.60133 | 1.58172 | 1.60557 | 1.61463 |
| Arrivals | ||
|---|---|---|
| MAP with HEX | 25 | 6 |
| 1.51374 | ||
| MAP with Erlang | 25 | 6 |
| 1.52501 | ||
| MAP with PC | 25 | 6 |
| 1.44390 | ||
| MAP with NC | 25 | 6 |
| 1.44877 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nithya, N.; Anbazhagan, N.; Amutha, S.; Jeganathan, K.; Park, G.-C.; Joshi, G.P.; Cho, W. Controlled Arrivals on the Retrial Queueing–Inventory System with an Essential Interruption and Emergency Vacationing Server. Mathematics 2023, 11, 3560. https://doi.org/10.3390/math11163560
Nithya N, Anbazhagan N, Amutha S, Jeganathan K, Park G-C, Joshi GP, Cho W. Controlled Arrivals on the Retrial Queueing–Inventory System with an Essential Interruption and Emergency Vacationing Server. Mathematics. 2023; 11(16):3560. https://doi.org/10.3390/math11163560
Chicago/Turabian StyleNithya, N., N. Anbazhagan, S. Amutha, K. Jeganathan, Gi-Cheon Park, Gyanendra Prasad Joshi, and Woong Cho. 2023. "Controlled Arrivals on the Retrial Queueing–Inventory System with an Essential Interruption and Emergency Vacationing Server" Mathematics 11, no. 16: 3560. https://doi.org/10.3390/math11163560
APA StyleNithya, N., Anbazhagan, N., Amutha, S., Jeganathan, K., Park, G.-C., Joshi, G. P., & Cho, W. (2023). Controlled Arrivals on the Retrial Queueing–Inventory System with an Essential Interruption and Emergency Vacationing Server. Mathematics, 11(16), 3560. https://doi.org/10.3390/math11163560










