Survey of Point Cloud Registration Methods and New Statistical Approach
Abstract
:1. Introduction
1.1. Optical Rangefinder
1.2. 3D Point Cloud
2. A Survey of Methods
2.1. ICP Algorithm
2.1.1. ICP Algorithm Results
2.1.2. ICP Algorithm Problem
2.2. Normal Distribution Transform (NDT)
2.3. Feature Based Registration
2.4. IDC
2.5. pIC
2.6. Point-Based Probabilistic Registration
2.7. Gaussian Fields
2.8. Quadratic Patches
2.9. Likelihood-Field Matching
2.10. CRF Matching
2.11. Branch-and-Bound Registration
2.12. Registration Using Local Geometric Features
2.13. PoitnReg
2.14. The Automatic Mapping of Parametric Objects (Buildings) from Indoor Point Clouds
2.15. Basic Registration Methods Comparison
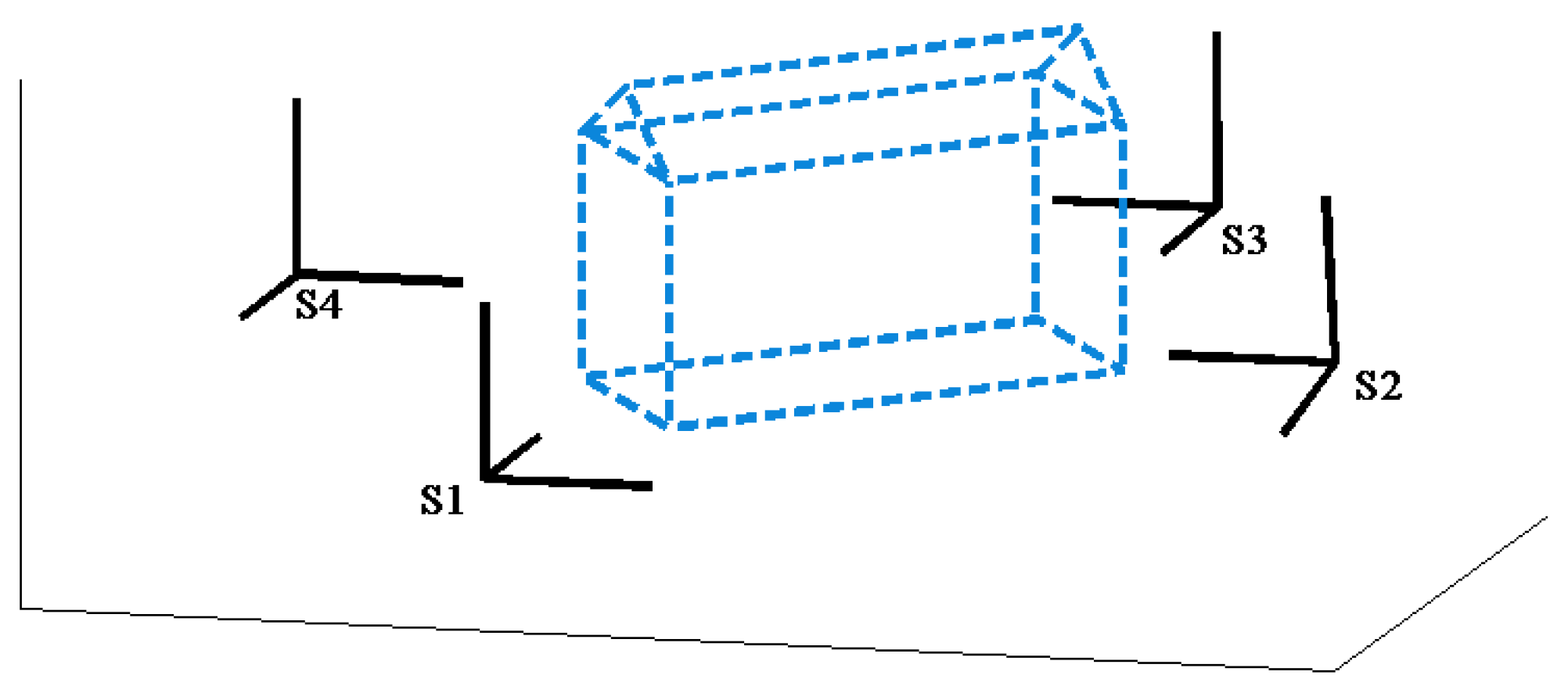
3. The Optimal Statistical Transformation Model Taking into Account Errors in Coordinate Systems
3.1. Model with Four Scans
3.2. Linearization of a Model with 4 Scans
3.3. The Estimates of Unknown Parameters in a Model with 4 Scans
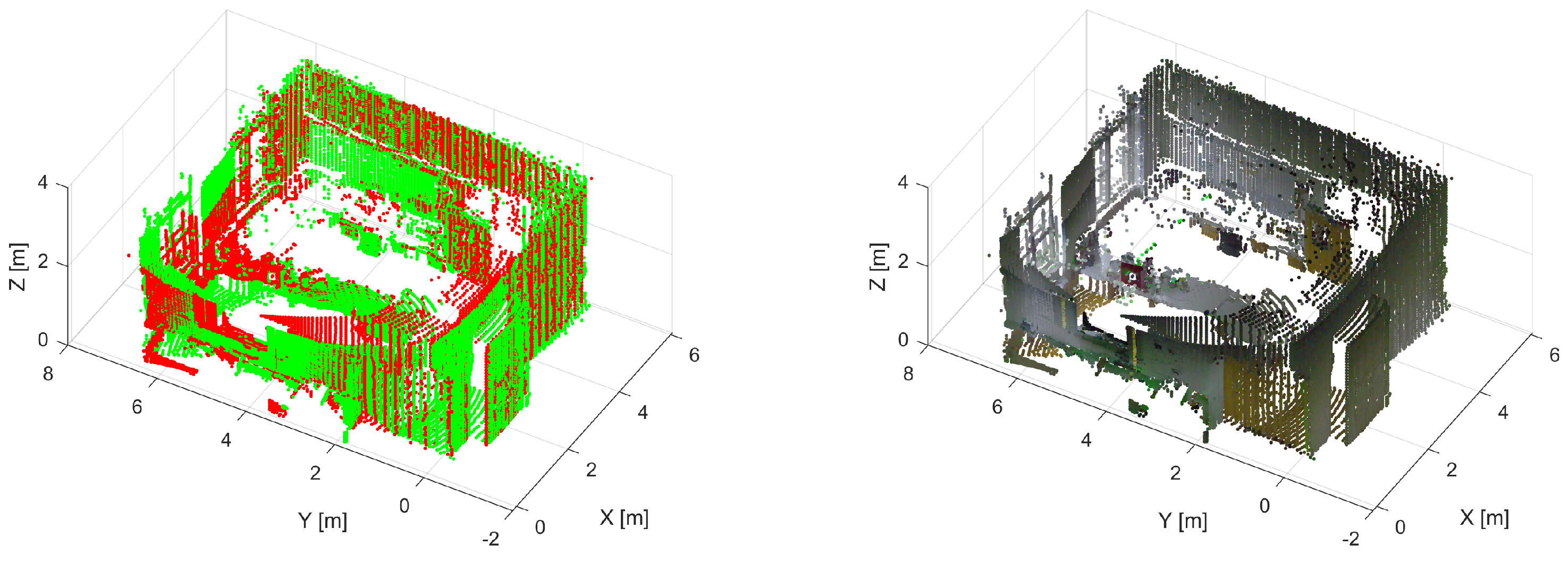
3.4. Numerical Study
4. Concluding Remarks
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| . |
References
- Goshtasby, A.A. Image Registration; Advances in Pattern Recognition; Springer: London, UK, 2012. [Google Scholar] [CrossRef]
- Pomerleau, F.; Colas, F.; Siegwart, R. A Review of Point Cloud Registration Algorithms for Mobile Robotics. Found. Trends Robot. 2015, 4, 1–104. [Google Scholar] [CrossRef]
- Cheng, L.; Chen, S.; Liu, X.; Xu, H.; Wu, Y.; Li, M.; Chen, Y. Registration of laser scanning point clouds: A review. Sensors. Multidisciplinary Digital Publishing Institute. Sensors 2018, 18, 1641. [Google Scholar] [CrossRef]
- Dong, Z.; Liang, F.; Yang, B.; Xu, Y.; Zang, Y.; Li, J.; Wang, Y.; Dai, W.; Fan, H.; Hyypp, J.; et al. Registration of large-scale terrestrial laser scanner point clouds: A review and benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 163, 327–342. [Google Scholar] [CrossRef]
- Kopacik, A.; Erdeeyi, J.; Kyrinovic, P. Engineering Surveys for Industry, Chapter Terrestrial Laser Scanning Systems; Springer: Berlin/Heidelberg, Germany, 2020; ISBN 9783030483081. [Google Scholar] [CrossRef]
- Chmelar, P.; Rejfek, L.; Nguyen, T.N.; Ha, D. Advanced Methods for Point Cloud Processing and Simplification. Appl. Sci. 2020, 10, 3340. [Google Scholar] [CrossRef]
- Chen, Y.; Gerard, M. Object modelling by registration of multiple range images. Image Vision Comput. 1991, 10, 145–155. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Nüchter, A. 3D Robotic Mapping: The Simultaneous Localization and Mapping Problem with Six Degrees of Freedom; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-354089883-2. ISSN 16107438. [Google Scholar] [CrossRef]
- Nüchter, A.; Elseberg, J.; Schneider, P.; Paulus, D. Study of parameterizations for the rigid body transformations of the scan registration problem. Comput. Vis. Image Underst. 2010, 114, 963–980. [Google Scholar] [CrossRef]
- Peter, B.; Wolfgang, S. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003; Volume 3, pp. 2743–2748. [Google Scholar]
- Magnusson, M.; Lilienthal, A.; Duckett, T. Scan registration for autonomous mining vehicles using 3D-NDT. J. Field Robot. 2007, 24, 803–827. [Google Scholar] [CrossRef]
- Magnusson, M. The Three-Dimensional Normal-Distributions Transform an Efficient Representation for Registration, Surface Analysis, and Loop Detection. In Studies in Technology; Örebro University: Örebro, Sweden, 2013. [Google Scholar]
- Beran, L.; Chmelar, P.; Rejfek, L. Navigation of Robotics Platform Using Advanced Image Processing Navigation Methods. In Proceedings of the VIPIMAGE (V. Eccomas Thematic Conference on Computional Vision and Medical Image Processing), Tenerife, Spain, 19–21 October 2015; ISBN 978-113802926-2. [Google Scholar]
- Beran, L.; Chmelar, P.; Rejfek, L. Navigation of Robotics Platform using Monocular Visual Odometry. In Proceedings of the Radioelektronika 25th International Conference, Pardubice, Czech Republic, 21–22 April 2015. [Google Scholar]
- Krajnik, T. Large-Scale Mobile Robot Navigation and Map Building. Ph.D. Thesis, Czech Technical University in Prague, Faculty of Electrical Engineering, Department of Cybernetics, Prague, Czech Republic, 2011. [Google Scholar]
- Lu, F.; Milios, E. Robot pose estimation in unknown environments by matching 2D range scans. J. Intell. Robot. Syst. 1997, 18, 249–275. [Google Scholar] [CrossRef]
- Montesano, L.; Minguez, J.; Montano, L. Probabilistic scan matching for motion estimation in unstructured environments. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2005. [Google Scholar] [CrossRef]
- Hähnel, D.; Burgard, W. Probabilistic Matching for 3D Scan Registration. In Proceedings of the VDI-Conference Robotik 2002 (Robotik), Forum am Schlosspark, Germany, 19–20 June 2002; Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=4f75beeeb9958a948492490f69c25f37165a3908 (accessed on 10 August 2023).
- Boughobel, F.; Muharrem, M.; Koschan, A.; Abidi, M. A new method for the registration of three-dimensional point-sets: The Gaussian Fields framework. Image Vis. Comput. 2010, 28, 124–137. [Google Scholar] [CrossRef]
- Boughorbel, F.; Koschan, A.; Abidi, B.; Abidi, M. Gaussian fields: A new criterion for 3D rigid registration. Pattern Recognit. 2004, 37, 1567–1571. [Google Scholar] [CrossRef]
- Mitra, N.J.; Gelfand, N.; Pottmann, H.; Guibas, L. Registration of point cloud data from a geometric optimization perspective. In Proceedings of the Symposium on Geometry Processing, Nice, France, 8–10 July 2004; pp. 22–31. [Google Scholar] [CrossRef]
- Burguera, A.; Gonz lez, Y.; Oliver, G. The likelihood field approach to sonar scan matching. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2008; pp. 2977–2982. [Google Scholar] [CrossRef]
- Lafferty, J.; McCallum, A.; Pereira, F. Conditional randomfields: Probabilistic models for segmenting and labeling sequence data. In Proceedings of the Eighteenth International Conference on Machine Learning (ICML), San Francisco, CA, USA, 28 June–1 July 2001; ISBN 1-55860-778-1. [Google Scholar]
- Forsman, P.; Halme, A. Feature based registration of range images for mapping of natural outdoor environments. In Proceedings of the International Symposium on 3D Data Processing, Visualization, and Transmission (3DPVT), Washington, DC, USA, 14–16 June 2004. [Google Scholar] [CrossRef]
- Johnson, A.E. Spin Images: A Representation for 3-D Surface Matching. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 1997. [Google Scholar]
- Olsen, M.; Johnstone, E.; Kuester, F.; Driscoll, N.; Ashford, S. New Automated Point-Cloud Alignment for Ground-Based Light Detection and Ranging Data of Long Coastal Sections. J. Surv. Eng. 2011, 137, 14–25. [Google Scholar] [CrossRef]
- Ochmann, S.; Vock, R.; Wessel, R.; Klein, R. Automatic reconstruction of parametric building models from indoor point clouds. Comput. Graph. 2016, 54, 94–103. [Google Scholar] [CrossRef]
- Marek, J.; Rak, J.; Jetensky, P. Statistical solution of 3D transformation problem. In Computer Science Research Notes, CSRN 2503; Zapadoceska Univerzita v Plzni: Plzen, Czech Republic, 2015; pp. 85–90. ISBN 978-808694367-1. [Google Scholar]
- Kubacek, L. Statistical Theory of Geodetic Networks; VUGTK: Zdiby, Czech Republic, 2013. [Google Scholar]



| Algorithm | Based on (Points/Model) | Covarience Matrix | Important Requirements | Speed Processing | Computation Complexity |
|---|---|---|---|---|---|
| 3D ICP | points | is estimated | - | slow for large datasets | |
| 3D NDT | 3D normal distribution | is estimated | - | faster than ICP | |
| Feature based | search space features | depends on application | varied environment | fast—depends on selected feature | depends on selected descriptor |
| IDC | points | is estimated | - | faster than ICP | similar to ICP but not specified |
| pIC | points | is estimated | - | slow for large datasets | similar to ICP but not specified |
| Point-based probabilistic | Probability functions | ss estimated | - | faster than ICP | similar to ICP but not specified |
| Gaussian fields | Gaussian mixture | is estimated | - | faster than ICP | |
| Quadratic patches | Quadratic approximation | is estimated | - | faster than ICP | not specified |
| Likelihood-fields | Likelihood-fields | uses identity matrix | - | similar to NDT | not specified |
| CRF matching | Conditional random fields | uses log-likelihood function | make sense only in 2D | slow for large datasets | in current scan, in reference scan |
| Branch and bound | Rotation symmetric features | is necessary, get from sensors | make sense only in 2D | not specified | not specified |
| Local geometric features | Local geometric features | Is estimated | - | Depending on used algorithm | Depending on used algorithm |
| PointReg | points | is necessary | only consistent object, moving has to be eliminated | slow due to user interaction | not specified |
| Algorithm | Precision | Advantages | Necessity of Human Intervention | Suitable Application | Origin |
|---|---|---|---|---|---|
| 3D ICP | good - depens on input data | precise with suitable data | initial parameters setup | precise 3D point clouds | 1992 |
| 3D NDT | good with suitable settings | space modeling, using of less accurate data | initial parameters setup | various input data | 2007 |
| Feature based | good, depens on environment | working with camera images | initial parameters setup | robotic navigation | 1998, 2006 (real time) |
| IDC | more robust, less precision than ICP | robustnes for bigger initial pose | initial parameters setup | similar to ICP | 1994 |
| pIC | better accuracy, robustness and convergence than ICP and IDC | incorporates sensors quality and noise | initial parameters setup | similar to ICP | 2005 |
| Point-based probabil | better than ICP | scans treating as probability function | initial parameters setup | large 3D scans | 2002 |
| Gaussian fields | good with suitable settings | similar to 3D NDT | initial parameters setup | various input data | 2004 |
| Quadratic patches | good with suitable settings | similar to 3D NDT | initial parameters setup | various input data | 2004 |
| Likelihood-fields | similar to NDT | possiblity to extend scans to get more points | initial parameters setup | various input data | 2008 |
| CRF matching | good with suitable settings | using od different user-features, robust to initial pose error | initial parameters setup | only for 2D scans | 2001 |
| Branch and bound | not specifed, dependent on set of common symetric features | using on highly unstructured environments | initial parameters setup | natural outdoor environment | 2004 |
| Local geometric feat | good depending on input data | matching local surfaces | initial parameters setup | point clouds wit varied objects | 1997 |
| PointReg | low RMS with the suitable settings and data handling | good with good data handling | manual | pitfalls 3D range scans | 2011 |
| Y | Y | Y | Y | Y | Y | Y | Y |
|---|---|---|---|---|---|---|---|
| 629.1793 | 629.0871 | 521.6030 | 533.7651 | −457.5236 | −446.6342 | 208.9794 | 223.0744 |
| 84.1583 | 84.0498 | −464.5526 | −469.4856 | −258.9134 | −265.6701 | 702.7168 | 691.0423 |
| 15.1976 | 4.0980 | 4.0980 | 16.6208 | 26.6208 | 17.8997 | 22.8997 | 30.1976 |
| 626.6654 | 638.7188 | 532.2563 | 536.3855 | −451.5327 | −445.1702 | 209.2158 | 218.5299 |
| 87.9686 | 90.5740 | −468.8736 | −462.9402 | −262.6306 | −263.4124 | 700.0364 | 690.6115 |
| 3.5058 | 7.8426 | 7.8426 | 7.7437 | 17.7437 | 12.0001 | 17.0001 | 18.5058 |
| 622.4489 | 640.0699 | 533.7651 | 536.7300 | −450.7452 | −444.5112 | 209.3221 | 210.9074 |
| 94.3597 | 91.4826 | −469.4856 | −462.0798 | −263.1193 | −262.3962 | 698.8299 | 689.8890 |
| 4.0666 | 5.5998 | 5.5998 | 3.3267 | 13.3267 | 14.6452 | 19.6452 | 19.0666 |
| 622.0117 | 536.5612 | −451.1310 | −443.3154 | 209.5151 | 210.1170 | ||
| 95.0224 | −462.5013 | −262.8799 | −260.5522 | 696.6406 | 689.8140 | ||
| 3.0727 | 16.2879 | 26.2879 | 17.3570 | 22.3570 | 18.0727 | ||
| 538.5282 | −446.6342 | −445.0099 | 209.2416 | ||||
| −457.5883 | −265.6701 | −263.1652 | 699.7429 | ||||
| 17.6355 | 27.6355 | 20.7081 | 25.7081 | ||||
| −439.5869 | 210.1170 | ||||||
| −254.8022 | 689.8140 | ||||||
| 14.7198 | 19.7198 | ||||||
| 629.2236 | 0.0134 | 629.2727 | 0.0151 | 639.9965 | 0.0254 | 632.7031 | 0.1205 |
| 84.0842 | 0.0162 | 84.1765 | 0.0108 | 91.4590 | 0.0235 | 102.1926 | 0.1057 |
| 14.8946 | 0.0180 | 4.2584 | 0.0149 | 16.7208 | 0.0232 | 7.9921 | 0.1125 |
| 626.7046 | 0.0121 | 638.7539 | 0.0133 | 636.1058 | 0.0753 | 630.6615 | 0.0852 |
| 87.9179 | 0.0107 | 90.4175 | 0.0154 | 97.5176 | 0.0541 | 100.7179 | 0.0816 |
| 3.4601 | 0.0155 | 7.8524 | 0.0151 | 7.5773 | 0.0429 | 2.0002 | 0.0344 |
| 622.3238 | 0.0142 | 640.0670 | 0.0180 | 635.6114 | 0.0907 | 629.4778 | 0.0233 |
| 94.3276 | 0.0139 | 91.4741 | 0.0189 | 97.8561 | 0.0687 | 99.8918 | 0.0422 |
| 4.1908 | 0.0188 | 5.6040 | 0.0201 | 3.2677 | 0.0789 | 4.6397 | 0.0179 |
| 621.9169 | 0.0190 | 635.8859 | 0.0595 | 627.7632 | 0.0912 | ||
| 95.0236 | 0.0224 | 97.9292 | 0.0614 | 98.7844 | 0.0894 | ||
| 2.9661 | 0.0256 | 16.2601 | 0.0209 | 7.4481 | 0.0796 | ||
| 632.8328 | 0.1003 | 630.4326 | 0.0488 | ||||
| 102.1181 | 0.0982 | 100.3622 | 0.0198 | ||||
| 17.6777 | 0.1143 | 10.7676 | 0.0158 | ||||
| 622.0444 | 0.0129 | ||||||
| 94.8902 | 0.0164 | ||||||
| 4.7548 | 0.0246 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marek, J.; Chmelař, P. Survey of Point Cloud Registration Methods and New Statistical Approach. Mathematics 2023, 11, 3564. https://doi.org/10.3390/math11163564
Marek J, Chmelař P. Survey of Point Cloud Registration Methods and New Statistical Approach. Mathematics. 2023; 11(16):3564. https://doi.org/10.3390/math11163564
Chicago/Turabian StyleMarek, Jaroslav, and Pavel Chmelař. 2023. "Survey of Point Cloud Registration Methods and New Statistical Approach" Mathematics 11, no. 16: 3564. https://doi.org/10.3390/math11163564
APA StyleMarek, J., & Chmelař, P. (2023). Survey of Point Cloud Registration Methods and New Statistical Approach. Mathematics, 11(16), 3564. https://doi.org/10.3390/math11163564






