Robust Model Predictive Control for Two-DOF Flexible-Joint Manipulator System
Abstract
:1. Introduction
- By means of the LFT technique, the LFT uncertain system of the two-DOF FJMS is constructed, which takes into account the parameter uncertainties of the spring-stiffness coefficients;
- The norm of system disturbances to the performance output and the input–output constraints of the two-DOF FJMS are transformed into the LMIs via the theory of control and the full-block multiplier technique;
- The robust constrained moving-horizon controller is designed for this LFT uncertain system, which can improve the performance of the controlled system while ensuring that the input–output constraints of this system are satisfied.
2. Problem Statement
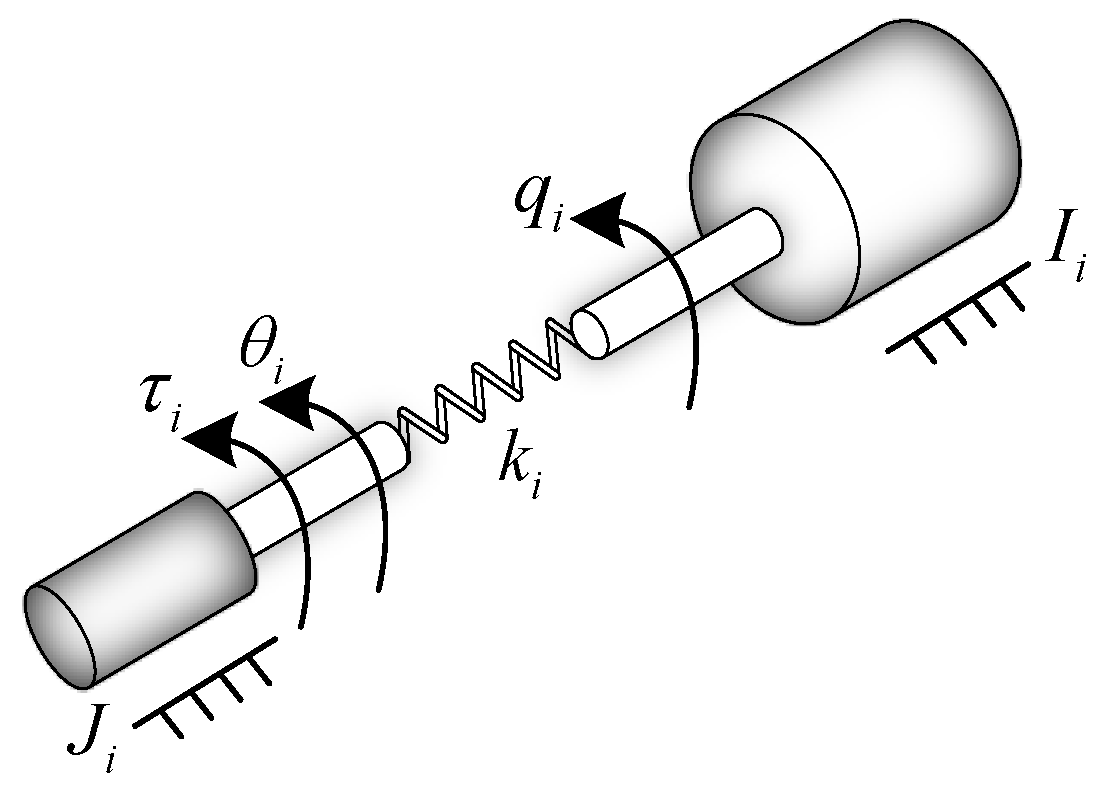
2.1. Dynamic Modeling of the Two-DOF FJMS
2.2. LFT Technique
2.3. State Transformation Procedure of the Two-DOF FJMS
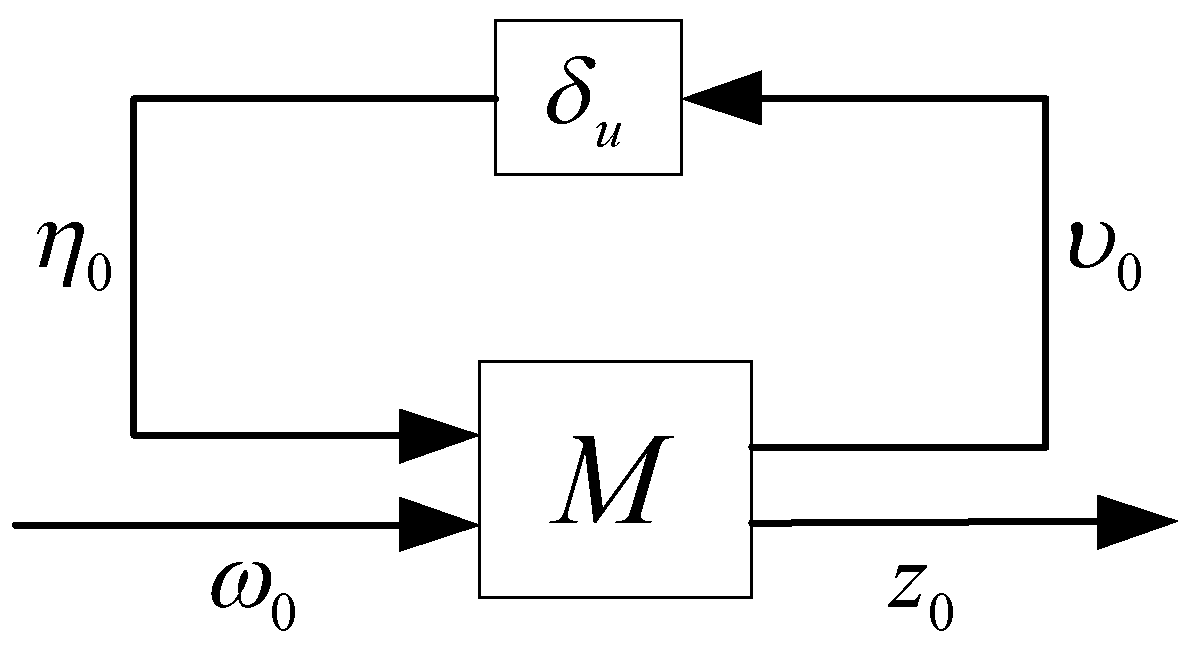
3. Analysis of the LFT Uncertain System
4. Robust Model Predictive Control with Constraints
4.1. Robust Constrained Control
4.2. Robust Constrained Moving-Horizon Control
5. Properties of the Closed-Loop System
- At every moment, the semi-definite programming (52) based on the state at the current moment has the results as , , , , and several multipliers;
- The performance optimization metricis bounded.
- Then, for all , the closed-loop controlled system under the action of would have the following properties:
- The constraints of the controlled system are all fulfilled;
- Under the perturbations of external limiting energy, the state of the system will converge to zero when ;
- The dissipation inequality is valid for any moment (), where ;
- The norm from the system perturbation to the performance output is always no greater than , where .
- The LMI (53) and LMI (54) are all feasible;
- The amplitude of the perturbations at any moment is not infinite;
- The performance optimization metric is bounded.
- Then, for all , the controlled system with the effect of the robust constrained moving-horizon controller would have the following properties:
- At every moment (), there is , and this relationship is established to symbolize that the constraint requirements of this controller are fulfilled;
- The last three properties of Theorem 1 are also present.
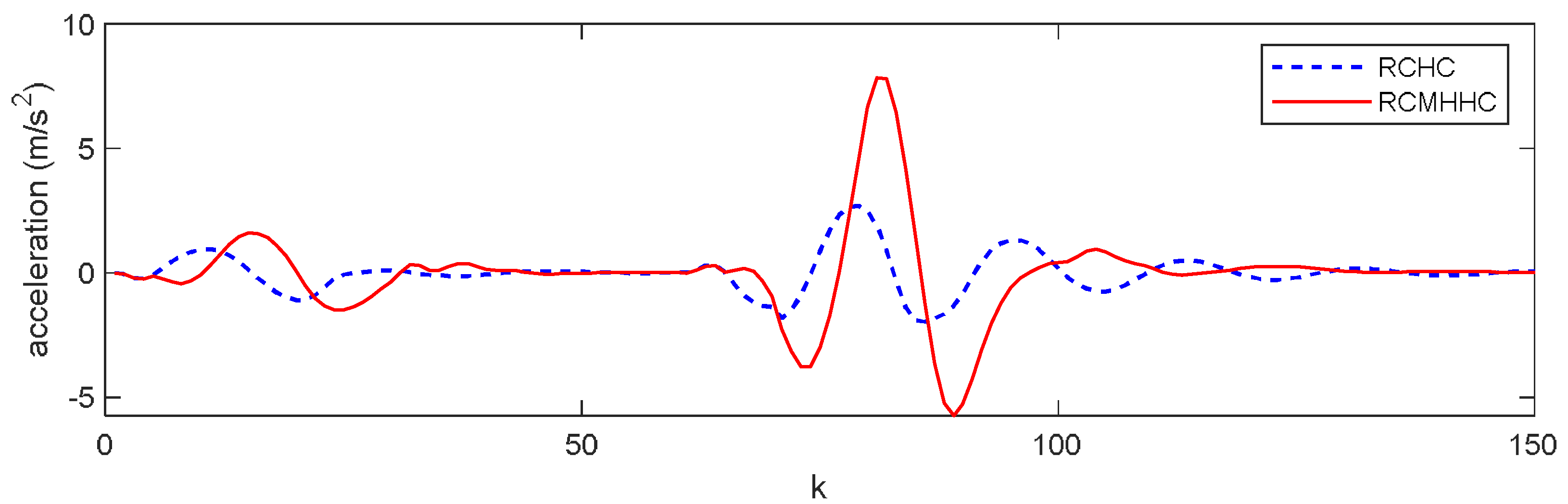
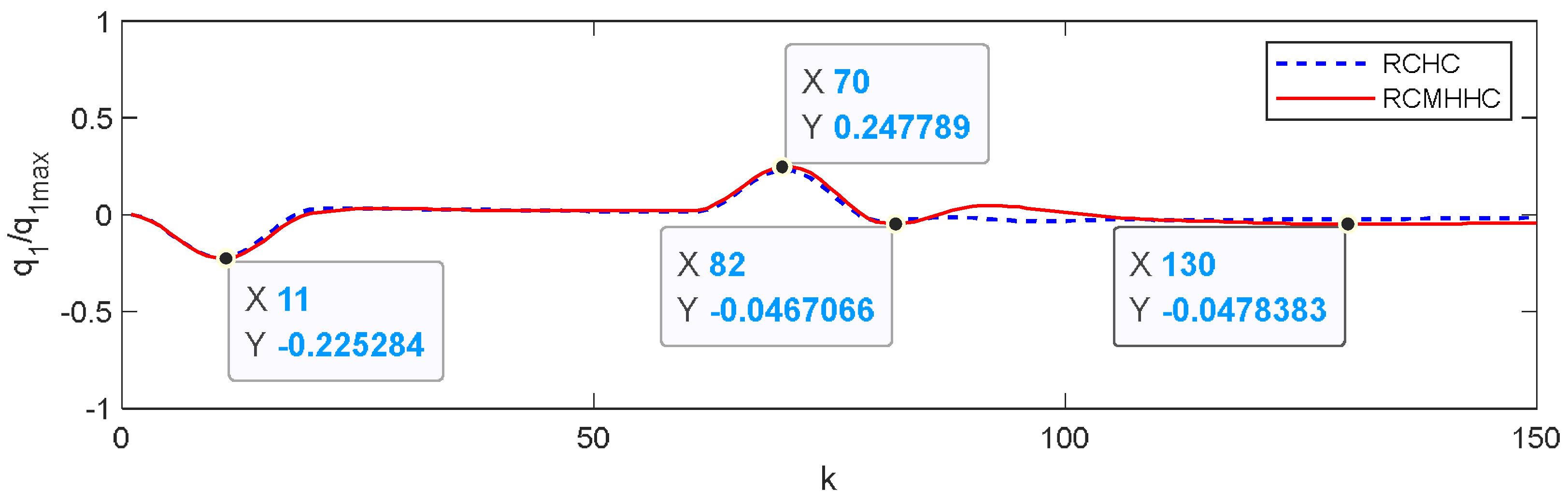
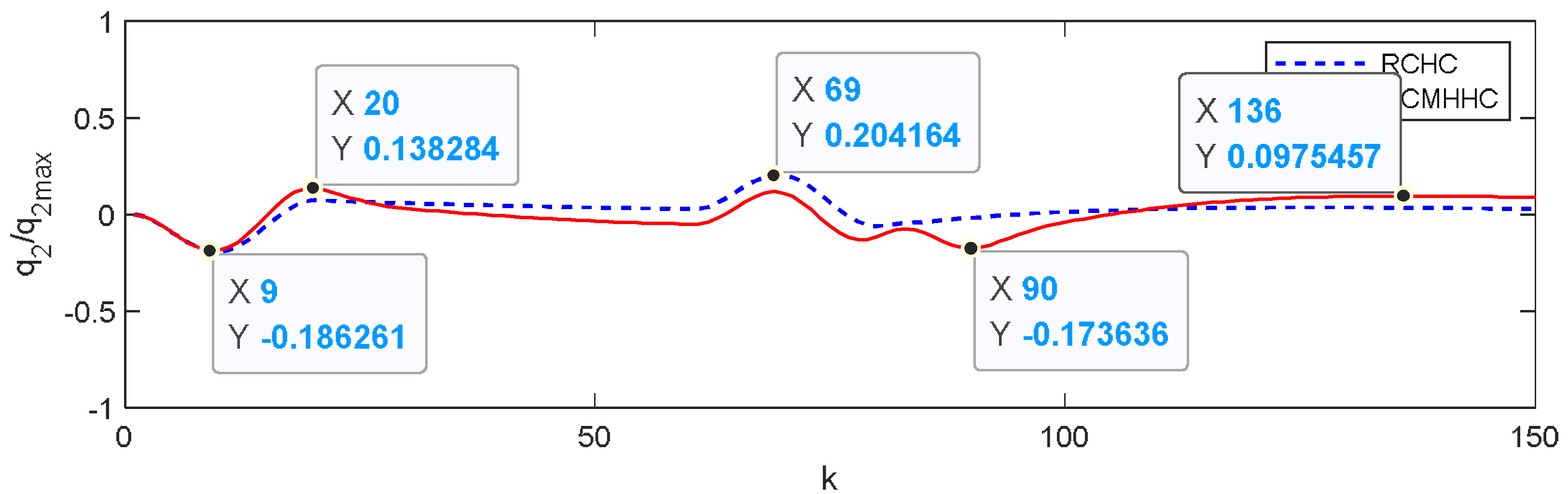
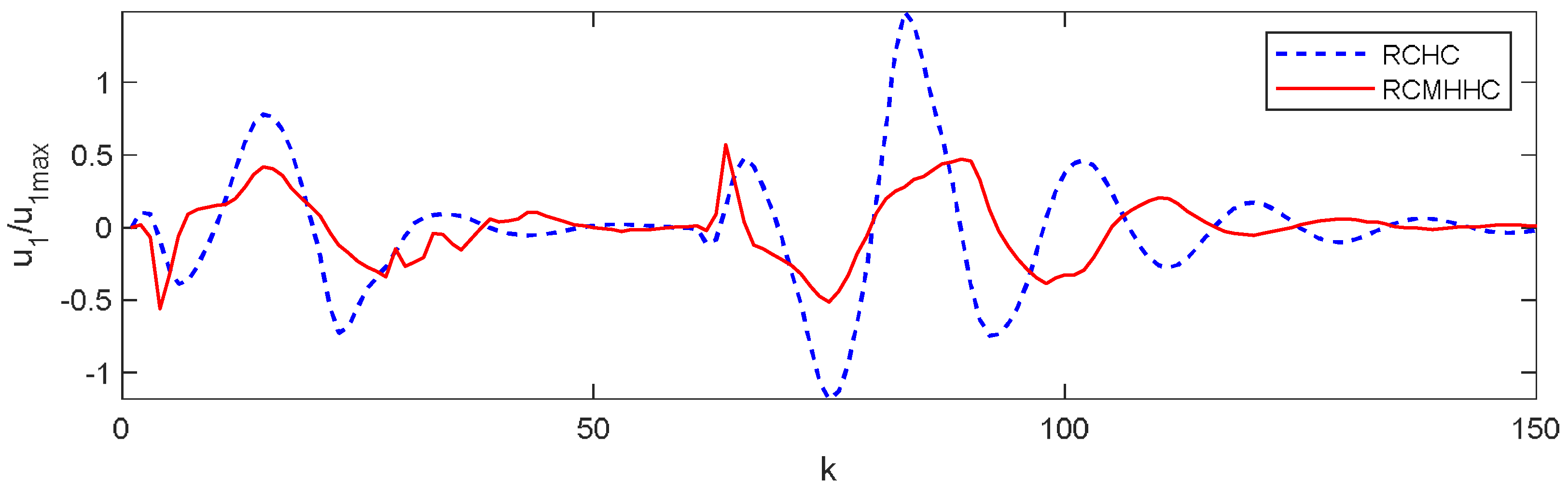
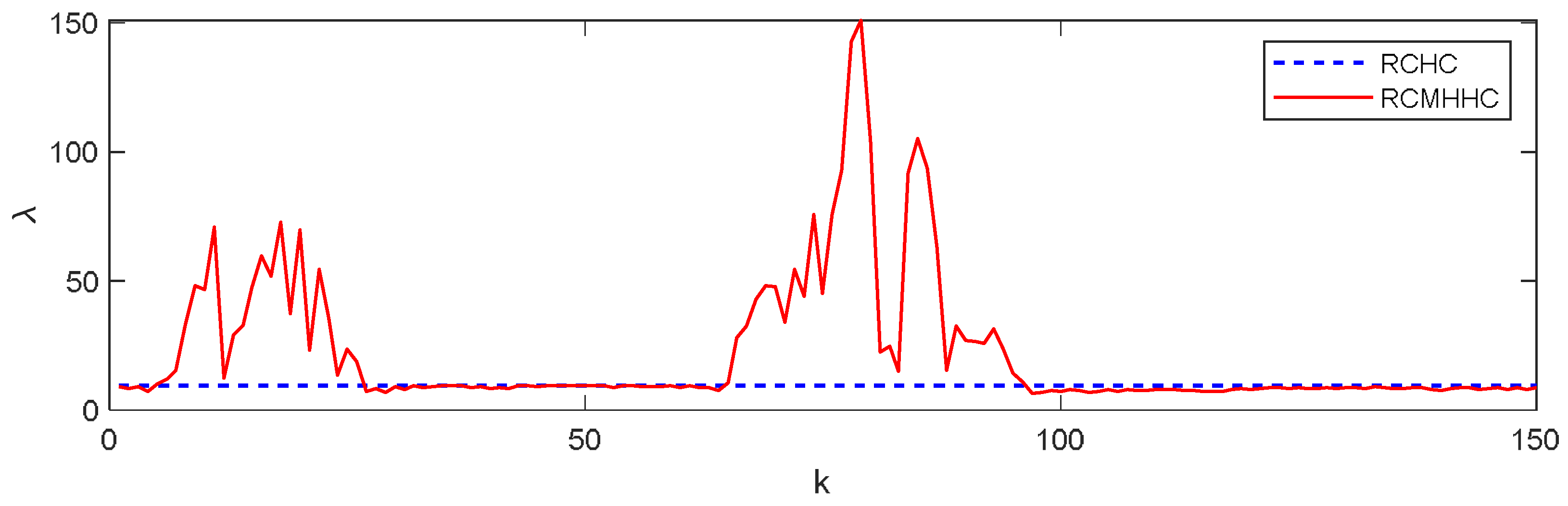
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.; Yang, X.; Xu, Z.; Zhang, W.; Yang, L.; Liu, X. An Adaptive Fault-Tolerant Control Method for Robot Manipulators. Int. J. Control Autom. Syst. 2021, 19, 3983–3995. [Google Scholar] [CrossRef]
- Phu, N.D.; Putov, V.V.; Su, C.T. Mathematical Models and Adaptive Control System of Rigid and Flexible 4-DOF Joint Robotic Manipulator with Executive Electric Drives. In Proceedings of the 2019 III International Conference on Control in Technical Systems (CTS), St. Petersburg, Russia, 30 October–1 November 2019. [Google Scholar]
- Naidu, D.S. Singular Perturbation Analysis of a Flexible Beam Used in Underwater Exploration. Int. J. Syst. Sci. 2011, 42, 183–194. [Google Scholar] [CrossRef]
- Nanos, K.; Papadopoulos, E.G. On the Dynamics and Control of Flexible Joint Space Manipulators. Control Eng. Pract. 2015, 45, 230–243. [Google Scholar] [CrossRef]
- Nubert, J.; Köhler, J.; Berenz, V.; Allgöwer, F.; Trimpe, S. Safe and Fast Tracking on a Robot Manipulator: Robust MPC and Neural Network Control. IEEE Robot. Autom. Lett. 2020, 5, 3050–3057. [Google Scholar] [CrossRef]
- Ahmadi, S.; Fateh, M.M. Control of Flexible Joint Robot Manipulators by Compensating Flexibility. Iran. J. Fuzzy Syst. 2018, 15, 57–71. [Google Scholar]
- Wei, J.; Cao, D.; Wang, L.; Huang, H.; Huang, W. Dynamic Modeling and Simulation for Flexible Spacecraft with Flexible Jointed Solar Panels. Int. J. Mech. Sci. 2017, 130, 558–570. [Google Scholar] [CrossRef]
- Zouari, L.; Abid, H.; Abid, M. Sliding Mode and PI Controllers for Uncertain Flexible Joint Manipulator. Int. J. Autom. Comput. 2015, 12, 117–124. [Google Scholar] [CrossRef]
- Fateh, M.M. Robust Control of Flexible-Joint Robots Using Voltage Control Strategy. Nonlinear Dyn. 2012, 67, 1525–1537. [Google Scholar] [CrossRef]
- Hassanzadeh, I.; Kharrati, H.; Bonab, J.R. Model Following Adaptive Control for a Robot with Flexible Joints. In Proceedings of the 2008 Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 4–7 May 2008. [Google Scholar]
- Korayem, M.H.; Shafei, A.M.; Doosthoseini, M.; Absalan, F.; Kadkhodaei, B. Theoretical and Experimental Investigation of Viscoelastic Serial Robotic Manipulators with Motors at the Joints Using Timoshenko Beam Theory and Gibbs-Appell Formulation. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2015, 230, 37–51. [Google Scholar] [CrossRef]
- Korayem, M.H.; Shafei, A.M.; Dehkordi, S.F. Systematic Modeling of a Chain of N-Flexible Link Manipulators Connected by Revolute–prismatic Joints Using Recursive Gibbs-Appell Formulation. Arch. Appl. Mech. 2014, 84, 187–206. [Google Scholar] [CrossRef]
- Marino, R.; Spong, M. Nonlinear Control Techniques for Flexible Joint Manipulators: A Single Link Case Study. In Proceedings of the 1986 IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 7–10 April 1986. [Google Scholar]
- Spong, M.W. Modeling and Control of Elastic Joint Robots. Math. Comput. Model. 1989, 12, 912. [Google Scholar] [CrossRef]
- Sun, L.; Yin, W.; Wang, M.; Liu, J. Position Control for Flexible Joint Robot Based on Online Gravity Compensation with Vibration Suppression. IEEE Trans. Ind. Electron. 2018, 65, 4840–4848. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, H.; Li, X.; Yu, H. Adaptive Command-Filtered Backstepping Control of Robot Arms with Compliant Actuators. IEEE Trans. Control Syst. Technol. 2018, 26, 1149–1156. [Google Scholar] [CrossRef]
- Rsetam, K.; Cao, Z.; Man, Z.; Mitrevska, M. Optimal Second Order Integral Sliding Mode Control for a Flexible Joint Robot Manipulator. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017. [Google Scholar]
- Qiu, B.; Guo, J.; Mao, M.; Tan, N. A Fuzzy-Enhanced Robust DZNN Model for Future Multi-Constrained Nonlinear Optimization with Robotic Manipulator Control. IEEE Trans. Fuzzy Syst. 2023, 1–13. [Google Scholar] [CrossRef]
- Xu, B.; Jiang, Q.; Ji, W.; Ding, S. An Improved Three-Vector-Based Model Predictive Current Control Method for Surface-mounted PMSM Drives. IEEE Trans. Transp. Electrif. 2022, 8, 4418–4430. [Google Scholar] [CrossRef]
- Kali, Y.; Saad, M.; Benjelloun, K.; Fatemi, A. Discrete-Time Second Order Sliding Mode with Time Delay Control for Uncertain Robot Manipulators. Robot. Auton. Syst. 2017, 94, 53–60. [Google Scholar] [CrossRef]
- Peng, Z.; Yan, W.; Huang, R.; Cheng, H.; Shi, K.; Ghosh, B.K. Event-Triggered Learning Robust Tracking Control of Robotic Systems with Unknown Uncertainties. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2540–2544. [Google Scholar] [CrossRef]
- Ma, L.; Mei, K.; Ding, S.; Pan, T. Design of Adaptive Fuzzy Fixed-Time HOSM Controller Subject to Asymmetric Output Constraints. IEEE Trans. Fuzzy Syst. 2023, 1–11. [Google Scholar] [CrossRef]
- Peng, Z.; Luo, R.; Hu, J.; Shi, K.; Ghosh, B.K. Distributed Optimal Tracking Control of Discrete-Time Multiagent Systems Via Event-Triggered Reinforcement Learning. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 3689–3700. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Higaki, S. Control of Flexible Joint Robot Manipulators Using a Combined Controller with Neural Network and Linear Regulator. J. Syst. Control Eng. 2011, 225, 798–806. [Google Scholar] [CrossRef]
- Yan, Z.; Lai, X.; Meng, Q.; Wu, M. A Novel Robust Control Method for Motion Control of Uncertain Single-Link Flexible-Joint Manipulator. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1671–1678. [Google Scholar] [CrossRef]
- Rsetam, K.; Cao, Z.; Man, Z. Cascaded-Extended-State-Observer-Based Sliding-Mode Control for Underactuated Flexible Joint Robot. IEEE Trans. Ind. Electron. 2020, 67, 10822–10832. [Google Scholar] [CrossRef]
- He, W.; Yan, Z.; Sun, Y.; Ou, Y.; Sun, C. Neural-Learning-Based Control for a Constrained Robotic Manipulator with Flexible Joints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5993–6003. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Zhou, Q.; Li, H.; Lu, R. Adaptive Prescribed Performance Control of a Flexible-Joint Robotic Manipulator with Dynamic Uncertainties. IEEE Trans. Cybern. 2022, 52, 12905–12915. [Google Scholar] [CrossRef]
- Dong, F.; Han, J.; Chen, Y.H. Improved Robust Control for Multi-Link Flexible Manipulator with Mismatched Uncertainties. In Proceedings of the 2015 International Conference on Fluid Power and Mechatronics (FPM), Harbin, China, 5–7 August 2015. [Google Scholar]
- Yim, J.G.; Yeon, J.S.; Park, J.H.; Lee, S.H.; Hur, J.S. Robust Control Using Recursive Design Method for Flexible Joint Robot Manipulator. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007. [Google Scholar]
- Abbas, H.S.; Cisneros, P.S.G.; Männel, G.; Rostalski, P.; Werner, H. Practical Model Predictive Control for a Class of Nonlinear Systems Using Linear Parameter-Varying Representations. IEEE Access 2021, 9, 62380–62393. [Google Scholar] [CrossRef]
- Cisneros, P.S.G.; Sridharan, A.; Werner, H. Constrained Predictive Control of a Robotic Manipulator Using Quasi-LPV Representations. Int. Fed. Autom. Control-Pap. 2018, 51, 118–123. [Google Scholar] [CrossRef]
- Do, T.T.; Vu, V.H.; Liu, Z. Linearization of Dynamic Equations for Vibration and Modal Analysis of Flexible Joint Manipulators. Mech. Mach. Theory 2022, 167, 104516. [Google Scholar] [CrossRef]
- Lai, X.Z.; She, J.H.; Yang, S.X.; Wu, M. Comprehensive Unified Control Strategy for Underactuated Two-Link Manipulators. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 39, 389–398. [Google Scholar]
- Spyrakos-Papastavridis, E.; Dai, J.S. Minimally Model-Based Trajectory Tracking and Variable Impedance Control of Flexible-Joint Robots. IEEE Trans. Ind. Electron. 2021, 68, 6031–6041. [Google Scholar] [CrossRef]
- Richiedei, D.; Trevisani, A. Simultaneous Active and Passive Control for Eigenstructure Assignment in Lightly Damped Systems. Mech. Syst. Signal Process. 2017, 85, 556–566. [Google Scholar] [CrossRef]
- Lai, X.Z.; Zhang, A.; She, J.H.; Wu, M. Motion Control of Underactuated Three-Link Gymnast Robot Based on Combination of Energy and Posture. IET Control Theory Appl. 2011, 5, 1484–1493. [Google Scholar] [CrossRef]
- Lynch, A.G.; Vanderploeg, M.J. A Symbolic Formulation for Linearization of Multibody Equations of Motion. J. Mech. Des. 1995, 117, 441–445. [Google Scholar] [CrossRef]
- Ghoreishi, A.; Nekoui, M.; Basiri, S. Optimal Design of LQR Weighting Matrices Based on Intelligent Optimization Methods. Int. J. Intell. Inf. Process. 2011, 2, 63–74. [Google Scholar]
- Peng, Z.; Hu, J.; Cheng, H.; Huang, R.; Luo, R.; Zhao, P.; Ghosh, B.K. Tracking Control for Motion Constrained Robotic System Via Dynamic Event-Sampled Intelligent Learning Method. In Proceedings of the 2022 IEEE 61st Conference on Decision and Control (CDC), Cancun, Mexico, 6–9 December 2022. [Google Scholar]
- Alam, W.; Mehmood, A.; Ali, K.; Javaid, U.; Alharbi, S.; Iqbal, J. Nonlinear Control of a Flexible Joint Robotic Manipulator with Experimental Validation. Stroj. Vestn. 2018, 64, 47–55. [Google Scholar]
- Akhtaruzzaman, M.; Akmeliawati, R.; Yee, T.W. Modeling and Control of a Multi Degree of Freedom Flexible Joint Manipulator. In Proceedings of the 2009 Second International Conference on Computer and Electrical Engineering, Dubai, United Arab Emirates, 28–30 December 2009. [Google Scholar]
- Bascetta, L.; Ferretti, G.; Scaglioni, B. Closed Form Newton-Euler Dynamic Model of Flexible Manipulators. Robotica 2017, 35, 1006–1030. [Google Scholar] [CrossRef]
- Bilal, H.; Yin, B.; Kumar, A.; Ali, M.; Zhang, J.; Yao, J. Jerk-Bounded Trajectory Planning for Rotary Flexible Joint Manipulator: An Experimental Approach. Soft Comput. 2023, 27, 4029–4039. [Google Scholar] [CrossRef]
- Hong, M.; Gu, X.; Liu, L.; Guo, Y. Finite Time Extended State Observer Based Nonsingular Fast Terminal Sliding Mode Control of Flexible-Joint Manipulators with Unknown Disturbance. J. Frankl. Inst. 2023, 360, 18–37. [Google Scholar] [CrossRef]
- Kostarigka, A.K.; Doulgeri, Z.; Rovithakis, G.A. Prescribed Performance Tracking for Flexible Joint Robots with Unknown Dynamics and Variable Elasticity. Automatica 2013, 49, 1137–1147. [Google Scholar] [CrossRef]
- Redheffer, R.M. On a Certain Linear Fractional Transformation. J. Math. Phys. 1960, 39, 269–286. [Google Scholar] [CrossRef]
- Pasha, S.A.; Tuan, H.D.; Vo, B.N. Nonlinear Bayesian Filtering Using the Unscented Linear Fractional Transformation Model. IEEE Trans. Signal Process. 2010, 58, 477–489. [Google Scholar] [CrossRef]
- Boukarim, G.E.; Chow, J.H. Modeling of Nonlinear System Uncertainties Using a Linear Fractional Transformation Approach. In Proceedings of the 1998 American Control Conference (ACC), Philadelphia, PA, USA, 26 June 1998. [Google Scholar]
- Andrea, R.D.; Khatri, S. Kalman Decomposition of Linear Fractional Transformation Representations and Minimality. In Proceedings of the 1997 American Control Conference (ACC), Albuquerque, NM, USA, 6 June 1997. [Google Scholar]
- Scherer, C.; Weiland, S. Linear Matrix Inequalities in Control, 2nd ed.; CRC Press: London, UK, 2011; pp. 123–142. [Google Scholar]
- Herrmann, G.; Turner, M.C.; Postlethwaite, I. Linear Matrix Inequalities in Control. In Mathematical Methods for Robust and Nonlinear Control: EPSRC Summer School; Turner, M.C., Bates, D.G., Eds.; Springer: London, UK, 2007; Volume 367, pp. 123–142. [Google Scholar]
- Chen, H. A Feasible Moving Horizon H∞ Control Scheme for Constrained Uncertain Linear Systems. IEEE Trans. Autom. Control 2007, 52, 343–348. [Google Scholar] [CrossRef]
- Chen, H.; Scherer, C.W. Moving Horizon H∞ Control with Performance Adaptation for Constrained Linear Systems. Automatica 2006, 42, 1033–1040. [Google Scholar] [CrossRef]
- Yaz, E.E. Linear Matrix Inequalities in System and Control Theory. Proc. IEEE 1998, 86, 2473–2474. [Google Scholar] [CrossRef]
- Heemels, W.P.M.H.; Kundu, A.; Daafouz, J. On Lyapunov-Metzler Inequalities and S-Procedure Characterizations for the Stabilization of Switched Linear Systems. IEEE Trans. Autom. Control 2017, 62, 4593–4597. [Google Scholar] [CrossRef]
- Scherer, C.W. Robust Mixed Control and Linear Parameter-Varying Control with Full Block Scalings. In Advances in Linear Matrix Inequality Methods in Control; Ghaoui, E.L., Niculescu, S.I., Eds.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999; pp. 187–207. [Google Scholar]
- Scherer, C.W. A Full Block S-Procedure with Applications. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 12 December 1997. [Google Scholar]
- Gyurkovics, É.; Takács, T. A Remark on Abstract Multiplier Conditions for Robustness Problems. Syst. Control Lett. 2009, 58, 276–281. [Google Scholar] [CrossRef]





| Symbol | Description |
|---|---|
| , | Lengths of manipulator links (m) |
| , | Distances between center-of-mass positions and joints (m) |
| , | Masses of manipulator links (kg) |
| , | Rotational inertias of manipulator links (kg·m2) |
| , | Rotational inertias of motor rotors (kg·m2) |
| , | Spring-stiffness factors of flexible joints (N·m/rad) |
| , | Output torques of motors (N·m) |
| Gravitational acceleration (m/s2) |
| Symbol | Values |
|---|---|
| , | 0.5 m, 0.5 m |
| , | 0.25 m, 0.25 m |
| , | 20 kg, 10 kg |
| , | 5.6 kg·m2, 2.8 kg·m2 |
| , | 6.183 kg·m2, 0.858 kg·m2 |
| , | 1000 N·m/rad, 1000 N·m/rad |
| 9.81 m/s2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Wang, H.; Yan, G.; Li, G.; Jian, L. Robust Model Predictive Control for Two-DOF Flexible-Joint Manipulator System. Mathematics 2023, 11, 3593. https://doi.org/10.3390/math11163593
Li R, Wang H, Yan G, Li G, Jian L. Robust Model Predictive Control for Two-DOF Flexible-Joint Manipulator System. Mathematics. 2023; 11(16):3593. https://doi.org/10.3390/math11163593
Chicago/Turabian StyleLi, Rong, Hengli Wang, Gaowei Yan, Guoqiang Li, and Long Jian. 2023. "Robust Model Predictive Control for Two-DOF Flexible-Joint Manipulator System" Mathematics 11, no. 16: 3593. https://doi.org/10.3390/math11163593
APA StyleLi, R., Wang, H., Yan, G., Li, G., & Jian, L. (2023). Robust Model Predictive Control for Two-DOF Flexible-Joint Manipulator System. Mathematics, 11(16), 3593. https://doi.org/10.3390/math11163593







