Robust Model Predictive Control for Two-DOF Flexible-Joint Manipulator System

Abstract

This paper presents a practical study on how to improve the ${\mathscr{H}}_{\infty }$ performance and meet the input–output constraints of the two-degrees-of-freedom (DOF) flexible-joint manipulator system (FJMS) with parameter uncertainties and external disturbances. For this reason, a robust constrained moving-horizon ${\mathscr{H}}_{\infty }$ controller is designed to improve the system ${\mathscr{H}}_{\infty }$ performance while still satisfying the input–output constraints of the uncertain system. First, the uncertain controlled system model of the two-DOF FJMS is established via the Lagrange equation method, Spong’s assumption, and the linear fractional transformation (LFT) technique. Then, the control requirements and input–output constraints of the uncertain system are transformed into the linear matrix inequality (LMI) via the theory of ${\mathscr{H}}_{\infty }$ control and the full-block multiplier technique. Next, the LMI optimization problem refreshed by the current state is addressed at each sample moment with the idea of the moving-horizon control of the model predictive control (MPC), and the calculated gain is implemented to the nonlinear closed-loop system under the state feedback structure. The validity and feasibility of the designed control scheme is finally verified via the results of simulation experiments.

1. Introduction

In recent years, due to the advantages of the lighter weight, higher flexibility, lower energy consumption, and higher load ratio of the FJMS compared with the traditional rigid-joint manipulator, the proportion of industrial processing, medical treatment, aerospace engineering, living services, and other application scenarios has increased dramatically. Thus, the control accuracy and robustness of the FJMS have become the key targets of researchers and users [1,2,3,4,5]. For the flexible joints of the manipulator, actuator motors are installed in the individual joints, driving each link to perform the specified actions. However, the rotors inside the motors and links are equipped with harmonic gears for transmission, which subsequently leads to extra errors and vibrations in the angles of the joints, and ultimately greatly influences the control accuracy of the FJMS [6,7]. In addition, because of the objective existence of external disturbances and parameter uncertainties, the conventional dynamic model of the manipulator is frequently impractical, and the above-mentioned factors must be considered when establishing the dynamic model of the FJMS in order to enhance the ${\mathscr{H}}_{\infty }$ performance of the controlled system with constraints.

With the improvement in the control accuracy requirements, the existence of the manipulator joint flexibility has already become a non-negligible matter, and a series of methods have been adopted by international scholars to control the FJMS. For example, L. Zouari et al. designed a sliding-mode controller to address the problem of uncertainties in the joint flexibility of the manipulator [8]. The robust controller was designed for the tracking control of the FJMS with the help of the voltage control strategy in [9]. I. Hassanzadeh et al. invoked an approach to the model following adaptive control when controlling a nonlinear FJMS [10]. The reason why the control performance is not good enough is that the system modeling is not modeled and analyzed for flexible joints. In the process of targeted modeling for the flexible joints of the manipulator, the order of the model is greatly increased to double, and thus the sophistication of the model is strengthened, which has attracted many scholars to explore this issue. The method of M. Spong has been the most broadly adopted and convenient in recent years [11,12,13]. His assumption is that there exists a linear-torsion spring, and the flexible deformation of the joint is equivalently replaced by the torsional deformation of the spring [14].

Up to now, numerous international scholars have conducted in-depth research to explore the control problem of suppressing perturbations for the FJMS, achieving some research results. L. Sun et al. proposed a PD control method with the help of online gravity compensation to achieve the position control of the FJMS [15]. Y. Pan et al. designed a simplified, adaptive command-filtered backstepping controller for the FJMS [16]. K. Rsetam et al. specifically designed the optimal second-order integral sliding-mode controller in order to improve the robustness of a single-link FJMS [17]. In addition, optimal controllers were designed for the discrete controlled systems in [18,19,20], and optimization control algorithms were designed to improve the control performance of the controlled systems while taking into account the existence of external disturbances and uncertainties in [21,22,23]. Z.H. Jiang et al. designed a linear-feedback- and neural-network-based controller to handle the control problem caused by the nonlinearity and dynamic instability of the FJMS [24]. Although several of the above approaches have suppressed the perturbations to some extent, they do not take into account the modeling errors due to the uncertainties of the model parameters. Z. Yan et al. proposed a robust control method based on the equivalent-input-perturbation method to achieve the high-precision motion control of an uncertain FJMS with a single link [25]. Although this method considers the errors caused by parameter inaccuracies, obtaining the real values of the parameters is required in the design of this controller, without realizing the true sense of considering the uncertainties of the system. For the problem of parameter uncertainties, the most realistic case is to be aware of the nominal values of the parameters and the possible variation ranges.

To this day, several control methods have been proposed to overcome the modeling uncertainties of the FJMS. K. Rsetam et al. designed a sliding-mode controller based on a cascaded extended state observer for the under-driven FJMS, where the sliding-mode control method was mainly used to diminish the error caused by uncertainties [26]. W. He et al. introduced the full-state feedback strategy in the neural network, which subsequently was used to respond to the uncertainties of the FJMS for guaranteeing the robustness of the system [27]. H. Ma et al. designed an adaptive fuzzy controller to improve the performance of the single-link FJMS via the performance functions, in which the dynamic signals were applied to replace the uncertainties of the system modeling [28]. F. Dong et al. designed a robust controller based only on the possible bounds of the system uncertainties and a consistent positive characterization of the inertia matrix to guarantee the robustness of the FJMS with uncertainties [29]. J.G. Yim et al. proposed a robust nonlinear recursive-control approach to design a virtually robust control for the FJMS, utilizing nonlinear ${\mathscr{H}}_{\infty }$ control with energy dissipation to attenuate the ${ℒ}_2$ gain from the performance impact of uncertainties [30]. In addition, designed control optimization algorithms were implemented on the real two-DOF manipulator to verify the controllers’ effectiveness in [31,32]. However, several of the above methods are not effective at achieving the control performance enhancement of the FJMS with constraints while dealing with the parameter uncertainties of the manipulator.

Most process models are nonlinear, but they are often linearized to perform the simulation and stability analysis. Linearization is the procedure of approximating and eliminating the higher-order nonlinear terms existing in the mathematical equations. Linear models are easier to understand than nonlinear models and are necessary to design the controllers for the controlled systems. T.T Do et al. established the dynamic equations of a general flexible-joint robot using the Lagrange formulation and linearized them on the basis of the Taylor series [33]. X.Z. Lai et al. divided the motion space of an underactuated two-link manipulator into two areas: the swing area and attractive area, and designed control laws for each system, where the controlled model in the attractive area was approximately linearized, while its controller was designed based on optimal control [34]. E. Spyrakos-Papastavridis et al. linearized an n-DOF flexible-joint robot at a desired operating point, and then utilized the LQR controller to obtain the full-state feedback gain of this system [35]. D. Richiedei et al. rationally performed the model linearization in the case of a two-DOF, two-link planar manipulator, producing small displacements to the configuration [36]. X.Z. Lai et al. approximately linearized the dynamic equations of an underactuated three-link gymnast robot in the attractive area and stabilized it at the straight-up equilibrium position using the balancing-control law [37]. A.G. Lynch et al. linearized nonlinear equations of the multibody dynamic systems around the equilibrium point [38]. A. Ghoreishi et al. linearized a single-link flexible robot around the origin (equilibrium point) [39]. One tends to linearize the nonlinear dynamic model around the equilibrium point, illustrating the fact that the nonlinear systems are locally linear at the equilibrium point. Motivated by the literature mentioned above, we selected the controlled system to be the two-DOF FJMS in the vicinity of the vertical equilibrium position.

As a matter of fact, there are inevitably constraints on the manipulator during the movement process, such as the control input constraints, joint angle constraints [40], etc. Accordingly, a controller that could improve the system ${\mathscr{H}}_{\infty }$ performance while still satisfying the input–output constraints of the system is necessary for this paper. For this paper, a robust constrained moving-horizon ${\mathscr{H}}_{\infty }$ controller is designed to enable the two-DOF FJMS to achieve the above control objectives under the consideration of external disturbances and parameter uncertainties.

The main contributions of this paper are as follows:

• By means of the LFT technique, the LFT uncertain system of the two-DOF FJMS is constructed, which takes into account the parameter uncertainties of the spring-stiffness coefficients;
• The ${\mathscr{H}}_{\infty }$ norm of system disturbances to the performance output and the input–output constraints of the two-DOF FJMS are transformed into the LMIs via the theory of ${\mathscr{H}}_{\infty }$ control and the full-block multiplier technique;
• The robust constrained moving-horizon ${\mathscr{H}}_{\infty }$ controller is designed for this LFT uncertain system, which can improve the ${\mathscr{H}}_{\infty }$ performance of the controlled system while ensuring that the input–output constraints of this system are satisfied.

The remainder of this paper is organized as follows. In Section 2, the dynamics of the two-DOF FJMS is modeled and converted to the state-space expression after linearization. In Section 3, the uncertainties of the spring coefficients in the two-DOF FJMS are investigated by means of the LFT technique, and the LFT uncertain model of this system is constructed. In Section 4, the robust constrained moving-horizon ${\mathscr{H}}_{\infty }$ controller is designed for the LFT uncertain system. In Section 5, the properties of the closed-loop system under the action of the optimization algorithm are given. In Section 6, the above controller implemented on the two-DOF FJMS for the simulation is described, and the experimental results are compared and analyzed. The conclusions are presented in Section 7.

2. Problem Statement

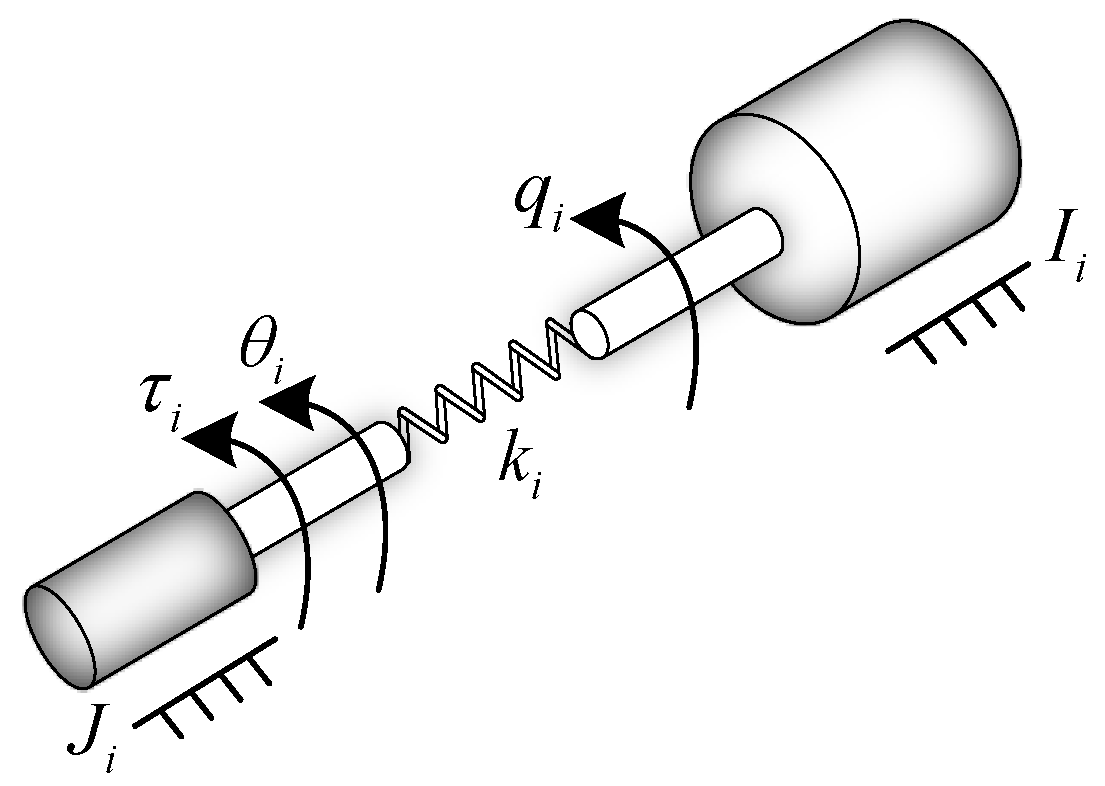
2.1. Dynamic Modeling of the Two-DOF FJMS

In this section, the dynamic characteristics of the studied two-DOF FJMS are discussed in detail. The simplified physical model of the two-DOF FJMS studied in this paper is established as shown in Figure 1. The manipulator system has two rotatable homogeneous links driven by motors at the shoulder joint and elbow joint, which can be moved in the vertical plane around their respective joints. The two-DOF FJMS moves around the vertical equilibrium position. The shoulder joint of the two-DOF FJMS is fixed, and the origin of the coordinate axis ($O$) is the point where the shoulder joint is located. After establishing the coordinate frame for the system, the horizontal plane where the $O$ axis is located is taken to be the surface of zero gravitational potential energy. In addition, due to the fact that both joints of the two-DOF FJMS considered in this paper are flexible joints, which are conceived as the linear springs between the motors and the links based on Spong’s assumption [14], the internal parts of the flexible joints are especially expanded, as shown in Figure 1, so that this relationship can be visualized.

The physical significances of the model parameters in Figure 1 are shown in

Table 1. The parameters of the two-DOF FJMS.

Symbol	Description
$L_1$, $L_2$	Lengths of manipulator links (m)
$L_{c1}$, $L_{\mathrm{c}2}$	Distances between center-of-mass positions and joints (m)
$m_1$, $m_2$	Masses of manipulator links (kg)
$I_1$, $I_2$	Rotational inertias of manipulator links (kg·m2)
$J_1$, $J_2$	Rotational inertias of motor rotors (kg·m2)
$k_1$, $k_2$	Spring-stiffness factors of flexible joints (N·m/rad)
${\tau }_1$, ${\tau }_2$	Output torques of motors (N·m)
$g$	Gravitational acceleration (m/s2)

. The $q_1$ and $q_2$ are the rotation angles of the first and second links, respectively, with the positive direction of the $Y$ axis. As well, the ${\theta }_1$ and ${\theta }_2$ are the rotation angles of the first and second motor rotors, respectively, with the positive direction of the $Y$ axis. The angle value formed by the clockwise rotation is set to be positive, and the angle value formed by the counterclockwise rotation is set to be negative.

At present, there are mainly two kinds of methods commonly used to establish the dynamic model for the system: the Lagrange equation method [41,42] and the Newton–Euler method [43]. In contrast to the latter method, the Lagrange equation method dramatically simplifies the complex dynamic equations due to the fact that it does not account for the internal binding forces of the system, and it allows the dynamic equations of the manipulator system to be expressed in a straightforward and concise manner. Therefore, the Lagrange equation method is chosen here in this paper.

The Lagrange equation method is based on the law of the conservation of energy by calculating the kinetic and potential energy of the system to accomplish the modeling. The system’s Lagrange function ($L\in \mathbb{R}$) is defined as the difference between the kinetic energy ($K\in \mathbb{R}$) and the potential energy ($P\in \mathbb{R}$) of the system [44]:

$$L=K-P.$$

(1)

The Lagrange equation is as follows:

$$\{\begin{array}{l}\frac{d}{dt}\frac{\partial L}{\partial {\dot{q}}_i}-\frac{\partial L}{\partial q_i}={\tau }_i\hfill \\ \frac{d}{dt}\frac{\partial K}{\partial {\dot{q}}_i}-\frac{\partial K}{\partial q_i}+\frac{\partial P}{\partial q_i}={\tau }_i\hfill \end{array}(i=1,2),$$

(2)

where $q_i$ is the rotation angle of the joint, and ${\tau }_i$ is the torque of the actuator.

In the two-DOF FJMS, how the flexible joints are handled is critical. Based on Spong’s simplified model, the flexible joint might be considered as a linear-torsion spring with zero inertia between the motor rotor and the link [13]. The simplified model of the flexible joint is shown in Figure 2, where $k_i$ is this spring’s stiffness factor. In this case, the motor rotor’s rotation angle (${\theta }_i$) will not always equal the link’s rotation angle ($q_i$) (i.e., ${\theta }_i\ne q_i$).

According to Lagrange’s second type Equation (2), the dynamic equations of the two-DOF FJMS are identified as follows [45,46]:

$$\{\begin{array}{c}M(q)\ddot{q}+C(q,\dot{q})\dot{q}+G(q)=k(\theta -q)\\ J\ddot{\theta }+k(\theta -q)=\tau \end{array},$$

(3)

where $\theta ={\left[\begin{array}{cc}{\theta }_1& {\theta }_2\end{array}\right]}^{\mathrm{T}}\in {\mathbb{R}}^{2\times 1}$, $q={\left[\begin{array}{cc}{q}_1& q_2\end{array}\right]}^{\mathrm{T}}\in {\mathbb{R}}^{2\times 1}$, $J=diag\left\{J_1,J_2\right\}\in {\mathbb{R}}^{2\times 2}$ is the diagonal and positive definite inertia matrix of the motors; $k=diag\left\{k_1,k_2\right\}\in {\mathbb{R}}^{2\times 2}$ is the simplified linear-torsion spring-stiffness-coefficient matrix of the flexible joints; $M(q)\in {\mathbb{R}}^{2\times 2}$ is the manipulator’s symmetric and positive definite inertia matrix; $C(q,\dot{q})\dot{q}\in {\mathbb{R}}^{2\times 1}$ is a column vector incorporating the Coriolis force and the centrifugal force; $G(q)\in {\mathbb{R}}^{2\times 1}$ represents the vector of the gravity; $\tau ={\left[\begin{array}{cc}{\tau }_1& {\tau }_2\end{array}\right]}^{\mathrm{T}}\in {\mathbb{R}}^{2\times 1}$ is the output torque of the motors. The specific forms of $M(q)$, $C(q,\dot{q})$, and $G(q)$ in Equation (3) are shown as follows:

$$\{\begin{array}{ccc}\hfill M(q)& =& \left[\begin{array}{cc}{\alpha }_1+{\alpha }_2+2{\alpha }_3\cos q_2& {\alpha }_2+{\alpha }_3\cos q_2\\ {\alpha }_2+{\alpha }_3\cos q_2& {\alpha }_2\end{array}\right]\hfill \\ \hfill C(q,\dot{q})& =& \left[\begin{array}{cc}-{\dot{q}}_2{\alpha }_3\sin q_2& -({\dot{q}}_1+{\dot{q}}_2){\alpha }_3\sin q_2\\ {\dot{q}}_1{\alpha }_3\sin q_2& 0\end{array}\right]\hfill \\ \hfill G(q)& =& \left[\begin{array}{c}-{\alpha }_4\sin q_1-{\alpha }_5\sin (q_1+q_2)\\ -{\alpha }_5\sin (q_1+q_2)\end{array}\right]\hfill \end{array},$$

(4)

where ${\alpha }_1=m_1{L}_{c1}^2+m_2{L}_1^2+I_1$, ${\alpha }_2=m_2{L}_{c2}^2+I_2$, ${\alpha }_3=m_2{L}_1{L}_{c2}$, ${\alpha }_4=(m_1{L}_{\mathrm{cl}}+m_2{L}_1)g$, and ${\alpha }_5=m_{2}g{L}_{c2}$.

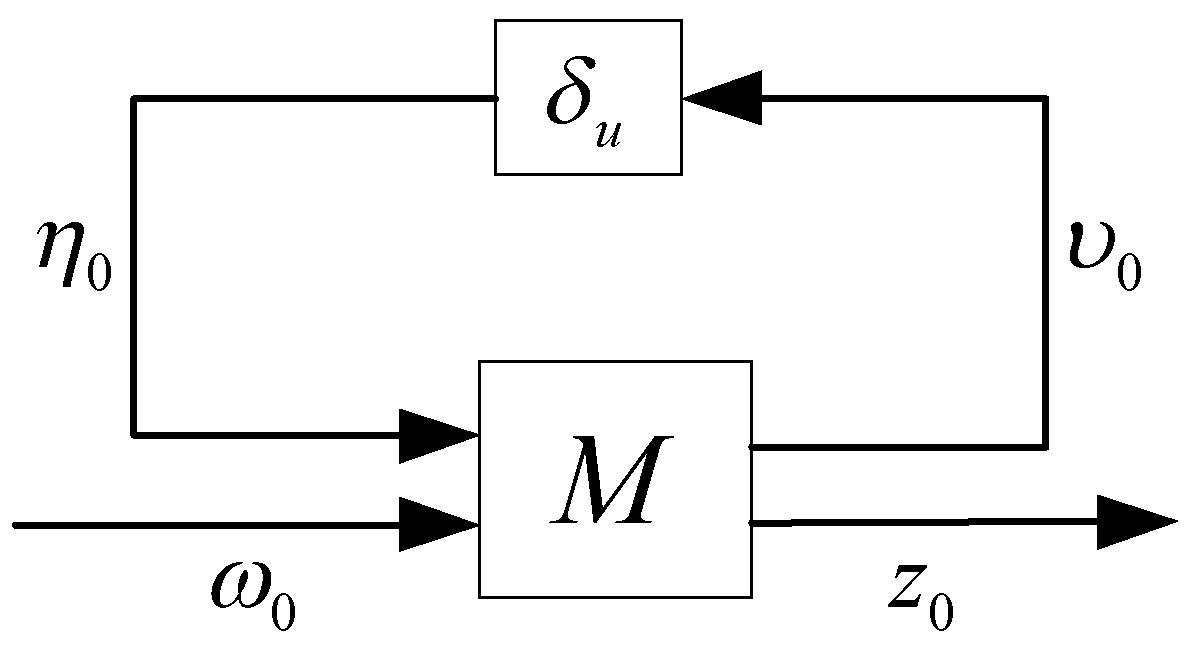
2.2. LFT Technique

LFT was proposed by Redheffer scholars in 1960 and has been widely applied in the research of robust control, as well as in the research of the control of linear parameter-varying systems [47]. LFT is a powerful technique for representing the uncertainties in matrices and systems that is able to perform structural analyses for uncertain systems, and to directly represent systems with uncertainties in the form of state-space expressions. This method has the advantage of decoupling the systems into deterministic and uncertain parts, and it provides an effective tool to construct parameter-uncertain system models. Ultimately, it is possible to make explicit considerations for such uncertainties during the designing of the system controllers [48,49]. The LFT contains the lower LFT and the upper LFT, and the upper LFT structure is highlighted here.

Consider the complex matrix $M$, the partition form of which is in [50]:

$$M=\left[\begin{array}{cc}{M}_{11}& M_{12}\\ M_{21}& M_{22}\end{array}\right]\in {\mathbb{C}}^{(p_1+p_2)\times (q_1+q_2)},$$

(5)

where each matrix has the appropriate dimension, and ${\delta }_u\in {\mathbb{C}}^{q_1\times p_1}$ is also a complex matrix. Assuming that there exists an inverse matrix of $(I-M_{11}{\delta }_u)$, then the upper LFT of the mapping corresponding to the matrix ${\delta }_u$ could be expressed as follows:

$$F_u\left(M,{\delta }_u\right)=M_{22}+M_{21}{\delta }_u{\left(I-M_{11}{\delta }_u\right)}^{-1}{M}_{12}:{\mathbb{C}}^{q_1\times p_1}\to {\mathbb{C}}^{p_2\times q_2}.$$

(6)

The graphical representation of the upper LFT is shown in Figure 3, where $M$ represents the known part of the system, the matrix ${\delta }_u$ represents all the uncertain components (including structural parameters, non-structural parameters, modeling uncertainties, etc.) with ${\delta }_u\in Y_{\delta }$, where $Y_{\delta }=\mathrm{diag}\left\{{\delta }_1{I}_1,\dots ,{\delta }_s{I}_s\right\}$ and $\left|{\delta }_i\right|\le 1(i=1,\dots ,s)$. In addition, ${\eta }_0$ and ${\upsilon }_0$ represent, respectively, the auxiliary input and output of the system, and ${\omega }_0$ and $z_0$ represent, respectively, the real input and output of the system.

The mathematical description of Figure 3 is as follows:

$$\left[\begin{array}{c}{\upsilon }_0\\ z_0\end{array}\right]=M\left[\begin{array}{c}{\eta }_0\\ {\omega }_0\end{array}\right]=\left[\begin{array}{cc}{M}_{11}& M_{12}\\ M_{21}& M_{22}\end{array}\right]\left[\begin{array}{c}{\eta }_0\\ {\omega }_0\end{array}\right],$$

(7)

$${\eta }_0={\delta }_u{\upsilon }_0.$$

(8)

By means of LFT, the uncertain part of the system model is separated and the connection with the known exact model part is established, which is convenient to analyze and design the system controller effectively.

2.3. State Transformation Procedure of the Two-DOF FJMS

The equation $x={\left[\begin{array}{cccccccc}{q}_1& {\dot{q}}_1& q_2& {\dot{q}}_2& {\theta }_1& {\dot{\theta }}_1& {\theta }_2& {\dot{\theta }}_2\end{array}\right]}^{\mathrm{T}}\in {\mathbb{R}}^{8\times 1}$ is selected as the state of the two-DOF FJMS, and $u={\left[\begin{array}{cc}{u}_1& u_2\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{cc}{\tau }_1& {\tau }_2\end{array}\right]}^{\mathrm{T}}\in {\mathbb{R}}^{2\times 1}$ is selected as the control input of this system. This manipulator system is known to be nonlinear according to Equations (3) and (4). As the angles and angular velocities of the first and second links are both close to zero in the attraction domain, the system may be approximately linearized around the equilibrium point, where the values of the variables are $q_1=0$, $q_2=0$, ${\dot{q}}_1=0$, and ${\dot{q}}_2=0$. The approximate linearization process via Taylor series expansion is performed as follows [33,34,37,39]:

$$\{\begin{array}{c}\cos q_1\approx 1,\sin q_1\approx q_1,{\dot{q}}_1\approx 0\\ \cos q_2\approx 1,\sin q_2\approx q_2,{\dot{q}}_2\approx 0\\ \sin (q_1+q_2)\approx q_1+q_2\end{array}.$$

(9)

Remark 1.

The controlled system investigated in this paper is the two-DOF FJMS moving around the vertical equilibrium position, and the types of control problems are addressed via the control algorithms designed in this paper when the manipulator is moving in the vicinity of the equilibrium point. Because the dynamic equation of this manipulator is nonlinear in nature, it thus requires linearization about the equilibrium point. Hereby, the higher-order nonlinear terms are eliminated to attain the linear model by using Taylor series expansion. Of course, considering that there are certain conditions for linearizing the two-DOF FJMS using Taylor series expansion, we have given some constraints on the two joint angles to ensure that this manipulator system moves around the equilibrium point.

Then, dynamic Equation (3) of the two-DOF FJMS is linearized and rewritten as a state-space expression with the following form:

$$\dot{x}=Ax+B_{u}u,$$

(10)

where the coefficient matrices $A$ and $B_u$ are as follows:

$$A=\left[\begin{array}{cccccccc}0& 1& 0& 0& 0& 0& 0& 0\\ A_{21}& 0& A_{23}& 0& A_{25}& 0& A_{27}& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ A_{41}& 0& A_{43}& 0& A_{45}& 0& A_{47}& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ A_{61}& 0& 0& 0& A_{65}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\\ 0& 0& A_{83}& 0& 0& 0& A_{87}& 0\end{array}\right],B_u=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ b_6& 0\\ 0& 0\\ 0& b_8\end{array}\right],$$

(11)

where $A_{ij}$ are represented as follows:

$$\{\begin{array}{l}{A}_{21}=\frac{{\alpha }_2{\alpha }_4-{\alpha }_3{\alpha }_5-k_1{\alpha }_2}{{\alpha }_1{\alpha }_2-{\alpha }_3^2},A_{23}=\frac{-{\alpha }_3{\alpha }_5+k_2({\alpha }_2+{\alpha }_3)}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}\\ A_{25}=\frac{k_1{\alpha }_2}{{\alpha }_1{\alpha }_2-{\alpha }_3^2},A_{27}=\frac{-k_2({\alpha }_2+{\alpha }_3)}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}\\ A_{41}=\frac{{\alpha }_1{\alpha }_5-{\alpha }_3{\alpha }_4-{\alpha }_2{\alpha }_4+{\alpha }_3{\alpha }_5+k_1({\alpha }_2+{\alpha }_3)}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}\\ A_{43}=\frac{({\alpha }_1+{\alpha }_3){\alpha }_5-k_2({\alpha }_1+{\alpha }_2+2{\alpha }_3)}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}\\ A_{45}=\frac{-k_1({\alpha }_2+{\alpha }_3)}{{\alpha }_1{\alpha }_2-{\alpha }_3^2},A_{47}=\frac{k_2({\alpha }_1+{\alpha }_2+2{\alpha }_3)}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}\\ A_{61}=\frac{k_1}{J_1},A_{65}=\frac{-k_1}{J_1},b_6=\frac{1}{J_1}\\ A_{83}=\frac{k_2}{J_2},A_{87}=\frac{-k_2}{J_2},b_8=\frac{1}{J_2}\end{array}.$$

(12)

3. Analysis of the LFT Uncertain System

The spring-stiffness coefficients are the key parameters of the flexible joints for the two-DOF FJMS, and the accuracy of their values plays a highly significant role in the overall controlled system. If there are fluctuations in the stiffness coefficients of the flexible joints, then this nominal manipulator system will become an uncertain dynamic system. The uncertainties of the $k_1$ and $k_2$ are described via the nominal values of the parameters themselves and their possible ranges of variation, as shown in the following equation:

$$\{\begin{array}{c}{k}_1={\overline{k}}_1(1+W_{k_1}{\delta }_{k_1})\\ k_2={\overline{k}}_2(1+W_{k_2}{\delta }_{k_2})\end{array},$$

(13)

where ${\overline{k}}_1$ and ${\overline{k}}_2$ represent, respectively, the nominal values of $k_1$ and $k_2$; $W_{k_1}$ and $W_{k_2}$ are the normalized weighted coefficients of uncertainties; ${\delta }_{k_1}$ and ${\delta }_{k_2}$ are used to describe the fluctuation ranges of the corresponding parameters; and $\left|{\delta }_i\right|\le 1(i=k_1,k_2)$.

To handle the problem of parameter uncertainties, the LFT technique is used to separate the uncertain part and the definite part of the system. Through the upper LFT, the $k_1$ and $k_2$ in Equation (13) are converted into the upper linear fraction structure described in Equation (6):

$$\{\begin{array}{c}{k}_1={\overline{k}}_1(1+W_{k_1}{\delta }_{k_1})={\overline{k}}_1+W_{k_1}{\delta }_{k_1}{(I-{\delta }_{k_1}\cdot 0)}^{-1}{\overline{k}}_1=F_u(M_{k_1},{\delta }_{k_1})\\ k_2={\overline{k}}_2(1+W_{k_2}{\delta }_{k_2})={\overline{k}}_2+W_{k_2}{\delta }_{k_2}{(I-{\delta }_{k_2}\cdot 0)}^{-1}{\overline{k}}_2=F_u(M_{k_2},{\delta }_{k_2})\end{array},$$

(14)

where

$$M_{k_1}=\left[\begin{array}{cc}0& {\overline{k}}_1\\ W_{k_1}& \overline{k_1}\end{array}\right],M_{k_2}=\left[\begin{array}{cc}0& {\overline{k}}_2\\ W_{k_2}& {\overline{k}}_2\end{array}\right].$$

(15)

The LFT uncertain model of the two-DOF FJMS considering parameter uncertainties and external disturbances can be obtained from Equations (10) and (14), as shown in Figure 4.

The uncertainties of the system considered during this research are categorized into internal and external uncertainties, where the parameter uncertainties are the internal uncertainties, and the external disturbances are the external uncertainties. Both of these have been considered and are presented in our system model. The approach of this research is capable of dealing with a class of control problems that consider the system’s uncertainties. The reason why only the spring-stiffness coefficients are considered with parameter uncertainties is that they have somewhat more inaccuracy compared to the other parameters.

In the case of the real system, this manipulator system is naturally subject to angular constraints and drive-torque constraints. This is why a new variable ($z_{\infty }$) is introduced to represent the constrained output of the uncertain system. The angular accelerations of the two joints are selected as the performance output of the system. Hence, the performance output and constrained output of this system are defined as follows:

$$\{\begin{array}{l}{z}_2={\left[\begin{array}{cc}{\ddot{q}}_1& {\ddot{q}}_2\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{cc}{\dot{x}}_2& {\dot{x}}_4\end{array}\right]}^{\mathrm{T}}\\ z_{\infty }={\left[\begin{array}{cccc}\frac{u_1}{u_{1\max }}& \frac{u_2}{u_{2\max }}& \frac{q_1}{q_{1\max }}& \frac{q_2}{q_{2\max }}\end{array}\right]}^{\mathrm{T}}\end{array}.$$

(16)

It can be derived from Figure 4 that the state space and the corresponding mapping relationships between ${\upsilon }_i(i=1,2)$ and ${\eta }_i(i=1,2)$ are as follows:

$$\left[\begin{array}{c}\dot{x}\\ \upsilon \\ z_2\\ z_{\infty }\end{array}\right]=\left[\begin{array}{cccc}A& B_{\eta }& B_u& B_{\omega }\\ C_{\upsilon }& 0& 0& 0\\ C_2& D_{2\eta }& D_2& 0\\ C_{\infty }& 0& D_{\infty }& 0\end{array}\right]\left[\begin{array}{c}x\\ \eta \\ u\\ \omega \end{array}\right],$$

(17)

$$\eta =\delta \upsilon =\left[\begin{array}{cc}{\delta }_{k_1}& 0\\ 0& {\delta }_{k_2}\end{array}\right]\upsilon ,$$

(18)

where $\omega ={\left[\begin{array}{cc}{\omega }_1& {\omega }_2\end{array}\right]}^{\mathrm{T}}\in {\mathbb{R}}^{2\times 1}$ is the external disturbance vector of the uncertain system; $\eta ={\left[\begin{array}{cc}{\eta }_1& {\eta }_2\end{array}\right]}^{\mathrm{T}}\in {\mathbb{R}}^{2\times 1}$ and $\upsilon ={\left[\begin{array}{cc}{\upsilon }_1& {\upsilon }_2\end{array}\right]}^{\mathrm{T}}\in {\mathbb{R}}^{2\times 1}$ are auxiliary vectors that represent, respectively, the uncertainty input and output vectors of this system; $\delta =diag\left\{{\delta }_{k_1},{\delta }_{k_2}\right\}\in Y_{\delta }$ represents the uncertainty matrix; and $Y_{\delta }$ is the collection of uncertainties.

Equations (17) and (18) could be transformed into state-space equations in which the uncertain and definite components of this system are separated, as follows:

$$\{\begin{array}{l}\dot{x}=(A+\Delta A)x+(B_u+\Delta B_u)u+B_{\omega }\omega \\ z_2=(C_2+\Delta C_2)x+(D_2+\Delta D_2)u\\ z_{\infty }=C_{\infty }x+D_{\infty }u\end{array},$$

(19)

where $A$, $B_u$, $B_{\omega }$, $C_2$, $D_2$, $C_{\infty }$, and $D_{\infty }$ are the known-constant-coefficient matrices describing the nominal system model of this manipulator; $\Delta A$, $\Delta B_u$, $\Delta C_2$, and $\Delta D_2$ are the uncertainty matrix functions of appropriate dimensions, representing the parameter uncertainties of the system model. Therefore, in order to extract the variables in the uncertainty matrices $\Delta A$, $\Delta B_u$, $\Delta C_2$, and $\Delta D_2$ containing ${\delta }_{k_1}$ and ${\delta }_{k_2}$, $\Delta A$, $\Delta B_u$, $\Delta C_2$, and $\Delta D_2$ could be written in the form of a bounded norm based on Equations (17) and (18), as follows:

$$\{\begin{array}{c}\left[\begin{array}{cc}\Delta A& \Delta B_u\end{array}\right]=E_1\delta \left[\begin{array}{cc}{F}_1& F_2\end{array}\right]\\ \left[\begin{array}{cc}\Delta C_2& \Delta D_2\end{array}\right]=E_2\delta \left[\begin{array}{cc}{F}_1& F_2\end{array}\right]\end{array},$$

(20)

where $E_1$, $E_2$, $F_1$, and $F_2$ are uncertain matrices of appropriate dimensions in the following forms, respectively:

$$\{\begin{array}{l}{E}_1={\left[\begin{array}{cccccccc}0& \frac{-{\alpha }_2{W}_{k_1}}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}& 0& \frac{({\alpha }_2+{\alpha }_3)W_{k_1}}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}& 0& \frac{W_{k_1}}{J_1}& 0& 0\\ 0& \frac{({\alpha }_2+{\alpha }_3)W_{k_2}}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}& 0& \frac{-({\alpha }_1+{\alpha }_2+2{\alpha }_3)W_{k_2}}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}& 0& 0& 0& \frac{W_{k_2}}{J_2}\end{array}\right]}^{\mathrm{T}},F_2=\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]\\ E_2=\left[\begin{array}{cc}\frac{-{\alpha }_2{W}_{k_1}}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}& \frac{({\alpha }_2+{\alpha }_3)W_{k_2}}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}\\ \frac{({\alpha }_2+{\alpha }_3)W_{k_1}}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}& \frac{-({\alpha }_1+{\alpha }_2+2{\alpha }_3)W_{k_2}}{{\alpha }_1{\alpha }_2-{\alpha }_3^2}\end{array}\right],F_1=\left[\begin{array}{cccccccc}{\overline{k}}_1& 0& 0& 0& -{\overline{k}}_1& 0& 0& 0\\ 0& 0& {\overline{k}}_2& 0& 0& 0& -{\overline{k}}_2& 0\end{array}\right]\end{array}.$$

(21)

4. Robust Model Predictive Control with Constraints

The solution to the optimization control problem addressed in this paper is to purposely design a controller that firstly ensures that this manipulator system maintains strong robustness and stability under the dual influence of parameter uncertainties and external disturbances, and secondly, that minimizes the ${\mathscr{H}}_{\infty }$ norm of system perturbation $\omega$ to performance output $z_2$ while ensuring that all the constraints of this system are satisfied. The final control goal is to design a controller to stabilize the two-DOF FJMS at the equilibrium point under the influence of a series of factors. In addition, the state feedback structure with $u=Kx$ is considered in the design process of the controller to ensure that a good control performance can be obtained. Therefore, the key point of our designed controller is how to calculate the feedback gain that satisfies the system constraints while guaranteeing the system performance.

4.1. Robust Constrained ${\mathscr{H}}_{\infty }$ Control

For the LFT uncertain system with constraints, this subsection focuses on the design of a robust constrained ${\mathscr{H}}_{\infty }$ controller to ensure the improvement in the ${\mathscr{H}}_{\infty }$ performance and the fulfillment of the input–output constraints. With the application of the LMI technique, the constrained ${\mathscr{H}}_{\infty }$ control problem can be converted into the convex optimization problem with LMIs as constraints to make it easier to solve. The lemmas about the LMIs used in this procedure are as follows:

Lemma 1

([51,52]). Suppose that $S=\left[\begin{array}{cc}M& N\\ N^{\mathrm{T}}& L\end{array}\right]\in {\mathbb{R}}^{(k+l)\times (k+l)}$ is non-singular and its inverse matrix is recorded as $S^{-1}=\left[\begin{array}{cc}\tilde{M}& \tilde{N}\\ {\tilde{N}}^{\mathrm{T}}& \tilde{L}\end{array}\right]\in {\mathbb{R}}^{(k+l)\times (k+l)}$. Then, the nonlinear matrix inequality

$$L\ge 0,{\left[\begin{array}{c}I\\ F\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}M& N\\ N^{\mathrm{T}}& L\end{array}\right]\left[\begin{array}{c}I\\ F\end{array}\right]\le 0,$$

(22)

is equivalent to the following LMI:

$$\tilde{M}\le 0,{\left[\begin{array}{c}-F^{\mathrm{T}}\\ I\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}\tilde{M}& \tilde{N}\\ {\tilde{N}}^{\mathrm{T}}& \tilde{L}\end{array}\right]\left[\begin{array}{c}-F^{\mathrm{T}}\\ I\end{array}\right]\ge 0.$$

(23)

Lemma 2

([53,54]). Suppose that there are three constant matrices, $E$, $F$, and $G$, and four affine-function matrices, $K(\beta )$, $L(\beta )$, $M(\beta )=M{(\beta )}^{\mathrm{T}}$, and $N(\beta )$, with the independent variable $\beta$. Which $L(\beta )$ can be decomposed into $Y^{\mathrm{T}}U{(\beta )}^{-1}Y$ and $U(\beta )<0$ is also affine depending on the variable $\beta$. Then, the nonlinear matrix inequality

$${\left[\begin{array}{c}E\\ \left[\begin{array}{c}K(\beta )\\ F\end{array}\right]\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}M(\beta )& \left[\begin{array}{cc}G& N(\beta )\end{array}\right]\\ \left[\begin{array}{c}{G}^{\mathrm{T}}\\ N{(\beta )}^{\mathrm{T}}\end{array}\right]& L(\beta )\end{array}\right]\left[\begin{array}{c}E\\ \left[\begin{array}{c}K(\beta )\\ F\end{array}\right]\end{array}\right]\le 0,$$

(24)

is equivalent to the following LMI:

$$\left(\begin{array}{cc}{E}^{\mathrm{T}}M(\beta )E+E^{\mathrm{T}}(GK(\beta )+N(\beta )F)+{(GK(\beta )+N(\beta )F)}^{\mathrm{T}}E& \left[\begin{array}{cc}K{(\beta )}^{\mathrm{T}}& F^{\mathrm{T}}\end{array}\right]Y\\ Y^{\mathrm{T}}\left[\begin{array}{c}K(\beta )\\ F\end{array}\right]& -U(\beta )\end{array}\right)\le 0.$$

(25)

Lemma 3

([55,56]). Suppose that $S_0,S_1,\cdots ,S_j\in {\mathbb{R}}^{\mathrm{n}\times \mathrm{n}}$ are the symmetric matrices. If there exists ${\phi }_1,{\phi }_2,\dots ,{\phi }_j\ge 0$ such that $S_0-{\displaystyle \sum _{i=1}^j{\phi }_i}{S}_i>0$ holds, then it is obtained as follows:

$${\zeta }^{\mathrm{T}}{S}_0\zeta >0 \mathrm{for} \mathrm{all} \zeta \ne 0 \mathrm{such} \mathrm{that} {\zeta }^{\mathrm{T}}{S}_i\zeta \ge 0(i=1,\dots ,j).$$

(26)

Due to the fact that the discrete-time model is applied to the conventional MPC, it is necessary to discretize the system (17), and the results are processed via the method of Equations (17)–(21), as follows:

$$\{\begin{array}{l}x(k+1)=(A_d+\Delta A_d)x(k)+(B_{ud}+\Delta B_{ud})u(k)+B_{\omega d}\omega (k)\\ z_2(k)=(C_{2d}+\Delta C_{2d})x(k)+(D_{2d}+\Delta D_{2d})u(k)\\ z_{\infty }(k)=C_{\infty d}x(k)+D_{\infty d}u(k)\end{array},$$

(27)

where $A_d=e^{A{T}_s}$, $\Delta A_d=E_{1d}\delta F_{1d}$, $E_{1d}=A^{-1}(e^{A{T}_s}-I)E_1$, $F_{1d}=F_1$, $B_{ud}=A^{-1}(e^{A{T}_s}-I)B_u$, $\Delta B_{ud}=E_{1d}\delta F_{2d}$, $F_{2d}=F_2$, $B_{\omega d}=A^{-1}(e^{A{T}_s}-I)B_{\omega }$, $C_{2d}=C_2$, $\Delta C_{2d}=E_{2d}\delta F_{1d}$, $E_{2d}=E_2$, $D_{2d}=D_2$, $\Delta D_{2d}=E_{2d}\delta F_{2d}$, $C_{\infty d}=C_{\infty }$, $D_{\infty d}=D_{\infty }$, and $T_s$ is the sample period. In addition, $\left|z_{\infty i}(k)\right|\le z_{\infty i,\max }=1(i=1,2,3,4)$ represents the four normalized constrained output values of this system. The state feedback control law $u(k)=Kx(k)$ is substituted into (27), and the closed-loop system can be written as follows:

$$\{\begin{array}{l}x(k+1)=A_{\delta }x(k)+B_{\omega d}\omega (k)\\ z_2(k)=C_{\delta }x(k)\\ z_{\infty }(k)=(C_{\infty d}+D_{\infty d}K)x(k)\end{array},$$

(28)

where $A_{\delta }=A_d+B_{ud}K+E_{1d}\delta (F_{1d}+F_{2d}K)$ and $C_{\delta }=C_{2d}+D_{2d}K+E_{2d}\delta (F_{1d}+F_{2d}K)$.

If there exists a non-negative value of $\lambda$ such that the system (28) satisfies the dissipation inequality shown below:

$$x{(k+1)}^{\mathrm{T}}Hx(k+1)-x{(k)}^{\mathrm{T}}Hx(k)\le {\lambda }^2{\Vert \omega (k)\Vert }_2^2-{\Vert z_2(k)\Vert }_2^2,$$

(29)

where $H\in {\mathbb{R}}^{8\times 8}$ is a positive definite symmetric matrix, and if the system is steady when $k\to \infty$, then $\underset{k\to \infty }{\lim }x(k+1)=0$ is true. This could be further deduced as follows:

$$\underset{\delta \in Y_{\delta }}{\max }\left({\displaystyle \sum _{k=0}^{\infty }\left({\Vert z_2(k)\Vert }_2^2-{\lambda }^2{\Vert \omega (k)\Vert }_2^2\right)}\right)\le x{(0)}^{\mathrm{T}}Hx(0),$$

(30)

where it is marked by the establishment of (30) that the ${\mathscr{H}}_{\infty }$ norm of this system from $\omega$ to $z_2$ is less than $\lambda$.

Replacing with the components of (29) by the closed-loop system (28) gives the following:

$${(A_{\delta }x(k)+B_{\omega d}\omega (k))}^{\mathrm{T}}H(A_{\delta }x(k)+B_{\omega d}\omega (k))-x{(k)}^{\mathrm{T}}Hx(k)\le {\lambda }^2{\Vert \omega (k)\Vert }_2^2-{\Vert C_{\delta }x(k)\Vert }_2^2.$$

(31)

The above inequality is organized and transformed into the quadratic form as follows:

$${\left[\begin{array}{c}x(k)\\ \omega (k)\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}{A}_{\delta }^{\mathrm{T}}H{A}_{\delta }-H+C_{\delta }^{\mathrm{T}}{C}_{\delta }& A_{\delta }^{\mathrm{T}}H{B}_{\omega d}\\ B_{\omega d}^{\mathrm{T}}H{A}_{\delta }& B_{\omega d}^{\mathrm{T}}H{B}_{\omega d}-{\lambda }^{2}I\end{array}\right]\left[\begin{array}{c}x(k)\\ \omega (k)\end{array}\right]\le 0.$$

(32)

The inequality (32) is equivalent to the following:

$$\left[\begin{array}{cc}I& A_{\delta }^{\mathrm{T}}\\ 0& B_{\omega d}^{\mathrm{T}}\end{array}\right]\left[\begin{array}{cc}-H& 0\\ 0& H\end{array}\right]\left[\begin{array}{cc}I& 0\\ A_{\delta }& B_{\omega d}\end{array}\right]+\left[\begin{array}{cc}0& C_{\delta }^{\mathrm{T}}\\ I& 0\end{array}\right]\left[\begin{array}{cc}-{\lambda }^{2}I& 0\\ 0& I\end{array}\right]\left[\begin{array}{cc}0& I\\ C_{\delta }& 0\end{array}\right]\le 0.$$

(33)

In order to separate $\delta$ from $A_{\delta }$ and $C_{\delta }$, the inequality (33) is modified into the following form:

$$\begin{array}{l}{\left[\begin{array}{cc}I& 0\\ 0& I\\ \delta (F_{1d}+F_{2d}K)& 0\end{array}\right]}^{\mathrm{T}}{\left[\begin{array}{ccc}I& 0& 0\\ A_d+B_{ud}K& B_{\omega d}& E_{1d}\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}-H& 0\\ 0& H\end{array}\right]\left[\begin{array}{ccc}I& 0& 0\\ A_d+B_{ud}K& B_{\omega d}& E_{1d}\end{array}\right]\left[\begin{array}{cc}I& 0\\ 0& I\\ \delta (F_{1d}+F_{2d}K)& 0\end{array}\right]\\ +{\left[\begin{array}{cc}I& 0\\ 0& I\\ \delta (F_{1d}+F_{2d}K)& 0\end{array}\right]}^{\mathrm{T}}{\left[\begin{array}{ccc}0& I& 0\\ C_{2d}+D_{2d}K& 0& E_{2d}\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}-{\lambda }^{2}I& 0\\ 0& I\end{array}\right]\left[\begin{array}{ccc}0& I& 0\\ C_{2d}+D_{2d}K& 0& E_{2d}\end{array}\right]\left[\begin{array}{cc}I& 0\\ 0& I\\ \delta (F_{1d}+F_{2d}K)& 0\end{array}\right]\le 0\end{array}.$$

(34)

Then, with the application of the full-block multiplier technique [57,58,59], it could be deduced that the holding of (33) is equivalent to the existence of an invertible multiplier matrix ($\tilde{T}$) such that

$${\left[\begin{array}{c}\delta \\ I\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}{\tilde{T}}_a& {\tilde{T}}_b\\ {\tilde{T}}_b^{\mathrm{T}}& {\tilde{T}}_c\end{array}\right]\left[\begin{array}{c}\delta \\ I\end{array}\right]\ge 0,$$

(35)

where ${\tilde{T}}_a<0$. Due to the invertibility of the multiplier matrix ($\tilde{T}$), the application of Lemma 1 to (35) results in the following:

$${\left[\begin{array}{c}I\\ -{\delta }^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}{T}_a& T_b\\ T_b^{\mathrm{T}}& T_c\end{array}\right]\left[\begin{array}{c}I\\ -{\delta }^{\mathrm{T}}\end{array}\right]\le 0 \mathrm{and} T={\tilde{T}}^{-1}=\left[\begin{array}{cc}{T}_a& T_b\\ T_b^{\mathrm{T}}& T_c\end{array}\right],$$

(36)

where $T_c$ is a positive definite diagonal matrix and $T_a=-T_c$, $T_b$ is a diagonal matrix, and all the elements of $T_b$ are antisymmetric matrices. Moreover, there is one thing worth noting:

$$\left[\begin{array}{cc}\delta & 0\\ I& 0\end{array}\right](F_{1d}+F_{2d}K)=\left[\begin{array}{ccc}0& 0& I\\ F_{1d}+F_{2d}K& 0& 0\end{array}\right]\left[\begin{array}{cc}I& 0\\ 0& I\\ \delta (F_{1d}+F_{2d}K)& 0\end{array}\right].$$

(37)

The following inequality could be further reasoned from (34)–(37):

$${\left[\begin{array}{ccc}I& 0& 0\\ A_d+B_{ud}K& B_{\omega d}& E_{1d}\\ 0& I& 0\\ C_{2d}+D_{2d}K& 0& E_{2d}\\ 0& 0& I\\ F_{1d}+F_{2d}K& 0& 0\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cccccc}-H& 0& 0& 0& 0& 0\\ 0& H& 0& 0& 0& 0\\ 0& 0& -{\lambda }^{2}I& 0& 0& 0\\ 0& 0& 0& I& 0& 0\\ 0& 0& 0& 0& {\tilde{T}}_a& {\tilde{T}}_b\\ 0& 0& 0& 0& {\tilde{T}}_b^{\mathrm{T}}& {\tilde{T}}_c\end{array}\right]\left[\begin{array}{ccc}I& 0& 0\\ A_d+B_{ud}K& B_{\omega d}& E_{1d}\\ 0& I& 0\\ C_{2d}+D_{2d}K& 0& E_{2d}\\ 0& 0& I\\ F_{1d}+F_{2d}K& 0& 0\end{array}\right]\le 0.$$

(38)

Then, the inequality (38) is subjected to the simple elementary matrix transformation, resulting in the following:

$${\left[\begin{array}{ccc}I& 0& 0\\ 0& I& 0\\ 0& 0& I\\ A_d+B_{ud}K& B_{\omega d}& E_{1d}\\ C_{2d}+D_{2d}K& 0& E_{2d}\\ F_{1d}+F_{2d}K& 0& 0\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cccccc}-H& 0& 0& 0& 0& 0\\ 0& -{\lambda }^{2}I& 0& 0& 0& 0\\ 0& 0& {\tilde{T}}_a& 0& 0& {\tilde{T}}_b\\ 0& 0& 0& H& 0& 0\\ 0& 0& 0& 0& I& 0\\ 0& 0& {\tilde{T}}_b^{\mathrm{T}}& 0& 0& {\tilde{T}}_c\end{array}\right]\left[\begin{array}{ccc}I& 0& 0\\ 0& I& 0\\ 0& 0& I\\ A_d+B_{ud}K& B_{\omega d}& E_{1d}\\ C_{2d}+D_{2d}K& 0& E_{2d}\\ F_{1d}+F_{2d}K& 0& 0\end{array}\right]\le 0.$$

(39)

Because ${\tilde{T}}_a<0$ and $H>0$, the $diag\left\{-H,-{\lambda }^{2}I,{\tilde{T}}_a\right\}<0$ holds. Applying Lemma 1 to (39) and performing the elementary matrix transformation, the result would be as follows:

$${\left[\begin{array}{ccc}I& 0& 0\\ 0& I& 0\\ 0& 0& I\\ -{(A_d+B_{ud}K)}^{\mathrm{T}}& -{(C_{2d}+D_{2d}K)}^{\mathrm{T}}& -{(F_{1d}+F_{2d}K)}^{\mathrm{T}}\\ -B_{\omega d}^{\mathrm{T}}& 0& 0\\ -E_{1d}^{\mathrm{T}}& -E_{2d}^{\mathrm{T}}& 0\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cccccc}N& 0& 0& 0& 0& 0\\ 0& I& 0& 0& 0& 0\\ 0& 0& T_c& 0& 0& T_b^{\mathrm{T}}\\ 0& 0& 0& -N& 0& 0\\ 0& 0& 0& 0& -{\lambda }^{-2}I& 0\\ 0& 0& T_b& 0& 0& T_a\end{array}\right]\left[\begin{array}{c}*\\ *\\ *\end{array}\right]\ge 0,$$

(40)

where $N=H^{-1}$. Due to $T_a<0$ and $N>0$, the $diag\left\{-N,-{\lambda }^{-2}I,T_a\right\}<0$ holds. With the help of Lemma 2, the nonlinear matrix inequality (40) is equivalent to the specific form of LMI, as follows:

$$\left[\begin{array}{cccccc}N& 0& -E_{1d}{T}_b& -A_d-B_{ud}K& -B_{\omega d}& -E_{1d}\\ 0& I& -E_{2d}{T}_b& -C_{2d}-D_{2d}K& 0& -E_{2d}\\ -T_b^{\mathrm{T}}{E}_{1d}^{\mathrm{T}}& -T_b^{\mathrm{T}}{E}_{2d}^{\mathrm{T}}& T_c& -F_{1d}-F_{2d}K& 0& 0\\ -{(A_d+B_{ud}K)}^{\mathrm{T}}& -{(C_{2d}+D_{2d}K)}^{\mathrm{T}}& -{(F_{1d}+F_{2d}K)}^{\mathrm{T}}& N^{-1}& 0& 0\\ -B_{\omega d}^{\mathrm{T}}& 0& 0& 0& {\lambda }^{2}I& 0\\ -E_{1d}^{\mathrm{T}}& -E_{2d}^{\mathrm{T}}& 0& 0& 0& -T_a^{-1}\end{array}\right]\ge 0.$$

(41)

Then, the above inequality (41) is subjected to the congruence transformation with $diag\left\{I,I,I,-N,I,T_a\right\}$, and defining $R=KN$ results in the following:

$$\left[\begin{array}{cccccc}N& 0& -E_{1d}{T}_b& A_{d}N+B_{ud}R& -B_{\omega d}& -E_{1d}{T}_a\\ 0& I& -E_{2d}{T}_b& C_{2d}N+D_{2d}R& 0& -E_{2d}{T}_a\\ -T_b^{\mathrm{T}}{E}_{1d}^{\mathrm{T}}& -T_b^{\mathrm{T}}{E}_{2d}^{\mathrm{T}}& T_c& F_{1d}N+F_{2d}R& 0& 0\\ {(A_{d}N+B_{ud}R)}^{\mathrm{T}}& {(C_{2d}N+D_{2d}R)}^{\mathrm{T}}& {(F_{1d}N+F_{2d}R)}^{\mathrm{T}}& N& 0& 0\\ -B_{\omega d}^{\mathrm{T}}& 0& 0& 0& {\lambda }^{2}I& 0\\ -T_a^{\mathrm{T}}{E}_{1d}^{\mathrm{T}}& -T_a^{\mathrm{T}}{E}_{2d}^{\mathrm{T}}& 0& 0& 0& -T_a\end{array}\right]\ge 0.$$

(42)

In summary, if there are variables ($R$, $N$, ${\lambda }^2$) and multipliers ($T_a$, $T_b$, $T_c$) making the LMI (42) be established, then the ${\mathscr{H}}_{\infty }$ norm of the controlled system (27) from $\omega$ to $z_2$ must be less than $\lambda$ under the action of the controller $K=R{N}^{-1}$ and $u(k)=Kx(k)$. Meanwhile, the above LMI also guarantees that $A_d+B_{ud}K$ is quadratically stable.

The treatment of the constraints existing in the system is discussed in this section. Firstly, an elliptic domain is defined as $\Omega (H,{\rho }_f):=\left\{x{(k)}^{\mathrm{T}}Hx(k)\le {\rho }_f\right\}$. If $x(k)\in \Omega (H,{\rho }_f)$, then it could be deduced from the closed-loop system (28) as follows:

$${\left|z_{\infty i}(k)\right|}^2={\left|e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)x(k)\right|}^2\le \underset{x(k)\in \Omega (H,{\rho }_f)}{\max }{\left|e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)x(k)\right|}^2(i=1,2,3,4),$$

(43)

where $e_i(i=1,2,3,4)$ are the standard basis vectors in the four-dimensional space. If ${\left|e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)x(k)\right|}^2\le z_{\infty i,\max }^2(i=1,2,3,4)$, then $\left|z_{\infty i}(k)\right|\le z_{\infty i,\max }(i=1,2,3,4)$ is valid, and it means that the constraints of the controlled system are satisfied. Let $S_0=z_{\infty i,\max }^2-{\left|e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)x(k)\right|}^2$ and $S_1={\rho }_f-x{(k)}^{\mathrm{T}}Hx(k)$. Applying Lemma 3, it is equivalent to the existence of $\phi >0$, which enables (44) to hold for all $\delta \in Y_{\delta }$:

$$z_{\infty i,\max }^2-x{(k)}^{\mathrm{T}}{(e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K))}^{\mathrm{T}}{e}_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)x(k)-\phi {\rho }_f+\phi x{(k)}^{\mathrm{T}}Hx(k)\ge 0(i=1,2,3,4).$$

(44)

And let $\phi =\frac{z_{\infty i,\max }^2}{{\rho }_f}$, then inequality (44) can be transformed into the following:

$${\left[\begin{array}{c}I\\ e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}-H& 0\\ 0& \frac{{\rho }_f}{z_{\infty i,\max }^2}\end{array}\right]\left[\begin{array}{c}I\\ e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)\end{array}\right]\le 0.$$

(45)

Using the technique of the full-block multiplier again, the holding of the above inequality is equivalent to the existence of four invertible multiplier matrices (${\tilde{V}}_i(i=1,2,3,4)$), satisfying the following:

$${\left[\begin{array}{cc}I& 0\\ e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)& 0\\ 0& I\\ F_{1d}+F_{2d}K& 0\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cccc}-H& 0& 0& 0\\ 0& \frac{{\rho }_f}{z_{\infty i,\max }^2}& 0& 0\\ 0& 0& {\tilde{V}}_{ai}& {\tilde{V}}_{bi}\\ 0& 0& {\tilde{V}}_{bi}^{\mathrm{T}}& {\tilde{V}}_{ci}\end{array}\right]\left[\begin{array}{cc}I& 0\\ e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)& 0\\ 0& I\\ F_{1d}+F_{2d}K& 0\end{array}\right]\le 0,$$

(46)

where ${\tilde{V}}_{ai}<0$. Then, the inequality (46) after the elementary matrix transformation is as follows:

$${\left[\begin{array}{cc}I& 0\\ 0& I\\ e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)& 0\\ F_{1d}+F_{2d}K& 0\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cccc}-H& 0& 0& 0\\ 0& {\tilde{V}}_{ai}& 0& {\tilde{V}}_{bi}\\ 0& 0& \frac{{\rho }_f}{z_{\infty i,\max }^2}& 0\\ 0& {\tilde{V}}_{bi}^{\mathrm{T}}& 0& {\tilde{V}}_{ci}\end{array}\right]\left[\begin{array}{cc}I& 0\\ 0& I\\ e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)& 0\\ F_{1d}+F_{2d}K& 0\end{array}\right]\le 0.$$

(47)

Owing to ${\tilde{V}}_{ai}<0$ and $H>0$, the $diag\left\{-H,{\tilde{V}}_{ai}\right\}<0$ holds. Applying Lemma 1 and performing the elementary matrix transformation, the inequality (47) is equivalent to the nonlinear matrix inequality shown below:

$${\left[\begin{array}{cc}I& 0\\ 0& I\\ -{(C_{\infty d}+D_{\infty d}K)}^{\mathrm{T}}{e}_i& -{(F_{1d}+F_{2d}K)}^{\mathrm{T}}\\ 0& 0\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cccc}\frac{z_{\infty i,\max }^2}{{\rho }_f}& 0& 0& 0\\ 0& V_{ci}& 0& V_{bi}^{\mathrm{T}}\\ 0& 0& -H^{-1}& 0\\ 0& V_{bi}& 0& V_{ai}\end{array}\right]\left[\begin{array}{c}*\\ *\\ *\end{array}\right]\ge 0,$$

(48)

where $V_{ci}(i=1,2,3,4)$ are four positive definite diagonal matrices and $V_{ai}=-V_{ci}$, $V_{bi}(i=1,2,3,4)$ are four diagonal matrices, and all elements of $V_{bi}$ are antisymmetric matrices. Because $V_{ai}<0$ and $H>0$, the $diag\left\{-H^{-1},V_{ai}\right\}<0$ holds. Applying Lemma 2, the inequality (48) is equivalent to the following LMI:

$$\left[\begin{array}{cccc}\frac{z_{\infty i,\max }^2}{{\rho }_f}& 0& -e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K)& 0\\ 0& V_{ci}& -F_{1d}-F_{2d}K& 0\\ -{(C_{\infty d}+D_{\infty d}K)}^{\mathrm{T}}{e}_i& -{(F_{1d}+F_{2d}K)}^{\mathrm{T}}& H& 0\\ 0& 0& 0& -V_{ai}^{-1}\end{array}\right]\ge 0.$$

(49)

Then, the inequality (49) is congruent transformed with $diag\left\{I,I,N,V_{ai}\right\}$, which results in the following:

$$\left[\begin{array}{cccc}\frac{z_{\infty i,\max }^2}{{\rho }_f}& 0& -e_i^{\mathrm{T}}(C_{\infty d}N+D_{\infty d}R)& 0\\ 0& V_{ci}& -F_{1d}N-F_{2d}R& 0\\ -{(C_{\infty d}N+D_{\infty d}R)}^{\mathrm{T}}{e}_i& -{(F_{1d}N+F_{2d}R)}^{\mathrm{T}}& N& 0\\ 0& 0& 0& -V_{ai}\end{array}\right]\ge 0(i=1,2,3,4).$$

(50)

Therefore, if the variables that enable LMI (42) to be feasible also make LMI (50) hold, then $\left|z_{\infty i}(k)\right|\le z_{\infty i,\max }(i=1,2,3,4)$, which indicates that all constraints are satisfied for the uncertainties considered by the system.

In summary, the robust constrained ${\mathscr{H}}_{\infty }$ controller with the state feedback structure is constructed by addressing the LMI optimization solution problem for the given ${\rho }_f>0$, as shown below:

$$\underset{{\lambda }^2,N,R,T_a,T_b,T_c,\left\{V_{ai},V_{ci}\right\}}{\min }{\lambda }^2 subject to (42) and (50).$$

(51)

In order to reduce the number of independent variables for this controller and the online computational burden of the algorithm, we may set $T_b=0$.

The method described above guarantees the ${\mathscr{H}}_{\infty }$ performance of the system with parameter uncertainties while satisfying the four constraints by addressing multiple LMIs. In addition, the trade-off between a good system performance and the satisfaction of the constraints can be achieved by defining the state elliptic domain ($\Omega (H,{\rho }_f)$) and selecting the appropriate controller parameter (${\rho }_f$).

4.2. Robust Constrained Moving-Horizon ${\mathscr{H}}_{\infty }$ Control

The concept of the control algorithm designed above highlights the inherent compromise between ensuring all the constraints and enhancing the control performance of the uncertain system. However, there might be a few large perturbations that cannot be anticipated in advance in the actual system, and it is possible to guarantee the system performance only by increasing the value of ${\rho }_f$ to expand the range of the elliptic domain $\Omega (H,{\rho }_f)$, yet the consequence of doing so would be extremely limited values of $N$ and $R$, ultimately resulting in the larger value of the performance index ($\lambda$), which, in turn, decreases the performance of the system. In contrast, the pursuit of a better performance could be achieved by lowering the value of ${\rho }_f$. But if the controlled system is subjected to larger external perturbations, there is no guarantee that the system constraints can be satisfied. Therefore, how to modify the LMI optimization control problem based on (51) is the top priority.

The stationarity and strong conservativeness of ${\rho }_f$, $H$, and $\lambda$ prompt us to incorporate the idea of the moving-horizon control of MPC to overcome the weaknesses of the current algorithm and to coordinate online the conflict between satisfying the constraints and improving the performance of the uncertain system. The moving-horizon control principle of predictive control is to address the objective optimization problem online at each sample moment, which is constantly renewed by the latest measurements of the controlled system, and the calculated control input is actioned on this system until the next sample moment.

The conflict between constraints and performance could be nicely settled by altering the range of the elliptic domain $\Omega (H,{\rho }_f)$ at any moment according to the extent of the disturbances to the uncertain system. Hence, the following LMI optimization problem is constantly refreshed with the latest state ($x(k)$) at each sample moment ($k$) and addressed:

$$\underset{{\rho }_k,{\lambda }_k^2,N_k,R_k,T_{ak},T_{bk},T_{ck},\left\{V_{aik},V_{cik}\right\}}{\min }{\chi }_1{\rho }_k+{\chi }_2{\lambda }_k^2 subject to,$$

(52)

$$\left[\begin{array}{cccccc}{N}_k& 0& -E_{1d}{T}_{bk}& A_d{N}_k+B_{ud}{R}_k& -B_{\omega d}& -E_{1d}{T}_{ak}\\ 0& I& -E_{2d}{T}_{bk}& C_{2d}{N}_k+D_{2d}{R}_k& 0& -E_{2d}{T}_{ak}\\ -T_{bk}^{\mathrm{T}}{E}_{1d}^{\mathrm{T}}& -T_{bk}^{\mathrm{T}}{E}_{2d}^{\mathrm{T}}& T_{ck}& F_{1d}{N}_k+F_{2d}{R}_k& 0& 0\\ {(A_d{N}_k+B_{ud}{R}_k)}^{\mathrm{T}}& {(C_{2d}{N}_k+D_{2d}{R}_k)}^{\mathrm{T}}& {(F_{1d}{N}_k+F_{2d}{R}_k)}^{\mathrm{T}}& N_k& 0& 0\\ -B_{\omega d}^{\mathrm{T}}& 0& 0& 0& {\lambda }_k^{2}I& 0\\ -T_{ak}^{\mathrm{T}}{E}_{1d}^{\mathrm{T}}& -T_{ak}^{\mathrm{T}}{E}_{2d}^{\mathrm{T}}& 0& 0& 0& -T_{ak}\end{array}\right]\ge 0,$$

(53)

$$\left[\begin{array}{cccc}\frac{z_{\infty i,\max }^2}{{\rho }_f}& 0& -e_i^{\mathrm{T}}(C_{\infty d}{N}_k+D_{\infty d}{R}_k)& 0\\ 0& V_{cik}& -F_{1d}{N}_k-F_{2d}{R}_k& 0\\ -{(C_{\infty d}{N}_k+D_{\infty d}{R}_k)}^{\mathrm{T}}{e}_i& -{(F_{1d}{N}_k+F_{2d}{R}_k)}^{\mathrm{T}}& N& 0\\ 0& 0& 0& -V_{aik}\end{array}\right]\ge 0(i=1,2,3,4),$$

(54)

$$\left[\begin{array}{cc}{\rho }_k& x{(k)}^{\mathrm{T}}\\ x(k)& N_k\end{array}\right]\ge 0,$$

(55)

$$\left[\begin{array}{cc}x{(k)}^{\mathrm{T}}{H}_{k-1}x(k)+h_0-h_{k-1}& x{(k)}^{\mathrm{T}}\\ x(k)& N_k\end{array}\right]\ge 0,$$

(56)

$${\rho }_k\le {\rho }_f,$$

(57)

where ${\chi }_1$ and ${\chi }_2$ are the weighting factors, which are used to adjust the weights between the minimization of the ${\mathscr{H}}_{\infty }$ norm from $\omega$ to $z_2$ and the minimization of the range of the elliptic domain $\Omega (H_k,{\rho }_k)$ while maintaining the constraints satisfied, thereby meeting the multifaceted requirements of the controlled system. The LMI (56) is an additional dissipation inequality that is implemented to ensure the dissipativity of the closed-loop system that is destroyed under the moving-horizon control scheme. Moreover, it is determined by the $H_{k-1}$ and dissipation index $h_{k-1}$ at the last moment, and the iterative updates of the $H_k$ and $h_k$ are calculated via $H_k:=N_k^{-1}$ and $h_k:=h_{k-1}-[x{(k)}^{\mathrm{T}}{H}_{k-1}x(k)-x{(k)}^{\mathrm{T}}{H}_{k}x(k)]$ with $h_0:=x{(0)}^{\mathrm{T}}{H}_{0}x(0)$.

At the moment $k$, if the semi-definite programming (52) can be addressed online for a given ${\rho }_f$, resulting in ${\rho }_k$, ${\lambda }_k$, $N_k$, $R_k$, and several multipliers, then the feedback gain at the current moment is considered as $K(k)=R_k{N}_k^{-1}$, and thus the closed-loop control input of the controlled system can be specified as follows:

$$u(k)=K(k)x(k),\forall k\ge 0.$$

(58)

At each sample moment, the values of the variables $R_k$ and $N_k$ are obtained by solving the LMI optimization problem (52), where $N_k$ is a positive definite symmetric matrix and $R_k=K(k)N_k$. Then, the feedback gain $K(k)=R_k{N}_k^{-1}$ at the current moment can be calculated after obtaining the values of the above variables. In addition, the state feedback structure is chosen in this paper during the controller design process, so the control input of the system is thus calculated with $u(k)=K(k)x(k)$.

The state $x(k)$ includes the information about the external disturbances to the system and the modeling mistakes caused by the parameter uncertainties. As a matter of fact, the $x(k)$ is used to calculate the value of the feedback gain $K(k)$ at the current moment, and it is also used as the feedback information of the closed-loop system. It should be noted here that the system state $x(k)$ in the control input $u(k)=K(k)x(k)$ and in the LMIs (55) and (56) are the state of the nonlinear system of the two-DOF FJMS. And it needs to be made clear that the purpose of linearizing the controlled system (3) is only to calculate the control feedback gain by solving the LMI optimization problem, and the feedback gain is subsequently used to calculate the control input of the two-DOF FJMS to act on the nonlinear system (3).

In addition to the introduction of the moving-horizon control strategy, another ingenious feature of the algorithm (52) is the treatment of ${\rho }_k$ as an independent variable and as a portion of the objective optimization function. Moreover, the coupling between the system constraints and the performance index is separated by the constant ${\rho }_f$, which consequently makes the optimization problem easily solvable numerically.

For the algorithm described above, the feasibility of the optimization problem at every sample moment is crucial. However, the feasibility of the above online optimization algorithm would not be guaranteed in the case of strong disturbances increasing suddenly at some random moment. Accordingly, borrowing the idea of the scaling method, a non-negative number ($\sigma \ge 0$) is introduced in this paper. The purpose of this improvement is simply to diminish the conservativeness of the algorithm (52) and to enhance its feasibility so that it is capable of coping with larger external disturbances. The robust constrained moving-horizon ${\mathscr{H}}_{\infty }$ control optimization algorithm is as follows:

$$\underset{{\rho }_k,{\lambda }_k^2,N_k,R_k,T_{ak},T_{bk},T_{ck},\left\{V_{aik},V_{cik}\right\}}{\min }{\chi }_1{\rho }_k+{\chi }_2{\lambda }_k^2 subject to (53), (54), (55), (56) and,$$

(59)

$${\rho }_k\le {\rho }_f(1+\sigma ).$$

(60)

Therefore, the robust constrained moving-horizon ${\mathscr{H}}_{\infty }$ control algorithm specifically addresses the LMI optimization problem (59) refreshed by the current moment state $x(k)$ at each sample moment, and if infeasibility occurs, then the value of $\sigma$ is augmented and the optimization problem is recalculated. For one moment, the process of expanding the range of the elliptic domain is diagrammed in Figure 5.

In the theory of robust model predictive control, we resort to the LMI technique to transform the constrained ${\mathscr{H}}_{\infty }$ control problem into a convex optimization problem with LMIs as constraints. In this way, multiple objectives in the controller design requirements could be transformed into multiple LMIs that are used as constraints on the objective function. Secondly, the optimization problem is solved to obtain the optimal control input at the current moment, which is implemented on the nonlinear controlled system, and then the optimization problem is refreshed with the latest state and is resolved again at the next moment, and ultimately the system performance is improved, and the system requirements are fulfilled through continuous moving-horizon optimization control.

5. Properties of the Closed-Loop System

In this section, the closed-loop characteristics of this system are discussed by implementing the above optimization algorithm (59) on the controlled system. The closed-loop system is mainly confronted with two situations: when the external disturbances in the system are relatively small, the optimization algorithm (52) is feasible at each sample moment, and when the external disturbances are sudden or large, it is only necessary to enlarge the value of $\sigma$ to guarantee the feasibility of the optimization algorithm (59) to achieve some degree of relaxation so that the controlled system can handle unpredictable and large disturbances.

Theorem 1.

Suppose the following:

• At every moment, the semi-definite programming (52) based on the state $x(k)$ at the current moment has the results as ${\rho }_k$, ${\lambda }_k$, $N_k$, $R_k$, and several multipliers;
• The performance optimization metric$\left\{{\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_{k-1},{\lambda }_k\right\}$is bounded.

• Then, for all $\delta \in Y_{\delta }$, the closed-loop controlled system under the action of $u(k)=K(k)x(k)$would have the following properties:

• The constraints of the controlled system are all fulfilled;
• Under the perturbations of external limiting energy, the state $x(k)$of the system will converge to zero when $k\to \infty$;
• The dissipation inequality ${\displaystyle \sum _{i=0}^k\left({\Vert z_2(i)\Vert }_2^2-{\overline{\lambda }}^2{\Vert \omega (i)\Vert }_2^2\right)}\le x{(0)}^{\mathrm{T}}{H}_{0}x(0)$ is valid for any moment ($k$), where $\overline{\lambda }=\max \left\{{\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_{k-1},{\lambda }_k\right\}$;
• The ${\mathscr{H}}_{\infty }$ norm from the system perturbation $\omega$ to the performance output $z_2$ is always no greater than ${\lambda }_{\infty }$, where ${\lambda }_{\infty }=\underset{k\to \infty }{\lim }\max \left\{{\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_{k-1},{\lambda }_k\right\}$.

Proof of Theorem 1.

If there is an appropriate ${\rho }_f$ such that LMIs (55) and (57) are valid, then it also means that the closed-loop system state $x(k)$ is within the elliptic domain $\Omega (H_k,{\rho }_k)=\left\{x{(k)}^{\mathrm{T}}{H}_{k}x(k)\le {\rho }_k\right\}$. For all $\delta \in Y_{\delta }$, the inequalities (43), (45), (50), and (54) are all equivalent to each other, which subsequently leads to $\left|z_{\infty i}(k)\right|\le z_{\infty i,\max }(i=1,2,3,4)$, and the first property is proved.

At any moment ($k$), if the optimization solution (${\rho }_k$, ${\lambda }_k$, $N_k$, $R_k$ and several multipliers) is valid by substitution in the LMIs (42) and (53), then the dissipative inequality (29) is expressed to work. Therefore, the following may be obtained:

$$x{(k+1)}^{\mathrm{T}}{H}_{k}x(k+1)-{\displaystyle \sum _{i=1}^k\left(x{(i)}^{\mathrm{T}}{H}_{i}x(i)-x{(i)}^{\mathrm{T}}{H}_{i-1}x(i)\right)}-x{(0)}^{\mathrm{T}}{H}_{0}x(0)\le {\displaystyle \sum _{i=0}^k\left({\lambda }_i^2{\Vert \omega (i)\Vert }_2^2-{\Vert z_2(i)\Vert }_2^2\right)}.$$

(61)

The (56) formed by the dissipation constraint satisfies ${\displaystyle \sum _{i=1}^k\left(x{(i)}^{\mathrm{T}}{H}_{i}x(i)-x{(i)}^{\mathrm{T}}{H}_{i-1}x(i)\right)}\le 0$. Letting $\overline{\lambda }=\max \left\{{\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_{k-1},{\lambda }_k\right\}$, the inequality (61) can be simplified as follows:

$$x{(k+1)}^{\mathrm{T}}{H}_{k}x(k+1)-x{(0)}^{\mathrm{T}}{H}_{0}x(0)\le {\displaystyle \sum _{i=0}^k\left({\overline{\lambda }}^2{\Vert \omega (i)\Vert }_2^2-{\Vert z_2(i)\Vert }_2^2\right)}.$$

(62)

Due to the fact that $H_k$ is positive definite and $\left\{{\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_{k-1},{\lambda }_k\right\}$ is bounded, then the third property is proved to be permanent. If there is finite energy of the perturbations to the controlled system, then it is obtained that ${\displaystyle \sum _{i=0}^{\infty }{\Vert z_2(i)\Vert }_2^2}\le x{(0)}^{\mathrm{T}}{H}_{0}x(0)+{\lambda }_{\infty }^2{\displaystyle \sum _{i=0}^{\infty }{\Vert \omega (i)\Vert }_2^2}$ when the limit of the inequality (62) at $k\to \infty$ is considered, where ${\lambda }_{\infty }=\underset{k\to \infty }{\lim }\max \left\{{\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_{k-1},{\lambda }_k\right\}$. Thus, the second property is evidenced by the above procedure. As for the last property, it is proved when the zero initial state is selected. □

Considering the circumstances of the optimization control algorithm (59) to be implemented, the following findings would be produced with less conservatism.

Theorem 2.

Suppose the following:

• The LMI (53) and LMI (54) are all feasible;
• The amplitude of the perturbations at any moment is not infinite;
• The performance optimization metric $\left\{{\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_{k-1},{\lambda }_k\right\}$ is bounded.

• Then, for all $\delta \in Y_{\delta }$, the controlled system with the effect of the robust constrained moving-horizon ${\mathscr{H}}_{\infty }$ controller would have the following properties:

• At every moment ($k$), there is $\left|e_i^{\mathrm{T}}(C_{\infty d}+D_{\infty d}K(k))x(k)\right|\le z_{\infty i,\max }(i=1,2,3,4)$, and this relationship is established to symbolize that the constraint requirements of this controller are fulfilled;
• The last three properties of Theorem 1 are also present.

Proof of Theorem 2.

The feasibility of the optimization algorithm (59) at any sample moment is guaranteed by the introduced factor $\sigma \ge 0$. The control gain is calculated with $K(k)=R_k{N}_k^{-1}$, and the first property is clearly well established. The proofs of the remaining properties are analogous to those of Theorem 1. □

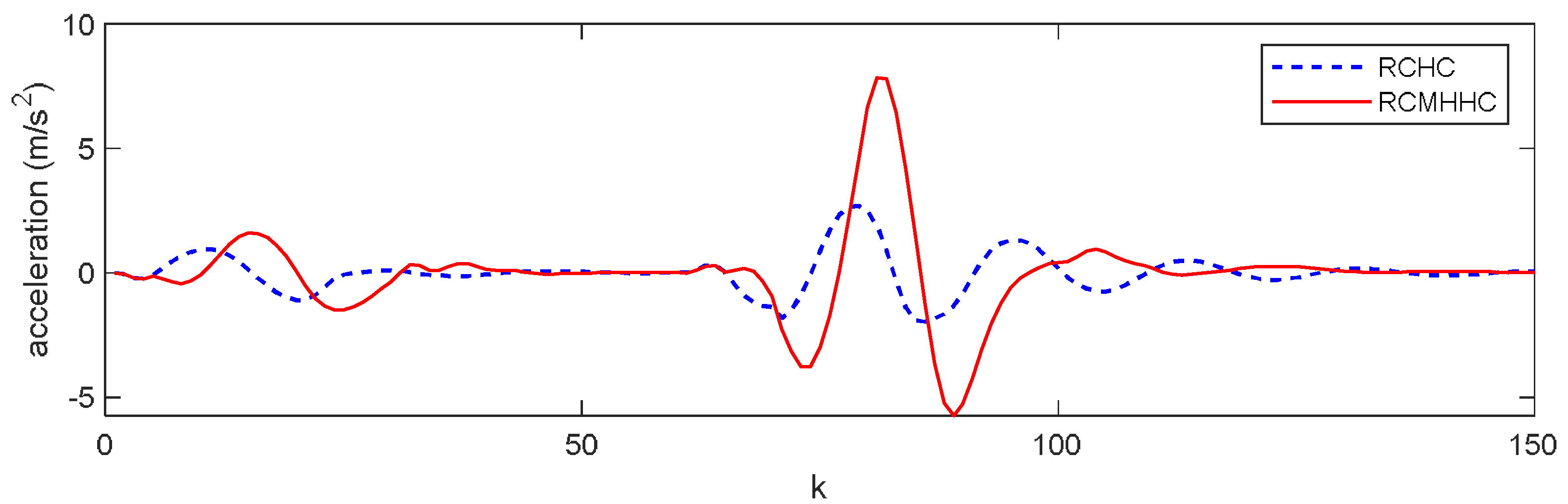
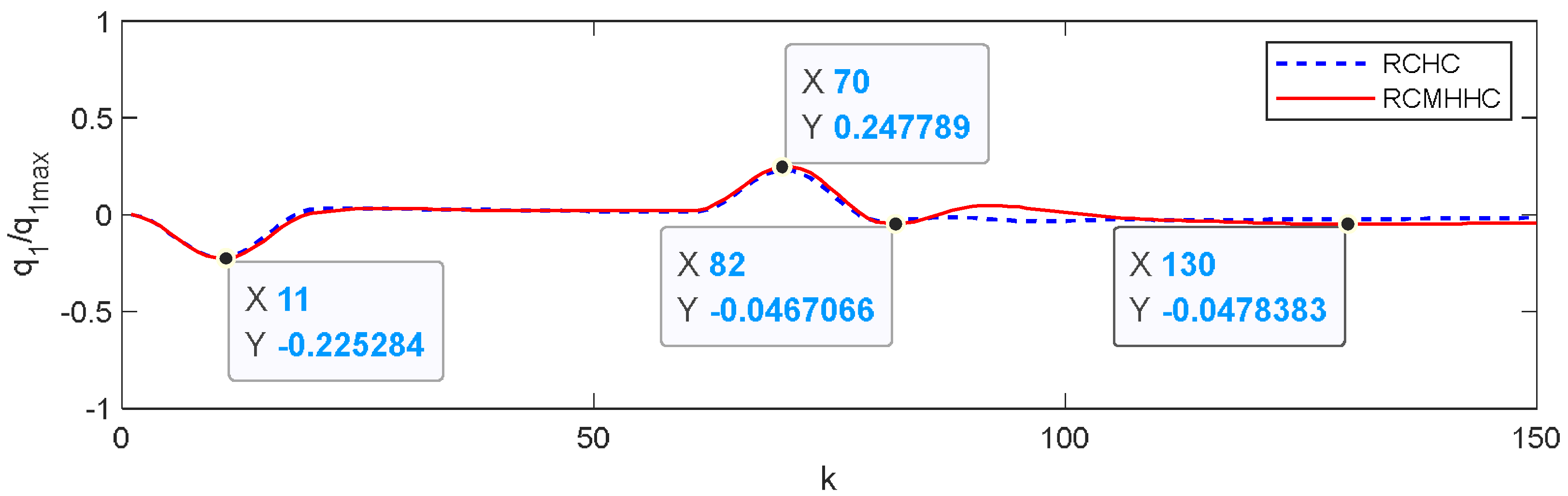
6. Simulation Results

In this section, the robust constrained moving-horizon ${\mathscr{H}}_{\infty }$ control algorithm is implemented for the dynamic model of the two-DOF FJMS, and the ${\mathscr{H}}_{\infty }$ performance of this controlled system is tested. The nominal values of the parameters of this manipulator system are shown in

Table 2. The nominal values of the parameters of the two-DOF FJMS.

Symbol	Values
$L_1$, $L_2$	0.5 m, 0.5 m
$L_{c1}$, $L_{\mathrm{c}2}$	0.25 m, 0.25 m
$m_1$, $m_2$	20 kg, 10 kg
$I_1$, $I_2$	5.6 kg·m2, 2.8 kg·m2
$J_1$, $J_2$	6.183 kg·m2, 0.858 kg·m2
${\overline{k}}_1$, ${\overline{k}}_2$	1000 N·m/rad, 1000 N·m/rad
$g$	9.81 m/s2

[46], selecting the sample time as $T_s=0.01\mathrm{s}$, and discretizing the two-DOF FJMS. In order to accomplish the stabilization of this system at the equilibrium point under the influence of external disturbances and parameter uncertainties, the whole system should have certain constraints on the sizes of both the joint angles of the two-DOF FJMS: $q_{1,\max }=0.15$ and $q_{2,\max }=0.15$. The main reason for constraining the maximum value of the two joint angles to be so small is mainly because of the consideration that there are certain conditions for linearizing the two-DOF FJMS using Taylor series expansion. Moreover, due to the saturation of the actuators, the torque values as the control input are also constrained: $u_{1,\max }=100$ and $u_{2,\max }=50$. To simplify the calculation procedure, the normalized control torques and joint angles are chosen as the constrained output here, where the system constraints are bounded by $z_{\infty i,\max }=1(i=1,2,3,4)$.

As for the parameter uncertainties, what are considered here are the spring-stiffness coefficients shown in Equation (13), where the normalized weighted coefficients are $W_{k_1}=0.2$ and $W_{k_2}=0.2$. In order to verify the feasibility and robustness of the designed control algorithm, the real values of the two uncertain parameters are set to different values at different time periods, as shown below:

$$k_1=\{\begin{array}{l}{\overline{k}}_1(1-0.2), 0\le k\le 30\\ {\overline{k}}_1(1+0.2), 30\le k\le 70\\ {\overline{k}}_1(1+0.6), 70\le k\le 150\end{array},k_2=\{\begin{array}{l}{\overline{k}}_2(1-0.2), 0\le k\le 30\\ {\overline{k}}_2(1+0.2), 30\le k\le 70\\ {\overline{k}}_2(1+0.6), 70\le k\le 150\end{array},$$

(63)

The external disturbances to the controlled system are assumed to be as follows:

$${\omega }_1={\omega }_2=\{\begin{array}{cc}\frac{\pi }{6}\sin (\frac{k\pi }{10}),\hfill & \hfill 0\le k\le 20\hfill \\ -\frac{\pi }{6}\sin (\frac{k\pi }{10}),\hfill & \hfill 60\le k\le 80\hfill \\ 0,\hfill & \hfill else\hfill \end{array},$$

(64)

For the design of the robust constrained moving-horizon ${\mathscr{H}}_{\infty }$ controller, the weight factors are selected as ${\chi }_1=0.1$ and ${\chi }_2=1$ to achieve a greater system performance and less energy consumption. Moreover, the size of the fixed elliptic domain $\Omega (H,{\rho }_f)$ is chosen as ${\rho }_f=10$. The RCHC (the LMI optimization algorithm (52))and RCMHHC (the LMI optimization algorithm (59)) were implemented on the two-DOF FJMS for simulation, and the comparative outputs of the experiments are shown in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12.

In Figure 10, it can be seen that the system under the action of RCHC has violated the control input constraint of $u_1$ at $74\le k\le 77$ and $82\le k\le 85$. The only way to make the system constraints satisfied is to increase the value of ${\rho }_f$ to expand the elliptic domain. However, the result of doing so would make the performance of this system worse, which fully illustrates the disadvantages of RCHC. In contrast, the control input constraints of the controlled system are well satisfied with the action of RCMHHC. In addition, we can discover that both joint angles are not out of our constraints during the whole process, according to the simulation results in Figure 8 and Figure 9. It should be noted here that the normalized values of the joint angles are shown in both images. Therefore, the actual maximum value of the two joint angles during the simulation is just $0.2478\times 0.15=0.03717 \mathrm{rad}$. In the later part of the simulation, the two joint angles of this system are basically stabilized around the $X$ axis, where the output curve of $q_2$ may not be as smooth as that of $q_1$ in the later stages, but the actual value of the joint angle of $q_2$ at $k=136$ is $0.0975\times 0.15=0.014625 \mathrm{rad}$. It is possible to determine that the designed controller is capable of stabilizing the nonlinear two-DOF FJMS at the vertical equilibrium position after acting on it. In Figure 6 and Figure 7, the reason why the system performance output under the action of RCMHHC does not perform as well as RCHC at some moments is caused by the concession of the system performance to the unsatisfied constraints due to the impact of larger disturbances. Figure 12 displays the variation curves of the performance indices of both algorithms. After the comparative analysis of the above output curves, the significant advantage of RCMHHC can be found in the online reconciliation of the conflict between satisfying the system constraints and improving the control performance at any moment. The coordination mechanism of RCMHHC is to decrease the performance requirements when necessary to make sure that the hard constraints are satisfied, and to enhance the performance requirements in time when the controlled system is far from the boundary of the constraints.

Both algorithms work by solving the LMI optimization problem. All the LMIs in the LMI optimization problem are derived based on the linear system, and the problem is solved through the toolbox of MATLAB and is thus less time-consuming. The value of the feedback gain obtained by solving RCHC is fixed, and the LMI optimization problem only needs to be solved once. However, the idea of moving-horizon control in RCMHHC makes the state of the system appear in the LMIs, so that its feedback gain value is not fixed, and it is necessary to solve the LMI optimization problem at every sample moment. In contrast, the real-time property of RCMHHC may not be as good as that of RCHC, but RCMHHC can improve the ${\mathscr{H}}_{\infty }$ performance of the two-DOF FJMS well while ensuring that the system constraints are satisfied. In conclusion, the real-time property of solving the LMI optimization problem at each moment can be satisfied for conventional PCs.

7. Conclusions

For the two-DOF FJMS, this paper designs a robust constrained moving-horizon ${\mathscr{H}}_{\infty }$ controller to accomplish the control objectives of this system while considering external disturbances, parameter uncertainties, and input–output constraints simultaneously. After establishing the LFT uncertain system of the two-DOF FJMS, the semi-definite programming problem with LMIs as constraints is developed via the full-block multiplier technique, ${\mathscr{H}}_{\infty }$ control, and MPC, for which the control feedback gain of the two-DOF FJMS can be obtained after solving the LMI optimization problem. The feedback gain is subsequently used to calculate the control input of the controlled system to act on the nonlinear two-DOF FJMS under the state feedback structure. Based on the moving-horizon control principle of MPC, this LMI optimization problem is refreshed with the current state of the system at each sample moment and solved online, and so on, in a continuous iterative loop. The simulation of the designed controller implemented on the two-DOF FJMS shows that the proposed control algorithm is able to improve the system ${\mathscr{H}}_{\infty }$ performance while ensuring that the system constraints are satisfied, and it could coordinate online the conflict between both requirements.