A Cooperative Game Hybrid Optimization Algorithm Applied to UAV Inspection Path Planning in Urban Pipe Corridors
Abstract
:1. Introduction
- (i)
- A cost function is formulated to transform path planning into an optimization problem. Considering all grids in the corridors as obstacles, the safety cost function is formulated for the corridor grid map model.
- (ii)
- A hybrid algorithm of SPSO and DE algorithms based on the Nash bargaining theory is proposed by introducing a Nash bargaining cooperation game model, which dramatically increases the searching ability of the algorithms.
- (iii)
- SPSO, PSO, and DE are introduced in comparative analysis experiments to evaluate the effectiveness of the GSPSODE algorithm.
- (iv)
- A high-precision urban pipe corridor 3D grid map model and scenario based on the RflySim platform are constructed as an experimental verification environment for UAV inspection path planning schemes to evaluate the effectiveness and feasibility of the path planning scheme generated by the GSPSODE algorithm.
2. Problem Formulation and Model Construction
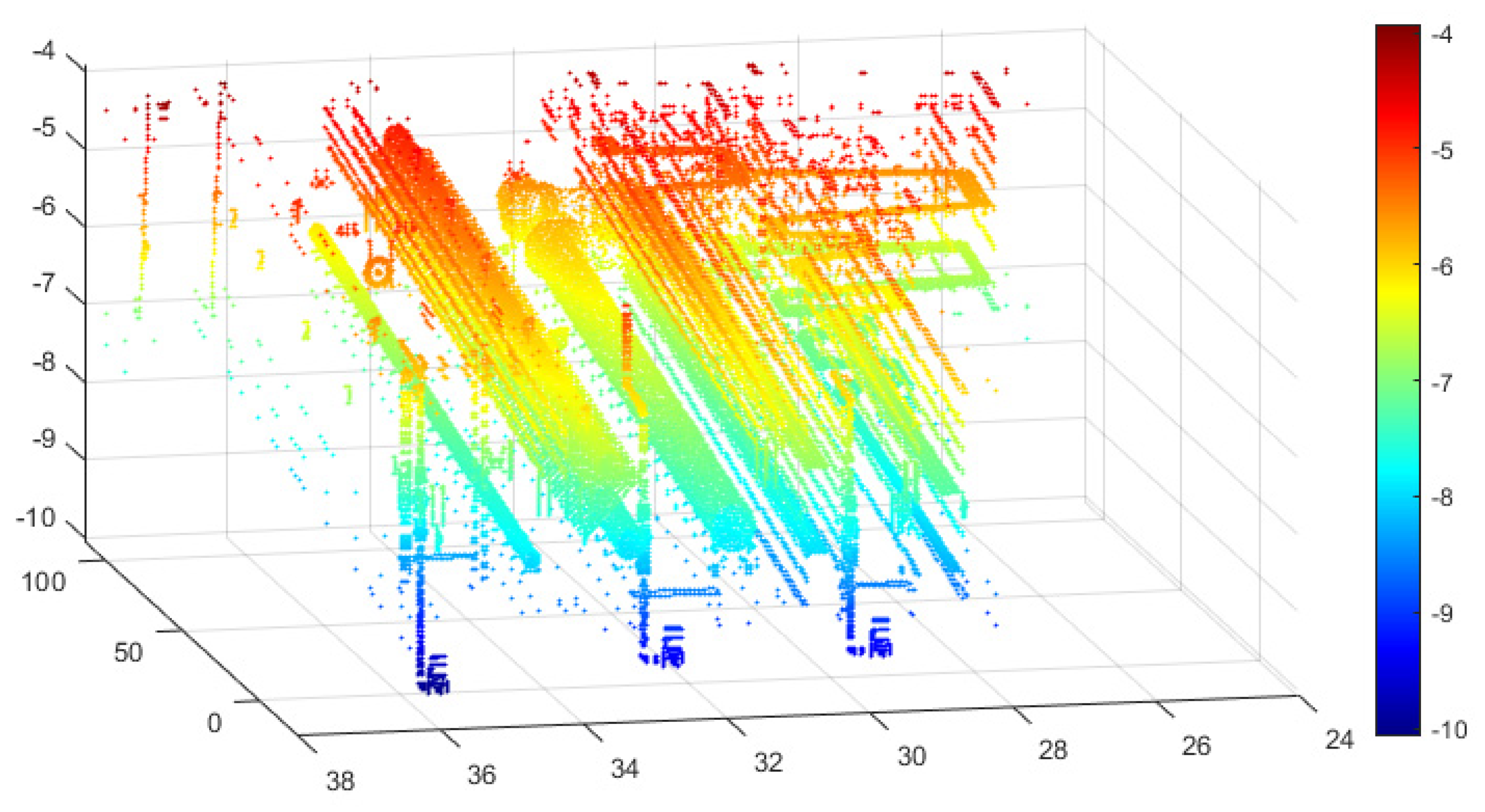
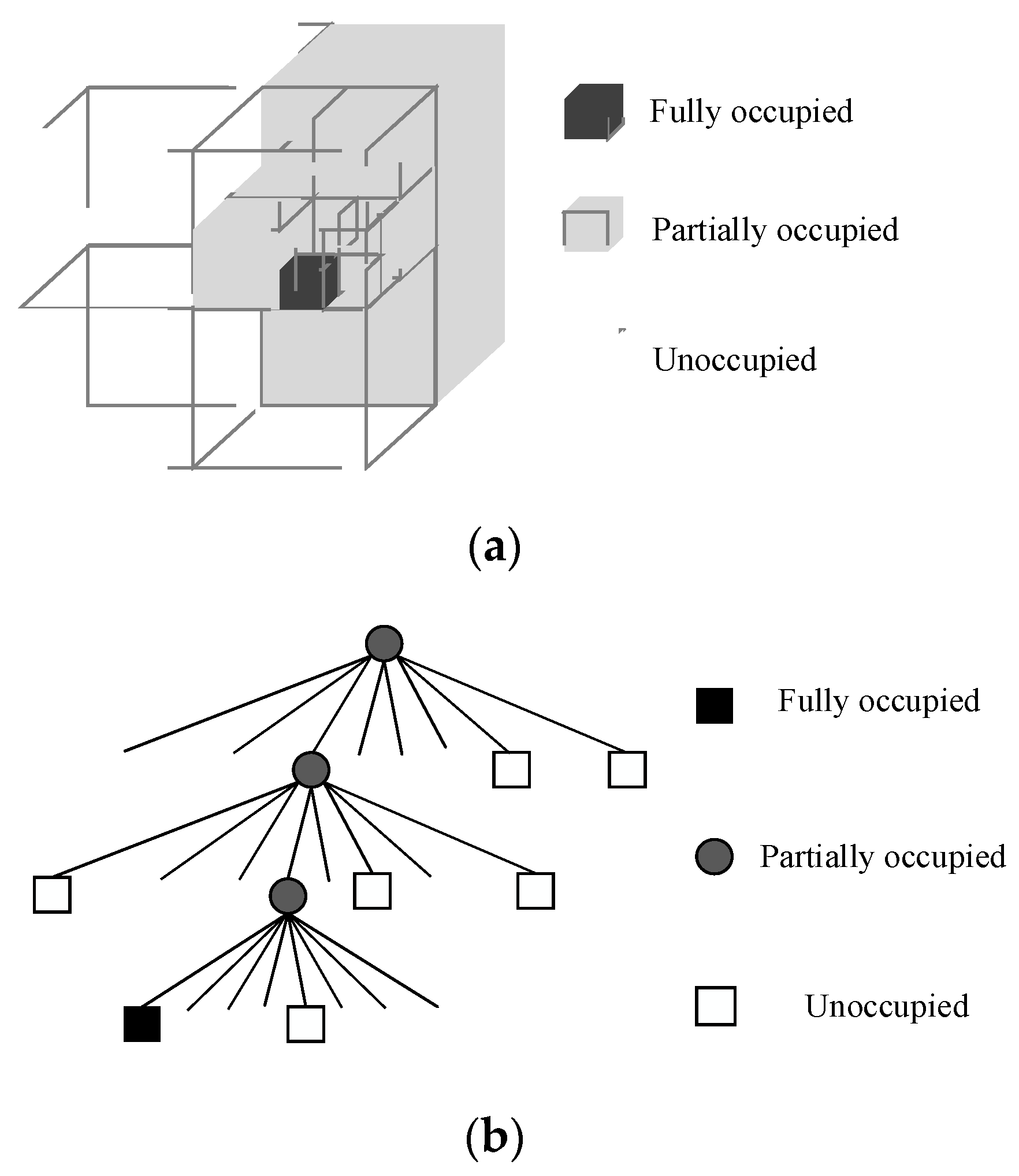
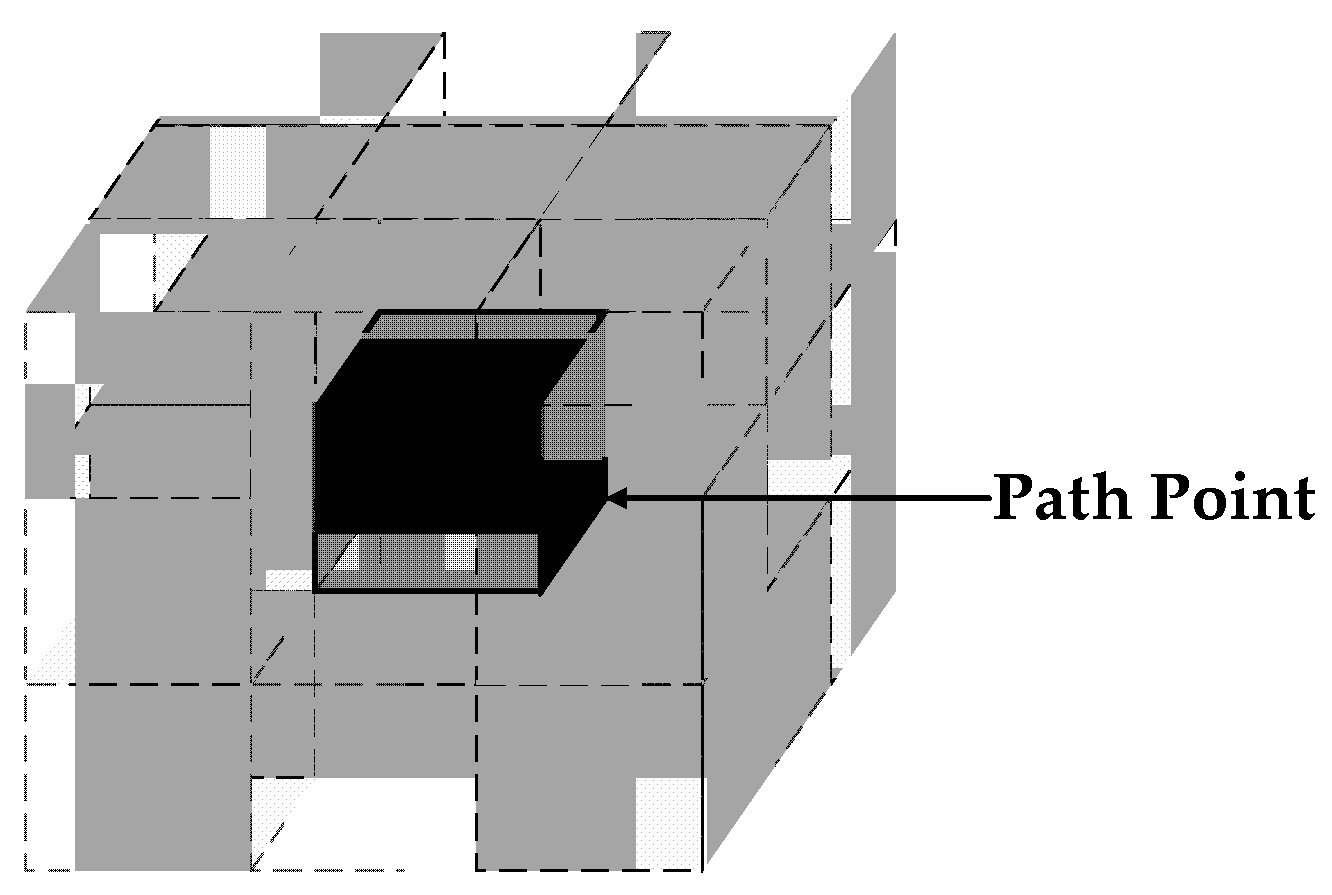
2.1. Map of Urban Pipe Corridors
2.2. Constraints
- (I)
- Path length constraints
- (II)
- Safety and feasibility constraints
- (III)
- Smooth constraints
2.3. Overall Cost Function
3. GSPSODE for UAV Path Planning
3.1. Nash Bargaining Cooperation Game Model
3.2. Spherical Vector Particle Swarm Optimization (SPSO)
- (I)
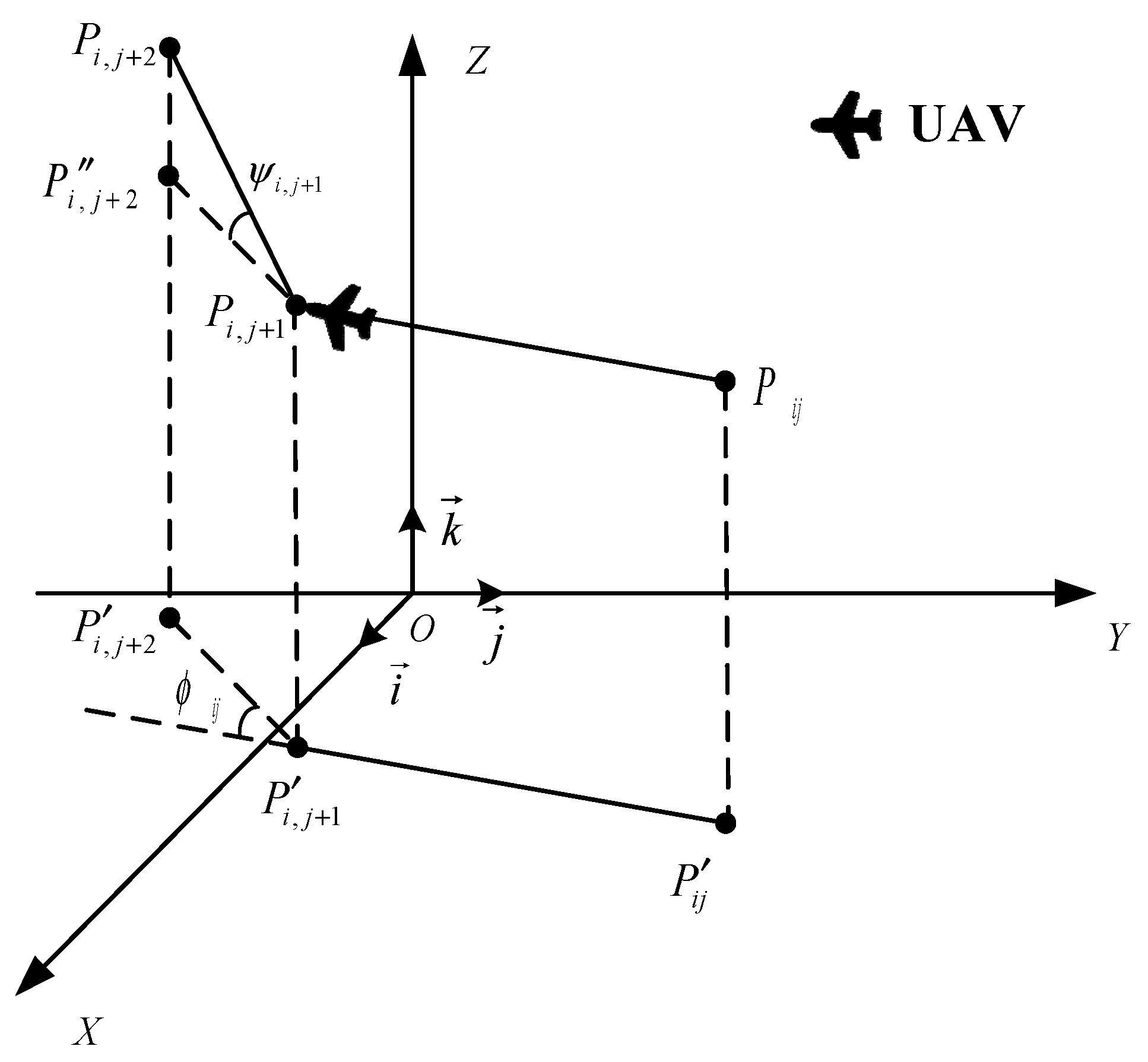
- SPSO is one of the PSO variants, which is created by introducing a spherical vector coordinate system. Each path is encoded as a set of vectors used to describe the movement of the UAV between neighboring waypoints, as represented by the three components of magnitude , elevation , and azimuth , corresponding to the UAV’s speed, turn angle, and climb angle. The flight path is represented by a N × 3D hyper spherical vector consisting of N nodes. The SPSO algorithm where is the position of the particle, and then, is the velocity increase in that particle, is shown in Equation (9):
- (II)
- Consider each path as a volume-less particle in a N × 3D search space, flying in the search space at a certain speed, which is dynamically adapted according to its own flight experience and that of its companions. The ith particle is denoted as = (,, …,), and the best position it experiences is denoted as a 1 × N-dimensional vector . The best position experienced by all particles in the population is denoted as a 1 × N-dimensional vector . and are, respectively, the 1 × 3D spherical vector and velocity . For each generation, the update is performed according to the following Equation (10):
- (III)
- To determine and , it is necessary to map the flight path in the spherical vector coordinate system to path used for evaluating the costs. The mapping ξ: of vector to waypoint and the local and global best positions can be computed as Equations (11) and (12):
3.3. Differential Evolution (DE)
- (I)
- First, a mutation operation is performed to select two individuals from among the parent individuals to generate a difference vector, which is scaled by a scale factor and then summed with the base vector to generate the experimental individual.
- (II)
- Then, crossover operations are performed on the parent individuals and the corresponding experimental individuals to generate new offspring individuals. Common types of crossovers are binomial and exponential, etc.
- (III)
- Finally, a selection operation is performed between the parent and offspring individuals, and individuals meeting the requirements are saved to the next generation population.
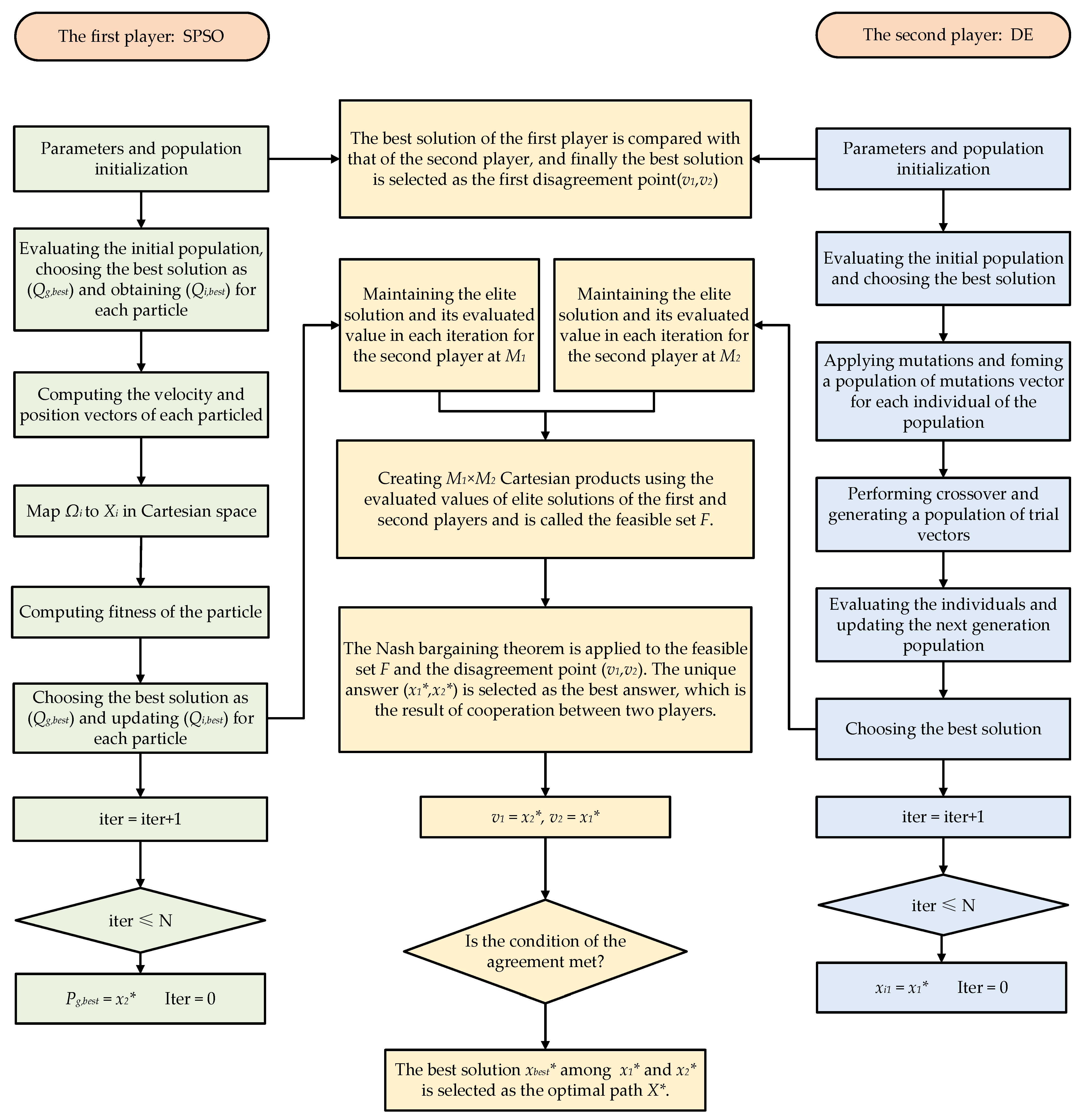
3.4. The Proposed Algorithm
- (I)
- The initial populations of the two players, SPSO and DE, are evaluated independently by the cost function, and all solutions of the two players are evaluated to select the best solution for the first and second players.
- (II)
- The two better solutions are compared, so that the best solution is chosen as the disagreement point in the first round of the game. Since the game has the same conditions for both players and is symmetric, the values are equal in the first round.
- (III)
- In each round of the game, the two players each run N times, and in each iteration, the best solutions and their evaluation values are stored for the first player in and the second player in , respectively, which means that N elite solutions are stored in the sets and for each iteration:
- (IV)
- The feasible set is the Cartesian product of the best solutions of the two players in N iterations:
- (V)
- After N iterations, SPSO and DE enter the game environment and play the cooperative game based on the Nash bargaining theory, and the unique solution = is selected as the best solution due to the Pareto optimality property.
- (V)
- is the game profit of the first player, which is used as the base vector in the DE mutation operator in the next iteration, resulting in a change in the DE mutation operator. is the second player’s game profit, which acts as the lead particle in SPSO to update the particle velocity vector in the next iteration, changing the direction of the particle’s motion. In addition, the only solution in this round of Nash bargaining is seen as a point of disagreement in the next round of Nash bargaining.
- (VII)
- If the conditions of the protocol are satisfied, the best value from the two values is chosen as the final solution; otherwise, the game is repeated for the next round.
4. Results and Analysis
4.1. Scenario Setup
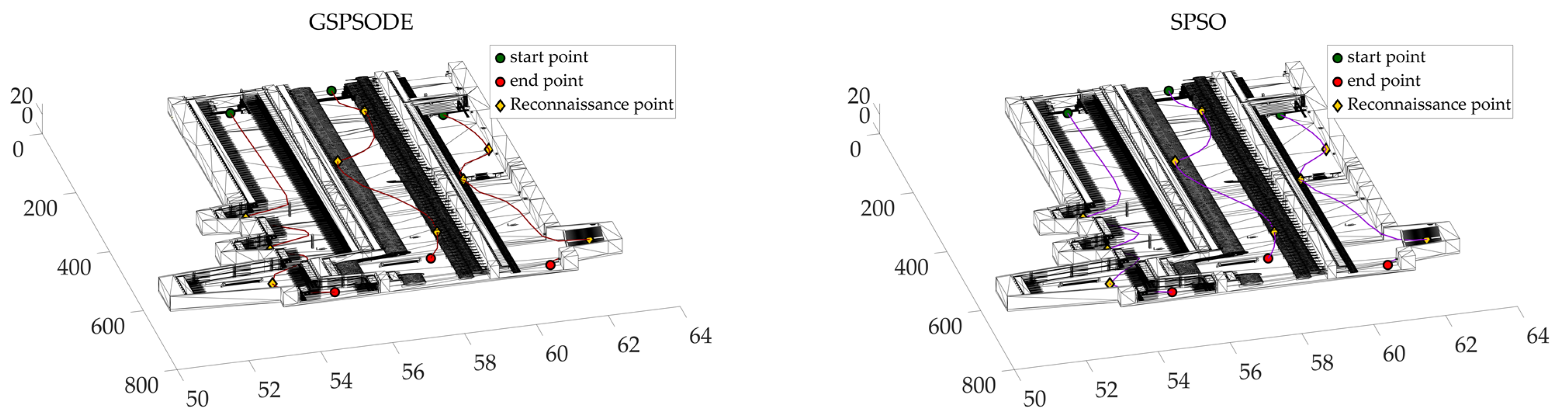
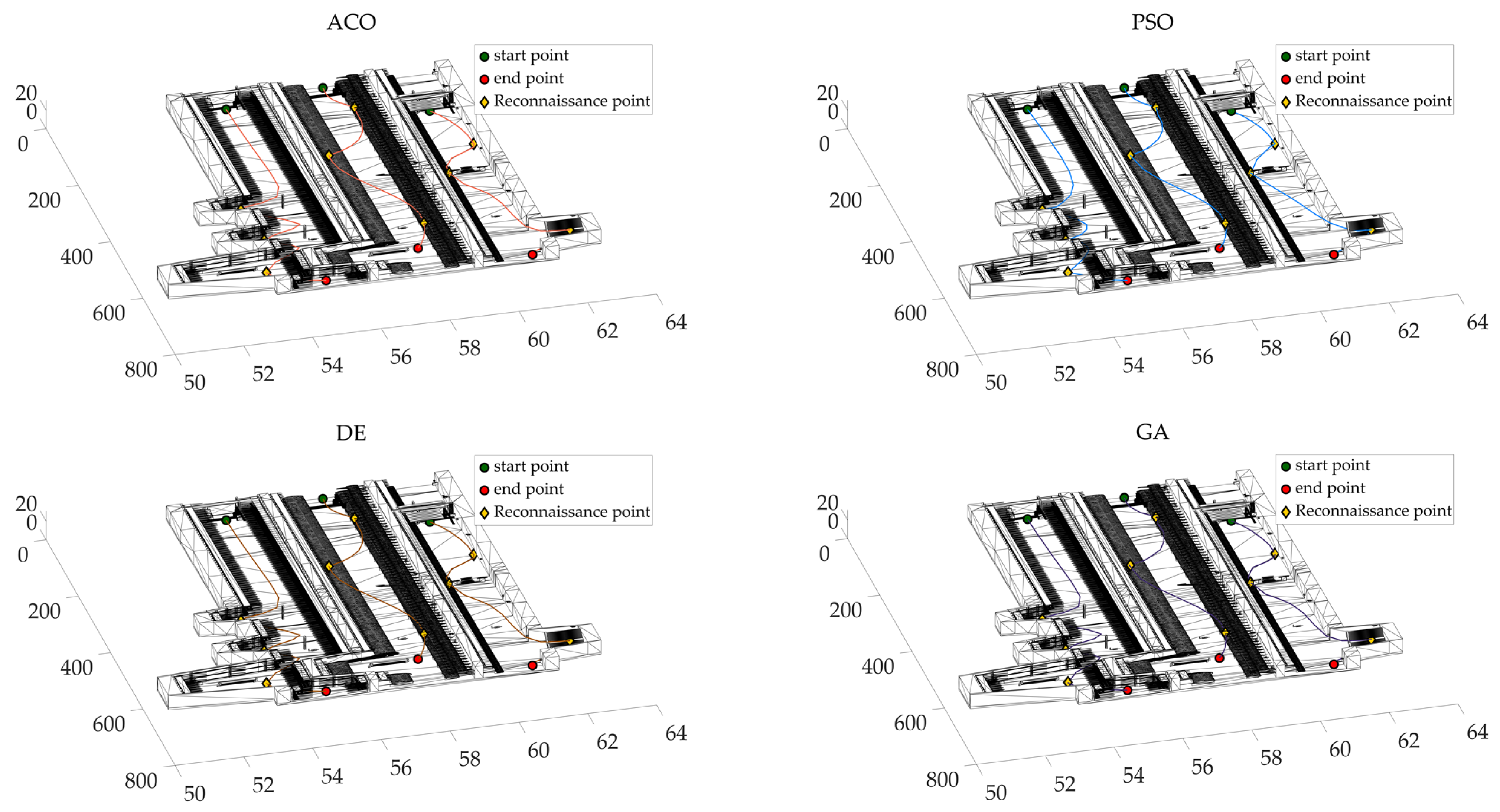
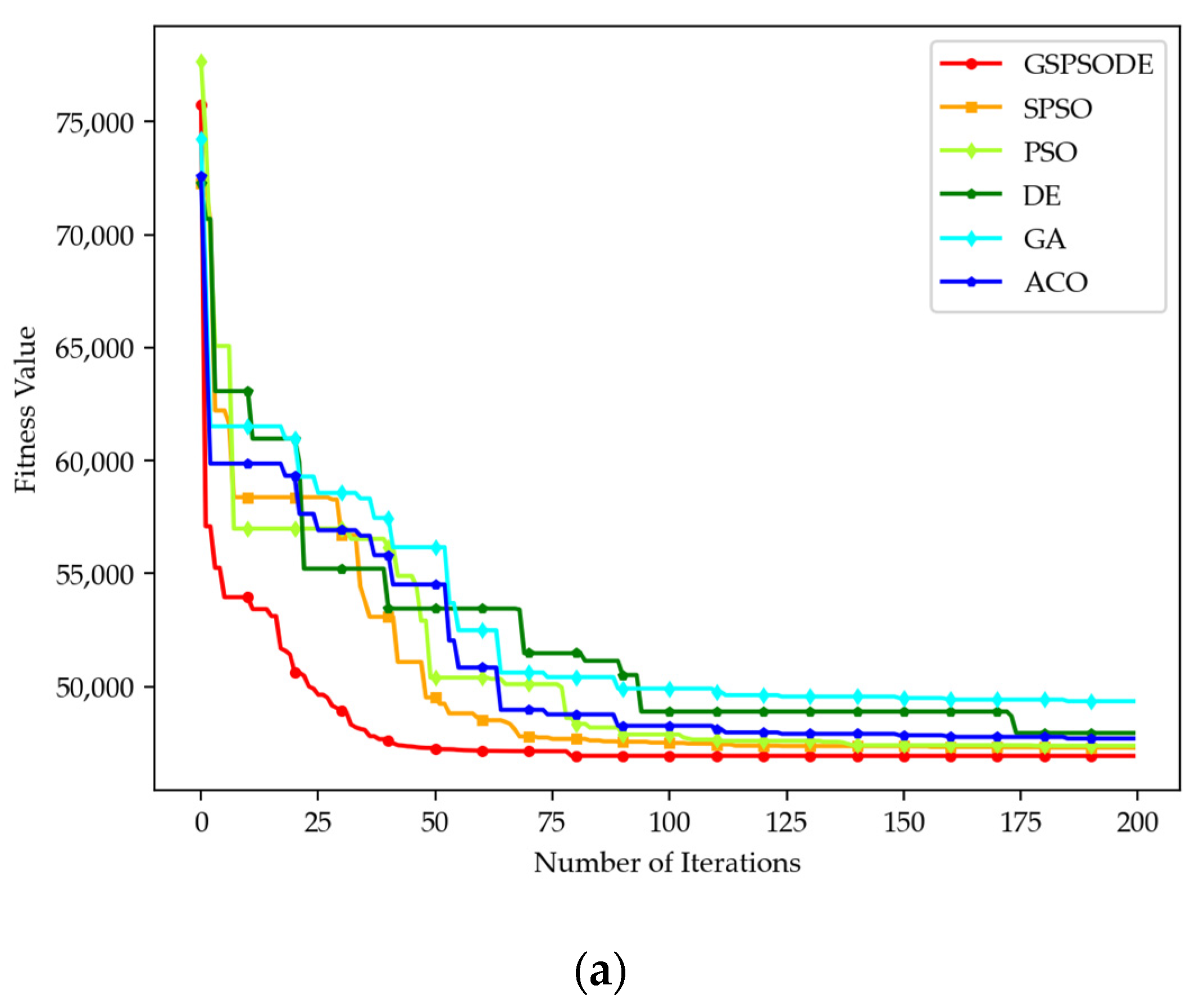
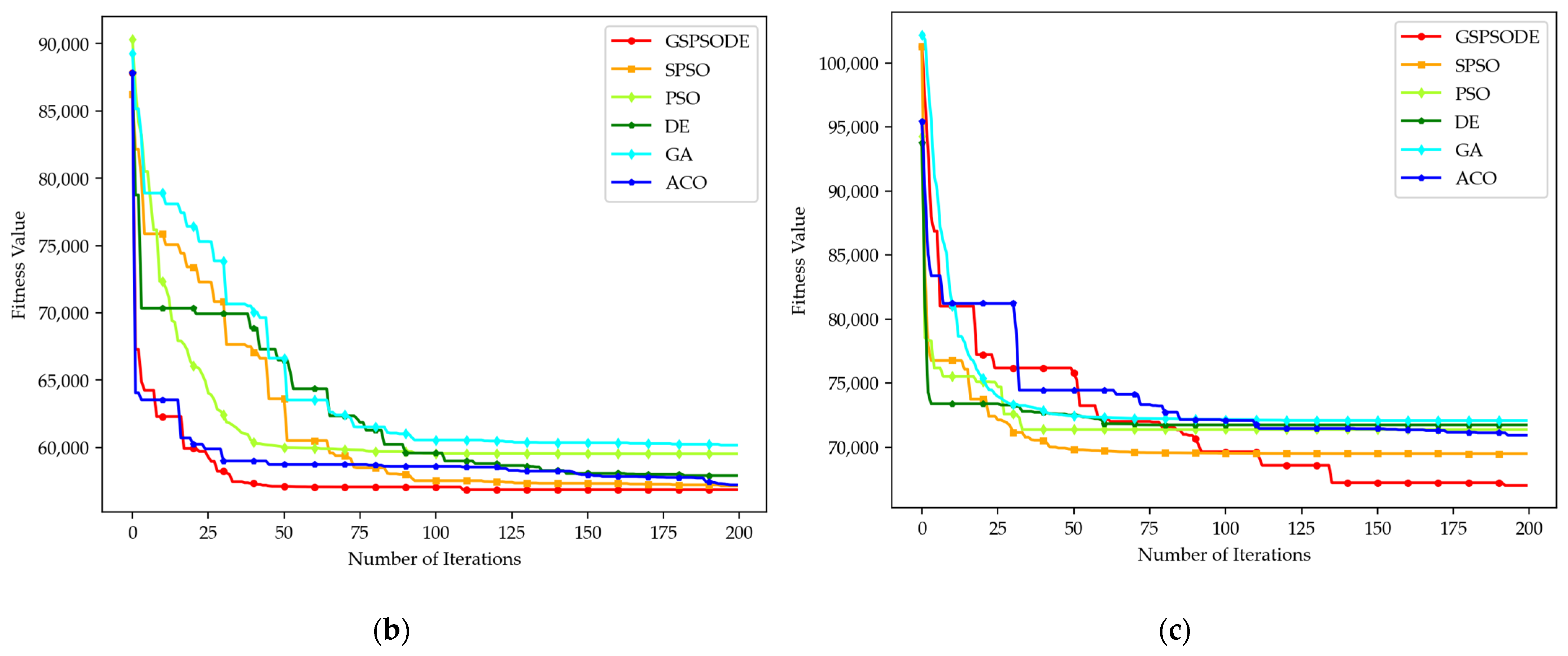
4.2. Comparative Analysis
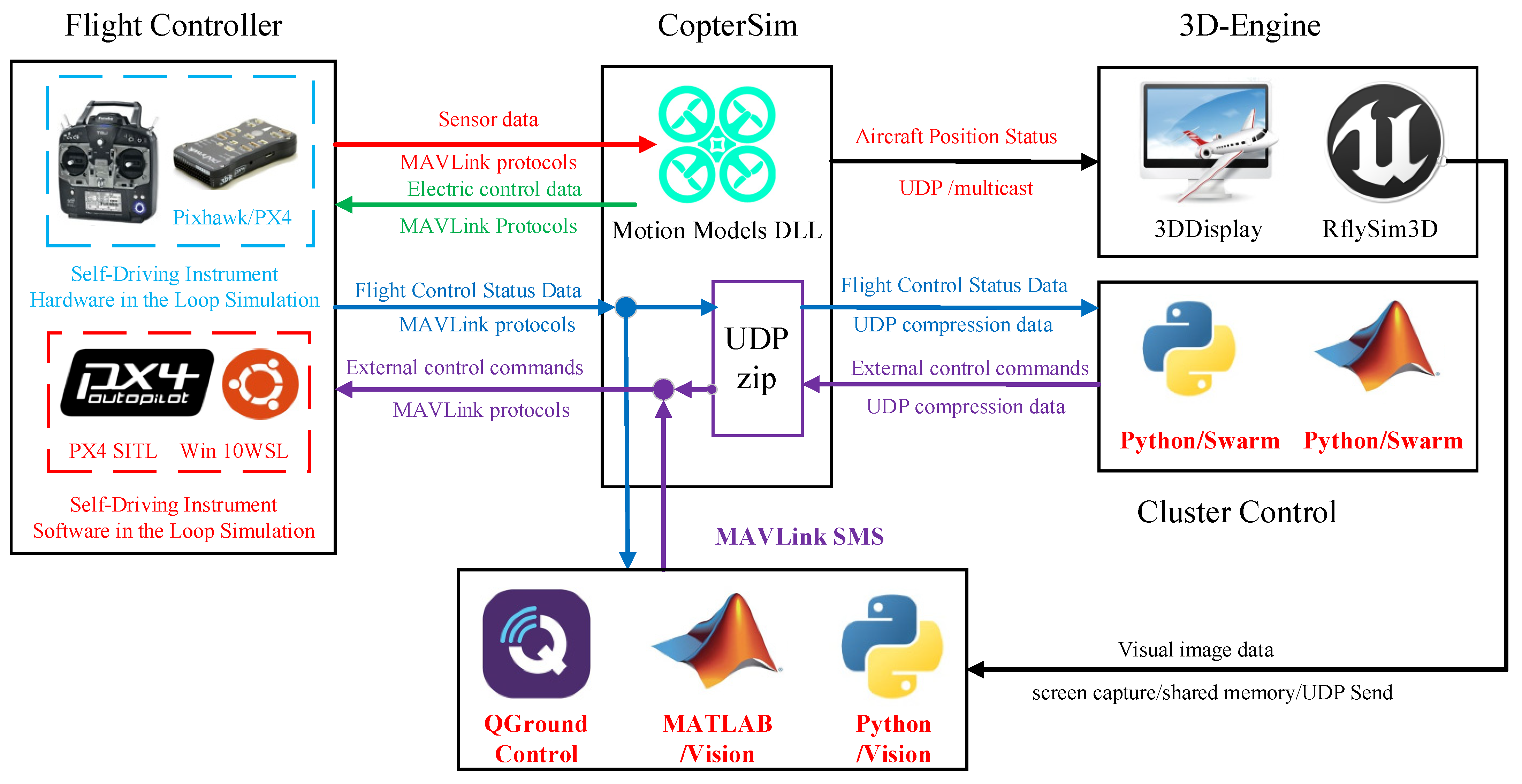
4.3. RflySim Simulation
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, D.; Zhang, Y.; Gong, Z.; Wu, T. A SLAM Method Based on Multi-Robot Cooperation for Pipeline Environments Underground. Sustainability 2022, 14, 12995. [Google Scholar] [CrossRef]
- Li, R.; Ma, H. Research on UAV Swarm Cooperative Inspection and Combat Technology. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27 November 2020; pp. 996–999. [Google Scholar]
- Aljalaud, F.; Kurdi, H.; Youcef-Toumi, K. Autonomous Multi-UAV Path Planning in Pipe Inspection Missions Based on Booby Behavior. Mathematics 2023, 11, 2092. [Google Scholar] [CrossRef]
- da Silva, Y.M.R.; Andrade, F.A.A.; Sousa, L.; de Castro, G.G.R.; Dias, J.T.; Berger, G.; Lima, J.; Pinto, M.F. Computer Vision Based Path Following for Autonomous Unmanned Aerial Systems in Unburied Pipeline Onshore Inspection. Drones 2022, 6, 410. [Google Scholar] [CrossRef]
- Cao, Y.; Wei, W.; Bai, Y.; Qiao, H. Multi-base multi-UAV cooperative inspection path planning with genetic algorithm. Clust. Comput. 2019, 22, 5175–5184. [Google Scholar] [CrossRef]
- Zhen, Z.; Xing, D.; Gao, C. Cooperative search-attack mission planning for multi-UAV based on an intelligent self-organized algorithm. Aerosp. Sci. Technol. 2018, 76, 402–411. [Google Scholar] [CrossRef]
- Wang, X.; Pan, J.-S.; Yang, Q.; Kong, L.; Snášel, V.; Chu, S.-C. Modified mayfly algorithm for UAV path planning. Drones 2022, 6, 134. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Ding, G.; Chen, J.; Gao, F.; Han, Z. Completion Time Minimization with Path Planning for Fixed-Wing UAV Communications. IEEE Trans. Wirel. Commun. 2019, 18, 3485–3499. [Google Scholar] [CrossRef]
- Radácsi, L.; Gubán, M.; Szabó, L.; Udvaros, J. A Path Planning Model for Stock Inventory Using a Drone. Mathematics 2022, 10, 2899. [Google Scholar] [CrossRef]
- Niewola, A.; Podsedkowski, L. L* algorithm—A linear computational complexity graph searching algorithm for path planning. J. Intell. Robot. Syst. 2018, 91, 425–444. [Google Scholar] [CrossRef]
- Julius Fusic, S.; Ramkumar, P.; Hariharan, K. Path Planning of Robot Using Modified Dijkstra Algorithm. In Proceedings of the 2018 National Power Engineering Conference (NPEC), Madurai, India, 9 March 2018. [Google Scholar]
- Zammit, C.; van Kampen, E.-J. Comparison Between A* and RRT Algorithms for 3D UAV Path Planning. Unmanned Syst. 2022, 10, 129–146. [Google Scholar] [CrossRef]
- Yang, J.; Xu, X.; Yin, D.; Ma, Z.; Shen, L. A Space Mapping Based 0–1 Linear Model for Onboard Conflict Resolution of Heterogeneous Unmanned Aerial Vehicles. IEEE Trans. Veh. Technol. 2019, 68, 7455–7465. [Google Scholar] [CrossRef]
- Shivgan, R.; Dong, Z. Energy-Efficient Drone Coverage Path Planning Using Genetic Algorithm. In Proceedings of the 2020 IEEE 21st International Conference on High Performance Switching and Routing (HPSR), Newark, NJ, USA, 11 May 2020. [Google Scholar]
- Sharma, A. Swarm Intelligence: Foundation, Principles, and Engineering Applications, 1st ed.; Mathematical Engineering, Manufacturing, and Management Sciences; CRC Press: Boca Raton, FL, USA, 2022; ISBN 978-0-367-54661-8. [Google Scholar]
- Sharma, A.; Shoval, S.; Sharma, A.; Pandey, J.K. Path Planning for Multiple Targets Interception by the Swarm of UAVs based on Swarm Intelligence Algorithms: A Review. IETE Tech. Rev. 2022, 39, 675–697. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.; Tu, L. A modified particle swarm optimization using adaptive strategy. Expert Syst. Appl. 2020, 152, 11335. [Google Scholar] [CrossRef]
- Shin, J.-J.; Bang, H. UAV Path Planning under Dynamic Threats Using an Improved PSO Algorithm. Int. J. Aerosp. Eng. 2020, 2020, 8820284–8820301. [Google Scholar] [CrossRef]
- Phung, M.; Ha, Q.P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization. Appl. Soft Comput. 2021, 107, 107376. [Google Scholar] [CrossRef]
- Xu, Z. Rotary unmanned aerial vehicles path planning in rough terrain based on multi-objective particle swarm optimization. J. Syst. Eng. Electron. 2020, 31, 130–141. [Google Scholar] [CrossRef]
- Huo, L.; Zhu, J.; Li, Z.; Ma, M. A hybrid differential symbiotic organisms search algorithm for UAV path planning. Sensors 2021, 21, 3037. [Google Scholar] [CrossRef]
- Abhishek, B.; Ranjit, S.; Shankar, T.; Eappen, G.; Sivasankar, P.; Rajesh, A. Hybrid PSO-HSA and PSO-GA algorithm for 3D path planning in autonomous UAVs. SN Appl. Sci. 2020, 2, 1805–1821. [Google Scholar] [CrossRef]
- Chen, Q.; He, Q.; Zhang, D. UAV Path Planning Based on an Improved Chimp Optimization Algorithm. Axioms 2023, 12, 702. [Google Scholar] [CrossRef]
- Hao, G.; Lv, Q.; Huang, Z.; Zhao, H.; Chen, W. UAV Path Planning Based on Improved Artificial Potential Field Method. Aerospace 2023, 10, 562. [Google Scholar] [CrossRef]
- Dadvar, M.; Navidi, H.; Javadi, H.H.S.; Mirzarezaee, M. A cooperative approach for combining particle swarm optimization and differential evolution algorithms to solve single-objective optimization problems. Appl. Intell. 2021, 52, 1–20. [Google Scholar] [CrossRef]
- Maalek, R. Field Information Modeling (FIM)™: Best Practices Using Point Clouds. Remote Sens. 2021, 13, 967. [Google Scholar] [CrossRef]
- Yu, C.; Cherfaoui, V.; Bonnifait, P.; Yang, D.-G. Managing Localization Uncertainty to Handle Semantic Lane Information from Geo-Referenced Maps in Evidential Occupancy Grids. Sensors 2020, 20, 352. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Molina, A.; Solís-Romero, J.; Villarreal-Cervantes, M.G.; Serrano-Pérez, O.; Flores-Caballero, G. Path-Planning for Mobile Robots Using a Novel Variable-Length Differential Evolution Variant. Mathematics 2021, 9, 357. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, X.; Ran, X.; Wang, J.; Chen, H.; Deng, W. Adaptive cylinder vector particle swarm optimization with differential evolution for UAV path planning. Eng. Appl. Artif. Intell. 2023, 121, 105942. [Google Scholar] [CrossRef]
- Gubán, M.; Udvaros, J. A Path Planning Model with a Genetic Algorithm for Stock Inventory Using a Swarm of Drones. Drones 2022, 6, 364. [Google Scholar] [CrossRef]
- Ji, H.; Hu, H.; Peng, X. Multi-Underwater Gliders Coverage Path Planning Based on Ant Colony Optimization. Electronics 2022, 11, 3021. [Google Scholar] [CrossRef]
- Dai, X.; Ke, C.; Quan, Q.; Cai, K.Y. RFlySim: Automatic test platform for UAV autopilot systems with FPGA-based hardware-in-the-loop simulations. Aerosp. Sci. Technol. 2021, 114, 106727–106742. [Google Scholar] [CrossRef]



| Reference | Contributions | Limitation |
|---|---|---|
| Hao, L. et al. (2020) [18] | This paper proposes a modified PSO called MPSO. A chaos-based non-linear inertia weight is used to balance capacities better. | Its convergence and stability lack theoretical support. There are some parameters in MPSO, which increase the difficulty of problem solving. |
| Shin, J.-J. et al. (2020) [19] | An improved particle swarm optimization (PSO) algorithm is proposed for finding an optimal path, which is composed of pre-processing steps, multi-swarm PSO algorithm, and post-processing steps. | It is not suitable to include constraints related to UAV maneuvering; therefore, this may lead to large errors between the planned path and the flight path. |
| Phung, M. et al. (2021) [20] | This paper presents a new algorithm named spherical-vector-based particle swarm optimization (SPSO) algorithm, which efficiently searches the configuration space of the UAV via the correspondence between the particle position and the speed, turn angle, and climb/dive angle of the UAV. | The optimization algorithm converges quickly and easily falls into local optimum. |
| Dadvar, M. et al. (2021) [26] | This paper proposes a new algorithm, which uses a coalition or cooperation model in the game theory to combine the DE and PSO algorithms to maintain a balance between the exploration and exploitation capabilities by preventing population stagnation and avoiding the local optimum. | Failure to incorporate the maneuvering characteristics of the UAV into the algorithm does not further improve its navigation capabilities. |
| This work |
| |
| Algorithm | Parameters |
|---|---|
| GSPSODE | = 1000, = 2000 |
| SPSO | = 1, = 1.5, = 1.5 |
| PSO | = 1, = 1.5, = 1.5 |
| DE | CR = 0.9, F = 0.5, r = 0.98 |
| GA | Pc = 0.2, Pm = 0.2 |
| ACO | α = 10, β = 1, γ = 1, τ0 = 1.2 |
| Algorithm | Evaluation Scores | Scene 1 | Scene 2 | Scene 3 |
|---|---|---|---|---|
| GSPSODE | Best | 5.68 × 104 | 4.69 × 104 | 6.70 × 104 |
| Mean | 5.70 × 104 | 4.70 × 104 | 6.70 × 104 | |
| Std | 24.58 | 35.46 | 30.77 | |
| Runtimes(s) | 151.25 | 122.16 | 166.58 | |
| SPSO | Best | 5.72 × 104 | 4.72 × 104 | 6.95 × 104 |
| Mean | 5.73 × 104 | 4.75 × 104 | 6.97 × 104 | |
| Std | 63.38 | 88.25 | 240.13 | |
| Runtimes(s) | 102.12 | 98.31 | 117.40 | |
| PSO | Best | 5.95 × 104 | 4.74 × 104 | 7.14 × 104 |
| Mean | 5.96 × 104 | 4.76 × 104 | 7.16 × 104 | |
| Std | 94.23 | 207.91 | 274.21 | |
| Runtimes(s) | 96.12 | 81.20 | 112.64 | |
| DE | Best | 5.79 × 104 | 4.79 × 104 | 7.17 × 104 |
| Mean | 5.80 × 104 | 4.83 × 104 | 7.20 × 104 | |
| Std | 102.73 | 132.53 | 310.13 | |
| Runtimes(s) | 80.28 | 72.61 | 105.83 | |
| GA | Best | 6.02 × 104 | 4.94 × 104 | 7.20 × 104 |
| Mean | 6.05 × 104 | 4.97 × 104 | 7.24 × 104 | |
| Std | 120.63 | 191.38 | 361.75 | |
| Runtimes(s) | 161.19 | 149.83 | 180.66 | |
| ACO | Best | 5.72 × 104 | 4.77 × 104 | 7.09 × 104 |
| Mean | 5.75 × 104 | 4.80 × 104 | 7.13 × 104 | |
| Std | 89.17 | 62.14 | 100.62 | |
| Runtimes(s) | 79.12 | 63.13 | 103.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhang, L.; Gao, Y.; Zheng, X.; Wang, Q. A Cooperative Game Hybrid Optimization Algorithm Applied to UAV Inspection Path Planning in Urban Pipe Corridors. Mathematics 2023, 11, 3620. https://doi.org/10.3390/math11163620
Wang C, Zhang L, Gao Y, Zheng X, Wang Q. A Cooperative Game Hybrid Optimization Algorithm Applied to UAV Inspection Path Planning in Urban Pipe Corridors. Mathematics. 2023; 11(16):3620. https://doi.org/10.3390/math11163620
Chicago/Turabian StyleWang, Chuanyue, Lei Zhang, Yifan Gao, Xiaoyuan Zheng, and Qianling Wang. 2023. "A Cooperative Game Hybrid Optimization Algorithm Applied to UAV Inspection Path Planning in Urban Pipe Corridors" Mathematics 11, no. 16: 3620. https://doi.org/10.3390/math11163620
APA StyleWang, C., Zhang, L., Gao, Y., Zheng, X., & Wang, Q. (2023). A Cooperative Game Hybrid Optimization Algorithm Applied to UAV Inspection Path Planning in Urban Pipe Corridors. Mathematics, 11(16), 3620. https://doi.org/10.3390/math11163620





