Abstract
An edge-weighted consensus-based formation control strategy is presented for mobile robots. In the edge-weighted strategy, a desired formation pattern is achieved by adjusting gain weights related to the distance between robots. Moreover, the edge-weighted formation control exploits the properties of weighted graphs to allow the formation to rotate and adapt its shape to avoid collision among robots. However, formation patterns are commonly defined by biases with respect to the centroid of the consensus rather than gain weights. This work proposes to optimize the gain weights in edge-weighted graphs, given a formation pattern in terms of biases. A multi-strategy mutation differential evolution algorithm is introduced to solve the optimization problem. Simulation and real-world experiments are performed considering multi-robot systems composed of differential drive robots. Additionally, the experimental setup includes Turtlebot3® Waffle Pi robots and an OptiTrack® motion capture system for control purposes. The experimental results verify the effectiveness of the proposed approach.
Keywords:
edge-weighted control; consensus-based control; differential evolution; evolutionary algorithms; mobile robots MSC:
93-10
1. Introduction
Cooperative work is the main advantage of multi-agent systems. A network of mobile robots is used for many applications, such as search-and-rescue (SaR) operations, cooperative transportation of objects, collaborative exploration, and mapping, along with others [1,2]. There is more than one strategy to solve the formation problem. Most of the time is solved as a consensus problem in which the states of all the agents converge to a common value [3]. In the case of mobile robots, this value defines the centroid of the desired formation.
Several works deal with formation problems based on the Laplacian properties [4]. The most common algorithms exploit the following control law , where corresponds to the position of the ith robot translated by a bias with respect to the centroid of the formation, and stands for the Laplacian matrix. One of the main advantages of this approach is that the formation is achieved even in the presence of delays in the communication if the communication topology is static, undirected, and connected [5]. Different approaches using a bias-based strategy have been proposed. For example, in [6], a hybrid technique to drive a group of mobile robots to a desired formation is presented, and Particle Swarm Optimization is applied for the exploration of unknown environments. In [7], a full consensus-formation is reached by a switching control law. Other examples under this strategy use single-integrator dynamics [8], pinning control of complex networks [9], and persistency of excitation to deal with non-holonomic constraints [10].
Nevertheless, solving the formation problem through a bias-based strategy does not void collisions while moving in unknown environments [11], and incorporates artificial potential fields for collision avoidance, producing an unstable behavior in the presence of communication delays [12]. The weighted graph strategy overcomes these drawbacks. In [11,13], an edge-weighted graph strategy is implemented to include collision avoidance among the robots.
This paper extends the results presented in [11], where an edge-weighted formation control is proposed. In this strategy, the distance between the ith robot and the jth robot is given by the minimum of the edge-tension function; thus, the choice of a constant gain in this function defines the desired distance for each couple of robots. However, a desired formation is usually given in cartesian coordinates rather than in terms of a gain related to the distance between robots. Optimization algorithms are applied under the edge-weighted graph scheme to find the best constant gain value corresponding to the desired formation given in cartesian coordinates.
Evolutionary Algorithms (EAs) have been widely used for intelligent optimization in many research areas such as electrical and electronics, path planning, trajectory design and tracking, automation control systems, interdisciplinary applications, and formation control [14,15]. In [15], the authors discussed the application of EAs to engineering problems. Particularly, the Differential Evolution (DE) algorithm stands out in the automation control and engineering civil areas.
Differential Evolution (DE) is commonly used to solve complex optimization problems [16]. Its flexibility and versatility have promoted several customized variants to solve real-world problems. Recently, many works have modified the conventional DE algorithm to enhance its effectiveness and efficiency [17]. In [17], the authors presented a recent review based on the state-of-the-art DE variants. The strengths and weaknesses of several DE modifications were carefully reviewed, followed by their potential application in solving real-world engineering problems. Among the reviewed variants, the multi-strategy different dimensional mutation differential evolution version stands out for its enhanced converge speed and exploitation search capacities, overcoming stagnation in local optima regions [18]. All these benefits motivated the authors to use the multi-strategy mutation scheme to deal with the drawbacks of conventional DE.
The contributions of this paper are summarized below: Given a desired formation in cartesian coordinates, it is proposed to optimize the constant gains of the edge-weighted graph, such that the edge-weight formation control drives the robots to the desired formation, keeping its capacities of collision avoidance among robots. Based on [18], a multi-strategy mutation differential evolution (MMDE) algorithm is proposed to solve this problem. MMDE enhances convergence speed rates and avoids premature convergence of the conventional DE algorithm. The proposed approach is called the MMDE-based formation pattern for edge-weighted formation control.
This article is organized as follows: The next section presents the kinematics model formulation for differential drive non-holonomic robots. Then, the edge-weighted formation control is described in Section 3. In Section 4, the description of the MMDE algorithm is provided. Moreover, the proposed MMDE-based formation pattern strategy is presented with details in Section 5. Simulation experiments and real-world implementation are performed in Section 6. An analysis of the reported results and the future research directions are given in Section 7. Finally, conclusions are presented in Section 8.
2. Kinematics Model Formulation
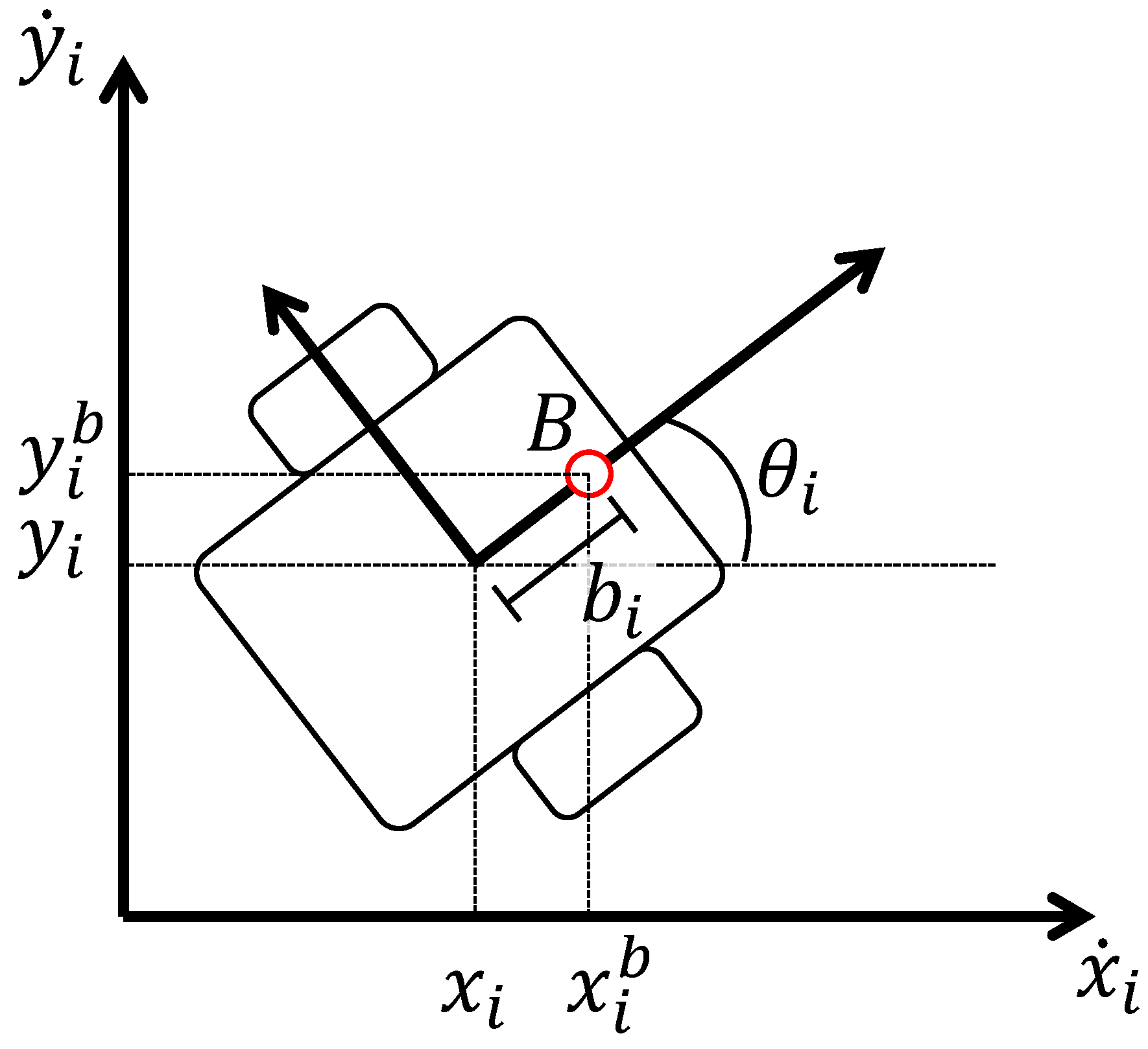
Consider a set of N differential drive non-holonomic robots, like the one depicted in Figure 1, each of them modeled as the unicycle kinematics (1) under the assumption that wheels are rolling without slippage, the steering axis is orthogonal to the -plane, and the geometry center Q coincides with the center of mass. The kinematics model is given by
where , stands as the cartesian coordinates, is the orientation with respect to the z-axis, and and are the linear and angular velocities, respectively. To deal with the non-holonomic constraints, the input/output linearization feedback in [19] is employed. Defining point B, from Figure 1, located along the sagittal axis of the robot at a distance from the contact point of the wheel with the ground, the cartesian coordinates are given by
with . After evaluating the time derivative of (2) yields
where the matrix is invertible as long as .
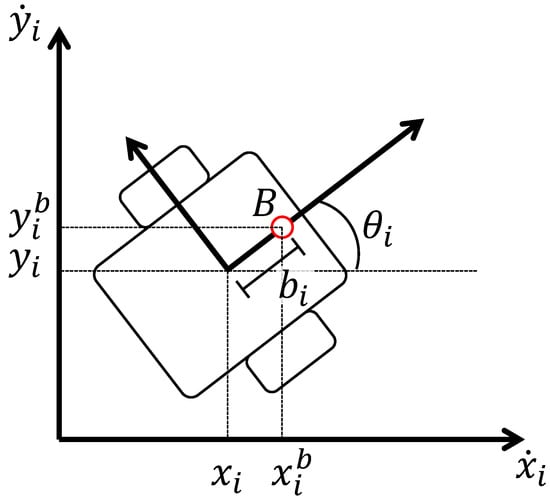
Figure 1.
Differential drive robot model.
To drive the robot, the input control is designed such as and . Then, using the following input transformation
the input/output linearization feedback is achieved
The communication topology is modeled as an undirected, static, connected, and weighted graph defined as a pair , where is the edge set of cardinality M and stands for the vertex set of cardinality N. Given a graph the Laplacian matrix, can be defined as
where is the incidence matrix whose components are given by
an edge represents the bidirectional communication between agents i and j. By construction, , such that , is symmetric, it has a unique zero eigenvalue, and the rest of its spectrum is strictly positive [20].
3. Edge-Weighted Formation Control
The consensus problem for N agents to drive the robots to a final common state can be solved with the Laplacian-based feedback method [11]. The feedback control is in the form
where , is the Neighbors subset of the ith robot, and is a positive edge-weight function in terms of . Defining a weight matrix as
and the weighted Laplacian matrix as follows
then the control law (8) can be recast as
where is an identity matrix, and ⊗ is the Kronecker product.
Regarding collision avoidance, the weight function is designed with a safety distance parameter among the robots. Therefore, the edge-weight function is defined as
where defines the inter-robot influence, stands for the position error, and is a constant related to the distance between robots.
The edge-weight function (12) was designed based on an edge-tension function that guarantees collision avoidance between agents i and j, if the parameter is strictly greater than the distance [11].
The distance between robots i and j is given by
The selection of the values determines the final formation. It means that the edge-weight control requires the appropriate selection of the values to drive the robots to a desired formation. Thus, given a formation pattern in cartesian coordinates, the goal is to adjust the gain such that
where is the desired bias of agent i, and is the desired bias of agent j, both biases defined with respect to the centroid of the desired formation.
This work proposes to solve the problem statement in (14), as an optimization problem. An objective function to deal with the optimization is described in the next subsection.
For further details of the Laplacian-based feedback method and collision avoidance, the reader is referred to read [11].
Objective Function Formulation
A candidate solution composed of a set of gains is defined as
where , since the cardinality of defines the dimension of the optimization problem.
Based on the edge-weight graph strategy, each element is related to a distance between agents i and j. The distance is computed as
On the other hand, a desired distance between agents i and j can be defined based on the desired formation pattern in cartesian coordinates. Distance is given by
An objective function can be designed such that . Then, an error is defined, .
Finally, the following objective function is proposed
where is a set of errors given by .
The optimization problem is expressed as
where each element is considered a feasible solution if . Otherwise, unfeasible solutions cause system instability while performing the formation control task.
In this work, the MMDE algorithm is used to solve this optimization problem stated in (19).
4. Multi-Strategy Mutation Differential Evolution
DE is a population-based stochastic algorithm for global optimization [21]. The DE algorithm uses D-dimensional parameter vectors , where , and denotes the nth individual in the gth generation. Every individual improves through three principal operations: mutation, crossover, and selection, performed every generation.
In conventional DE, the mutation strategy DE/rand/1 is utilized for global optimization, but its convergence ability is often insufficient with low convergence speed. On the other hand, the mutation strategy DE/best/1 is utilized for local optimization, but it suffers from premature convergence. Based on [18], this work presents the MMDE scheme to enhance the convergence speed while avoiding premature convergence of the conventional DE algorithm. The procedure of MMDE to solve minimization problems is shown below.
In the mutation operation, a mutant vector is generated for each individual n according to
where , , and are randomly selected individuals such as and . The parameter is called the amplification factor, and it controls the amplification of the differential variation . Moreover, is the best individual in the population at generation g, and G is the total number of generations.
As shown in (20), the mutation scheme is divided into four generation units. The first and the third generation promote exploitation search and speed convergence. The second and fourth generation units prevent population stagnation in local optima regions [18].
A trial vector is generated based on the following binomial crossover operation
where and is the crossover constant. and are uniform random numbers defined as and . The number ensures that the trial vector obtains at least one element from the mutation vector to avoid evolutionary stagnation [22].
In the selection operation, the trial vector is compared to the actual vector based on the evaluation of an objective function f. If yields a better solution than , then replaces . Otherwise, is retained to the next iteration . The selection scheme is defined as
A detailed description of conventional DE and its modifications can be found in [17,21,22].
5. Description of the Mmde-Based Formation Pattern Algorithm
In consensus-based formation control strategies using bias , the formation patterns are defined by translating (in cartesian coordinates) the position of the ith robot with respect to the centroid of the formation. The advantage of bias-based strategies is the easy proposal of formation patterns. However, these strategies do not allow the formation to rotate and adapt its shape to avoid collisions [11].
In edge-weighted formation control, the formation patterns are defined by edge-weighted values . Given the appropriate values, , the desired formation is achieved without the definition of any bias, with the advantage of collision avoidance [11]. However, the choice of values can be difficult to propose for some formation patterns. Moreover, the more edge-weighted values the graph contains, the more difficult it will be to propose the values.
This work proposes to optimize the values for the edge-weighted formation control, , such that each robot i achieves the desired formation defined with cartesian coordinates.
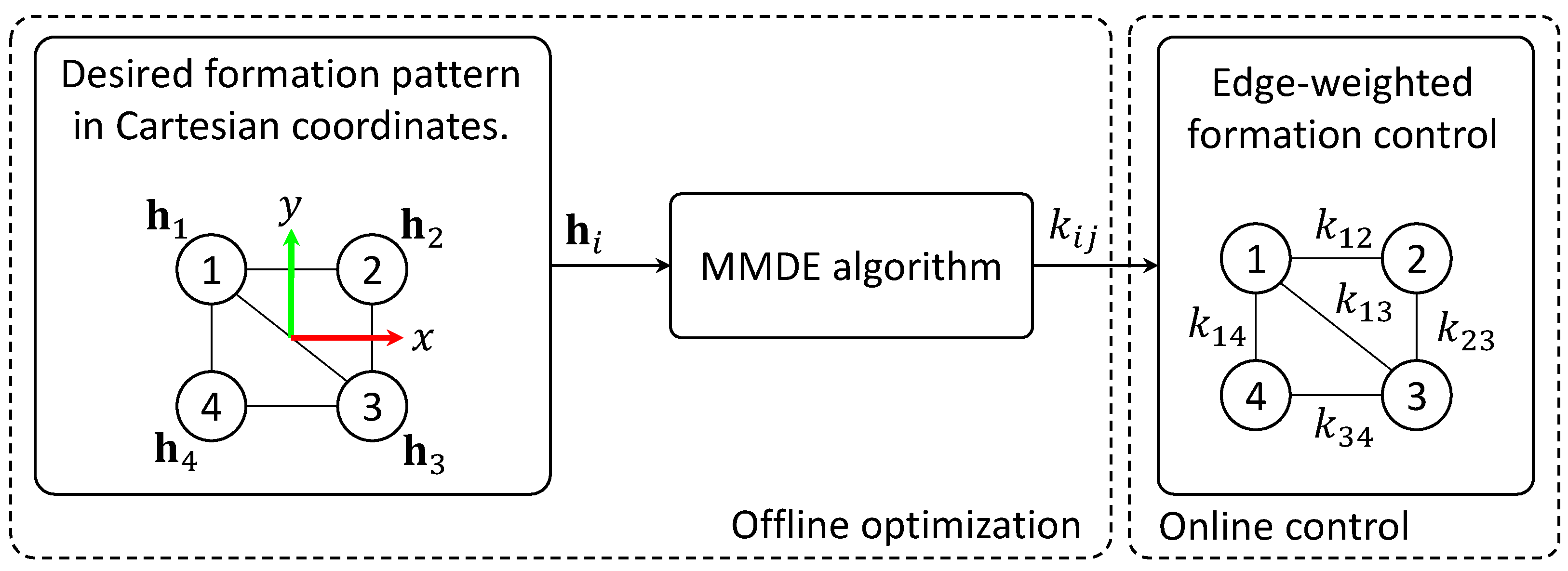
The description of the proposed approach is illustrated in Figure 2. The MMDE-based formation pattern scheme consists of two stages: The first stage involves offline optimization. In this phase, the MMDE algorithm determines the corresponding values based on a desired formation pattern with respect to the centroid of the formation. In the second stage, the edge-weighted control strategy is employed to achieve the desired formation using the calculated values.
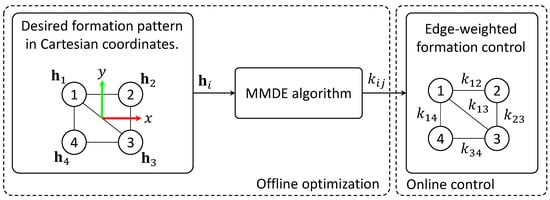
Figure 2.
Proposed MMDE-based formation pattern scheme.
The following subsections provide a detailed description of the MMDE-based formation pattern algorithm presented in Figure 2.
Mmde-Based Formation Pattern Algorithm
This work proposes to optimize the objective function (18) using the MMDE algorithm. The MMDE algorithm requires the initialization of each individual in the population. Usually, individuals are randomly initialized considering lower and upper bounds.
To generate random individuals , it is proposed to use the following equation
where and are the lower and upper bounds, respectively. Moreover, is a uniform random number. This boundary must be selected such as .
It is important to notice that some elements of the trial vector may represent unfeasible solutions due to the impact of the mutation operation. To deal with unfeasible solutions, it is proposed to follow the next scheme
where each value is randomly computed to make it feasible. A summary of the MMDE algorithm to adjust the values, for the edge-weighted formation control is shown in Algorithm 1.
| Algorithm 1 MMDE algorithm to adjust the values, for the edge-weighted formation control |
|
6. Experimental Results
The applicability of the proposed approach is demonstrated through simulation and real-world experiments. All parameter settings used for both experiments are provided below.
The settings of the MMDE algorithm are defined as follows: The amplification factor and the crossover constant , as suggested in [17]. Moreover, a total of iterations and population members were selected. With respect to the edge-weight formation strategy settings, the safety distance was set to , and the inter-robot influence was fixed to . These parameters were experimentally selected.
For simplicity, the physical parameter is set to meters for all robots. Additionally, the linear and angular velocities have been bounded to and . This saturation is imposed to protect the equipment, especially for real-world implementations.
All experiments are conducted as follows: First, a desired formation pattern is provided in cartesian coordinates with respect to the centroid of the formation. Then, the MMDE algorithm optimizes offline the values for the edge-weighted formation control. Finally, the edge-weighted formation control was performed online to achieve the desired formation.
For real-world experimentation, up to five Turtlebot3 (Turtlebot3 is a registered trademark of ROBOTIS Inc. USA) Waffle Pi mobile robots have been considered. The Turtlebot3® Waffle Pi is a modular differential drive mobile robot, compact and customizable, programmable and ROS-based platform for education, research, and product development applications [23] (see Figure 3).

Figure 3.
Turtlebot3® Waffle Pi. Onboard cubes of silver reflective fabric are used for tracking purposes.
The ROS (ROS is a registered trademark of Open Robotics, Mountain View, CA, USA) packages of Turtlebot3® provide access to send velocity control inputs and read its odometry. However, odometry measures lack precision due to the sensor’s tell, terrain conditions, and slipping. To deal with this problem, it is proposed to use an OptiTrack (OptiTrack is a registered trademark of NaturalPoint Inc., Corvallis, OR, USA) tracking system to estimate the poses of the robots with precision, instead of reading the robot’s odometry.
The OptiTrack® system is composed of six cameras Flex3 (OptiTrack Flex 3 is a registered trademark of NaturalPoint Inc., Corvallis, OR, USA) and a computer with the software Motive for streaming. Tracking information is sent using ROS® packages. The space for real-world implementations is presented in Figure 4.

Figure 4.
OptiTrack® setup for real-world implementations. The six cameras Flex3® are installed on the ceiling.
Another computer is used to receive the poses of the robots from the OptiTrack® system, and it sends the respective control signals to each Turtlebot3®. The proposed scheme is programmed on this computer using MATLAB (MATLAB is a registered trademark of Mathworks Inc., Torrance, CA, USA) and its ROS® toolbox.
6.1. Simulation Experiments
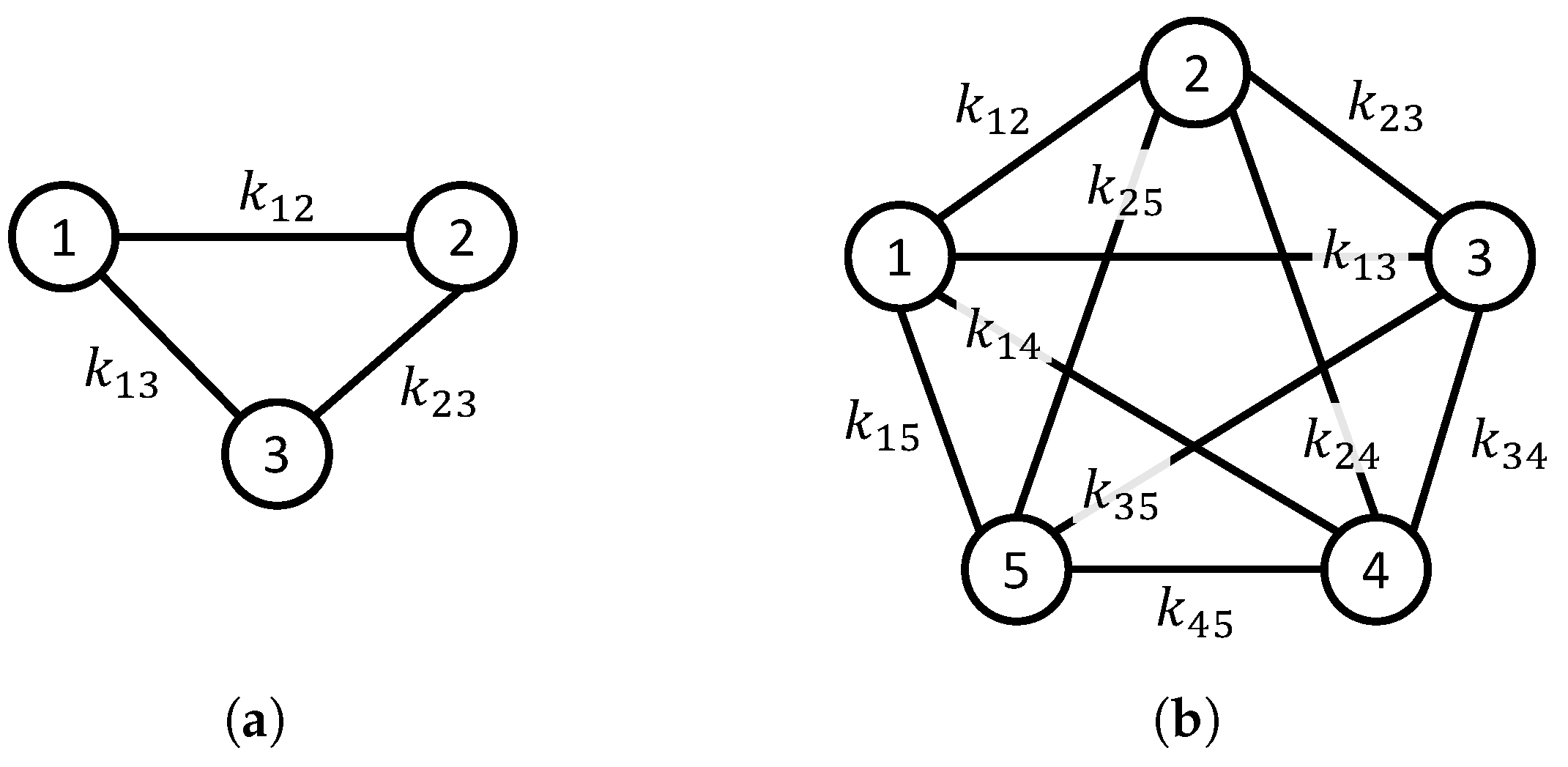
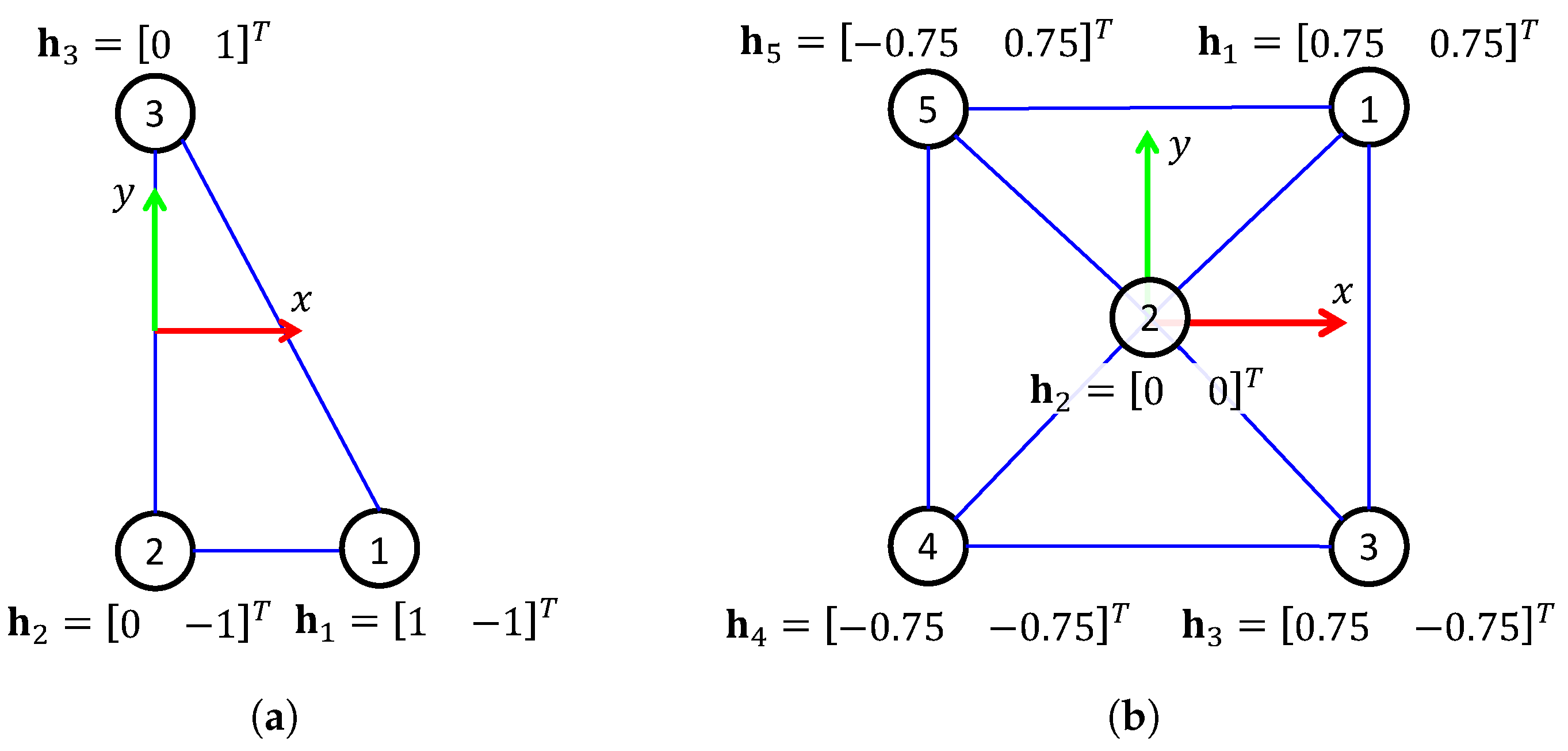
The simulation experiments were carried out using a network of four robots interconnected as illustrated in Figure 5, where the dimensionality of the problem is . Moreover, two tests were performed called Simulations 1 and 2 Simulation 2. The desired formation patterns for the considered tests are shown in Figure 6.
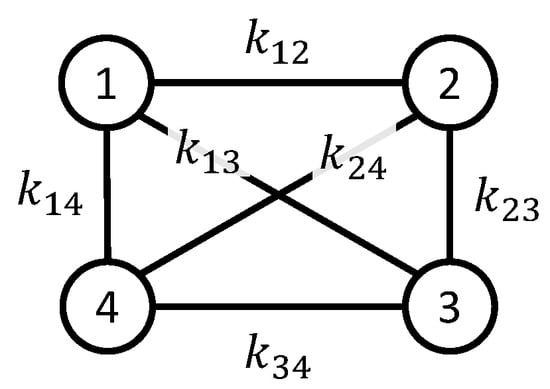
Figure 5.
Communication topology among robots for simulation experiments. Each value must be adjusted to define a desired formation.
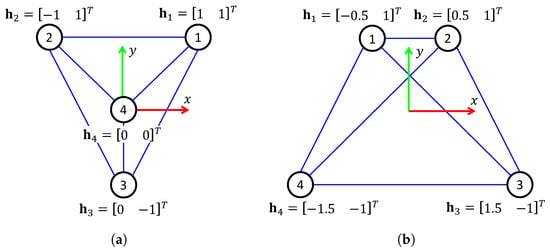
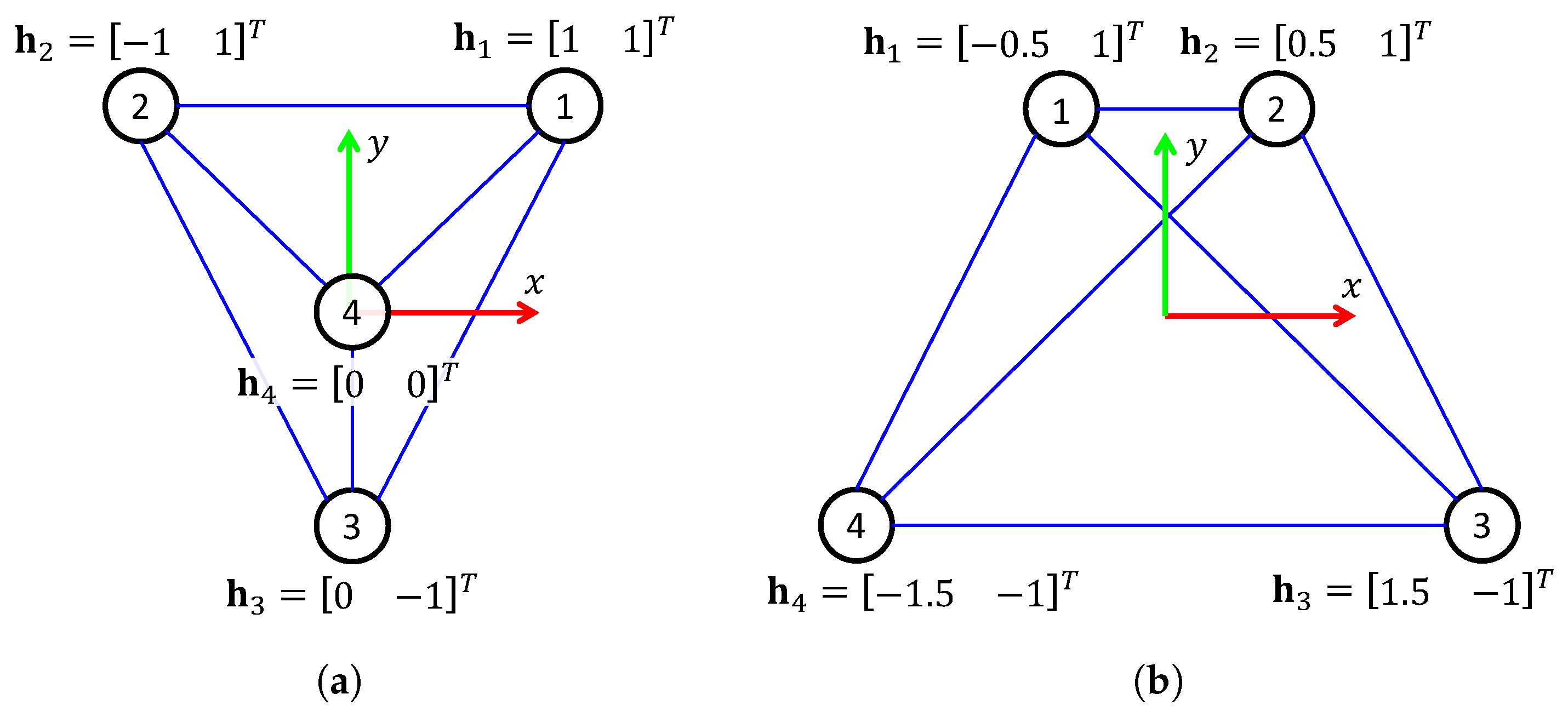
Figure 6.
Desired formation patterns in cartesian coordinates used for simulation. The frame represents the centroid of the formation pattern. (a) Formation pattern for Simulation 1. (b) Formation pattern for Simulation 2.
Table 1 reports the optimal values of both simulation tests. In the case of Simulation 1, the values and were expected to be equal due to the shape of its desired formation pattern (see Figure 6). Similarly, the values and were expected to be the same for Simulation 2.

Table 1.
Optimization results of MMDE. The table reports the optimal values. Moreover, is the objective function evaluation at the final generation.
Table 1 also shows the objective function evaluation at the final generation called . The performance of MMDE is similar in both tests. After a total of 150 generations, the algorithms report an objective function evaluation of and , for Simulations 1 and 2 2, respectively. The reported values are small enough to consider the values optimal for the edge-weighted formation control.
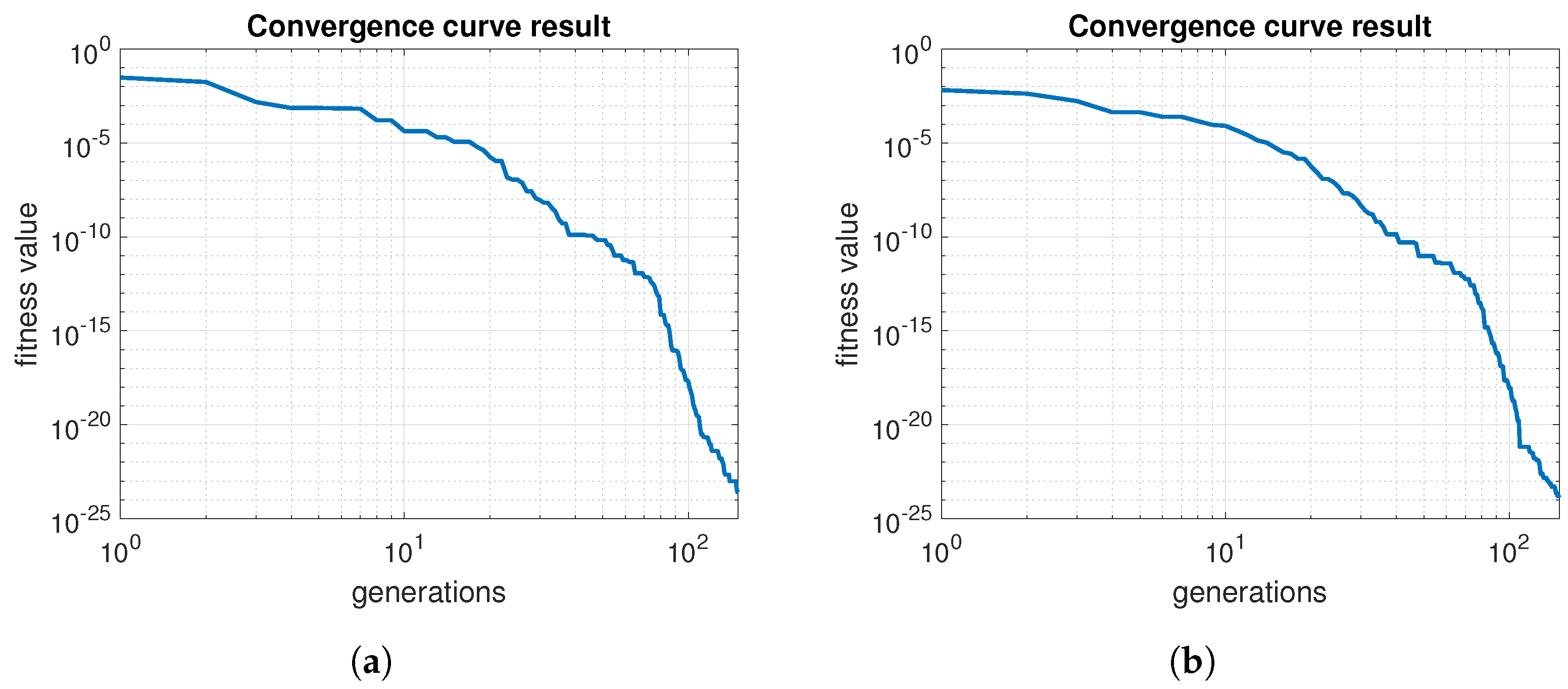
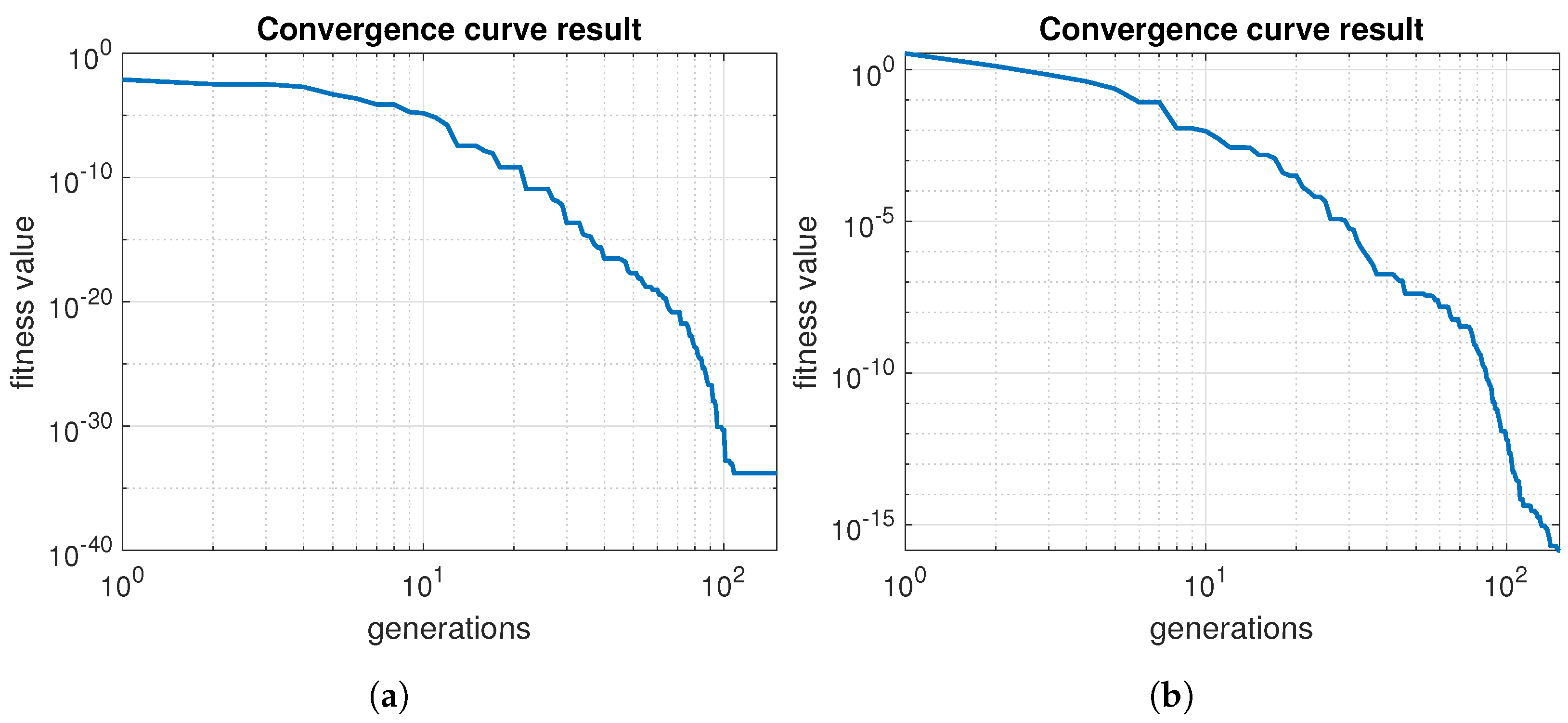
The convergence curves results for simulation experiments are illustrated in Figure 7. These results exhibit the fast convergence speed of the MMDE algorithm. Moreover, the algorithm also demonstrates its exploitation search capability.
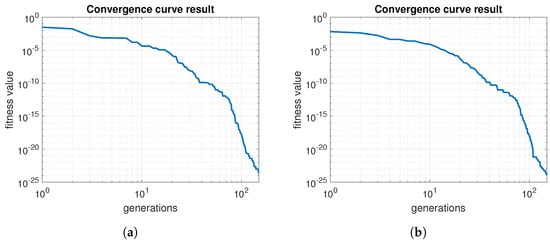
Figure 7.
Convergence curve results of simulations. The fitness value represents the objective function evaluation. (a) Convergence curve of Simulation 1. (b) Convergence curve of Simulation 2.
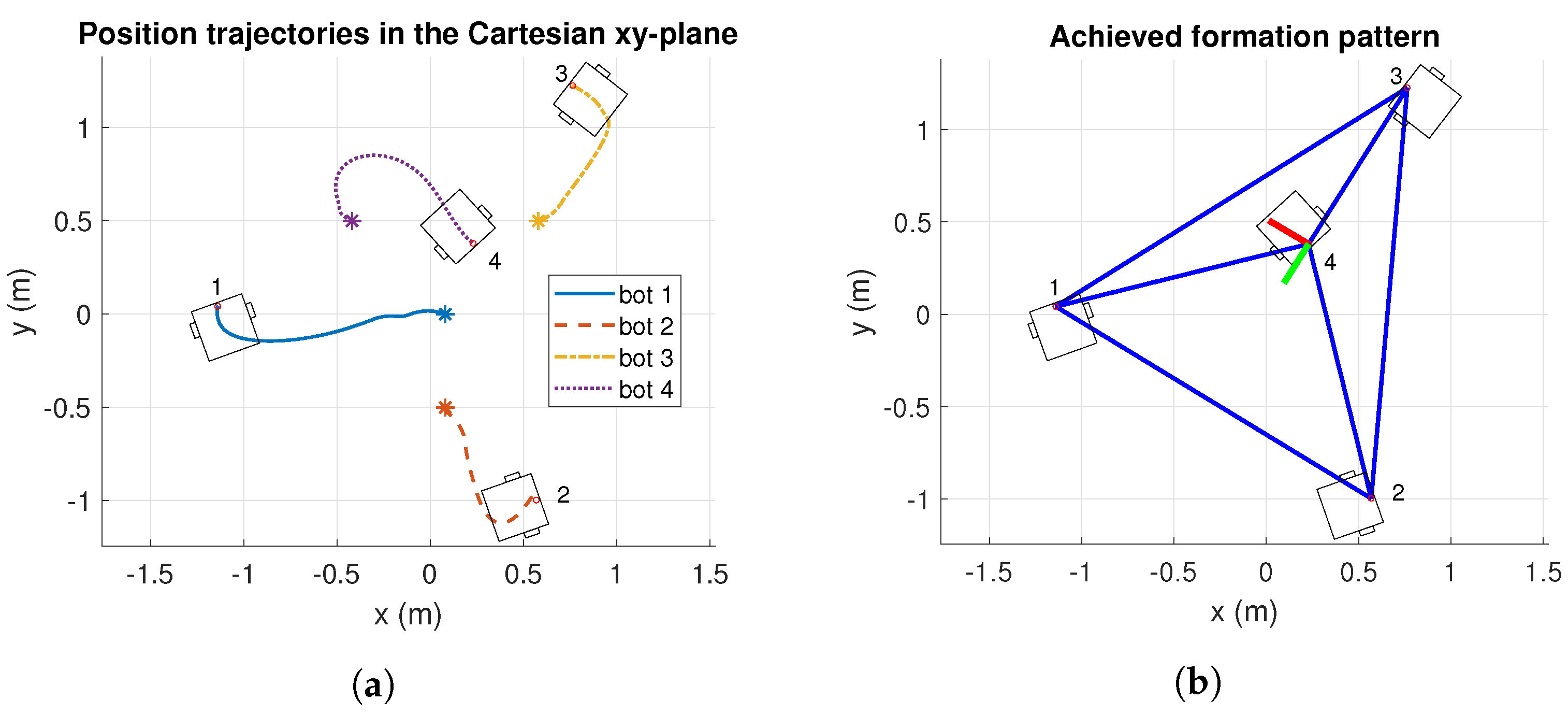
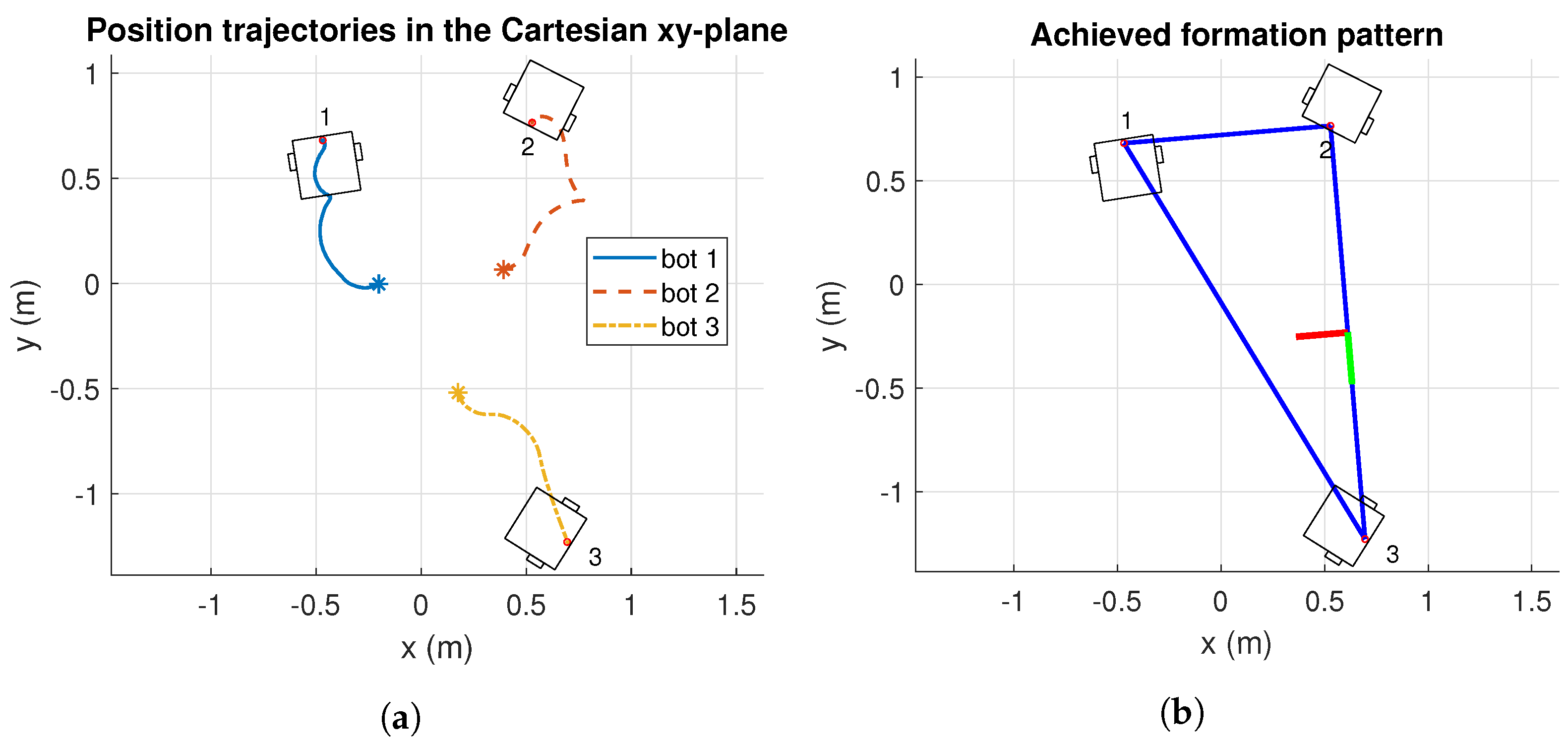
As it may be appreciated from Figure 8, the robots converge to the desired formation pattern for Simulation 1. Figure 8a reports the position trajectories of each robot, in cartesian coordinates. Additionally, the achieved formation pattern is drawn in Figure 8b. Notice that the formation shape rotates to avoid collision among robots, reaching the desired formation from Figure 6a.
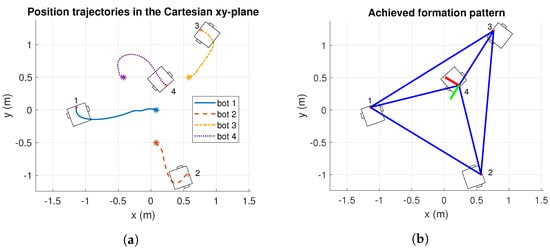
Figure 8.
Results of position trajectories and achieve formation pattern, in cartesian -plane of Simulation 1. The initial robot’s positions are identified with asterisk markers. m: meters. (a) Position trajectories of Simulation 1. (b) Achieved formation of Simulation 1.
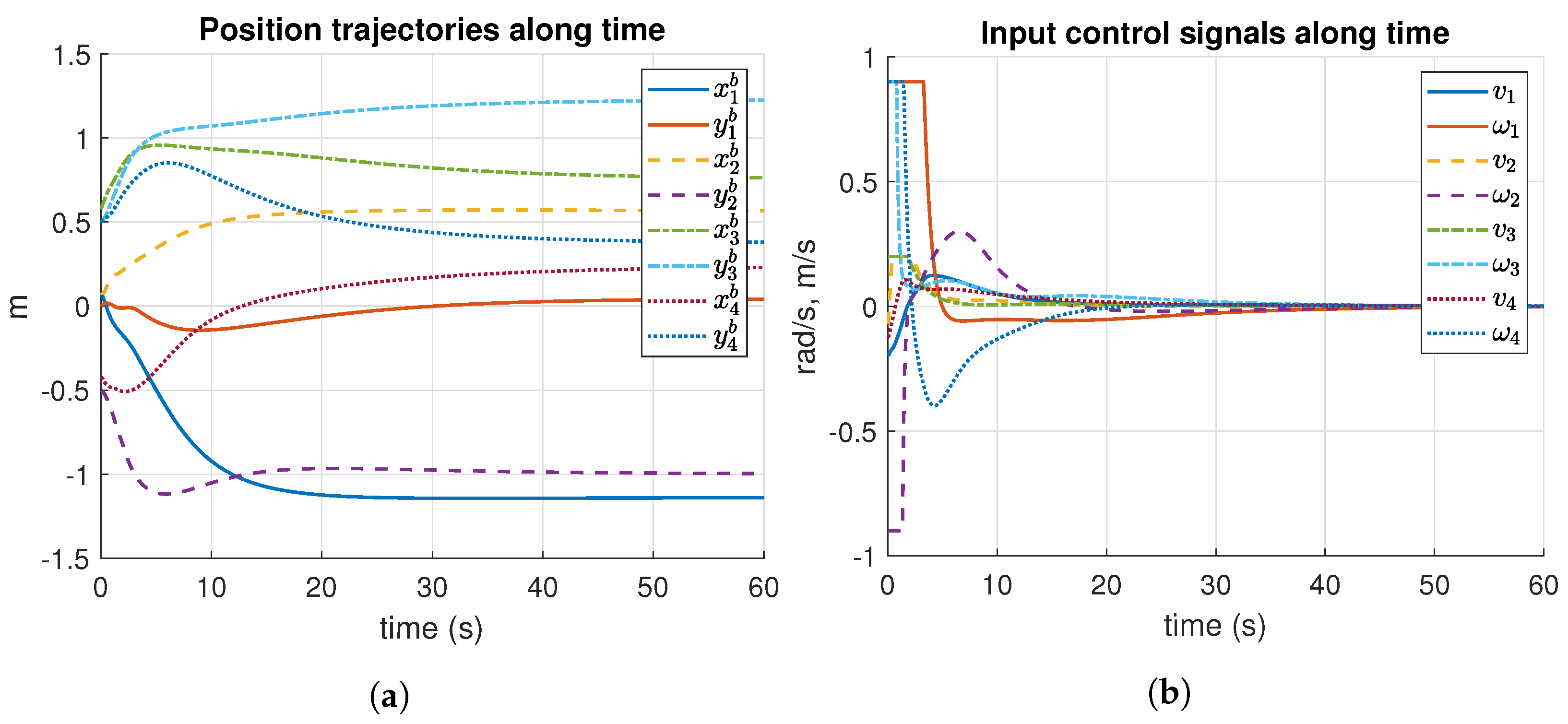
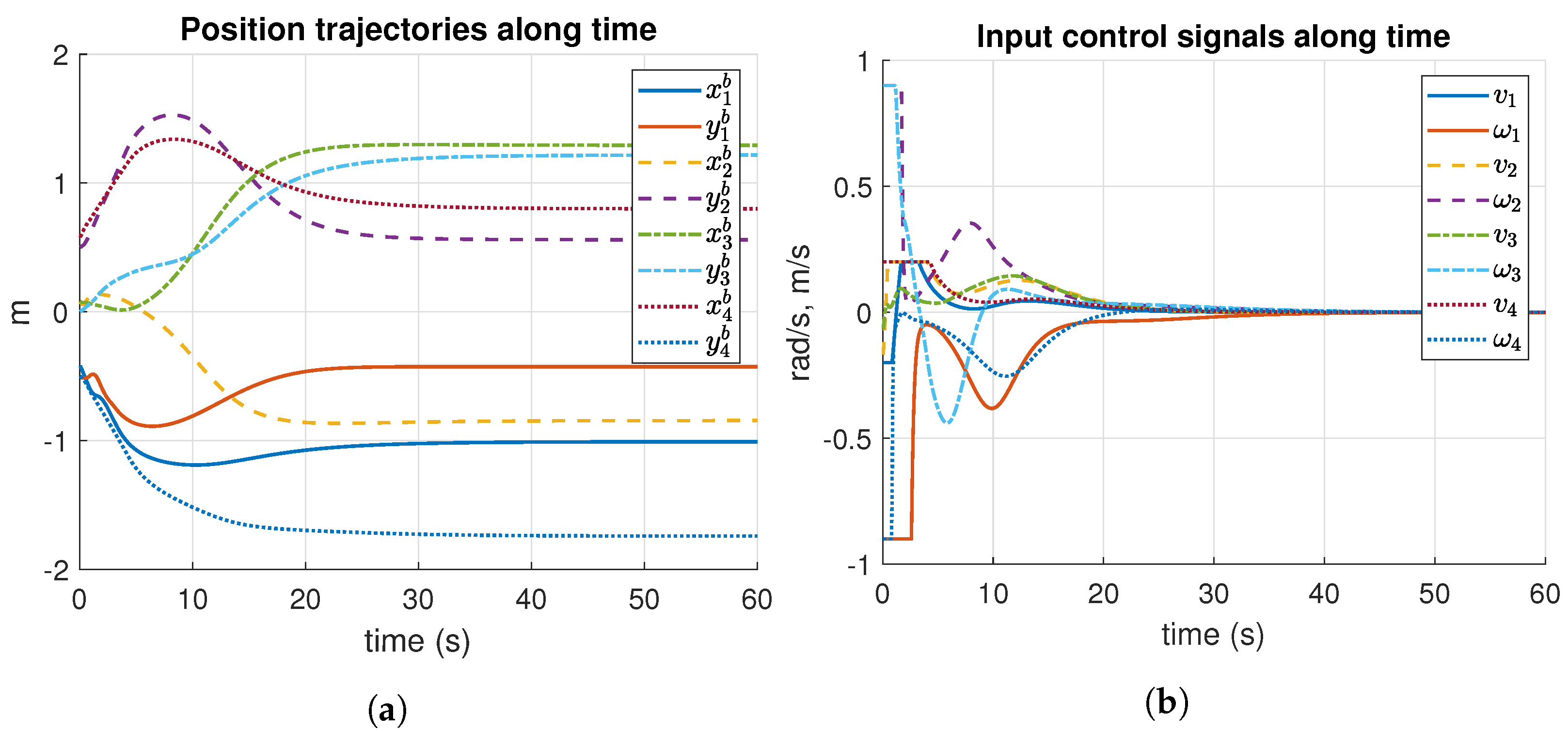
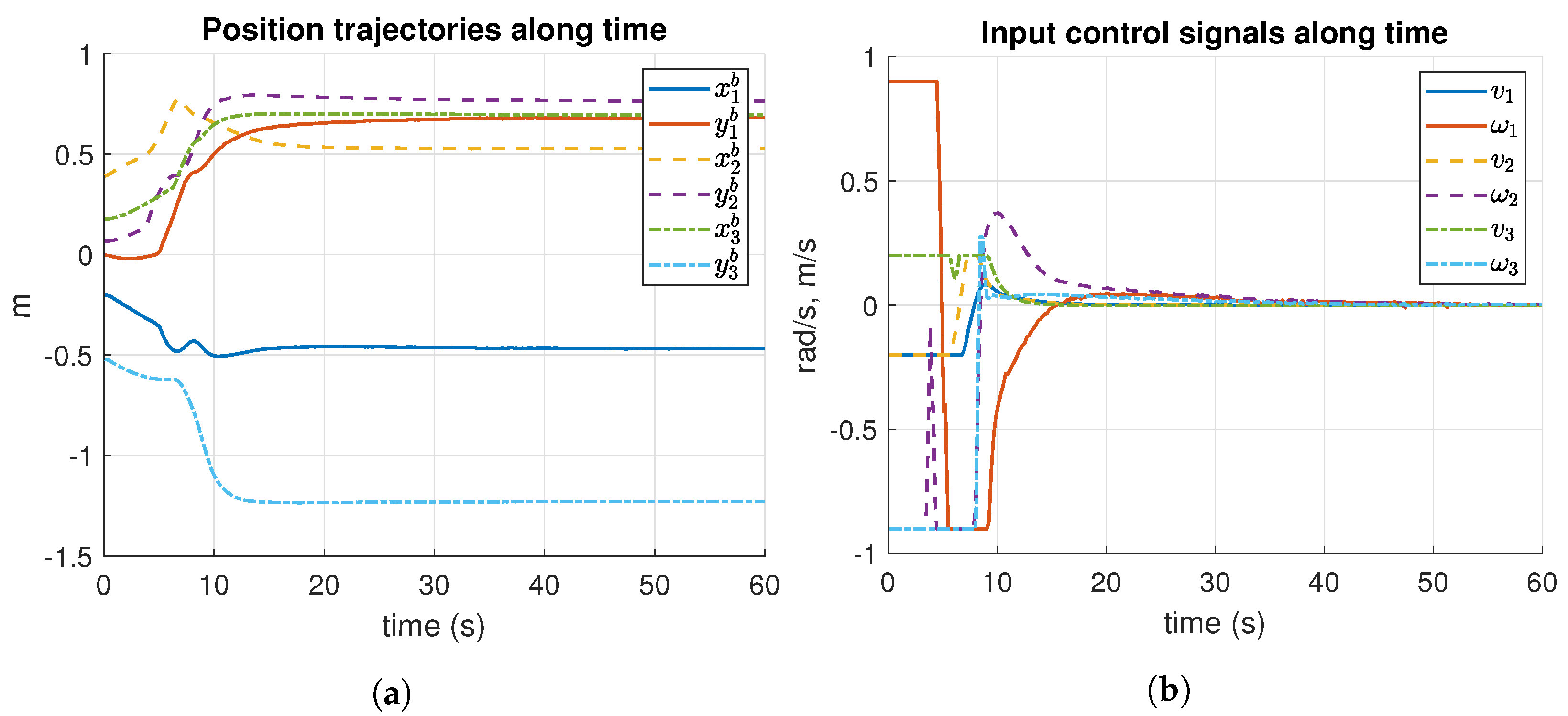
The formation control results along time of Simulation 1 are reported in Figure 9. The position trajectories show smooth displacements (see Figure 9a). The control signals are also smooth, as can be seen in Figure 9b. Moreover, the robot reached its formation after 30 s.
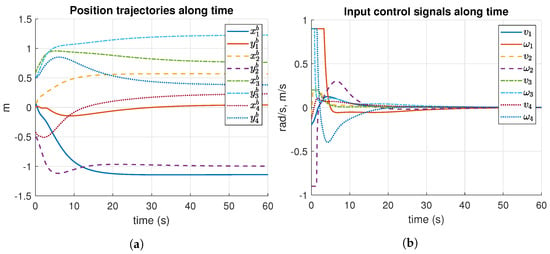
Figure 9.
Results of position trajectories and input control signals, along time of Simulation 1. m: meters, s: seconds. (a) Position trajectories of Simulation 1. (b) Input control signals of Simulation 2.
Cartesian paths followed by the robots reached the desired formation (see Figure 10a). Notice that Robot 2 and Robot 3 avoid a possible collision. Moreover, the achieved formation in Figure 10b is the one expected in Figure 6b. As can be observed, the final formation is rotated since the formation adapts its shape to avoid collisions.
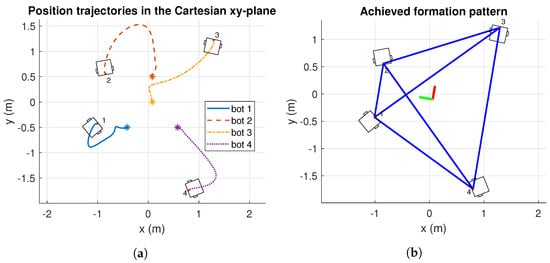
Figure 10.
Results of position trajectories and achieve formation pattern, in cartesian -plane of Simulation 2. The initial robot’s positions are identified with asterisk markers. m: meters. (a) Position trajectories of Simulation 2. (b) Achieved formation of Simulation 2.
Figure 11 presents the results of Simulation 2, which are the position trajectories and the input control signals along time. Both the position displacements and the control signals of each robot are smooth, as shown in Figure 11a and Figure 11b, respectively. In this case, the robots reached the desired formation after 25 s.
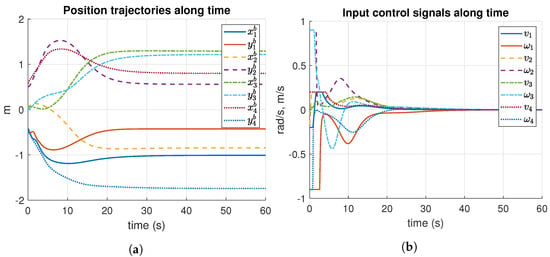
Figure 11.
Results of position trajectories and input control signals, along time of Simulation 2. m: meters, s: seconds. (a) Position trajectories of Simulation 2. (b) Input control signals of Simulation 2.
6.2. Real-World Experiments
Two tests were performed in real-world experiments called Experiment 1 and Experiment 2. Experiment 1 considers a network of three robots interconnected as illustrated in Figure 12a, and Experiment 2 considers five interconnected robots, as shown in Figure 12b. Notice that the dimensionality of these tests is quite different since in Experiment 1, while in Experiment 2. Moreover, the desired formation patterns for Experiments A and B, are included in Figure 13a and Figure 13b, respectively.
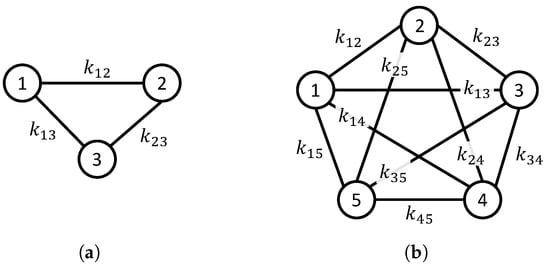
Figure 12.
Communication topology among robots for real-world experiments. Each value must be adjusted to define a desired formation. (a) Communication topology for Experiment 1. (b) Communication topology for Experiment 2.
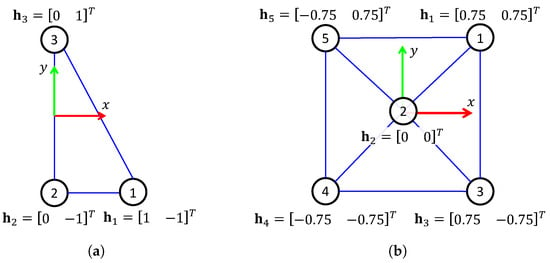
Figure 13.
Desired formation patterns in cartesian coordinates used for real-world experiments. The frame represents the centroid of the formation pattern. (a) Formation pattern for Experiment 1. (b) Formation pattern for Experiment 2.
Table 2 reports the optimal values of Experiment 1. In this case, as expected (see Figure 13a). The result is smaller than the previous tests since the formation pattern is easier with lower dimensionality.

Table 2.
Optimization results of MMDE in Experiment 1. The table reports the optimal values. Moreover, is the objective function evaluation at the final generation.
Table 3 shows the optimal values of Experiment 2. The obtained results are , , and , as required by the desired formation pattern in Figure 13b. Notice that is the most significant result among tests since the required formation pattern is more challenging to solve. However, the optimal values are still small enough for the formation control task.

Table 3.
Optimization results of MMDE in Experiment 2. The table reports the optimal values. Moreover, is the objective function evaluation at the final generation.
The convergence curve results for real-world experiments are illustrated in Figure 14. As can be seen, the convergence curve looks similar in both tests. These curves are also similar to the simulation experiment results (see Figure 7). However, previous objective function evaluations suggest that more generations are required for more complex communications topologies.
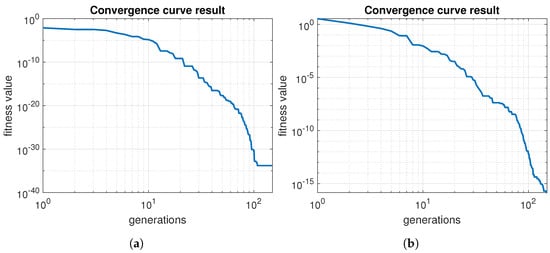
Figure 14.
Convergence curve results of real-world experiments. The fitness value represents the objective function evaluation. (a) Convergence curve of Experiment 1. (b) Convergence curve of Experiment 2.
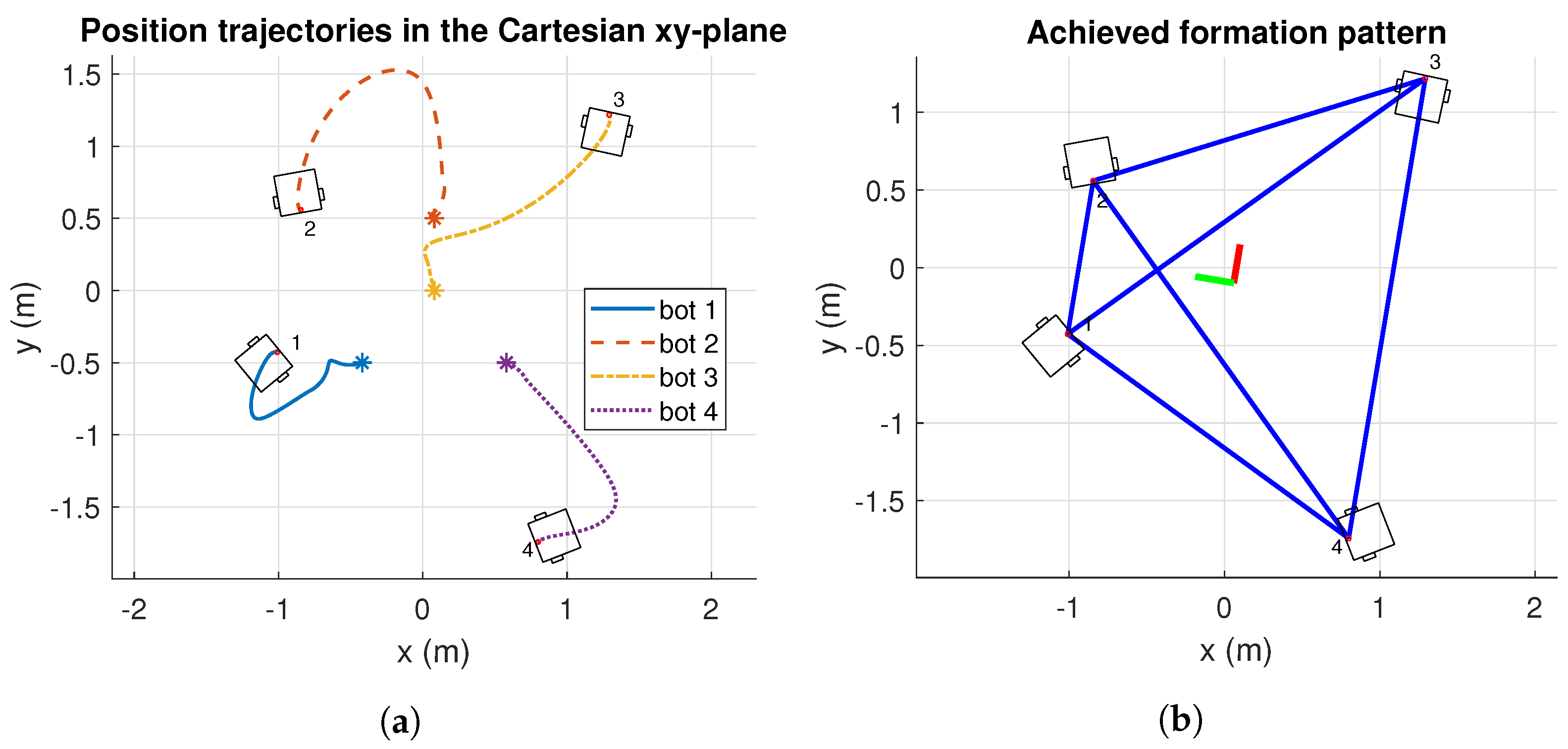
Figure 15 illustrates that robots reached the desired formation pattern for Experiment 1. In this case, Figure 15a shows that position trajectories in the plane are smooth. Moreover, there was no risk of collision. However, the edge-weight control still rotates the center of the formation to best achieve the desired formation pattern (see Figure 15b).
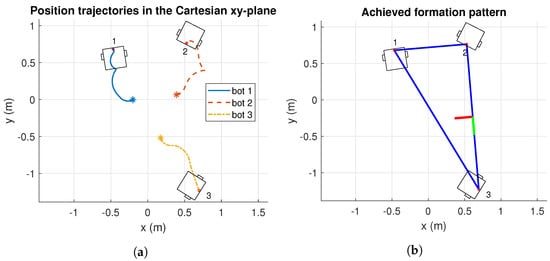
Figure 15.
Results of position trajectories and achieve formation pattern, in cartesian -plane of Experiment 1. The initial robot’s positions are identified with asterisk markers. m: meters. (a) Position trajectories of Experiment 1. (b) Achieved formation of Experiment 1.
Figure 16 presents the position trajectories and input control signals along time of Experiment 1. As it may be appreciated from Figure 16a, trajectories reached the formation pattern around 20 s. Clearly, the control signals start saturated, but after 10 s their performance becomes smooth (see Figure 16b).
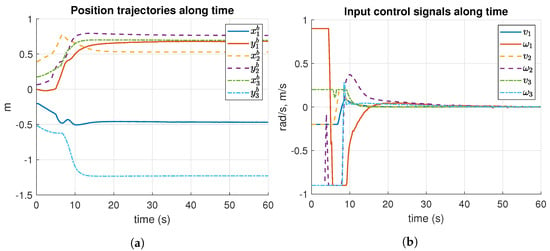
Figure 16.
Results of position trajectories and input control signals, along time of Experiment 1. m: meters, s: seconds. (a) Position trajectories of Experiment 1. (b) Input control signals of Experiment 1.
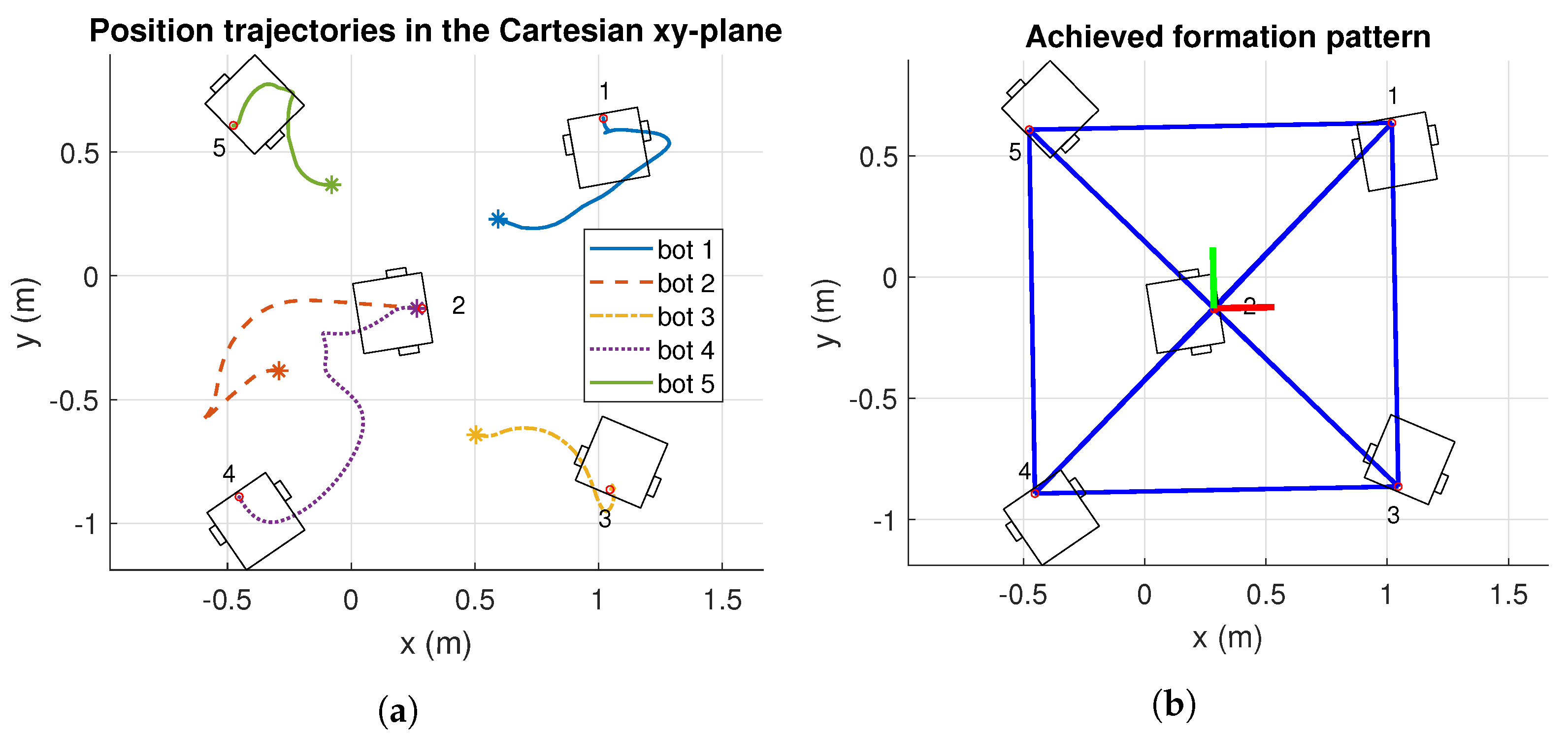
Regarding Experiment 2, the formation pattern results are provided in Figure 17. In this case, the initial positions of robots 2 and 4 are proposed in a way that their trajectories cross to show that the controller avoids the collision. However, the cartesian path followed by the robots reported that the collision is avoided (see Figure 17a). Moreover, the formation pattern is achieved successfully, as illustrated in Figure 17b.
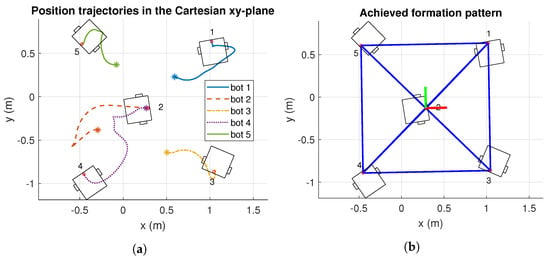
Figure 17.
Results of position trajectories and achieve formation pattern, in cartesian -plane of Experiment 2. The initial robot’s positions are identified with asterisk markers. m: meters. (a) Position trajectories of Experiment 2. (b) Achieved formation of Experiment 2.
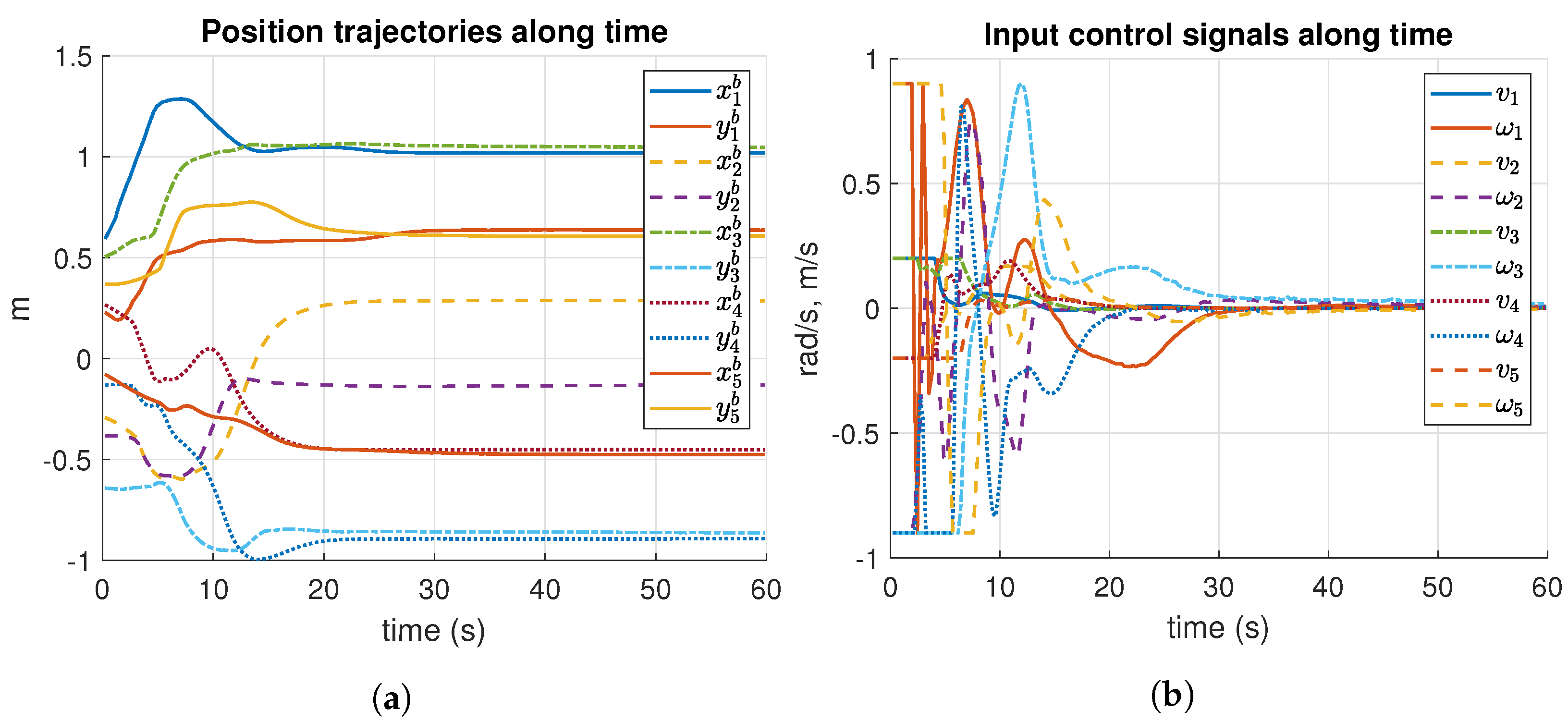
Figure 18 reports the formation control results along time of Experiment 2. The desired formation is reached after 30 s. Figure 18a shows that the robots converge smoothly to the desired formation pattern at around 30 s. However, input control signals reported in Figure 18b are not smooth as previous tests. Although this test is more complex than the previous ones, many drawbacks of the real-world implementations arose, such as non-modeled dynamics, external perturbations, robot wear conditions, and imperfections in the surface. Moreover, ROS® packages pass through a local network via Wi-Fi communications involving loss of packages and delays. Despite all these drawbacks, the control strategy succeeds in achieving the required formation.
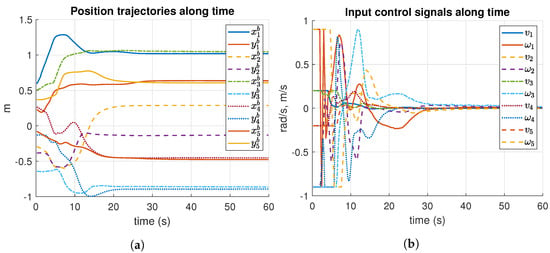
Figure 18.
Results of position trajectories and input control signals, along time of Experiment 2. m: meters, s: seconds. (a) Position trajectories of Experiment 2. (b) Input control signals of Experiment 2.
Finally, the results of the real-world implementations using Turtlebot3® Waffle Pi robots are included in Figure 19. The achieved formations patterns are highlighted with green lines which approximate the reached formations.

Figure 19.
Achieved formation pattern in the real-world implementation using Turtlebot3® Waffle Pi robots. Green lines approximate the reached formation pattern. Each number indicates the ith robot. (a) Achieved formation of Experiment 1. (b) Achieved formation of Experiment 2.
7. Discussion
Desired formation patterns are often given in cartesian coordinates instead of providing gain weights since cartesian coordinates are easier to define with respect to the center of the formation. The formation pattern choosing the gain weights in edge-weighted graphs can be complicated, especially for complex robot networks. The proposed MMDE-based formation pattern algorithm has successfully provided optimal gain weights given cartesian coordinates, which was the main contribution of the paper.
It has been shown that the edge-weighted formation control exploits the properties of weighted graphs to allow the formation to rotate and adapt its shape to avoid collision among robots.
Moreover, all experiments were performed based on a complete graph topology. However, not all the vertices are required to be connected, since the communication topology only requires an undirected, static, connected, and weighted graph [11]. It is let as a future work to study the impact of the MMDE-based formation pattern, varying the vertices connections.
The performance of the edge-weight control scheme was admirable in real-world implementations since ROS® packages pass through a local network via Wi-Fi communications involving loss of packages and delays. Additionally, the results of simulations and real-world experiments indicate that the robots reached the desired formation patterns with smooth trajectories in the -plane. However, the input control signals of the experiments were not as smooth as in the simulation. This is mainly due to non-modeled dynamics, external perturbations, loss of packages, and other drawbacks of the physical implementations which are not considered in simulated scenarios. Despite all these inconveniences, the edge-weight control performs well.
In this work, the MMDE-based formation pattern algorithm is performed offline, while the edge-weighted formation control drives the mobile robots online. It is left to future work to propose an online optimization-based formation pattern. In this manner, the desired formation pattern can be changed during online operation.
Moreover, the collision avoidance capacities of edge-weighted formation control can be combined with pin control of complex networks, adding a dynamic topology without restricting complete graph connection in complex networks [9].
8. Conclusions
This paper addressed an edge-weighted consensus-based formation control for differential drive robots. An MMDE-based formation pattern algorithm was proposed to provide the gain weights in edge-weighted graphs, given a desired formation in cartesian coordinates. Then, the edge-weighted formation control drives the mobile robots to the desired formation control, based on the adjusted gain weights. Simulation and real-world experiments were performed to verify the effectiveness and applicability of the proposed approach. Experiments considered a communication topology for multi-robot systems composed of three, four, and five mobile robots.
For the MMDE-based formation pattern algorithm, MMDE demonstrated its exploitation capacities with fast learning rates. MMDE has provided objective function evaluations below to 1.1843 × 10−16 for a network of five robots, which was the most challenging experiment. The smaller the objective function evaluations, the better precision the formation achieved will have.
Moreover, the reported optimal gain weights were adequate in all experiments. With respect to the edge-weighted formation control, the simulation and real-world implementation demonstrates the capacity of the control scheme to avoid collision among robots.
The applicability of the proposed method was tested with an experimental setup composed of an OptiTrack® motion capture system and up to five Turtlebot3® Waffle Pi. The main difference between simulation and real-world experiments was the computed control signals. The control signals results of real experiments were not smooth as the simulation results, due to non-modeled dynamics, external perturbation, imperfection in the surface, and robot wear conditions. However, mobile robots converge to the desired formation pattern performing smooth position trajectories in the -plane.
Finally, besides using different robots in the network topology, more future studies can be proposed, including trajectory tracking in formation with collision avoidance in the presence of dynamic objects.
Author Contributions
Conceptualization, J.H.-B. and T.H.; Data curation, J.D.R. and J.H.-B.; Funding acquisition, A.Y.A. and M.P.-C.; Investigation and software, J.D.R. and T.H.; Methodology, J.H.-B. and T.H.; Project administration and supervision, A.Y.A. and M.P.-C.; Validation, J.H.-B., T.H. and J.D.R.; Visualization and Writing, J.H.-B., J.D.R., T.H. and A.Y.A. All authors read and agreed to the published version of the manuscript.
Funding
This research was funded by CONAHCYT Mexico, through Project PCC-2022-319619.
Data Availability Statement
The data analyzed are available from the authors upon request.
Acknowledgments
The authors also thank Universidad de Guadalajara for their support in this research.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EAs | Evolutionary Algorithms |
| DE | Differential Evolution |
| MMDE | Multi-strategy Mutation Differential Evolution |
| ROS | Robot Operating System |
References
- Issa, B.A.; Rashid, A.T. A survey of multi-mobile robot formation control. Int. J. Comput. Appl. 2019, 181, 12–16. [Google Scholar]
- Latora, V.; Nicosia, V.; Russo, G. Complex Networks: Principles, Methods and Applications; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control. 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Godsil, C.; Royle, G.F. Algebraic Graph Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 207. [Google Scholar]
- Ren, W.; Beard, R.W.; Atkins, E.M. Information consensus in multivehicle cooperative control. IEEE Control. Syst. Mag. 2007, 27, 71–82. [Google Scholar]
- Grandi, R.; Falconi, R.; Melchiorri, C. Coordination and control of autonomous mobile robot groups using a hybrid technique based on particle swarm optimization and consensus. In Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1514–1519. [Google Scholar]
- Jin, J.; Kim, Y.G.; Wee, S.G.; Gans, N. Consensus based attractive vector approach for formation control of non-holonomic mobile robots. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Republic of Korea, 7–11 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 977–983. [Google Scholar]
- Molinari, F.; Raisch, J. Efficient consensus-based formation control with discrete-time broadcast updates. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4172–4177. [Google Scholar]
- Rios, J.D.; Ríos-Rivera, D.; Hernandez-Barragan, J.; Pérez-Cisneros, M.; Alanis, A.Y. Formation Control of Mobile Robots Based on Pin Control of Complex Networks. Machines 2022, 10, 898. [Google Scholar] [CrossRef]
- Nuno, E.; Loria, A.; Hernández, T.; Maghenem, M.; Panteley, E. Distributed consensus-formation of force-controlled non-holonomic robots with time-varying delays. Automatica 2020, 120, 109114. [Google Scholar] [CrossRef]
- Falconi, R.; Sabattini, L.; Secchi, C.; Fantuzzi, C.; Melchiorri, C. Edge-weighted consensus-based formation control strategy with collision avoidance. Robotica 2015, 33, 332–347. [Google Scholar] [CrossRef]
- Secchi, C.; Fantuzzi, C. Formation control over delayed communication networks. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 563–568. [Google Scholar]
- Falconi, R.; Sabattini, L.; Secchi, C.; Fantuzzi, C.; Melchiorri, C. A graph–based collision–free distributed formation control strategy. IFAC Proc. Vol. 2011, 44, 6011–6016. [Google Scholar] [CrossRef]
- Darvishpoor, S.; Darvishpour, A.; Escarcega, M.; Hassanalian, M. Nature-Inspired Algorithms from Oceans to Space: A Comprehensive Review of Heuristic and Meta-Heuristic Optimization Algorithms and Their Potential Applications in Drones. Drones 2023, 7, 427. [Google Scholar] [CrossRef]
- Slowik, A.; Kwasnicka, H. Evolutionary algorithms and their applications to engineering problems. Neural Comput. Appl. 2020, 32, 12363–12379. [Google Scholar] [CrossRef]
- Bilal; Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar] [CrossRef]
- Ahmad, M.F.; Isa, N.A.M.; Lim, W.H.; Ang, K.M. Differential evolution: A recent review based on state-of-the-art works. Alex. Eng. J. 2022, 61, 3831–3872. [Google Scholar] [CrossRef]
- Xiao, P.; Zou, D.; Xia, Z.; Shen, X. Multi-strategy different dimensional mutation differential evolution algorithm. Proc. AIP Conf. Proc. 2019, 2073, 020102. [Google Scholar]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Force Control; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ren, W.; Cao, Y. Distributed Coordination of Multi-Agent Networks: Emergent Problems, Models, and Issues; Springer: Berlin/Heidelberg, Germany, 2011; Volume 1. [Google Scholar]
- Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341. [Google Scholar] [CrossRef]
- Simon, D. Evolutionary Optimization Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Amsters, R.; Slaets, P. Turtlebot 3 as a robotics education platform. In Robotics in Education: Current Research and Innovations 10; Springer: Berlin/Heidelberg, Germany, 2020; pp. 170–181. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).