Macroeconomic Effects of Maritime Transport Costs Shocks: Evidence from the South Korean Economy
Abstract
:1. Introduction
2. Literature Review
3. DSGE Model
3.1. Composition of the DSGE Model
3.1.1. Household
3.1.2. Domestic Firms
3.1.3. Law of One Price, Import/Export Retailers, and Incomplete Exchange Rate Pass-Through
3.1.4. Terms of Trade and Real Exchange Rates
3.1.5. International Risk Sharing and UIP
3.1.6. Equilibrium in the Goods Market
3.1.7. Decomposition of Real Marginal Costs
3.1.8. Computation of Natural Output
3.1.9. Representation of the Total CPI
3.1.10. Monetary Policy and Foreign Shocks
3.1.11. Linearized Equilibrium System
3.2. Model Parameterization
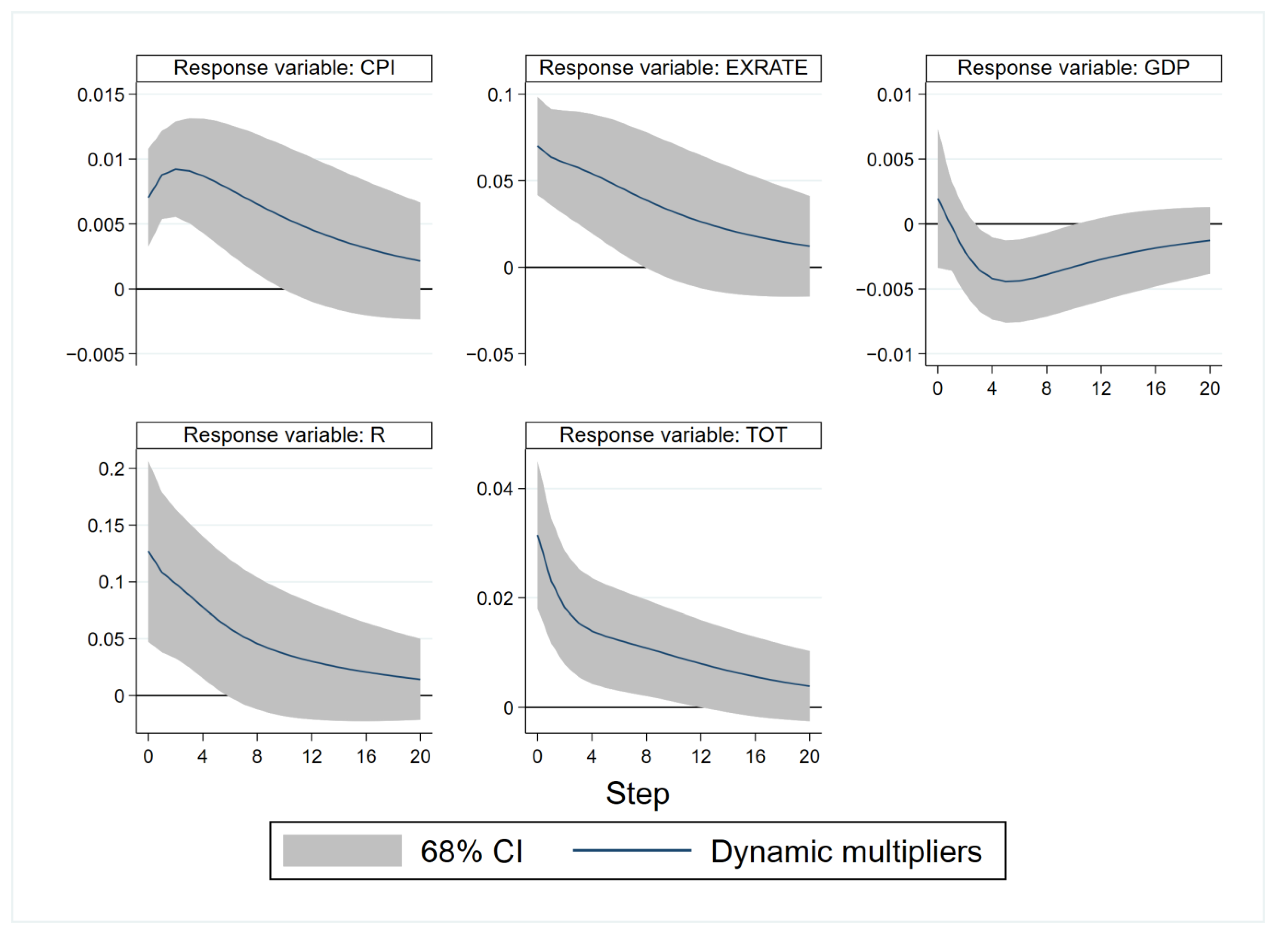
3.3. Impulse Response Analysis Results
4. VARX Analysis
4.1. VARX Model and Data
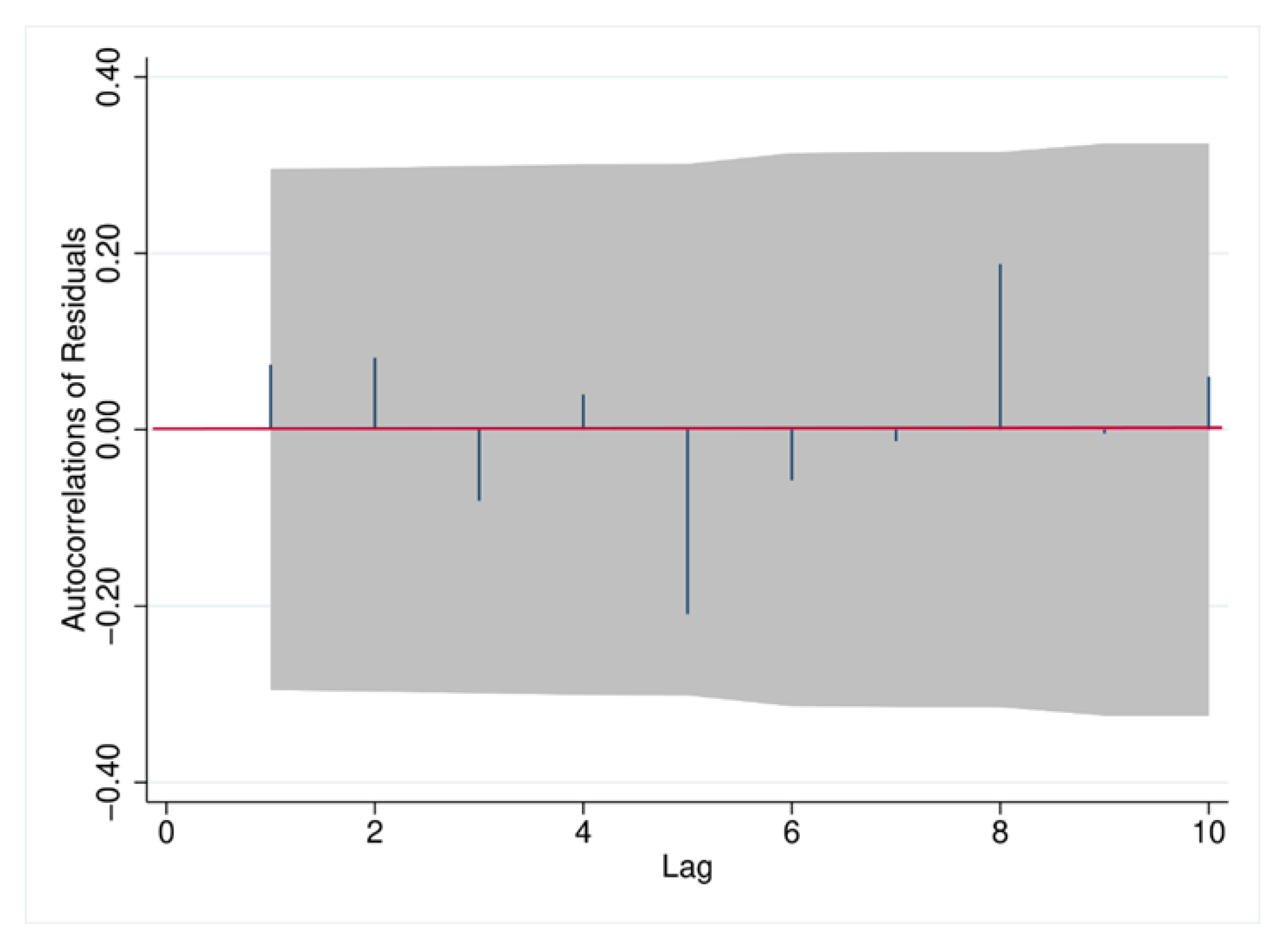
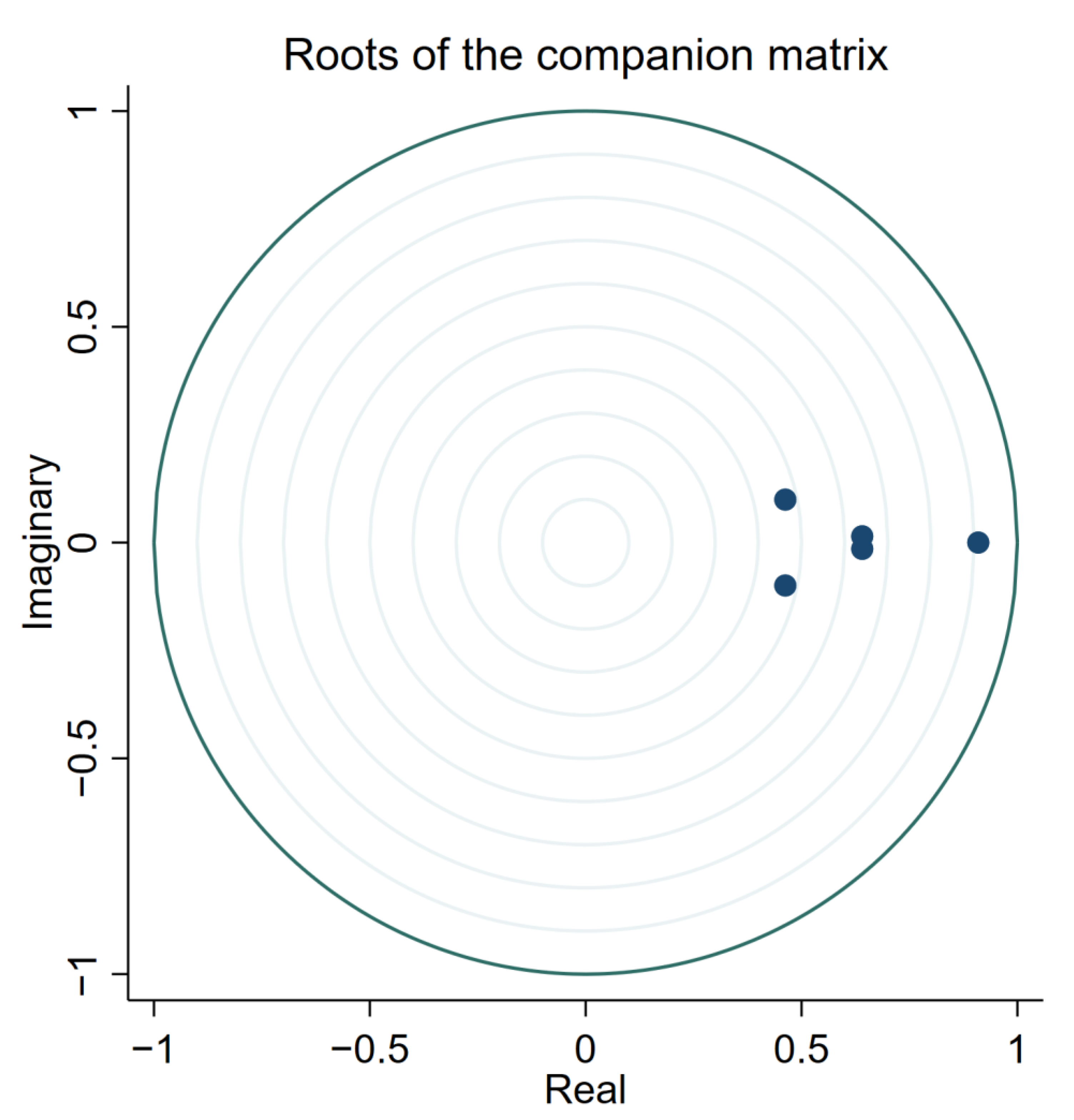
4.2. Analysis of Dynamic Multiplier Functions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- United Nations Conference on Trade and Development (UNCTAD). Review of Maritime Transport 2021; UNCTAD: Geneva, Switzerland, 2021. [Google Scholar]
- Fernando, L.; Dunn, J. The Dynamics of International Shipping Costs; Federal Reserve Bank of St. Louis: St. Louis, MI, USA, 2022; Available online: https://www.stlouisfed.org/on-the-economy/2022/january/dynamics-international-shipping-costs (accessed on 3 January 2022).
- Carrière-Swallow, Y.; Deb, P.; Furceri, D.; Jiménez, D.; Ostry, J.D. How Soaring Shipping Costs Raise Prices around the World; International Monetary Fund: Washington, DC, USA, 2022; Available online: https://www.imf.org/en/Blogs/Articles/2022/03/28/how-soaring-shipping-costs-raise-prices-around-the-world (accessed on 28 March 2022).
- Michail, N.A.; Melas, K.D.; Cleanthous, L. The Relationship between Shipping Freight Rates and Inflation in the Euro Area. Int. Econ. 2022, 172, 40–49. [Google Scholar] [CrossRef]
- United Nations Conference on Trade and Development (UNCTAD). Container Shipping in Times of COVID-19: Why Freight Rates Have Surged, and Implications for Policymakers; UNCTAD Policy Brief No. 84; UNCTAD: Geneva, Switzerland, 2021. [Google Scholar]
- United Nations Conference on Trade and Development (UNCTAD). Shipping During COVID-19: Why Container Freight Rates Have Surged; UNCTAD: Geneva, Switzerland, 2021; Available online: https://unctad.org/news/shipping-during-covid-19-why-container-freight-rates-have-surged (accessed on 23 April 2021).
- Rožić, T.; Naletina, D.; Zając, M. Volatile Freight Rates in Maritime Container Industry in Times of Crises. Appl. Sci. 2022, 12, 8452. [Google Scholar] [CrossRef]
- Park, J.S.; Seo, Y.-J. The Impact of Seaports on the Regional Economies in South Korea: Panel Evidence from the Augmented Solow Model. Transp. Res. Part E Logist. Transp. Rev. 2016, 85, 107–119. [Google Scholar] [CrossRef]
- Ding, X.; Wang, M. Container Freight Rates and International Trade Causality Nexus: Evidence from Panel Var Approach for Shanghai and Asean-6 Countries. Discret. Dyn. Nat. Soc. 2022, 2022, 2415914. [Google Scholar] [CrossRef]
- Organisation for Economic Co-operation and Development (OECD). Oecd Economic Outlook; OECD: Paris, France, 2021; Volume 2021. [Google Scholar]
- Carrière-Swallow, Y.; Deb, P.; Furceri, D.; Jiménez, D.; Ostry, J.D. Shipping Costs and Inflation. J. Int. Money Financ. 2023, 130, 102771. [Google Scholar] [CrossRef]
- Adolfson, M.; Laséen, S.; Lindé, J.; Villani, M. Evaluating an Estimated New Keynesian Small Open Economy Model. J. Econ. Dyn. Control 2008, 32, 2690–2721. [Google Scholar] [CrossRef]
- Costa, C.J., Jr. Understanding Dsge Models: Theory and Applications; Vernon Press: Wilmington, DE, USA, 2016. [Google Scholar]
- Monacelli, T. Monetary Policy in a Low Pass-through Environment. J. Money Credit. Bank. 2005, 37, 1047–1066. [Google Scholar] [CrossRef]
- Nicholson, W.B.; Matteson, D.S.; Bien, J. Varx-L: Structured Regularization for Large Vector Autoregressions with Exogenous Variables. Int. J. Forecast. 2017, 33, 627–651. [Google Scholar] [CrossRef]
- OECD/European Union Intellectual Property Office. Misuse of Containerized Maritime Shipping in the Global Trade of Counterfeits; Illicit Trade; OECD Publishing: Paris, France, 2021.
- Kim, J.W. What Determines the Volume of Maritime Containers in Korea? KIET Ind. Econ. Rev. 2011, 16, 14–25. [Google Scholar] [CrossRef]
- Pham, N.T.A.; Sim, N. Shipping Cost and Development of the Landlocked Developing Countries: Panel Evidence from the Common Correlated Effects Approach. World Econ. 2020, 43, 892–920. [Google Scholar] [CrossRef]
- Yin, J.; Shi, J. Seasonality Patterns in the Container Shipping Freight Rate Market. Marit. Policy Manag. 2018, 45, 159–173. [Google Scholar] [CrossRef]
- Yonhap, S. Korea Introduces Own Container Cargo Index; Yonhap News Agency: Seoul, Republic of Korea, 2022; Available online: https://en.yna.co.kr/view/AEN20221107007400320 (accessed on 7 November 2022).
- Macera, A.P.; Divino, J.A. Import Tariff and Exchange Rate Transmission in a Small Open Economy. Emerg. Mark. Financ. Trade 2015, 51, S61–S79. [Google Scholar] [CrossRef]
- Bae, B.-H. Results from the Construction of New Bok-Dsge Model for Economic Forecasting and Policy Analysis. Bank Korea Mon. Bull. 2013, 68, 16–52. [Google Scholar]
- Kim, T.B. Analysis on Korean Economy with an Estimated Dsge Model after 2000. KDI J. Econ. Policy 2014, 36, 1–64. [Google Scholar]
- Choi, J.; Hur, J. An Examination of Macroeconomic Fluctuations in Korea Exploiting a Markov-Switching Dsge Approach. Econ. Model. 2015, 51, 183–199. [Google Scholar] [CrossRef]
- Yie, M.-S.; Yoo, B.H. The Role of Foreign Debt and Financial Frictions in a Small Open Economy Dsge Model. Singap. Econ. Rev. 2016, 61, 1550077. [Google Scholar] [CrossRef]
- Kang, H.; Suh, H. Macroeconomic Dynamics in Korea During and after the Global Financial Crisis: A Bayesian Dsge Approach. Int. Rev. Econ. Financ. 2017, 49, 386–421. [Google Scholar] [CrossRef]
- Engel, C.; Wang, J. International Trade in Durable Goods: Understanding Volatility, Cyclicality, and Elasticities. J. Int. Econ. 2011, 83, 37–52. [Google Scholar] [CrossRef]
- Galí, J.; Monacelli, T. Monetary Policy and Exchange Rate Volatility in a Small Open Economy. Rev. Econ. Stud. 2005, 72, 707–734. [Google Scholar] [CrossRef]
- Galí, J. Monetary Policy, Inflation, and the Business Cycle: An Introduction to the New Keynesian Framework and Its Applications; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Calvo, G.A. Staggered Prices in a Utility-Maximizing Framework. J. Monet. Econ. 1983, 12, 383–398. [Google Scholar] [CrossRef]
- Gao, Y.; Yao, X.; Wang, W.; Liu, X. Dynamic Effect of Environmental Tax on Export Trade Based on Dsge Mode. Energy Environ. 2019, 30, 1275–1290. [Google Scholar] [CrossRef]
- Kilian, L.; Zhou, X. Modeling Fluctuations in the Global Demand for Commodities. J. Int. Money Financ. 2018, 88, 54–78. [Google Scholar] [CrossRef]
- Kilian, L. Not All Oil Price Shocks Are Alike: Disentangling Demand and Supply Shocks in the Crude Oil Market. Am. Econ. Rev. 2009, 99, 1053–1069. [Google Scholar] [CrossRef]
- Borchert, I.; Yotov, Y.V. Distance, Globalization, and International Trade. Econ. Lett. 2017, 153, 32–38. [Google Scholar] [CrossRef]
- Luo, M.; Fan, L.; Liu, L. An Econometric Analysis for Container Shipping Market. Marit. Policy Manag. 2009, 36, 507–523. [Google Scholar] [CrossRef]
- Das, R.C. Forecasting Incidences of COVID-19 Using Box-Jenkins Method for the Period July 12–Septembert 11, 2020: A Study on Highly Affected Countries. Chaos Solitons Fractals 2020, 140, 110248. [Google Scholar] [CrossRef]
- Jiang, Y.; Wei, W.; Das, R.C.; Chatterjee, T. Analysis of the Strategic Emission-Based Energy Policies of Developing and Developed Economies with Twin Prediction Model. Complexity 2020, 2020, 4701678. [Google Scholar] [CrossRef]
- Das, R.C. Prediction of Number of Cases and Deaths Due to the Second Wave of COVID-19 Using Arima Model for May 11–June 30, 2021: A Study on India and Its Major States. Asian J. Res. Soc. Sci. Humanit. 2021, 11, 1–27. [Google Scholar] [CrossRef]
- Justiniano, A.; Preston, B. Monetary Policy and Uncertainty in an Empirical Small Open-Economy Model. J. Appl. Econom. 2010, 25, 93–128. [Google Scholar] [CrossRef]
- Justiniano, A.; Preston, B. Macroeconomic Effects of Energy Price: New Insight from Korea? Mathematics 2022, 25, 93–128. [Google Scholar]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer Science & Business Media: Berlin, Germany, 2005. [Google Scholar]
- Anwar, S.; Nguyen, L.P. Channels of Monetary Policy Transmission in Vietnam. J. Policy Model. 2018, 40, 709–729. [Google Scholar] [CrossRef]
- Afrin, S. Monetary Policy Transmission in Bangladesh: Exploring the Lending Channel. J. Asian Econ. 2017, 49, 60–80. [Google Scholar] [CrossRef]
- Pham, V.A. Impacts of the Monetary Policy on the Exchange Rate: Case Study of Vietnam. J. Asian Bus. Econ. Stud. 2019, 26, 220–237. [Google Scholar] [CrossRef]
- Köse, N.; Aslan, Ç. The Effect of Real Exchange Rate Uncertainty on Turkey’s Foreign Trade: New Evidences from Svar Model. Asia Pac. J. Account. Econ. 2023, 30, 553–567. [Google Scholar] [CrossRef]
- Ravn, M.O.; Schmitt-Grohé, S.; Uribe, M. Consumption, Government Spending, and the Real Exchange Rate. J. Monet. Econ. 2012, 59, 215–234. [Google Scholar] [CrossRef]
- Baek, J. Not All Oil Shocks on the Trade Balance Are Alike: Empirical Evidence from South Korea. Aust. Econ. Pap. 2022, 61, 291–303. [Google Scholar] [CrossRef]

| * | * | |
| Parameter | Calibration | Description | Source |
|---|---|---|---|
| Households | |||
| 0.99 | Discount factor | Choi and Hur [24], He and Lee [40] | |
| 1.2 | The inverse of Frisch elasticity of labor supply | Bae [22] | |
| 0.04 | Coefficient of risk aversion | Choi and Hur [24] | |
| 0.4 | Level of economic openness | Yie and Yoo [25] | |
| 4.460 | Elasticity of substitution between domestic and imported goods | Bae [22] | |
| Firms | |||
| 0.8 | Domestic prices stickiness | Bae [22] | |
| 0.69 | Import price stickiness | Bae [22] | |
| 0.82 | Export price stickiness | Kang and Suh [26] | |
| Monetary policy rule | |||
| 1.5 | Inflation reaction coefficient in the Taylor rule | Bae [22], Kang and Suh [26], Kim [23] | |
| 0.2 | Output gap reaction coefficient in the Taylor rule | Bae [22], Kang and Suh [26], Kim [23] | |
| Parameter | Calibration | Description | Source |
|---|---|---|---|
| AR coefficients | |||
| 0.98 | Technology | Choi and Hur [24] | |
| 0.82 | Maritime transport costs | Authors’ estimate | |
| 0.93 | Impact of foreign output on maritime transportation costs | Authors’ estimate | |
| 0.49 | Foreign Output | Choi and Hur [24] | |
| 0.85 | Foreign interest rates | Choi and Hur [24] | |
| 0.76 | Foreign Inflation | Choi and Hur [24] | |
| 0.9 | Interest rate smoothing | Bae [22], Kang and Suh [26], Kim [23] | |
| Standard deviations | |||
| 3.06 | Technology | Choi and Hur [24] | |
| 0.08 | Maritime transport costs | Authors’ estimate | |
| 0.41 | Foreign Output | Choi and Hur [24] | |
| 0.41 | Foreign interest rates | Choi and Hur [24] | |
| 0.52 | Foreign Inflation | Choi and Hur [24] | |
| 0.002 | Monetary policy exogenous shocks | Bae [22] | |
| * | * | ||
| * |
| Variable Definition | Abbreviation | Period | Source |
|---|---|---|---|
| Domestic block (Endogenous variables) | |||
| Seasonally Adjusted Real GDP | GDP | 2002:Q1–2022:Q4 | Bank of Korea’s Economic Statistics System database (BOK-ECOS) |
| Nominal exchange rate (base rate of KRW to USD) | EXRATE | 2002:Q1–2022:Q4 | BOK-ECOS |
| Nominal interest rate (unsecured overnight borrowing rate) | R | 2002:Q1–2022:Q4 | BOK-ECOS |
| Terms of Trade | TOT | 2002:Q1–2022:Q4 | BOK-ECOS |
| Seasonally Adjusted Consumer Price Index | CPI | 2002:Q1–2022:Q4 | BOK-ECOS |
| Foreign block (Exogenous variables) | |||
| West Texas Intermediate (WTI) crude oil price | OIL | 2002:Q1–2022:Q4 | Energy Information Administration |
| U.S. Federal Funds Rate | R_US | 2002:Q1–2022:Q4 | Board of Governors of the Federal Reserve System |
| China Containerized Freight Index | CCFI | 2002:Q1–2022:Q4 | Shanghai Shipping Exchange |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, X.; Choi, Y.-J. Macroeconomic Effects of Maritime Transport Costs Shocks: Evidence from the South Korean Economy. Mathematics 2023, 11, 3668. https://doi.org/10.3390/math11173668
Ding X, Choi Y-J. Macroeconomic Effects of Maritime Transport Costs Shocks: Evidence from the South Korean Economy. Mathematics. 2023; 11(17):3668. https://doi.org/10.3390/math11173668
Chicago/Turabian StyleDing, Xingong, and Yong-Jae Choi. 2023. "Macroeconomic Effects of Maritime Transport Costs Shocks: Evidence from the South Korean Economy" Mathematics 11, no. 17: 3668. https://doi.org/10.3390/math11173668
APA StyleDing, X., & Choi, Y.-J. (2023). Macroeconomic Effects of Maritime Transport Costs Shocks: Evidence from the South Korean Economy. Mathematics, 11(17), 3668. https://doi.org/10.3390/math11173668






