Joint Optimization of Maintenance and Spare Parts Inventory Strategies for Emergency Engineering Equipment Considering Demand Priorities
Abstract
:1. Introduction
- (1)
- Construct a joint optimization model of spare parts inventory and maintenance strategies for the service system comprising two types of emergency engineering equipment;
- (2)
- Consider the diverse priorities of the demands needed to be accomplished by emergency engineering equipment in accordance with the real situation;
- (3)
- Employ the Markov process imbedding approach efficiently to formulate a group of system reliability indexes, including the availability of spare parts, maintenance engineer and entire service system;
- (4)
- Apply the branch-and-bound method successfully to address the joint optimization model and derive the joint optimum decisions of spare part inventory strategy and maintenance engineer allocation.
2. Model Descriptions and Assumptions
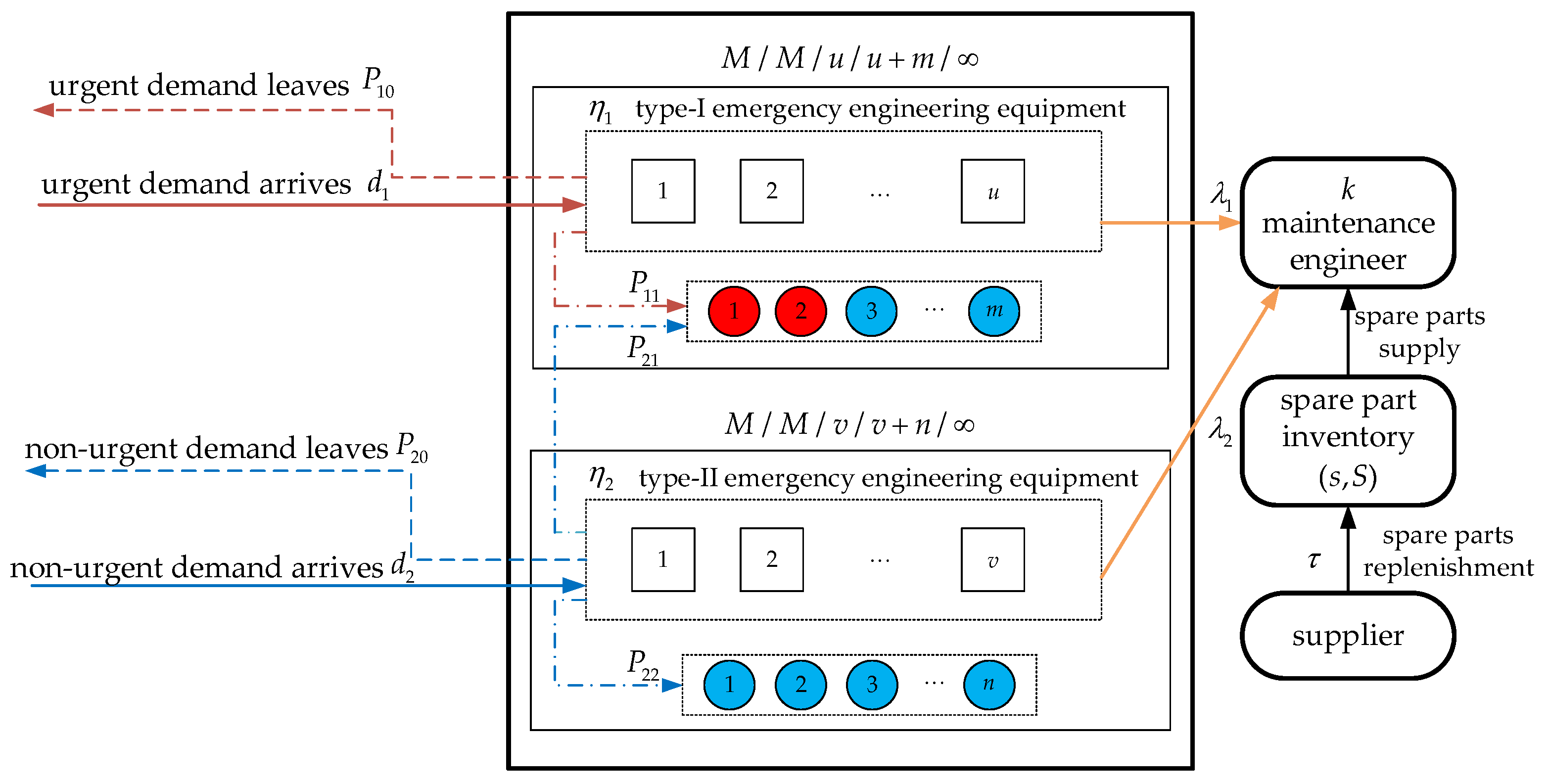
2.1. System Description
- (1)
- If the urgent demands reach the service system, the operation situations are described as follows. Customers with urgent demands automatically choose the type-I emergency engineering systems to acquire the express service. If there is no available type-I emergency engineering equipment, the customer may leave the service system directly with a probability , or wait in the queue of type-I emergency engineering equipment with a probability , satisfying .
- (2)
- When the non-urgent demands arrive at the service system, the operation scenarios are introduced as follows. The primary choice of customers with non-urgent demands is the type-II emergency engineering systems, owing to the less pressure of time. If no available type-II emergency engineering equipment exists upon the arrival of the demands, the customers may leave the system directly with a probability . Alternatively, they may continue waiting in the queue for the type-II emergency engineering equipment with a probability . Another possible choice is switching to the queue of type-I emergency engineering equipment with a probability , while the unsatisfied non-urgent demands may still wait to be served due to the fully occupied type-I emergency engineering equipment. Particularly, in the queue of type-I emergency engineering equipment, the customers with urgent demands take priority for service over those with non-urgent demands. It is obvious that .
2.2. Maintenance and Spare Parts Inventory Strategies
2.3. Basic Assumptions
- (1)
- The arrival of urgent and non-urgent demands follows the Poisson process with rates and , respectively.
- (2)
- Each piece of emergency engineering equipment functions independently. The service time of type-I and type-II emergency engineering equipment fulfilling the demands follows the exponential distribution with rates and , respectively. Obviously, .
- (3)
- The lifetimes of type-I and type-II emergency engineering equipment are exponentially distributed with rates and , respectively.
- (4)
- The maintenance times of type-I and type-II emergency engineering equipment follow exponential distributions with parameters and , respectively.
- (5)
- The lead time of spare parts replenishment obeys an exponential distribution with a replenishment rate .
3. Markov Process Descriptions
- (1)
- Condition: and ;Transition: ;Transition rate: .
- (2)
- Condition: and ;Transition: ;Transition rate: .
- (3)
- Condition: and ;Transition: ;Transition rate: .
- (4)
- Condition: and ;Transition: ;Transition rate: .
- (5)
- Condition: and ;Transition: ;Transition rate: .
- (6)
- Condition: and ;Transition: ;Transition rate: .
- (7)
- Condition: and ;Transition: ;Transition rate: .
- (8)
- Condition: and ;Transition: ;Transition rate: .
- (9)
- Condition: and ;Transition: ;Transition rate: .
- (10)
- Condition: and ;Transition: ;Transition rate: .
- (11)
- Condition: and ;Transition: ;Transition rate: .
- (12)
- Condition: and ;Transition: ;Transition rate: .
- (13)
- Condition: and ;Transition: ;Transition rate: .
- (14)
- Condition: and ;Transition: ;Transition rate: .
- (15)
- Condition: and ;Transition: ;Transition rate: .
- (16)
- Condition: and ;Transition: ;Transition rate: .
- (17)
- Condition: and ;Transition: ;Transition rate: .
- (18)
- Condition: and ;Transition: ;Transition rate: .
- (19)
- Condition: and ;Transition: ;Transition rate: .
4. Formulation of the Joint Optimization Model
4.1. Derivation of Reliability Indexes
4.2. Cost Analysis
4.3. Joint Optimization Model
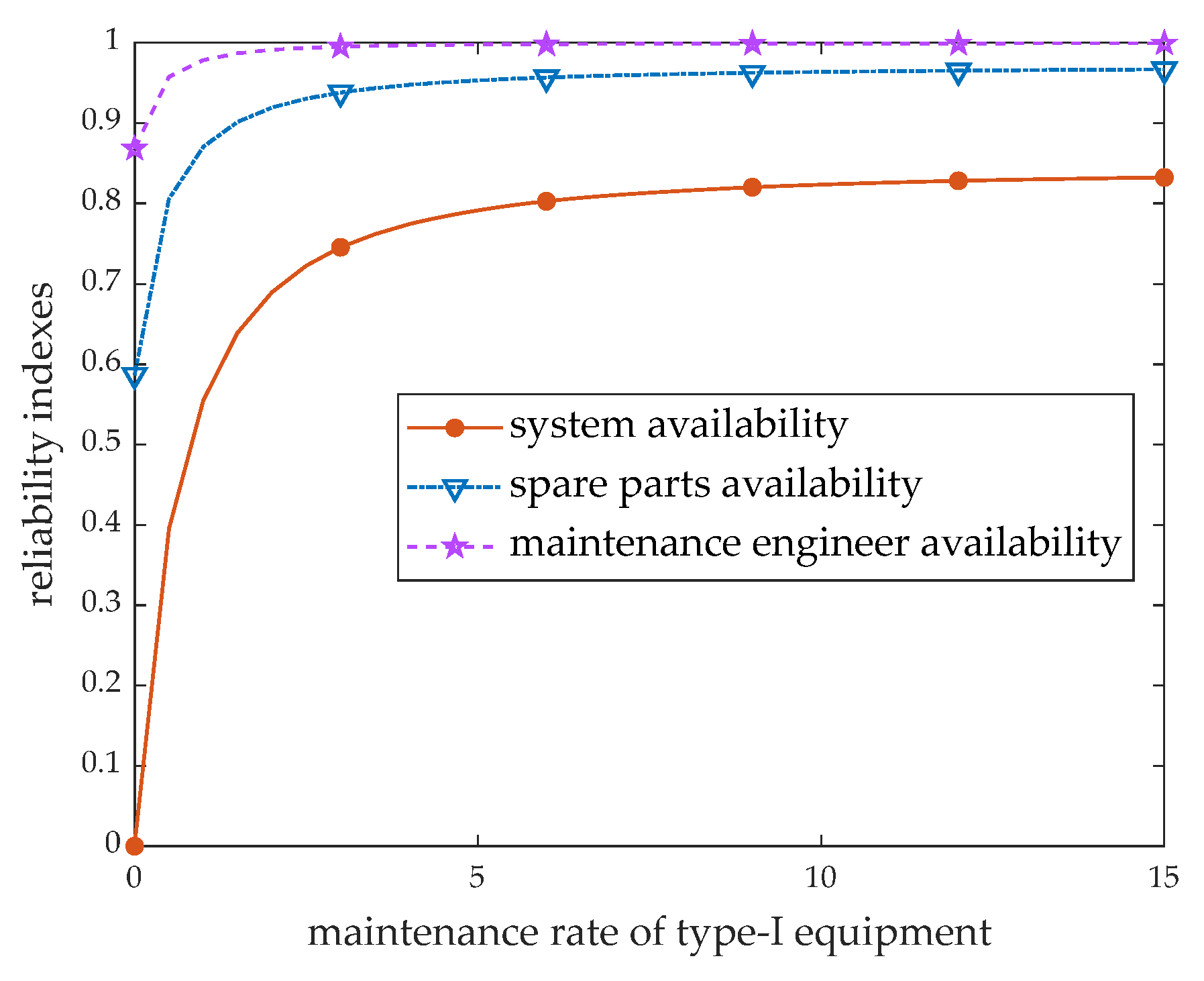
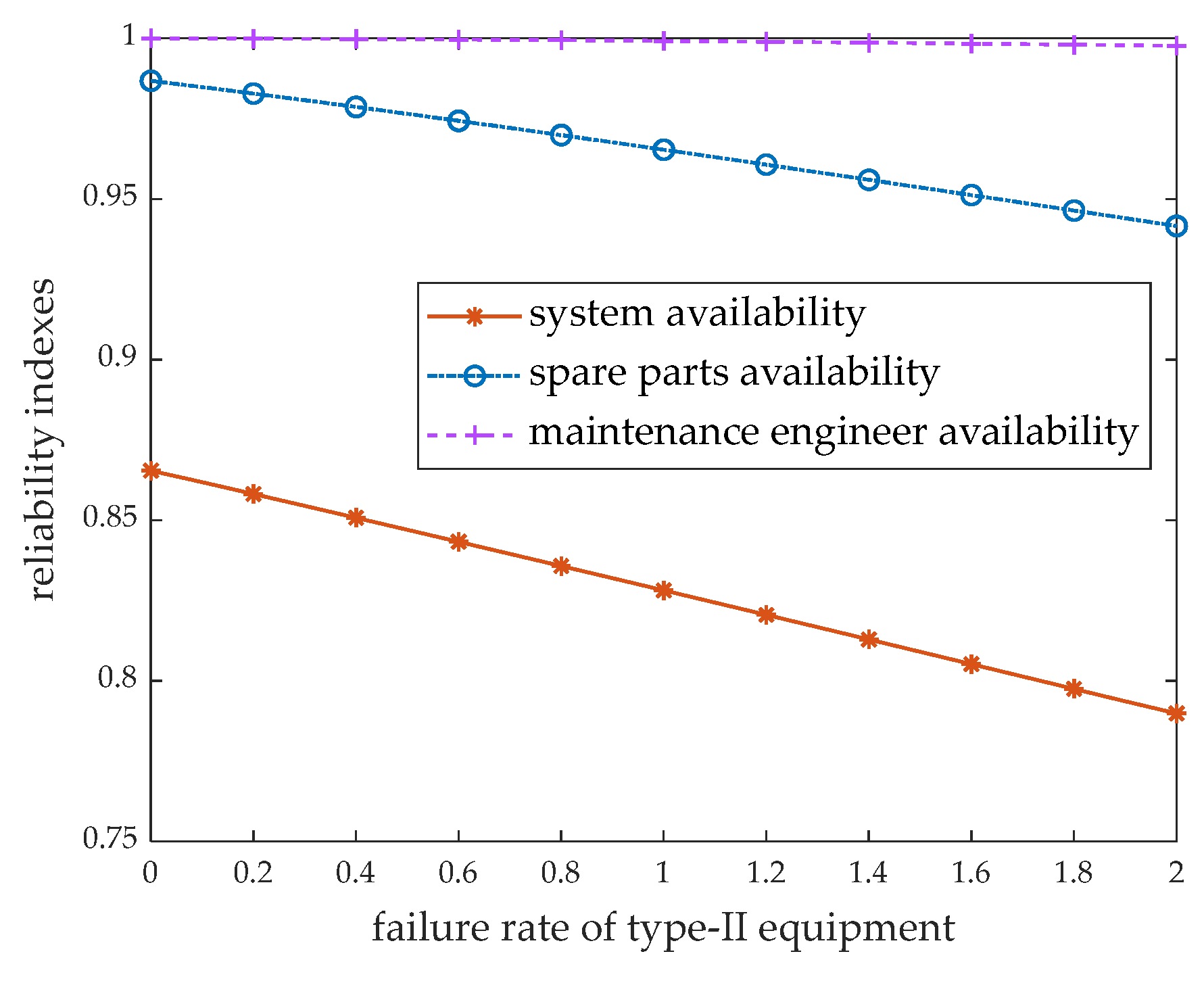
5. Numerical Examples
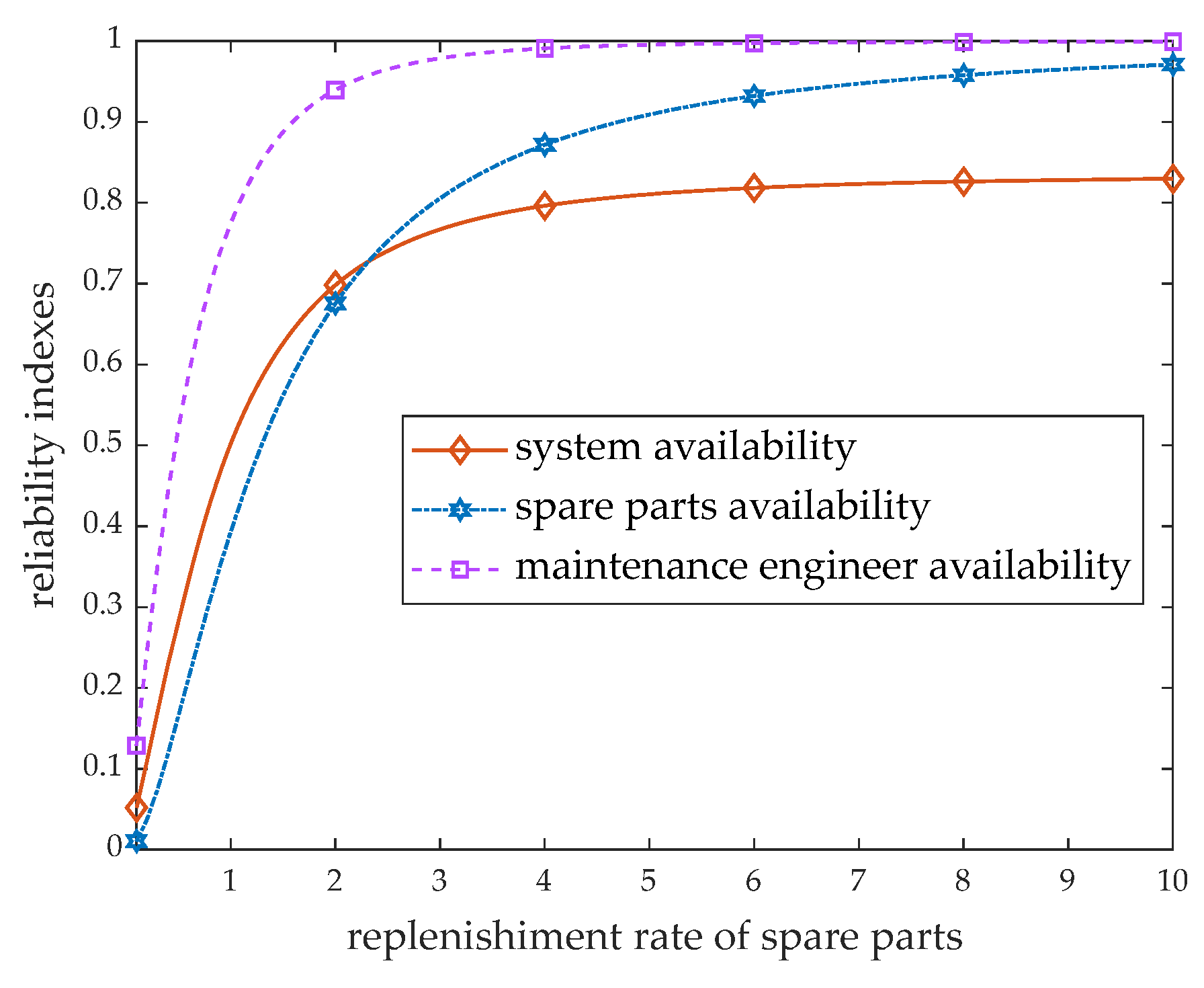
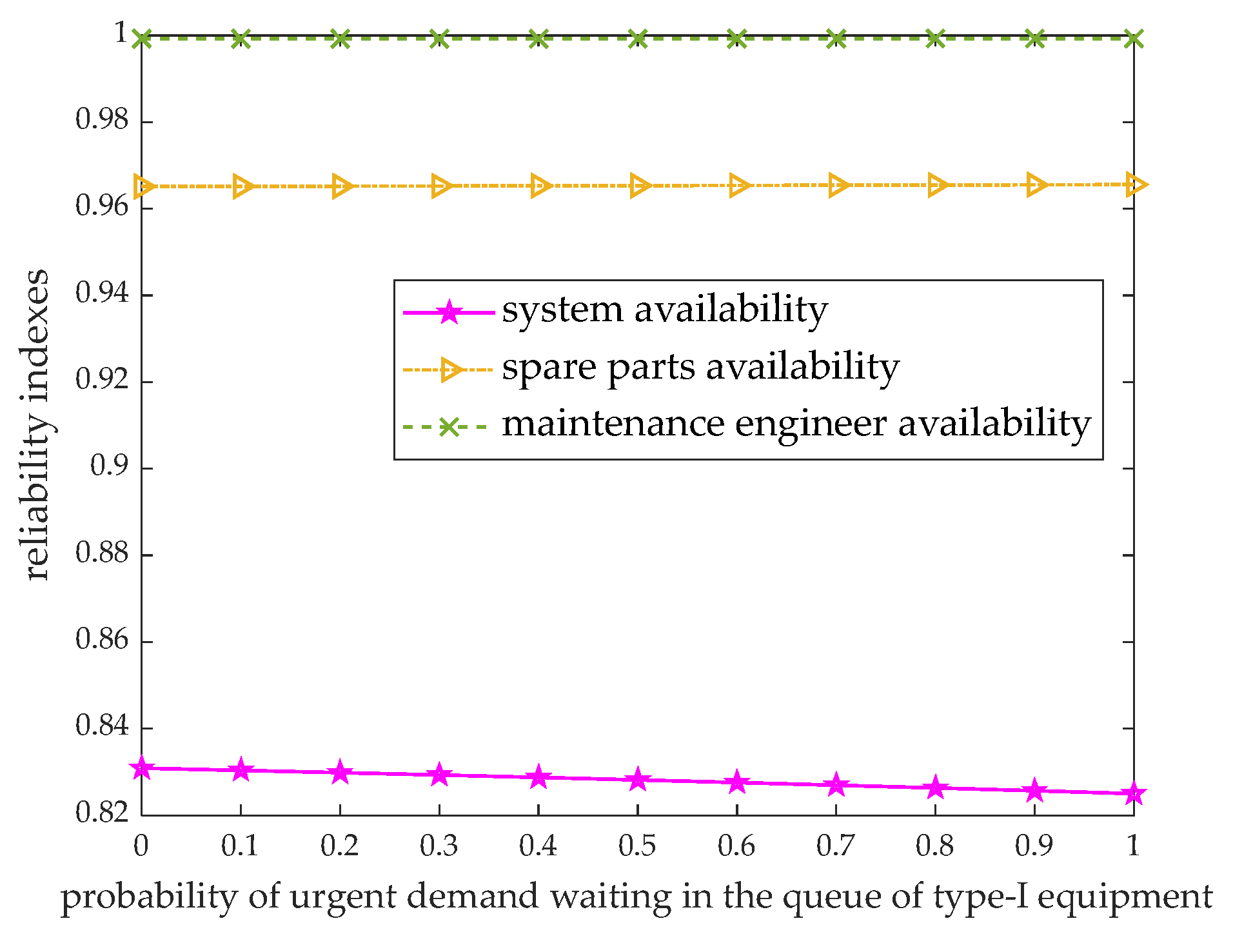

6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.Y.; Zhao, X.; Wang, S.Q.; Sun, L.P. Reliability and maintenance for performance-balanced systems operating in a shock environment. Reliab. Eng. Syst. Saf. 2020, 195, 106705. [Google Scholar] [CrossRef]
- Dui, H.Y.; Yang, X.J.; Fang, Y.N. Evaluation methodology for preventive maintenance in multi-state manufacturing systems considering different costs. Int. J. Prod. Res. 2022. [Google Scholar] [CrossRef]
- Li, J.L.; Yin, G.H.; Wang, X.F.; Yan, W.X. Automated decision making in highway pavement preventive maintenance based on deep learning. Autom. Constr. 2022, 135, 104111. [Google Scholar] [CrossRef]
- Wang, S.Q.; Zhao, X.; Wu, C.S.; Wang, X.Y. Joint optimization of multi-stage component reassignment and preventive maintenance for balanced systems considering imperfect maintenance. Reliab. Eng. Syst. Saf. 2023, 237, 109367. [Google Scholar] [CrossRef]
- Dong, E.Z.; Gao, T.L.; Cheng, Z.H.; Wang, R.C.; Bai, Y.S. Opportunistic maintenance strategy for complex equipment with a genetic algorithm considering failure dependence: A two-dimensional warranty perspective. Sensors 2022, 22, 6801. [Google Scholar] [CrossRef]
- Li, H.; Huang, C.G.; Soares, C.G. A real-time inspection and opportunistic maintenance strategies for floating offshore wind turbines. Ocean Eng. 2022, 256, 111433. [Google Scholar] [CrossRef]
- Broek, M.; Teunter, R.H.; de Jonge, B.; Veldman, J. Joint condition-based maintenance and condition-based production optimization. Reliab. Eng. Syst. Saf. 2021, 214, 107743. [Google Scholar] [CrossRef]
- Zheng, R.; Makis, V. Optimal condition-based maintenance with general repair and two dependent failure modes. Comput. Ind. Eng. 2020, 141, 106322. [Google Scholar] [CrossRef]
- Shen, J.Y.; Cui, L.R.; Ma, Y.Z. Availability and optimal maintenance policy for systems degrading in dynamic environments. Eur. J. Oper. Res. 2019, 276, 133–143. [Google Scholar] [CrossRef]
- Liu, Q.N.; Ma, L.; Wang, N.C.; Chen, A.K.; Jiang, Q.H. A condition-based maintenance model considering multiple maintenance effects on the dependent failure processes. Reliab. Eng. Syst. Saf. 2022, 220, 108267. [Google Scholar] [CrossRef]
- Dui, H.Y.; Zhang, C.; Tian, T.Z.; Wu, S.M. Different costs-informed component preventive maintenance with system lifetime changes. Reliab. Eng. Syst. Saf. 2022, 228, 108755. [Google Scholar] [CrossRef]
- Tusar, M.I.H.; Sarker, B.R. Spare parts control strategies for offshore wind farms: A critical review and comparative study. Wind Eng. 2022, 46, 1629–1656. [Google Scholar] [CrossRef]
- Dendauw, P.; Goeman, T.; Claeys, D.; De Turck, K.; Fiems, D.; Bruneel, H. Condition-based critical level policy for spare parts inventory management. Comput. Ind. Eng. 2021, 157, 107369. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Li, H.; Hu, S.Q.; Yu, X.Z. Two-stage supply chain inventory management based on system dynamics model for reducing bullwhip effect of sulfur product. Ann. Oper. Res. 2022. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Zhang, J.X.; Du, D.B.; Li, T.M.; Si, X.S. A lifetime estimation method for multi-component degrading systems with deteriorating spare parts. Reliab. Eng. Syst. Saf. 2023, 238, 109427. [Google Scholar] [CrossRef]
- Yan, T.; Lei, Y.; Wang, B.; Han, T.; Si, X.; Li, N. Joint maintenance and spare parts inventory optimization for multi-unit systems considering imperfect maintenance actions. Reliab. Eng. Syst. Saf. 2020, 202, 106994. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, X.; Peng, R.; Kang, J. Joint optimization of inspection and spare ordering policy with multi-level defect information. Comput. Ind. Eng. 2020, 139, 106205. [Google Scholar] [CrossRef]
- Zhang, J.X.; Du, D.B.; Si, X.S.; Hu, C.H.; Zhang, H.W. Joint optimization of preventive maintenance and inventory management for standby systems with hybrid-deteriorating spare parts. Reliab. Eng. Syst. Saf. 2021, 214, 107686. [Google Scholar] [CrossRef]
- Cai, B.P.; Wang, Y.D.; Zhang, Y.P.; Liu, Y.L.; Ge, W.F.; Li, R.K.; Liu, Y.H.; Liu, G.J. Condition-based maintenance method for multi-component system based on RUL prediction: Subsea tree system as a case study. Comput. Ind. Eng. 2022, 173, 108650. [Google Scholar] [CrossRef]
- Zahedi-Hosseini, F.; Scarf, P.; Syntetos, A. Joint maintenance-inventory optimisation of parallel production systems. J. Manuf. Syst. 2018, 48, 73–86. [Google Scholar] [CrossRef]
- Salmasnia, A.; Talesh-Kazemi, A. Integrating inventory planning, pricing and maintenance for perishable products in a two-component parallel manufacturing system with common cause failures. Oper. Res. 2022, 22, 1235–1265. [Google Scholar] [CrossRef]
- Zhu, M.X.; Zhou, X.J. Hybrid opportunistic maintenance policy for serial-parallel multi-station manufacturing systems with spare part overlap. Reliab. Eng. Syst. Saf. 2023, 236, 109304. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, X.Y. Joint optimization of condition-based maintenance and inventory control for a k-out-of-n: F system of multi-state degrading components. Eur. J. Oper. Res. 2021, 290, 514–529. [Google Scholar] [CrossRef]
- Zheng, M.M.; Lin, J.; Xia, T.B.; Liu, Y.; Pan, E.R. Joint condition-based maintenance and spare provisioning policy for a K-out-of-N system with failures during inspection intervals. Eur. J. Oper. Res. 2023, 308, 1220–1232. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Wang, J.; Coit, D.W. Joint optimization of spare part supply and opportunistic condition-based maintenance for onshore wind farms considering maintenance route. IEEE Trans. Eng. Manag. 2022. [Google Scholar] [CrossRef]
- Wang, J.J.; Qiu, Q.G.; Wang, H.H. Joint optimization of condition-based and age-based replacement policy and inventory policy for a two-unit series system. Reliab. Eng. Syst. Saf. 2021, 205, 107251. [Google Scholar] [CrossRef]
- Liu, X.B.; Yang, T.J.; Pei, J.; Liao, H.T.; Pohl, E.A. Replacement and inventory control for a multi-customer product service system with decreasing replacement costs. Eur. J. Oper. Res. 2019, 273, 561–574. [Google Scholar] [CrossRef]
- Yi, H.; Cui, L.R. A new computation method for signature: Markov process method. Nav. Res. Log. 2018, 65, 410–426. [Google Scholar] [CrossRef]
- Cui, L.R.; Gao, H.D.; Mo, Y.C. Reliability for k-out-of-n: F balanced systems with m sectors. IISE Trans. 2018, 50, 381–393. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, J.; Wang, X.Y. Joint optimization of components redundancy, spares inventory and repairmen allocation for a standby series system. Proc. Inst. Mech. Eng. Part O-J. Risk Reliab. 2019, 233, 623–638. [Google Scholar] [CrossRef]
- Dui, H.Y.; Lu, Y.H.; Gao, Z.F.; Xing, L.D. Performance efficiency and cost analysis of multi-state systems with successive damage and maintenance in multiple shock events. Reliab. Eng. Syst. Saf. 2023, 238, 109403. [Google Scholar] [CrossRef]
- Wang, X.Y.; Ning, R.; Zhao, X.; Wu, C.S. Reliability assessments for two types of balanced systems with multi-state protective devices. Reliab. Eng. Syst. Saf. 2023, 229, 108852. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Z.Y.; Wang, X.Y.; Guo, B. Reliability of performance-based system containing multiple load-sharing subsystems with protective devices considering protection randomness. Reliab. Eng. Syst. Saf. 2023, 239, 109508. [Google Scholar] [CrossRef]
- Song, Y.B.; Wang, X.Y. Reliability analysis of the multi-state k-out-of-n: F systems with multiple operation mechanisms. Mathematics 2022, 10, 4615. [Google Scholar] [CrossRef]
- Wu, C.S.; Zhao, X.; Wang, X.Y.; Wang, S.Q. Reliability analysis of performance-based balanced systems with common bus performance sharing. Reliab. Eng. Syst. Saf. 2021, 215, 107865. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhao, X.; Wu, C.S.; Lin, C. Reliability assessment for balanced systems with restricted rebalanced mechanisms. Comput. Ind. Eng. 2020, 149, 106801. [Google Scholar] [CrossRef]
- Wang, X.Y.; Ning, R.; Zhao, X.; Zhou, J. Reliability evaluations for a multi-state k-out-of-n: F system with m subsystems supported by multiple protective devices. Comput. Ind. Eng. 2022, 171, 108409. [Google Scholar] [CrossRef]
- Xie, W.; Liao, H.T.; Jin, T.D. Maximizing system availability through joint decision on component redundancy and spares inventory. Eur. J. Oper. Res. 2014, 237, 164–176. [Google Scholar] [CrossRef]
- Abdelmaguid, T.F. Bi-objective dynamic multiprocessor open shop scheduling for maintenance and healthcare diagnostics. Expert Syst. Appl. 2021, 186, 115777. [Google Scholar] [CrossRef]
- Yu, V.F.; Salsabila, N.Y.; Siswanto, N.; Kuo, P.H. A two-stage genetic algorithm for joint coordination of spare parts inventory and planned maintenance under uncertain failures. Appl. Soft. Comput. 2022, 130, 109705. [Google Scholar] [CrossRef]
- Yang, M.; Li, C.B.; Tang, Y.; Xiong, M.K. Availability-oriented maintenance strategy of key equipment in automated production line considering performance degradation. IEEE Robot. Autom. Lett. 2023, 8, 3182–3189. [Google Scholar] [CrossRef]

| Study | System Structure | Optimized Policy | Methodology | Demand Priority |
|---|---|---|---|---|
| Ref. [16] | Series system with identical units | Preventive maintenance (PM) and inventory | Stochastic dynamic programming and simulation | None |
| Ref. [17] | Single-unit system | Condition-based maintenance (CBM) and threshold of ordering spares | Enumeration algorithm | None |
| Ref. [18] | Standby system | PM and inventory | Simulation | None |
| Ref. [19] | Multi-component system | CBM and inventory | Genetic algorithm | None |
| Refs. [20,21,22] | Parallel or series-parallel system | PM and inventory [20,21]; Opportunistic maintenance and inventory [22] | Simulation [20]; Particle swarm optimization [21]; Hierarchical optimization [22] | None |
| Refs. [23,24,25,26] | k-out-of-n: F system [23,24]; Onshore Wind Farm [25]; Two-unit series system [26] | CBM and inventory | Markov decision process (MDP) and dynamic programming [23]; MDP and value iteration [24]; Clustering and simulation [25]; Semi-MDP [26] | None |
| Ref. [27] | Use-oriented product service system | CBM and inventory | MDP and sequential heuristic solution | None |
| This paper | Service system with two types of equipment | Corrective maintenance engineer allocation and inventory | Markov process imbedding and branch-and-bound method | Urgent demands given higher priority |
| Rule | Common Trigger | Distinctive Condition | Transition | Rate |
|---|---|---|---|---|
| (1) | An urgent demand arrives | (1) Type-I equip. is available. | ||
| (2) | (2) Demand waits in type-I queue due to the unavailability of type-I equip. | |||
| (3) | A non-urgent demand arrives | (3) Type-II equip. is available. | ||
| (4) | (4) Type-II and type-I equip. is unavailable and available, respectively. | |||
| (5) | (5) Demand waits in type-I queue due to the unavailability of type-I and type-II equip. | |||
| (6) | (6) Demand waits in type-II queue due to the unavailability of type-II equip. |
| Rule | Common Trigger | Distinctive Condition | Transition | Rate |
|---|---|---|---|---|
| (7) | A piece of equip. fails | (7) A piece of type-I equip. fails. | ||
| (8) | (8) A piece of type-II equip. fails. | |||
| (9) | A piece of type-I equip. completes the service | (9) There is no waiting demand. | ||
| (10) | (10) There exists at least one waiting urgent demand. | |||
| (11) | (11) There is no waiting urgent demand but at least one waiting non-urgent demand. | |||
| (12) | A piece of type-II equip. completes the service | (12) There is no waiting demand. | ||
| (13) | (13) There exists at least one waiting non-urgent demand. |
| Rule | Common Trigger | Distinctive Condition | Transition | Rate |
|---|---|---|---|---|
| (14) | A piece of type-I equip. is completely repaired | (14) There is no waiting demand. | ||
| (15) | (15) There exists at least one waiting urgent demand. | |||
| (16) | (16) There is no waiting urgent demand but at least one waiting non-urgent demand. | |||
| (17) | A piece of type-II equip. is completely repaired | (17) There is no waiting demand. | ||
| (18) | (18) There exists at least one waiting non-urgent demand. |
| 5 | 4 | 0.5 | 0.5 | 0.5 | 0.25 | 0.25 | 9 | 7 | 1.5 | 1 | 12 | 10 | 9 |
| No. | Joint Optimization Policy | Reliability Indexes | ||||
|---|---|---|---|---|---|---|
| 1 | 7 | 3 | 8 | 23.8372 | ||
| 2 | 1 | 3 | 8 | 24.4232 | ||
| 3 | 15 | 3 | 8 | 24.6996 | ||
| 4 | 7 | 1 | 8 | 22.9336 | ||
| 5 | 7 | 10 | 8 | 21.9344 | ||
| 6 | 7 | 3 | 1 | 18.0879 | ||
| 7 | 7 | 3 | 17 | 24.7137 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, J.; Ning, R.; Chen, X. Joint Optimization of Maintenance and Spare Parts Inventory Strategies for Emergency Engineering Equipment Considering Demand Priorities. Mathematics 2023, 11, 3688. https://doi.org/10.3390/math11173688
Wang X, Wang J, Ning R, Chen X. Joint Optimization of Maintenance and Spare Parts Inventory Strategies for Emergency Engineering Equipment Considering Demand Priorities. Mathematics. 2023; 11(17):3688. https://doi.org/10.3390/math11173688
Chicago/Turabian StyleWang, Xiaoyue, Jingxuan Wang, Ru Ning, and Xi Chen. 2023. "Joint Optimization of Maintenance and Spare Parts Inventory Strategies for Emergency Engineering Equipment Considering Demand Priorities" Mathematics 11, no. 17: 3688. https://doi.org/10.3390/math11173688
APA StyleWang, X., Wang, J., Ning, R., & Chen, X. (2023). Joint Optimization of Maintenance and Spare Parts Inventory Strategies for Emergency Engineering Equipment Considering Demand Priorities. Mathematics, 11(17), 3688. https://doi.org/10.3390/math11173688






