Equilibrium Position of a Particle in a Microchannel Flow of Newtonian and Power-Law Fluids with an Obstacle
Abstract
:1. Introduction
2. Numerical method
2.1. Lattice Boltzmann Method (LBM)
2.2. Boundary Treatment
2.3. Hydrodynamic Force and Torque
2.4. Lubrication Force
2.5. Power-Law Fluid
3. Verification
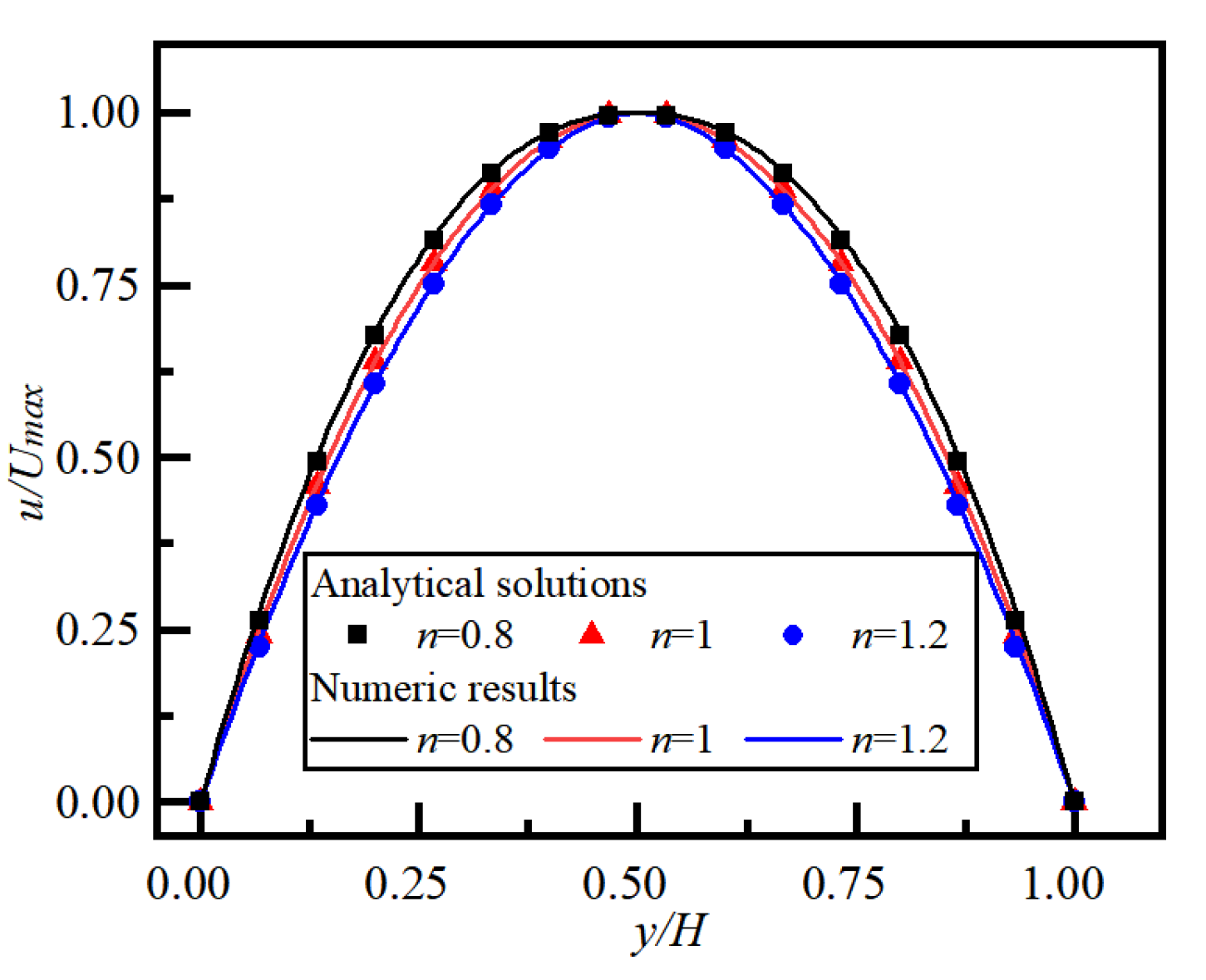
3.1. Velocity Distribution for the Power-Law Fluid
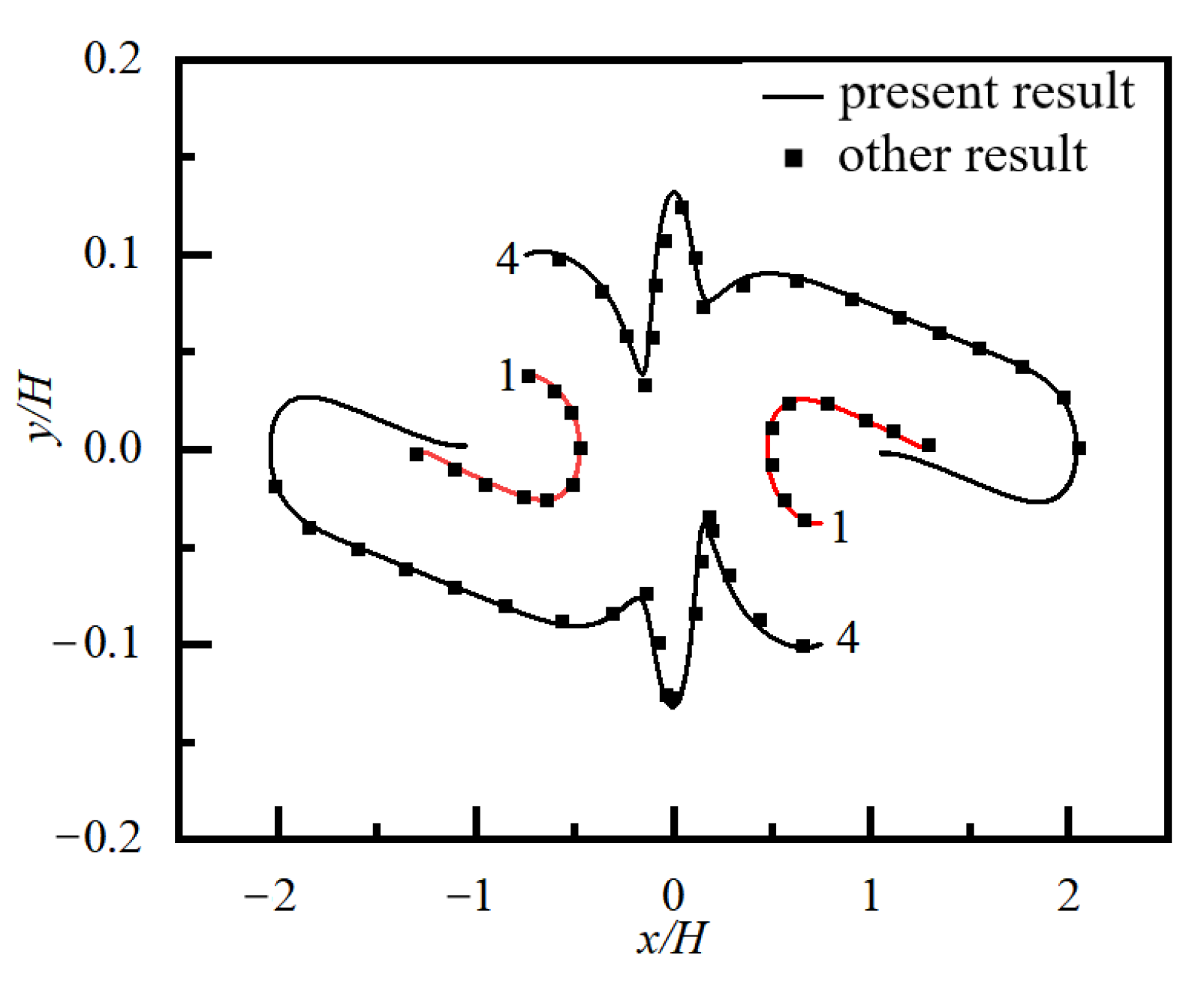
3.2. Particle Trajectory
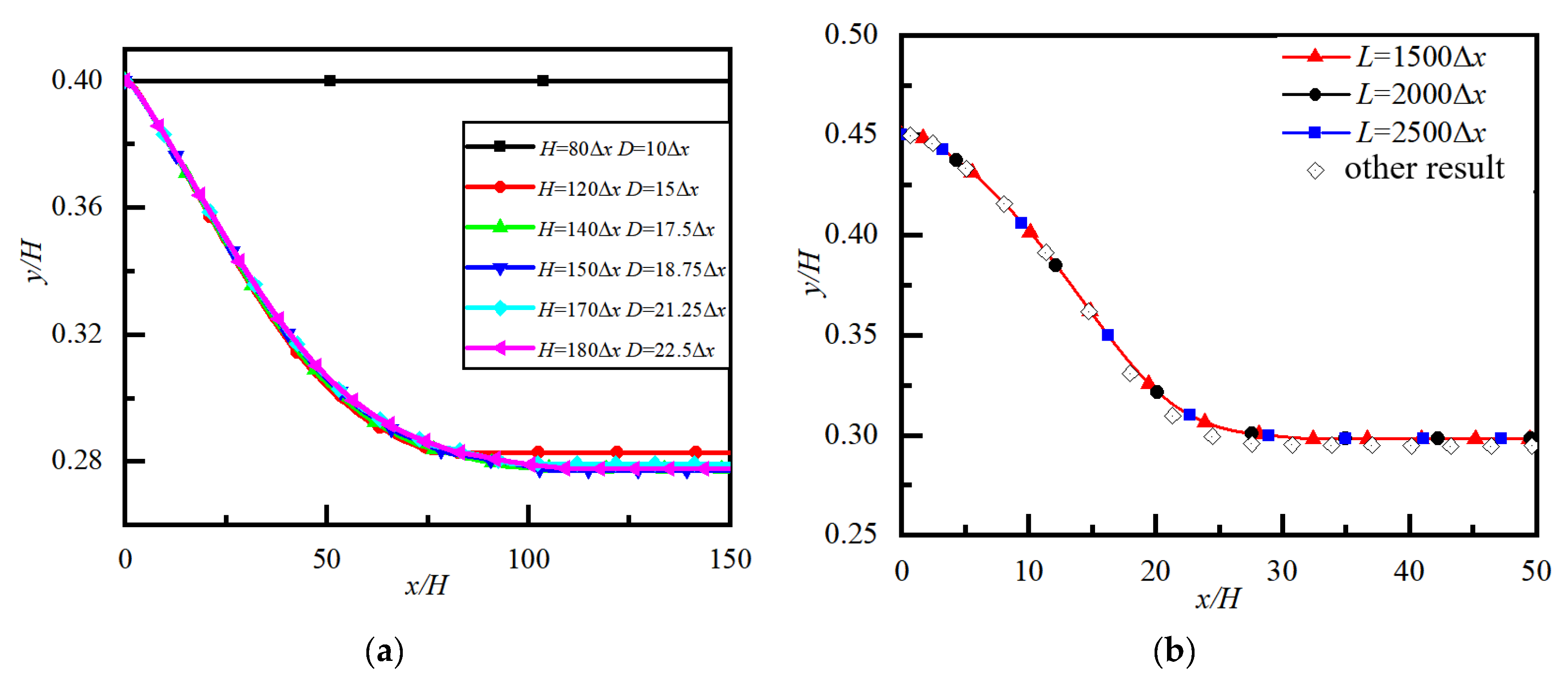
3.3. Grid Resolution and Compute-Domain Independence
4. Results and Discussion
4.1. Flow and Parameters
4.2. Lateral Migration and Equilibrium Position of a Particle without Obstacle
4.3. Effect of Obstacle Size on Particle Migration and Lateral Position
4.3.1. Situation near Obstacle
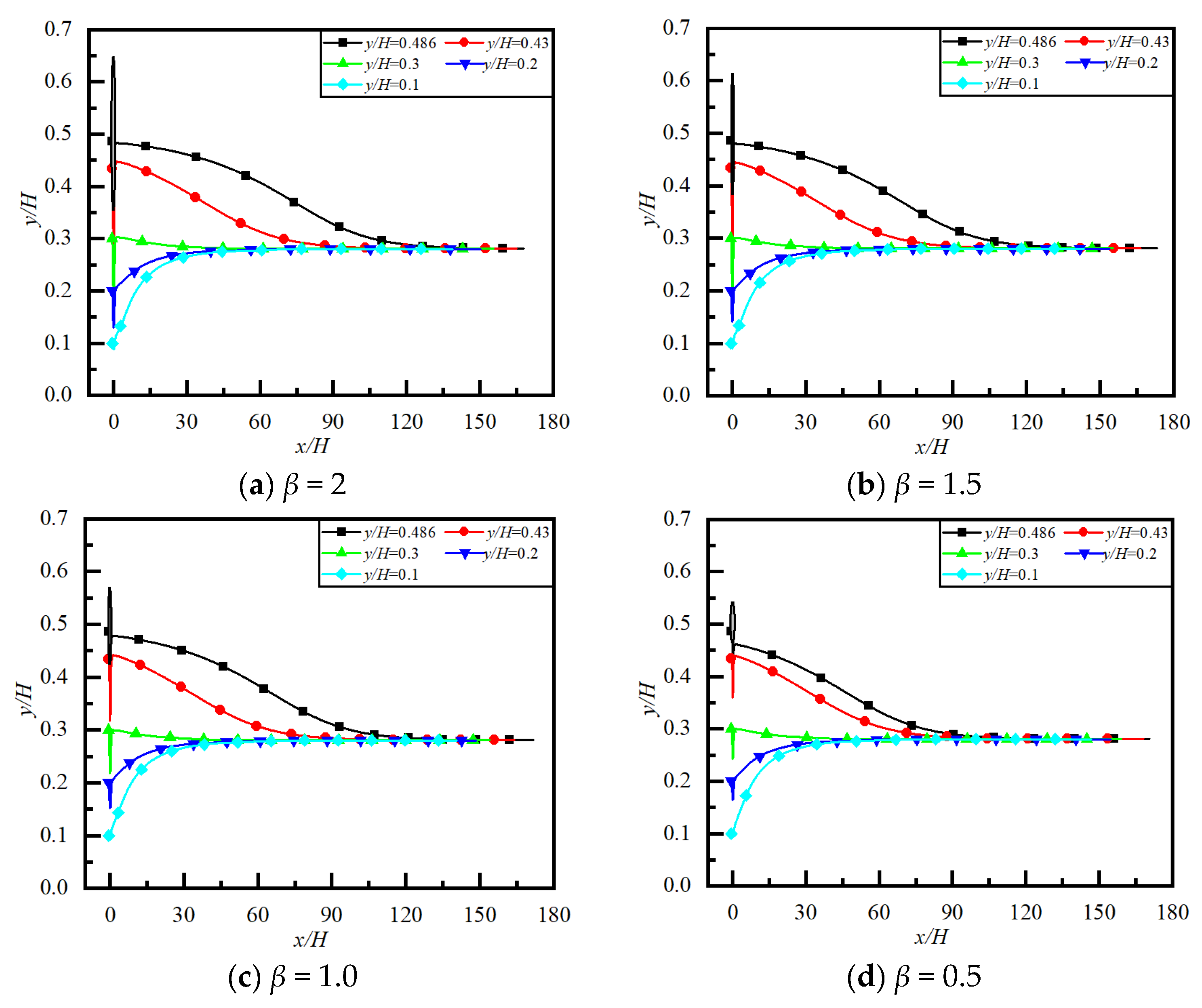
4.3.2. Situations Far Downstream of Obstacle
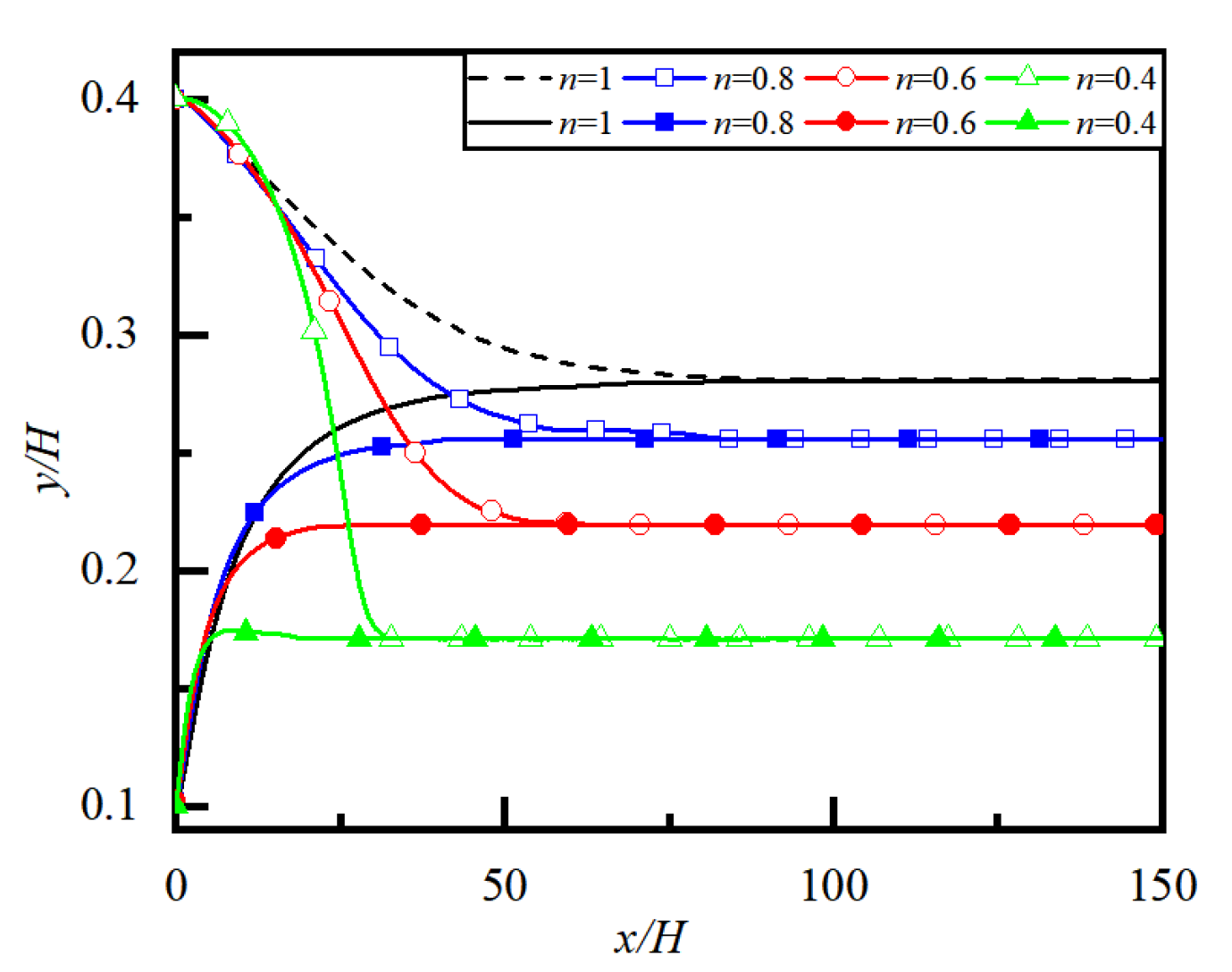
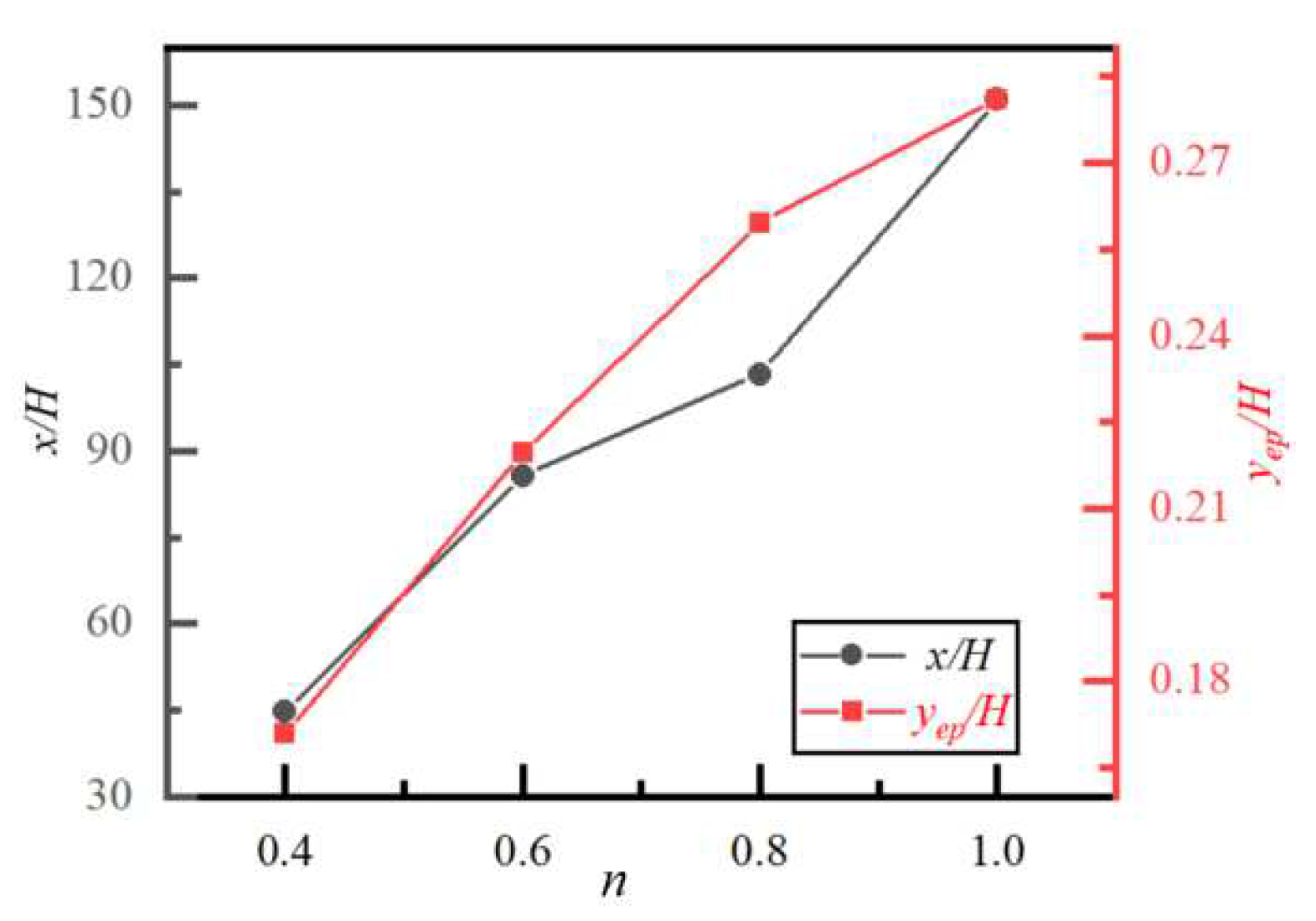
4.4. Effect of Power-Law Index n on Particle Migration and Lateral Equilibrium Position
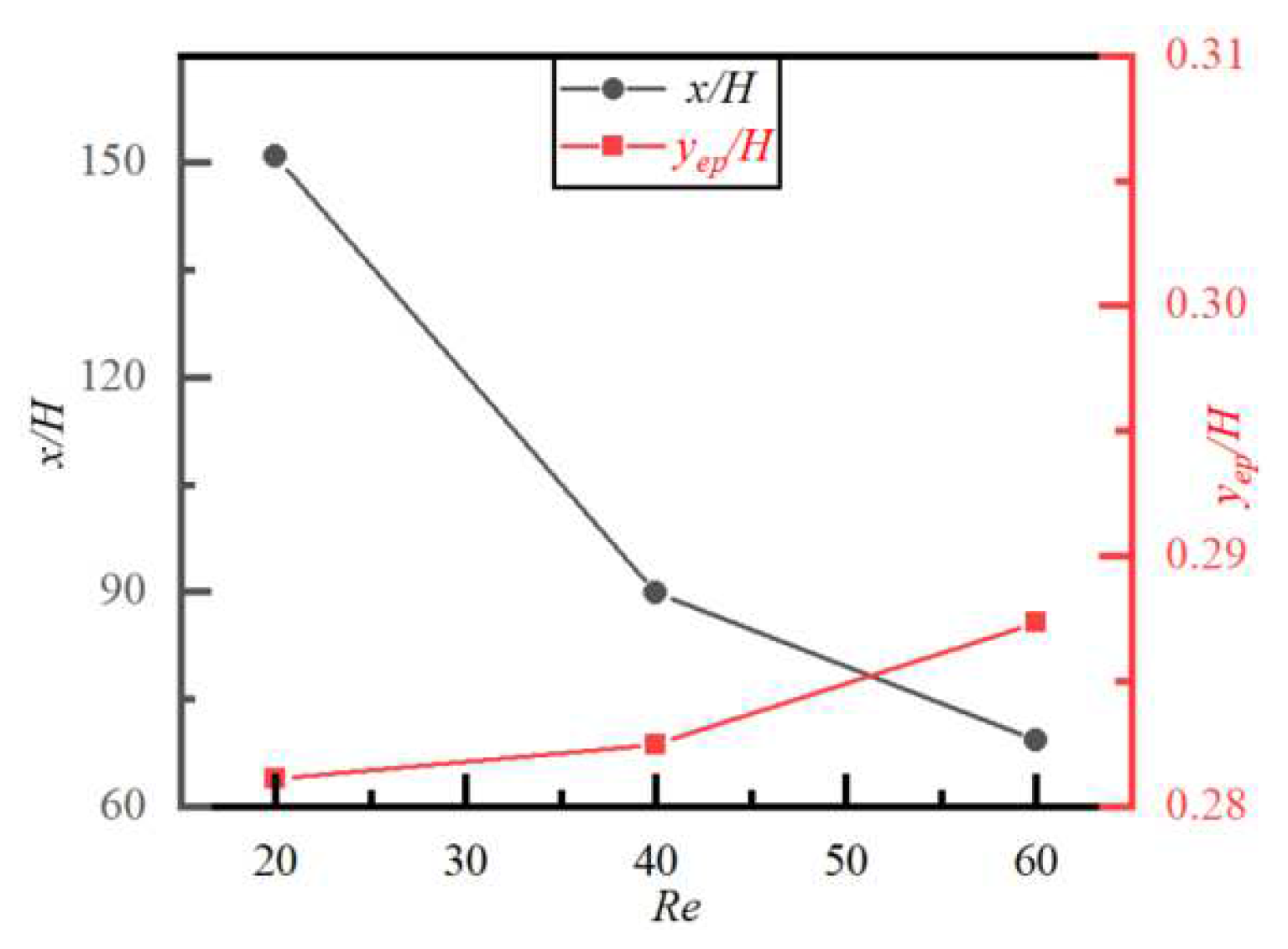
4.5. Effect of Reynolds Number Re on Particle Migration and Lateral Equilibrium Position
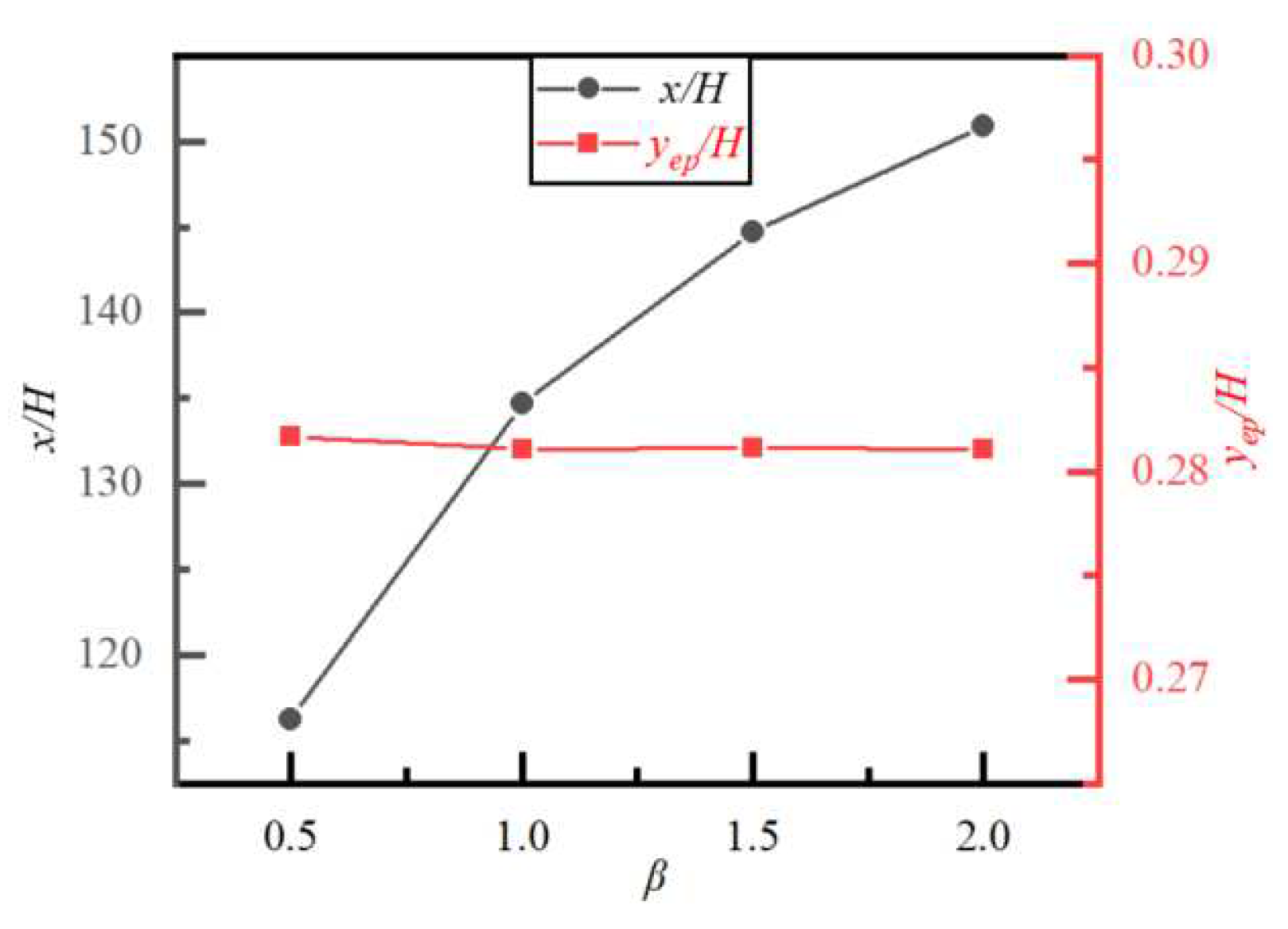
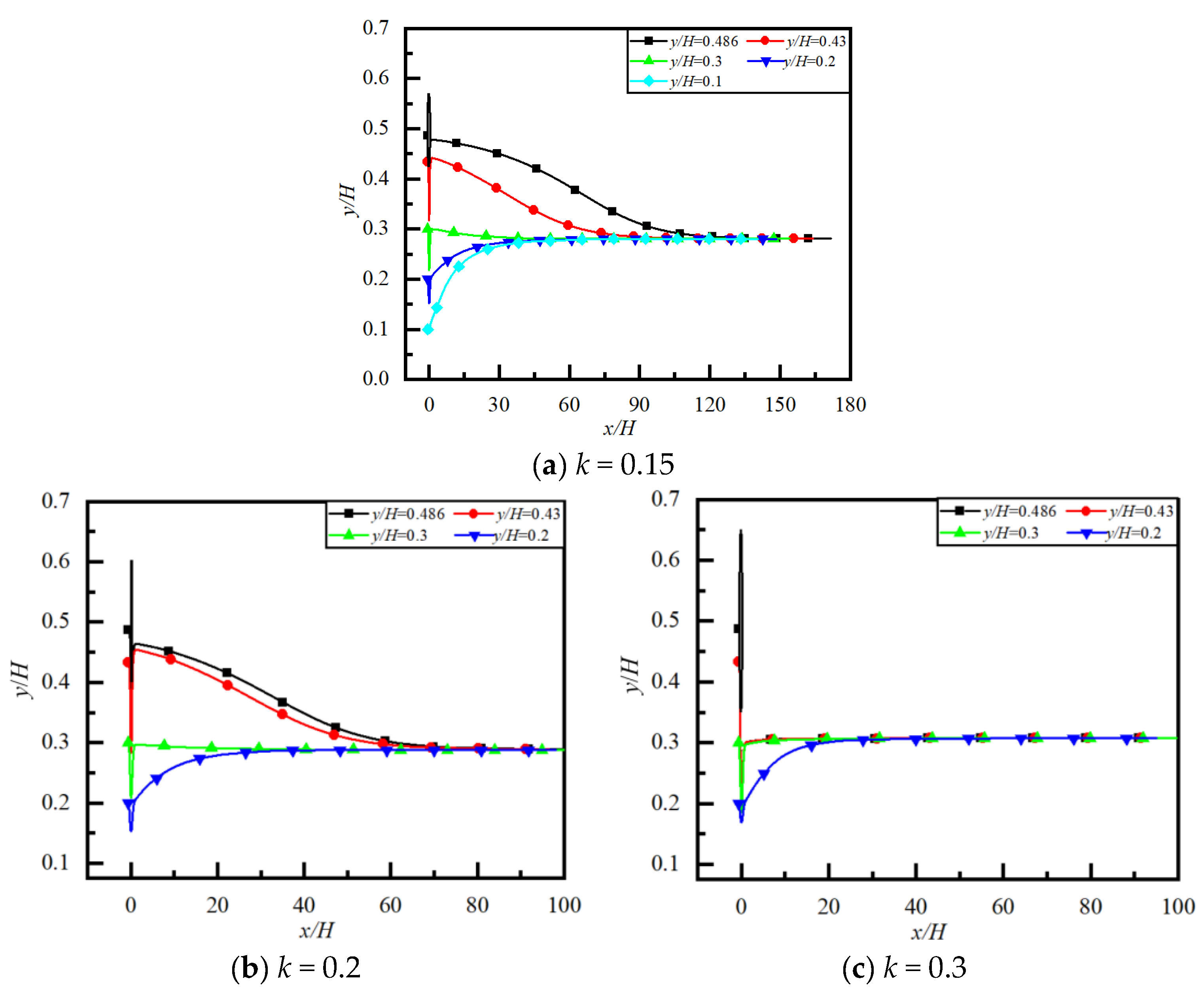
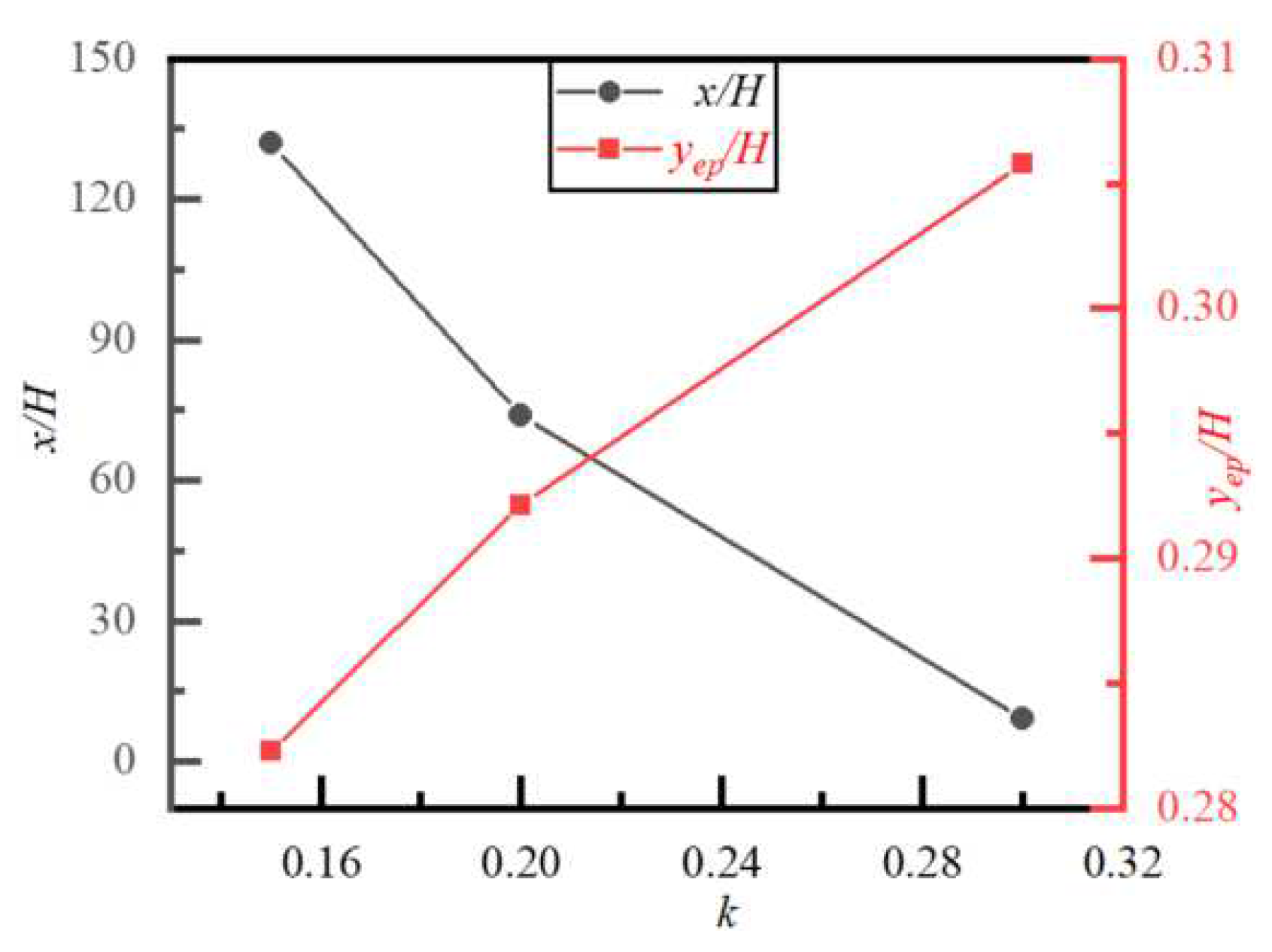
4.6. Effect of Blockage Ratio k on Particle Migration and Lateral Equilibrium Position
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Di Carlo, D. Inertial microfluidics. Lab A Chip 2009, 9, 3038–3046. [Google Scholar] [CrossRef]
- Duffy, D.C.; McDonald, J.C.; Schueller, O.J.A.; Whitesides, G.M. Rapid prototyping of microfluidic systems in poly (dimethylsiloxane). Anal. Chem. 1998, 70, 4974–4984. [Google Scholar] [CrossRef] [PubMed]
- Martel, J.M.; Toner, M. Inertial focusing in microfluidics. In Annual Review of Biomedical Engineering; Yarmush, M.L., Ed.; Annual Reviews: SAN Mateo, CA, USA, 2014; pp. 371–396. [Google Scholar]
- Wang, R.J.; Lin, J.Z.; Li, Z.H. Analysis of electro-osmotic flow characteristics at joint of capillaries with step change in zeta-potential and dimension. Biomed. Microdevices 2005, 7, 131–135. [Google Scholar]
- Gossett, D.R.; Weaver, W.M.; Mach, A.J.; Hur, S.C.; Tse, H.T.K.; Lee, W.; Amini, H.; Di Carlo, D. Label-free cell separation and sorting in microfluidic systems. Anal. Bioanal. Chem. 2010, 397, 3249–3267. [Google Scholar] [CrossRef]
- Lagus, T.P.; Edd, J.F. High-throughput co-encapsulation of self-ordered cell trains: Cell pair interactions in microdroplets. RSC Adv. 2013, 3, 20512–20522. [Google Scholar] [CrossRef]
- Godino, N.; Jorde, F.; Lawlor, D.; Jaeger, M.; Duschl, C. Purification of microalgae from bacterial contamination using a disposable inertia-based microfluidic device. J. Micromechanics Microengineering 2015, 25, 084002. [Google Scholar] [CrossRef]
- Horsman, K.M.; Bienvenue, J.M.; Blasier, K.R.; Landers, J.P. Forensic DNA analysis on microfluidic devices: A review. J. Forensic Sci. 2007, 52, 784–799. [Google Scholar] [CrossRef]
- Kang, K.; Lee, S.S.; Hyun, K.; Lee, S.J.; Kim, J.M. DNA-based highly tunable particle focuser. Nat. Commun. 2013, 4, 2567. [Google Scholar] [CrossRef]
- Yan, S.; Zhang, J.; Yuan, D.; Li, W.H. Hybrid microfluidics combined with active and passive approaches for continuous cell separation. Electrophoresis 2017, 38, 238–249. [Google Scholar] [CrossRef] [PubMed]
- Garcia, A.L.; Akhtar, J.; Saenz, L.; Shu, F.J.; Kuravi, S.; Kota, K. Waviness-induced passive particle manipulation of very dilute suspensions in confined microfluidic flows. Microfluid. Nanofluidics 2023, 27, 30. [Google Scholar] [CrossRef]
- Segré, G.; Silberberg, A. Radial particle displacements in poiseuille flow of suspensions. Nature 1961, 189, 209–210. [Google Scholar] [CrossRef]
- Oliver, D.R. Influence of particle rotation on radial migration in the poiseuille flow of suspensions. Nature 1962, 194, 1269–1271. [Google Scholar] [CrossRef]
- Goldsmith, H.L.; Mason, S.G. Axial migration of particles in poiseuille flow. Nature 1961, 190, 1095–1096. [Google Scholar] [CrossRef]
- Ho, B.P.; Leal, L.G. Inertial migration of rigid spheres in two-dimensional unidirectional flows. J. Fluid Mech. 1974, 65, 365–400. [Google Scholar] [CrossRef]
- Feng, J.; Hu, H.H.; Joseph, D.D. Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 2. Couette and Poiseuille flows. J. Fluid Mech. 1994, 277, 271–301. [Google Scholar] [CrossRef]
- Fox, A.J.; Schneider, J.W.; Khair, A.S. Inertial bifurcation of the equilibrium position of a neutrally-buoyant circular cylinder in shear flow between parallel walls. Phys. Rev. Res. 2020, 2, 013009. [Google Scholar] [CrossRef]
- Fox, A.J.; Schneider, J.W.; Khair, A.S. Dynamics of a sphere in inertial shear flow between parallel walls. J. Fluid Mech. 2021, 915, A119-1-23. [Google Scholar] [CrossRef]
- Wen, B.; Li, H.B.; Zhang, C.Y.; Fang, H.P. Lattice-type-dependent momentum-exchange method for moving boundaries. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 2012, 85, 016704. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.S.; Seo, K.W.; Lee, S.J. Lateral and cross-lateral focusing of spherical particles in a square microchannel. Lab A Chip 2011, 11, 460–465. [Google Scholar] [CrossRef]
- D’Avino, G.; Maffettone, P.L. Particle dynamics in viscoelastic liquids. J. Non-Newton. Fluid Mech. 2015, 215, 80–104. [Google Scholar] [CrossRef]
- Yu, Z.S.; Wang, P.; Lin, J.Z.; Hu, H.H. Equilibrium positions of the elasto-inertial particle migration in rectangular channel flow of Oldroyd-B viscoelastic fluids. J. Fluid Mech. 2019, 868, 316–340. [Google Scholar] [CrossRef]
- Yang, S.; Kim, J.Y.; Lee, S.J.; Lee, S.S.; Kim, J.M. Sheathless elasto-inertial particle focusing and continuous separation in a straight rectangular microchannel. Lab Chip 2011, 11, 266–273. [Google Scholar] [CrossRef] [PubMed]
- Chrit, F.E.; Bowie, S.; Alexeev, A. Inertial migration of spherical particles in channel flow of power law fluids. Phys. Fluids 2020, 32, 083103. [Google Scholar] [CrossRef]
- Hu, X.; Lin, J.Z.; Ku, X.K. Inertial migration of circular particles in Poiseuille flow of a power-law fluid. Phys. Fluids 2019, 31, 073306. [Google Scholar] [CrossRef]
- Tong, S.H.; Han, X.F.; Zhou, F.K.; Xu, X.F. Study on particle aggregation behavior in shear-thinning fluid. Chin. J. Process Eng. 2022, 22, 792–801. [Google Scholar]
- Ghomsheh, M.J.; Jafari, A.; Funfschilling, D. Inertial lift on a particle in a straight microchannel of Newtonian, power-law and Carreau-Yasuda fluids: A simulation study toward optimized particle separation. J. Non-Newton. Fluid Mech. 2023, 312, 104977. [Google Scholar] [CrossRef]
- Li, B.T.; Chen, X.; Zheng, L.C.; Zhu, L.L.; Zhou, J.L.; Wang, T.T. Precipitation phenomenon of nanoparticles in power-law fluids over a rotating disk. Microfluid. Nanofluidics 2014, 17, 107–114. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, B.; Wang, N. Lattice BGK model for incompressible Navier–Stokes equation. J. Comput. Phys. 2000, 165, 288–306. [Google Scholar] [CrossRef]
- Nie, D.M.; Lin, J.Z. A LB-DF/FD method for Particle Suspensions. Commun. Comput. Phys. 2010, 7, 544–563. [Google Scholar]
- Qian, Y.H.; Dhumieres, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- He, X.Y.; Shan, X.W.; Doolen, G.D. Discrete Boltzmann equation model for nonideal gases. Phys. Rev. E 1998, 57, R13–R16. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Ladd, A.J.C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 1994, 271, 285–309. [Google Scholar] [CrossRef]
- Ladd, A.J.C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 1994, 271, 311–339. [Google Scholar] [CrossRef]
- Aidun, C.K.; Lu, Y.; Ding, E.J. Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 1998, 373, 287–311. [Google Scholar] [CrossRef]
- Glowinski, R.; Pan, T.W.; Hesla, T.I.; Joseph, D.D.; Periaux, J. A Fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: Application to particulate flow. J. Comput. Phys. 2001, 169, 363–426. [Google Scholar] [CrossRef]
- Zhu, Q.Y.; Zhuang, Y.J.; Yu, H.Z. Three-dimensional numerical investigation on thermosolutal convection of power-law fluids in anisotropic porous media. Int. J. Heat Mass Transf. 2017, 104, 897–917. [Google Scholar] [CrossRef]
- Drazer, G.; Koplik, J.; Gabbanelli, S. Lattice Boltzmann method for non-Newtonian (power-law) fluids. Phys. Rev. E 2005, 72, 046312. [Google Scholar]
- Bird, R.B.; Dai, C.C.; Yarusso, B.J. The rheology and flow of viscoplastic materials. Rev. Chem. Eng. 1983, 1, 1–70. [Google Scholar] [CrossRef]
- Yan, Y.; Morris, J.F.; Koplik, J. Hydrodynamic interaction of two particles in confined linear shear flow at finite Reynolds number. Phys. Fluids 2007, 19, 113305. [Google Scholar] [CrossRef]
- Hu, X.; Lin, J.Z.; Guo, Y.; Ku, X.K. Motion and equilibrium position of elliptical and rectangular particles in a channel flow of a power-law fluid. Powder Technol. 2021, 377, 585–596. [Google Scholar] [CrossRef]
- Jefri, M.A.; Zahed, A.H. Elastic and viscous effects on particle migration in plane-Poiseuille flow. J. Rheol. 1989, 33, 691–708. [Google Scholar] [CrossRef]
- Nakayama, S.; Yamashita, H.; Yabu, T.; Itano, T.; Sugihara-Seki, M. Three regimes of inertial focusing for spherical particles suspended in circular tube flows. J. Fluid Mech. 2019, 871, 952–969. [Google Scholar] [CrossRef]

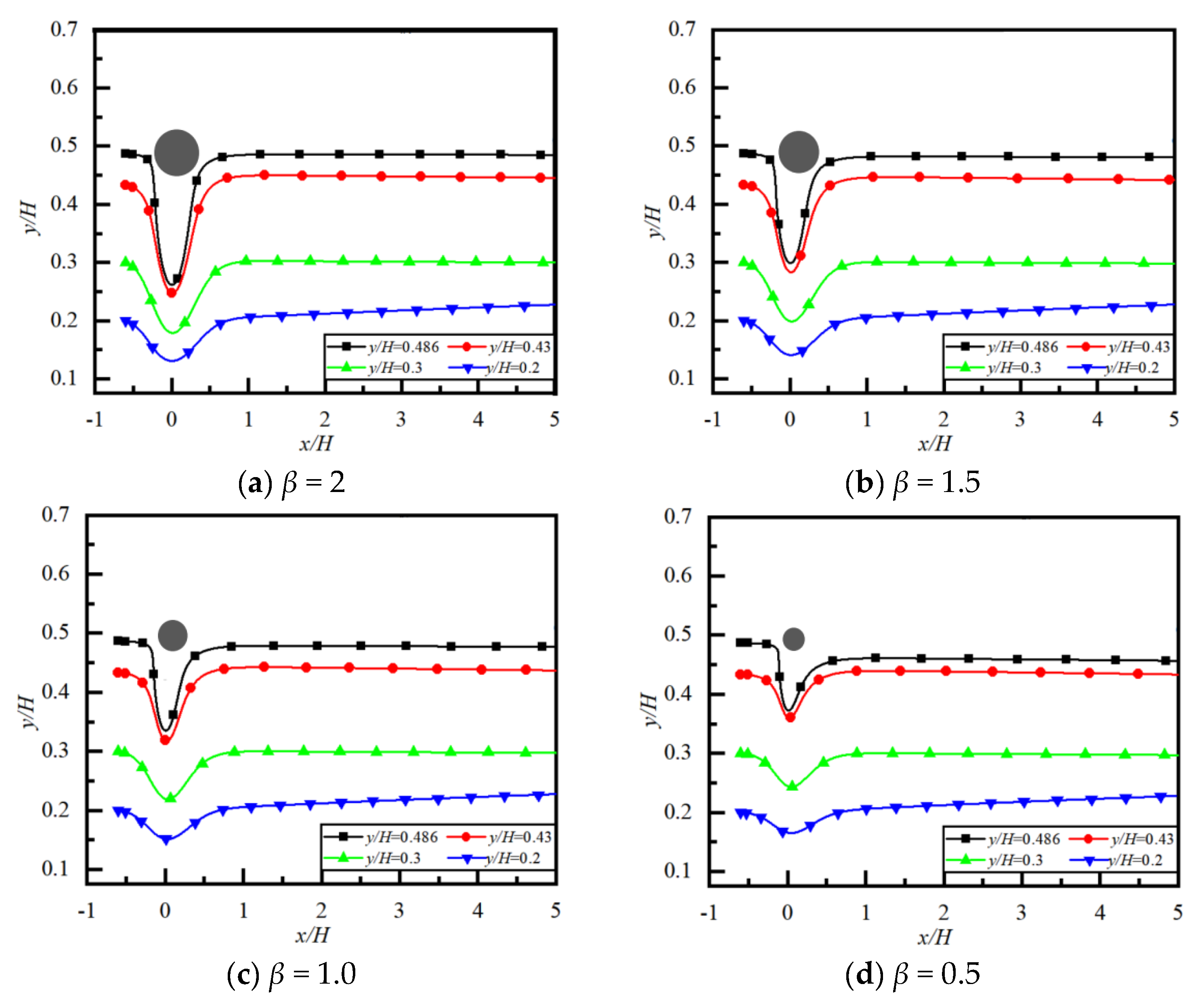


| y/H = 0.2 | y/H = 0.3 | y/H = 0.43 | y/H = 0.486 | |
|---|---|---|---|---|
| β = 2 | 0.23 | 0.3 | 0.448 | 0.485 |
| 1.5 | 0.23 | 0.298 | 0.443 | 0.481 |
| 1.0 | 0.228 | 0.298 | 0.439 | 0.477 |
| 0.5 | 0.225 | 0.297 | 0.435 | 0.457 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Lin, J. Equilibrium Position of a Particle in a Microchannel Flow of Newtonian and Power-Law Fluids with an Obstacle. Mathematics 2023, 11, 3700. https://doi.org/10.3390/math11173700
Chen D, Lin J. Equilibrium Position of a Particle in a Microchannel Flow of Newtonian and Power-Law Fluids with an Obstacle. Mathematics. 2023; 11(17):3700. https://doi.org/10.3390/math11173700
Chicago/Turabian StyleChen, Dongmei, and Jianzhong Lin. 2023. "Equilibrium Position of a Particle in a Microchannel Flow of Newtonian and Power-Law Fluids with an Obstacle" Mathematics 11, no. 17: 3700. https://doi.org/10.3390/math11173700
APA StyleChen, D., & Lin, J. (2023). Equilibrium Position of a Particle in a Microchannel Flow of Newtonian and Power-Law Fluids with an Obstacle. Mathematics, 11(17), 3700. https://doi.org/10.3390/math11173700







