Global Properties of HIV-1 Dynamics Models with CTL Immune Impairment and Latent Cell-to-Cell Spread
Abstract
:1. Introduction
2. Model with Latent CTC Transmission and CTL Immune Impairment
2.1. System Description
2.2. Basic Properties
2.2.1. Nonnegativity and Boundedness of the Solutions
2.2.2. Reproduction Number and Equilibria
- (i)
- there exists only one equilibrium point when , and
- (ii)
- there exists two equilibria and when
- If , then we have . In this case, let us define a function on as:
2.2.3. Stability of Equilibria and
3. Model with Distributed Time Delays
3.1. System Description
3.2. Basic Properties
3.2.1. Nonnegativity and Ultimate Boundedness of the Solutions
3.2.2. Reproduction Number and Equilibria
- (i)
- there exists only one equilibrium point when and
- (ii)
- there exists two equilibria and when
- If , then we have In this case, let us define a function on as:
3.2.3. Stability of Equilibria and
4. Numerical Simulations
4.1. Numerical Simulation for Model (8)
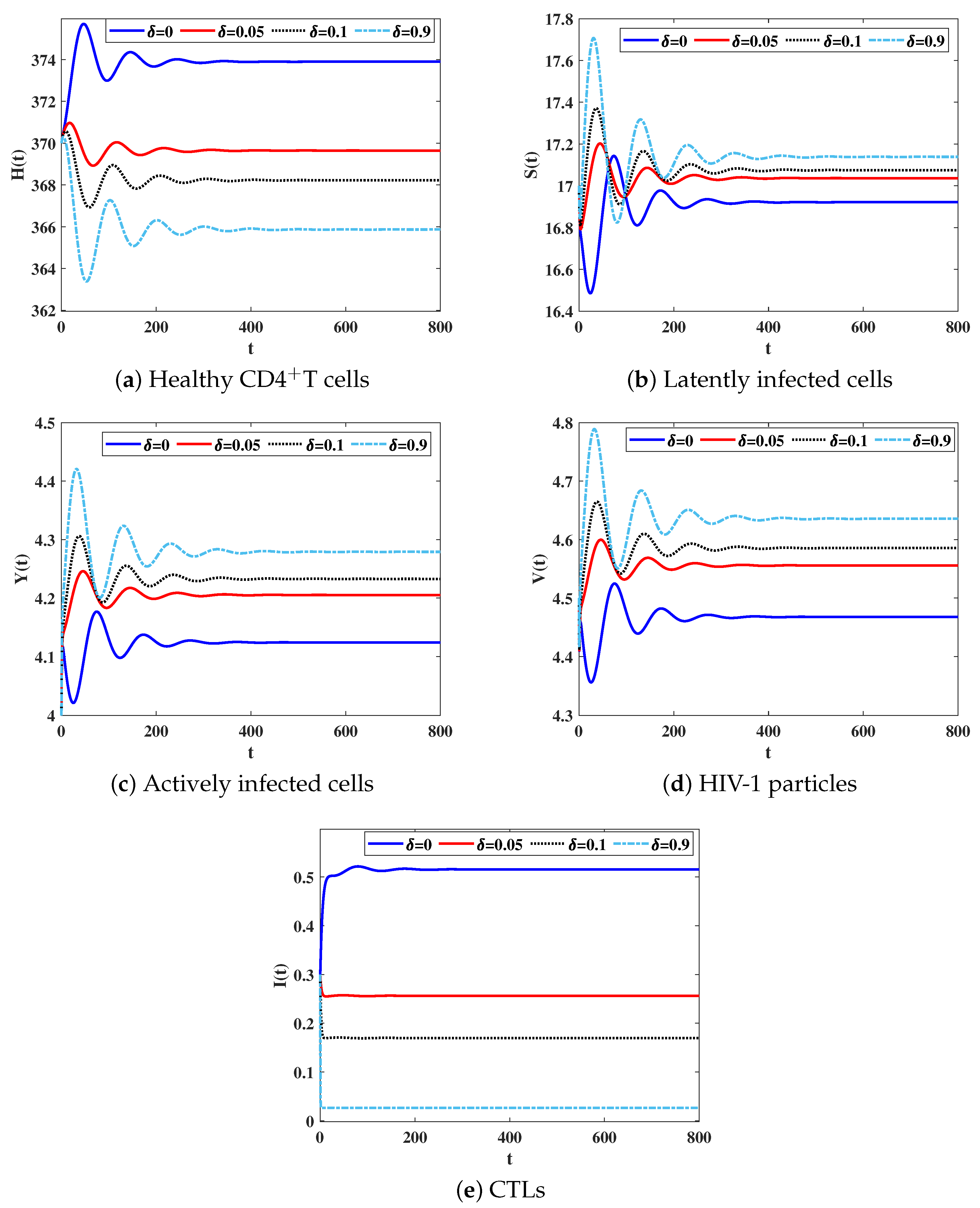
4.1.1. Effect of and on Stability of Equilibria
4.1.2. Effect of the CTL Immune Impairment
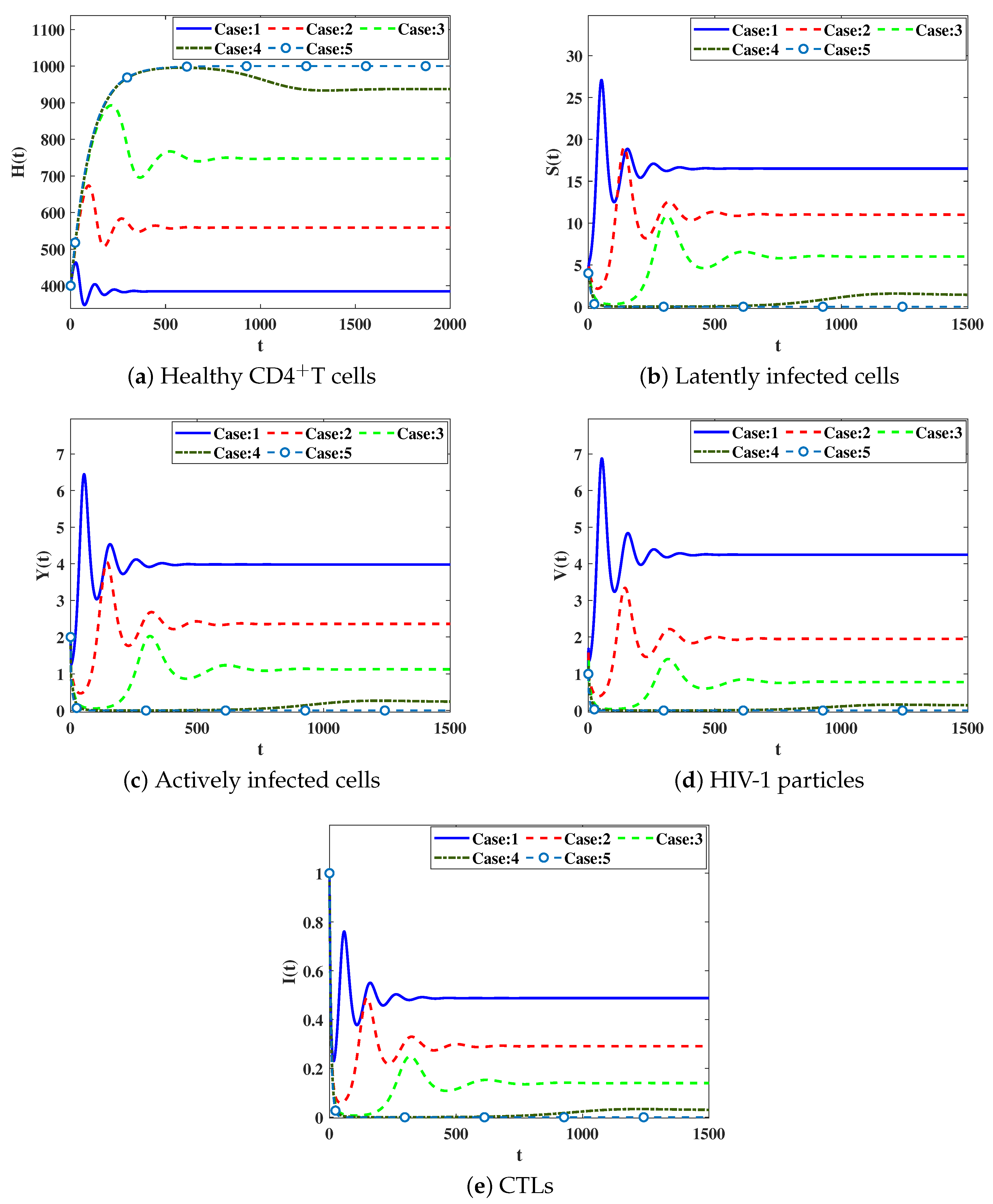
4.2. Numerical Simulation for Model (23)
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nowak, M.A.; Bangham, C.R.M. Population dynamics of immune responses to persistent viruses. Science 1996, 272, 74–79. [Google Scholar] [CrossRef]
- Nowak, M.A.; May, R.M. Virus Dynamics; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Arnaout, R.; Nowak, M.; Wodarz, D. HIV-1 dynamics revisited: Biphasic decay by cytotoxic lymphocyte killing? Proc. R. Soc. Lond. Ser. Biol. Sci. 1450, 267, 1347–1354. [Google Scholar] [CrossRef] [PubMed]
- Adak, D.; Bairagi, N. Bifurcation analysis of a multidelayed HIV model in presence of immune response and understanding of in-host viral dynamics. Math. Methods Appl. Sci. 2019, 42, 4256–4272. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Lu, X.; Liu, S. A delayed HIV-1 model with virus waning term. Math. Biosci. Eng. 2016, 13, 135–157. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Wang, W.; Liu, X. Global Stability in a viral infection model with lytic and nonlytic immune response. Comput. Math. Appl. 2006, 51, 1593–1610. [Google Scholar] [CrossRef]
- Lv, C.; Huang, L.; Yuan, Z. Global stability for an HIV-1 infection model with Beddington-DeAngelis incidence rate and CTL immune response. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 121–127. [Google Scholar] [CrossRef]
- Jiang, C.; Kong, H.; Zhang, G.; Wang, K. Global properties of a virus dynamics model with self-proliferation of CTLs. Math. Appl. Sci. Eng. 2021, 2, 123–133. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, W. Complete classification of global dynamics of a virus model with immune responses. Discret. Contin. Dyn.-Syst.-Ser. 2014, 19, 1087–1103. [Google Scholar] [CrossRef]
- Ren, J.; Xu, R.; Li, L. Global stability of an HIV infection model with saturated CTL immune response and intracellular delay. Math. Biosci. Eng. 2020, 18, 57–68. [Google Scholar] [CrossRef]
- Wang, A.P.; Li, M.Y. Viral dynamics of HIV-1 with CTL immune response. Discret. Contin. Dyn.-Syst.-Ser. 2021, 26, 2257–2272. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, R. Mathematical analysis of a delayed HIV infection model with saturated CTL immune response and immune impairment. J. Appl. Math. Comput. 2022, 68, 2365–2380. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.-F. Dynamics of two time delays differential equation model to HIV latent infection. Phys. A 2019, 514, 384–395. [Google Scholar] [CrossRef]
- Perelson, A.; Neumann, A.; Markowitz, M.; Leonard, J.; Ho, D. HIV-1 dynamics in vivo: Virion clearance rate, infected cell life-span, and viral generation time. Science 1996, 271, 1582–1586. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Zou, X. Dynamics of a HIV-1 infection model with cell-mediated immune response and intracellular delay. Discret. Continuous Dyn.-Syst.-Ser. 2009, 12, 511–524. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, X.; Song, X. Dynamical behavior of a delay virus dynamics model with CTL immune response. Nonlinear Anal. Real World Appl. 2010, 11, 1795–1809. [Google Scholar] [CrossRef]
- Li, X.; Fu, S. Global stability of a virus dynamics model with intracellular delay and CTL immune response. Math. Methods Appl. Sci. 2015, 38, 420–430. [Google Scholar] [CrossRef]
- Shu, H.; Wang, L.; Watmough, J. Global stability of a nonlinear viral infection model with infinitely distributed intracellular delays and CTL immune responses. Siam J. Appl. Math. 2013, 73, 1280–1302. [Google Scholar] [CrossRef]
- Jolly, C.; Sattentau, Q. Retroviral spread by induction of virological synapses. Traffic 2004, 5, 643–650. [Google Scholar] [CrossRef]
- Sato, H.; Orenstein, J.; Dimitrov, D.; Martin, M. Cell-to-cell spread of HIV-1 occurs within minutes and may not involve the participation of virus particles. Virology 1992, 186, 712–724. [Google Scholar] [CrossRef] [PubMed]
- Iwami, S.; Takeuchi, J.S.; Nakaoka, S.; Mammano, F.; Clavel, F.; Inaba, H.; Kobayashi, T.; Misawa, N.; Aihara, K.; Koyanagi, Y.; et al. Cell-to-cell infection by HIV contributes over half of virus infection. eLife 2015, 4, e08150. [Google Scholar] [CrossRef]
- Komarova, N.L.; Wodarz, D. Virus dynamics in the presence of synaptic transmission. Math. Biosci. 2013, 242, 161–171. [Google Scholar] [CrossRef]
- Sourisseau, M.; Sol-Foulon, N.; Porrot, F.; Blanchet, F.; Schwartz, O. Inefficient human immunodeficiency virus replication in mobile lymphocytes. J. Virol. 2007, 81, 1000–1012. [Google Scholar] [CrossRef]
- Sigal, A.; Kim, J.T.; Balazs, A.B.; Dekel, E.; Mayo, A.; Milo, R.; Baltimore, D. Cell-to-cell spread of HIV permits ongoing replication despite antiretroviral therapy. Nature 2011, 477, 95–98. [Google Scholar] [CrossRef] [PubMed]
- Martin, N.; Sattentau, Q. Cell-to-cell HIV-1 spread and its implications for immune evasion. Curr. Opin. HIV AIDS 2009, 4, 143–149. [Google Scholar] [CrossRef]
- Guo, T.; Qiu, Z. The effects of CTL immune response on HIV infection model with potent therapy, latently infected cells and cell-to-cell viral transmission. Math. Biosci. Eng. 2019, 16, 6822–6841. [Google Scholar] [CrossRef] [PubMed]
- Elaiw, A.M.; AlShamrani, N.H. Global stability of a delayed adaptive immunity viral infection with two routes of infection and multi-stages of infected cells. Commun. Nonlinear Sci. Numer. Simul. 2020, 86, 105259. [Google Scholar] [CrossRef]
- Regoes, R.; Wodarz, D.; Nowak, M.A. Virus dynamics: The effect to target cell limitation and immune responses on virus evolution. J. Theor. Biol. 1998, 191, 451–462. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Zhang, J.; Wang, H.; Ma, W.; Liao, F. Dynamics analysis of a delayed viral infection model with logistic growth and immune impairment. Appl. Math. Model. 2014, 38, 524–534. [Google Scholar] [CrossRef]
- Krishnapriya, P.; Pitchaimani, M. Modeling and bifurcation analysis of a viral infection with time delay and immune impairment. Jpn. J. Ind. Appl. Math. 2017, 34, 99–139. [Google Scholar] [CrossRef]
- Eric, A.V.; Noe, C.C.; Gerardo, G.A. Analysis of a viral infection model with immune impairment, intracellular delay and general non-linear incidence rate. Chaos Solitons Fractals 2014, 69, 1–9. [Google Scholar]
- Wang, S.; Song, X.; Ge, Z. Dynamics analysis of a delayed viral infection model with immune impairment. Appl. Math. Model. 2011, 35, 4877–4885. [Google Scholar] [CrossRef]
- Krishnapriya, P.; Pitchaimani, M. Analysis of time delay in viral infection model with immune impairment. J. Appl. Math. Comput. 2017, 55, 421–453. [Google Scholar] [CrossRef]
- Wang, Z.P.; Liu, X.N. A chronic viral infection model with immune impairment. J. Theor. Biol. 2007, 249, 532–542. [Google Scholar] [CrossRef] [PubMed]
- Jia, J.; Shi, X. Analysis of a viral infection model with immune impairment and cure rate. J. Nonlinear Sci. Appl. 2016, 9, 3287–3298. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Raezah, A.A.; Azoz, S.A. Stability of delayed HIV dynamics models with two latent reservoirs and immune impairment. Adv. Differ. Equ. 2018, 50, 1–25. [Google Scholar] [CrossRef]
- Bai, N.; Xu, R. Mathematical analysis of an HIV model with latent reservoir, delayed CTL immune response and immune impairment. Math. Biosci. Eng. 2021, 18, 1689–1707. [Google Scholar] [CrossRef]
- Raezah, A.A.; Elaiw, A.M.; Alofi, B.S. Global properties of latent virus dynamics models with immune impairment and two routes of infection. High-Throughput 2019, 8, 16. [Google Scholar] [CrossRef] [PubMed]
- Alofi, B.S.; Azoz, S.A. Stability of general pathogen dynamic models with two types of infectious transmission with immune impairment. AIMS Math. 2020, 6, 114–140. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, R. Dynamics analysis of an HIV infection modelwith latent reservoir, delayed CTL immune response and immune impairment. Nonlinear Anal. Model. Control. 2023, 28, 1–19. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Raezah, A.; Alofi, B.S. Dynamics of delayed pathogen infection models with pathogenic and cellular infections and immune impairment. AIP Adv. 2018, 8, 025323. [Google Scholar] [CrossRef]
- Agosto, L.; Herring, M.; Mothes, W.; Henderson, A. HIV-1-infected CD4+ T cells facilitate latent infection of resting CD4+ T cells through cell-cell contact. Cell 2018, 24, 2088–2100. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Wang, X.; Guo, K.; Ma, W. Global analysis of a diffusive viral model with cell-to-cell infection and incubation period. Math. Methods Appl. Sci. 2020, 43, 5963–5978. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Stability of a general CTL-mediated immunity HIV infection model with silent infected cell-to-cell spread. Adv. Differ. Equ. 2020, 2020, 355. [Google Scholar] [CrossRef]
- Alshamrani, N.H. Stability of a general adaptive immunity HIV infection model with silent infected cell-to-cell spread. Chaos Solitons Fractals 2021, 150, 110422. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Stability of a delayed adaptive immunity hiv infection model with silent infected cells and cellular infection. J. Appl. Anal. Comput. 2021, 11, 964–1005. [Google Scholar] [CrossRef]
- Hattaf, K.; Dutta, H. Modeling the dynamics of viral infections in presence of latently infected cells. Chaos Solitons Fractals 2020, 136, 109916. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H.; Hobiny, A.D. Stability of an adaptive immunity delayed HIV infection model with active and silent cell-to-cell spread. Math. Biosci. Eng. 2020, 17, 6401–6458. [Google Scholar] [CrossRef] [PubMed]
- AlShamrani, N.H.; Elaiw, A.M.; Dutta, H. Stability of a delay-distributed HIV infection model with silent infected cell-to-cell spread and CTL-mediated immunity. Eur. Phys. J. Plus 2020, 135, 593. [Google Scholar] [CrossRef]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Willems, J.L. Stability Theory of Dynamical Systems; Wiley: New York, NY, USA, 1970. [Google Scholar]
- Hale, J.K.; Lunel, S.M.V. Introduction to Functional Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Sahani, S.K.; Yashi, P. Effects of eclipse phase and delay on the dynamics of HIV infection. J. Biol. Syst. 2018, 26, 421–454. [Google Scholar] [CrossRef]
- Allali, K.; Danane, J.; Kuang, Y. Global analysis for an HIV infection model with CTL immune response and infected cells in eclipse phase. Appl. Sci. 2017, 7, 861. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Al Agha, A.D. Analysis of a delayed and diffusive oncolytic M1 virotherapy model with immune response. Nonlinear Anal. Real World Appl. 2020, 55, 103116. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Al Agha, A.D. Global Stability of a reaction-diffusion Malaria/COVID-19 coinfection dynamics model. Mathematics 2022, 10, 4390. [Google Scholar] [CrossRef]
- Bellomo, N.; Painter, K.J.; Tao, Y.; Winkler, M. Occurrence vs. Absence of taxis-driven instabilities in a May-Nowak model for virus infection. SIAM J. Appl. Math. 2019, 79, 1990–2010. [Google Scholar] [CrossRef]
- Ren, X.; Tian, Y.; Liu, L.; Liu, X. A reaction-diffusion within-host HIV model with cell-to-cell transmission. J. Math. Biol. 2018, 76, 831–1872. [Google Scholar] [CrossRef] [PubMed]
- Bellomo, N.; Outada, N.; Soler, J.; Tao, Y.; Winkler, M. Chemotaxis and cross-diffusion models in complex environments: Models and analytic problems toward a multiscale vision. Math. Model. Methods Appl. Sci. 2022, 32, 713–792. [Google Scholar] [CrossRef]


| Parameter | Value | Reference | Parameter | Value | Reference |
|---|---|---|---|---|---|
| 10 | [54] | 0.8 | [32] | ||
| 0.01 | [54] | 0.04 | [32] | ||
| varied | - | 2.6 | [55] | ||
| varied | - | 2.4 | [55] | ||
| varied | - | 0.025 | [32] | ||
| 0.2 | [54] | 0.2 | [32] | ||
| 0.17 | [54] | varied | - |
| Equilibria | |
|---|---|
| Delay Parameters | Equilibria | |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlShamrani, N.H.; Halawani, R.H.; Shammakh, W.; Elaiw, A.M. Global Properties of HIV-1 Dynamics Models with CTL Immune Impairment and Latent Cell-to-Cell Spread. Mathematics 2023, 11, 3743. https://doi.org/10.3390/math11173743
AlShamrani NH, Halawani RH, Shammakh W, Elaiw AM. Global Properties of HIV-1 Dynamics Models with CTL Immune Impairment and Latent Cell-to-Cell Spread. Mathematics. 2023; 11(17):3743. https://doi.org/10.3390/math11173743
Chicago/Turabian StyleAlShamrani, Noura H., Reham H. Halawani, Wafa Shammakh, and Ahmed M. Elaiw. 2023. "Global Properties of HIV-1 Dynamics Models with CTL Immune Impairment and Latent Cell-to-Cell Spread" Mathematics 11, no. 17: 3743. https://doi.org/10.3390/math11173743






